两种不同风切变指数计算方法在风速垂直外推中的对比分析

刘航，薛文亮

(中节能风力发电股份有限公司，北京 100082)

风能资源评估中采用轮毂高度的风速测算风电机组发电量，《风电场风能资源测量方法》(GB/T 18709-2002)中明确规定需在拟选风电机组轮毂中心高度处安装风速和风向传感器。由于前期初步评估存在误差，以及大叶轮和高塔筒技术的快速迭代更新，导致前期的测风高度有时并不与所选机组的轮毂高度相一致，此时需要根据风切变指数垂直外推轮毂高度处的风速[1]。

在风电领域，风切变专指在大气边界层内水平风速在垂直高度内的变化，可用风速随高度变化的风速廓线表示。风切变指数表征风速随高度变化的快慢程度，如果以幂律方程描述风速廓线，那么幂律指数即为风切变指数。风切变指数的确定直接影响垂直外推风速的准确度，进而对风机选型、发电量评估和收益率测算产生重大影响[2-3]。

当有多个高度的风速数据时，应用最小二乘法拟合幂律风速廓线来确定风切变指数，该方法基于多个高度的完整的风速廓线，能综合反映风切变状况[4]，本文中的计算都采用该方法；当仅有两个高度的风速数据时，根据风切变幂律公式求出风切变指数，计算公式如下[5]：

(1)

(2)

式(1)～(2)中，α表示为风切变指数；Z1和Z2表示为高度，m；V1是高度Z1对应的风速，m/s；V2是高度Z2对应的风速，m/s。

王炎等[6]人应用10 min、小时、月份、年平均的风切变指数进行风速的垂直外推，论证了风切变指数的计算与时间尺度的大小有关；李鹏等[7]人论述了风切变指数与下垫面的地形和粗糙度关系密切。本文在全面分析风切变综合影响因素的基础上，通过两种常用的风切变指数计算方法垂直外推某一高度的时序风速，并与实测风速及各自对应的单机发电量进行偏差对比，以此判断两种方法的优劣。

1 风切变的影响因素分析

造成风在近地层中随高度变化的原因有动力和热力这两个因素。前者主要来源于地面的摩擦效应，即地面的粗糙度，以及地形影响，后者主要表现为与近地层大气热稳定度的关系[8]。

通常地表粗糙度越大，风切变指数也越大。例如建筑物密集的城市和森林，近地面高度对风的减速效应显著，导致近地面风速较低，呈现出风切变指数大的特征，而开阔的水面正好相反[9]。因不同方向上地表植被不同，以及地表植被随季节的周期性变化，风切变指数随方向和季节而变化。当大气层结为中性稳定条件时，湍流将完全依靠动力原因来发展，这时风速随高度z的变化服从普朗特经验公式[10]：

(3)

(4)

式(3)和式(4)中，u*表示为摩擦速度，m/s；k表示为冯卡门常数，k=0.4；τ表示为地面剪切应力，N/m2；ρ表示为空气密度，kg/m3；z0表示为地表粗糙度，m。

在山地风电场中，风切变受地形影响较为明显。山地场址的风切变往往较小，甚至出现负切变。因为当气流通过山顶位置时，下层的气流受到明显的挤压，根据通量守恒，下层气流加速效应大于上层气流，导致整体的风切变指数变小。当下层气流的加速效应显著时，而上层加速效应较弱或没有时，就会出现负切变[9]。

在不同的大气热稳定度下，会有不同的风切变指数。在不稳定的大气条件下，风切变指数较小，在稳定的大气条件下，风切变指数较大。出现这样的现象是因为当大气不稳定的时候，上下层大气混合增强，气流上下交互较为频繁，导致上下层风速差异变小，总体表现为风切变较小[11-12]，而在稳定大气条件下情况正好相反。图1为某测风塔位置全年的风切变指数和气温日变化曲线，白天地表受阳光加热影响，气温升高，近地层大气变得不稳定，上下层气流交互加剧，各层高度风速差异变小，风切变较小；而在夜间，地表温度降低，大气变得稳定，上下层气流交互减弱，风切变增大。

图1 测风塔位置全年的风切变指数和气温日变化曲线

粗糙度和地形是导致风切变产生的空间因素，在较大的时间尺度上(如季度)对风切变的影响相对固定；而大气热稳定度对风切变的影响表现为在小尺度时间上的动态变化的过程。因此，风切变的产生是多种因素综合作用的结果，要想科学合理的评估风切变，就不能忽视其随时间和空间变化的关系。

2 两种常用的风切变指数计算方法对比分析

工程中常用两种风切变指数进行风速的垂直外推，第一种是依据每个时间步长的风速计算时序风切变指数，通常测风数据为逐10 min的时间序列，全年会计算出52 560个风切变指数。时序风切变指数考虑了其在10 min时间尺度上受大气热稳定度动态变化的影响，另外，10 min内风向相对稳定，也即考虑了该风向上对应的地形和粗糙度的影响。第二种是依据几个不同高度的全扇区平均风速计算出1个风切变指数；或者根据各风向扇区的平均风速计算出12个或16个不同风向扇区的风切变指数。这种方法计算出的风切变指数虽然也考虑了大气热稳定度的影响，但在计算平均风速时，该影响在整个测风时长内也一同被平均了。分扇区计算的风切变指数考虑了不同方向上地形和粗糙度的影响，但未考虑地表植被随时间的周期性变化。为便于描述，将这两种方法分别称为时序风切变法和扇区平均风切变法。

下面通过一个实例说明应用上述两种风切变指数计算方法进行风速垂直外推时的优劣。首先针对同一个测风塔数据，应用上述两种方法分别计算风切变指数，然后根据风切变指数与幂律公式(1)垂直外推出已测的某一高度的风速，再将其与实测风速及各自对应的发电量进行对比分析。

2.1 数据准备和介绍

在我国中东部的丘陵地带选取一个测风塔M，该测风塔风速仪安装高度分别为30 m、50 m、70 m、80 m、90 m、100 m和120 m处，风向仪安装高度为120 m。依据《风电场风能资源评估方法》(GB/T 18710-2002)中规定的方法对2018年全年逐10 min共计52 560个测风数据进行验证和处理后，有效数据完整率为99.0%，满足标准中规定的风能资源评估要求。设定120 m为垂直外推和实测风速的对比高度，考虑到30 m和50 m距离分析高度120 m较远，计算风切变指数时不考虑这两个高度，最终使用70 m、80 m、90 m和100 m处高度的测风数据计算风切变指数。

表1为测风塔M处全年的风切变指数日变化情况，该位置的风切变指数随时间变化显著，最大值为0.532，最小值为0.121，分别发生在子夜和正午。表2为测风塔M处的全年风切变指数随方向的变化情况，风切变指数随方向变化明显，最大值和最小值分别为0.544和0.243，分别发生在SSE和NE扇区。测风塔M处全年的风切变指数方向玫瑰图如图2所示。

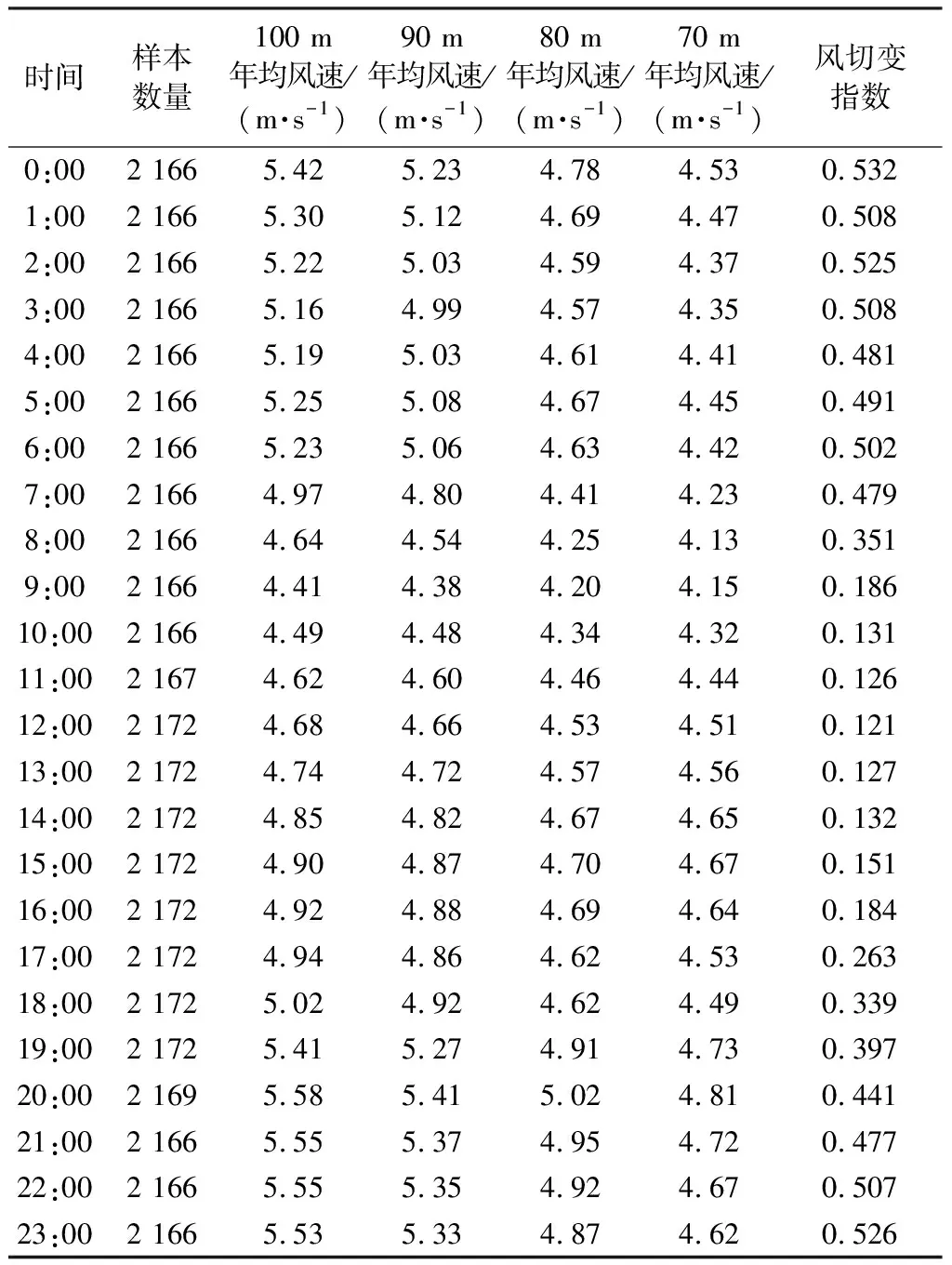
表1 测风塔M处全年的风切变指数日变化情况

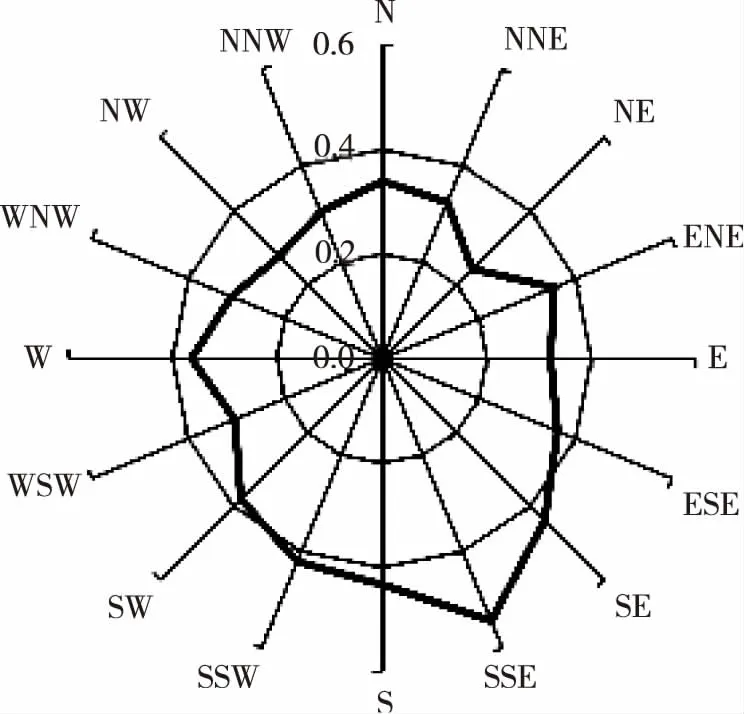
图2 测风塔M处全年的风切变指数方向玫瑰图

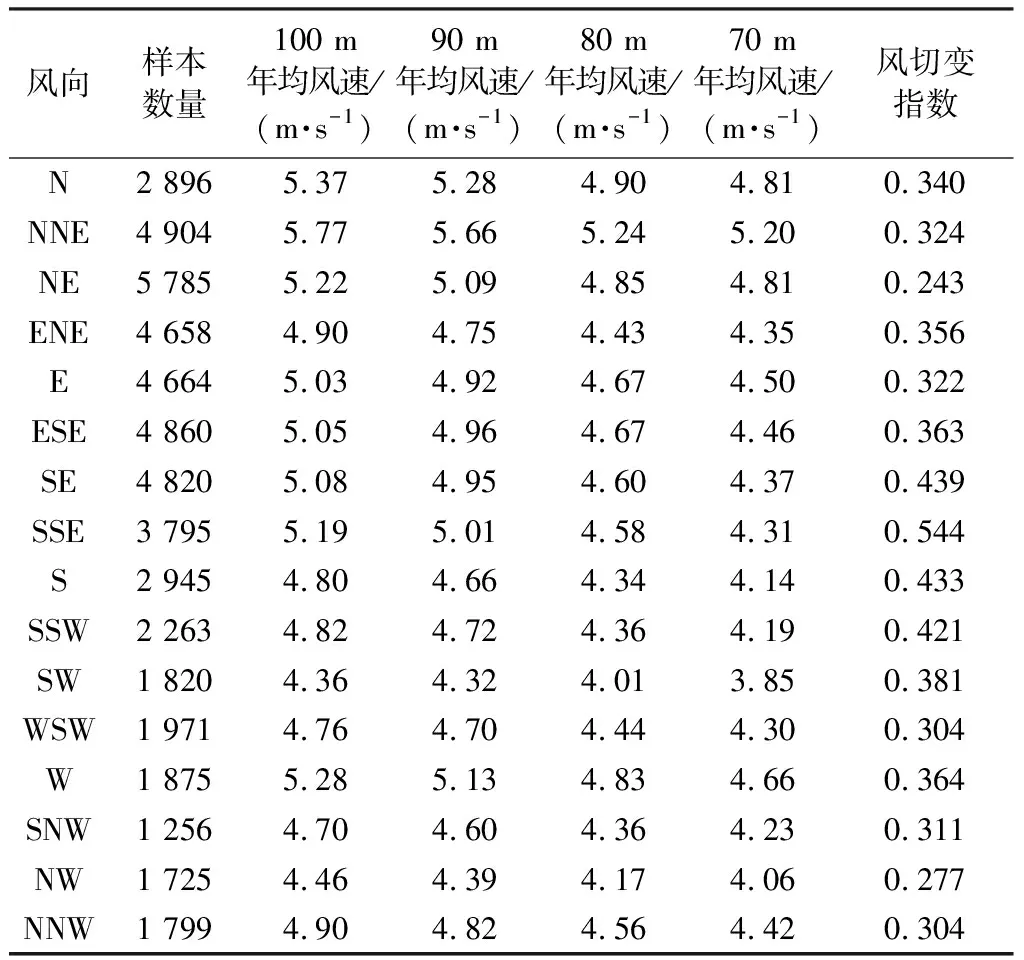
表2 测风塔M处全年的风切变指数随方向的变化情况

2.2 风速对比分析

按照前面介绍的两种方法分别计算风切变指数，再根据实测的100 m时序风速和风切变幂律公式(1)垂直外推出两套120 m高度的时序风速数据。由于风电机组的切入风速一般在3 m/s以上，并且风速较低时，风速受湍流影响严重，表现出不稳定的特点。因此在分析时，去除掉3 m/s以下的小风速段。推算的120 m风速频率分布对比见表3，推算的120 m风频偏差如图3所示，从中可以看出，使用基于时序风切变法推算的120 m风频分布更接近实测情况，其风频偏差明显小于扇区平均风切变法。此外，从图3的风频偏差对比可以看出，当风速在11.5 m/s以上时，即在大风速区间，使用两种方法推算的风速的风频偏差趋于稳定，偏差都接近于零；当风速小于11.5 m/s时，两种方法推算的结果都存在一定程度的偏差。

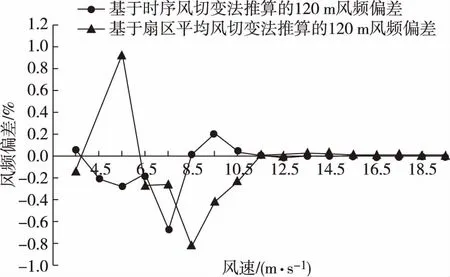
图3 推算的120 m风频偏差

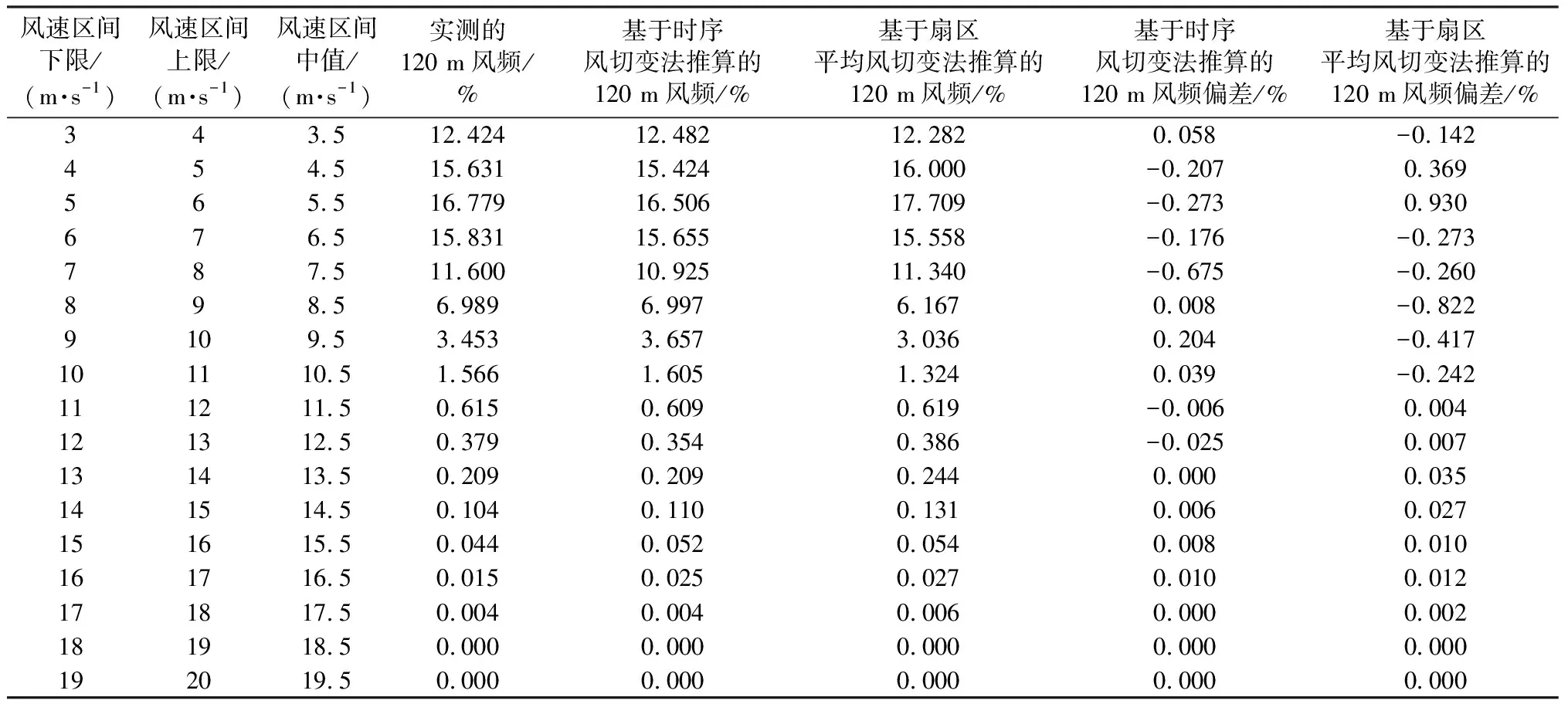
表3 推算的120 m风速频率分布对比表

2.3 年发电量对比分析

使用垂直外推出的120 m时序风速计算单机年发电量，将其与实测的120 m风速计算的单机年发电量进行对比分析。计算时选用低风速机型WTG 164-3.3MW，采用该机型在场址相应空气密度下的动态功率曲线、并取相同的综合折减系数75%进行计算。年发电量对比及其相对偏差见表4，应用基于时序风切变法计算的年发电量偏差较小，更接近实测风速计算的年发电量。

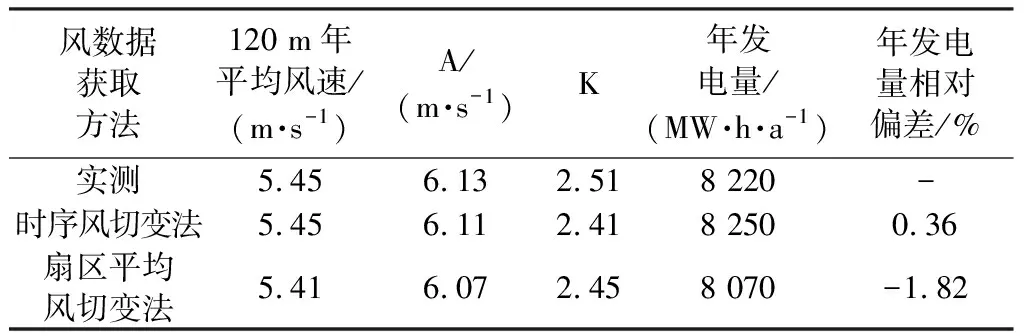
表4 年发电量对比表及其相对偏差

3 结语

1)风切变指数受地表粗糙度、地形和近地层大气热稳定度因素的综合影响，随时间和空间的改变而动态变化。

2)通过对推算风速的频率分布及其对应的发电量进行偏差分析可知，因时序风切变法较全面地考虑了风切变的影响因素，其推算的准确性优于扇区平均风切变法，其计算结果更接近实际情况。

3)在大风速区间，使用两种方法推算出的风速，其偏差趋于稳定，偏差都接近于零；而在小风速区间，使用两种方法推算的结果都存在一定程度的偏差。