预制混凝土管组合柱-钢梁节点核心区受力性能分析

张锡治，李星乾，章少华，张天鹤 ，闫翔宇，于志双

预制混凝土管组合柱-钢梁节点核心区受力性能分析

张锡治1, 2，李星乾1，章少华1, 2，张天鹤1，闫翔宇2，于志双3

(1. 天津大学建筑工程学院，天津 300072；2. 天津大学建筑设计规划研究总院有限公司，天津 300072；3. 中铁建大桥工程局集团建筑装配科技有限公司，天津 300300)

建立了预制混凝土管组合柱-钢梁节点在往复荷载作用下受力性能分析的精细化有限元计算模型．根据已完成的6个“弱节点”试验结果，对比分析试验与模拟试件的破坏模式、梁端荷载-位移骨架曲线和特征点荷载，验证了有限元模型的准确性．研究了预制混凝土管组合柱-钢梁节点核心区受力全过程工作机理，并对各关键组件的应力、应变发展规律及其相互作用进行分析．通过有限元模型参数化分析，研究了轴压比、钢套箍厚度、钢套箍延伸高度、预制混凝土管强度及芯部混凝土强度等因素对节点承载力和变形能力的影响．分析结果表明：在梁端往复荷载作用下，钢套箍屈服“拉力带”和核心区混凝土“斜压杆”机构共同抵抗节点剪力；峰值荷载时钢套箍以刚体变形为主，极限荷载时钢套箍腹板大面积屈服；芯部混凝土、钢套箍与预制混凝土管之间界面接触相互作用力分布不均匀；轴压比、钢套箍厚度、预制混凝土管和芯部混凝土强度对节点承载力及变形能力影响较大，增大钢套箍厚度可以显著提高节点承载力及变形能力；钢套箍延伸高度增加可以提高节点变形能力，但对承载力影响不明显．建立了预制混凝土管组合柱-钢梁节点受剪计算模型，理论值与模拟值吻合较好且偏于安全．

预制混凝土管组合柱；RCS节点；数值模拟；受力机理；受剪承载力

钢筋混凝土柱-钢梁混合框架结构(RCS混合框架结构)充分利用和发挥钢筋混凝土和钢在强度、刚度和延性等方面优势，具有良好的建筑功能适用性，在工程中得到了较为广泛的应用．针对钢筋混凝土柱-钢梁节点(RCS节点)，国内外学者已开展了一系列研究工作，提出了不同构造形式的RCS节点，建立了相应的计算模型和设计理论[1-4]．

目前，RCS节点的研究主要集中于其在低周反复荷载作用下的受力性能．李贤[5]、张锡治等[6]和Wu等[7]对端板螺栓连接RCS边节点进行了抗震试验研究，指出端板-预应力高强螺栓连接可以提高节点受剪承载力和减小节点核心区损伤．郭子雄等[8]、Zhang等[9]、Khaloo等[10]、Kim等[11]、Zibasokhan等[12]、Alizadeh等[13]针对不同构造形式柱贯通型和梁贯通型RCS中节点的抗震性能已开展了大量试验研究，分析了节点在往复荷载作用下的受力机理．Cheng 等[14]、Men等[15]对带楼板的RCS节点抗震性能进行了试验研究，结果表明楼板的存在对节点的受力特征和破坏模式等有显著影响．

传统的结构抗震试验目前已比较成熟，但由于结构缩尺、量测范围受限等缺点，难以完全反映结构构件在荷载作用下受力全过程的弹塑性力学行为[16].为深入研究RCS节点的传力特征及其在结构体系中的受力性能，部分学者利用有限元方法对RCS节点进行了分析，主要包括：Mirghaderi等[17]采用ABAQUS软件对其所提出的RCS节点进行了数值模拟，指出混凝土斜压杆提供的承载力占节点总剪力的55%；李贤[5]采用ANSYS软件对端板螺栓连接RCS节点建立了三维实体有限元模型，参数分析结果表明端板厚度和轴压力对节点抗震性能影响较大，螺栓预紧力对节点整体性能影响不大，但对节点局部受力性能有一定影响；Chou等[18]利用PISA程序对一栋三层后张预应力RCS混合框架进行了动力弹塑性时程分析，验证了采用转动弹簧单元模拟梁柱节点自复位特征的可行性和准确性．

目前以RCS节点核心区为对象的相关研究较为缺乏，试验研究大多关注承载力和耗能能力等宏观抗震性能指标，对此类节点的工作机理和力学行为尚未明晰．特别地，节点核心区各组件受力全过程应力、应变发展及各组件之间的相互作用规律需进一步研究．基于现有研究成果，结合装配式建筑的发展需求，提出了一种预制混凝土管组合柱-钢梁节点形式，完成了6个“弱节点”试件的低周反复加载试验[19]. 本文分析了其轴压比、芯部混凝土强度、钢套箍厚度和延伸高度等参数对节点核心区受剪性能的影响．为深入研究预制混凝土管组合柱-钢梁节点核心区受力性能，明确其受力全过程工作机理和破坏机制，采用通用有限元分析软件ABAQUS建立了预制混凝土管组合柱-钢梁节点精细化三维数值模型，考虑材料非线性、几何非线性和接触非线性，对试验结果进行全过程计算，扩展参数范围分析关键参数对节点受力性能的影响规律，建立节点受剪承载力计算方法，为工程应用提供理论依据．

1 有限元模型建立与验证

1.1 模型建立

本文研究的预制混凝土管组合柱-钢梁节点形式如图1所示，采用ABAQUS/Standard建立其精细化数值模型，如图2所示．其中，混凝土、钢梁、八边形外加强环、钢套箍、栓钉和加载板均采用8节点线性减缩积分三维实体单元(C3D8R)，钢筋采用2节点三维桁架单元(T3D2)，采用结构化网格划分技术对模型进行网格划分．为研究节点核心区受力全过程，对模型进行非均匀网格划分，即对节点核心区部件进行细网格划分，非节点核心区部件进行粗网格划分．

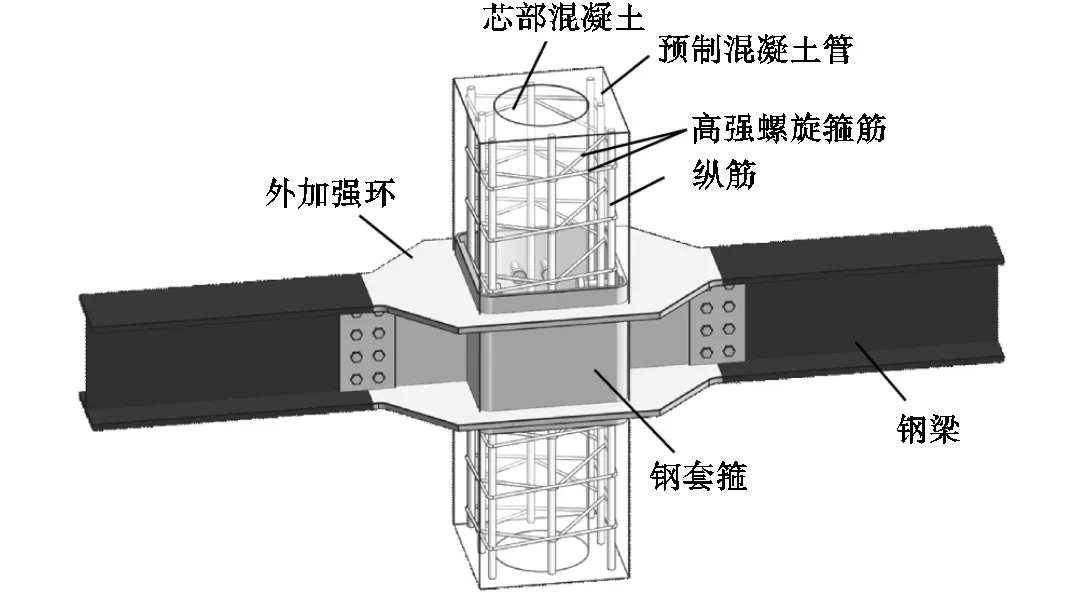
图1 预制混凝土管组合柱-钢梁节点示意

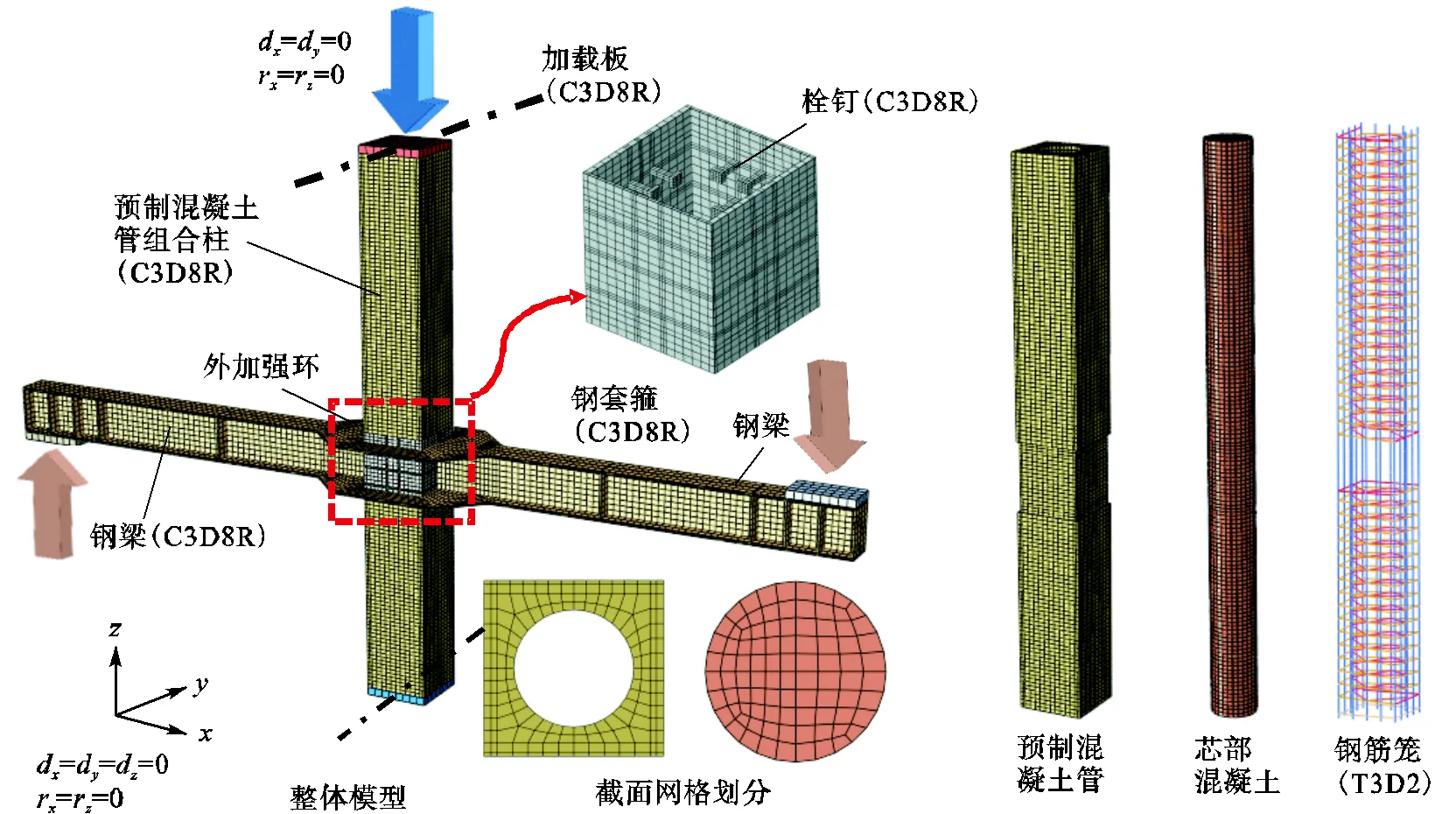
图2 预制混凝土管组合柱-钢梁节点有限元模型

1.2 材料本构关系

1.2.1 钢 材

预制混凝土管组合柱-钢梁节点中的钢材包括钢套箍、栓钉、纵筋和箍筋．在有限元模型中，采用各向同性强化与双线性随动硬化混合模型模拟钢材材料性能，多轴应力下满足von Mises屈服准则，并服从相关联的塑性流动法则．其单轴应力-应变关系采用线性强化模型，强化段弹性模量取0.01s，s为钢材弹性模量，s＝206000N/mm2，泊松比s＝0.3．钢材的屈服强度和极限强度按文献[19]实测数据取值．

1.2.2 混凝土

采用塑性损伤模型(CDP模型)模拟混凝土材料性能，该模型考虑各向同性损伤并服从非关联的塑性流动法则，控制参数取值见表1．将混凝土截面划分为钢管约束混凝土、箍筋约束混凝土和非约束混凝土(图2)以考虑混凝土约束条件的不同．其中，钢管约束混凝土受压本构关系采用韩林海模型[20]；箍筋约束混凝土受压本构关系采用Mander等模型[21]；保护层非约束混凝土受压本构关系采用文献[22]建议的单轴受压本构模型．由于约束对混凝土受拉性能影响较小，故混凝土受拉应变-应变关系采用文献[22]建议的模型．混凝土弹性模量c＝105/(2.2＋34.7cu)[22]，cu为混凝土立方体抗压强度，泊松比c＝0.2．

引入受拉损伤因子和受压损伤因子模拟混凝土受拉和受压状态下的损伤，其值采用Sidoroff能量等价原理[23]计算得到．

表1 混凝土塑性损伤控制参数

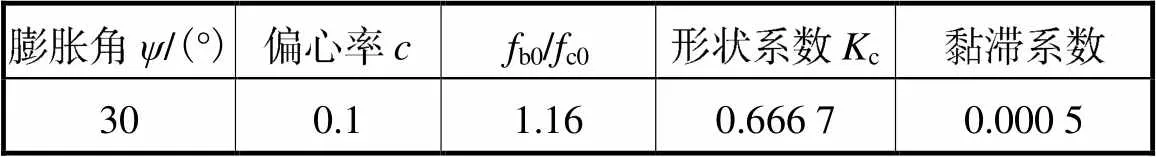
Tab.1 Plastic coefficient of concrete damage

1.3 界面关系与边界条件

钢筋骨架、栓钉和混凝土之间的界面关系使用嵌入区域(embedded region)约束，定义绝对容差和相对公差分别为0和0.05，分析中使用较小容差进行计算.钢套箍和混凝土的相互作用关系选用面-面(surface-to-surface)接触[24]，其中界面法向接触关系采用“硬接触”模型，允许钢套箍与混凝土在受力过程中发生分离，当发生接触时法向接触应力在二者之间可以完全传递；界面切向接触关系采用“库伦摩擦模型”模拟，其特征为当界面切向应力达到临界应力值(crit)时发生相对滑移，此时界面剪应力保持crit不变，该法则采用摩擦系数f1表征二者之间的摩擦行为，本文中取f1＝0.6[20]．类似地，预制混凝土管与芯部混凝土之间的界面法向和切向接触关系也采用“硬接触”和“库伦摩擦”模拟，根据预制混凝土管内壁表面粗糙处理方法，取摩擦系数f2＝0.6[25]．钢材与焊缝之间采用绑定(tie)约束．

为模拟试件实际受力状态，模型中预制混凝土管组合柱柱底约束3个方向的平动，释放轴方向的转动自由度，以模拟固定铰支座；柱顶释放轴方向的平动和轴方向的转动自由度，允许柱顶发生竖向位移和平面内转动，如图2所示．加载过程中，在柱顶和梁端加载点设置参考点，参考点与加载板表面耦合(coupling)，避免加载过程中出现应力集中．其中，柱顶施加的轴向荷载为

＝(c,oc1＋c,ic2)

式中：为试验轴压比；c,o、c,i分别为预制混凝土管和芯部混凝土轴心抗压强度；c1、c2分别为预制混凝土管和芯部混凝土截面面积．梁端采用反对称位移控制加载，如图2所示．

1.4 有限元模型验证

文献[19]中研究了6个预制混凝土管组合柱-钢梁节点在柱顶施加恒定轴压力、梁端施加低周反复荷载作用下的受剪性能，主要参数见表2．其中：为钢套箍厚度；e为钢套箍延伸高度；cu,o、cu,i分别为预制混凝土管和芯部混凝土立方体抗压强度；y、u分别为钢套箍的屈服强度和极限强度；y、m分别为节点屈服和峰值受剪承载力；y、m分别为节点屈服和峰值受剪承载力有限元结果与试验结果的相对误差．试验试件几何尺寸及构造如图3所示．为验证有限元模型的准确性，将数值模拟结果和试验结果进行对比．以试件CRCS1和试件CRCS2为例，图4给出了有限元模拟的破坏模式与试验结果对比．图中t、c分别为混凝土受拉和受压损伤因子，ep为等效塑性应变，为von Mises应力．由等效塑性应变图可知，试件CRCS1和试件CRCS2的节点累积塑性应变较大区域主要集中于节点核心区钢套箍，其值分别为56500ε和74200ε，最大应力分别为401MPa和405MPa，与试验试件节点核心区发生剪切破坏现象相吻合．节点核心区整体刚度较大，其变形以刚体转动为主，有限元模型可以较好地模拟节点变形特征．由混凝土损伤云图可知，柱身以弯曲裂缝为主，并在后期向柱中轴线斜向发展．节点核心区钢套箍上下柱端混凝土受压损伤严重，试件CRCS1和CRCS2混凝土受压损伤高度分别约为60mm和40mm，与试验现象较为吻合．与试件CRCS1相比，试件CRCS2钢套箍延伸高度增加，柱端混凝土受压损伤程度减弱，混凝土压碎剥落高度减小，其损伤分布规律与试验现象基本一致．因此，本文建立的有限元模型可以较为准确地预测预制混凝土管组合柱-钢梁节点的整体破坏模式．

表2 参考文献[19]中试件主要参数

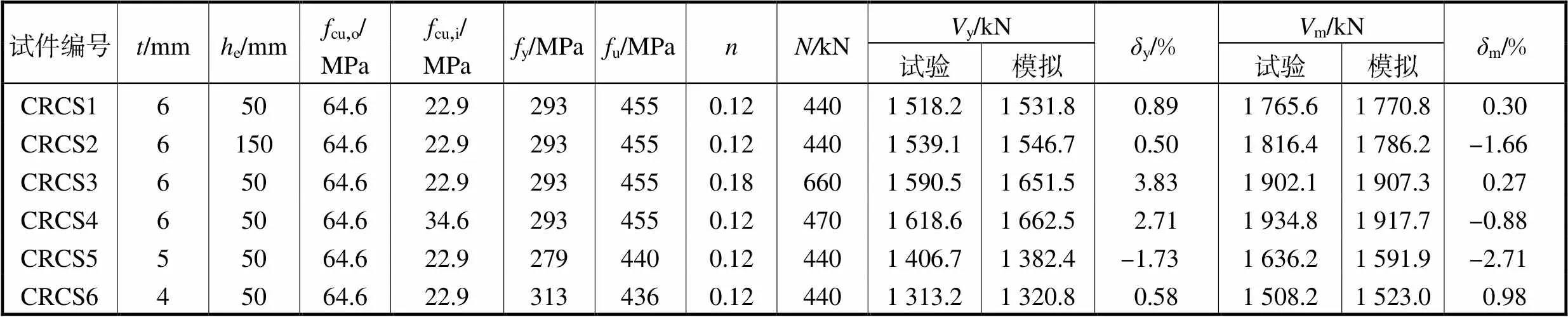
Tab.2 Main parameters of the test specimens in Ref.[19]

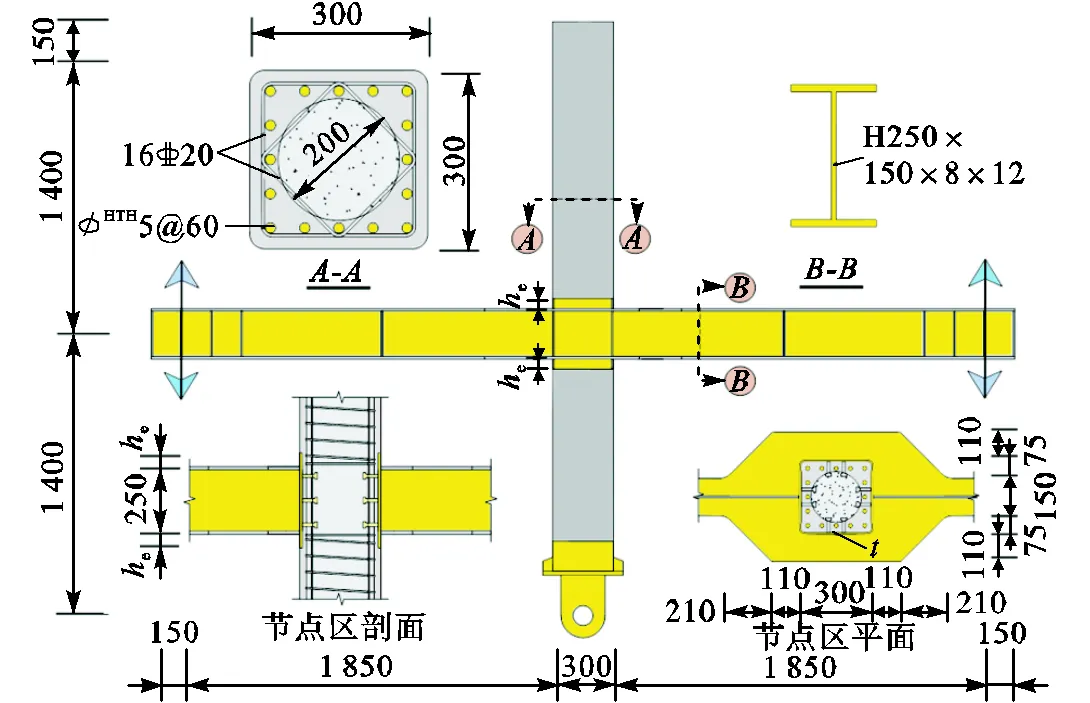
图3 试件几何尺寸及构造

图5为有限元和试验得到的梁端荷载-位移骨架曲线对比．由图5可见，有限元模型计算结果与试验结果吻合较好，有限元分析能较为准确地模拟试验曲线的上升段和峰值荷载后的下降段刚度退化．有限元模拟得到的节点受剪屈服和峰值承载力见表2．由表可知，有限元模型对节点承载力和变形能力模拟精度较好，屈服承载力误差在3.83%以内，峰值承载力误差在2.71%以内．

综上所述，本文建立的有限元模型可以较准确地模拟预制混凝土管组合柱-钢梁节点的整体变形特征、节点核心区破坏模式，同时对节点核心区特征点承载力计算具有良好的精度．因为主要分析特征点节点核心区受力机理和承载力计算方法，有限元单调加载得到的荷载-位移关系曲线与试验骨架曲线基本一致，为提高计算效率和减少计算量，后文有限元分析中采用单调加载模式．

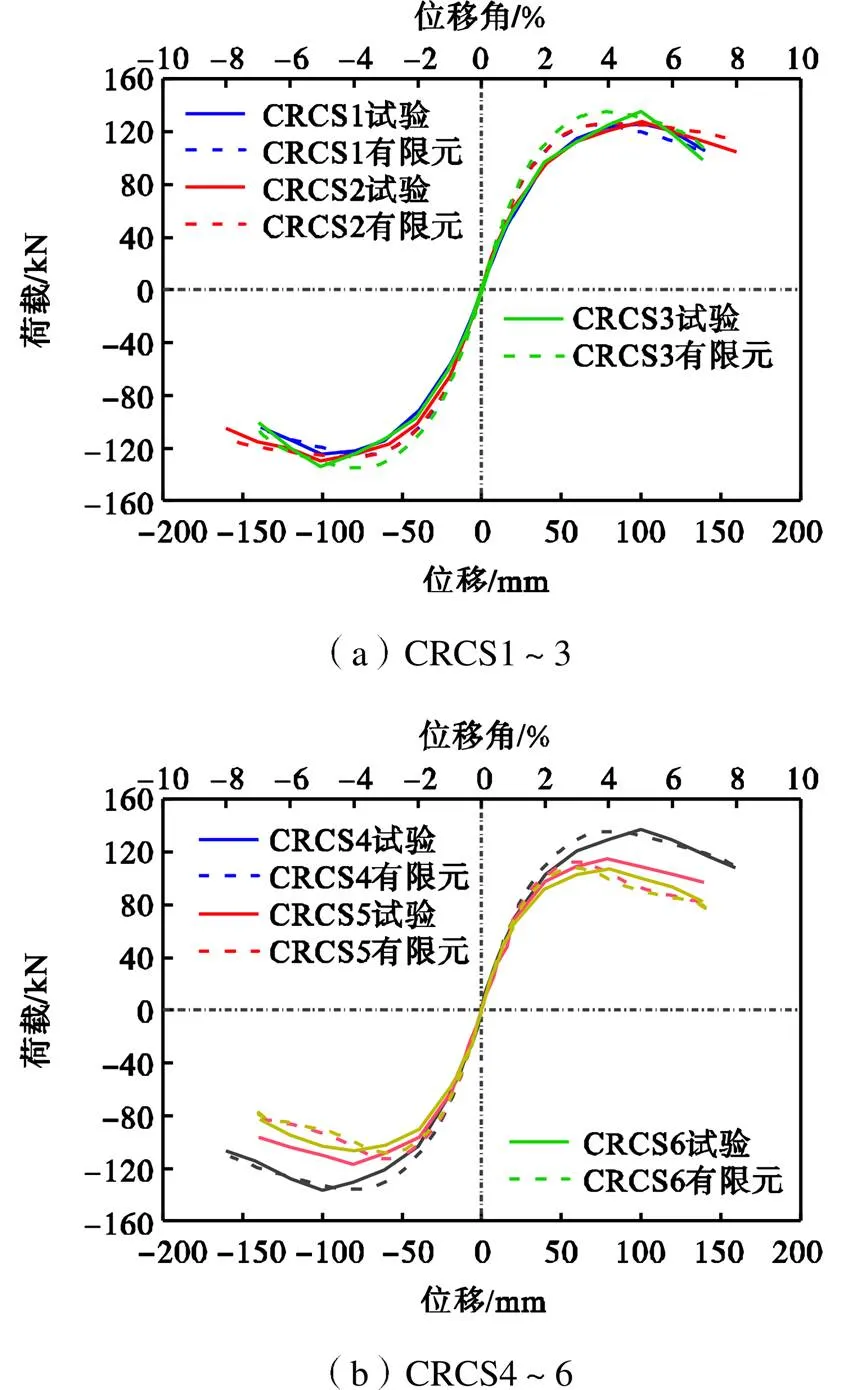
图5 有限元计算结果与试验骨架曲线对比

2 节点核心区受力性能分析

2.1 受力全过程工作机理分析

利用经过验证的有限元模型，对预制混凝土管组合柱-钢梁节点核心区受力性能进行分析，探讨节点核心区受力全过程工作机理．章少华等[19]的试验研究表明，采用外加强环连接的预制混凝土管组合柱-钢梁节点具有明确的传力途径和可靠的传力性能，所有试件主要发生节点核心区受剪破坏，钢套箍与柱连接过渡区域混凝土保护层局部压碎剥落，未发生焊缝断裂失效等非试验预期现象，与有限元分析中设定的理想接触关系基本相同．选取试验基准试件CRCS1作为典型试件分析节点核心区全过程工作机理，典型的荷载-位移骨架曲线如图6所示．图中标志出骨架曲线上3个特征点、、分别对应屈服荷载y、峰值荷载m和极限荷载u，其对应的位移分别为y、m和u．通过分析节点各部件在各特征点下的应力云图和应力、应变矢量图，明晰该节点的受力状况和工作机理．

图7所示为钢梁和外加强环在各特征点沿全局坐标系轴方向纵向应力(S11)云图．由图可知，点时，较大应力集中于钢梁与外加强环交界处，外加强环开始显现其良好的应力扩散作用．点时，钢梁受压和受拉翼缘范围沿梁长度方向达到最大，钢梁受拉屈服区域从翼缘扩展到腹板，但未出现局部屈曲现象，同时外加强环应力传递路径愈发显著；对受拉的外加强环而言，较大应力集中于与柱交界处角部区域，对受压的外加强环而言，应力较为均匀地分布在与柱接触的宽度范围内．点时，靠近节点核心区的外加强环应力进一步增大，钢梁应力逐渐减小，表明大部分梁端荷载通过外加强环传递到节点核心区，最终发生节点核心区破坏．

图6 典型试件的荷载-位移曲线及特征点定义

图7 钢梁和外加强环S11应力分布

核心区钢套箍von Mises应力在各特征点的分布情况如图8所示．由图可知，点时，腹板受拉角部区域开始进入屈服，此时最大应力值＝281.3MPa，形成“拉力带”抵抗节点核心区剪切作用；点时，腹板屈服区域进一步扩大，最大应力值＝298.6MPa，钢套箍变形以整体刚体转动为主，剪切变形不明显，同时钢套箍翼缘与腹板交界处应力集中发生屈服．点时，腹板屈服区域无显著扩大，在柱宽度和梁高度范围内，钢套箍腹板大面积屈服，应力水平增长明显，最大应力值＝321.5MPa，钢套箍出现明显的剪切变形，同时钢套箍翼缘部分区域屈服．

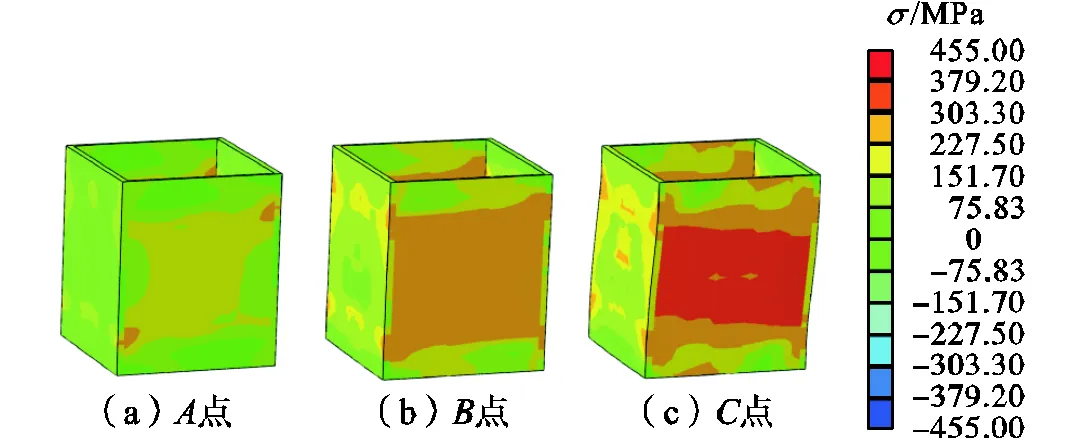
图8 钢套箍von Mises应力分布

图9为预制混凝土管和芯部混凝土各特征点最小主应力矢量图．最小主应力代表混凝土主压应力，其矢量方向可作为判断主斜裂缝发展方向的依据．由图可知，不同特征点下预制混凝土管主压应力流发展趋势有明显差异．点时，预制混凝土管主压应力基本沿核心区对角线方向，反映了节点核心区预制混凝土管混凝土在受力过程中形成“斜压杆”机构抵抗核心区受剪作用．点时，预制混凝土管主压应力除沿核心区对角线形成“主斜压杆”外，由于钢套箍翼缘对核心区混凝土的约束作用，节点核心区混凝土形成“次斜压杆”抵抗外力，如图9所示．点时，主斜压杆作用减小，次斜压杆与柱纵轴夹角增大，混凝土受剪承载力下降，核心区预制混凝土管受剪破坏，节点发生显著的剪切变形．根据芯部混凝土主压应力矢量图可知，芯部混凝土也形成了“斜压杆”机构抵抗节点剪力，其应力流发展趋势与预制混凝土管类似，表明芯部混凝土与预制混凝土管具有较好的共同工作性能．

图9 预制混凝土管和芯部混凝土最小主应力矢量图

上述工作机理分析结果表明，采用外加强环连接的预制混凝土管组合柱-钢梁节点具有明确合理的传力路径和良好的受力性能，核心区的钢套箍屈服形成“拉力带”与预制混凝土管组合柱和芯部混凝土“斜压杆”机构共同参与节点受剪．随着梁端位移的增加，核心区预制混凝土管混凝土与芯部混凝土承担的剪力逐步增加，达到峰值荷载后下降；钢套箍承担的剪力逐步上升后基本保持恒定，峰值荷载后屈服区域应力水平增长显著．节点破坏时，核心区混凝土破坏，钢套箍腹板大面积屈服，发生较大的剪切变形．

2.2 相互作用

通过提取有限元模型法向相互作用应力(CPRESS)等线图，可综合分析预制混凝土管组合柱-钢梁节点各组件之间的共同工作性能．图10所示为点时芯部混凝土与预制混凝土管相互作用力分布图．由图可知，在节点核心区二者法向相互作用力分布不均匀，靠近受压翼缘的芯部混凝土区域相互作用力最大(50.6MPa)，远离受压翼缘的芯部混凝土相互作用力逐渐减小，表明受压翼缘的芯部混凝土区域提供的节点受剪承载力更大．在节点核心区以外的区域，相互作用力等线图近似沿环向呈水平分布，表明芯部混凝土与预制混凝土管在受力过程中具有良好的协同工作性能．

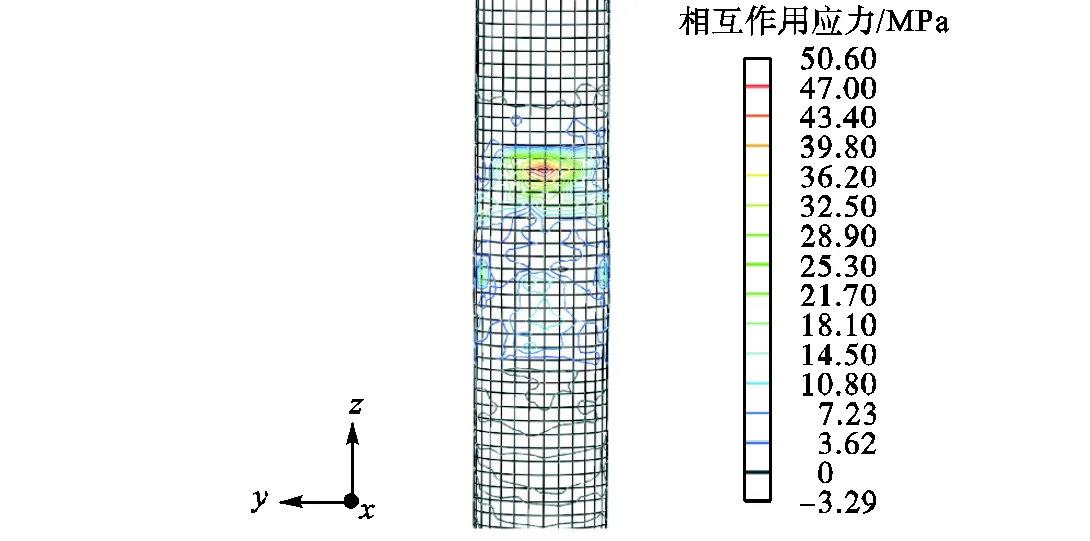
图10 芯部混凝土与预制混凝土管相互作用力分布

图11为点时钢套箍与预制混凝土管之间的法向相互作用应力分布．由图可知，钢套箍翼缘和腹板区域的相互作用力分布不均匀，钢套箍受压翼缘处相互作用力最大(149MPa)，受拉翼缘处相互作用力最小．此外，由于栓钉的抗剪和抗拔作用，栓钉与钢套箍接触面的相互作用力较大，表明栓钉起到了较好的剪力传递效果，增强了钢套箍与节点核心区混凝土之间的共同工作性能．

图11 钢套箍与预制混凝土管相互作用力分布

3 参数分析

为研究预制混凝土管组合柱-钢梁节点参数对其核心区承载力和变形能力的影响，以试验试件CRCS1为基准，通过不同参数变化分析其对节点核心区剪力-剪切变形(-)曲线和承载力的影响．节点核心区剪切变形计算简图如图12所示，计算公式为

式中：、分别为节点核心区对角测点相对压缩和伸长位移；a、b分别为节点核心区对角测点的宽度和高度．

有限元模型主要分析参数包括：轴压比()、钢套箍厚度()、钢套箍延伸高度(e)、预制混凝土管混凝土强度(cu,o)以及芯部混凝土强度(cu,i)．除6个试验试件有限元模型外，根据分析参数建立了15个有限元模型，具体参数取值及计算结果见表3．表中：y,FEM、m,FEM分别为有限元计算得到的节点屈服承载力和峰值承载力；u,FEM为节点承载力下降至85%峰值承载力时对应的层间位移角．

表3 有限元模型计算参数

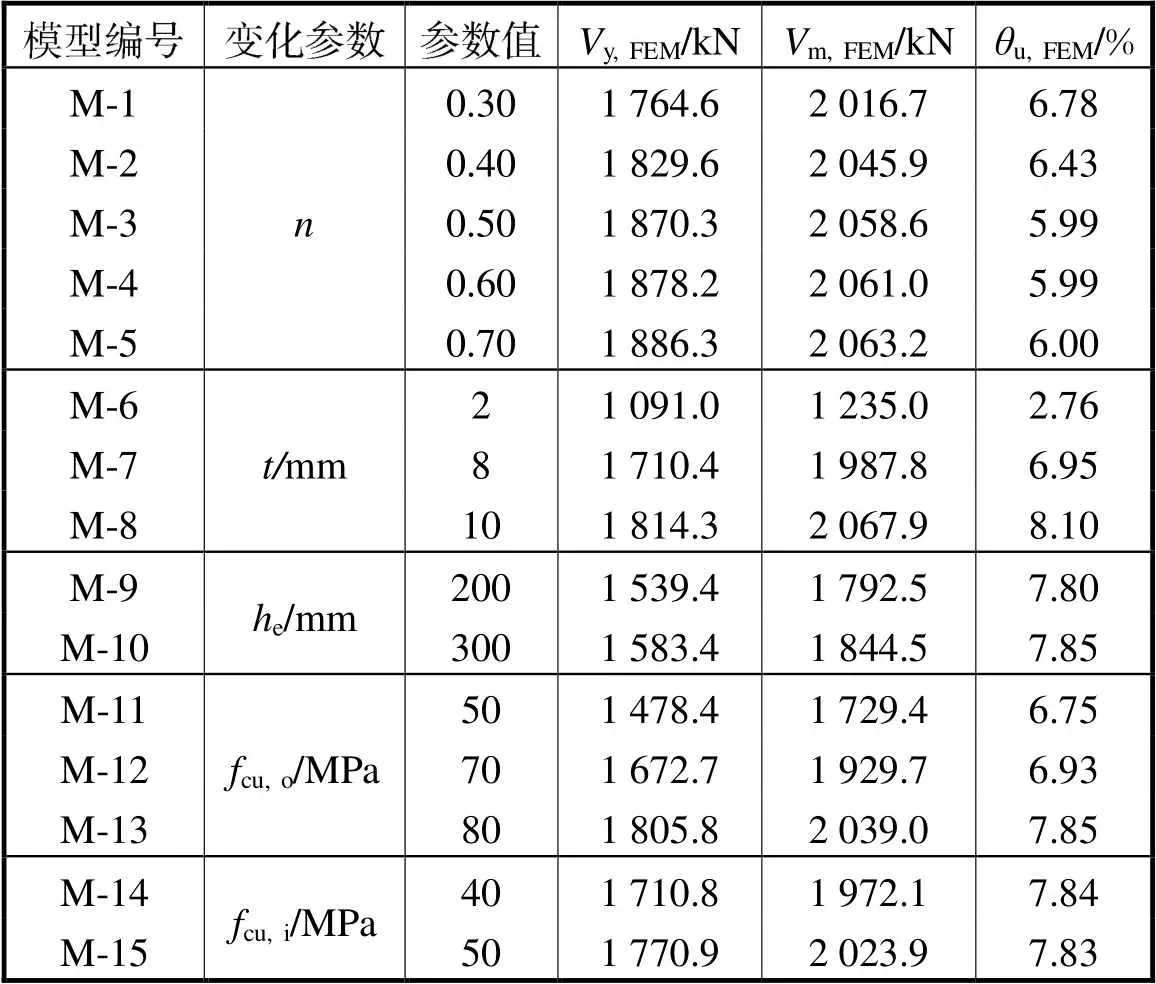
Tab.3 Parameter of finite element modes

3.1 轴压比

图13(a)、(b)给出了不同轴压比下预制混凝土管组合柱-钢梁节点核心区的-关系曲线．由图13(a)、(b)和表3可知：①在一定范围内，节点剪切刚度随轴压比的增加而增大，但破坏时其极限位移角减小，当从0.30增加到0.40、0.50时，极限位移角分别降低了5.2%和11.7%，当达到0.60、0.70时，增加轴压比对节点极限位移角的影响不明显；②当≤0.4时，增加轴压比可以显著提高节点核心区的屈服和峰值受剪承载力，这是由于轴压力可以抑制混凝土裂缝发展，增强核心区混凝土三向约束效果；③当＞0.4时，轴压比对节点屈服和峰值受剪承载力影响较小，从0.40增加到0.50、0.60、0.70，屈服和峰值受剪承载力仅分别提高了2.2%、2.7%、3.1%和0.6%、0.7%、0.8%．

3.2 钢套箍厚度

钢套箍厚度的增加会显著提高节点的承载力和变形能力，但对节点初始剪切刚度无明显影响，如图13(c)和(d)所示．当从2mm增加到4mm、5mm、6mm、8mm、10mm，节点受剪峰值承载力分别提高了20.5%、26.7%、41.9%、56.8%和66.3%．这是因为增加钢套箍厚度相当于增加节点核心区截面含钢率，钢套箍直接参与节点受剪并为核心混凝土提供约束作用，极大地提高了节点承载性能和变形能力．因此，在设计中通过增加钢套箍厚度是提高节点承载力和变形能力的有效途径之一．

3.3 钢套箍延伸高度

节点承载力随着钢套箍延伸高度的增加有一定提高，但增幅较小，如图13(e)和(f)所示．当e从50mm增加到150mm、200mm、300mm时，节点承载力分别提高了0.9%、1.2%和4.2%，这是因为钢套箍延伸高度增加可以在一定程度上减小节点核心区上下柱端混凝土保护层碎裂剥落．当e从50mm增加到150mm时，节点极限位移角增加了19.1%，但当e＞150mm时，节点变形能力受e影响很小．可见，在一定范围内增加钢套箍延伸高度可以增大节点变形能力，但超过一定范围后钢套箍延伸高度对节点的变形能力影响较小．

3.4 预制混凝土管强度

预制混凝土管强度对节点-关系曲线的影响如图13(g)和(h)所示．由图可知，节点承载力随预制混凝土管强度的提高呈线性增长趋势，当cu,o从50MPa增加到60MPa、70MPa、80MPa时，节点承载力分别提高了4.7%、13.1%和22.1%，极限位移角分别提高了2.4%、2.7%和16.3%．由于混凝土的脆性随强度的增加而增大，对cu,o较大的节点，其峰值荷载后核心区剪力-剪切角曲线下降段较陡，因此在设计中提高预制混凝土管强度时应考虑其对节点变形能力的不利影响．

3.5 芯部混凝土强度

如图13(i)和(j)所示，节点屈服和峰值受剪承载力随芯部混凝土强度的提高而增大，当cu,i从20MPa增加到30MPa、40MPa、50MPa时，节点屈服和峰值受剪承载力分别提高了8.5%、11.7%、15.6%和8.3%、11.4%、14.3%，同时其极限位移角分别提高了10.1%、16.3%和16.2%．因此，适当提高芯部混凝土强度可增强节点变形能力．建议实际工程中芯部混凝土强度不宜低于C30，且不宜高于预制混凝土管强度.

4 节点受剪承载力计算

4.1 力学模型建立

根据对预制混凝土管组合柱-钢梁节点核心区的工作机理分析，可知该类节点受剪承载力由核心区钢套箍腹板“拉力带”和核心区混凝土“斜压杆”两部分组成．本文中，“斜压杆”机构除沿节点核心区对角线方向形成的主斜压杆外，还考虑了钢套箍翼缘对核心混凝土约束的有利作用，形成的次斜压杆与主斜压杆共同抵抗节点剪力．基于上述分析，建立适用于预制混凝土管组合柱-钢梁节点受剪计算模型如图14所示．

图14 节点核心区受剪计算模型

4.2 节点受剪承载力计算

由以上分析可知，预制混凝土管组合柱-钢梁节点受剪承载力由钢套箍腹板抗剪承载力和节点核心区混凝土受剪承载力两部分组成，后者考虑了钢套箍翼缘约束作用．因此，节点受剪承载力可表示为

节点核心区钢套箍处于压剪复合作用应力状态如图14(a)所示，图中，为钢套箍腹板所受的轴压应力，为腹板剪应力．根据第四强度理论，当节点达到峰值荷载时，钢套箍腹板处于剪切流变状态，可得腹板受剪承载力，即

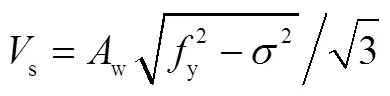
式中：w为钢套箍腹板面积；按钢套箍和混凝土强度按比例分配，即

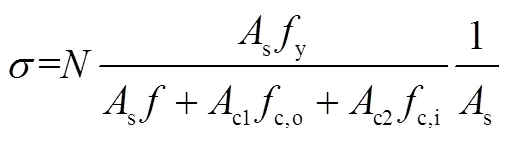
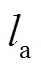
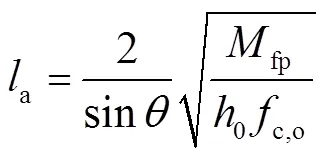
式中：0为核心混凝土截面高度，0＝c－2sf，c为柱截面高度，sf为钢套箍翼缘厚度；fp为钢套箍翼缘塑性极限弯矩，fp＝y(2/4)；为斜压杆与柱纵轴之间的夹角，其表达式[26]为

式中，b、c分别为钢梁和柱的截面高度．

考虑预制混凝土管与芯部混凝土强度不同，将混凝土斜压杆受剪承载力视为二者承载力的叠加，则混凝土斜压杆提供的受剪承载力为

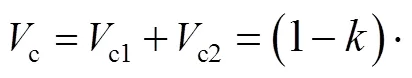
式中：c1、c2分别为预制混凝土管和芯部混凝土受剪承载力；为折减系数，取＝/c，为芯部混凝土直径，c为柱截面宽度．

计算节点受剪屈服承载力时，采用Fukumoto等[26]基于回归分析得到的核心区混凝土受剪屈服荷载与峰值荷载比例系数1、2分别对预制混凝土管和芯部混凝土提供的受剪承载力进行折减，即

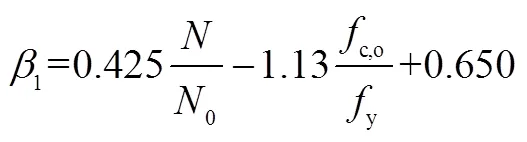
式中：/0为柱轴压比；0＝sy＋c1c,o＋c2c,i．

按式(8)和式(2)计算得到的节点屈服受剪承载力y,cal和峰值受剪承载力m,cal与数值分析所得的y,FEM、m,FEM进行对比，结果如图15所示．由计算结果可知，y,cal/y,FEM的平均值和均方差分别为0.796、0.077，变异系数为0.097；m,cal/m,FEM的平均值和均方差分别为0.878、0.095，变异系数为0.108，计算值与模拟值吻合较好，且偏于安全．由于本文模型中未考虑轴压力对混凝土斜压杆机制的有利作用，仅将轴压力作为设计时的安全储备，当柱轴压比增大时，理论计算结果更偏于保守．

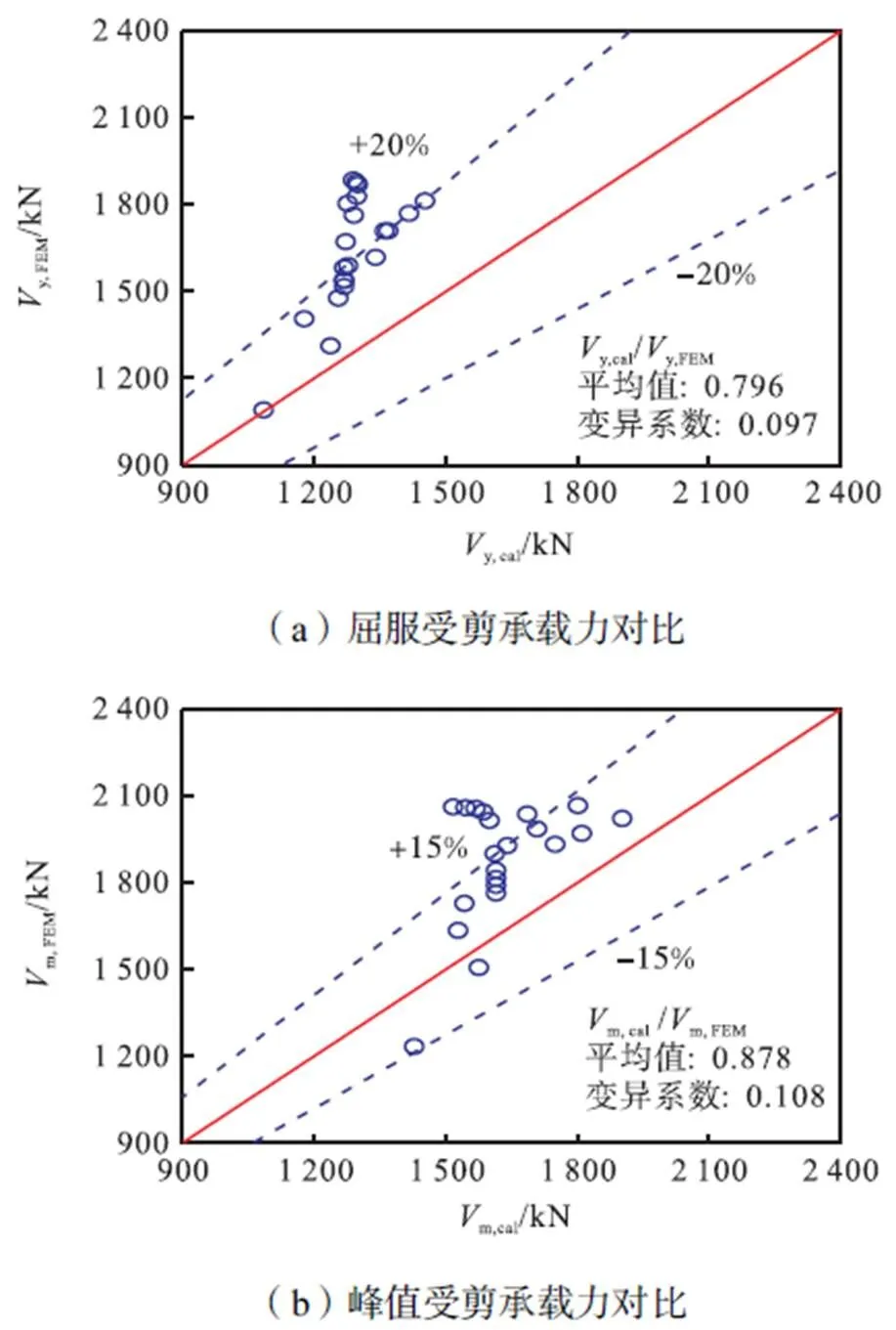
图15 节点受剪承载力计算值与试验及有限元结果对比

5 结 论

(1) 建立了预制混凝土管组合柱-钢梁节点精细化数值模型，典型试件模拟的破坏模式与试验现象基本一致，模拟得到的节点屈服受剪承载力和峰值受剪承载力与试验值的误差分别在3.83%和2.71%以内，验证了数值模型的准确性．

(2) 全过程工作机理分析结果表明，在梁端往复荷载作用下，钢套箍屈服形成“拉力带”抵抗节点剪力，核心区混凝土形成“斜压杆”抵抗节点剪力；达到峰值点时钢套箍以刚体变形为主，极限点时钢套箍腹板大面积屈服，发生明显剪切变形．芯部混凝土与预制混凝土管、钢套箍与预制混凝土管之间相互作用力分布不均匀．

(3) 在一定范围内，增加轴压比可以提高节点承载力和初始剪切刚度，但当＞0.4时，轴压比对节点承载力影响较小；增加钢套箍厚度对提高节点承载力和变形能力作用显著，是工程设计的推荐方法之一；节点承载力随预制混凝土管和芯部混凝土强度的增加而提高，但预制混凝土管强度较高时使节点核心区剪力-剪切角曲线下降段变陡，变形能力降低；在分析参数范围内，节点变形能力随钢套箍延伸高度和芯部混凝土强度的增加而提高．

(4) 考虑钢套箍翼缘约束对核心混凝土的有利作用，建立了预制混凝土管组合柱-钢梁节点受剪计算模型，提出了节点受剪承载力计算公式.y,cal/y,FEM的平均值和变异系数分别为0.796和0.097，m,cal/m,FEM的平均值和变异系数分别为0.878和0.108，理论屈服受剪承载力和峰值受剪承载力与有限元分析结果吻合较好，且偏于安全．

［1］ Deierlein G G. Design of Moment Connections for Composite Framed Structures[D]. Austin：The University of Texas，1988.

［2］ ASCE. Guidelines for design of joints between steel beams and reinforced concrete columns[J]. Journal of Structural Engineering，1994，120(8)：2330-2357.

［3］ Parra-Montesinos G，Wight J K. Modeling shear behavior of hybrid RCS beam-column connections [J]. Journal of Structural Engineering，2001，127(1)：3-11.

［4］ 门进杰，周婷婷，张雅融，等. 钢筋混凝土柱-钢梁组合框架结构基于性能的抗震设计方法和量化指标[J]. 建筑结构学报，2015，36(增2)：28-34.

Men Jinjie，Zhou Tingting，Zhang Yarong，et al. Performance-based seismic design method and quantified performance index of RCS composite frame structure [J]. Journal of Building Structures，2015，36(Suppl2)：28-34(in Chinese).

［5］ 李 贤. 端板螺栓连接钢-混凝土组合节点的抗震性能研究[D]. 长沙：湖南大学，2009.

Li Xian. Seismic Behavior of Bolted End-plate Connections for Composite Steel and Concrete Structures[D]. Changsha：Hunan University，2009(in Chinese).

［6］ 张锡治，章少华，徐盛博，等. 端板与柱间灌浆层对端板连接RCS节点抗震性能影响的试验研究[J]. 天津大学学报(自然科学与工程技术版)，2020，53(7)：674-684.

Zhang Xizhi，Zhang Shaohua，Xu Shengbo，et al. Experimental study on influence of a grout layer between an end-plate and a column on seismic of end-plate-connection RCS joints[J]. Journal of Tianjin University(Science and Technology)，2020，53(7)：674-684(in Chinese).

［7］ Wu Y T，Xiao Y，Anderson J C. Seismic behavior of PC column and steel beam composite moment frame with posttensioned connection[J]. Journal of Structural Engineering，2009，135(11)：1398-1407.

［8］ 郭子雄，朱奇云，刘 阳，等. 装配式钢筋混凝土柱-钢梁框架节点抗震性能试验研究[J]. 建筑结构学报，2012，33(7)：98-105.

Guo Zixiong，Zhu Qiyun，Liu Yang，et al. Experimental study on seismic behavior of a new type of prefabricated RC column-steel beam frame connections[J]. Journal of Building Structures，2012，33(7)：98-105(in Chinese).

［9］ Zhang X Z，Zhang J W，Gong X J，et al. Seismic performance of prefabricated high-strength concrete tube column-steel beam joints[J]. Advances in Structural Engineering，2017，21(5)：658-674.

［10］ Khaloo A，Doost B R. Seismic performance of precast RC column to steel beam connections with variable joint configurations[J]. Engineering Structures，2018，160：408-418.

［11］ Kim J H，Cho Y S，Lee K H. Structural performance evaluation of circular steel bands for PC column-beam connection[J]. Magazine of Concrete Research，2013，65(23)：1377-1384.

［12］ Zibasokhan H，Behnamfar F，Behfarnia K. The new proposed details for moment resisting connections of steel beam to continuous concrete column [J]. Advances in Structural Engineering，2016，19(1)：156-169.

［13］ Alizadeh S，Attari N K A，Kazemi M T. Experimental investigation of RCS connections performance using self-consolidated concrete[J]. Journal of Constructional Steel Research，2015，114：204-216.

［14］ Cheng C T，Chen C C. Seismic behavior of steel beam and reinforced concrete column connections[J]. Journal of Constructional Steel Research，2005，61(5)：587-606.

［15］ Men J J，Xiong L Q，Wang J C，et al. Effect of different RC slab widths on the behavior of reinforced concrete column and steel beam-slab subassemblies[J]. Engineering Structures，2021，229(2)：111639.

［16］ 聂建国，王宇航. ABAQUS中混凝土本构模型用于模拟结构静力行为的比较研究[J]. 工程力学，2013，30(4)：59-67.

Nie Jianguo，Wang Yuhang. Comparison study of constitutive model of concrete ABAQUS for static analysis of structures[J]. Engineering Mechanics，2013，30(4)：59-67(in Chinese).

［17］ Mirghaderi S R，Eghbali N B. Analytical investigation of a new through column-type joint for composite reinforced concrete and steel frames[C]//The 2013 World Congress on Advances in Structural Engineering and Mechanics(ASEM13). Jeju，Korea，2013：3158-3170.

［18］ Chou C C，Chen J H. Tests and analyses of a full-scale post-tensioned RCS frame subassembly[J]. Journal of Constructional Steel Research，2010，66(11)：1354-1365.

［19］ 章少华，张锡治，张天鹤，等. 预制混凝土管组合柱-钢梁连接节点抗震性能试验研究[EB/OL]. https:// kns.cnki.net/kcms/detail/detail.aspx?dbcode=CAPJ&dbname=CAPJLAST&filename=JZJB2020101000H&uniplatform=NZKPT&v=0dxdBFFT2iD%25mmd2FCu9Mu1-s%25mmd2B0EkMQLIWgI7iF6SUU4vLltFU7G1Ms8xtFLi0C0wSxtPI，2021-03-09.

Zhang Shaohua，Zhang Xizhi，Zhang Tianhe，et al. Experimental study on seismic behavior of concrete-filled precast concrete tube column to steel beam connections[EB/OL]. https://kns.cnki.net/kcms/detail/detail.as-px?dbcode=CAPJ&dbname=CAPJLAST&filename=JZJB2020101000H&uniplatform=NZKPT&v=0dxdBFFT2i-D%25mmd2FCu9Mu1s%25mmd2B0EkMQLIWgI7iF6SUU4vLltFU7G1Ms8xtFLi0C0wSxtPI，2021-03-09.(in Chinese).

［20］ 韩林海. 钢管混凝土结构——理论与实践[M]. 3版. 北京：科学出版社，2016.

Han Linhai. Concrete Filled Steel Tubular Strutures—Theory and Practice[M]. 3rd ed. Beijing：Science Press，2016(in Chinese).

［21］ Mander J B，Priestley M J N，Park R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering，1988，114(8)：1804-1826.

［22］ GB 50010—2010 混凝土结构设计规范[S]. 北京：中国标准出版社，2015.

GB 50010—2010 Code for Design of Concrete Strutures [S]. Beijing：Standards Press of China，2015(in Chinese).

［23］ Sidoroff F. Description of anisotropic damage applica-tion to elasticity[C]//Proceeding of IUTAM Colloqui-um on Physical Nonlinearities in Structural Analysis. Berlin，Germany，1981：237-244.

［24］ ACI 318 Committee. Building code requirements for structural concrete(ACI 318-19) and commentary (ACI 318R-19)[S]. Farmington Hills：American Concrete Institute，2014.

［25］ 张锡治，章少华，牛四欣，等. 钢-混凝土预制混合梁受弯性能有限元分析[J]. 天津大学学报(自然科学与工程技术版)，2018，51(增)：143-150.

Zhang Xizhi，Zhang Shaohua，Niu Sixin，et al. Finite element analysis of flexural behavior of precast hybrid steel-concrete beam[J]. Journal of Tianjin University(Science and Technology)，2018，51(Suppl)：143-150(in Chinese).

［26］ Fukumoto T，Morita K. Elastoplastic behavior of panel zone in steel beam-to-concrete filled steel tube column moment connections[J]. Journal of Structural Engineering，2005，131(12)：1841-1853.

Mechanical Behavior Analysis of Panel Zone in Concrete-Filled Precast Concrete Tube Column-to-Steel Beam Connections

Zhang Xizhi1, 2，Li Xingqian1，Zhang Shaohua1, 2，Zhang Tianhe1，Yan Xiangyu2，Yu Zhishuang3

(1.School of Civil Engineering，Tianjin University，Tianjin 300072，China；2. Tianjin University Research Institute of Architectural Design and Urban Planning Co.，Ltd.，Tianjin 300072，China；3. China Railway Construction Bridge Engineering Bureau Group Construction Assembly Technology Co.，Ltd.，Tianjin 300300，China)

The mechanical behavior of concrete-filled precast concrete tube(CFPCT)columns-to-steel beam connections under cyclic loading was studied using precise finite element models. Based on the experimental results of six “weak-joint” specimens，the failure modes，beam end skeleton curves，and characteristic loads were compared，validating the accuracy of the finite element models. The full-range behavior of the panel zone was investigated，and the development rules of stress and strain on key components as well as their interaction relationships were analyzed. The influence of axial compression ratio，steel jacket thickness，extended steel jacket height，precast concrete strength，and filled concrete strength on joint strength and deformation capacity were studied using parametric analysis of the finite element model. The results show that the tension band provided by the yielded steel jacket and diagonal compression strut provided by the panel zone concrete worked together to resist shear loading. The deformation of the steel jacket is mostly rigid when the peak load is reached. However，when the ultimate load is reached，the steel jacket yields over a large area. Hence，the distribution of interactions between the filled and precast concrete tubes，steel jacket，and the precast concrete tube is heterogeneous. The axial compression ratio，steel jacket thickness，precast concrete strength，and filled concrete strength have a significant impact on joint strength and deformation capacity. The load-bearing and deformation capacity of joints improve with an increase in steel jacket thickness. The influence of extended steel jacket height is not obvious，and the deformation ability of the joints increases as height increases. The shear model of the CFPCT column-to-steel beam joint is proposed in this study. The results show that the theoretical results agree well with the simulated ones and are conservative.

concrete-filled precast concrete tube(CFPCT)columns；RCS connection；numerical analysis；mechanical mechanism；shear strength

10.11784/tdxbz202103049

TU317.9；TU398.9

A

0493-2137(2022)04-0428-13

2021-03-24；

2021-04-27.

张锡治（1967—  ），男，博士，研究员，zhang_xz@tju.edu.cn.

李星乾，Lixq@tju.edu.cn.

国家自然科学基金资助项目(51578369)；天津市科技计划资助项目(19YDLYSN00120)；住建部科技计划资助项目(2020-S-020).

Supported by the National Nature Science Foundation of China(No.51578369)，Tianjin Science and Technology Projects(No.19YDLYSN 00120)，the Science and Technology Projects of Ministry of Housing and Urban-Rural Development of China(No.2020-S-020)．

(责任编辑：许延芳)