基于出行阻抗的城市地铁网络客流分布计算

杨群，罗钦，赖怡纯，郭政阳，赖志鹏

深圳技术大学 城市交通与物流学院，广东 深圳 518118

0 引言

随着城市的发展，城市轨道交通线路不断增加，定性、定量预测客流分布有助于分析掌握轨道交通客流的分布变化规律，对制定轨道交通整体运营组织管理政策以及改善轨道交通网络结构具有重要作用[1]。当前国内大中城市客流构成复杂[2]，客流成长快[3]，成长规律多变[4-5]，增加了城市客流分配预测的难度。目前传统的交通流分配理论主要分为均衡分配模型[6-7]和非均衡分配模型[8-9]，基于主观经验或实际观测数据进行预测。Chan等[10]提出一种与城市人口和经济发展相关联的地铁客流预测方法；Wei等[11]结合神经网络提出基于经验模态分析的客流预测方法；Zhang等[12]提出基于波动分析的短时客流预测方法；Ma等[13]通过长短期神经网络获取非线性交通动态，对短时交通客流进行了预测；Kumar等[14]结合神经网络与交通流密度预测了短期交通量；Roos等[15]通过动态贝叶斯网络预测巴黎铁路的短期客流。

在线路较多的情况下，乘客出行有了更多的选择。有的乘客注重换乘次数、有的在意到达目的地时间、有的更在乎舒适程度等[16]。这些出行的阻抗因素对客流预测及客流分配提出了更高要求，而传统的交通流分配理论难以满足客流预测需求[17]。因此，构建基于出行阻抗的多路径客流分布模型，分析计算网络客流分布非常必要。

本文结合轨道交通网络客流分配理论，分析乘客出行时的阻抗来源，构建新线接入后的乘客综合出行阻抗函数，建立基于出行阻抗的多路径客流分布模型，并设立换乘惩罚系数对不同路径的客流分配进行合理修正，以期提高城市地铁网络客流分布计算的准确性。

1 轨道交通网络客流分布预测模型

1.1 乘客综合出行阻抗函数

出行者在出行过程中对轨道交通起止点的距离感比较模糊，故OD(O为始发站，D为目的站)的距离不作为出行阻抗的因素。出行者一般比较在意出行的价格、时间和换乘次数等因素[18]。在价格方面，假定乘客在乘车前已经确定了出行OD，根据现行票价制定规则，无论乘客最终选择哪条路径，票价都是按照最短路径计算的，所以价格在OD确定的情况下是常量。根据实际需求可知，时间是出行者出行的首要阻抗因素。本文仅将出行者的出行时间作为出行阻抗，出行阻抗是影响交通流分配的一项重要指标。

1.1.1 进站候车阻抗

根据当前轨道交通出行的特点以及对深圳市既有地铁线路工作日列车发车间隔的统计，列车发车间隔在高峰期一般为3～6 min，在平峰期一般为4～10 min，故乘客一般不会按照列车时刻表来刻意踩点和安排自己的时间[19]。假设乘客到达站台候车的时间具有相互独立性和均衡性，且为了方便后续研究，假设乘客上下车时间等于列车到站停站时间，而列车到站停站时间相对于列车发车间隔可以忽略不计。假定乘客进站候车所花费的时间为列车发车间隔的一半，乘客在换乘时所产生的进站候车时间阻抗(乘客从车站入口到站台的时间)

th=tl/2，

(1)

式中tl为线路l中列车的发车间隔时间。

1.1.2 乘车阻抗

影响乘客选择不同路径的最重要因素是出行时间[20-21]。列车在运行过程中的时间是乘客最直观的感受，根据乘车时间对乘客出行的影响设定相应的乘车时间阻抗

tc=∑l∈L∑u∈Ultl,u+∑l∈L∑m∈Mltl,m,

(2)

式中：L为列车在运行中所经过的线路集合，Ul为途经线路l上区间的集合，Ml为途经线路l上的车站集合，tl,u为线路l上列车在区间u的运行时间，tl,m为线路l上列车在车站m的停站时间。

tl,u与tl,m仅与列车的运行状态有关，可根据列车实际运行情况得到。

1.1.3 换乘阻抗

出行者在出行过程中，对换乘次数以及换乘需要的走行时间尤为看重[22]。不少乘客宁愿多乘坐一段时间的地铁，也不愿意换乘次数太多[23]。换乘阻抗主要由乘客在换乘过程中的走行时间和在换乘站的站台候车时间组成。换乘走行过程消耗的时间与普通的候车时间给乘客带来的感受不同，需要设定放大系数δ对乘客换乘行走过程中产生的急躁情绪进行描述，则乘客在a站换乘过程中的换乘阻抗

ta=δ(ta,w+ta,h)，

(3)

式中：ta,w为乘客在a站换乘的走行时间(乘客从当前列车到换乘列车的走行时间)，由实测得出；ta,h为在a站的换乘候车时间，设定为列车发车间隔的一半。

δ过大，相关换乘的路径被选择的概率大幅下降;δ过小，需要多次换乘的路径被选中的概率增加。δ需要根据实际情况而定。

1.1.4 综合出行阻抗

结合当前轨道交通的特点可知，在一般情况下乘客更在意出行时的准时性和可靠性，而拥挤程度所带来的影响较小，本文考虑乘客的乘车阻抗、候车阻抗以及换乘阻抗，不考虑乘客在列车里的拥挤感受，所以综合出行阻抗

tz=th+tc+ta。

(4)

1.2 乘客综合出行路径选择

在不断有新线开通的情况下，线网越来越复杂，乘客的选择路径集变得更大，存在寻求最短路径及次短路径等问题。已有研究中，有使用Dijkstra算法和遗传算法等进行K短路搜索[10-11]，但由于K难以确定，在路网复杂的情况下，容易漏掉部分路径。本文直接计算所有用户可选的出行路径，不通过其他算法进行筛选，直接进入多路径客流分布计算。

1.3 基于出行阻抗的多路径客流分布计算模型

在列出所有可选择路径后，仍有不被乘客选择的不合理路径，在此，需要对这些路径进行合理性判断，筛选有效路径集。本文基于轨道交通运营时间和乘客综合出行阻抗筛选有效路径集。

1.3.1 基于运营时间的有效路径集筛选

搜集得到的路径中，有些路径换乘时还未到运营时间或超过了运营时间，需要对这些路径进行剔除。起点站时间和终点站时间可以通过列车运行图以及各换乘站所需时间进行判断。

1.3.2 基于乘客综合出行阻抗容许区域的有效路径集筛选

搜集得到的路径中，有些路径远远超过最短路径的阻抗，乘客通常不会去选择，需要进行剔除。

在已知的OD集合中，若上述搜索到的有效路径集中只有一条路径，则将所有客流分配至该路径，若搜集得到多条路径，则需要按比例将客流分配至各路径。

一个OD中第i条路径的综合出行阻抗相对于最短路径综合出行阻抗的偏差

(5)

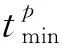
C的概率密度分布函数

(6)

式中：r为C取最大期望的概率，此处r=0；σ为常量，其取值决定正态函数曲线的陡峭程度。

路径i的效用

Si=e-[(C-r)2]/(2σ2),

(7)

路径i的客流分配比例

(8)

当某条路径的阻抗较小时，该路径被乘客选择的概率较大，客流分配比例也越大。当2条路径的阻抗相近时，若其中一条路径的换乘次数更多，乘客会重新考虑该选择哪一条路径，所以在客流分配模型中需要考虑换乘因素。为了适时调整路径的客流分配比例，在考虑综合出行阻抗的情况下，设置与换乘次数线性相关的换乘惩罚系数λ，其函数表达式为：

λ(n)=ω0n，

(9)

式中：ω0为换乘修正系数的转换因子，n为路径的换乘次数。

考虑乘客λ的客流分配比例计算公式为：

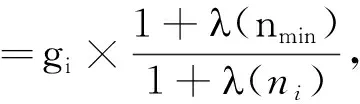
(10)

gmin′=∑(gmin+gi-gi′),

(11)

式中：gi′为经λ修正后路径i的客流分配比例，nmin为最短路径的换乘次数，ni为路径i的换乘次数，gmin′为经λ修正后的最短路径客流分配比例，gmin为最短路径的初始客流分配比例。

由式(6)～(11)可知，在已知OD的有效路径集中，客流分配模型同时考虑了路径阻抗和换乘次数。路径的客流分配规则是：有效路径集中所有路径的客流分配比例之和为1；式(11)同时考虑路径阻抗和λ，tz、λ大的路径被乘客选择的概率较小；tz、λ小的路径被乘客选择的概率较高。

2 轨道交通网络客流分布预测算例

基于式(1)～(11)，以深圳地铁1号线、2号线、3号线、5号线、11号线为例进行客流分布计算。

2016年7月某工作日深圳地铁自动售票系统中的1号线、2号线、3号线、5号线、11号线的单位时间最大断面客流(列车在1 h内某方向运送的最大客流量)数据如表1所示。由表1可知：11号线为近期开通的线路，所以客流偏少，初始分配比例小。

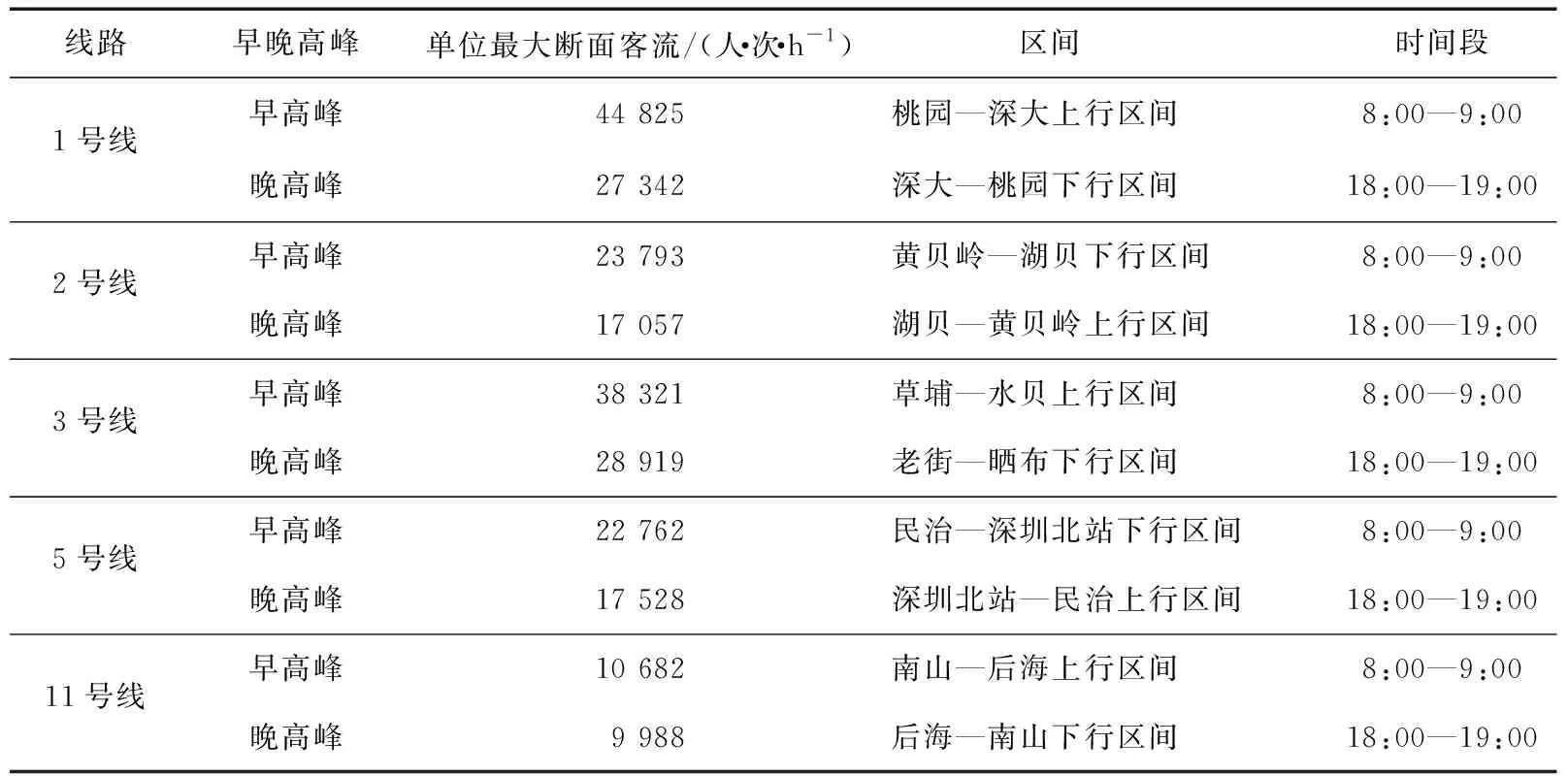
表1 11号线开通后各线路小时最大断面客流

11号线开通后增加了换乘站，各相关OD路径的换乘次数n发生了相应的变化，如前海湾站、车公庙站、福田站、后海站都增加了换乘次数。根据式(9)对λ进行调整，λ调整前后各线路日客运量的变化如表2所示。由表2可知：λ调整后，11号线日客运量达20.61万人·次，客运量明显增加。全网日客运量达到324.75万人·次。各线路客流增幅与实际运营中的客流特征相符。

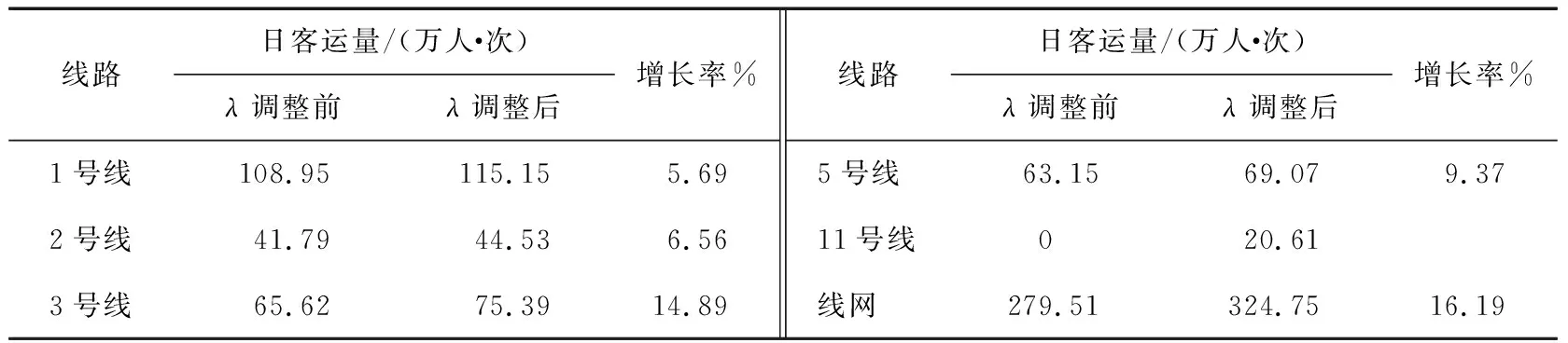
表2 λ调整前后各线路及线网的日客运量对比

客流增长的主要原因是随着深圳地铁11号线的开通，深圳市轨道交通路网串联起福田、前海、宝安中心等多个关键产业集聚区域，增强了线网的连通性。随着11号线运营时间的增加，新线车站附近将形成新的人口及岗位聚集圈，原有的土地利用性质和交通平衡状态将会被打破，这将进一步增加11号线自身的客流量，进而使得线网客运总量增加。

11号线开通前后各线路的客流强度(客流量除以运营里程)如表3所示。

由表3可知：11号线开通后，各线路的客流强度都有所增加，线路的利用率得到了一定程度的提升。3号线的客流强度增长率最大，为14.38%，客流强度达1.83万人·次/(km·d)，说明3号线的客流强度受11号线的影响较大。1号线的客流强度增加了5.58%，说明11号线的接入促使1号线的利用率进一步提高。整个线网总客流强度下降较为明显，主要原因是11号线的客流较少，自身客流还处在培养阶段，降低了整个线网的客流强度。

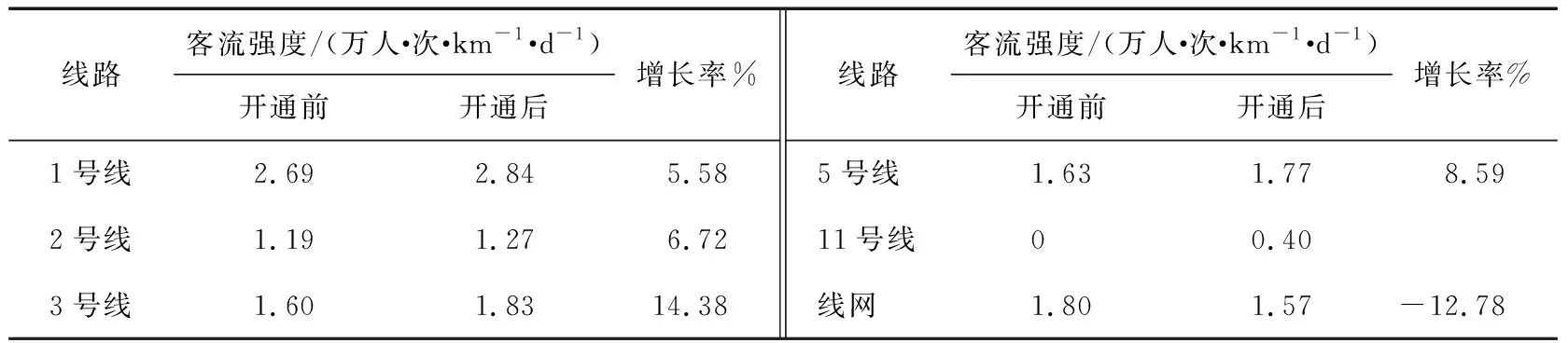
表3 11号线开通前后各线路及线网的客流强度对比

结合表1及式(9)～(11)可得11号线接入后各既有线路及线网的λ变化情况，如表4所示。

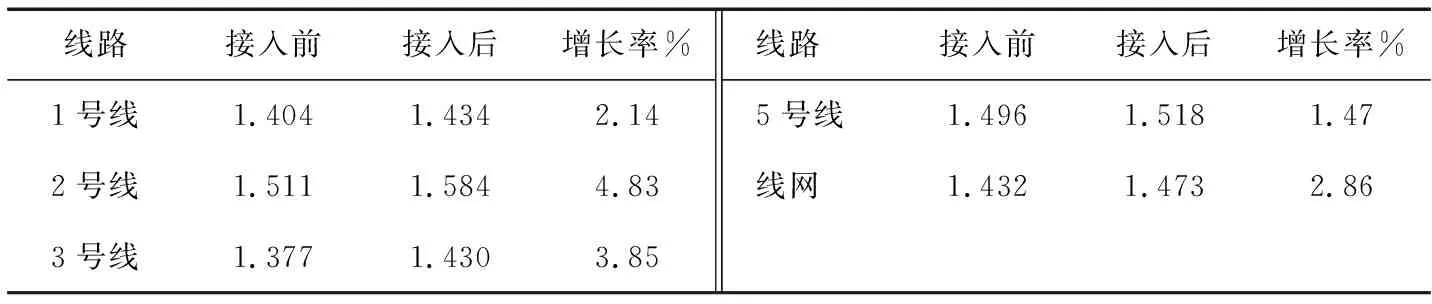
表4 11号线开通前后各线路及线网的λ

由表4可知：11号线开通后，1号线、2号线、3号线、5号线的λ分别提升2.14%、4.83%、3.85%、1.47%，整个线网的λ提升2.86%，说明11号线开通后使得线网中的换乘客流增大，乘客在出行过程中可以通过换乘到达更多的目的地，路网的连通性得到了进一步增强。11号线与1号线、2号线、3号线、5号线都交叉衔接，其中后海站和车公庙站由中间站变为换乘站。因此，11号线的开通增加了乘客出行的可选路径，进而提升了各个线路的λ。

3 结论

本文通过设立乘客综合出行阻抗函数，基于各路径的效用，结合有效路径集的搜索与筛选，构建基于时间阻抗的多路径客流分布模型，并设立换乘惩罚系数对不同路径的客流分配进行合理修正。以深圳地铁1号线、2号线、3号线、5号线、11号线的运营为例进行客流分析，新开通的11号线使得各个线路中的换乘客流有不同程度的增大，增加了乘客出行的可选路径，且11号线车站附近形成新的人口及岗位聚集圈，进一步增加了11号线自身的客流，使得线网客运总量增加，与实际运营中的客流特征相符，进一步验证了本文提出的基于时间阻抗的多路径网络客流分布模型的适用性与有效性。