规则波下刚性植物根茎对边界层最大剪切力特性影响研究

李勰，陈杰,2,3,4*，蒋昌波,2,3,4，姚震，罗元拼，罗婉娇

( 1. 长沙理工大学 水利与环境工程学院，湖南 长沙 410114；2. 洞庭湖水环境治理与生态修复湖南省重点实验室，湖南 长沙 410114；3. 水沙科学与水灾害防治湖南省重点实验室，湖南 长沙 410114；4. 湖南省环境保护河湖疏浚污染控制工程技术中心，湖南 长沙 410114)

1 引言

近岸植物与波浪的相互作用一直是海岸研究领域的热点[1-4]。以红树林为代表的刚性植物近岸消波减浪效果显著[5]，其作为一种新型生态屏障，可起到保护海岸的作用。

许多学者开展了以概化模型模拟近岸植物的研究工作，包括数值模拟[6-7]和实验研究。在实验方面，起初学者们多以立体圆柱来模拟刚性植物，如Dalrymple等[8]忽略植物的部分结构特性，以垂直圆柱模拟植物，对规则波下的沿程能量损失做了研究。在此基础上，部分学者考虑到植物结构上的差异性，以不同的模型模拟植物的根、茎、叶。如Husrin等[9]以真实植物根和茎的刚性模型探究了孤立波下红树林的消波特性。但这些学者只考虑了单独的根、茎、叶对波浪的影响，而忽略了根茎叶之间的配合，三者组合共同对波浪的影响。所以，一些学者优化了实验及实验模型，进一步考虑了植物根、茎、叶组合对波浪的影响[10]以及单株和簇状植物不同的消波特性[11]。但前人的研究大多是分析了波浪的波高[5]、流速[12]、波能衰减[8]等特性，而对波浪经过植物带的过程中沿程剪切力变化的分析很少。

底部剪切力是引起泥沙输运而导致泥沙淤积的主要动力，波浪作用下的泥沙运动已有许多学者[13-15]研究，对于波浪剪切力[16-20]研究工作也已经开展。在波浪传播至红树林时，大量刚性植物的存在会引起波浪剪切力的变化，国内外已开展了一些研究工作[21-22]。红树林根系发达，专门针对刚性植物根茎结构对波浪剪切力的影响，还有待进一步研究。因此，为弥补现有研究不足，设计了根茎定量概化植物模型，分析刚性植物的根、茎对于规则波下边界层最大剪切力特性的影响。

2 实验设置

实验在长沙理工大学长40.0 m、高0.8 m、宽0.5 m波浪水槽中进行。图1给出实验布置情况，水槽右侧设置了消能坡，消除波浪反射的干扰，左侧设有推板式造波机。水槽中分别设置了编号为G1至G8的浪高仪。2.0 m长的植物模型带设置在水槽中部。

图1 实验布置（单位：m）Fig. 1 Sketch of experment (unit：m)

如图2a和图2b所示，实验设计了变态比尺红树林模型，横向比尺为8∶39，竖向比尺为1∶10。茎高45.0 cm，采用直径2.0 cm的空心有机玻璃圆柱进行模拟。根高14.1 cm，采用直径0.8 cm的空心有机玻璃圆柱进行模拟，有机玻璃圆管动态弹性模量E动=4.35×109N/m2、静态弹性模量E静=3.15×109N/m2。由于树根根须数量、根须直径、对底面投影面积等几何因素非常复杂，对植物树根部分仅做概化模型，且该模型材料，在波浪作用下不会产生变形，可以较好地模拟植物树干部分。如图2d所示在底部采用有机玻璃底板来固定植物模型，底板尺寸长×宽×高为200.0 cm ×49.5 cm×0.8 cm。单个植物模型根群直径为10.0 cm，模型横向边距为2.6 cm，间距为3.2 cm；纵向边距为1.975 cm，间距为1.85 cm。

如表1所示，实验采用规则波为入射波，考虑了两种水深h、4种波高H和4种周期T。模型分别采用根茎组合（如图2b所示）、单独根（图2b中去掉长茎即为单独根模型）两种植物模型型式。

表1 实验工况Table 1 Expermental cases

图2 植物模型Fig. 2 Plant models

3 理论分析

对于黏性很小的流体或大雷诺数的流体运动，黏性影响主要限于边界层，在边界层内存在着很大的速度梯度和相应的剪切力。针对此次试验，结合边界层理论和前人的试验经验，可将整个植物带根群视为边界层[12]。故在无植物带水流中，边界层最大剪切力的位置在底床附近；而含植物带水流中，边界层最大剪切力出现在植物带根群顶部附近。

Jonsson[22]在总结前人研究工作基础上，对波浪底部边界层作了较全面的探讨，提出波浪作用下边界层最大剪切力τm可由下式计算：式中，ρ为流体密度，取1 000 kg/m3；fw为波浪底摩阻系数；um为近底波浪质点水平速度的最大值。层流边界层下的波浪摩阻系数计算式如下：

式中，雷诺数Re计算如下：

式中，μ为水的黏滞系数，实验室温度为20℃，取1.01×10-6kPa·s。

底部水质点最大运动振幅am可由下式计算：

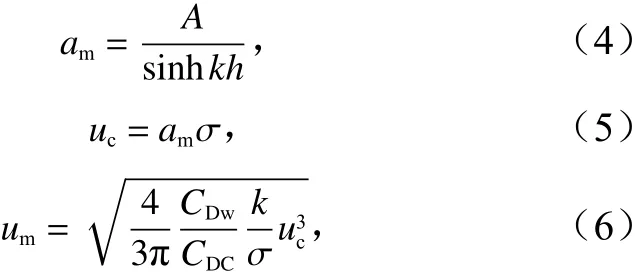
式中，A为振幅，取A=H/2；H为波高；h为水深；k为波数；σ为圆频率；CDW是瞬时阻力系数；CDC是时均阻力系数，比值取为1.0[21]。

式（5）是基于微幅波理论计算的近底质点水平速度，式（6）则是由Luhar等[12]基于含植物带的规则波，经过推导，得出的在植物带中边界层流速的计算公式。

Jonsson[22]给出波浪的边界层从层流状态进入紊流状态的判断依据为Re≥1.26×104。

图3 给出了G3至G7位置的雷诺数计算结果，图中显示所有工况下边界层雷诺数均满足Jonsson[22]给出的判别式，故边界层处于层流状态。

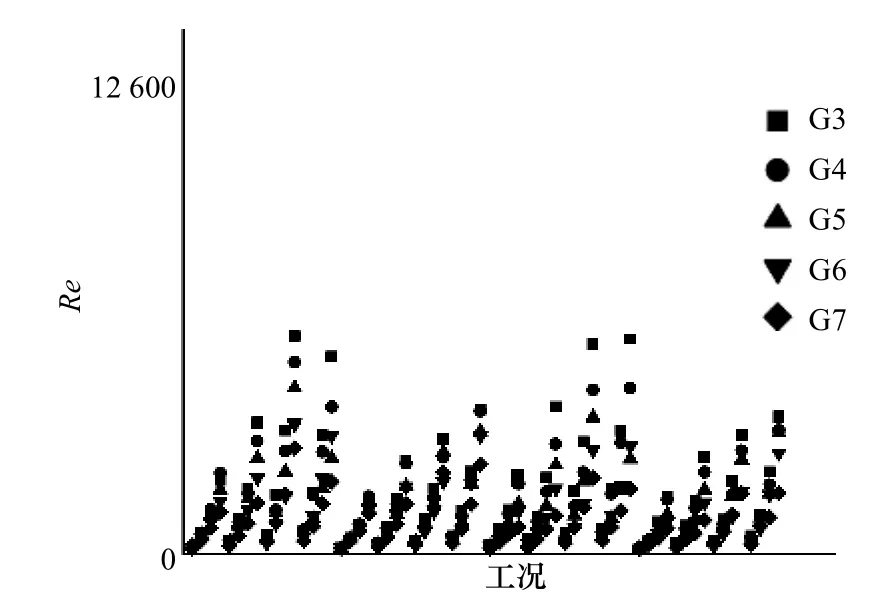
图3 雷诺数计算结果Fig. 3 Reynolds number calculation results

边界层最大剪切力可由Jonsson[22]和Luhar等[12]公式计算得到，其中影响边界层最大剪切力的变量是波高H。植物能够引起波浪的波高衰减，已经在很多研究中证明。因而以波高为主要影响因素，来探讨刚性植物对规则波下边界层最大剪切力特性的影响。

4 结果分析

4.1 剪切力沿程变化分析

如图1所示，以G1浪高仪处为原点，沿流向方向为x轴正方向，沿水流正向设计了15株植物模型，沿水流垂向设计了4株植物，共计植物60株，分析图中植物模型仅为植物带位置示意，植物个数以图1为准。G1与G2浪高仪用于验证入射波波形，G8浪高仪用于分析数据时分离反射波，G3浪高仪放置在植物带前0.2 m处，用来测量进入植物带前波浪的波高数据。沿程共设置了5个断面，分别为G3、G4、G5、G6和G7。为更直观地体现植物模型对规则波剪切力的影响，对边界层最大剪切力相对衰减比例τi/τ0在沿程5个断面的变化进行分析。其中，τ0为基于入射波高所计算的剪切力，τi为特定断面的剪切力。

图4 a至图4h给出单独根模型下剪切力的沿程变化情况。从总体上看，边界层最大剪切力τm的衰减效果随入射波高H的增大而增大。在波浪开始进入植物带时，波速较大，在刚接触会产生较大的紊动效应，导致剪切力会有一定幅度的上涨。当h=30 cm时，在x=4.3 m和x=4.9 m位置，边界层最大剪切力会有一定幅度的增大，且当T=1.9 s时，在x=6.1 m位置，也出现了边界层最大剪切力变大的情况。而当h=35 cm时，变大位置基本上后移到了x=5.5 m或x=6.1 m处，而在部分工况下，出现了明显的边界层效应；在x=6.7 m位置，会出现边界层最大剪切力衰减强度的回升。在单独根模型下，波浪在穿过植物带后，x=6.7 m位置的τi/τ0范围是0.46～0.85，平均为0.67。

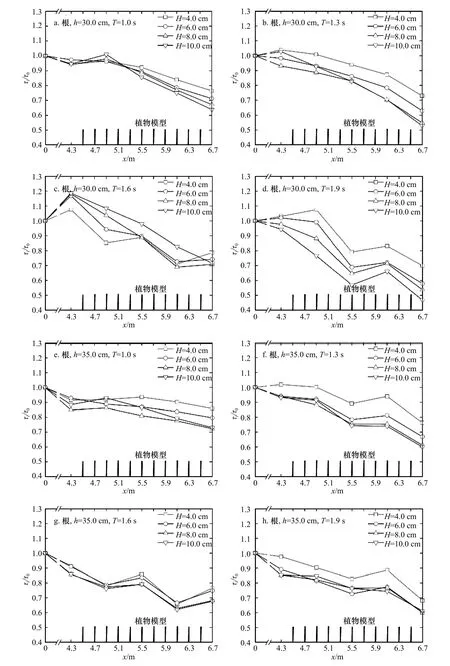
图4 单独根模型剪切力沿程衰减规律Fig. 4 The variation of shear force attenuation along the way with roots alone

图5a至图5h给出根茎模型下边界层最大剪切力的沿程变化情况。图5a至图5c中，边界层最大剪切力τm初始有些许增加，随后急剧下降。图5d至图5f中边界层最大剪切力τm上涨后移到了x=6.1 m位置，在最后一段，会有一个快速的下降。图5g和图5h除了在植物带中出现了上涨情况外，在最后位置也出现了上涨。对比单独根模型实验结果，总体上，剪切力的衰减效果随入射波高的增大而增大，上涨的规律也与根模型类似。根茎模型对剪切力的消减效果是强于根模型的，x=6.7 m位置的τi/τ0范围由0.46～0.85减小至0.46～0.76，综合所有工况计算得到x=6.7 m位置的τi/τ0的平均值，可发现平均值由根模型的0.67下降至根茎模型的0.58。由此可见，茎有助于根群减小底部剪切力。

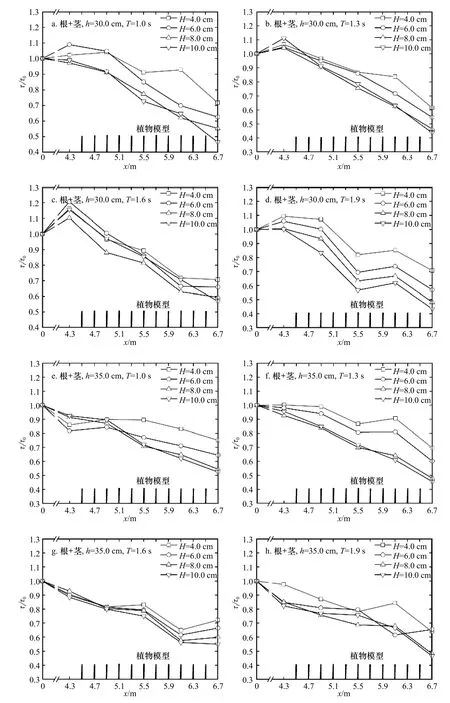
图5 根+茎模型影响下的剪切力沿程衰减规律Fig. 5 The variation of shear force attenuation along the way with roots and stems

4.2 剪切力衰减系数变化分析

为了更好地分析边界层最大剪切力在不同模型及不同工况下的变化规律，定义一个剪切力衰减系数K，计算式如下：

式中，τ6和τ3分别是G6和G3断面的剪切力值。

图6 给出式（7）计算得到边界层最大剪切力消减系数随波高的变化规律。其中图6a和图6b是根模型的边界层最大剪切力消减系数随波高的变化图。从图中可以看出，虽然有部分区域由于水流的紊流效应，消减系数会有降低的趋势，但整体上看消减系数还是随入射波高的增大而增大。T=1.3 s和1.9 s时的消减系数时大于T=1.0 s和1.6 s。图6c和图6d是根茎模型的边界层最大剪切力消减系数随波高的变化图。消减系数也是随入射波高的增大而增大，且根茎模型的消减系数整体略大于单独根模型的消减系数。同样于根模型T=1.3 s和1.9 s时的消减系数时大于T=1.0 s和1.6 s。根茎组合模型消减系数范围为0.12～0.61，单独根模型消减系数范围为0.06～0.51。

4.3 剪切力消减系数与水动力因素、植物因素之间的关系

波浪传播过程中的边界层最大剪切力变化与诸多因素有关。目前学者主要将其分为两类：水动力因素和植物因素[23]。本实验中，影响规则波与植物相互作用的水动力因素包括入射波高H、周期T、水深h、波长L等，影响其规律的植物因素包括：植物高度hv、植被区沿流线长度B、淹没体积Vv。因而剪切力消减系数与要素之间存在以下关系：

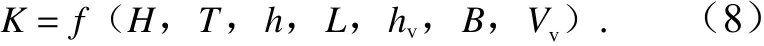
将式（9）中的参数无量纲化得到式（10）

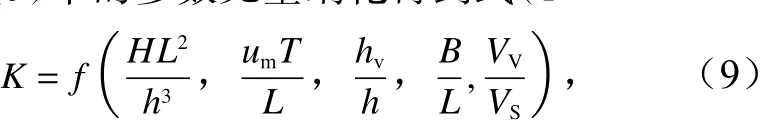
式中，HL2/h3为厄塞尔数，表示流体层中长的表面重力波的非线性程度；umT/L为KC数，表示黏性力相对惯性力之间的关系；hv/h为淹没度，从垂向方面考虑植物高度与水深的影响；B/L为植被区相对宽度，是从纵向方面考虑植物带长度和波长的影响；Vv/Vs为植被区相对淹没体积，来表示植物相对体积的影响。

为进一步分析式（9）中边界层最大剪切力消减系数K与各影响因子之间的关系，基于单独根和根茎植物模型的实验数据，对式（9）进行多元非线性回归拟合。得到了剪切力消减系数K与厄塞尔数HL2/h3，KC数umT/L、淹没度hv/h、植被区相对宽度B/L、植被区相对淹没体积Vv/Vs之间的关系，结果如式（10）所示。由于受到多个水动力因素和植物因素的影响，植物对边界层最大剪切力的消减机理十分复杂，拟合情况如图7所示，虽然整体数据点和拟合曲线存在部分偏差，但整体呈现幂函数的关系。拟合公式与实验数据之间拟合度达到0.772。其中，实测值与理论值相

差30%的工况有：单独根模型8个（h=35 cm，H=4 cm，T=1 s；h=35 cm，H=8 cm，T=1 s；h=35 cm，H=10 cm，T=1 s；h=35 cm，H=4 cm，T=1.3 s；h=35 cm，H=6 cm，T=1.6 s；h=35 cm，H=8 cm，T=1.6 s；h=35 cm，H=10 cm，T=1.6 s；h=35 cm，H=4 cm，T=1.9 s）。根+茎模型4个（h=35 cm，H=4 cm，T=1 s；h=35 cm，H=4 cm，T=1.6 s；h=35 cm，H=6 cm，T=1.6 s；h=35 cm，H=6 cm，T=1.9 s）。综合来看，误差较大的点均为水深h为35 cm的工况，故此拟合公式更适用于水深较浅的情况。且单独根模型的误差点多于根+茎模型，也从侧面体现了茎有助于根群减小波浪底部剪切力。式（10）体现了消减系数变化与水动力因素和植物因素均存在着物理联系，其中，消减系数K与厄塞尔数HL2/h3、植被区相对宽度B/L呈负相关，与KC数umT/L、淹没度hv/h，植被区相对淹没体积Vv/Vs呈正相关。

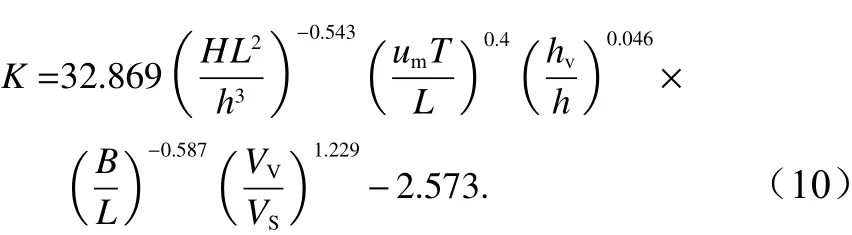
5 结论

本实验研究探究的主要内容是规则波经过含植物带水流时，位于边界层的最大剪切力是如何变化的。着重讨论植物模型对于边界层最大剪切力的影响特性，为以后学者研究红树林带边界层最大剪切力提供理论依据。通过概化植物模型实验，探究了单独根、根茎共同作用下近岸刚性植物对规则波沿程剪切力衰减特性及衰减系数变化规律，研究发现边界层最大剪切力的衰减系数的范围为0.06～0.61，说明红树林是能够影响到波浪边界层最大剪切力，且能使其减小。规则波下边界层最大剪切力衰减效果随波高的增大而增大，且红树林的茎有助于根群减小底部剪切力。植物根茎模型对边界层最大剪切力变化特性的影响与淹没度、植被区相对淹没体积、植被区相对宽度、厄塞尔数及KC数均有关系。本实验仅考虑含植物带水流边界层最大剪切力的理论研究，研究有助于进一步探究以红树林为代表的近岸刚性植物对波浪边界层剪切力的特性影响，为合理利用近岸刚性植物减少海岸带泥沙淤积、抵御海浪侵蚀提供一定指导。