基于演化算符的南海海面高度异常中长期统计预报

李美莲，金慕君，纪增华，李威,2*，梁康壮

( 1. 天津大学 海洋科学与技术学院，天津 300072；2. 天津市海洋气象重点实验室，天津 300074)

1 引言

水下移动平台在执行任务时，通常要在水下潜行3个月左右，出于隐蔽考虑，需要提前预知移动平台周围一定范围之内的海洋环境信息，而移动平台自身所携带的观测设备只能观测到航迹上当前的海洋环境信息，故需要海洋数值预报系统[1]为其提供时效为1～3个月左右海洋数值预测预报结果，作为海洋环境信息保障的支撑。

当前，基于海洋数值模式的海洋预测技术受对应的气象驱动场预报时效只有10 d的限制，难以提供准确的10 d以上的数值预报产品。为了获得10 d以上海洋环境数值预报结果，美国海军采用将10 d的气象驱动场预报[2]结果与气候态气象驱动场结果加权平均作为气象驱动场的方式（在10～30 d的预报时段，其气象驱动场预报逐渐松弛到气候态），实现了10～30 d的海洋环境趋势预测； 在最新的延伸期海洋要素预报系统中，美国海军特别采用了高分辨率的大气-海洋-陆地-海冰-海浪耦合模式[3]（Earth System Prediction Capability, ESPC）进行预报，并采用了弱耦合数据同化方法提升预报准确度 ，实现了高分辨率（大气水平19 km、垂向60层，海洋水平（1/25）°、垂向41层，海冰（1/25）°，海浪（1/8）°）的16 d预报，以及较低分辨率（大气水平37 km、垂向60层，海洋水平（1/12）°、垂向41层，海冰（1/12）°，海浪（1/4）°）的45 d预报。在预报中，数值模式运行于3 000核的高性能计算平台，且每个模型天需要计算1 h的时间。另外，欧洲中期天气预报中心（European Centre for Medium-Range Weather Forecasts, ECMWF）一直以来也是借助超级计算机和最先进的同化技术来开展较长时间尺度的数值大气和海洋分析预报业务。以上预报方式均需要在高性能计算平台上运行高分辨率的海洋预报模式，运算量巨大，无法在一般计算平台上运行。

相对大气而言，海洋具有较大的运动惯性，这使得采用统计学方法通过对历史资料分析建模，完成海洋要素预报成为可能。尤其是随着近年来卫星资料的积累，为统计预报方法提供了充分的数据支撑。传统统计方法通常采用线性模型[4]。例如，对单一站点的观测数据或经过正则相关分析（Canonical Correlation Analysis，CCA）和经验正交函数（Empirical Orthogonal Function，EOF）分解处理后的时间模态进行线性回归[5-6]。针对海洋要素的非线性物理过程，采用线性方法与非线性方法结合的方法也有许多研究。Niedzielski和Kosek[7]利用多项式谐波模型的外推与LS（Leastsquare）残差的自回归方法，预测赤道太平洋的海面高度异常。Ubilava和Helmers[8]指出，平滑过渡自回归模型（Smooth Transition Autoregressive，STAR）预测海面温度异常的效果优于线性自回归模型。随着预报时段的延长，海洋各要素变化逐渐以非线性过程为主导。Garcia-Gorriz和Garcia-Sanchez[9]采用人工神经网络方法，利用气象数据预报海面温度，可以很好地对海温季节变化及年际变化进行预测，相关系数高达0.99。孙文等[10]利用卫星测高数据得到海平面异常序列，发现神经网络的长期预报效果较好。由李晓静[11]提出的一种基于多重分形与概率神经网络相结合的海温预测方法，对厄尔尼诺综合区平均海温进行1～3个月的预报，取得了较好的结果。但以上方法要么没有保持小运算量，要么没有考虑空间相关性，也没有实现对以天平均为单位的海洋时空多尺度过程进行预测。

鉴于海水在动力热力上具有较大的惯性，海洋内区有其自身的演化规律，在不考虑外强迫的前提下，可以通过对资料的分析构建统计预测方法。本文旨在利用历史卫星遥感资料构建海洋状态变量中长期演化矩阵，研制一种全新的、小型化的海洋中长期统计预测方法和模型，有效降低预测所需的运算量，大幅提高预测预报的时效，并开展数值试验验证该方法的有效性。

2 数据介绍

在构建预报模型、开展预报试验和效果检验过程中，所采用的数据来自法国CLS（Collecte Localisation Satellites）公司1993年至2017年的逐日全球多源卫星观测海面高度异常（Sea Surface Height Anomaly，SSHa）水平空间分辨率为0.25°的网格化融合资料[12]。该数据集由多颗卫星高度计海面高度异常数据融合而成，融合而成的平均值可以在某些区域或期间提供比任何单独的遥感产品更可靠的估计，具有较高的可信度和准确性。

3 方法介绍

不失一般性，假设海洋数值模式为

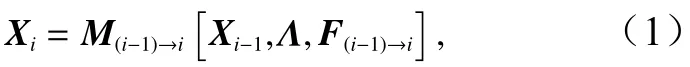
式中，Xi-1为第 (i-1)时 刻的状态变量；Xi为 第i时刻的状态变量； F(i-1)→i为 第 (i-1)时 刻到第i时刻的外界强迫场，包括上边界气象驱动场、底边界条件和侧向开边界条件；Λ为模式参数，包含了模式的偏差；M(i-1)→i[·]为从时刻 (i-1)到 时刻i的演化算符，可以是线性的也可以是非线性的。

模式状态变量Xi可 以表示为累年日平均气候态结果和相对于气候态的距平结果之和的形式，即同样的，外界强迫场也可以表示为能够驱动出气候态结果的气候态外界强迫场和相对于气候态外界强迫场的距平场于是，上述海洋数值模式可以表示为

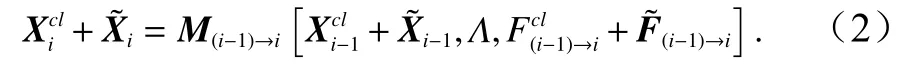
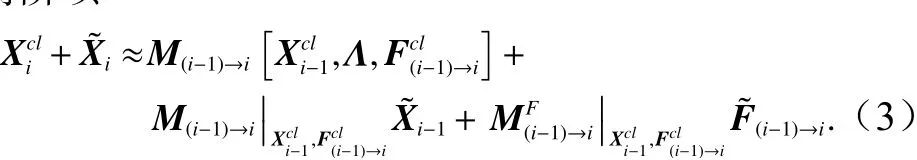
按照上述定义，累年日平均气候态状态变量与气候态外界强迫场满足方程

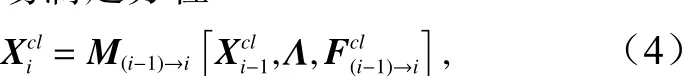
于是我们可以获得距平场满足的方程为

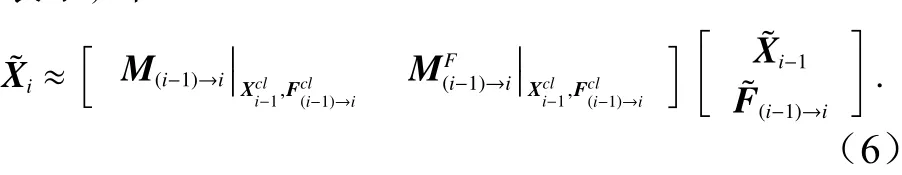
利用大量的逐日的卫星遥感海面高度异常距平结果和对应的气象驱动场与开边界条件等外界强迫场距平结果，可以反推出线性演化算符和具体的做法是上式两端同乘以并取数学期望E{·}，然后两边再同乘以的逆矩阵，即可反推出上述线性演化算符

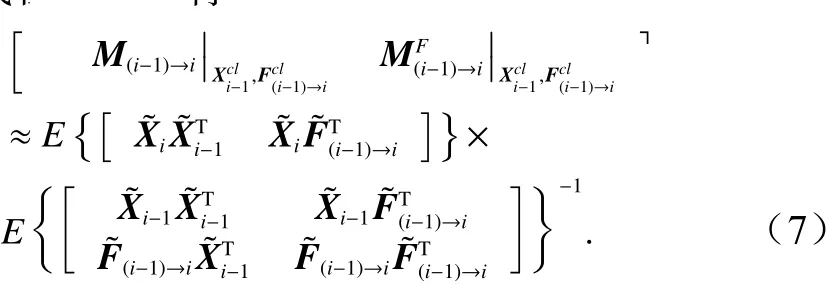
因为未来时刻的外界驱动场与当前海洋状态变量是不相关的，所以我们可以认为和因此，可以得出

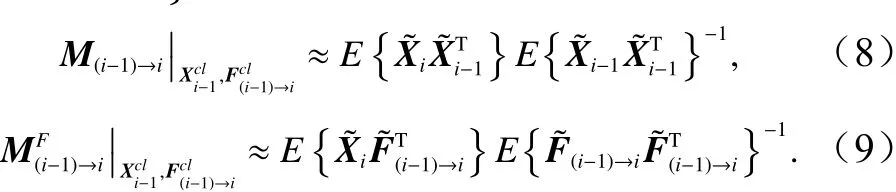
本文拟开展60 d时长的中长期预测，考虑到实际情况下，很难事先得到如此长时效的气象驱动场和开边界条件，因此本文暂不考虑外界强迫项的影响，于是上述距平场的线性演化方程式（5）简化为

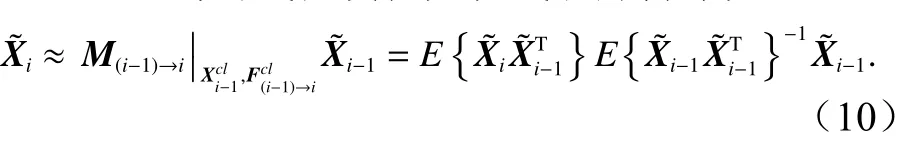
利用上述反推出的线性演化算符，我们可以对距平结果的演化进行计算，但在做真实预报的时候，我们需要进一步叠加累年逐日卫星遥感海面高度异常统计分析气候态结果，以获得最终的海面高度异常场的预报结果。

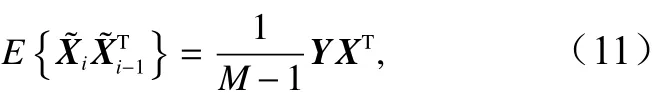
同理，令Y为与第i时刻相对应的历史上的逐日的卫星遥感海面高度异常距平向量排列成的大矩阵，则有

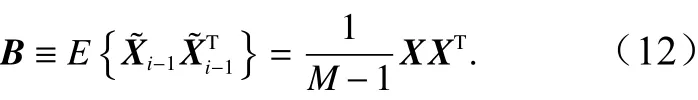
海洋数值模式网格点状态变量个数是极其巨大的，远远多于样本个数，因此用集合样本计算得到的背景场误差协方差矩阵，其特征值数量不会超过样本个数，这样的背景场误差协方差矩阵是不存在逆的，只能对其计算伪逆。对于这样的背景场误差协方差矩阵，可以采用递归最小二乘算法（Recursive Least-Square，RLS）来递归求解逆矩阵，除此之外，也可以采用如下的方法来计算。可以先计算XTX的Jacobi分解

式 中，v˜ 为 正 交 矩 阵；的 特 征 值 构 成 的 对 角阵。显然，分 别 为XXT的 特征 向量和特征值。因此，有X的广义逆矩阵为

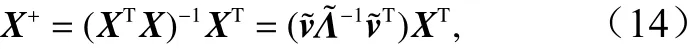
背景误差协方差矩阵的广义逆矩阵可以写为

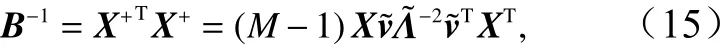
我们可以如下验证所得的广义逆矩阵的正确性

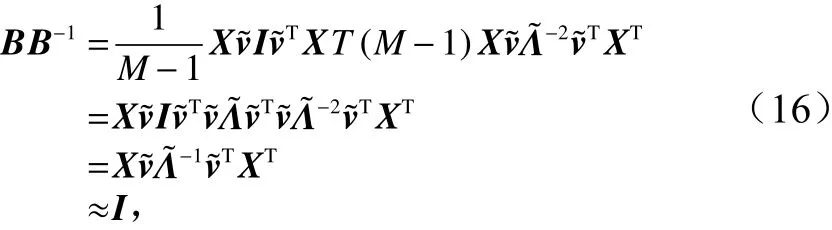
或者

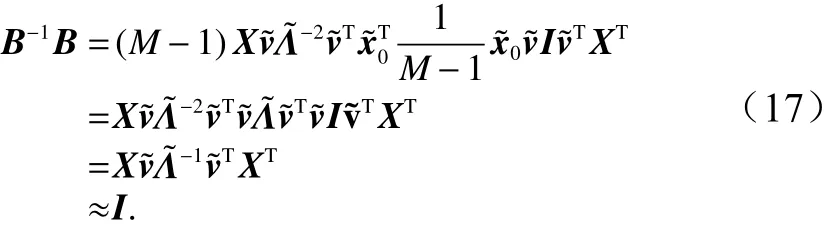
对于任意时间跨度的预报，我们可以利用递推的方法直接表示出从m时刻到n时刻的演化算符：

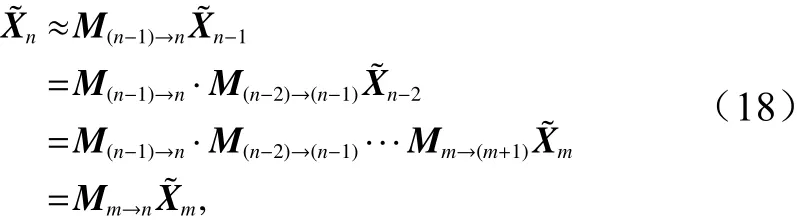
其中定义

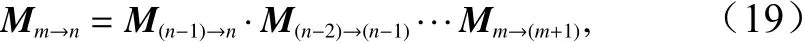
将上式（8）、式（11）、式（12）代入式（18）化简可得：

此外，为进一步减弱由有限样本造成的伪长程相关问题，从而提高起报时刻的预报精度，我们还可以在上述基础上引入Schur乘积[13]进行局地化，令Bnm=式中，ρ表示采用Schur乘积中使用的局地化因子。由式（20）可知

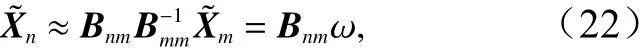
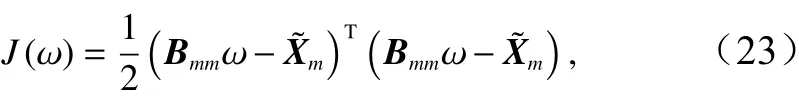
要使J(ω)最小，则计算其梯度方向有

将式（24）放入最优化程序中即可快速算得最优解，进而代入式（22）即可算得第n时刻的预报结果。但由于篇幅所限，本文在以下试验中并未引入Schur乘积进行局地化，在未来的工作中将对此作进一步研究，提升起报时刻的预测精度。

4 演化算符预报试验和效果检验

4.1 预报试验设置

预报试验所用的是“数据介绍”所述卫星遥感海面高度异常产品南海区域的数据。预报流程主要包括4部分：海陆分离、季节信号与非季节信号分离、距平信号的模型预测、预测结果与季节信号结合。

首先通过数据判断陆地与海洋区域并进行标记，然后对历年同月同日的数据作平均，得到累年逐日海面高度异常统计分析数据。之后用历年逐日卫星遥感海面高度异常结果扣除上述累年逐日海面高度异常统计分析结果，获得历年逐日的海面高度异常距平结果，完成季节信号与非季节信号的分离。将所得的海面高度异常距平结果放入基于演化算符的预报模型中，得到预报时长内的逐日海面高度异常距平预测结果。最后将所得的海面高度异常距平预测结果与对应日期的累年逐日海面高度异常统计分析结果相加，即可获得最终的海面高度异常预测结果。

为检验本研究的预报方法的准确性与可行性，将预测所得的海面高度异常预测结果与真实的卫星数据相比较，计算出二者的相关系数与均方根误差（RMSE）[14]。以此可分析基于演化算符的预报方法的预测时长及其相对于其他预测模型的优势。

4.2 惯性预报、气候态预报与基于演化算符的统计预报的相关系数比较

为了证明演化算符的预报方法具有可行性，本研究基于具有统计代表性的数据进行了多次试验模拟，具体如下：利用本研究的统计方法进行2007年1月1日至2010年11月30日共1 429 d的观测预报，每一天预报的时间跨度都以该日为起点往后从1 d取到61 d。

在这1 429次试验中，我们将预报初始时刻与预报时刻历年同月同日的卫星遥感海面高度异常距平数据分别排列成大矩阵Xm和Xn。矩阵中各列代表不同年份的数据，即矩阵的列数代表集合的样本数；而每一列的各行则是空间有效点的数据。由此构建演化算符矩阵，并进行运算得出预报结果，然后计算出预测值与真实值之间的相关系数。

为与传统方法进行比较，我们将历年同时刻的历史数据的平均值作为该时刻的预报值进行气候态预报；将初始时刻的距平场作为预报时刻的距平场再加上预报时刻的气候态平均场即可获得惯性预报的结果。然后按相同的方法计算出气候态预报以及传统惯性预报的相关系数，并将三者结果进行对比。

图1 为本研究方法的预报、惯性预报以及气候态预报与真实场分别计算其相关系数的比较。从图1中可以看出，气候态预报的相关系数稳定在0.5左右，在约30 d内明显低于基于演化算符的预报方法和惯性预报方法计算出的相关系数，在约30 d后其相关系数大于惯性预报的相关系数。而演化算符预报与惯性预报相比，虽然惯性预报在前15 d内的相关系数较大，与真实场的相关程度更大，但随着预报时长的增加，惯性预报与真实值的相关系数发生了较大幅度的下降，相关性逐渐减弱。而本文所采用的基于演化算符的统计预报方法虽然在短时预报中无法与惯性预报相比较，但对于中长期的预报有着自己的明显优势，在预报时长为20～60 d的中长期预报中，基于演化算符的统计预报方法的相关系数较传统惯性预报更大，与真实值的相关性强。

图1 3种预报方法与真实值的相关系数Fig. 1 Correlation coefficients between three forecasting methods and real values

4.3 惯性预报、气候态预报与基于演化算符的统计预报的均方根误差比较

为了进一步比较基于演化算符的统计预报方法与传统惯性预报方法以及气候态预报方法的准确性，用上述相同的样本分别计算演化算符预报、惯性预报以及气候态预报与真实场的RMSE，并作图进行比较，如图2所示：气候态预报所求出的RMSE在0.08 m以上，其数值在任意时效长度内都高于演化算符预报和惯性预报的RMSE数值，相较于其他两种方法准确性较低。对于惯性预报而言，其RMSE数值随预报时效的增长而迅速增大。虽然在短期海洋预报中，惯性预报的准确性高于演化算符预报，但当预报时效超过15 d时，惯性预报的RMSE超过演化算符预报并逐渐升高至0.08 m以上，趋近气候态预报的RMSE曲线。而演化算符预报在时效长达20～60 d时RMSE在三者中最小，缓慢升高至0.06 m与0.07 m之间，所以基于演化算符的预报方法在中长期预报中准确度最高。

综合考虑，当预报时长为20～60 d时，基于演化算符的统计预报方法所得出的预报结果与真实值的RMSE最小，相关系数最大，是可信程度最高的中长期海洋预报方法。

4.4 惯性预报、气候态预报与基于演化算符的统计预报的预报图比较

为了能够更加直观地看出3种方法的预测精准程度，本文分别采用基于演化算符的统计预报、惯性预报以及气候态预报方法进行了同上4.2节所述的1 429次实验，利用所得的预测数据绘制了预报图，并将预报结果与卫星遥感资料相对比，验证该方法的准确性。

在这里特举通过3种方法分别以2010年11月1日为预测起始点预测同年12月1日的预测结果为例，如图3所示。

从图3中可以看出，基于演化算符的统计预报方法对于中长期的预报有着明显的优势。相对于惯性预报以及气候态预报而言，基于演化算符的统计预报方法预测结果更加接近2010年12月1日的真实场。

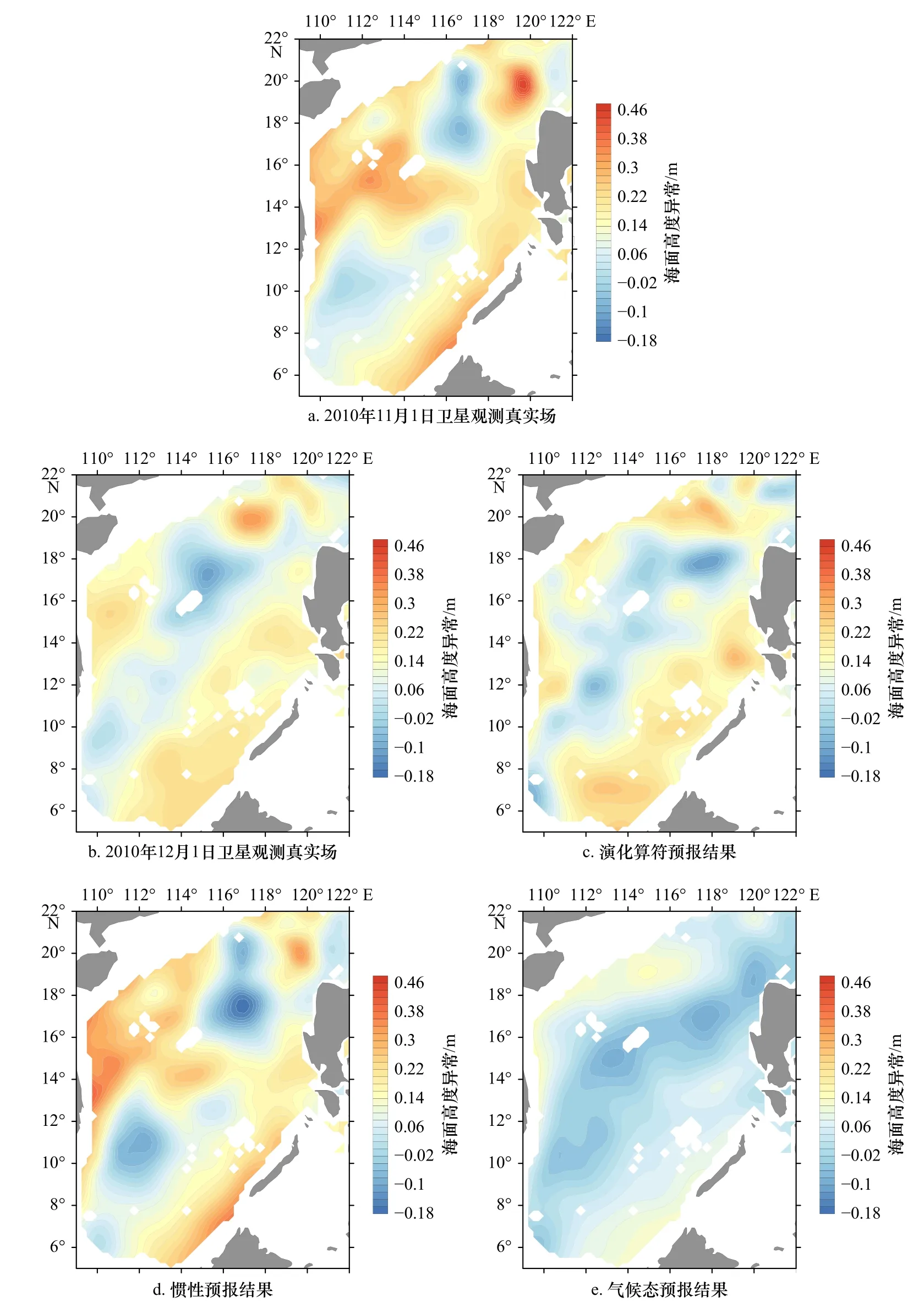
图3 海面高度异常统计预报结果与卫星观测结果Fig. 3 Statistical prediction results and satellite observation results of sea surface height anomalies

为了更好地看出3种方法对于海洋要素发展趋势的预测，我们将卫星观测的真实值与预报结果分别与预测起始点（即2010年11月1日）的真实值相减，计算出增量，如图4所示。通过图4的对比可以看出，相对于惯性预报与气候态预报而言，基于演化算符的统计预报方法的增量与真实值的增量更为接近。通过增量的绘图与观察，进一步验证了本方法能准确预报SSHa增量，可以在一定程度上把握海洋要素的发展趋势。

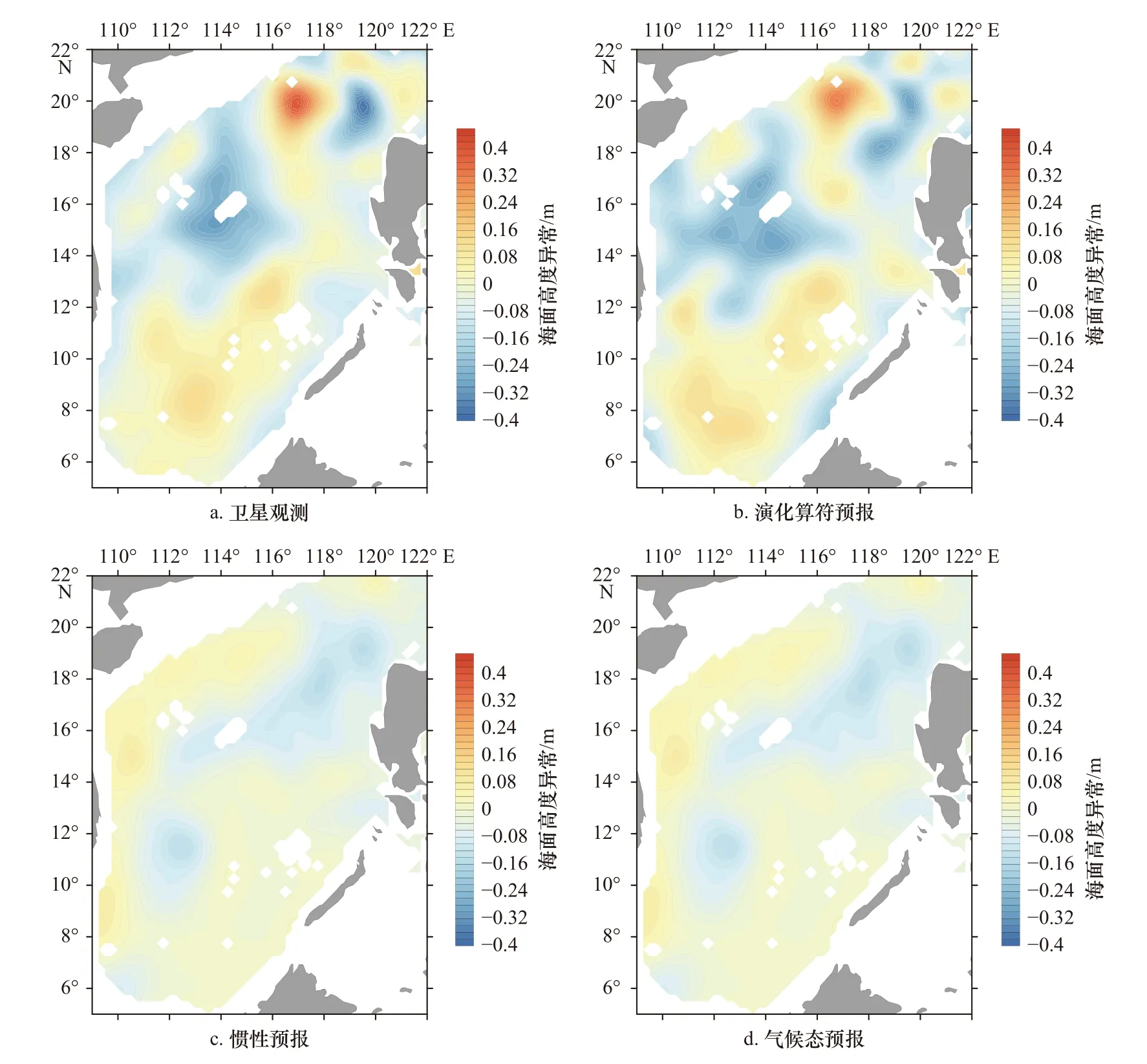
图4 海面高度异常预测结果与卫星观测结果相对于预测起始点的增量Fig. 4 The increment of prediction results and satellite observation results relative to the predicted starting point of sea surface height anomaly

4.5 结果检验小结

总的来说，与惯性预报和气候态预报相比，对于15 d以上时效的预报，基于演化算符的统计预报准确度更高，相关性更好，无论在预报时效还是预报精度上都有着绝对优势。传统惯性预报虽然对短时预报有着自己的优势，但对时长为20～60 d的中长期预报却有着明显的不足。基于演化算符的统计预报方法能很好地进行时长长达20～60 d的中长期预报，提供更为精准的预报结果，这是目前传统惯性预报和气候态预报难以达到的。

5 综合预测模型构建与检验

5.1 综合预测模型构建

根据上述结果可以看出，在短期预报中演化算符预报结果在很大程度上敌不过惯性预报。为发挥惯性预报在短期预报中的优势与演化算符预报在中长期预报中的优势，我们采用惯性预报和演化算符预报加权平均的形式来进行预报：以两者的预报方差的倒数为权重，对两者进行加权平均，将惯性预报与演化算符预报的结果进行融合，构建出误差更小的南海海面高度异常中长期统计预测模型，从而使得综合预测模型无论在短期还是中长期都可实现良好的预报效果。这里惯性预报只是对距平场进行惯性预报，这种做法可以有效保留最终结果里的季节信号。对于第tl时刻的预报，令

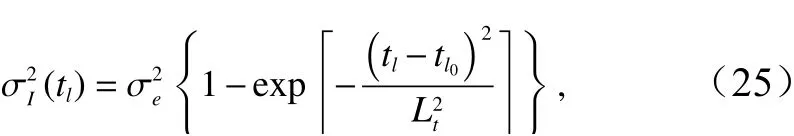
为惯性预报的方差，tl为 预报时效；Lt为衰减时间尺度，经研究发现此处Lt取 21 d曲线拟合效果最好；是惯性预报无限长时间的方差，此处取通过对演化算符预报的方差曲线进行多项式拟合，可以得出演化算符预报的方差表达式为

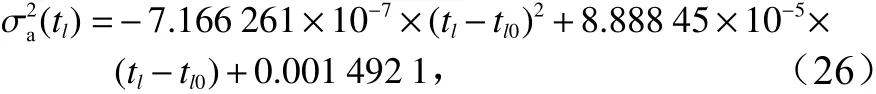
方差曲线的拟合效果如图5。

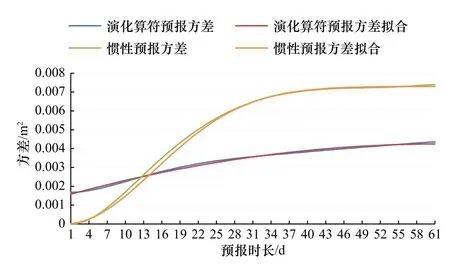
图5 演化算符预报与惯性预报方差的曲线拟合Fig. 5 Curve fitting of evolutionary operator prediction and inertial prediction error

上述方差曲线是基于我们在4.2节所做的1 429次试验的方差的均值，由于试验次数已经具有很强的统计意义，使所得的方差曲线趋于稳定，因此我们通过曲线拟合所得到的权重也具有一定的普适性。

综合考虑惯性预报和演化算符预报，我们可以得出最终的预报为

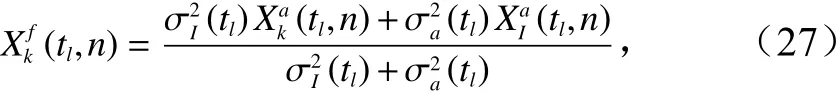
据此将惯性预报与演化算符预报相结合，构建最终的海洋中长期统计预测模型。

5.2 综合预测模型的结果检验

为了证明最终融合的海洋中长期统计预测模型的准确性，本研究基于与上述3种预报所用的相同的数据，运用融合而成的综合模型进行实验模拟，计算出2007年1月1日至2010年11月30日共1 429 d的观测预报，每一天的预测时效长为61 d，计算出预测值与真实值之间的RMSE与相关系数，并将其与未融合的演化算符预报、气候态预报以及传统惯性预报的结果进行对比，得出了以下结果：最终的海洋中长期统计预测模型在整个预报时长上（0～61 d）都明显优于单独的演化算符预报和惯性预报以及气候态预报的结果，表现为RMSE在其中处于最低水平，相关系数在其中处于最高水平图6。由此说明本研究最终的海洋中长期统计预测模型构建的合理性与预报的准确性。

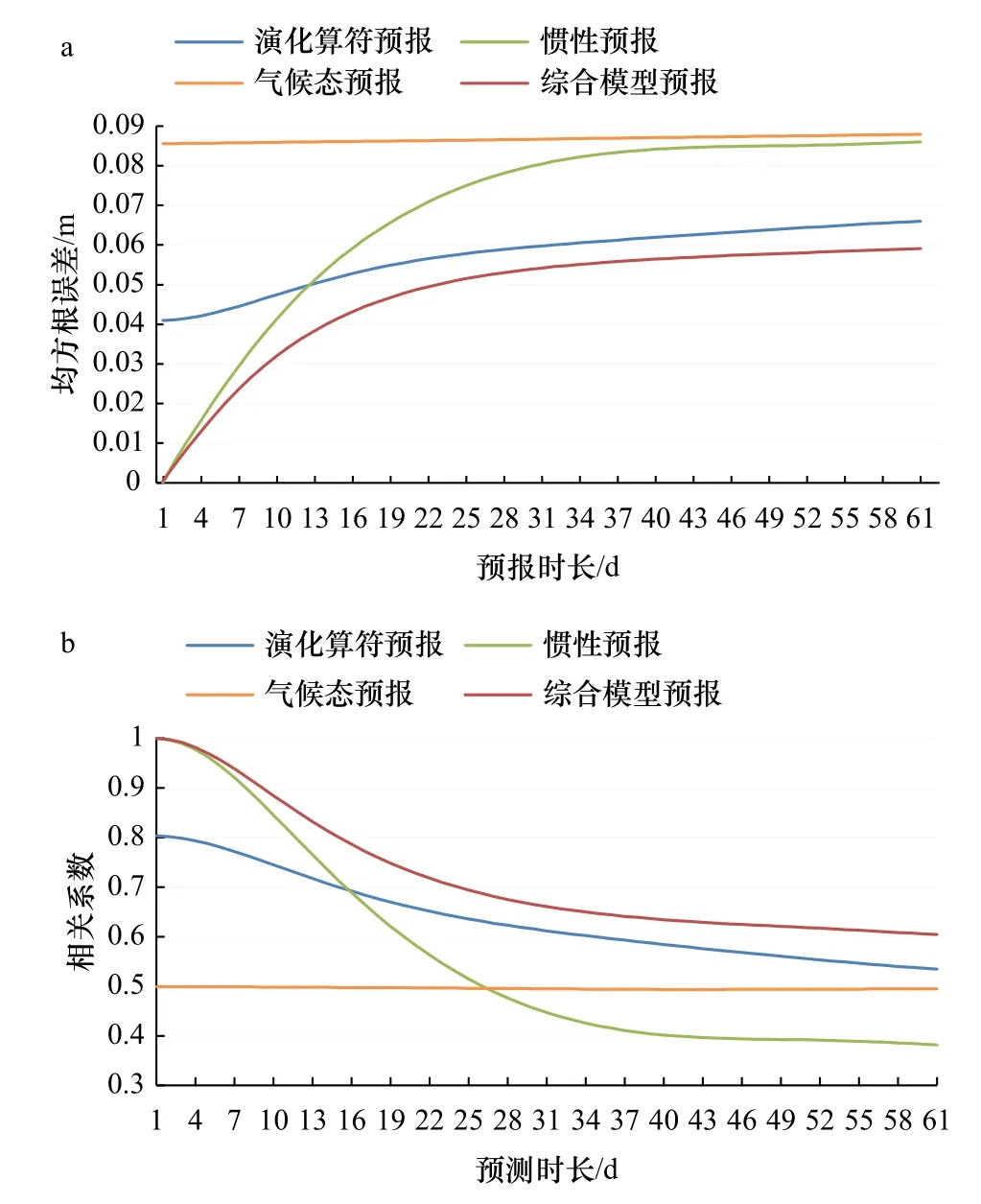
图6 综合模型与3种模型的均方根误差与相关系数对比Fig. 6 Comparison of root mean square error and correlation coefficients between the comprehensive model and the three models

此外，为了更好地看出4种预测方法对于海洋要素发展趋势的预测，本文以选取的断面（图7）上的站点为横坐标，以预测时长（0～61 d）为纵坐标，作出时间-站点图，以此可观察南海区域中波的传播。以2008年7月1日起预测61 d的结果为例，4种预测方法的时间-站点图如图8所示。

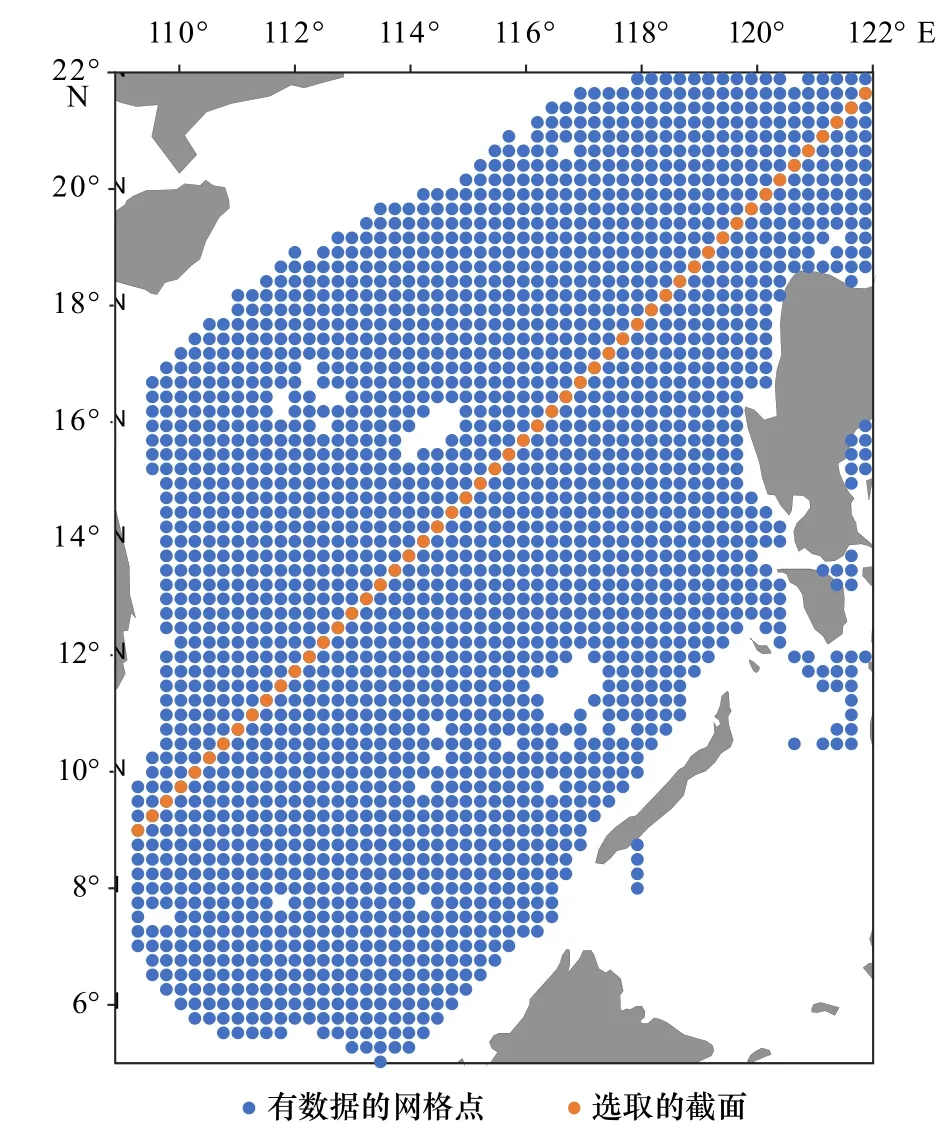
图7 选取的截面Fig. 7 Selected sections

从图8可看出，构建的综合模型与演化算符模型预测的结果相比于惯性预报以及气候态预报更为准确，与真实的观测更为相近。从综合模型预报的时间-站点图可以看出较为明显的波的传播趋势，即波从吕宋海峡向西传播进入南海，但惯性预报与气候态预报对于波的传播趋势预测结果较差。因此，本文构建的综合模型预报能够对海洋要素的发展趋势，如波的传播等，具有良好的预测效果，从而也能反映出综合模型的准确性较高。

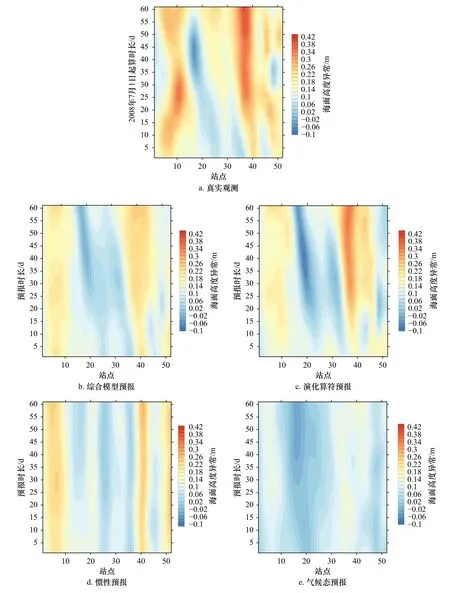
图8 综合模型与3种模型的时间-站点图Fig. 8 Time-to-site diagram of the synthesis model and the three models

综上，可以看出，将演化算符预报与惯性预报进行加权平均融合而成的综合模型无论是短期，还是中长期的预报结果都明显优于单独的演化算符预报、惯性预报以及气候态预报的结果，且能对海洋要素的发展趋势进行较好的预测。

6 结语

本研究采用南海历史卫星遥感海面高度异常资料构建了海面高度异常距平场的演化算符，并结合累年日平均卫星遥感海面高度异常气候态场，实现了小运算量（使用PC机单次60 d预报的时间约为5 min）的南海海面高度异常场的中长期统计预测，预测时效长达60 d。

开展了基于演化算符的南海海面高度异常场的中长期预测试验，将预测结果与真实的卫星遥感海面高度异常资料进行对比，计算相关系数和均方根误差，并与常规的惯性预测和气候态预测结果进行了比较，结果表明，本文的方法能够较为快捷、准确地提供预报时长为20～60 d的中长期预测，优于常规的惯性预测和气候态预测结果。最后，结合惯性预报的短期预报优势和本文基于演化算符方法的中长期预报优势，以两者的预报方差的倒数为权重，对两者进行加权平均，构建出误差更小的南海海面高度异常中长期统计预测模型，并用试验证实了其准确性。

本文实际上采用了历史卫星遥感数据构成集合来估计线性演化矩阵，但由于集合成员不充足（本文试验中集合成员数目为所用不同年份的历史数据的年数，即14～16个），势必会造成伪长程相关，影响预报精度，在未来的研究中，笔者将考虑在算法中通过Schur乘积引入局地化，改善预测效果。

本文并未考虑气象强迫场和开边界条件的作用，尽管如此，本文的方法仍然给出了较好的预测结果，这可能是因为，对于南海这样较深的有层结的水体，在1～2个月的时间尺度上，海洋的内部动力过程占据主导作用，外界强迫尚未来得及显著改变内部运动状态；在未来的研究中，笔者将进一步考虑用历史数据构建与外界强迫相对应的演化矩阵。

正如本文在第3节“方法介绍”中所述，不论原模式状态变量满足的海洋数值模式是线性的还是非线性的，其距平场满足的方程可以近似为线性的，尽管海洋过程满足非线性演化方程，但本文关注于距平场所满足的演化算符，因此，本文能够得到较好的预测结果也表明，在1～2个月的时间尺度上，距平场中的波动和涡旋运动以线性为主；在距平场所满足的方程中，我们实际上略去了高阶项，而这些高阶项恰恰是非线性项，在未来的研究中，我们拟采用人工智能的手段来处理这些非线性项。

需要指出的是，本文的方法还可以应用于卫星遥感海面温度资料的中长期统计预测，甚至可以应用于卫星遥感海面高度异常和卫星遥感海面温度的中长期联合统计预测，将这些海面信息的预测结果进一步采用模块化海洋数据同化系统（Modular Ocean Data Assimilation System，MODAS）[15]或者改进的合成海洋剖面系统（Improved Synthetic Ocean Profile，ISOP）[16]向水下投影，构造出水下的三维温盐场，即可实现水下温度和盐度的中长期统计预测。