西太平洋黑洞涡旋物质输运能力分析
田丰林,杨笑坤,刘潇,何遒,陈戈*
( 1. 中国海洋大学 信息科学与工程学部 海洋技术学院,山东 青岛 266100;2. 青岛海洋科学与技术试点国家实验室 区域海洋动力学与数值模拟功能实验室,山东 青岛 266237)
1 引言
中尺度涡旋是一种海洋中广泛存在,空间尺度从数十千米至数百千米不等,寿命从数十天至数百天不等的旋转水体。根据旋转方向,中尺度涡旋可以分为气旋型(北半球为逆时针)和反气旋型(北半球为顺时针)[1-2],它的运动影响着海洋环流、大规模水体和生物分布,对盐度、热量和其他海水化学元素的混合、输运也非常重要[3-6]。
中尺度涡旋的识别方法可分为欧拉方法和拉格朗日方法。欧拉方法根据瞬时海表面高度或海流瞬时特征来识别涡旋,可以利用卫星高度计数据实现自动化识别全球涡旋[7]。近期的欧拉涡旋识别和追踪方法采用并行计算的方法[3,8-9],大大提高了对全球欧拉涡旋的识别效率。欧拉方法的识别结果会随着参考系的旋转或线性加速而变化,使研究结果的不确定性增加[10]。欧拉方法高估了中尺度涡旋的输运能力[7],在非稳定流场中,不依赖于参考系的拉格朗日拟序结构(Lagrangian Coherent Structures,LCSs)方法能更客观地描述涡旋对水体的输运能力[11]。欧拉涡旋描述短期内物质的输运很有效,但在非稳定流场中,欧拉涡旋边界随流场运动会很快失去连贯性,沿涡旋移动轨迹出现拉伸和成丝的现象;而拉格朗日涡旋可以描述一定时间尺度内涡旋的边界,在时间尺度内,涡旋的边界作为物质屏障可以携带内部的水体运动,并且不会产生大量的泄露[7]。黑洞涡旋是一种连贯性很强的拉格朗日涡旋,Beron-Vera等[7]认为黑洞涡旋的定义是涡旋边界所处的物质带符合条件:涡旋在随着流场变形后,边界所处的物质带的变形应该与边界的变形一致,不应该出现显著的拉伸或者剪切变形。黑洞涡旋边界的理论是寻找流场平流输运下具有最小变形的边界,在计算中,求得嵌套的椭圆拉格朗日拟序结构(eLCSs)的最外层闭合曲线,即为黑洞涡旋的边界,由于该边界的数学解和宇宙中黑洞边界的数学解等价,且物质进入涡旋内部就很难出来,故被命名为黑洞涡旋[12]。与其他拉格朗日涡旋相比,黑洞涡旋的识别过程比较复杂,对涡旋的连贯性要求很高,要求在给定时间尺度内没有任何水体的丢失,相比于其他的拉格朗日涡旋能更好地评估涡旋的输运能力[13],它具有很好的包裹性和连贯性[14]。
在LCSs的早期研究中,有限时间李雅普诺夫指数方法(Finite-time Lyapunov Exponent, FTLE)[15]和有限空间李雅普诺夫指数方法(Finite-size Lyapunov Exponent, FSLE)[16-17]被用来评估海洋流场的扰动增长[18]。虽然FTLE在无剪切LCSs提取中发挥了重要作用并得到了广泛应用,但其连贯性比较差,会在特定情况下产生错误[19]。因此,一种新的拉格朗日变分测地线理论被提出[20],它能更准确地描述物质输运并且可以通过流体变形有效地提取LCSs,这一方法也经过了理论流场的验证[3]。Haller和Beron-Vera[12]提出黑洞涡旋的识别方法,并比较了拉格朗日涡旋和欧拉涡旋的物质输运能力,Beron-Vera等[14]通过二维遥感数据和Drifter数据证明了拉格朗日涡旋确实具有强连贯性。由于黑洞涡旋的识别方法对涡旋的连贯性要求较高并且计算过程比较复杂,Haller等[21]以及Abernathey和Haller[22]又提出通过计算拉格朗日平均涡度偏差(Lagrange Averaged Vorticity Deviation, LAVD)的方法识别亚中尺度拉格朗日涡旋。相比于LAVD涡旋,黑洞涡旋的连贯性更强,也能更好地反映拉格朗日涡旋对物质的输运能力。Abernathey和Haller[22],Rypina等[23]都使用地转流数据识别涡旋边界。
中尺度涡旋三维结构的研究主要基于卫星高度计数据和观测数据的综合分析,可以使用遥感数据和浮标数据来评估涡旋对物质的输运能力[5,24]。Dong等[25]利用卫星高度计数据和Argo数据分析涡旋在水平和垂直方向上热量和盐度的输运能力,并比较了不同区域涡旋对热量和淡水的输运能力。目前关于欧拉涡旋的三维结构研究较多[26-27]。Hu等[28]基于卫星高度计和Argo数据研究一个气旋涡的三维结构和物理性质。Xu等[26]利用Argo剖面数据观察不同深度上中尺度涡旋对模态水俯冲和输运的影响,并计算了北太平洋涡旋扩散系数。Dong等[29]和Lin等[30]在南海和南加州湾采用了三维欧拉涡旋识别方法获得三维涡旋数据集,证明了大多数涡旋的垂直结构不超过400 m。Blazevski和Haller[31]研究了非稳定流场中eLCSs的三维结构,在二维流场的基础上证明了三维流场中拉格朗日运输边界的稳定性和有效性。总体来说,与欧拉涡旋相比,基于三维观测数据的拉格朗日涡旋研究较少。
为了补充拉格朗日涡旋的研究,验证黑洞涡旋的物质输运能力,本文使用卫星高度计数据和Argo浮标数据来分析涡旋在水平和垂直方向上输运物质的能力。首先,识别出不同时间尺度(T=30 d,60 d,90 d和120 d)的黑洞涡旋边界,同时使用虚拟粒子来验证黑洞涡旋的强连贯性,并与欧拉边界进行对比。然后,将海表盐度(Sea Surface Salinity,SSS)、海表温度(Sea Surface Temperature,SST)和叶绿素浓度(Chlotophyll Concentration,CHL)数据与边界进行叠加分析,研究黑洞涡旋在水平方向上对物质的输运能力。最后,利用Argo浮标提供的三维采样数据绘制Eddy A的剖面图,验证黑洞涡旋垂直方向上作为输运边界的有效性,以补充拉格朗日涡旋的三维验证。我们利用Argo剖面数据(盐度、温度和溶解氧(Dissolved Oxygen,DO))分析不同深度黑洞涡旋的物质输运能力,还通过剖面图发现了黑洞涡旋盐度异常的三明治结构。
2 数据和方法
2.1 数据
2.1.1海平面高度异常数据和速度场数据
本文使用法国AVISO(Archiving Validation and Interpretation of Satellite Oceanographic)数据中心的海平面高度异常(MSLA-H)数据和通过地转流公式计算得到的速度场数据(MSLA-UV, https://www.aviso.altimetry.fr/index.php?id=1271),空间分辨率为25 km×25 km,时间分辨率为1 d。
2.1.2海表面温度数据
本文使用美国国家航空航天局(NASA)(https://podaac.jpl.nasa.gov)的高分辨率红外辐射计(AVHRR)提供的海表温度数据,空间分辨率为25 km×25 km,时间分辨率为1 d。
2.1.3海表面盐度数据
本文使用哥白尼海洋环境监测中心(CMEMS)(http://marine.copernicus.eu/)提供的周平均SSS数据,空间分辨率为25 km×25 km。
2.1.4叶绿素浓度数据
叶绿素浓度数据由CMEMS (http://marine.copernicus.eu/)提供。本文使用基于SeaWiFS、MODIS、MERIS和OLCI-S3A&S3B等传感器的融合四级地图产品,空间分辨率为4 km×4 km,时间分辨率为1 d。
2.1.5Argo浮标数据
本文使用2014年3月底投放的17个Argo浮标(世界气象组织的IDs 2901550-2901566)具有增强时空分辨率的采样数据(温度、盐度和溶解氧数据,垂直分辨率为2 m)[26],时间分辨率为1 d,初始位置如图1所示。其中一个ID为2901552的Argo大部分盐度数据标记较差,我们在研究过程中删除了该浮标的数据。
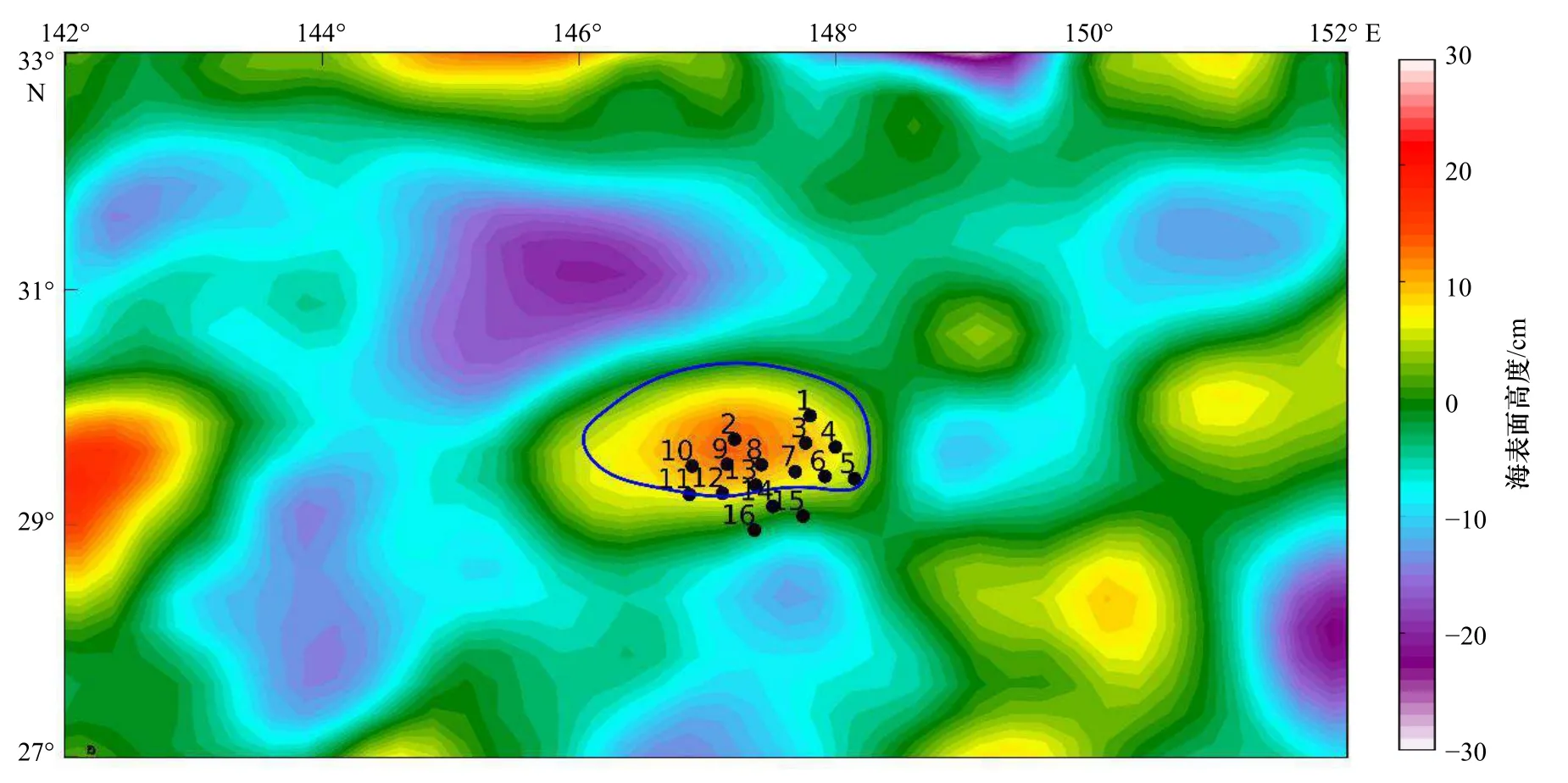
图1 2014年3月28日Eddy A的黑洞涡旋边界(蓝色闭合曲线)与海表面高度异常值和16个Argo(除No. 2901552)的初始位置(黑色点)叠加图Fig. 1 Satellite-derived sea surface height anomalies with Eddy A (blue line) detected by the ELCSs method on March 28, 2014 and theinitial positions (black points) of the 16 Argo floats (except for No. 2901552)
2.1.6澳大利亚联邦科学与工业研究组织区域海洋地图数据
本文使用澳大利亚联邦科学与工业研究组织(CSIRO)(http://www.marine.csiro.au/~dunn/)提供的区域海洋地图数据(CARSs)计算温度异常和盐度异常。在现代海洋测量的时间尺度上,CARSs数据提供了空间分辨率为50 km×50 km的海洋气候态平均网格数据。
2.1.7研究范围
基于Argo浮标与Eddy A整个生命周期的轨迹,我们选取西太平洋(20°~50°N,130°~160°E)作为研究区域。
2.2 黑洞涡旋识别方法
在二维速度场v(x,t)作用下,一个区域内的粒子经过时间t后的运动轨迹为对速度场求偏导

定义流场的轨迹场如下:
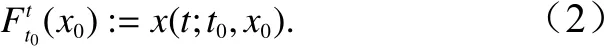
这表示粒子在初始时刻t0的初始位置x0在流场中经过时间t后到达新位置的运动轨迹。
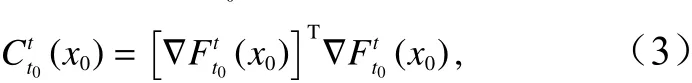
式中,∇表示梯度计算。
物质曲线η是在时间区间 [t0,t1]内同一拉伸系数λ的封闭环。在t0时刻,物质曲线是由柯西格林应变张量的两个线性无关特征值和对应的特征向量组成
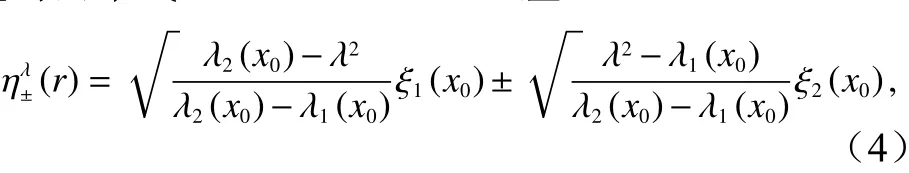
式中,λ1和λ2为特征值;ξ1和ξ2是对应的特征向量,
闭合曲线r(s)满足下列微分公式

选取适当庞加莱截面上的点由式(5)进行积分计算得到的封闭曲线即为λ-lines[32]。为了适应不同的涡旋,从庞加莱截面定义的λ-lines的数量( λnumber)为

式中,LPS是庞加莱截面的长度;lRes是速度场辅助网格的长度。
图2 详细介绍了黑洞涡旋边界的提取。选取涡旋内涡度极值点作为涡心[12]。基于张量场,选取一个明显在涡旋外部的点,两点相连即为庞加莱截面,进行积分计算得到不同的λ-lines,如图2所示。如果存在外层的闭合λ-line,该涡旋就是黑洞涡旋,其边界就是最外层的闭合λ-line,其λ值不一定等于1。如果存在λ=1的闭合λ-line,那么涡旋表现出极强的连贯性。当涡旋只包含λ≠1的最外层边界时,该涡旋为次连贯拉格朗日涡旋,λ<1连贯性增强,λ>1连贯性减弱[12]。基于本文的识别结果,Eddy A存在封闭的λ=1的λ-line,也有一个λ=0.9(连贯性增强)的最外层边界,因此,Eddy A是一个连贯性很强的黑洞涡旋[12]。
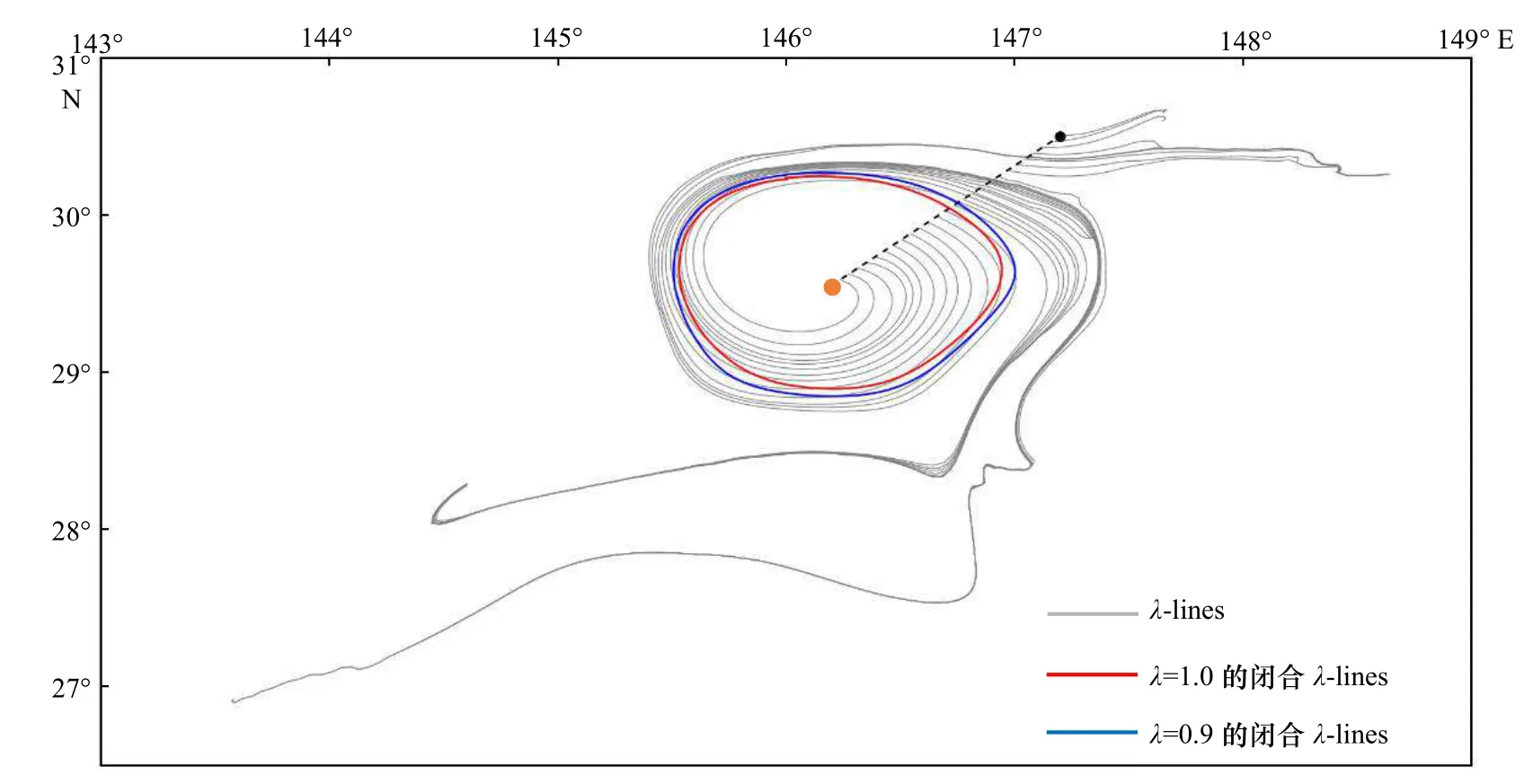
图2 以Eddy A为例,t0以2014年4月10日为初始时刻,积分时间为30 d的黑洞涡旋提取λ=1边界(红色曲线)和最外层边界(蓝色曲线)的比较Fig. 2 Black-hole eddy’s boundaries for t0=April 10, 2014, with a detection time scale of 30 d, are extracted in red (λ=1) and blue (λ=0.9)橙色点为涡心,黑色为涡旋外的点,黑色虚线为庞加莱截面The red point is the eddy center, the black point is the point outside the eddy, and the black dotted line is the Poincare section
3 结果与讨论
3.1 遥感数据验证
为了分析不同时间尺度的黑洞涡旋的物质输运能力,我们识别初始时刻为2014年4月10日,时间尺度为T=30 d,60 d,90 d和120 d的黑洞涡旋边界。研究中使用的欧拉边界是一种基于海平面高度(Sea Surface Height, SSH)得到的有效边界[33]。本文通过虚拟粒子随流场的运动轨迹来比较黑洞涡旋边界和欧拉边界的连贯性[14](图3)。通过观察初始位置(图3a),我们发现欧拉边界的面积大于所有时间尺度的黑洞涡旋边界,时间尺度越长的黑洞涡旋边界的面积越小。边界随流场运动到第30 d时,欧拉边界出现了严重的成丝现象,时间尺度为30 d的黑洞涡旋边界保持着很好的连贯性(图3b)。时间尺度为60 d、90 d和120 d的黑洞涡旋边界在随地转流运动的过程中,位置发生了改变,但是没有出现明显的丝状结构,仍然包裹着边界内部的粒子移动(图3c,图3d)。由此可见,黑洞涡旋边界在时间尺度内保持着连贯性,边界阻碍着粒子与周围水体混合。对于一些黑洞涡旋边界,即使随流场运动的时间超过时间尺度,边界出现丝状结构,但粒子还是被包围在边界内,没有分散。这体现出黑洞涡旋的边界随流场运动时具有稳定性,并且对其内部的物质具有较强的包裹能力。
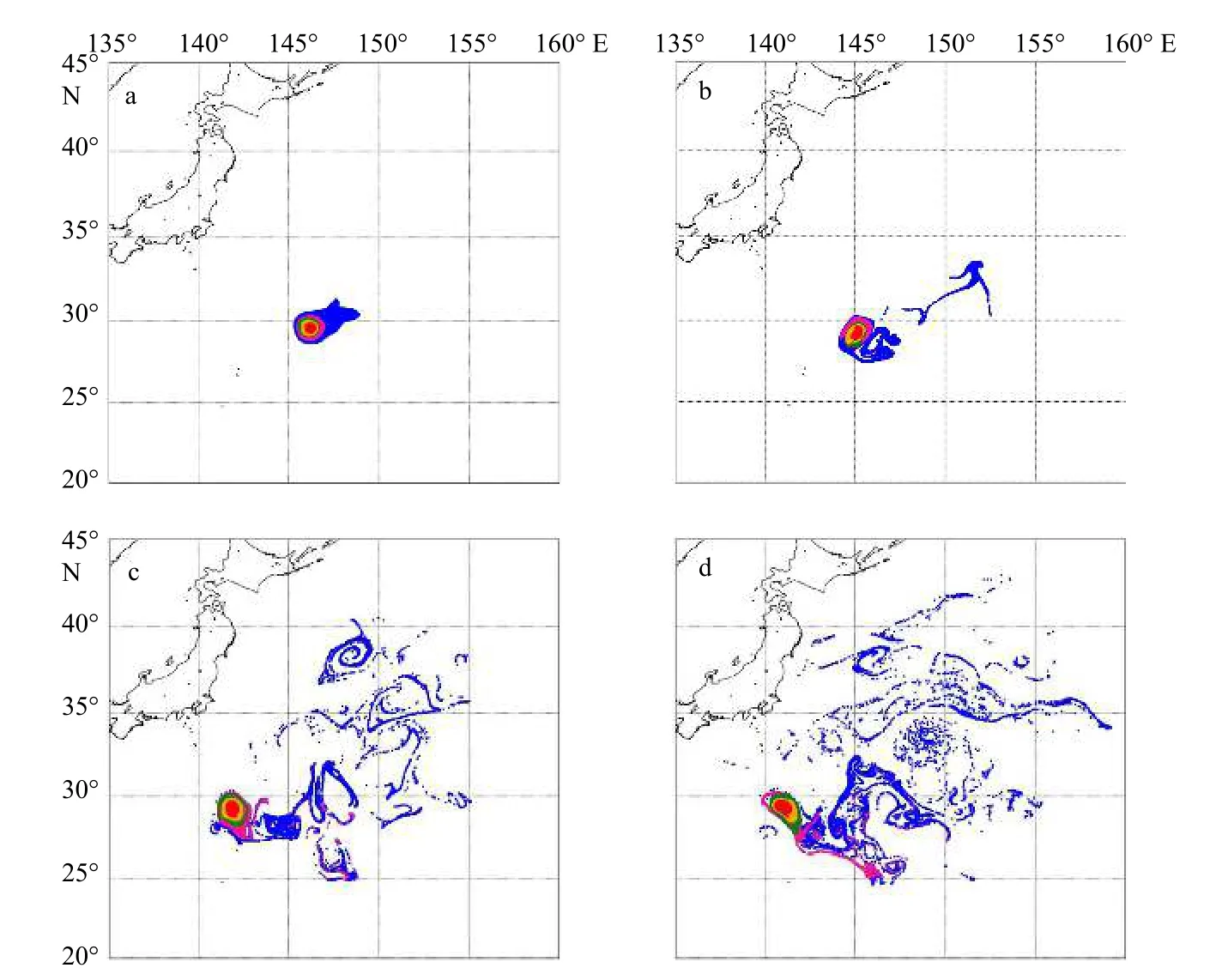
图3 黑洞涡旋边界(粉色、绿色、橙色和红色线分别为积分时间30 d、60 d、90 d和120 d)和欧拉边界(蓝色线)随流场运动其内部虚拟粒子的移动轨迹Fig. 3 Eddy boundaries of the black-hole (pink, green, orange and red lines are with detection time scale of 30 d, 60 d, 90 d and 120 d respectively) and Eulerian boundary (blue) filled with virtual particles moves with the geostrophic a. 2014年4月10日各边界的初始位置;b-d. 分别为5月9日、7月8日和8月7日的粒子轨迹a. The initial position of the boundary on April 10, 2014; b-d. particles tracks on May 9, July 8 and August 7, respectively
本文将海表面遥感数据(SST异常、SSS异常和CHL异常数据)与黑洞涡旋边界进行叠加,分析黑洞涡旋在水平方向上对物质的输运能力(图4至图6)。图4a展示了初始时刻(2014年4月10日)Eddy A的欧拉边界,以及时间尺度分别为30 d,60 d,90 d和120 d的黑洞涡旋边界。通过观察图4,我们发现黑洞涡旋边界内存在高温度异常。随着地转流运动,欧拉边界分散严重,而黑洞涡旋的位置发生变化,但在时间尺度内仍保持连贯性,并且图4c和图4d的黑洞涡旋边界内存在明显的高温度异常。通过SSS异常与Eddy A边界的叠加分析可以发现,黑洞涡旋内部对应低盐度异常特征,并且这一特征在黑洞涡旋边界和地转流运动的整个周期中都存在(图5)。图6a中,黑洞涡旋内叶绿素浓度较低,图6b、图6c和图6d中Eddy A的黑洞涡旋边界内也对应低叶绿素浓度。综上所述,黑洞涡旋边界被认为是物质输运的屏障,与海表面物质分布密切相关,证明了黑洞涡旋边界可以描述海表面属性的边界。Eddy A作为一个反气旋涡使海表面水体向下运动,表现为高海表面温度异常、低盐度异常和低叶绿素浓度异常[34],这与我们的研究结果一致。图4a中海表面温度异常与涡旋边界没有严格对应,这是由于我们使用的是海表面温度异常数据,但涡旋是三维水体,所引起的是三维上的温度异常,Eddy A的暖核可能在海表面以下,在海表面体现的温度异常不够典型。图4b右侧的子图中,由于欧拉边界随地转流变形扭曲,在黑洞涡旋旁边出现旋转结构可能是没有在积分时间内保持连贯性的涡旋或涡流结构。图6b中叶绿素浓度异常与边界的对应不如图6a和图6c严谨,这是因为叶绿素浓度受光照、降水和生物因素等一系列海洋参量的影响,影响原因比较复杂,但是根据图6a和图6c,我们认为该涡旋在大部分时间内可以很好的对应。另外,时间尺度90 d和120 d的黑洞涡旋边界会在切向上出现细小的成丝现象,这是切向上的剪切力导致的,不影响边界的连贯性。总体来说,尽管欧拉边界可以描述瞬时的涡旋位置和范围,但是高估了欧拉涡旋对物质的输运能力,而黑洞涡旋能更客观地描述在一定时间内的物质的输运边界。
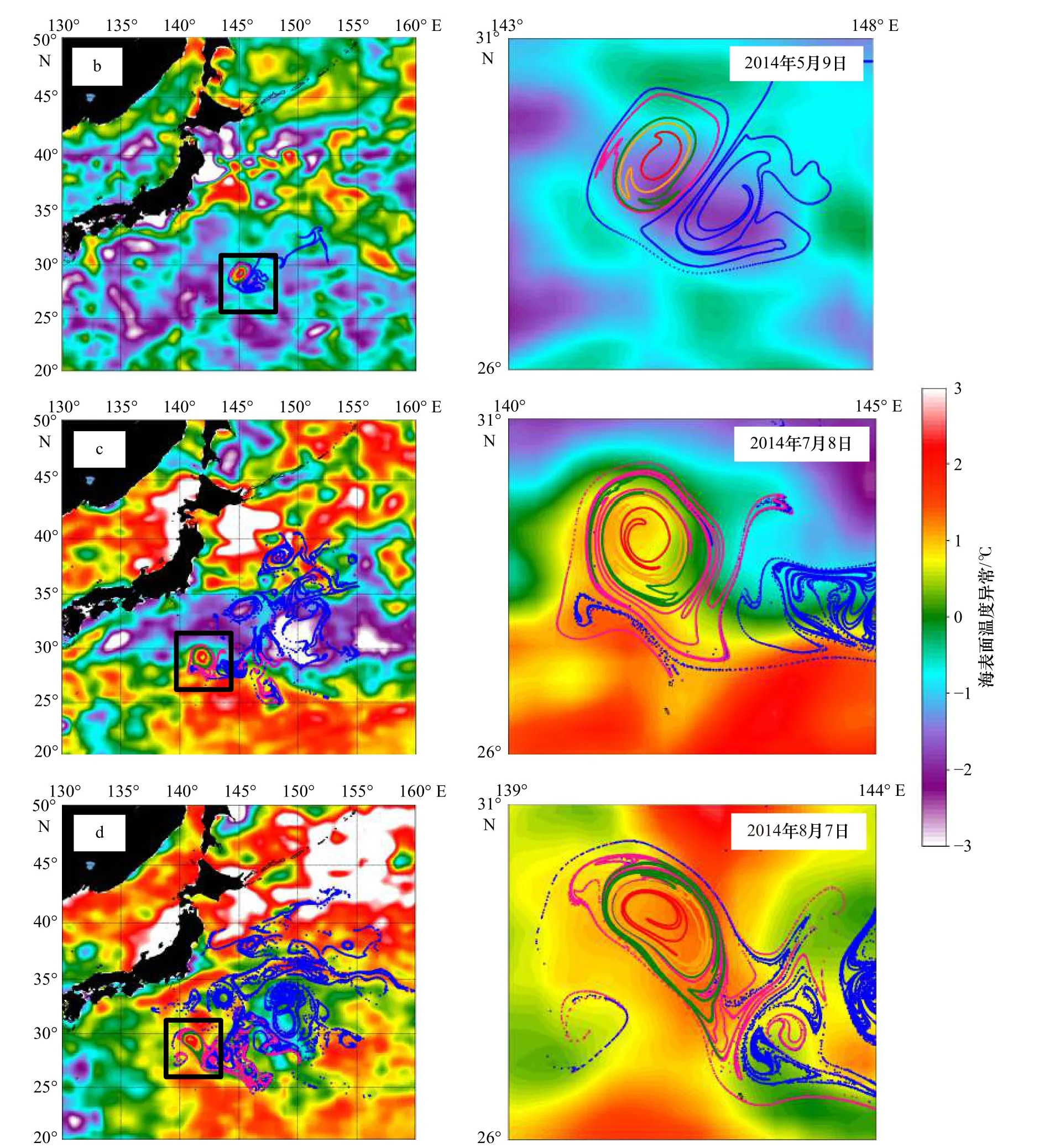
图4 黑洞涡旋边界(粉色、绿色、橙色和红色线分别为积分时间30 d、60 d、90 d和120 d)和欧拉边界(蓝色)随流场运动的轨迹Fig. 4 The trajectories of black-hole (pink, green, orange and red lines are with detection time scale of 30 d, 60 d, 90 d and 120 d respectively) and Eulerian boundary (blue) under the geostrophic a为2014年4月10日各边界的初始位置;b-d分别为5月9日、7月8日和8月7日的粒子轨迹;右列为对应的左列图中黑色框内的放大图a. The initial position of the boundary on April 10, 2014; b-d. particles tracks on May 9, July 8 and August 7, respectively; the right column is the enlarged image in the black box of the left column
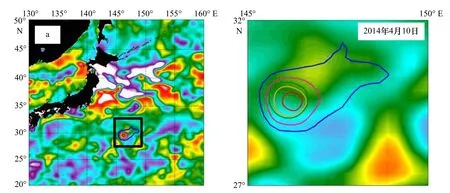
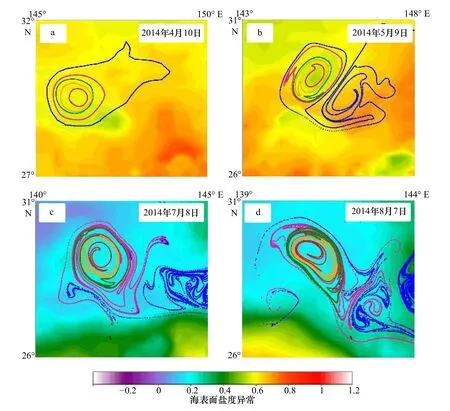
图5 黑洞涡旋边界(粉色、绿色、橙色和红色线分别为积分时间30 d,60 d,90 d和120 d)和欧拉边界(蓝色线)随流场运动轨迹Fig. 5 The trajectories of black-hole (pink, green, orange and red lines are with detection time scale of 30 d, 60 d, 90 d and 120 d respectively) and Eulerian boundary (blue) under the geostrophic a. 2014年4月10日各边界的初始位置;b-d分别为5月9日、7月8日和8月7日的粒子轨迹a. The initial position of the boundary on April 10, 2014; b-d. particles tracks on May 9, July 8 and August 7, respectively
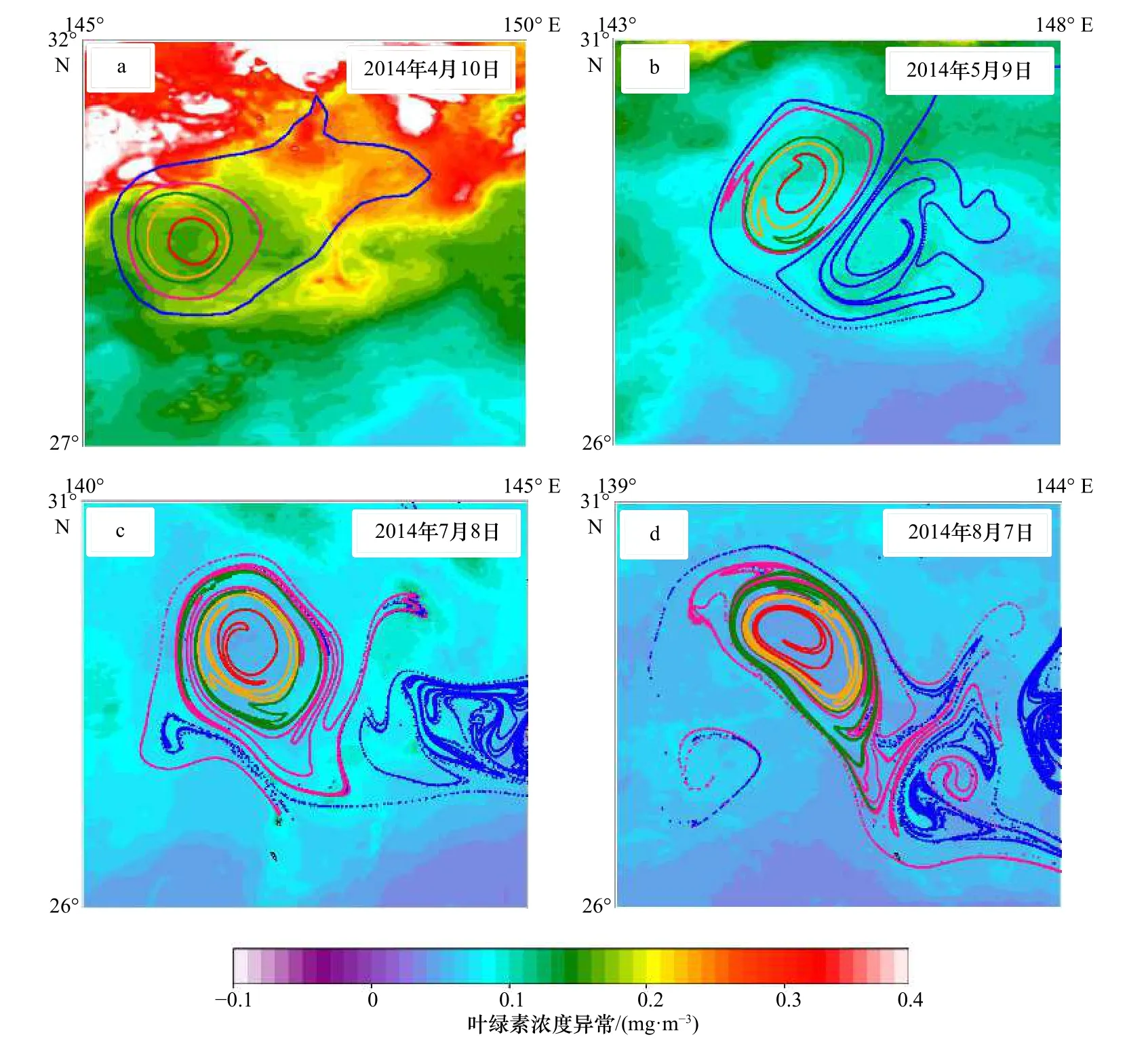
图6 黑洞涡旋边界(粉色、绿色、橙色和红色线分别为积分时间30 d、60 d、90 d和120 d)和欧拉边界(蓝色线)随流场运动的轨迹Fig. 6 The trajectories of black-hole (pink, green, orange and red lines are with detection time scale of 30 d, 60 d, 90 d and 120 d respectively) and Eulerian boundary (blue) under the geostrophic a. 2014年4月10日各边界的初始位置;b-d分别为5月9日、7月8日和8月7日的粒子轨迹a. The initial position of the boundary on April 10, 2014; b-d. particles tracks on May 9, July 8 and August 7, respectively
3.2 Argo数据验证
本文利用Argo浮标得到的温度、盐度和溶解氧数据,对Eddy A进行不同深度的物质输运能力分析。将Argo数据和CARSs的气候态数据进行处理得到不同深度的温度异常、盐度异常和溶解氧数据,用于追踪涡旋内部的物质变化。通过图7可以看到在90 d内有多个Argo浮标位于Eddy A内部,然而,Argo浮标本身的密度和物理特性与海水不同,所以浮标轨迹不能精确地反映海流方向,但Argo的观测数据可以反映涡旋内部盐度、温度和溶解氧的属性。
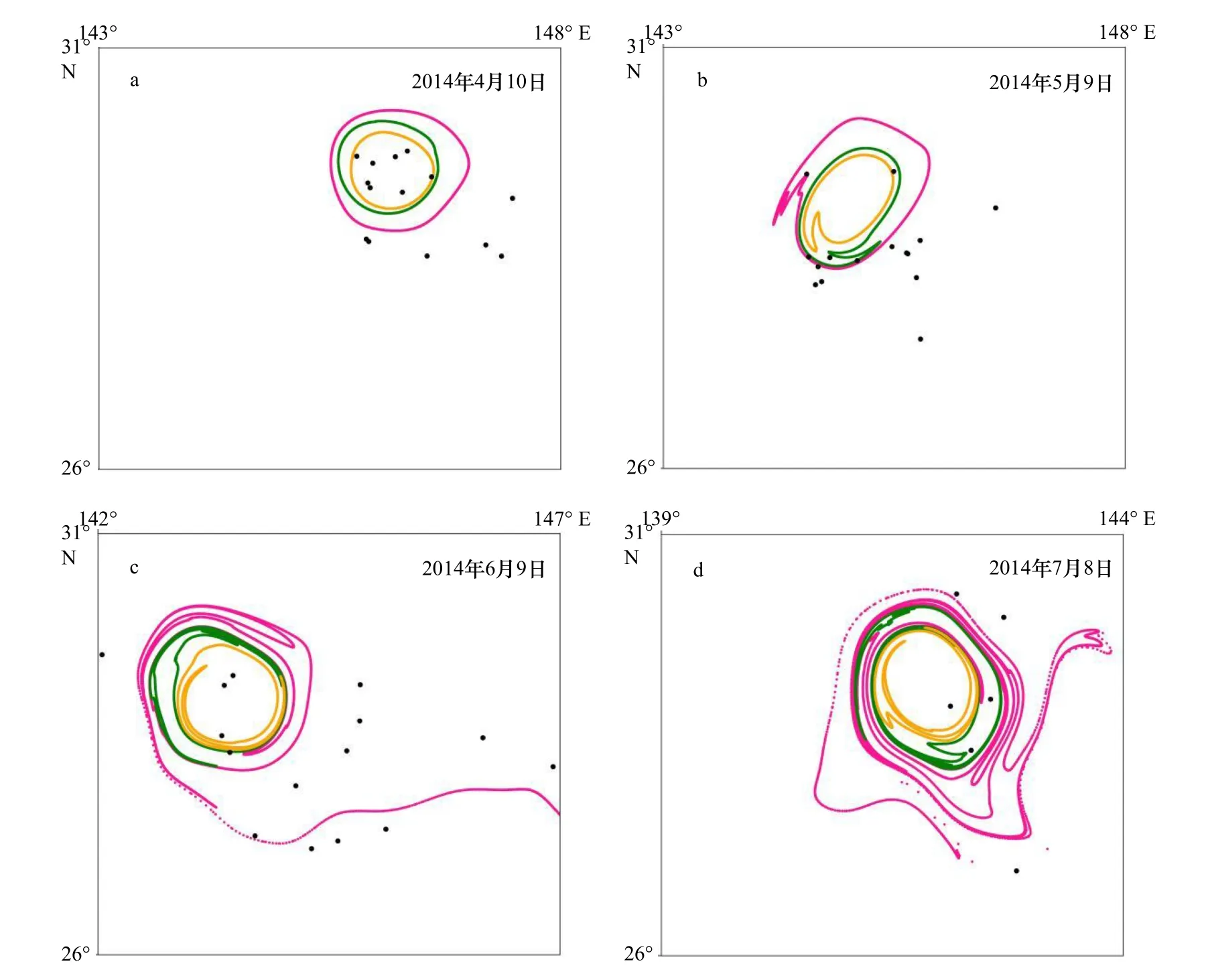
图7 Argo浮标(黑色点)与涡旋Eddy A边界的相对位置Fig. 7 The relative position of Argo buoy (black dots) and Eddy A曲线为t0=2014年4月10日的T=30 d(粉色)、T=60 d(绿色)和T=90 d(黄色)的拉格朗日边界Each black-hole eddy boundary has a different detection time scale T of 30-days (pink), 60-days (green), 90-days (yellow) and t0= April 10, 2014 on April 10,2014 (a), May 9, 2014 (b), June 9, 2014 (c) and July 8, 2014 (d)
欧拉方法描述的是涡旋的瞬时边界,随流场运动会很快失去连贯性,因此本文只研究黑洞涡旋边界在一定时间内的剖面结构。图8为Eddy A边界内外温度和盐度异常随深度变化图。温度异常的峰值出现在深度为400 m附近(图8a、图8d、图8g和图8j)。盐度异常在深度为200 m时出现峰值后迅速下降,然后从500 m又开始上升,在700 m附近再次出现峰值(图8b、图8e、图8h和图8k),形成很明显的三明治结构。水体的垂直分布是决定盐度异常剖面的重要因素,Eddy A的上升运动使盐度较低的北太平洋中间层水(North Pacific Intermediate Water)上升,降低北太平洋热带水(North Pacific Tropical Water)的盐度,所以深度为200~500 m时,深度越小盐度异常越低;而盐度较高的北太平洋热带水被抬升后使浅层海水(0~200 m)呈现正盐度异常。在更深层的海水,由于北太平洋深层水(the North Pacific Deep Water)的盐度相对较高,Eddy A的运动将其抬升,使得深度为500~800 m时低盐度异常减弱[35]。溶解氧的浓度随深度不断增加,在深度为0~400 m时变化最快。由于受到各种海面因素的影响,海表面的信号可能与深层信号不一致。不同时间,不同深度涡旋内外物质分布不同,但涡旋内物质随深度变化基本保持一致,特别是温度和盐度,这充分说明黑洞涡旋在垂直方向上也能包裹物质运动。
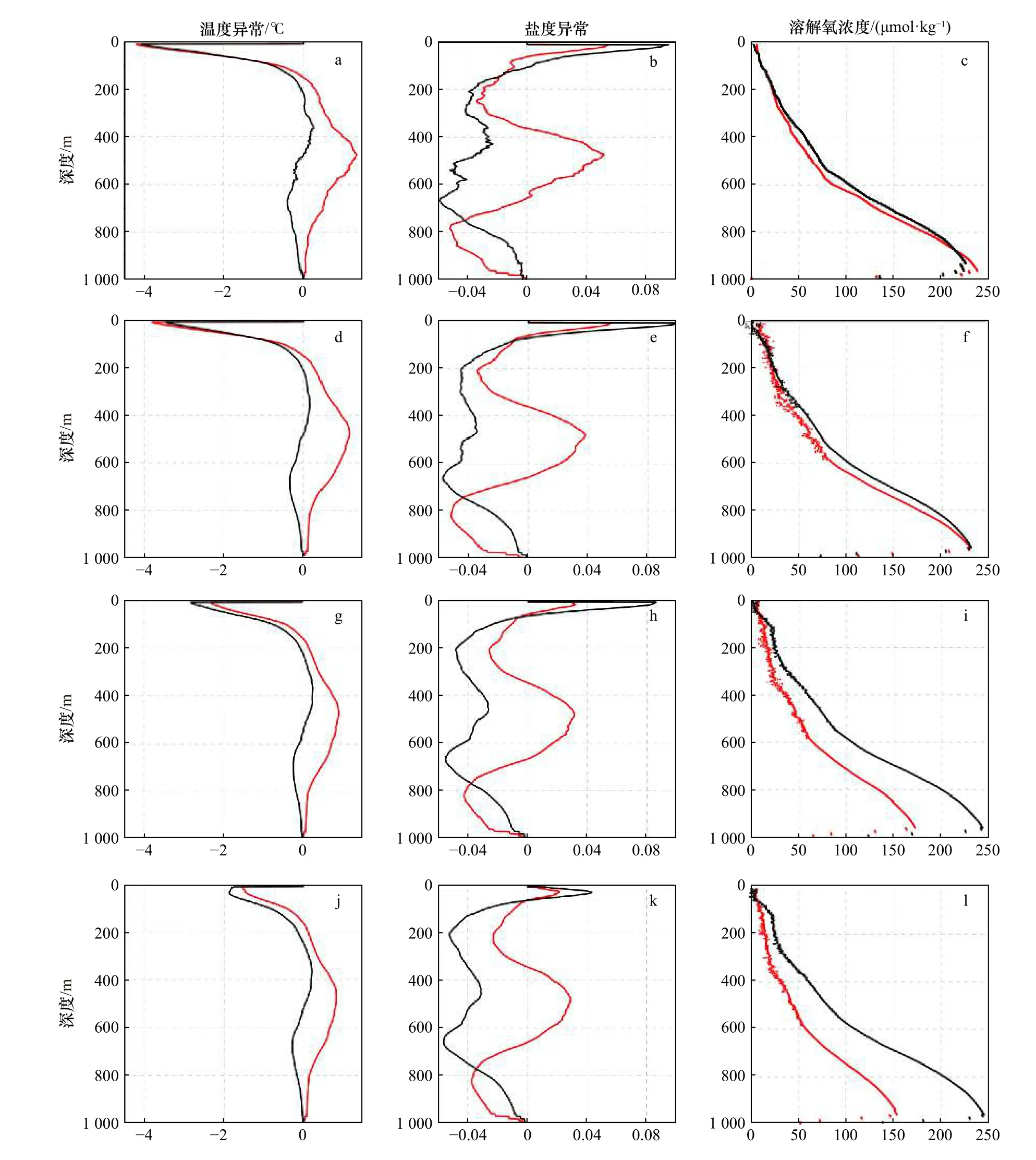
图8 垂直方向上不同时间积分的黑洞涡旋边界内(红色曲线)外(黑色曲线)物质分布差异比较Fig. 8 The difference of material distribution inside (red curve) and outside (black curve) the black-hole eddy boundaries in vertical a, d, g, j. 温度异常剖面;b,e, h, k. 盐度异常剖面;c, f, i, l. 溶解氧浓度剖面。第1行和第2行分别为T=30 d边界在4月10日和5月9日的剖面,第3行和第4行为T=60 d边界在7月8日 和T=90 d边界在8月7日的剖面a, d, g, j. The temperature anomaly profiles; b, e, h, k. the salinity anomaly profiles; c, f, i, l. the dissolved oxygen concentration profiles. The first and second lines are profiles of the boundary T=30 d on April 10 and May 9, the third and fourth lines are profiles of the boundary T=60 d on July 8 and T=90 d on August 7
通过建立Argo数据点坐标系,可以观察到不同深度的温度和盐度异常分布与黑洞涡旋边界的关系(图9)。通过计算边界经过流场运动后与涡旋中心的距离,得到不同时间积分的平均拉格朗日边界,根据Eddy A的空间范围,我们忽略与涡心相对距离超过500 km的Argo数据点。根据温度和盐度异常数据得到拟合曲线并计算拟合曲线二阶导数为0的点,该点坐标表示拟合曲线变化最快的位置。虽然温度异常和盐度异常的拟合曲线在浅层海水比较平缓(图9a,图9b),但还是和较深层一样呈现涡旋中心高异常值,涡旋边界低异常值的趋势。随着深度的增加,相较于图9a、图9b、图9i和图9j,Argo数据点的温盐异常值距涡心越远下降趋势越明显(图9c至图9h),这一趋势在深度为900 m时减弱(图9i,图9j)。结合不同深度来看,二阶导数为0的点几乎总是在积分时间大于等于90 d的平均黑洞涡旋边界附近,即长时间积分的黑洞涡旋边界可以反映垂直方向上物质和热量变化最快的位置。
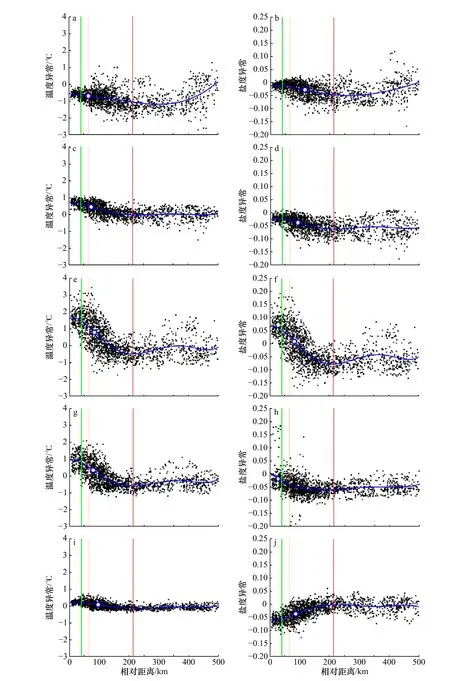
图9 Argo数据点的温度异常和盐度异常与涡心相对距离统计Fig. 9 The statistical graphs of relative distance between Argo data point of temperature anomaly and salinity anomaly and eddy center a, c, e, g, i. 为温度异常;b, d, f, h, j. 盐度异常。第1行至第5行的深度分别为100 m,300 m,500 m,700 m,900 m。红色、橙色和绿色竖线分别代表随流场运动后T=30 d,90 d和120 d的平均黑洞边界,蓝色的线代表拟合曲线,蓝色空心点为拟合曲线二阶导数为0的点a, c, e, g, i. Temperature anomaly; b, d, f, h, j. salinity anomaly. The depth of the first to fifth rows is 100 m, 300 m, 500 m, 700 m and 900 m respectively. The red, orange and green vertical lines represent the average black-hole eddy boundaries of T=30 d, 90 d and 120 d after moving with the flow field. The solid blue lines represent the fitting curve, and the blue edge dots show where the second derivative is 0
从图10中可以观察到,随着海表面水从辐合中下降,不同深度的DO值变低。并且在较深层的水体中,涡旋中心附近的DO值高于边缘处。随着深度的增加,拟合曲线的下降趋势更加明显,说明在深水中,靠近涡旋中心的水体相对于边缘水体富氧程度更高。和温度异常和盐度异常相同,DO梯度变化最大的点总是在长时间积分的拉格朗日边界附近。这表明Eddy A具有将上层富氧水汇聚并将其输送到底层的能力。这些发现证明了随着流场变化,黑洞涡旋在垂直方向也具有对内部物质的包裹能力,并且能将上层热量和物质输运到深层。

图10 Argo数据点的溶解氧浓度与涡心相对距离统计Fig. 10 The statistical graphs of relative distance between Argo data point of dissolved oxygen concentration and eddy center点的颜色代表所属深度范围,红色、橙色和绿色竖线分别代表随流场运动后T=30 d、90 d和120 d的平均黑洞涡旋边界。黑色的线代表拟合曲线,蓝色空心点为拟合曲线二阶导数为0的点The color of points represents the depths. The red, orange and green vertical lines represent the average black-hole eddy boundaries of T=30 d, 90 d and 120 d after moving with the flow field. The black lines represent the fitting curve, and the blue edge dots show where the second derivative is 0
4 结语
本文使用基于eLCSs的黑洞涡旋识别方法,确定西太平洋一个典型的黑洞涡旋边界。通过虚拟粒子随着流场的变化来验证黑洞涡旋比欧拉涡旋更具有连贯性。利用遥感数据SST、SSS和CHL数据分析黑洞涡旋在水平方向上的物质输运能力,随着时间的变化,黑洞涡旋边界的移动与海表面温度、海表面盐度和叶绿素浓度的移动相吻合,证明了黑洞涡旋在海表面方向上作为输运边界的客观性。首次利用Argo浮标获取的采样数据(温度、盐度和DO)形成黑洞涡旋剖面图,证明了不同时间尺度的黑洞涡旋在垂直方向上可以裹挟涡旋内部的水体运动,而不同深度的温度、盐度和DO变化最快的点与长时间尺度的黑洞涡旋边界的一致性体现了其作为物质输运边界的可靠性。
LCS方法强调了物质在流场中的连贯性,因此拉格朗日涡旋具有非常卓越的客观性。我们将着重于利用拉格朗日方法的优点来推进涡旋的识别和验证工作。随着更高时空分辨率遥感数据的出现,我们能更精细地分析海洋结构,更准确地评估物质输运情况,本文中黑洞涡旋不能准确地反映海表面物质分布的问题也可以得到解决。此外,随着模式数据和再分析数据的不断升级,对海洋涡旋二维和三维结构的细致刻画值得进一步研究,也需要具有更精确的空间和时间分辨率的观测数据来精细地评价中尺度涡旋的三维物质输运能力。在未来工作中,我们会对黑洞涡旋边界内存在的高温度异常、低盐度异常和低叶绿素浓度异常进行定量刻画,并进一步定量分析光照、降水和生物因素等对涡旋物质包裹性的影响。

