基于新型变指数趋近律的智能小车轨迹跟踪

李 艳， 孙 蕊

(1.陕西科技大学电气与控制工程学院， 西安 710021; 2.陕西农产品加工技术研究院， 西安 710021)

近年来，随着四驱车式移动机器人制造技术的飞速发展，机器人越来越多地广泛应用于人类生活用品服务、生产设备制造、太空空间探测等领域中，所以机器人的运动控制是研究的重要领域。对于各行业领域广泛应用的车式移动机器人，精确的轨迹运动跟踪控制能力，无疑是实现小车自主运动并正确执行相应工作任务的重要技术能力基础。然而由于智能化的小车运动是一个典型的强高度耦合、强非线性的多种可变量复杂运动系统，再加上实际小车运动过程中外部环境干扰的普遍存在和智能小车轨迹运动模型的不确定性存在，导致小车轨迹跟踪控制器的设计工作难度较高。所以为了实现快速高精度的自动轨迹跟踪运动控制，必须采用合适的控制策略[1-2]。在自动控制策略上, 滑模控制[3-5]技术具有物理控制实现简单、快速自动响应、易于模拟实现等几大优点，对于机器人的控制非常有利，所以在车式机器人轨迹跟踪控制等方面具有广泛的应用。

对于传统的车式机器人快速轨迹跟踪问题，侯明冬等[6]提出一种新的抗饱和无模型的自适应终端积分滑膜控制方法，该方法响应速度快且跟踪精度高，但是其跟踪偏差的抖振较为明显，不利于实际情况下小车的轨迹跟踪实现。对于车类移动机器人的滑模轨迹跟踪技术问题，潘天宇等[7]将滑模控制器的等速趋近律进行改进，与自动导航车的轨迹跟踪进行结合，该方法能较快地纠正不同转弯半径和不同速度的误差，但该方法角度偏差的超调较大且跟踪时间较长，并没有保证轨迹的跟踪精度。赖欣等[8]提出一种自适应模糊滑模轨迹跟踪控制器，该控制器实现了大幅度削弱抖振、降低稳态误差的功能，且能在较短时间内进行轨迹跟踪，但是其设计过程较为复杂。对于车式机器人的鲁棒性弱的轨迹跟踪运动控制问题，李爱娣等[9]利用反步法来设计车辆轨迹快速跟踪控制器，该控制器使得车式机器人能快速且准确地跟踪给定期望的轨迹，姜立标等[10]将特殊幂次函数和反双曲正弦函数相结合，设计了一种组合公式的轨迹趋近律，实现了跟踪控制器在车辆平顺快速轨迹跟踪时的参考期望轨迹。智能控制理论的发展使得车式移动机器人在轨迹跟踪控制方面出现了许多新的控制算法[11-17]。文献[18-19]将模糊算法和神经网络相结合对智能车进行轨迹跟踪控制研究，文献[20]将模糊控制器与型预测控制方法相结合对智能车辆进行路径跟踪控制，提高控制效果。然而在实际控制应用中，神经网络控制算法往往需要大量的实验数据和高昂的计算控制成本，而模型预测控制算法更是由于需要较高的控制精度和过长的线性优化实现时间，不能完全满足跟踪控制数据实时性的严格要求。

针对跟踪运动精度低、鲁棒稳定性弱的新型智能滑模小车的轨迹跟踪控制问题，提出一种新型滑模趋近律的轨迹跟踪运动控制器，该趋近律加入了变指数幂次项，并且可以在有限时间内达到稳定，提高了智能小车轨迹跟踪系统的收敛速度，同时限制了其抖振现象的产生，使得小车的轨迹跟踪误差快速收敛到0，从而完成智能小车的稳定轨迹跟踪运动控制。

1 运动学及轨迹误差模型

1.1 运动学模型的建立

当智能小车进行轨迹跟踪运动时，转弯期间车体绕其几何中心O点运动，如图1所示。假设车身的质心点与几何中心点相重合，由图1可知ω为小车本身转弯时的角速度；Ro为点O距离车体几何中心点M的直线距离；Ri(i=1,2,…,4)为点O距离每个车轮中心的距离；vo为智能小车几何中心点M前进时的运动速度，其运动方向与纵轴y方向垂直，vo与ω的关系为vo=ωRo；vi(i=1,2,…,4)为小车每个轮子的中心运动速度，其与ω的关系为vi=ωRi。所以得到等式为

图1 平面转弯示意图Fig.1 Plane turning diagram

(1)

当小车忽略侧向滑动时，为了轻松完成跟踪车辆给定期望轨迹的目标，需要控制其几何中心线速度vo和旋转角速度ω。由于智能小车的各种运动状态都会随着时间改变，如旋转角速度、线速度、空间中位置状态等。所以引入一个整体坐标系和一个部分坐标系来分别描述智能小车运动跟踪的期望坐标轨迹和实际跟踪轨迹，如图2所示。

图2 整体坐标系和部分坐标系Fig.2 Global coordinate system and partial coordinate system

以整个大地为参照系建立整体坐标系XOY，以小车本身为参照系建立部分坐标系xoy。其中整个车身的几何中心在整体坐标系的坐标用点M(x，y)表示；点D为小车在整体坐标系中的一个位置点，用坐标(xD,yD)表示；θ是小车车头运动方向与整体坐标系X轴之间的夹角[21-22]。由图2可以看出点D在两坐标系之间的数学关系表达式为

(2)

式(1)中：x′和y′分别表示图2中点D在部分坐标系中的横坐标和纵坐标值。所以得到智能小车的运动在整体坐标系XOY和部分坐标系xoy之间的映射关系，可以用正交旋转矩阵公式表示为

(3)

1.2 轨迹跟踪误差模型的建立

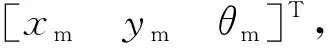
图3 智能小车运动学位姿误差坐标图Fig.3 Smart car movement degree and attitude error coordinate map

假设小车本身无任何滑动，可以得到智能小车运动学的方程为

(4)

所以智能小车的轨迹跟踪误差模型为

(5)

又由图3可得

(6)

则有

(7)

由式(5)可得

(8)

对式(8)求导并结合式(6)、式(7)，可得智能小车的轨迹误差模型为

(9)

2 小车轨迹跟踪控制器设计

为了严格有效地进行轨迹跟踪运动，设计出一种新型变指数幂次趋近律滑模控制的轨迹跟踪运动控制器，所以得图4所示的结构控制框图。

图4 结构控制框图Fig.4 Structure control block diagram

2.1 新型变指数幂次趋近律

通过参考文献[23]的新型变指数幂次趋近律来设计滑模轨迹跟踪运动控制器，该新型趋近律在传统趋近律的基础上加入了变指数幂次项，且可以在有限时间内达到稳定，具体方程为

(10)

(11)

式中：s表示系统状态；α表示大于0小于1之间的实数；λ表示新型变指数幂次趋近律中的指数取值;sgn表示符号函数。从式(10)、式(11)可以看出，对于s的取值范围不同，λ的取值结果也就不同，从而对应幂次趋近律中的指数的选取不同，所以通过λ的自适应变化就可以使得系统在不同的阶段分别获得比较快速的趋近速率。当|s|<1趋近律等同于双幂次组合函数的形式；当|s|≥1趋近律又相当于变指数幂次趋近律的形式。两种形式都具有较快的趋近速率，对比传统趋近律显然拥有一定的优胜性。

2.2 滑模面的设计

根据新型幂次趋近律即式(10)的时间收敛特性设计滑模面为

(12)

式(12)中：n1、n2表示大于0的正实数参数值；ωr≠0且为常数。

式(12)满足新型幂次趋近律公式，即

(13)

2.3 稳定性分析

定理1小车在基于新型变指数趋近律滑模控制器式(12)和式(13)的作用下，xe、ye和θe均可在有限时间内收敛至0。

证明时间收敛特性证明：假如系统的初始状态so=si(0)>1(i=1,2)。那么将系统从初始连续运动状态到滑模面的连续收敛过程一般可以大致分为2主要个阶段。第一阶段：从最初状态si(0)到si=1；第二阶段：从si=1到滑模切换面[23]。

(1)滑模面s1=θe在有限的时间内连续趋近到0的证明。

第一阶段：当系统从最初状态so=si(0)>1到si=1时，可知|s1|>1。

此时趋近律可以写为

(14)

求解式(11)需要考虑如下方程，即

(15)

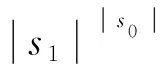
(16)

得

(17)

(18)

解出上述的一阶线性微分方程，得

(19)

又因为s1(0)=s0，所以可得常数C为

(20)

由式(19)、式(20)得到收敛时间为

(21)

即可求得从s0到s1=1的时间，即

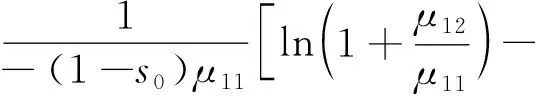
(22)

综上可知，系统从s0到s1=1所需时间小于t。

第二阶段：系统从s1=1到达切换滑模面的阶段，可知|s1|<1。

此时趋近律可以写为

(23)

根据对应的收敛时间，同理计算得

(24)

综上可知，两个阶段的趋近情况在s1>0时，系统从初始状态s0到s1=0的时间应该小于上述两个阶段所需时间的总和t1+t2。

当系统的初始状态s1<0时，其收敛到滑模面的时间同样分为2个阶段：从初始状态s0到s1=-1和从s1=-1到滑模面，分析与计算原理与上述系统初始状态s1>0时相同。

(2)滑模面s2=n1xe-n2ωrye在有限的时间内趋近到0的证明。

记滑模面s1、s2的收敛时间分别为ts1、ts2。所以当总时间t>ts1+ts2时，滑模面s1、s2可以收敛到0，此时的角速度和线速度可分别表示为

ωm=ωr

(25)

(26)

此时式(9)可变形为

(27)

(28)

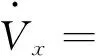
(29)

因为xe渐近收敛到0，并且滑模面s1和s2已经证明可以在有限时间内收敛到0，所以可得ye也会渐近收敛到0。

综上所述，小车在基于新型变指数趋近律滑模控制器的作用下，xe、ye和θe均可在有限时间内收敛至0。

所以由式(10)、式(12)、式(13)可以得到轨迹跟踪运动控制器的式子分别为

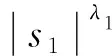
(30)

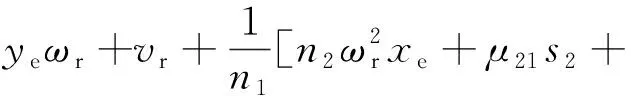
(31)

3 仿真结果及分析

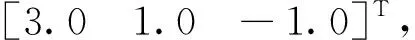
由图5可知，智能小车的轨迹跟踪误差可以在0.5 s内收敛到0。图6所示为速度控制器的曲线变化图，由图6可知，在新型幂次趋近律滑模轨迹跟踪控制器v和ω的作用下，智能小车可以很好地跟踪参考轨迹。

图5 轨迹跟踪误差曲线Fig.5 Trajectory tracking error curve

为了更深入地验证新型滑模幂次运动趋近律对轨迹跟踪运动控制的联合仿真有效性，将基于新型幂次趋近律的滑模控制器与基于双幂次趋近律的滑模控制器[26]进行联合仿真及其实验对比，图7、图8分别为智能小车在新型幂次趋近律和双幂次趋近律滑模控制作用下的实际轨迹与参考轨迹的曲线对比图，然后选择适当的参数，得到如图9所示的系统轨迹跟踪误差xe、ye、θe的仿真对比结果图。

图8 两趋近律跟踪正弦型参考轨迹曲线Fig.8 Two reaching laws tracking sinusoidal reference trajectory curve

图9 系统轨迹跟踪误差仿真对比Fig.9 System trajectory tracking error simulation comparison

由图9可知，基于新型幂次趋近律滑模控制器控制的轨迹跟踪误差的收敛速度明显快于基于双幂次趋近律滑模的轨迹跟踪误差控制器，而且其超调也明显小于双幂次趋近律滑模控制器，由此可知本文趋近律的跟踪效果更好。

4 实际环境下的测试

为了充分验证本文新型幂次趋近律滑模控制器的准确性，将自主研发的智能小车放于实际环境中进行轨迹跟踪实验，硬件系统以树莓派为核心控制器，智能小车的接收设备为WHEELTEC IMU惯性导航模块，其速度精度为0.05 m/s，角度分辨率小于0.01°，角度重复性小于0.1°，位置测量精度为0.01 m， 智能小车跟踪的轨迹选取为“8”字形，表达式为

(32)

图10 实验中的智能小车Fig.10 Smart car in experiment

由图11可知，基于新型幂次趋近律的智能小车除了“8”字圆弧位置，其他位置均能较为平滑的跟踪给定轨迹。图12为该控制器下的跟踪误差曲线，可知由于其给定起始位姿与参照轨迹起始位姿不一致，导致较大的初始位姿偏差，在18～22 s和38～45 s区间，由于处于“8”字形弧度拐弯处，轨迹曲率大，导致就小车所受的侧滑现象产生，同时伴随离心力的影响，造成位姿偏差较大。其中xe、ye、θe的偏差范围分别是：-0.32～0.36 m、-0.5～0.5 m、-0.4～0.2 rad。当曲率较小时，智能小车可以做平滑的跟踪运动，且跟踪偏差趋于0。图13为速度趋近律输出变量变化曲线，可知：由于实际摩擦力的存在会导致速度的波动产生，但小车基本可以很好地跟踪参考轨迹。 上述结果更加准确的验证了本文所提基于新型变指数趋近律的智能小车具有很好的跟踪效果。

图11 轨迹跟踪曲线Fig.11 Trajectory tracking curve

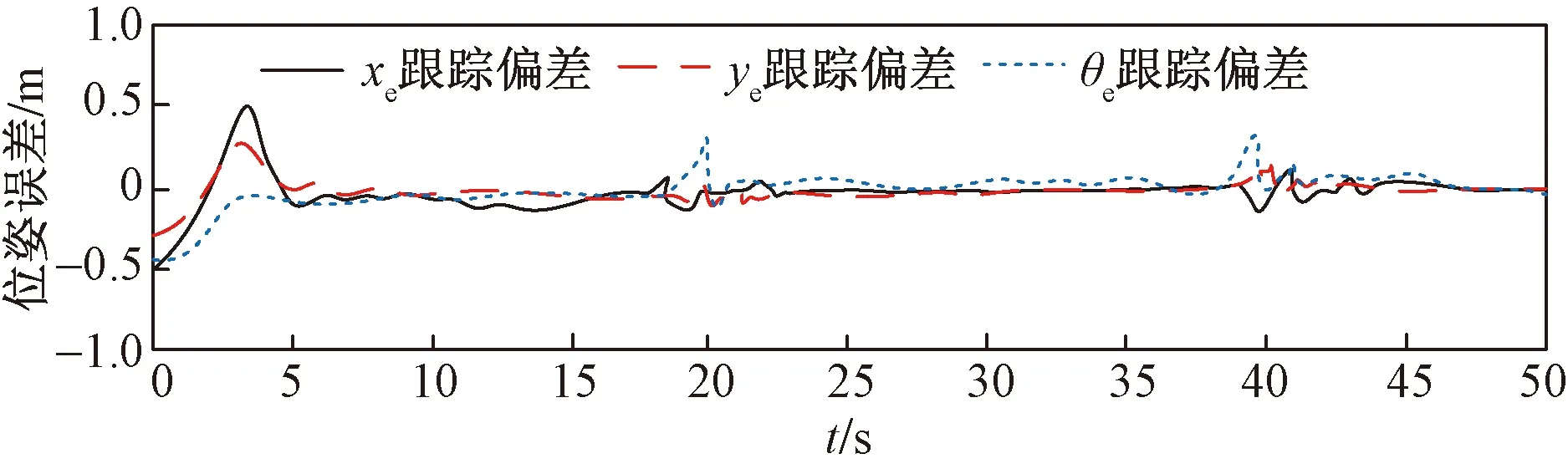
图12 轨迹跟踪误差曲线Fig.12 Trajectory tracking error curve

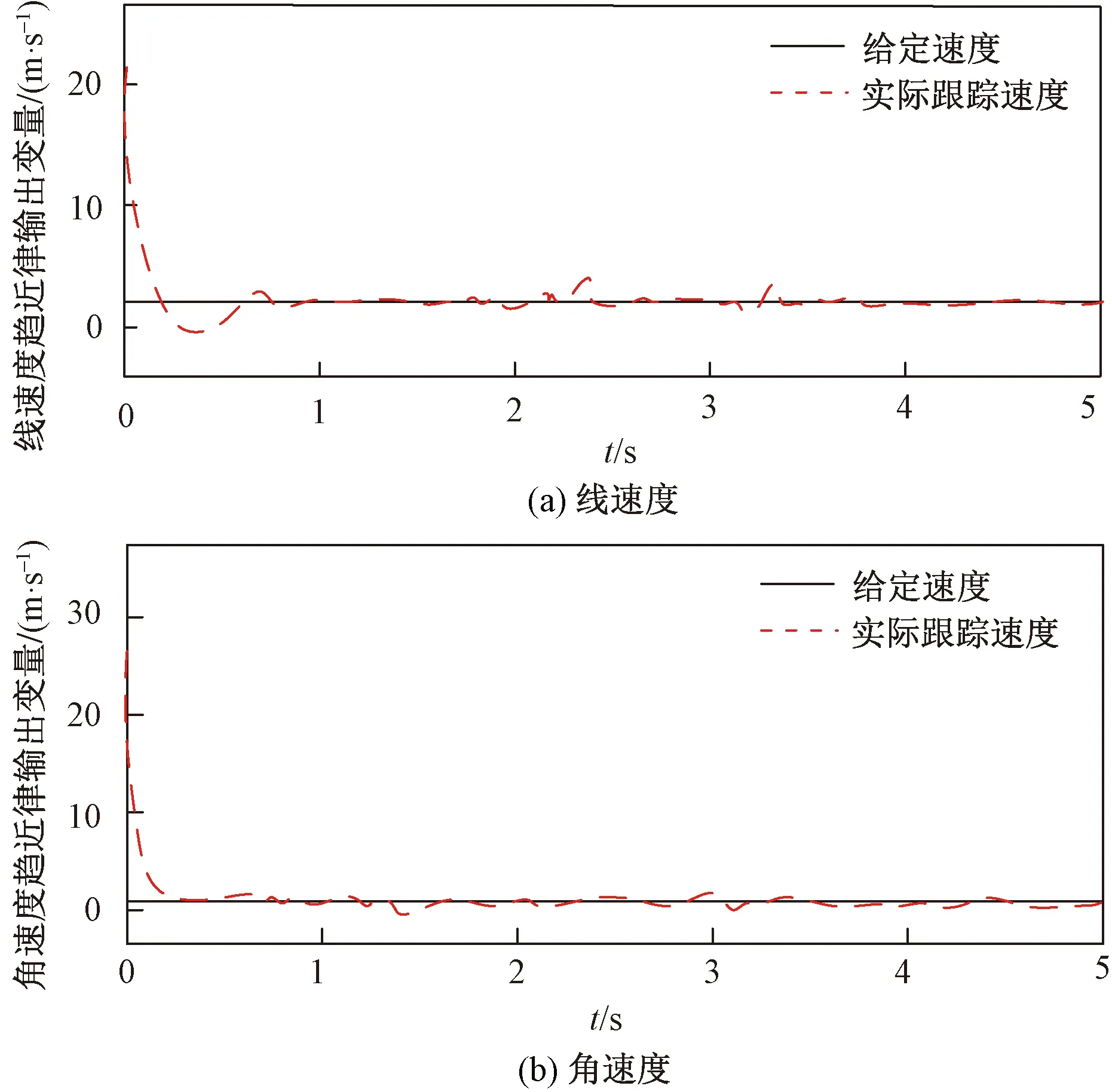
图13 速度趋近律输出变量变化曲线Fig.13 The output variable curve of the speed approaching law

5 结论

以新型智能滑模小车为主要研究实验对象，建立其小车轨迹快速运动学原理控制系统模型并对其进行系统设计分析，提出一种基于新型变指数幂次趋近律滑模运动控制的小车轨迹快速跟踪运动控制解决方案。提高轨迹跟踪时指数趋近速度的同时不仅大大削弱了小车控制系统本身的抖振运动现象，并且还能使其具有很强的运动抗干扰能力，使得小车控制系统在进行轨迹跟踪时的误差快速收敛并能及时达到0。并且将其与双幂次趋近律作用下的轨迹跟踪控制算法仿真进行实验对比，同时将小车在实际环境中进行了实验，仿真的实验结果充分验证了本文所提控制策略的正确有效性，使智能小车在轨迹跟踪时能够具有更优的轨迹跟踪效果和更高的运动品质。