一种耦合算法的三维弹性空腔声振特性分析
文润旭, 袁丽芸*, 刘嘉明, 刘丽萍
(1.广西科技大学机械与交通工程学院, 柳州 545006; 2.广西汽车零部件与整车技术重点实验室, 柳州 545006)
弹性空腔结构应用在工程中的各个领域,如船舶的船舱、飞机的机舱等,可以进一步简化为弹性空腔的模型。对于弹性空腔的振动与噪声问题一直是迫切需要研究人员解决的,提高弹性空腔声振特性性能是科技前瞻性的研究。有限元法是现如今工程分析中最广泛的数值方法,并随着计算机技术的不断发展有限元法受到科技工作者的高度重视并得以应用,它具有灵活性、高效性、边界适应性好等特点,并且能够适应于多物理场的数值分析,如声固耦合、磁固耦合等。有限元数值方法的主要思想是通过把问题域离散为若干单元,并将它们的边界上的结点相互连接,用近似函数表示求解域的未知变量,使用变分原理建立求解未知的代数方程。其中,二维板结构的三角形单元,由于边界适应性强,位移函数构造简单,计算规模小,得到了广泛的应用。顾太平等[1]基于直角坐标系的三角形离散网格,采用面积坐标构造了薄板三角形单元内部任意一点的挠度位移插值函数。薛俊好等[2]在文献[1]的基础上,进一步给出了该三角形板单元的应变矩阵计算公式。然而,上述两篇文献均缺少进一步的算例分析。由于插值型函数直接由原始网格生成,当单元网格畸变时,其精度将难以保证,角形板在进行弹性板的动力学问题分析中,具有较好的边界适应性,然而需要进一步处理单元畸变引起的精度较差问题。
针对三维空腔问题,常采用的方法包括有限元法、边界元法、光滑有限元法等,应用广泛的三维单元包括四面体单元和六面体单元。闵祥斗等[3]利用有限元方法对高速列车车室进行声固耦合建模,经过Ansys软件仿真预测中低段噪声。杨年炯等[4]针对驾驶室轰鸣声问题使用有限元方法对引气管仿真继而优化,其中在引气管不平整面采用三角形网格划分,避免了网格畸变产生的计算误差。Du等[5]对弹性板为边界的三维空腔进行了声振耦合分析,并且使用Rayleigh-Ritz法,基于结构-声学耦合系统的能量表达式,确定了其低阶模态频率。白洁[6]采用Galerkin法对三维声场进行离散,生成四面体单元,车身采用四边形单元,构造了车身三维弹性空腔的有限元耦合模型,采用Virtual Lab获得了耦合系统的固有频率。结果表明在驾驶舱不规则区域边界采用四边形网格离散,会产生奇异点,从而影响计算精度,甚至发生不收敛现象。姚昊萍等[7]构建了由2块弹性板和4块刚性板构成的声-固耦合空腔模型,利用了瑞利-里茨方法求解耦合系统的特征值,使用纽曼边界条件,分析了空腔内的声压响应,通过算例结果验证了此模型解析解与实验值一致性。戴腾飞[8]应用光滑有限元法对柴油机缸盖内外声学建模,并验证此方法的可行性。需要指出的是,上述研究中声场区域均采用有限元法构造声学刚度矩阵,由于有限元本身的局限性,其刚度矩阵偏硬,因此,计算精度有待进一步的提高。而光滑有限元法在处理声学问题上具有对刚度“软化”的作用,逐渐得到了学者们的青睐。郭小斌等[9]总结了光滑有限元法的类型和优点,此方法能够软化刚度矩阵、处理体积锁定问题,应用也极其广泛,其中在声学的应用中具有较高的收敛性和精度。Li等[10]使用光滑有限元法对结构-声学耦合问题分析,由于板和弹性空腔都是采用光滑有限元法进行模型的建立,所以具有对有限元“过硬”情况软化的效果,因此比有限元法精度更高,但其弹性板所采用的三角形单元面内位移采用了一阶剪切变形理论,与横向位移相关,仍具有一定的局限性。张智琅等[11]基于光滑有限元-解耦有限粒子法(smooth finite element method, decoupled finite particle method, SFEM-DFPM)模拟流固耦合问题,能够解决传统有限元“过刚”的问题,此耦合方法能有效处理自由液面的流固耦合问题。
综上所述,目前对弹性空腔的研究多采用有限元法或光滑有限元法进行,其中声场区域采用光滑技术处理可以将声刚度矩阵进行“软化”,从而提高计算精度;而弹性板采用4节点3自由度单元或3节点3自由的板单元进行离散,面内位移与横向位移相关,计算精度有待进一步的提高。最近,刘嘉明等[12]用边光滑有限元进行二维约束层阻尼( constrained layer damping ,CLD)全敷设矩形腔的声振分析,并与有限元法比对,具有较好的计算精度,其研究思路可进一步拓展到三维情形。基于此,拟采用3节点5自由度的三角形单元对薄板进行离散处理,以便得到边界适应性好、精度较高的薄板有限元模型;再对弹性空腔的声刚度矩阵进行光滑处理,以软化声场刚度矩阵;然后考虑弹性板和空腔的耦合条件,从而得到三维弹性空腔的一种新的声振耦合模型,并进一步对该类模型的声振特性进行数值探讨。
1 三维弹性空腔声固耦合模型
如图1所示,三维弹性空腔是由声腔域和柔性板组成,其中顶部采用柔性板,其他五个壁是刚性的,对于此类弹性空腔使用一种新方式组合建模,分别对板进行三角形单元有限元法建模、声腔域进行光滑有限元建模。下面分别阐述板有限元模型、声腔域光滑有限元模型,以及三维弹性空腔耦合模型。

图1 三维弹性空腔耦合模型Fig.1 Three-dimensional elastic cavity coupling model
1.1 薄板有限元模型的建立
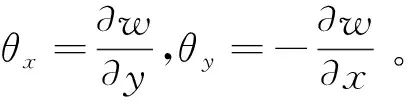
针对上述板单元,引入薄板的中面位移向量,即
Δ=[u,v,w,θx,θy]T
(1)
根据文献[1],采用边界适应性较好三角形单元对板结构进行离散。引入面积坐标L1、L2、L3,则单元内任意点(xi,yi)的挠度可写为
(2)
式(2)中:形函数具体表达为
(3)
(4)
(5)
同时,考虑三节点三角形单元任意点(x,y)独立于横向位移的面内位移,即
(6)
由式(2)、式(6)引入形函数矩阵Ns,即
(7)
为了尽量减少网格畸变所带来的计算误差,将采用等参单元进行坐标映射,将物理坐标映射到自然坐标系中进行计算。此时,可将单元内部任意点的坐标用节点坐标和形函数表达为

L3=1-ξ-η
(8)
用变分法可得板结构的动力平衡方程为
(9)
式(9)中:us为板节点位移向量;Ms为板质量矩阵;Ks为板的刚度矩阵;Fs为结构的节点等效外部激励向量;Ffs为流体在流固耦合边界作用在结构上的节点等效声压向量。其表达式为
(10)
(11)
(12)
(13)

1.2 声腔域光滑有限元模型的建立
通过标准的伽辽金方法,得到声腔域Helmholtz方程的加权残值弱形式,即

(14)
式(14)中:kω为声场波数;ρc为声场介质密度;ΓN为边界条件。

(15)
采用光滑梯度技术,声学问题的光滑声压梯度可表示为

(16)
式(16)中:Bfi(x,y)表示光滑梯度矩阵;M为局部光滑域的节点总数。
将式(15)和式(16)代入式(14)中,运用变分原理,并通过单元集成分析,可以得到声学域光滑有限元动力学方程为
(17)
式(17)中:Kf表示声学光滑刚度矩阵;Mf表示声学质量矩阵;Ff为空腔在边界处的振动所引起的激励力向量,其表达式[12]为
(18)
(19)
(20)
1.3 三维弹性空腔声固耦合方程的建立
在声腔域板的耦合处,板的振动法向速度会对声腔产生耦合力,并结合式(20),该耦合作用力可以表示为
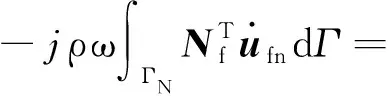
(21)
结合式(9)、式(17)可得弹性空腔耦合方程为
(22)
对于自由振动问题,式(22)的右边激励力向量为0,代入位移和声压边界条件(一般为0)后,不难获得该类问题的特征方程为
|K-λM|=0
(23)
式(23)中:K和M是代入边界条件后,划掉边界向量为0时对应的各行和各列元素后,整理所得的刚度矩阵和质量矩阵。进一步求解得可得耦合系统的固有频率和振型。
2 数值算例
2.1 柔性板的模态分析
为了验证文中三角形板单元有限元法的准确性及良好的适应性,此算例对矩形薄板进行模态分析,几何和材料参数取自参考文献[10],该矩形薄板为柔性铝板,长a=0.4 m、宽b=0.32 m、厚h=0.001 m、弹性模量E=71 GPa、泊松比υ=0.3、密度ρ=2.7×103kg/m3,约束条件采用四边简支。
用本文数值解与文献[10]中的有限元方法(finite element mothod,FEM)、光滑有限元方法(smoothed finite element mothod,SFEM)数值进行固有频率及误差大小的对比,结果见表1所示。图2、图3则给出了ANSYS和本文所用方法所得简支板的前两阶振型图。其中本文方法所得振型图根据MATLAB编程所得模态振型矩阵,代入Tecplot软件绘制所得。
从表1可知,在低阶时,本文数值算法的计算结果误差稍高于SFEM计算结果,但在中高阶时,其误差低于SFEM计算结果;本文方法整体上计算结果误差小于文献[10]FEM和ANSYS的计算结果;此外,图2、图3给出了ANSYS和本文所用方法所得简支板的前两阶振型对比图,极度相似。综上,本文数值算法结果接近SFEM结果,并且本文的计算精度比传统有限元精度高。因此,使用本文数值算法对板进行模态分析是精确的,且计算规模小。
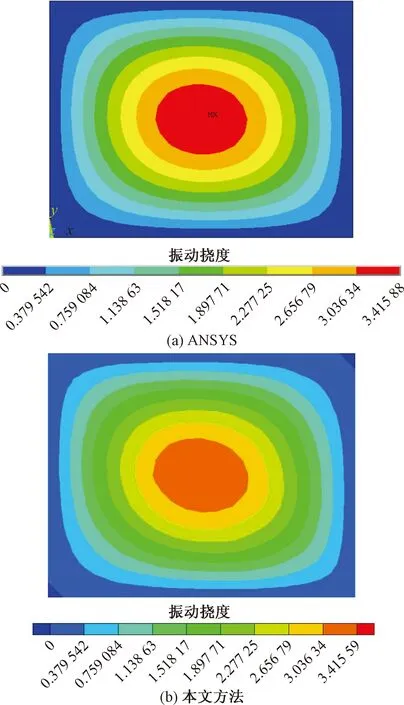
图2 矩形薄板第一阶模态振型Fig.2 The first mode of the rectangular plate

图3 矩形薄板第二阶模态振型Fig.3 The second mode of the rectangular plate

表1 四边简支矩形薄板前十阶固有频率对比Table 1 Comparison of the first ten natural frequencies of the triangular thin plate
2.2 三维弹性空腔声振特性分析
为了评估本文方法对三角形单元的薄板理论推导的合理性,进一步考查本文中使用的柔性板有限元建模、声腔域光滑有限元建模,再进行新耦合方式的合理性,及三角形单元与四面体单元的适应性效果,对此分析三维弹性空腔声固耦合的声振性能。
本例中,为了跟文献[10]作对比,封闭矩形空腔的尺寸参数选为:长为0.4 m、宽为0.32 m、高为0.36 m。板材为铝制,同算例1中柔性薄板的几何参数和物理参数一致。柔性薄板由三角形网格建模,该简支板的边界条件位于边缘。空腔内的三维空气是由四面体网格模拟,其空气的物理参数:密度ρ=1.225 kg/m3、声速c=340 m/s,计算得出了由柔性板组合三弹性空腔前十阶固有频率结果见表2所示。其中,本文模型的网格尺寸为0.04 m,ANSYS有限元网格尺寸为0.02 m。
从表2可知,三维弹性空腔模型固有频率的对比中SFEM的计算结果误差小于ANSYS的计算结果;本文数值算法比SFEM计算精度更高,并且更接近参考解,在中高阶模态中计算结果较明显;进一步分析图4、图5可得,ANSYS和本文所用方法所得三维弹性空腔前两阶振型基本相同。

图4 三维弹性空腔模型的一阶模态振型Fig.4 The first mode of the three-dimensional elastic cavity model

图5 三维弹性空腔模型的二阶模态振型Fig.5 The second mode of the three-dimensional elastic cavity model

表2 三维弹性空腔模型前十阶固有频率对比Table 2 Comparison of the first ten natural frequencies of the three-dimensional elastic cavity model
综上,验证了FEM与SFEM耦合算法是正确的,并且计算效果较好,说明了在保证计算规模较小的前提下,本文方法仍具有较好的计算精度。
3 结论
本文中三维弹性空腔声固耦合新模型是分别采用三角形单元对板进行有限元建模、光滑有限元法对声腔域进行光滑处理,再考虑二者的边界耦合条件进一步建立的。通过与文献[10]和ANSYS仿真结果对比可得出以下结论。
(1)采用3节点5自由度的三角形单元对薄板进行离散处理计算规模小,精度足够。
(2)基于FEM与SFEM耦合算法的声固耦合模型,计算精度高,规模也相对较小。
(3)由于采用的三角形板单元具有良好的边界适应性和较小的计算规模,声腔域的光滑处理也软化了声场域的刚度矩阵,可保证较好的计算精度,本文中所建立的声振耦合模型可进一步地应用于实际工程中形状更复杂弹性空腔结构的声振特性分析中。

