应急物资多式联运鲁棒路径优化

刘 松， 郭 敏， 乐美龙， 彭 勇

(1.南京航空航天大学民航学院， 南京 211106； 2.重庆交通大学交通运输学院， 重庆 400074； 3.山地城市交通系统与安全重庆市重点实验室， 重庆 400074)

近几十年来，地震、洪水、台风等各种类型的自然灾害频发，造成大量的经济损失与人员伤亡。灾害发生后，能否在道路塌陷、运力不足、交通受阻等情况下找到一条时间成本较低、效率较高的运输路线将救援物资尽快调拨到灾区成为了抢险救灾、降低人员伤亡与经济损失的关键。

路径优化问题受到了学者的广泛关注，这些研究主要集中在增加运输模型约束条件或算法设计方面。祝新等[1]考虑到路况对于传统医疗冷链物流配送模型的影响，建立了以综合成本为目标的配送模型。陈畴镛等[2]研究了在时间窗及配送公平性影响下的运输路径规划问题。何婷等[3]研究了疫情背景下生鲜电商企业的车辆路径优化问题。Jiang等[4]建立了将多项目包装与车辆路径和分批配送相结合的优化模型。刘松等[5]研究了碳排放限制下冷藏集装箱的路径优化问题。陈汨梨等[6]研究了不确定条件下多式联运路径优化问题。

在应急物资运输方面，许多学者在研究确定环境下的多目标优化及物资调度与选址问题。宋英华等[7]建立了双目标应急物资配送车辆路径问题整数规划模型，并验证了模型的有效性。薛星群等[8]研究了通行约束和运力限制条件下的应急物资联合调度问题。刘倩宇[9]将选址问题与路径优化问题进行了结合，考虑到备选配送中心的优先级，对应急物流的选址——路径优化进行了研究。吕伟等[10]研究了应急物资需求紧迫程度差异下的物资配送路径优化问题。刘晋等[11]运用自适应遗传算法，对应急物资储备库选址及调度问题进行了研究。

随着研究的深入，有学者注意到确定环境下给出的应急物资运输方案难以满足实际中的应急物资运输要求，对不确定环境下的应急物资运输开展了研究。张梦玲等[12]研究了不确定需求下考虑供应商参与机制的应急物资配置问题。Wang等[13]提出了一种海运不确定性条件下的多式联运综合调度模型。王妍妍等[14]研究了模糊信息下多种类应急物资多周期分配优化问题。葛显龙等[15]针对动态事件对配送过程的干扰问题，研究了多品类共同配送车辆路径优化问题。但是已有的研究大多假设已知部分参数的概率分布，而在实际运输作业过程中，尤其是发生突发事件后的应急物资运输，这些参数却因缺少历史数据而无法知道其概率分布情况，而更应该寻求鲁棒运输路径。然而，单一运输方式下的鲁棒路径优化问题已经被证明是NP-Hard(nondeterministic polynomial-hard)问题[16]，对该类问题的研究一直以来都是学者研究的热点。孙秀巧等[17]运用改进遗传退火算法，对高速公路巡逻车辆路径优化调度问题进行了研究。康斌等[18]建立了多目标应急救援物资配送路径优化模型，并利用改进后的遗传算法验证了模型的正确性。昝新宇等[19]提出一种基于改进蚁群算法的救援路径规划方法。赵邦磊等[20]建立了多目标优化的冷链物流配送模型，并设计改进ACO(ant clony optimization)算法对模型进行了求解。而应急物资多式联运鲁棒路径优化问题需要同时考虑不同运输方式之间的转运以及铁路、水路等的发班时刻限制等，对其求解相较于单一运输方式下的路径优化问题更为困难，需要针对模型的独特性设计专门的算法。

综上所述，当前中外学者对确定环境下的路径优化问题研究较多，而不确定环境下的成果较少，这类研究忽略了外部环境对于系统的影响，得到的运输优化路径在应用于复杂多变的应急物资运输网络时鲁棒性较差。且少有学者同时考虑到应急物资运输途中的不确定性以及水路、铁路等运输方式的发班时刻限制。基于此，针对应急物资运输的不确定性和铁路、水路等的发班时刻限制，构建应急物资多式联运鲁棒路径优化模型，并针对模型求解的NP难特点，设计大变异遗传算法与自适应遗传算法，并进行了算例应用，可为应急物资决策者提供一定的参考。

1 问题描述及建模

1.1 问题描述

在如图1所示的多式联运网络图中，假设现需将应急物资从起点1运输到终点8，物资在不同的运输方式间存在着转运时间。同时，由于运输环境的不确定性，各节点之间所需要的运输时间是不确定的。另外，水路及铁路运输需要按照发班时刻表发班，求一条时间成本较低且鲁棒性能较好的物资调拨路径。

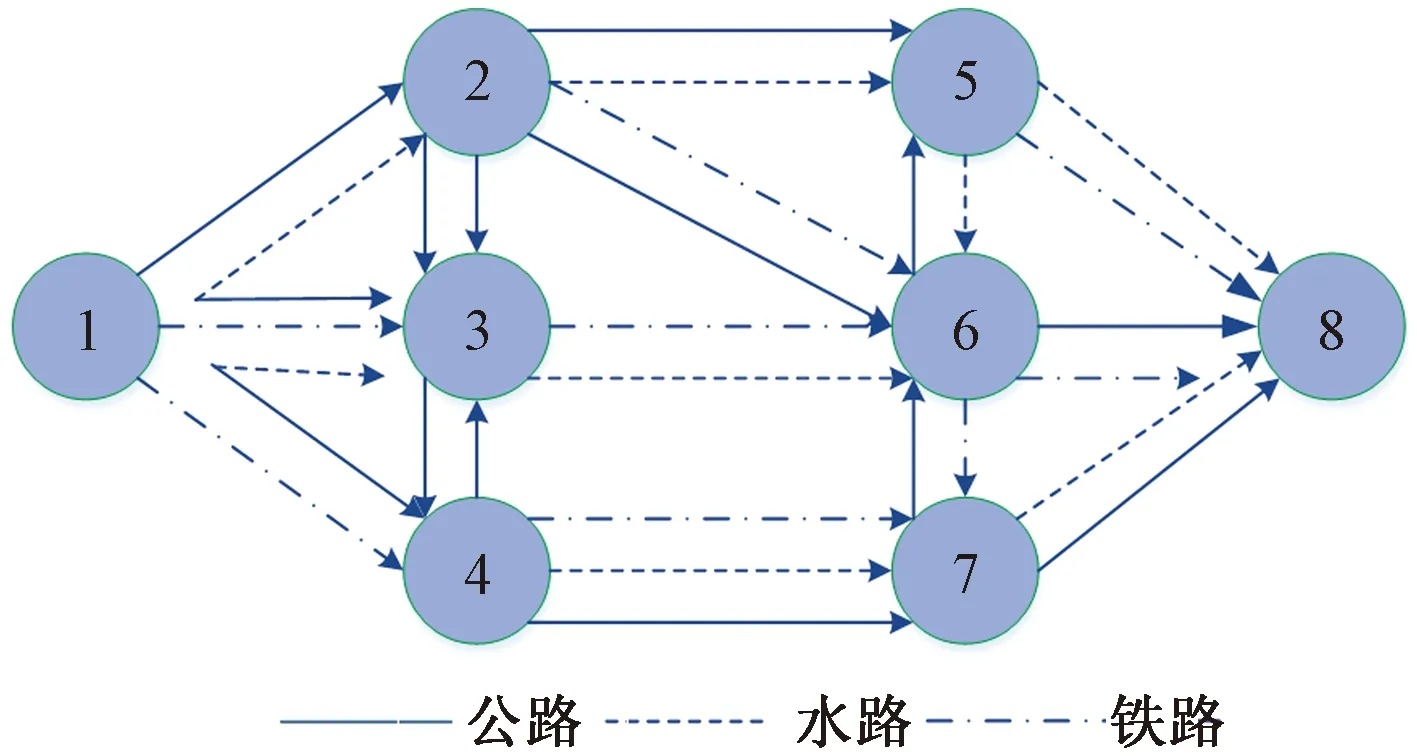
图1 多式联运运输网络Fig.1 Multimodal transport network

1.2 模型假设与变量

1.2.1 模型假设

(1)货物在运输节点只可转运一次。

(2)运输途中并不发生货物的装卸，即运输全程货运量保持不变。

(3)相邻两节点之间，只能采用一种运输方式进行运输。

(4)每个运输节点最多被经过一次，即运输途中不出现封闭回路。

(5)运输途中除了由于班期限制导致等待外，其他地方无需等待。

1.2.2 模型参数及变量

本文模型参数及变量如表1所示。

表1 模型参数

1.3 目标函数及运输条件

1.3.1 目标函数

应急物资运输最主要的特点是时效性要求高，因此将运输时间最短作为决策目标，另外，鲁棒优化分为绝对鲁棒、相对鲁棒以及偏差鲁棒3种，采用绝对鲁棒优化方法，构建目标函数，即

(1)

式(1)中：第一项为运送时间；第二项为转运时间；第三项为由于班期限制导致的等待时间。

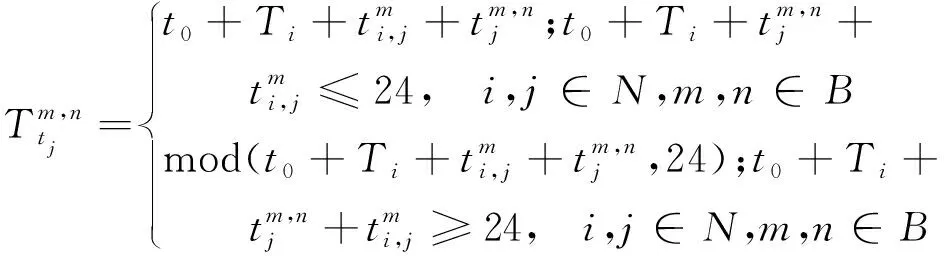
(2)

(3)

1.3.2 约束条件

(1)需要满足流量守恒约束。即起点净流量为1，转运点净流量为0，终点净流量为-1。表达式为

(4)

(2)应急物资在相邻两个节点之间只能选择一种运输方式，表达式为

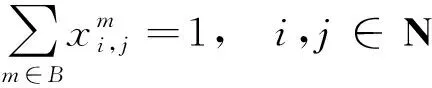
(5)

(3)运输连续性约束，即

(6)

(4)应急物资在节点处只能转运一次，即

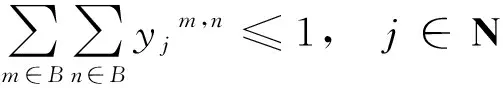
(7)

(5)决策变量只能取0或者1。

(8)

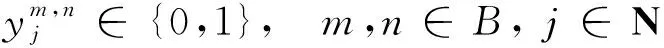
(9)

2 问题求解

由于传统的最短路算法不能求解应急物资多式联运鲁棒路径优化模型，现设计遗传算法进行求解。

2.1 编码及初始种群的生成

2.1.1 编码

由于多式联运运输方式，运输路线都未知，故采用可变长的路径编码方法。具体编码过程如下。

(1)染色体的编码由两段组成，第一段采用Floyd法生成一条从起点到终点的运输路径。

(2)第二段是在第一段生成运输路径的基础上，随机生成一种对应节点间已存在的运输方式，用数字1表示公路运输；2表示铁路运输；3表示水路运输，如图2所示。

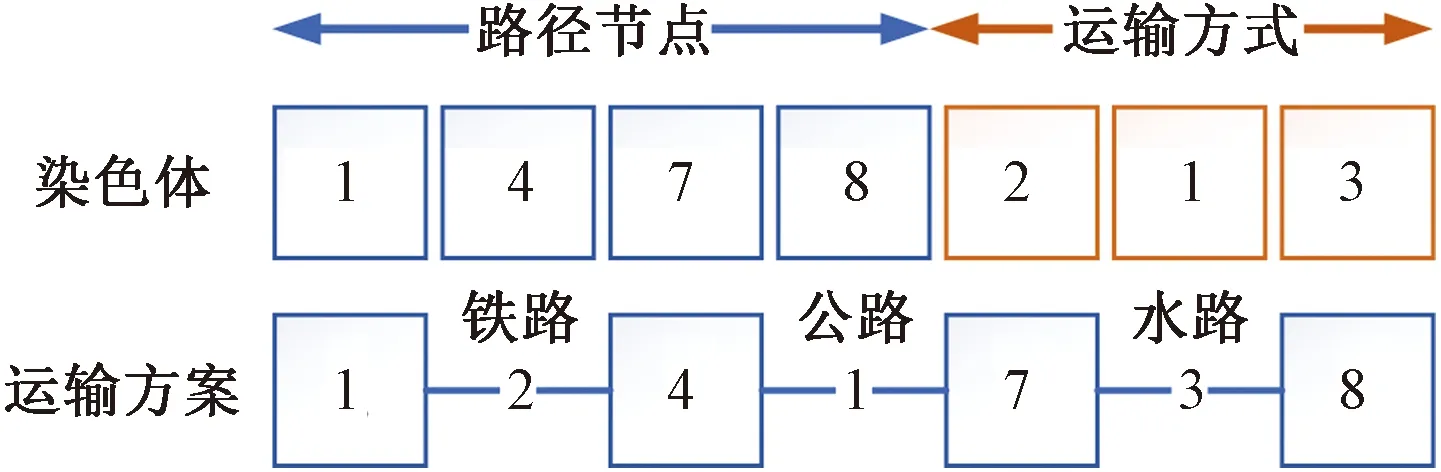
图2 编码示意图Fig.2 Coding diagram

2.1.2 初始种群的生成

采用如下方法生成初始种群。

(1)根据多式联运网络图生成稀疏矩阵，稀疏矩阵中的非零元素对应于边的权值，即路径长度。

(2)利用Floyd法生成染色体第一段编码，接着随机选择节点间的运输方式，生成第二段编码，得到一条初始染色体。

(3)判断染色体数量是否达到种群规模，若已达到，则终止；否则将染色体第一段编码所对应的各节点间的路权扩大一个较小倍数，返回(2)。

2.2 适应度评价与约束条件判断

因本文中以时间成本最小为目标，而遗传算法的适应值越大越好，故采用目标函数的倒数为适应值函数，即

f=1/Z

(10)

2.3 遗传操作

2.3.1 选择

采用轮盘赌选择方法。

2.3.2 交叉

对第一段染色体采用两点交叉的遗传方式，并对于交叉后可能产生的非法染色体通过Floyd法进行修复，具体过程如下。

(1)若第一个交叉节点直接与起点相连，且与起点之间没有通路，则可通过Floyd法找到两点间的一条连通路。同样的方法也可处理第二个交叉节点与终点相连时的阻断情况。

(2)若两个交叉点皆在路径中间位置，则任意交叉点和相邻节点无法连通时，都可以通过找到与之相邻的上一节点之间的连通路径进行方案改进。若无连通路径，则继续探查再上一节点。如图3所示:染色体U1与染色体U2交叉后得到的染色体U3为非法染色体。因节点2和节点4之间存在连通路，则无需继续探查节点2与上一节点7之间的连通情况，可直接用Floyd法找到节点2与节点4之间的一条连通路2-3-4使染色体U3为合法染色体。

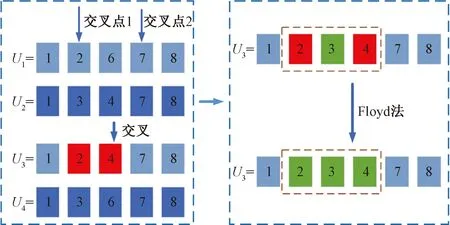
图3 Floyd法寻找连通路Fig.3 Floyd’s method to find the connecting pathway

2.3.3 变异

采用的变异方法如下：随机选择第k个基因位作为变异位，去除该基因位上的基因，接着判断第k-1个基因与第k+1个基因所对应的节点间是否存在连通路。若连通，则直接在染色体第二段编码对应位置随机生成一种运输方式；反之，则利用Floyd法找到两点之间的一条最短路，将其连通，后续编码过程同上。如图4所示，若有染色体1-2-6-8-2-3-1，现将第二个基因位上的基因2去掉，因为节点1和节点6之间无连通路，所以可利用Floyd法生成一条1和6之间的最短连通路。假设生成的连通路为1-3-6，接着便随机生成节点1和节点3、节点3和节点6之间的运输方式，假设生成的运输方式为公路运输与铁路运输，则最终该染色体将变异为1-3-6-8-1-2-1。

图4 变异操作示意图Fig.4 mutation operation diagram

2.4 算法说明

在上述理论基础上，本文中设计大变异遗传算法和自适应遗传算法对应急物资多式联运鲁棒路径优化模型进行求解。

2.4.1 大变异遗传算法

大变异遗传算法的主要思想如下：为避免算法出现“早熟”现象，当某代的所有个体集中在一起时，便以一个远大于设置概率的大变异概率进行变异操作，将集中了的参数进行“打散”，进而跳出局部最优，保持种群多样性；反之，则继续采用设置的变异概率进行遗传操作，具体过程如图5所示。

Fmax为代代最大适应度；Favg为当代平均适应度；α为密集因子图5 大变异遗传算法流程图Fig.5 Flow chart of large mutation genetic algorithm

2.4.2 自适应遗传算法

自适应遗传算法的关键在于算法运行过程中，会针对每个染色体的适应值匹配专属的交叉概率与变异概率。对于适应值较高的个体，采用较低的交叉-变异概率组合，使其被保留进入下一代的概率加大；对于适应值较低的个体，则采用较高的交叉-变异概率组合，使其被淘汰的概率增加，具体过程如图6所示。

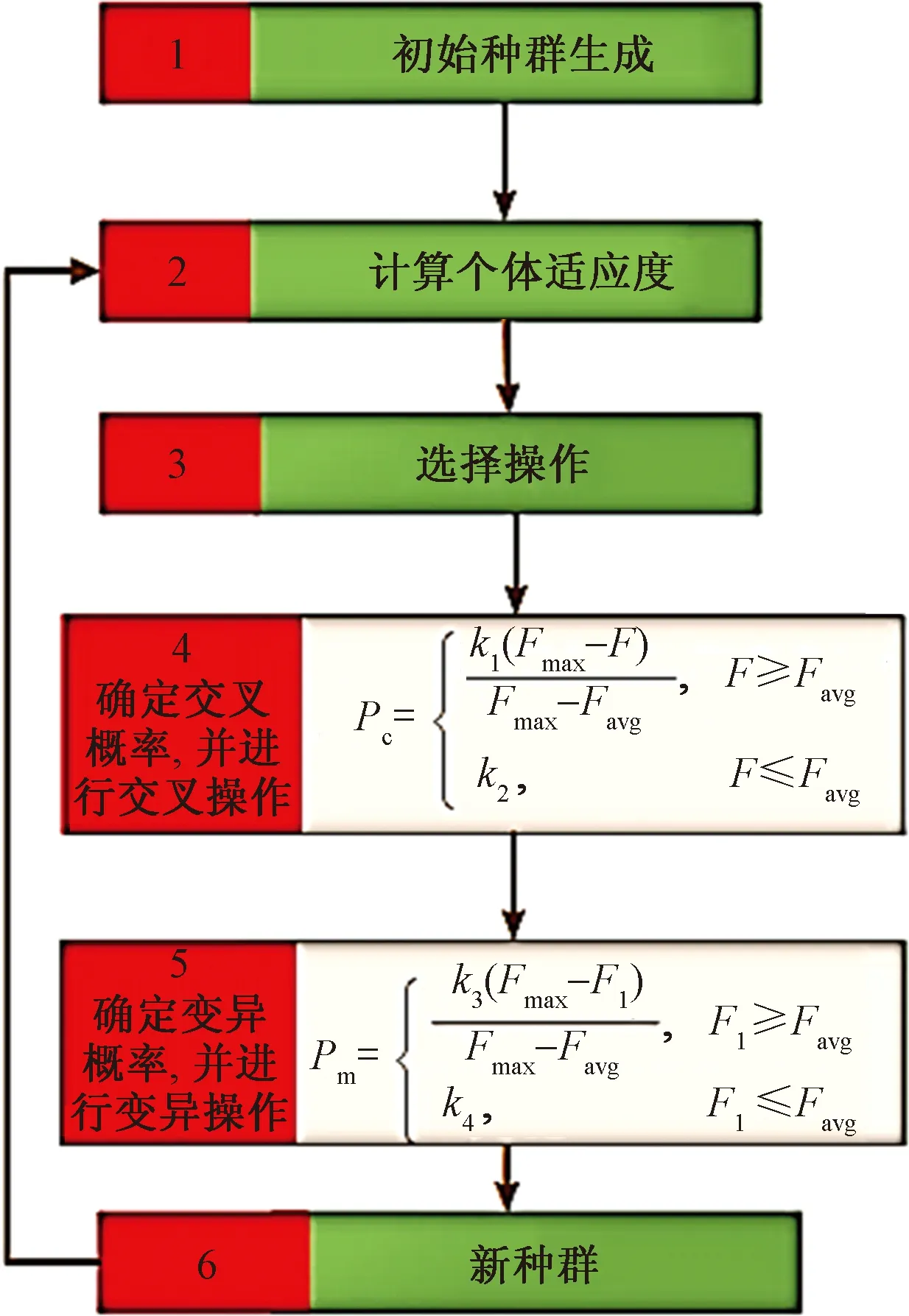
Pc为交叉概率；Pm为变异概率；F为要交叉的两个个体中交大的适应度值；k1、k2、k3、k4为常数图6 自适应遗传算法流程图Fig.6 Flow chart of adaptive genetic algorithm

3 算例分析

3.1 算例设计

为验证模型和算法的有效性，采用如图7所示的多式联运网络进行验证。节点1为运输起点，节点25为运输终点，各节点坐标由Solomon benchmark C102列的前25个数据确定，将两点间的欧几里得距离扩大10倍作为两点间的运输距离。由于运输环境的不确定性，运输速度为不确定值，各运输方式的转运时间、运输速度和班期如表2和表3所示。假设现需要将一批应急救援物资于起点1运出，求从节点1～节点25总运输时间最少的鲁棒运输方案。

图7 多式联运网络Fig.7 Multimodal transport network

表2 不同运输方式的转运时间

表3 各运输方式的运输速度及班期

3.2 结果分析

采用MATLAB R2017a编程实现算法。设置种群规模为70，遗传代数为50。使交叉概率为0.9、0.8、0.7、0.6、0.5，变异概率为0.05、0.04、0.03、0.02、0.01两两组合计算，两种算法在不同的交叉-变异概率组合下连续运行10次，计算得到均值、最优值、运行时间等结果如表4、表5所示。

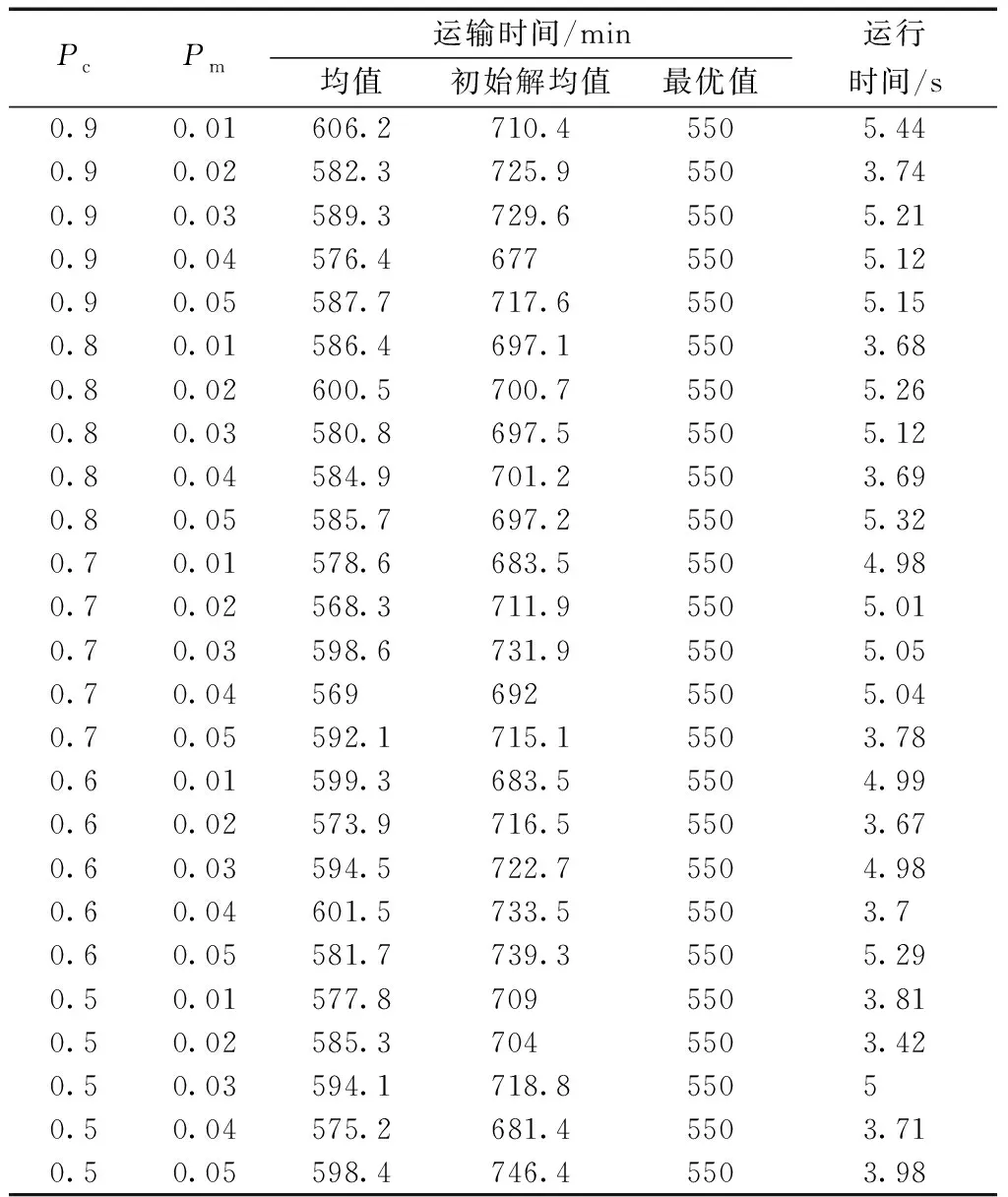
表4 大变异遗传算法实验结果

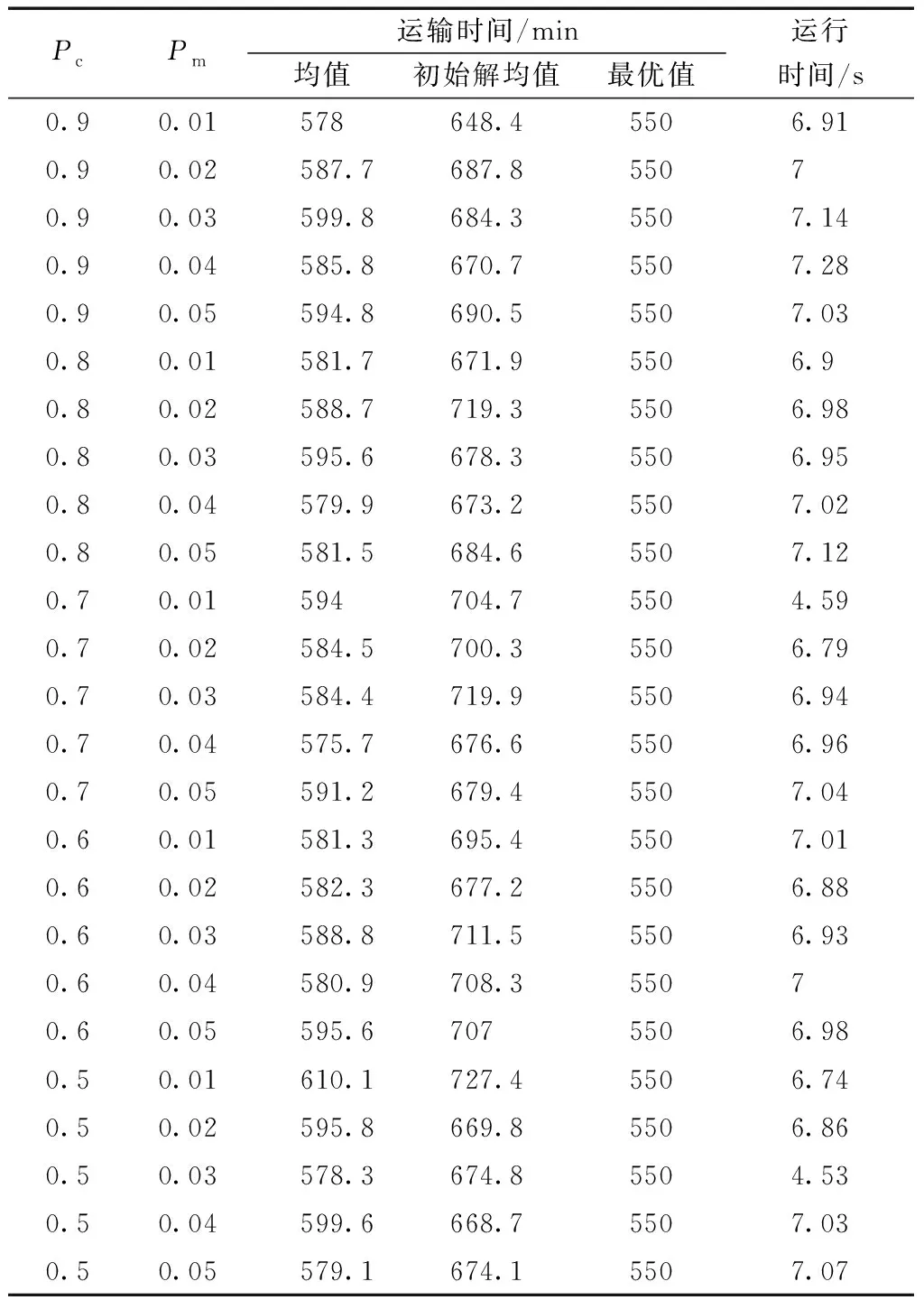
表5 自适应遗传算法实验结果

下面根据两种遗传算法所得到的结果确定本文中具体的求解算法以及合适的概率组合。

3.2.1 求解算法以及概率组合的确定

(1)最优解方面。如图8所示，两种算法在不同的概率组合下连续运行10次找到的最优解均为550，说明两种算法求解得到的应急物资调拨方案所消耗的总运输时间均为550 min，求解效果都相对较好。

图8 不同交叉-变异概率下两种算法的最优解Fig.8 Optimal solutions of two algorithms under different crossover mutation probabilities

(2)初始解均值方面。如图9所示，每种算法在25种不同的交叉-变异概率组合下，连续运行10次，每次运行的种群规模为70，一共会有17 500个初始解。分别运行两种算法，则一共会有35 000个初始解。但是，这35 000个初始解所求得的平均初始解均未超过760，而最优解为550，说明两种算法所产生的初始解均为连通路。

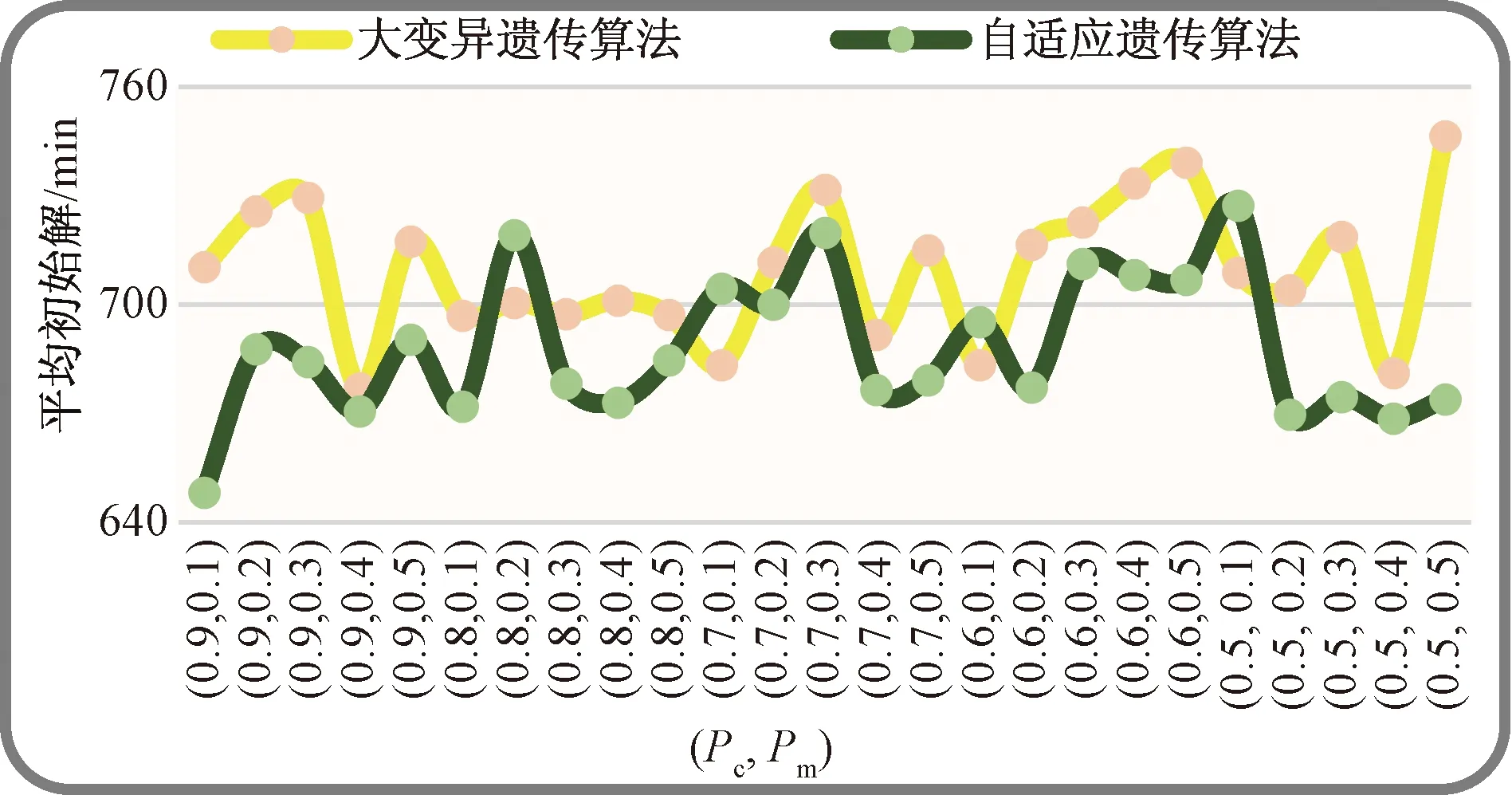
图9 两种算法的平均初始解Fig.9 The average initial solution of two algorithms

(3)运行时间方面。如图10可知，不管变异概率与交叉概率如何组合，在相同的概率组合下，大变异遗传算法的运行时间总会低于自适应遗传算法。由前文可知，两种算法生成的初始解均为连通路，而且求解得到的应急物资运输时间总是相同的，说明大变异遗传算法求解更快更高效。且当Pc=0.5、Pm=0.02时，大变异遗传算法运行时间最短。

图10 两种算法在不同交叉-变异概率组合下的平均运行时间Fig.10 The average running time of two algorithms under different combination of crossover mutation probability

3.2.2 运输方案的确定

运用大变异遗传算法，在Pc=0.5、Pm=0.02下对算例进行求解，得到结果如图11所示。

图11 迭代图Fig.11 Iterative graph

如图11所示，大变异遗传算法存在“阶梯状”的迭代过程，表明其在运行过程中跳出了局部最优解，进行了更大范围的搜索。所需的运输总时间为550 min，运输方案如表6、图12所示。

表6 运输方案

图12 运输方案示意图Fig.12 Schematic diagram of transportation scheme

4 结论

自然灾害发生后，对于应急物资的输送问题引起了运输领域专家与学者的广泛关注。因为在救援物资运输途中，存在各种不确定因素的影响，鉴于此，研究不确定环境下的应急物资多式联运鲁棒路径优化问题，得到如下结论。

(1)将快速、有效地组合应急物资多式联运作为出发点，考虑到运输途中各种不确定情况对于运输结果的扰动以及各运输方式的发班时刻限制，运用鲁棒优化方法，建立了不确定环境下带班期限制的应急物资多式联运鲁棒路径优化模型，并设计了大变异遗传算法和自适应遗传算法对模型进行了求解，求解结果较好。

(2)通过对已有实例进行修改，将大变异遗传算法以及自适应遗传算法的求解结果进行了对比分析，最终确定采用大变异遗传算法在Pc=0.5、Pm=0.02的概率组合下进行算例求解，求解结果可以为应急物资运输决策者提供一定的参考。