例谈初中数学起始课教学

韩光东

摘要：在初中数学的学习中，章节起始课对于一章节的学期起到了统领全局的作用，是学生建立知识架构的重要阶段。本文以苏科版初中数学八年级《6.1函数》为例，体会初中数学章起始课教学的重要价值以及起始课学习的各种策略。

关键词：初中数学;函数;章起始课;策略

中图分类号：G4 文献标识码：A

在初中数学的一线教学中，我们经常会听到关于章节起始课这样的声音：这节课没有什么内容，简要提一下，直接上下一节课就可以了;这节课的内容在接下来的课中有所涉及，到时候我们再重点解剖......种种类似的声音都传递了一个认识，章节起始课没有那么重要，可有可无。笔者认为，缺少了或简化章节起始课会让整个章节的学习少了数学的味道，知识变得零散，学生的学习机械而没有趣味。下面以“函数”教学为例，与大家共同研究思考。

一、教学过程设计

1.创设情境，定义生成

问题1：老师每天早晨骑自行车到学校，老师从家出发匀速行驶，自行车行驶过程中，有那些量没有改变？有哪些量发生了改变？

学生1：自行车行驶的速度不变，行驶的时间在改变，行驶的路程在改变.

学生2：老师从家到学校的总路程不变.

给出常量与变量的定义：在某一变化过程中，

数值保持不变的量叫做常量，

可以取不同数值的量叫做变量. （老师板书常量、变量）

刚刚两个同学提到的4個量中，自行车行驶的速度、从家到学校的总路程是常量，自行车行驶的路程、行驶的路程是变量.

功能分析：从教师自身的例子出发，能迅速引导学生进入到问题情境中去，帮助学生建立“常量”与“变量”的概念.

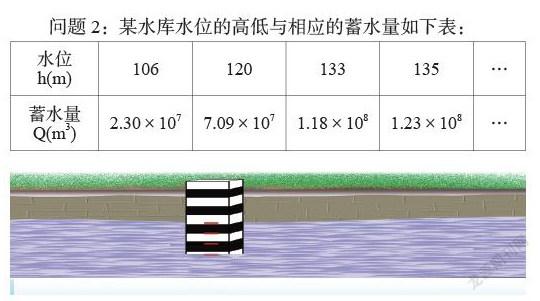
问题2：某水库水位的高低与相应的蓄水量如下表：

水位h（m） 106 120 133 135 …

蓄水量Q（m3） 2.30×107 7.09×107 1.18×108 1.23×108 …

说说表格里有哪几个变量？它们有怎样的关系呢？

学生3：有两个变量，水位h与蓄水量Q，水位在逐渐升高，蓄水量也在逐渐增大.

老师追问：水位与蓄水量之间有没有联系？

学生3：随着水位升高，蓄水量增大.

老师：刚刚你是从左往右观察表格得到的关系，如果从右往左观察，你又能得到什么？

学生3：随着水位降低，蓄水量减少.

老师：如果我给定了一个确定的水位，大家说蓄水量是怎样的？

学生齐答：有一个确定的蓄水量与它对应.

老师总结：可以看出，随着水位升高，蓄水量增大;随着水位降低，蓄水量减少;当水位确定时，蓄水量也随着确定.

功能分析：帮助学生建立“对应”的概念，初步感知一个变量随另一个变量变化的例子，学生在见到这样的表格时，不一定会立马将两个变量之间建立联系，老师及时追问让学生立刻意识到两个变量还存在联系，从而向函数内涵靠拢.

问题3：用火柴棒搭金鱼

搭1条金鱼需要8根火柴，每多搭1条金鱼就要增加6根火柴.设搭n条金鱼所需要火柴的根数为S，则S= .

学生4：搭n条金鱼，比搭第1条多出了（n-1）条，增加6（n-1）根火柴，

所以

S=8+6（n-1），化简得S=6n+2 .

老师：在这一变化过程中，有常量吗？

注：设计这一问题，进一步揭示常量、变量的概念， 对于给定的关系式，指明如何确定常量、变量，学生在回答这个问题时可能会存在疑虑，需要老师指明这里的6、2就是常量.

老师：有哪几个变量，它们之间有怎样的关系？

学生5：有两个变量需火柴棒根数S和小鱼的条数n，n每增加1，S就增加6.

老师：当搭10条小鱼，需要多少根火柴？搭50条呢？搭100条呢？

学生齐答：62，302，602.

老师：也就是说当小鱼条数n确定时，S呢？

学生齐答：也随着确定.

学生6回答，学生一齐复述.（教师板书）

功能分析：本问题出现了一个具体的关系式，进一步体现了两个变量之间的对应关系，本问题比上一个问题更加具体，更能凸显出一个变量随另一个变量的变化规律，揭示函数的本质.后面的填空设计是引导学生这样的思路去思考一个变化的过程，更利于函数概念的建立.

二、基于课例谈起始课的学习

1.总领全章，系统建构知识

对于函数这一章节的学习，我们主要会研究函数的三种表达形式、图像与性质以及应用。本节课的教学设计，为了引出函数的定义，设计了表格、关系式、图像三种不同形式的情境问题，对应于接下来要研究的三种表达形式。在学习的过程中，学生已经能够根据已知信息列出简单的函数关系式，就是接下来要研究的应用类问题。问题4的天气预报曲线图在实际生活中经常会见到，学生很容易说出气温随着时间如何变化，为研究函数图像的性质作了铺垫。整章的内容在起始课的教学中都有所体现，因为起始课的学习，使得接下来的学习很自然，是对起始课的细化与深入学习。我们可以通过起始课的学习，建构起整章的知识架构，让学生体会到数学是一个整体，真正要想认识数学，就要具备基本的系统思维，注重知识与知识的联系，这样更利于学生整合知识，系统性地学习，这样的系统思维我们应该从起始课就开始培养。

2.联系生活，从抽象到具体

章节起始课不是空洞的、没有内容的课，它往往也是一节概念新授课。看似简单的一个概念学生要真正的理解需要借助生活实践，把生活情境中的问题转化为数学的表达。单纯地去说函数的概念是很抽象的，本节课我们通过引入一个行程类问题认识了变量与常量为函数概念的形成做好铺垫，接下来给出三个生活实例，概括出实例中的共同特征，借助这三个生活实例，我们就赋予了抽象的函数概念具体的载体，从而归纳出函数的概念。函数是两个变量之间关系，对函数的内涵理解不透，后续的学习必然会出现障碍。起始课的学习要化抽象为具体，帮助学生理解概念，也为接下来知识的学习打下了坚实的基础。

参考文献

1.雷晓莉.数学起始课教学认识的偏差[J].中学数学教学参考，2010（7）.

2.熊海斌.上好数学起始课的策略探微明.中学教学参考，2015（08） .