连铸板坯三维二冷动态配水与精准压下研究与应用
张炯明,周青海,尹延斌,吴星星,刘华阳
北京科技大学钢铁冶金新技术国家重点实验室,北京 100083
近十几年来中国钢产量飞速上升,去年中国钢产量占全世界总产量的一半以上,连铸是钢铁厂主要流程中的重要环节,连铸坯的质量也成为影响钢材质量的重要因素. 连铸坯表面横裂纹及角部横裂纹在连铸过程中时有发生,特别是中碳钢、中碳合金钢及微合金化钢,该类铸坯的表面缺陷与连铸的二次冷却工艺及压下位置有直接关系;而铸坯的中心偏析、中心缩孔及中心疏松在中碳钢、中碳合金钢及高碳钢上表现得尤为突出,这类质量缺陷与连铸二次冷却及压下工艺有非常大的关系;目前这两种缺陷是制约连铸生产的主要因素,严重影响企业的生产和经济效益. 针对上述问题,本文从连铸坯的主要缺陷入手,弄清缺陷形成的主要机理,提出相应的技术措施,减少上述铸坯的缺陷,提高铸坯的质量.
1 连铸板坯常见的主要缺陷及技术措施
1.1 连铸坯的主要缺陷
连铸坯质量很大程度上影响着钢材产量及其产品质量,连铸坯的缺陷时常会制约企业的生产,典型的铸坯表面缺陷有表面裂纹(纵裂及横裂纹),内部缺陷有中心偏析和中心疏松等,如图1[1]和图2[2]所示. 弄清表面横裂纹、角横裂纹、铸坯中心偏析、中心疏松、中心缩孔的形成机理,采用相应的工艺措施,减少这些缺陷的发生率,是十分重要的课题.

图1 高强汽车板铸坯角横裂纹[1]Fig.1 Corner crack of high-strength automotive steel [1]

图2 微合金钢铸坯中心偏析[2]Fig.2 Central segregation of micro-alloyed steel[2]
1.2 连铸坯缺陷的形成机理
1.2.1 连铸坯表面裂纹形成机理
连铸坯表面横裂纹包括表面横裂纹及角横裂纹,这种裂纹具有多发性,主要发生在微合金钢、中碳钢及有些合金钢上,很多企业采用铸坯下线,角部火焰清理后,再装入加热炉,这种工序严重影响了企业的生产经营[3−5]. 为了解决这一问题,目前相应开发了倒角结晶器等技术[6−8]. 关于这种裂纹形成机理有很多研究工作[9−16],研究多集中在析出物对单相奥氏体下部塑性的影响、对铁素体析出过程的影响、对奥氏体和铁素体两相区上部塑性的影响等. 减少这类裂纹的关键是弄清该钢种的高温力学性能及裂纹开裂方式. 实验钢种成分如表1所示.

表1 实验钢种化学成分(质量分数)Table 1 Chemical composition of experimental steel grades (mass fraction) %
图3为某厂两个微合金化钢种铸坯样断面收缩率(简称RA,下同)随温度的变化曲线. 从图3中可以看出,A32钢零塑性温度(ZDT)在1375 ℃左右,温度低于1375 ℃后,随温度的降低断面收缩率值迅速上升,1300 ℃时断面收缩率接近80%,1250 ℃ 时即增加到92.5%,在1050~1300 ℃之间,断面收缩率基本在80%及以上,在950~1050 ℃范围内,钢的断面收缩率明显降低,在950 ℃时降为40.1%,在700~950 ℃之间断面收缩率基本在40%以下,其中775~825 ℃之间断面收缩率达到最小值约15%,温度低于775 ℃后断面收缩率逐渐升高.
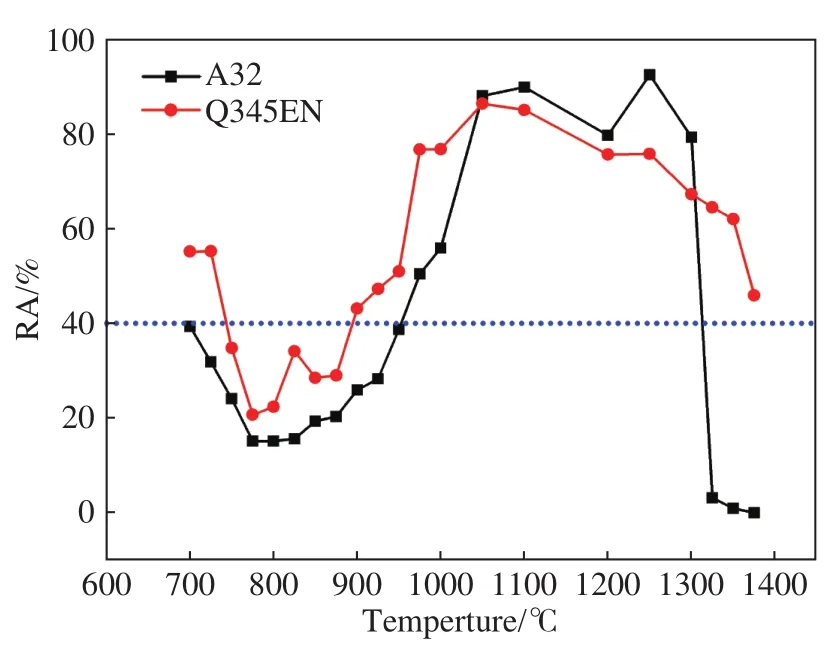
图3 微合金钢A32和Q345EN的RA变化结果Fig.3 Results of RA of A32和Q345EN
图4是铸坯表面冷却速率实测与模型计算结果,现场实际测量了铸坯矫直前后边部(距角部50 mm)的温度,同时采用数学模型对铸坯边部(距角部50、150和500 mm)温度进行了计算,确定冷却速率约为 2.5 ℃·min−1,通过取 Q345EN 铸坯试样10 mm×10 mm,在马弗炉里加热保温5 min,然后以2.5 ℃·min−1降温到各个温度进行析出物检测.析出物采用萃取复型方法检测,对铸坯在各个温度的析出物进行了分析,由图5、图6可知,可以看出900 ℃时,析出物尺寸较大,主要组成为铌、钛的碳、氮化物,随后温度降低,850 ℃时析出物尺寸小于900 ℃时析出物尺寸.

图4 连铸坯表面冷却速率实测与模型计算结果Fig.4 Results of the measured and modeled cooling rates on the surface of the continuous casting slab

图5 不同温度铸坯试样的析出物Fig.5 Precipitates at different temperature
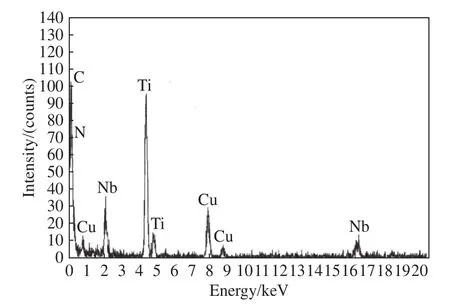
图6 试样900℃时析出物的成分Fig.6 Composition of precipitates at 900℃
此外,进行高温力学性能拉伸试验,经过有限元模型计算,连铸坯角部的应变速率最大为0.0004 s−1[17],本次拉伸试样应变速率为 0.001 s−1.试样拉断后,对A32断口金相组织及形貌进行测定. 825~900 ℃处于奥氏体低温区,变形时奥氏体晶界发生滑移导致低塑性沿晶脆性断裂;750~800 ℃时钢组织处于奥氏体和α铁素体两相区,先共析铁素体在原奥氏体晶界析出,形成铁素体膜,此温度区间铁素体强度大约是奥氏体强度的1/4[18]. 拉伸测试时,变形应力作用主要集中在奥氏体晶界的α铁素体网膜上,造成沿晶界破坏.据图7显示,750 ℃以后奥氏体晶界处的铁素体网膜向晶粒内部发展,晶粒内部也发生共析反应,原奥氏体晶界处应力集中减少,钢的延塑性回升,同时750 ℃、825 ℃断口金相组织显示,晶粒尺寸不均匀,混晶严重,所以造成钢的延性变坏. 由图8可知, 950 ℃时,拉断后同时存在沿晶断裂和穿晶断裂,属于混合断裂;750~875 ℃时,断口呈典型沿晶塑性断裂模式,晶界上布满浅韧窝. 温度为725 ℃时,断口仍然是沿晶断裂模式,但韧窝明显加深、加大. 高温力学测试结果为合理设定目标温度奠定了基础,可使连铸矫直过程避开脆性区进行矫直,最终制定更加合理的二冷制度,使铸坯表面温度分布更加均匀.

图7 A32各温度下的断口金相组织Fig.7 A32 organization of A32 at different temperatures
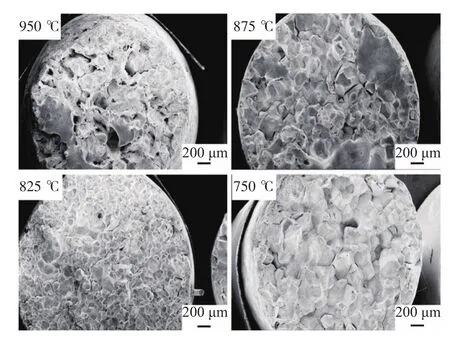
图8 A32各温度下的断口形貌Fig.8 Fracture surface of A32 at different temperatures
1.2.2 连铸坯中心偏析形成机理
钢水凝固过程中,合金元素在固相中的溶解度低于其在液相中的溶解度,凝固过程中合金元素逐渐聚集到液相,因而最后凝固部分的合金元素含量高于其他部分,即铸坯中心位置合金元素含量高于其他位置,最终形成中心偏析. 钢的凝固组织由边部到中心分别为细等轴晶区、柱状晶区和和粗大等轴晶区. 柱状晶由于传热的作用会形成二次枝晶,在一次、二次枝晶间存在液相,液相所含的合金元素溶质成分高于固相的一次、二次枝晶,形成微观偏析(枝晶偏析),在流动的作用下,这些微观未凝固的小液相区聚集在一起就形成宏观偏析,表现为中心偏析或1/4偏析.
1.2.3 连铸坯的中心疏松、缩孔形成机理
连铸是钢水发生相变、液态变成固态、体积发生收缩的过程,而在固−液相线温度区间内,钢水处于糊状区,既有液相、也有固相,钢水流动状态发生变化,当固相率很高时,钢水流动性很差,无法起到补缩作用,此时形成的缩孔保留在铸坯内,有些微小缩孔称为疏松,钢水的最后凝固阶段在铸坯的中心,所以称为中心缩孔及中心疏松,通过现场低倍检验结果的照片可以对中心缩孔及中心疏松进行评级.
1.3 连铸板坯常规技术措施
1.3.1 连铸二冷配水
铸坯出一冷后,需要继续冷却,在二次冷却区继续对铸坯表面温度进行喷水,目前二冷配水有两种方式,一种是静态水表配水[19−20],水表中冷却水量是拉速的二次函数,当拉速变化时,冷却水量立即发生变化,铸坯的热滞后明显,带来表面温度的波动,其凝固组织不稳定,会出现凝固搭桥现象,形成偏析. 另一种是动态配水,国内外很多学者进行了相关研究[21−24]. 动态配水又分两类,第一类是等效拉速方法,计算机记录铸坯到达某一位置经历的时间,将铸坯到弯月面距离除以该时间得到过往拉速,再将过往拉速与即时拉速加权平均得到等效拉速,二冷的水量是等效拉速的二次函数. 第二类动态配水是利用数学模型模拟浇注过程,拉速发生变化时首先按等效拉速法给出冷却水量进行控制,然后根据实际水量计算铸坯某冷却区出口的表面温度,求出计算温度与该位置设定温度的差,以此调整二冷各区的冷却水量,最终达到一致. 达涅利铸机很多采用等效拉速方法进行配水,是一种简易的动态配水,这种控制对非稳态铸坯表面温度的波动有一定的改善作用,但还是存在一定的热滞后现象,还会造成非稳态铸坯表面温度的波动.
在第二类动态配水基础上,又发展了一种闭环动态配水,采用的是二维数学模型,避开脆性区矫直,然后根据钢种、锰硫质量比、压缩比、钢材用途等确定冷却方式,给出每个钢类典型的冷却曲线.有些具有幅切功能的铸机,边部可单独控制,边部的水量为模型计算出中部的水量乘以系数,这一系数凭经验而定,给出各铸坯宽度对应的系数表,该系数不能随铸机状况变化进行调整,给实际操作带来很大困难,但目前多家钢厂均采用这种模式进行配水,实际生产中,这种配水方式会产生很多困难.如某厂4号机投用这种配水方式时,对某一钢种调整好边部系数后,当铸机状态发生改变导致铸坯出现表面裂纹时就需要重新调整边部系数,最终导致同一钢种可能出现多个边部系数. 关于配水的另一个问题是不同季节的温度差异对于铸坯的冷却有不同影响,铸机开始浇注和浇注一段时间后,铸机本身的温度有较大变化,其对铸坯的冷却也有一定影响,目前二冷配水没有考虑这一问题,而且这一问题在北方钢厂表现的尤为突出.
1.3.2 连铸轻压下技术
通过在连铸坯凝固末端附近施加压力(热应力和机械压力)以产生一定的压下量,阻碍含富集偏析元素的钢液流动从而消除中心偏析,同时补偿连铸坯的凝固收缩量以消除中心疏松,即为铸坯凝固末端轻压下技术,目前轻压下主要分为辊式轻压下、热应力轻压下和凝固末端连续锻压技术[24],如图9所示.
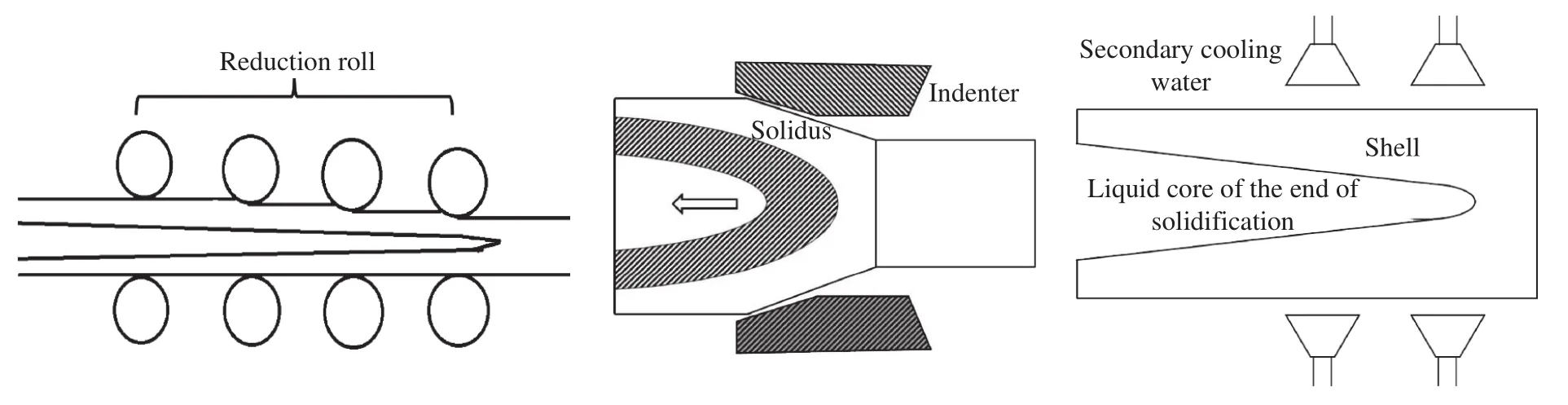
图9 轻压下分类示意图[25]Fig.9 Different types of soft reduction[25]
20世纪90年代末出现了实施跟踪凝固终点并据此调整辊缝的压下方法,即动态轻压下方法,其中基于辊缝动态控制的辊式压下技术是轻压下技术应用的主要方向,该法将凝固终点附近辊列的收缩锥度由常规的0.2 mm·m−1左右增加到0.8~1.4 mm·m−1,以补偿钢水凝固造成的收缩,消除由此引起的钢水流动,使中心偏析显著减轻. 在压下工艺中有两个重要参数,一是压下量、二是压下位置,普遍认为这两个参数是通过实验确定的经验值,通过不同的压下量、压下位置的组合进行某个钢种的压下实验,然后取低倍试样进行对比,找出优化方案,确定压下量与压下位置. 目前的压下方式中的总压下量基本为一定值,多数铸机的总压下量是5 mm或者6 mm,压下量分配通过固相率插值方式分给各个扇形段,压下区间经常出现在两个扇形段上,有时能达到三个扇形段压下,甚至四个扇形段压下. 两段压下量的设定如图10所示.
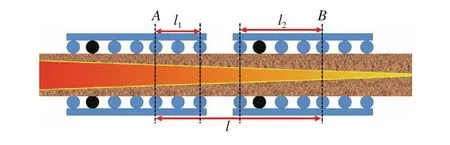
图10 压下示意图Fig.10 Schematic of soft reduction
压下通过设定两个固相率作为轻压下的开始与结束位置,开始位置A的铸坯中心固相率在某一扇形段内,结束位置B在另一个扇形段内,如图10所示. 设定总压下量为S,则每扇形段的压下量计算公式如下,第一个扇形段的压下量为公式(1):
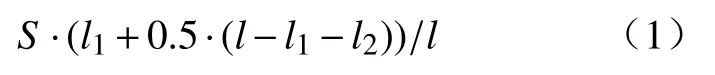
第二个扇形段的压下量为公式(2):
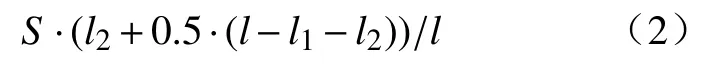
当A到B区间长度横跨三个扇形段时,每个扇形段的压下量按照上述插值方法进行计算. 非稳态压下是当拉速发生变化时,模型计算出压下起止固相率,即确定了发生变化后新的A、B位置,模型通过插值运算计算出相应的位置与压下量,发送给可编程逻辑控制器(简称 PLC),PLC 立即控制扇形段的位移传感器,进行压下控制. 当拉速发生波动时,压下段对应的铸坯固相率发生波动,压下量和压下位置重新计算引起波动,最终导致非稳态压下波动. 图 11(a)是某厂稳态时第 8 扇形段压下量的变化情况, 稳态时压下量控制的较为理想. 图 11(b)、图 11(c)分别为非稳态时第 7、 8扇形段压下量变化情况,压下量随拉速波动较大,这种波动对设备损害较大,为此宝钢一些生产低碳钢的铸机取消了压下功能. 此外,大多数企业实际生产中,当拉速降低到 0.5 m·min−1以下时,会切换成手动模式,然后模型按开浇方式重新投入轻压下模式,造成很长一段铸坯(长度约为 20 m)未被压下,这段铸坯的偏析、疏松级别较重.
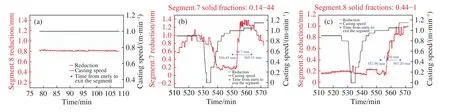
图11 稳态与非稳态过程典型扇形段压下量的变化. (a)稳态时第8扇形段压下量变化;(b)为非稳态时第7扇形段压下量变化;(c)为非稳态时第8扇形段压下量变化Fig.11 Variation of the typical soft reduction at the steady state and nonsteady state: (a) variation of the reduction amount of seg.8 at the steady state;(b)variation of the reduction amount of segment.7 at the nonsteady state;(c) variation of the reduction amount of segment.8 at the nonsteady state
1.3.3 模型数据库及异钢种混浇计算
通常动态配水及压下模型对应有一个数据库,数据库中包含目标温度、钢种代码及所对应的成分、各钢种在不同温度的焓或者比热容、密度以及各钢种压下参数等. 目前很多二冷配水及压下模型使用等效比热法来计算铸坯的温度,等效比热的核心是将凝固潜热平均分配到固−液两相区,而实际上凝固潜热并非平均分布,在液相线附近凝固潜热的放出要快于固相线附近,所以采用等效比热法会影响二冷水量和压下参数的准确计算. 异钢种混浇是指在不更换中间包时更换浇注钢种,从浇注第二个钢种的某时刻开始,中间包里的钢水成分会发生变化,最终完全达到第二个钢种钢水成分. 为了降低成本,这种现象普遍存在于各个钢铁企业. 目前二冷配水和压下模型没有考虑到这一问题,通常采用的是质量加权平均来计算成分,没有考虑到中间包钢水的死区和钢水流动对合金元素浓度分布的影响,计算结果不准确.目前的混浇操作中,浇注第二个钢种时,二冷和压下模型对应的钢种成分会突然修改为第二个钢种的成分,固−液相线温度会突然变化,目标温度也会发生突然变化,导致二冷水量、压下位置和压下量等参数突然变化,最终导致混浇坯铸坯质量变差,混浇坯长度计算不准确等问题. 综上所述,现有二冷配水和压下存在的问题制约了二冷配水和压下的效果,导致实际生产过程不能很好地利用二冷配水和压下技术,产品质量得不到很好的改善甚至恶化,基于此,本团队近年来就相关问题展开研究,开发了三维二冷动态配水与精准压下模型,形成了双目标温度设定、精准可控单段压下、连铸非稳态压下、异钢种混浇二冷与压下控制和凝固终点W形预测与控制等几项技术,通过现场实施和应用,铸坯质量得到了有效改善.
2 三维二冷动态配水与精准压下模型建立与应用
2.1 模型建立与技术应用
三维二冷动态配水及精准压下的模型建立了钢水在连铸过程三维数学模型[26],三维数学模型考虑铸坯宽度方向、厚度方向和拉坯方向三个方向的边界条件进行水量计算,模型可显示三个方向上的温度场. 首先建立传热方程,忽略了拉坯方向的热量传递,故板坯凝固的二维传热微分方程为:
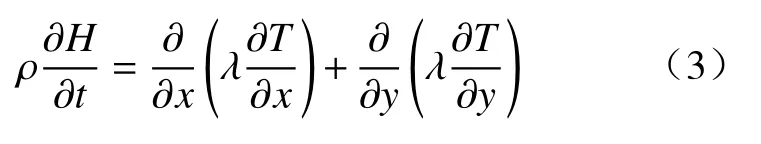
其中,H为钢的热焓,J·kg−1;T为温度,℃; λ为导热系数,W·m−1·K−1; ρ为钢的密度,kg·m−3.
模型的假设条件如下:
(1)忽略拉坯方向传热和结晶器弯月面处的传热;(2)结晶器钢水液面的温度为中间包钢水的温度;(3)将铸坯内液相穴的对流换热等效为传导传热来处理;(4)认为铸坯中心对称,只研究1/4铸坯断面. 初始及边界条件为:
t=0时,结晶器的钢液温度和中间包浇注温度(Tp)相同:
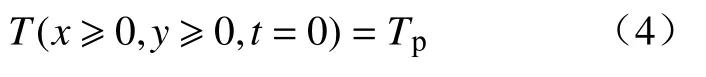
1) 铸坯中心,凝固传热模型中心对称:

2) 铸坯表面,结晶器(Mold,第二类边界条件)、足辊区(FR,第三类边界条件)二冷区(SC,第三类边界条件)以及空冷区(AC,第一类边界条件)的边界条件分别考虑:

其中,qxy为 单位面积热通量,W·m−2;h1、h2分别为足辊区和二冷区换热系数,W·m−2·℃−1; σ为波尔茨曼常数,取1.380649×10−23, J ·K−1;ε为铸坯外表面的辐射率,钢一般取0.85;Ta、Tb、Tw分别为各区设定目标温度、铸坯表面中心温度、二冷水温度,℃.
3) 二冷的各冷却区的换热系数h[27]:

其中:w为水流密度,L·m−2·s−1;A、B、n为常数.
采用显式和隐式组合而成的交替方向隐式差分法进行求解[28]. 以“坯龄”(坯壳生成后所经历的时间)为控制参数进行冷却控制,建立起“坯龄”和传热的关系,求出换热系数h,再根据换热系数h和冷却水量的对应关系,确定二冷各区的冷却水量. 在非稳态控制中,拉速不再直接决定水量的大小,而是通过拉速计算出铸坯所在位置,从而决定在二冷区相应的位置供给铸坯冷却所需的水量.
2.1.1 三维二冷动态配水及精准压下数据库
2.1.1.1 凝固降温路径和相组成
由铁碳相图(图12)[29]可知,不同碳含量的钢种从液相降温凝固到常温过程中会经历不同的相变过程,考虑到钢种中其他元素对铁碳相图中相组成的影响,根据国际焊接学会(IIW)碳当量公式碳当量={w(C) +w(Mn)/6+[w(Cr)+w(Mo)+w(V) ]/5+[w(Ni)+w(Cu)]}/15对碳含量进行修正,下文中的碳含量[C]值均是修正后碳当量的值. 根据相图中相变点如P点、H点、J点、B点、S点及E点的碳含量作为分界点,其中C为碳含量,将不同碳含量分为0<[C]≤0.028%、0.028%<[C]≤0.09%、0.09%<[C]≤0.17%、0.17%<[C]≤0.53%、0.53%<[C]≤0.77%、0.77%<[C]≤2.11% 划分成 1 到 6 类钢(Type1~Type6),同一类钢降温过程中的相变和相组成是相同的. 降温过程中,用T1~T5分别表示凝固过程中发生相变时的温度,六类钢的相变路径如图13所示. 对于第一类钢,降温至铁碳相图PQ线时,渗碳体析出量极低,可忽略不计,故忽略了这一类钢的PQ相变.
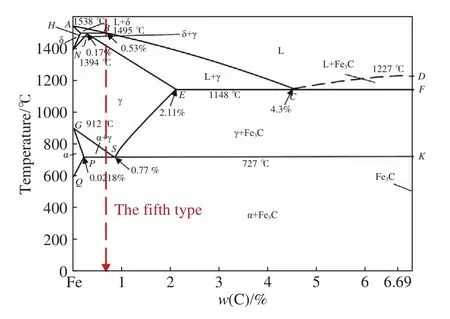
图12 铁碳相图[29]Fig.12 Phase diagrams[29]

图13 六类钢凝固降温相变路径Fig.13 Six phase change paths of steel solidification cooling
液相线温度Tl和固相线温度Ts公式见文献[30],T1~T5由公式 (12)~(16)计算:

其中,T1表示L相开始向L+δ相转化时的温度;T2表示δ相开始向δ+γ相转化时的温度;T3表示γ相开始向γ+α相转化时的温度;T4表示γ+α相全部转化为α相时的温度;T5表示γ相开始向γ+Fe3C相转化时的温度;液相向固相发生转变时,平衡凝固是极难实现的,实际的凝固过程都是非平衡凝固,固−液两相的均匀化来不及通过传质而充分进行,则除界面处能处于局部平衡状态外,固−液两相中平均成分势必偏离平衡相图所确定的数值. 钢的固相分数fs和液相分数fl通过Scheil−Gulliver方程[31]求解. 钢发生固态相转变时,固−固两相区之间的相组成根据相图采用杠杆定律计算.
2.1.1.2 钢种热物性参数的计算
(1)钢种固相热焓、密度及导热系数计算.
计算钢种的固相热焓、密度及导热系数时,首先根据上一部分内容确定该钢种各温度段的相组成. 基于该钢种各相的化学成分及已有数据分析计算该相的物性参数,如公式(17)所示,进而得到该相的物性参数与温度的对应关系,如公式(18)所示.
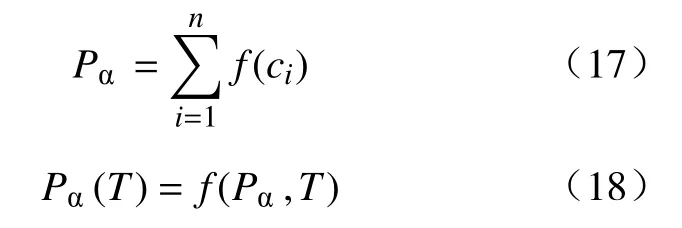
其中,Pα为钢种某一温度下α相的物性参数(固相热焓、密度、导热系数);ci为第i个成分组元的质量分数,%;n为钢种计算所用到的成分组元数量;f(ci)第i个成分组元与纯相α某一物性参数之间的函数关系;Pα(T)—纯相α在T温度下的某一物性参数;f(Pα,T)为Pα(T)与Pα和T的函数关系式.
根据钢种的相组成及每个相的性能利用混合定律计算出材料的整体性能,如式(19):

其中,P为钢种某一温度下的物性参数;Pα为钢种某一温度下α相的物性参数;χα为钢种某一温度下α相的相分数,%;Pβ为钢种某一温度下β相的物性参数;χβ为钢种某一温度下β相的相分数,%.
(2)钢种液相热焓值及凝固潜热处理.
钢在凝固时会释放凝固潜热,凝固潜热按下面方法计算. 钢种在温度T时的焓值HT由公式(20)~(21)计算,固液相率fs及fl由前面提到的Scheil−Gulliver[31]方程确定.

其中,Hs为钢种固态时在温度T时的焓值;Hl为钢种液态时在温度T时的焓值;Δh为钢的过热焓;h为钢的显焓;L为钢种的凝固潜热;单位均为J·kg−1.
2.1.1.3 导热系数修正
连铸过程中,钢水在液相穴内的湍流流动导致钢水的导热系数明显大于坯壳(固态钢)的导热系数. 因此,数据库中钢的导热系数分为两个部分,首先是固态钢的导热系数,其次是以固态钢导热系数和湍流效应为基础对钢水导热系数进行修正的修正因子M(常数). 通过数值模拟计算得到连铸过程中液相穴内钢水的有效导热系数,进而得出了导热系数的修正因子,模拟计算中流动、传热、凝固方程及参数见文献[32−33]. 图14(a)为通过数值模拟计算得出的Q345的有效导热系数云图分布,在铸坯各横向截面作有效导热系数平均化处理,得出了钢水有效导热系数随拉坯方向的变化曲线(图14(b)),根据该曲线确定了软件中结晶器及二冷各区的钢水的有效导热系数值,结晶器区域M为4,二冷区M为3. 在数据库中写入各分区M值,即实现了对导热系数的修正.

图14 Q345有效导热系数分布及M值沿拉坯方向变化. (a)有效导热系数分布;(b) M值沿拉坯方向变化Fig.14 Effective thermal conductivity and M: (a) distribution of effective thermal conductivity; (b) variation of M on the direction of casting
2.1.2 双目标温度设定技术及其应用
对于具有幅切功能的铸机,通常是确定中心的冷却水量,边部的冷却水量为中心的冷却水量乘以一系数,数据库中有一数据表,可根据实际情况进行调整,本研究采用双目标温度,即设定铸坯表面中心、铸坯表面角部的目标温度不同,计算达到铸坯中心、边部的目标温度所需要的中部、边部的冷却水量并进行设定. 这样设定的边部水量更为合理、准确. 以这种控制方式控制,能够使二冷水量分布均匀,减少铸坯表面裂纹和角横裂纹,减轻W形状凝固终点.
2.1.3 压下量及压下位置确定技术
压下技术是将凝固终点附近辊列的收缩锥度由常规的 0.2 mm·m−1左右增加到 0.8~1.4 mm·m−1,以补偿钢水凝固造成的收缩,消除由此引起的钢水流动,使中心偏析显著减轻.
轻压下工艺压下位置和压下量是两个重要参数,关于这两个参数普遍认为由实际经验确定. 本文提出的压下量的计算公式如下:

其中,S为总压下量,mm;S1为中心偏析沿厚度方向带宽,mm;S2为中心疏松或缩孔沿厚度方向的带宽,mm;n为压下效率,为芯部变形量与铸坯厚度方向总变形量之比;S3为铸坯凝固收缩量,mm;S4为板坯鼓肚量,mm;S5为铸坯因温度降低引起的热收缩量,mm.
2.1.4 精确可控单段压下技术
以Q345钢为例,首先将中心固相率为0.9对应的位置作为该钢种轻压下的结束位置,考虑将该位置设定在某一扇形段的出口处,模型可以根据这一设定值反向计算拉坯速度,给出合理的建议拉速. 通常上V型偏析开始形成位置对应铸坯中心固相率为0.55,结合模型计算和经验参数,中心固相率0.55~0.9这个区间对应铸坯长度约为1.5 m,而一个扇形段长度在2.0 m左右,可实现在一个扇形段内压下. 以此可实施精准压下,同时能避开损坏的扇形段进行压下. 奥钢联轻压下通常将压下区间对应铸坯中心固相率设置为0.3~0.95,即中心固相率为0.3时开始压下,中心固相率为0.95时结束压下. 本技术将钢种分为几个大类,取铸坯的纵剖试样做低倍检验,找出V型偏析的形成位置,测量其到铸坯中心线的距离δ,认为V型偏析形成点的坯壳固相率为0.9~1.0,由δ可计算该位置对应的中心固相率,以此确定压下开始位置. 图15为不同末端压下量铸坯中心偏析情况,其中图15(a)为C偏析度,图15(b)为末端轻压下2 mm铸坯的低倍检验结果,图15(c)为末端压下10 mm铸坯的低倍检验结果,可以看出末端压下量增大后岛状偏析加重,形成带状偏析,中心偏析度高达1.15. 通过低倍检验结果,测量铸坯岛状偏析的形貌及岛状偏析的尺寸,确定岛状偏析边界距离铸坯中心的距离,岛状偏析边界固相率为1,计算出铸坯中心所对应的固相率,即为压下的结束位置.
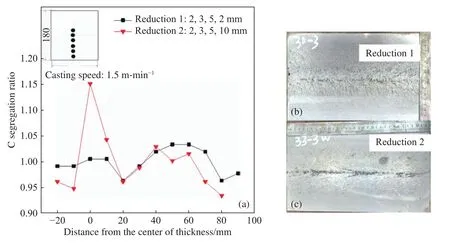
图15 不同末端压下量铸坯中心偏析情况. (a)两种末端压下量对应C偏析度结果;(b)末端压下2 mm低倍结果;(c)末端压下10 mm低倍结果Fig.15 Center segregation of different reduction amount at the end of solidification:(a) result of C segregation ratio;(b) macrostructure of C segregation of 2 mm reduction amount;(c) macrostructure of C segregation of 10 mm reduction amount
2.1.5 连铸非稳态压下技术
连铸生产过程受铸机状态和生产计划等多因素影响,拉速变化,即非稳态状态时常发生. 目前普遍采用的压下方式是通过模型计算压下起止点的位置来实时指导压下过程,拉速波动时,模型计算的起点和结束点位置发生变化,压下位置和各段压下量随即发生变化,如图16(a)所示,这就容易造成压下位置和压下量的频繁波动,而本技术采用临界点控制法,可有效解决压下位置和压下段的频繁波动现象. 在压下结束位置两侧200 mm处设置两个临界点,当拉速变化时,临界点位置均有变化,临界点位置变化幅度小于200 mm时,模型锁定压下位置及压下量均固定不变,只有当两个临界点位置移动超过200 mm时,才按照模型的计算结果进行控制,调节压下量和压下位置,同时压下量分多次调节,每次调节量不超过0.5 mm,调节量可根据液压阀的灵敏度进行修正. 由此在非稳态过程中实现对压下量的稳定控制,如图16(b)所示.
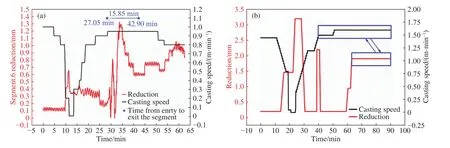
图16 非稳态压下控制对比. (a)常规压下方式非稳态过程控制;(b)本技术非稳态压下控制Fig.16 Comparison of different controls of reduction at the nonsteady state:(a)regular control of reduction at the nonsteady state;(b) this research control of reduction at the nonsteady state
此外,针对切换过程造成的很长一段铸坯未被压下的情况,提出全过程自适应压下控制方式,拉速降到0.5 m·min−1以下时,模型同样可以计算连铸过程钢水的温度及凝固状况,跟踪液芯长度、压下起止位置的变化,仍按照模型的计算结果进行压下,同时本技术的压下方式中锁死前三段,使其不可执行压下,以这样的方式进行,降低拉速时凝固终点沿拉坯方向反向移动,若移动到前三段位置处,则不再执行压下,以保证结晶器液面稳定和生产安全.
2.1.6 异钢种混浇二冷及压下技术
异钢种混合浇注在连铸生产中普遍存在. 异钢种钢水在中间混合后,其固−液相线温度、导热系数、热焓值等热物性参数势必发生变化,成分的变化就要求目标温度做相应调整,二冷控制中考虑这一变化,首先对连铸中间包中的混浇过程进行数值模拟,计算了混浇时中间包内钢水溶质组元的扩散过程,在中间包出口处对钢水溶质组元、固−液相线温度进行监测,从而确定混浇过程时间及钢水溶质组元变化特征. 溶质组元传输方程见文献[34]. 钢水中各溶质组元扩散过程基本是一致的,而且钢水固液相线温度主要由C、Si、Mn、S、P决定. 计算中对钢水中五个组元进行求解,根据五个组元的浓度计算钢水的固−液相线温度.表2中列出了AH36与Q345两个钢种的成分. 图17为混合浇注数值模拟计算的中间包内钢水碳含量分布及进入结晶器钢水的碳含量、固−液相线温度随时间变化曲线. 可以看出,混合浇注开始后100 s内,从中间包进入结晶器内的钢水依然是AH36.混合浇注100 s后,进入结晶器内钢水的成分、固−液相线温度开始发生变化,逐渐变为Q345钢. 将数值模拟计算的混合浇注时间、混合浇注过程中的钢水成分及固−液相线温度变化特征嵌入数据库中,对现场生产中混合浇注过程的钢水成分、固−液相线温度、中心固相率及混浇坯长度进行预报,进而对铸坯目标温度和压下区间进行相应的调整.

表2 混合浇注钢种成分及其固−液相线温度Table 2 Composition of mixed cast steel and solid-liquid phase line temperature
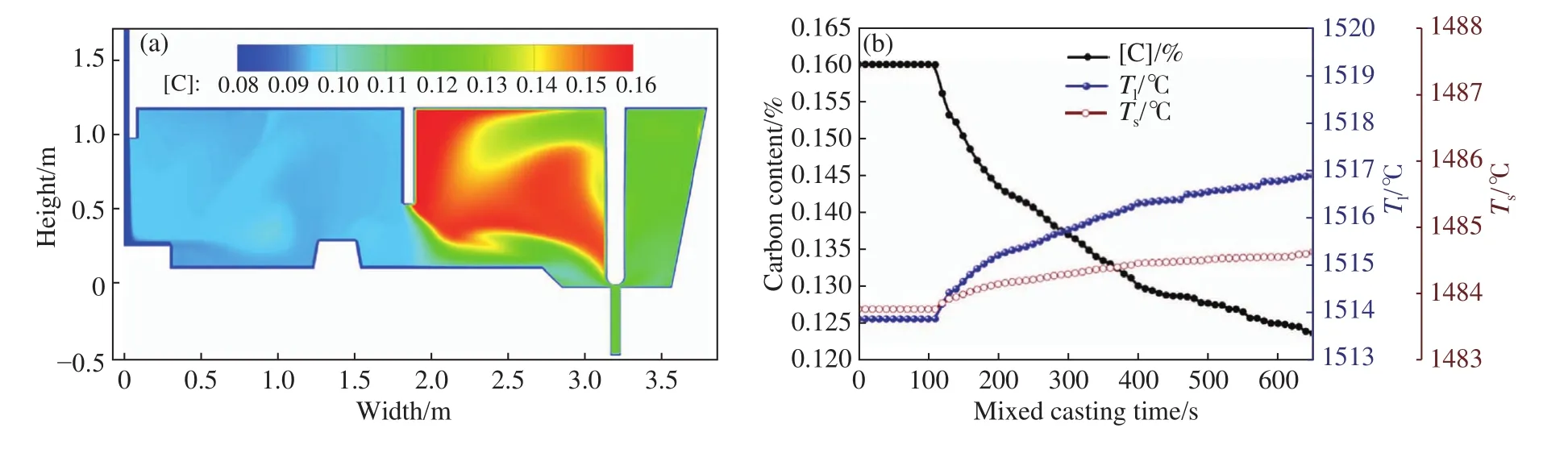
图17 混合浇注数值计算结果. (a)碳元素质量分数分布;(b)碳含量和固−液相线温度变化Fig.17 Results of numerical calculation:(a) distribution of C mass fraction; (b) variation of carbon content and solid-liquid line
2.1.7 W形凝固终点形状预测与控制技术
针对目前连铸坯生产过程中普遍存在的W形凝固终点进行研究. 如图18(a)所示为实际生产的有W形凝固状况铸坯,这种不均匀凝固终点的形成对铸坯内部质量有很大影响. 通过输入实际产生的边界条件,喷水的不均匀会造成这类凝固状况,如图18(b)示. 通过模拟能够预测传统二冷水分布存在问题. 通过测温实验和喷嘴特性研究,给出合理的边界条件,优化压下和二冷工艺参数,应用三维动态配水模型,对喷嘴分布、型号和安装方式进行优化设计,然后在国内L厂进行实验并取得了较好的效果,如图18(c)、18(d)所示,W形凝固终点消除.

图18 W形凝固终点形状预测与控制. (a)凝固终点W形;(b)W形模型预测;(c)W形消除;(d)W形模型消除Fig.18 Prediction and control of W-shape at the end of solidification:(a) W-shape at the end of solidification; (b) model prediction of W-shape;(c) elimination of W-shape; (d) model elimination of W-shape
2.2 三维二冷动态配水与精准压下模型效果评价
分别于国内A厂、B厂、L厂、Y厂投用三维二冷动态配水与精准压下模型,其中A厂三维二冷动态模型投入使用后,裂纹试枪合格率由79.58%提高到95.74%,提高了16.16%,如图19所示. B厂4号机投用前后,超高强钢和裂纹发生率如图20所示,由图20可知模型投入后,该厂裂纹发生率和封锁率分别从5.77%和10.23%改善到4.61%和5.53%. 裂纹发生率和封锁率最低为3.88%和3.77%. 铸坯质量得到有效改善.

图19 投用前(1~4月)和投用后(5月)裂纹试枪合格率Fig.19 Cracking rate before and after using the model
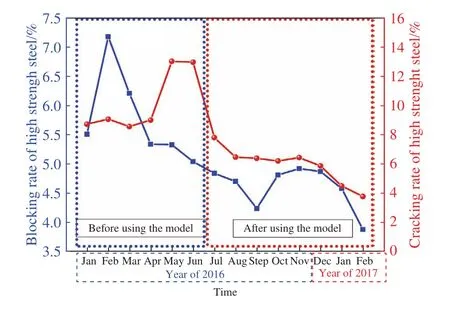
图20 模型投用前后裂纹发生率统计Fig.20 Crack rate before and after using the model
L厂三维动态配水与轻压下软件于全钢种上线前、后各一个季度统计的铸坯轧后缺陷率如表3所示:模型上线前,典型 355 类钢种铸坯的中心偏析评级多为C1.0~C1.5级,上线投用后偏析评级多为C0.5~C1.0. 偏析缺陷试验对比样品如图21所示,可以看到应用该模型后偏析缺陷明显改善.在Y厂进行了二冷水调整试验与测温试验. 模型调整应用后分别在最后3个段出口采用红外热成像仪测量各段出口温度,调整前后模型计算温度与实测值如图22所示,由图22可知,铸坯表面实测结果与模型计算结果基本吻合,验证了模型的准确性,水量调整后,二冷区下部铸坯表面温度适当调高,矫直段温度由870 ℃提高至900 ℃,避开了第三脆性区,有效减轻了表面裂纹,改善了铸坯质量. Y厂三维动态配水与轻压下软件全钢种投用前、后一个季度,中心偏析评级C0.5~C1.0的比例由65%提高到85%以上,铸机稳态状况下未出现A类偏析,裂纹发生率由10.47%降低到1.29%,有效改善了铸坯表面质量.

表3 模型上线前后轧后缺陷率统计Table 3 Crack rate before and after using the model

图21 投用前(a)和投用后(b)偏析缺陷对比Fig.21 Comparison of segregation before and after using the model used for the Plant L

图22 模型计算温度与实测温度对比Fig.22 Comparison of the model’s calculated temperature and measured temperature
3 结论
(1) 开发并应用三维二冷动态配水与精准压下模型并现场应用,实施三维二冷动态配水与精准压下后,有效改善裂纹发生和中心偏析等问题,提高了铸坯表面质量和内部质量.
(2) 开发新型二冷和压下数据库和双目标温度控制技术,均匀铸坯宽度方向表面温度. 模型可容纳更多边界条件,同时开发异钢种混浇过程二冷控制技术和W形凝固终点形状预测与控制技术,提高了模型计算精度和准确度,增强了模型的现场适用性,实现了二冷水量和压下参数的优化,有效改善连铸板坯角部裂纹问题.
(3) 提出新的压下参数确定公式和方法,实现了精确可控单段压下控制、非稳态过程压下控制和包括异钢种混浇过程压下控制,优化各工况条件下的压下效果,改善连铸板坯中心偏析、中心疏松和缩孔等问题.

