压下对重轨钢大方坯内裂纹敏感性的影响
马海涛,张炯明,尹延斌
北京科技大学冶金新技术国家重点实验室,北京 100083
随着社会的发展,铁路的运输压力增加,对钢轨的性能提出了更高的要求[1],重轨钢多采用大断面方坯连铸生产,由于碳含量高,易出现连铸坯中心偏析[2−3]. 中心偏析极大地影响了产品的性能.因此,更好地了解连铸坯质量控制技术是进一步提高连铸坯质量的关键[4]. 在连铸过程中,低过热度浇注[5−6]、电磁搅拌[7−10]、铸坯压下[11]和凝固末端强冷[12]等技术均可以有效改善铸坯质量. 其中,压下技术是提高连铸坯质量最有效的方法,现在已经在各钢铁企业得到了广泛应用[13].
虽然在连铸坯凝固末端进行压下可以有效地控制连铸坯质量,但压下参数不当往往会使连铸坯产生内部裂纹,造成连铸坯质量恶化[14−16]. 根据相关研究表明[17],铸坯内部裂纹一般与凝固前沿的强度和塑性直接相关. Won等[18]、Seol等[19]与Cornelissen[20]提出了一种基于实测临界应变的临界断裂应力模型,该模型考虑了脆性温度范围和应变速率,分析了脆性温度范围和应变速率对内部裂纹临界应变的影响,当脆性温度范围和应变速率增大时,临界应变减小,内部裂纹形成的可能性增大;Yamanaka等[21]和Kobayashi[22]得到了零强度温度(Zero strength temperature, ZST)和零塑性温度(Zero ductility temperature, ZDT)温度区间对应的铸坯中心固相率在0.8~0.99之间. Nakagawa等[23]在碳钢高温力学实验中认为ZDT对应的铸坯中心固相率为0.98. Kim等[24]研究结果表明ZDT对应的温度是固相线温度. 所以,以上多位学者的研究结果表明,ZST和ZDT温度区间对应的铸坯中心固相率多集中在0.8~1.0之间. 此外,很多学者对铸坯压下产生内裂纹展开研究,王一成和胡鹏[25]研究了方坯压下内裂纹的形成机理,研究结果表明由于压下变形过程中的拉应变撕裂是形成内部裂纹的主要原因. 宋潇[26]对280 mm×380 mm大方坯重轨钢进行了压下热力耦合数值模拟研究,计算结果表明,压下量在3 mm内不会产生内裂纹,压下量为4 mm的情况下固相率不超过0.6时不会产生内裂纹,压下量为5 mm时固相率不超过0.4不会产生内裂纹. Li等[27]研究了轴承钢连铸坯压下内裂纹的形成,研究发现沿脆性断裂的内裂纹在糊状区位于ZST与ZDT之间,并且裂纹区域的等效塑性应变为2.34%~2.45%,大于临界应变(0.4%~1.5%).
目前,国内外学者对于连铸坯压下已有大量研究,但是铸机不同、生产的钢种不同,压下后产生的效果也不尽相同,有学者认为在铸坯靠后(高固相率)的位置压下不会出现裂纹,在铸坯靠前(低固相率)的位置压下容易出现裂纹,但是并没有统一规律[28−29]. 本文针对230 mm×280 mm断面重轨钢、大方坯展开了压下研究,通过ABAQUS有限元软件建立了铸坯压下模型,分析了U71Mn铸坯在压下过程中产生内部裂纹的工艺条件,优化工艺参数,为现场生产提供数据支撑.
1 数学模型
1.1 几何模型
压下几何模型主要由三部分组成,铸坯、压下辊以及支撑辊,大方坯压下有限元模型示意图如图1所示,由于铸坯的屈服应力远小于压下辊和支撑辊,所以将铸坯作为弹性材料,压下辊和支撑辊作为刚性材料. 辊子和铸坯之间属于库伦摩擦,摩擦系数选取0.3[30]. 考虑到铸坯压下时在宽度方向上的对称性,在铸坯宽度方向上建立了1/2模型,模型的断面尺寸为230 mm×280 mm,模型长度为500 mm,压下辊的半径为150 mm,压下辊的宽度为300 mm,模型网格数为16100.

图1 大方坯压下有限元模型Fig.1 Reduction finite-element model of the bloom
1.2 模型假设
在保证计算结果精度的前提下,对压下有限元模型做如下假设:
(1)铸坯在拉坯方向温度一致,凝固壳厚度均匀,不考虑钢水静压力对铸坯的影响;
(2)考虑到铸坯不同成分材料的物性差别较小,忽略铸坯不同物性差异,将材料视为各处均匀分布;
(3)假设材料满足小变形理论,压下辊对铸坯的作用力方向不会随着变形发生变化;
(4)在应力应变分析中假设材料为各项同性,忽略微观结构的影响.
1.3 连铸凝固传热模型与压下模型
(1)连铸凝固传热模型[30].
连铸坯温度场是压下模型计算的基础,为此,采用二维切片法建立连铸凝固传热模型,获得压下模型连铸坯的温度场信息,模型忽略了连铸坯拉坯方向的传热,同时不考虑结晶器振动对传热的影响,连铸坯的凝固传热方程为:

其中,cp为 有效比热容,J·kg−1·K−1; ρ为钢液密度,kg·m−3;T为温度,K;t为时间,s; λ 为导热系数,W·m−1·K−1.
(2)连铸压下模型.
连铸坯凝固过程中温度变化会引起热变形,同时铸坯受到压下作用发生变形. 所以,在压下变形过程中同时含有弹性变形与塑性变形,而在压下过程中铸坯温度变化引起的热变形相对于压下的影响不大,不考虑铸坯高温蠕变变形,将铸坯凝固过程的应力应变看作是稳态过程,即与时间无关.因此,弹塑性模型常被用来计算铸坯的应力场[31].
按照弹塑性增量理论,铸坯的总应变量表达式为:
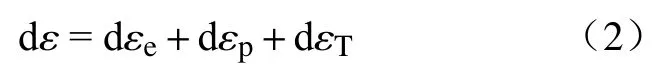
其中, d ε为总的应变增量; d εe为弹性应变增量;dεp为塑性应变增量; d εT为热应变增量.
1)弹性应变增量.
根据胡克定律,在弹性形变阶段可得弹性应变增量的表达式:

其中, [De]为弹性矩阵;σ为应力,MPa.
2)塑性应变增量.
材料进入塑性变形阶段后塑性应变增量的表达式为:

其中,κ为常数;φ为米泽斯屈服函数.
3)热应变增量.
热应变增量表达式为:

其中, [ α]为热膨胀系数矩阵.
1.4 求解细节
本文主要采用ABAQUS/Explict有限元软件进行建模求解. 首先,通过建立铸坯传热模型对铸坯进行温度场求解,温度场模型采用八节点线性传热单元(DC3D8),温度计算模型采用温度瞬态分析;根据温度场的求解结果作为压下模型的初始条件进行压下模型的求解计算. 其中,压下辊作为刚性材料,铸坯作为可变形体,压下模型采用八节点传热耦合位移单元(C3D8T),并采用瞬态温度−位移显性分析.
1.4.1 初始条件
①热分析初始条件:将中间包的温度作为浇注温度;
②铸坯压下初始条件:根据传热模型计算铸坯在压下区域的温度场,提取压下区域的温度场作为初始温度场加载到压下模型中,铸坯拉速为1 m·min−1;辊的初始温度为 200 ℃,辊的转速为 0.11 rad·s−1.
1.4.2 边界条件
①热分析边界条件:热分析边界条件分为结晶器、二冷区以及空冷区三部分,按照胡文广等[32]的铸坯传热模型的边界条件进行设定;
②压下模型边界条件:设定铸坯Y−Z面为对称面.
1.5 物理参数
本文研究对象为U71Mn重轨钢,其成分如表1所示. 采用JMatPro热力学软件对U71Mn重轨钢的物性参数进行计算,其密度、导热系数、弹性模量、泊松比,热膨胀系数、比热和流变应力等参数计算结果如图2(a)和(b)所示. 本研究选取900~1600 ℃范围内U71Mn重轨钢的热物性参数. 弹性模量和泊松比是描述材料力学变形行为最基本的参数,弹性模量在固相区至液相区逐渐减小,在液相区弹性模量值为0;泊松比随温度的增加逐渐增加,在液相区泊松比值为0.5;考虑到压下模型主要计算的是凝固前沿变形行为,连铸过程中铸坯在高温状态下属于低应变速率. 因此,应力应变曲线的选取主要集中在960~1460 ℃之间的值,应变速率为0.001 s−1. 图2(c)为U71Mn重轨钢的液相分数和固相分数,其中fs为 固相率.

表1 U71Mn钢种的化学成分(质量分数)Table 1 Chemical composition of U71Mn steel (mass fraction) %

图2 U71Mn 重轨钢物性参数. (a)热物性参数;(b)流变应力(应变速率为 0.001 s−1);(c)固相分数和液相分数Fig.2 Parameters of U71Mn steel: (a) physical parameters; (b) flow-stress (strain rate is 0.001 s−1); (c) solid and liquid fraction
1.6 内部裂纹出现的判据
在连铸坯凝固过程中,受坯壳所处温度状态不同的影响,坯壳裂纹敏感性分布也不尽相同. 但通常认为内部裂纹多数是在凝固前沿形成的,凝固前沿一般认为是固相线(Ts)和液相线(Tl)之间的凝固区域,如图3所示. Clyne[33]、Li和Thomas[34]以及Kim等[24]引入黏滞性温度(Liquid impenetrable temperature,LIT)进一步划分裂纹敏感区. 因此,将凝固前沿划分为三个部分,分别是:

图3 铸坯凝固前沿温度分布[37]Fig.3 Temperature distribution at the solidification front in the bloom[37]
(1)液相线温度至零强度温度(ZST)区间,ZST对应的固相率在0.8左右,材料特性表现为液相,钢的强度和塑性为零;
(2)黏滞性温度(LIT)和零强度温度(ZST)温度区间,LIT对应的固相率在0.9左右,此区域晶界并非完全封闭,位于坯壳枝晶紧凑程度较低的区域,钢液可及时填充裂纹[35],称之为填充区. 从而抑制裂纹的产生,此区域钢的凝固组织具有一定的强度但无延展变形的能力;
(3)在黏滞性温度(LIT)与零塑性温度(ZDT)温度区间,ZDT对应的固相率在1.0左右,此区域为温度脆性区间,在温度脆性区间内累积应力超过临界应力时便会产生内裂纹[36],这是内裂纹形成的高发区. 因此,铸坯内裂纹多是在凝固前沿中的该区域内形成的.
对铸坯压下后内裂纹进行预测,根据学者[38]研究内部裂纹的判定依据,如图4所示. 通过计算钢种碳当量Ceq以及锰硫比,可得到裂纹产生固−液界面的临界等效塑性应变. 通过公式(6)计算U71Mn碳当量Ceq为0.69%,根据钢种化学成分计算w[Mn]/w[S]比为143.8,根据图4可以得到U71Mn钢种在凝固前沿的临界应变为0.4%.


图4 碳当量与临界应变的关系Fig.4 Relationship between the carbon equivalent and critical strain
2 结果与讨论
2.1 大方坯温度场计算
为验证网格数量的无关性,选取中心固相率0.6位置处的铸坯作为计算对象,对铸坯不同网格数的温度场进行计算,连铸坯模型划分网格数分别是7920,16100和28000. 铸坯温度场计算结果如图5所示,计算结果表明,网格数量对计算结果几乎无影响,为提高计算结果图片的清晰度以及提高运算效率,本模型对铸坯划分网格数为16100.

图5 不同网格数温度场计算结果Fig.5 Temperature field calculation results of different grid numbers
图6(a)是大方坯表面温度与中心温度分布.从图6(a)可以看出,大方坯的压下区间在距离弯月面14.9 m至20.5 m之间,通过红外测温仪对铸坯表面进行温度测量,测量结果与计算结果基本一致,验证了铸坯传热模型的准确性. 图6(b)为铸坯上表面(内弧侧)到下表面(外弧侧)温度分布,对比了在中心固相率为0.3~0.7位置处铸坯厚度方向的温度分布. 在中心固相率为0.3、0.4、0.5、0.6和0.7位置处的铸坯中心两相区厚度分别是104.4、97.2、87.4、82.2和73.0 mm. 由此可见,铸坯中心两相区的厚度随着固相率的增加而减小. 因此,在中心固相率为 0.3、0.4、0.5、0.6和0.7位置处的铸坯凝固前沿至铸坯中心的距离分别是52.2、48.6、43.7、41.1和36.5 mm.

图6 大方坯温度分布. (a)铸坯中心及表面温度;(b)铸坯液芯温度分布Fig.6 Temperature distribution in the bloom: (a) center and surface temperature of bloom; (b) temperature distribution of the bloom liquid core
本文对铸坯温度场进行数值模拟计算,铸坯在压下区间内处于空冷区,铸坯通过辐射传热进行冷却. 通过JMatPro热力学软件对U71Mn钢种进行计算得到液相线温度为1475 ℃,固相线温度为1370 ℃. 对铸坯温度场计算得到在中心固相率为0.3、0.4、0.5、0.6和0.7位置处的铸坯中心温度分别为 1459、1453、1446、1437和 1426 ℃. 图 7为铸坯横截面温度场分布云图,横截面的右侧为中心对称面. 从计算云图可以看出,随着铸坯中心固相率的增加,铸坯中心温度降低,中心两相区厚度减小,即凝固前沿至铸坯中心的距离减小.

图7 不同铸坯中心固相率铸坯温度场分布Fig.7 Temperature distribution at different central solidification fractions
2.2 压下区间对压下裂纹敏感性的影响
本文研究了压下区间对铸坯产生内裂纹的影响,对不同中心固相率位置处的铸坯进行压下数值模拟计算,将2.1节中铸坯温度场的计算结果作为初始条件加载到铸坯压下模型中,然后对铸坯进行热力耦合计算,现将模拟计算结果做如下讨论.
图8给出了不同固相率位置处铸坯压下7 mm,铸坯横截面上的等效塑性应力分布,横截面的右侧为中心对称面,从图8中可以看出,等效塑性应变主要集中在铸坯的上表面(内弧侧)和下表面(外弧侧). 铸坯中心固相率为0.3时等效塑性应变区域在宽度方向上主要集中在铸坯角部以及铸坯1/4之间区域;铸坯中心固相率为0.4时等效塑性应变区域在宽度方向上向铸坯1/4处延伸;当中心固相率为0.5时等效塑性应变区域在宽度方向上主要集中在角部与铸坯3/8区域内;当中心固相率为0.6时等效塑性应变区域在宽度方向上继续向铸坯中心延伸,同时应变区域在厚度方向上向铸坯中心扩大;当中心固相率为0.7时等效塑性应变区域在宽度方向上接近铸坯中心,同时应变区域在厚度方向上向铸坯中心继续扩大. 由此可知,随着铸坯中心固相率的提高,铸坯表面温度降低,等效塑性应变值变大,铸坯的塑性应变区域在宽度方向上逐渐向铸坯中心延伸,同时等效塑性应变在铸坯厚度方向上向铸坯中心扩大.
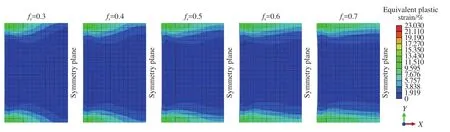
图8 铸坯横截面等效塑性应变分布Fig.8 Equivalent plastic strain distribution in the cross section of the bloom
图9给出了在不同固相率位置处铸坯压下7 mm后铸坯等效塑性应变分布与温度分布. 其中点线图代表等效塑性应变,直线图代表温度. 从图9(a)中可以看出,等效塑性应变从表面到中心逐渐减小. 对中心固相率为 0.3、0.4、0.5、0.6和0.7位置处的铸坯分别进行压下,铸坯表面产生的最大等效塑性应变值分别为6.93%、8.29%、9.72%、10.73%和11.97%. 因此,中心固相率越高,铸坯表面温度越低,压下后铸坯产生的等效塑性应变越大.
大多数压下引起的内部裂纹主要是在凝固前沿出现的,为研究对不同中心固相率位置处的铸坯进行压下,铸坯出现内裂纹的问题,对铸坯凝固前沿的等效塑性应变进行计算分析,评估铸坯产生内裂纹的风险. 图9(b)给出了不同中心固相率位置处的铸坯压下7 mm凝固前沿等效塑性应变,其中竖直虚线代表不同固相率位置处铸坯的凝固前沿,水平虚线代表临界应变. 从图9(b)可以看出,对中心固相率为0.3、0.4、0.5、0.6和0.7位置处的铸坯分别进行压下,铸坯凝固前沿的等效塑性应变分别是0、0、0.03%、0.16%和0.04%. 结果表明,凝固前沿的等效塑性应变随着中心固相率的增加先增加然后逐渐减小,当铸坯中心固相率比较低(0.3~0.6)时,铸坯表面温度高,坯壳抵抗变形的能力差,压下使铸坯在上表面(内弧侧)至凝固前沿产生的等效塑性应变随固相率的增加而增加;当中心固相率较高(0.6~0.7)时,铸坯表面温度低,坯壳抵抗变形的能力强,压下使铸坯在凝固前沿产生的等效塑性应变随固相率的增加而减小. 因此,铸坯凝固前沿的等效塑性应变随着铸坯中心固相率的增加先增加后减小. 通过模型计算结果表明,对中心固相率在0.3~0.7范围内的铸坯压下7 mm,凝固前沿的最大等效塑性应变为0.16%,均未超过临界应变(0.4%). 所以,在中心固相率0.3~0.7范围内单辊压下7 mm不会产生内裂纹.
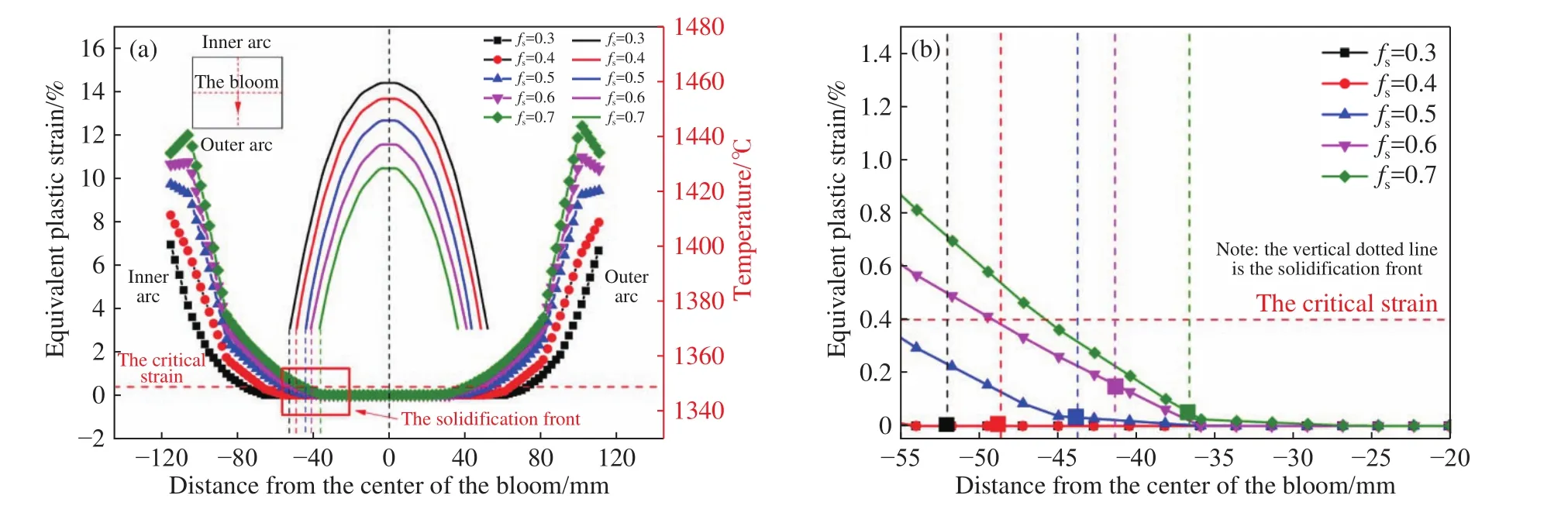
图9 铸坯等效塑性应变. (a)不同固相率下等效塑性应变;(b)凝固前沿等效塑性应变Fig.9 Equivalent plastic strain of the bloom at: (a) different solid fractions; (b) solidification front
2.3 压下量对压下裂纹敏感性的影响
对铸坯不同中心固相率进行压下裂纹敏感性研究,其结果表明,对中心固相率为0.6位置处的铸坯进行压下,铸坯凝固前沿出现裂纹的风险较高. 为进一步优化工艺参数,对铸坯中心固相率为0.6位置处的铸坯进行不同压下量的压下数值模拟计算,研究不同压下量对铸坯凝固前沿裂纹敏感性的影响.

图10 铸坯等效塑性应变. (a)不同压下量等效塑性应变;(b)凝固前沿等效塑性应变Fig.10 Equivalent plastic strain of the bloom (a) at different reduction amounts and (b) at the solidification front
图10给出了对中心固相率为0.6位置处的铸坯进行不同压下量时的等效塑性应变. 从图10(a)可以看到随着压下量的增加,铸坯产生的等效塑性应变逐渐增加. 从图10(b)中可以看出铸坯压下5 mm凝固前沿的等效塑性应变为0,也就是说,压下5 mm对凝固前沿等效塑性应变没有影响. 当压下量7、8、10和12 mm时,其凝固前沿的等效塑性应变分别为0.16%、0.65%、2.30%、3.85%. 随着压下量的增加,凝固前沿的等效塑性应变逐渐增加. 所以,增加压下量凝固前沿产生裂纹的风险大大提高. 压下量为7 mm时凝固前沿的等效塑性应变为0.16%;压下量为 8 mm时,等效塑性应变为0.65%,超过了U71Mn重轨钢的临界应变(0.4%).因此,对于U71Mn重轨钢在铸坯中心固相率为0.6时,压下量超过7 mm铸坯会产生内部裂纹.
2.4 压下模型验证
为了验证压下模型的准确性,对230 mm×280 mm断面重轨钢铸坯进行了压下试验,试验工艺参如下数:拉速为 1 m·min−1,比水量为 0.3 L·kg−1,过热度为31 ℃. 在铸坯中心固相率0.6位置处进行压下. 设计了5种试验方案,分别为方案一压下5 mm、方案二压下7 mm、方案三压下8 mm、方案四压下10 mm和方案五压下12 mm. 通过五组压下试验对铸坯进行取样,对所取试样沿拉坯方向取铸坯中心面的纵剖试样,试样尺寸为300 mm×230 mm×30 mm,取样示意图如图11(a)所示,对所取试样进行锯切、磨铣和酸侵等处理,观察铸坯内部质量.

图11 试样纵剖酸侵低倍照片. (a)取样示意图;(b)压下 5 mm;(c)压下 7 mm;(d)压下 8 mm;(e)压下 10 mm;(f)压下 12 mmFig.11 Acid erosion pictures of the longitudinal section sample: (a) sampling diagram; (b) reduction of 5 mm; (c) reduction of 7 mm; (d) reduction of 8 mm; (e) reduction of 10 mm; (f) reduction of 12 mm
图11(b)~(f)为不同压下量下纵剖试样低倍照片. 图11(b)为压下量为5 mm时铸坯试样低倍照片,低倍照片中未出现裂纹,但是存在“V”型偏析,说明压下5 mm时不会出现内裂纹,但是并不能解决“V”偏析;图11(c)为压下量7 mm铸坯试样低倍照片,低倍照片中也没有出现裂纹,同时“V”型偏析消失,说明压下量足够大,即避免了“V”型偏析又防止内裂纹的出现;图11(d)、图11(e)和图11(f)分别为压下量8、10和12 mm铸坯试样低倍照片,可以看到低倍照片均出现了内裂纹,并且随着压下量的增大,内裂纹也越严重. 因此,在铸坯中心固相率为0.6时,单辊压下量超过7 mm就会出现内裂纹,试验结果与模型计算结果基本一致,模型计算结果可靠.
3 结论
本文采用ABAQUS有限元软件对230 mm×280 mm断面重轨钢铸坯进行压下模型计算,同时经过工业试验的验证,得到以下几点结论:
(1) 对重轨钢铸坯进行凝固传热模型计算,计算了铸坯中心固相率为0.3、0.4、0.5、0.6和0.7时铸坯的温度分布,分别为1459、1453、1446、1437和1426 ℃,中心两相区的厚度分别是104.4、97.2、87.4、82.2和73.0 mm. 因此,铸坯中心两相区的厚度随着固相率的增加而减少.
(2) 压下模型压下区间计算结果表明,对中心固相率为 0.3,0.4,0.5,0.6和 0.7位置处的铸坯压下7 mm时,其凝固前沿等效塑性应变分别为0、0、0.03%、0.16%和0.04%,均未超过临界应变. 因此,对中心固相率 0.3、0.4、0.5、0.6和0.7位置处的铸坯进行7 mm压下,铸坯不会产生内裂纹.
(3) 压下模型压下量计算结果表明,在铸坯中心固相率为0.6时,压下量为5、7、8、10和12 mm,铸坯凝固前沿等效塑性应变分别为0、0.16%、0.65%、2.30%和3.85%. 随着压下量的增加,凝固前沿的等效塑性应变逐渐增加. 同时,压下量超过7 mm,凝固前沿的等效塑性应变超过临界应变.因此,铸坯出现内裂纹. 另外,压下试验验证了压下模型的可靠性.

