基于均匀试验的重轨最优复合矫直规程
宋 华 廉法博 李奎星 童山虎 贾 昊 原思宇 王忠强
1.辽宁科技大学,鞍山,114051 2.鞍山钢铁集团公司,鞍山,114021
3.南车石家庄车辆有限公司,石家庄,050000
0 引言
轨底纵向残余应力和平直度是衡量矫后重轨质量的2个重要指标。轨底纵向残余应力过大会造成重轨使役中的应力超过疲劳极限而失效,平直度则直接影响重轨成材率及列车运行的平稳性。国标GB258-2007《铁路用热轧钢轨》规定,矫后重轨轨底纵向残余应力必须小于250MPa,轨身平直度在垂直方向上每3m长度内轨身挠度小于等于0.5mm,且每3m长度内轨身挠度小于等于0.4mm,在水平方向上每1.5m轨身挠度小于等于0.7mm。平立复合矫直作为重轨生产中的最后一道变形工艺,所采用的复合矫直规程最终决定矫后重轨的轨底应力和平直度。目前生产中,对重轨进行试矫以寻找最优复合矫直规程,造成了大量的浪费,因此通过仿真分析和统计学试验对重轨复合矫直规程进行研究和优化具有重要意义。
目前,国内外对重轨复合矫直的研究主要集中在矫直过程中及矫直后重轨应力和平直度方面,采用统计学试验方法对最优复合矫直规程进行探索的文献极少。文献[1-4]对重轨矫直过程进行了仿真,并分析了矫后重轨的残余应力,但均未对矫直规程进行研究。文献[5]建立了简化的矫直辊模型,采用了正交试验方法对复合矫直规程进行了统计学研究,但需进行50次模拟计算,计算量非常大。本文采用均匀试验方法,仅需10次试验即可达到50次正交试验的统计精度。同时,本文在考虑重轨预弯冷却后残余应力的基础上,建立了精确的矫直辊模型,提高了重轨的网格密度。
1 重轨复合矫直模型的建立
采用ANSYS有限元软件对U75V百米高速重轨进行建模,考虑到冷床间距、矫直机辊距和计算时间,重轨模型长取5000mm,共划分了88 000个单元、114 729个节点,单元类型选用具有动力学特性的8节点6面体单元的Solid164,重轨截面及网格划分情况如图1所示。在采用ANSYS隐式热分析对重轨热预弯冷却过程进行求解后,通过隐显转换(implicit to explicit)方法将终冷时刻具有残余应力和几何变形状态的重轨导入矫直模型。导入前的重轨终冷时刻整体纵向应力分布如图2所示。

图1 重轨模型截面和网格划分

图2 重轨终冷时刻形状和纵向应力分布云图

图3 矫直辊有限元模型
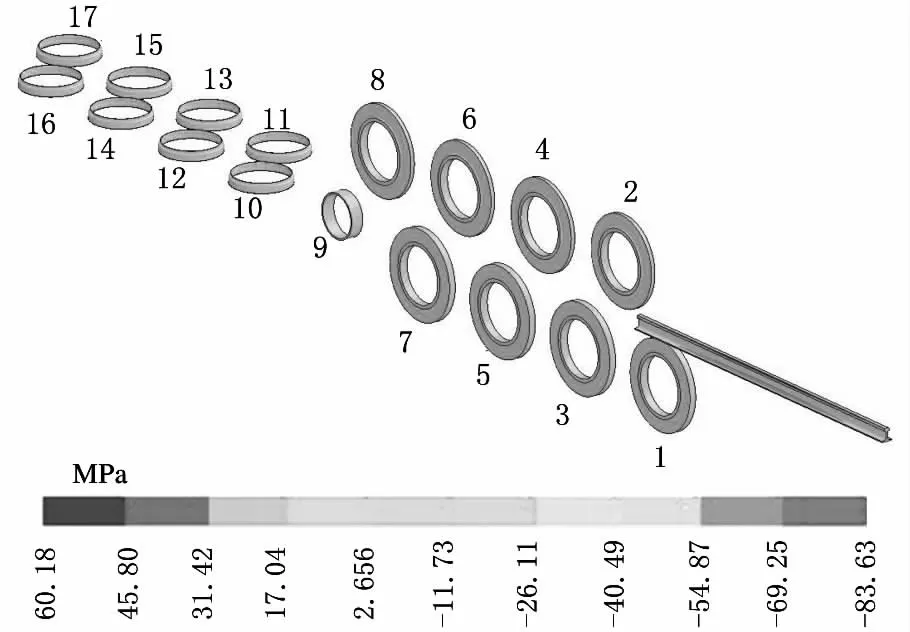
图4 应力初始化后的重轨矫直系统模型
具有精确辊型的矫直辊有限元模型如图3所示。导入后的重轨矫直模型及其纵向应力分布如图4所示。重轨复合矫直模型共划分358 440个单元、422 969个节点,重轨材料模型为双线性随动强化模型,矫直辊均为刚性体。重轨平立复合矫直机各辊依与重轨的先后接触顺序编号为1~17(图4),水平矫直辊距为1600mm,立式矫直辊距为1300mm,9#辊为无辊型辅助辊。重轨水平矫直上侧的2#、4#、6#、8#辊和立矫右侧的11#、13#、15#、17#辊可进行压下量的调节(17#辊的压下量一般为0)。各辊的压下量组合称为矫直规程。以某厂采用的复合矫直规程(表1)为基准规程,在此基础上对每个矫直辊的压下量进行调节,并按照均匀试验设计方法进行模拟试验和统计分析。重轨及矫直辊的有限元材料参数如表2所示。

表1 重轨平立复合矫直各辊压下量 MPa

表2 重轨及矫直辊的有限元材料性能参数
2 均匀设计和试验方案
均匀试验设计根据具体试验来选择适用的均匀设计表,按对应的均匀设计使用表来安排试验方案,设计时不考虑因素的交互作用[6]。均匀设计表与正交表类似,是一种规格化的试验工具表格,用Un(mk)表示,其中,U为均匀设计表代号,n为试验总次数,m为水平数,k为最大因素数。n、k分别表示行数和列数,m表示每列中字码的个数。
采用不同压下量组合进行试验以找到最优的矫后重轨残余应力和平直度的矫直规程是本文试验设计的指导思想。将可控并影响试验结果的7个矫直辊(2#、4#、6#、8#水平矫直辊和11#、13#、15#立式矫直辊)的压下量作为因素。各矫直辊的压下量以现场压下量为基准,将现行压下量(减小2mm、减小1mm、增加1mm、增加2mm)作为各因素的5个水平。故本试验共有7个因素、5个水平,全面试验需进行57=78 125次,正交试验需进行50次,采用均匀试验设计方法,并使用拟水平法即将每个水平重复一次,选用10水平的均匀设计表,则仅需进行10次模拟试验即可获得较高试验精度。因此,选用U10(1010)的设计表(表3)安排试验方案(试验号1~10),再根据U10(1010)使用表(表4)设计本试验表头,如表5所示。

表3 U10(1010)均匀设计表
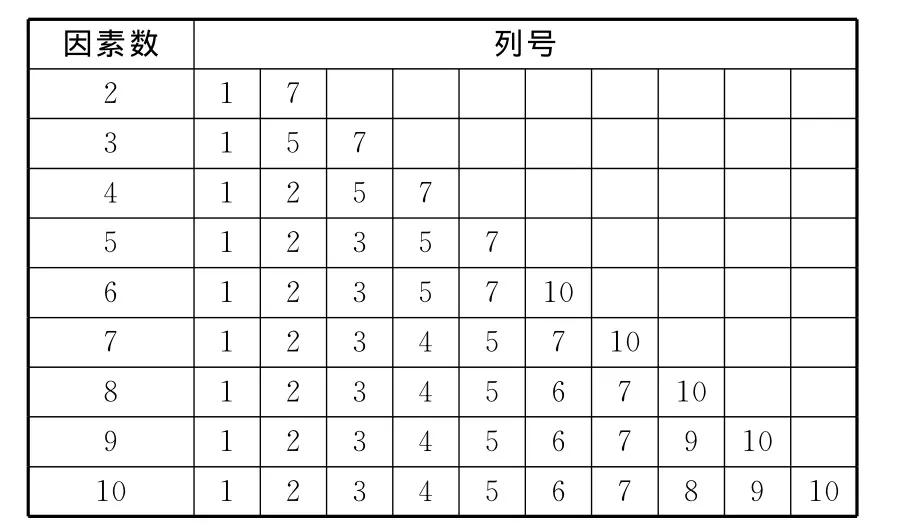
表4 U10(1010)的使用表

表5 均匀试验表头设计
均匀试验表头设计完成后,再结合U10(1010)使用表,将每个因素的5个水平(压下量,单位mm)按照拟水平的原则填入U10(1010)均匀设计表中,即得到本次均匀试验方案,如表6所示,按照该试验方案进行试验,试验结果见表7。表7中,X11表示1号因素的第1水平,即表示2#矫直辊的压下量为17.2mm,其他类推。

表6 试验方案
由于均匀设计的试验点分布均匀,因此可采用直观分析法直接对试验结果进行比较,并从中选出试验指标最好的矫直规程。各辊压下量的调节作用则属于多元线性回归问题,需采用回归分析法,并借助相关计算分析软件进行分析计算。本文选用软件 SPSS(statistical product and solution)13.0对试验结果进行数据处理和回归分析。

表7 试验结果
3 试验结果分析和最优矫直规程的确定
3.1 最优轨底纵向残余应力规程
以矫后重轨轨底中线上节点的纵向应力为研究对象,对矫后重轨轨底纵向残余应力进行分析以找到最优规程和调节方法。由表7可知,3号试验应力最小,为残余应力最佳规程。对试验结果进行回归分析,得到回归方程:
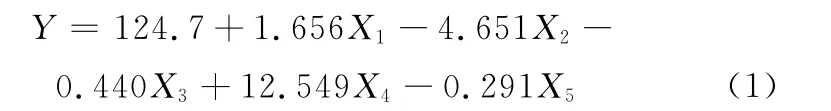
最大拉应力回归分析结果的相关系数为0.418 518,判定系数为0.175 157,校正判定系数为-1.3559,标准差为54.715 73,观测值为10。相关方差分析结果如表8所示,由于显著值大于0.05,说明回归方程可信。将回归方程各项的回归系数标准化后,由于X2、X3和X5的系数为负数,且以应力最小为佳,因此2#、8#辊压下量取值应偏下限,同理,4#、6#、11#压下量取值应偏上限。将以上各值代入式(1),得到Y=102.184 MPa,该应力不仅大于3号试验的应力89.033 MPa和10号试验的应力89.747MPa,且大于作为对照的现场压下量的模拟结果94.587MPa。

表8 最大拉应力结果方差分析表
由于最大拉应力回归统计的相关系数仅为0.418 518,说明回归方程的显著性不高,即各辊压下量的调节对轨底最大应力仅存在一定程度的影响,但并不会使应力出现大幅度的波动,而仅会在一定范围内变化。
由回归方程各项系数可判断各因素影响大小的主次顺序为8#、4#、2#、6#、11#。该顺序说明若要得到较小的轨底应力,压下量的调节优先顺序如下:减小8#辊压下量、增大4#辊压下量、减小2#辊压下量、增大6#辊压下量、增大11#辊压下量。
3.2 最优平直度规程
根据表5所示的平直度结果,通过直观分析法可知,虽然3号和7号试验的垂直方向的平直度结果(0.231mm、0.252mm)最好,8号试验的水平方向平直度结果(0.379mm)最好,但仅7号试验平直度结果在垂直方向和水平方向同时满足国标要求,为最佳试验结果。对比对照组的平直度结果(垂直方向0.317mm和水平方向0.342 mm),7号试验组水平方向平直度并不理想。
(1)用回归分析方法,得到垂直方向平直度的回归方程:
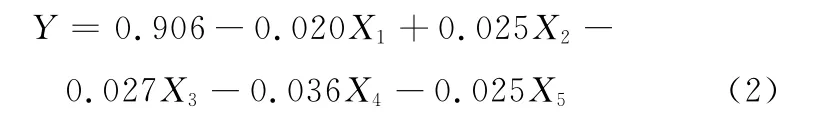
由式(2)、垂直方向平直度回归统计结果(相关系数0.880 053、判定系数0.774 494、校正判定系数-0.007 39、标准差0.076 082、观测值10)和表9的相关性分析可知,垂直方向平直度与13#、15#辊的压下量没有线性关系,与其他几个辊的压下量的相关系数接近1,表明回归方程显著相关。再由各项回归系数可知,各因素的主次顺序为X4、X3、X2、X5、X1,因此为了得到更好的垂直方向平直度,调节各辊压下量的效果和方法依次为:增大8#辊压下量,增大6#辊压下量,减小4#辊压下量或增大11#压下量,增大2#辊压下量。

表9 垂直方向平直度结果方差分析表
(2)用回归分析方法得到的水平方向平直度的回归方程:
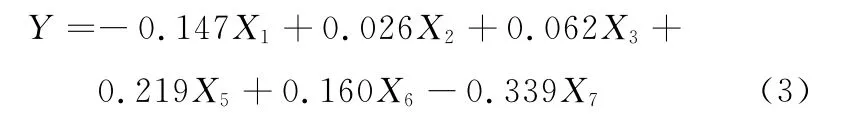
同理,由式(3)、水平方向平直度回归统计的结果(相关系数0.976 728、判定系数0.953 998、校正判定系数0.396 495、标准差0.269 011、观测值10)和表10可知,各因素的主次顺序为X7、X5、X6、X1、X3、X2,且水平方向平直度与以上各辊压下量的调节有直接关系,与8#没有线性关系。因此为了得到更好的水平方向平直度,调节各辊压下量的效果和方法依次为:增大15#辊、2#辊的压下量,减小11#辊、减小13#辊、6#辊、4#辊的压下量。

表10 水平方向平直度结果方差分析表
3.3 重轨最优复合矫后规程
综上所述,7号试验和对照组试验结果在各个指标上均满足国标要求,其中,7号试验的轨底最大应力为150.080MPa,垂直方向平直度为0.252mm/1m,水平方向平直度为0.586mm/1.5m;而现场生产中采用的矫直规程19.2mm-11.2mm-7.9mm-3.5mm-12.0mm-6.0mm-2.5 mm,采用现场规程的对照组试验的轨底最大应力为94.587MPa,垂直方向平直度为0.317mm/1m,水平方向平直度为0.342mm/1.5m。可见采用现场矫直规程所得到的轨底最大应力更小,平直度指标也更优。因此,通过对U75V重轨最优矫直规程的理论研究,证明通过大量生产实践逐渐摸索出并在现场生产中所采用的矫直规程为最优规程。
3 结论
(1)矫直过程中各矫直辊压下量的单独调节不会对矫后重轨轨底纵向应力产生较大影响。减小重轨轨底纵向应力的压下量调节方法和效果依次为:减小8#辊压下量,增大4#辊压下量,减小2#辊压下量,增大6#辊压下量,增大11#辊压下量。
(2)矫直过程中各个矫直辊压下量的单独调节对矫后重轨的平直度指标影响很大。提高垂直方向平直度的压下量调节方法和效果依次为:增大8#辊压下量,增大6#辊压下量,减小4#辊压下量或者增大11#辊压下量,增大2#辊压下量;提高水平方向平直度的压下量调节方法及效果依次为:增大15#辊压下量,减小11#辊压下量,减小13#辊压下量,增大2#压下量,减小6#辊压下量,减小4#辊压下量。
(3)通过对重轨最优复合矫直规程的均匀试验优化研究,证明现场生产中采用的矫直规程即为最优规程,即19.2mm-11.2mm-7.9mm-3.5 mm-12.0mm-6.0mm-2.5mm,其结果是:轨底最大应力为94.587MPa,垂直方向的平直度为0.317mm/1m,水平方向平直度为0.342mm/1.5m。
[1] Chen Lin,Wang Jianguo,Li Ge.The Simulated Calculation and Optimizing Experimental Research of the Residual Stress of the Heavy Rail[J].Materials Science Forum,2012,704/705:296-301.
[2] Chen Lin,Tian Zhongliang,Gao Michao,et al.Researches on Rules of the Longitudinal Residual Stress Distribution in Straightening Deformation Zone of Heavy Rail with Multi-rollers[J].Materials Science Forum,2008,575/578:231-236.
[3] Talamini B,Gordon J,Perlman A B,et al.Finite Element Estimation of the Residual Stresses in Rollerstraightened Rail[C]//ASME Proceedings Rail Transportation.Anaheim,CA,USA,2004:123-131.
[4] 周剑华,吉玉,吴迪.辊式水平矫直60kg/m重轨断面应力应变分析[J].塑性工程学报,2011,18(6):39-42.Zhou Jianhua,Ji Yu,Wu Di.Analysis of the Stress and Strain on the Section of 60kg/m Heavy Rail in the Process of Level Roller,Straightening[J].Journal of Plasticity Engineering,2011,18(6):39-42.
[5] 王培龙.重轨辊式复合矫直数值模拟研究[D].鞍山:辽宁科技大学,2009.
[6] 方开泰.均匀试验设计的理论、方法和应用——历史回顾[J].数理统计与管理,2004,23(3):89-99.

