雷击高速铁路牵引网引发的跳闸率分析

段启凡，杨 桐

0 引言

截至2020年底，全国铁路营业里程达14.63万公里，电气化率达72.8%，其中高速铁路营业里程3.79万公里。随着电气化铁路营业里程和运行速度的不断提高，开展电气化铁路牵引网安全运行相关课题的研究十分重要。随着高速铁路的桥占比越来越高，迫切需要结合接触网自身特点对雷电防护问题开展系统研究。

目前，我国高速铁路采用高架长桥结构模式的占比较高，高速铁路牵引网在高架长桥处对地高度相当于110 kV架空输电线路的对地高度，而由于牵引网不设避雷线，导致牵引网系统受直击雷影响的概率较大[1]。

近年来研究高速铁路牵引供电系统的耐雷特性主要持有下述几种观点：AT供电方式是我国高速铁路主要采用的一种供电方式，文献[2]利用ATP-EMTP仿真平台搭建T-F-R接触网线路和牵引变压器等模型，通过仿真得到当雷电流击中牵引供电系统时，牵引供电系统的雷电过电压幅值可以达到1.2 MV，远远大于线路绝缘子所能承受的雷电过电压幅值，给电气化铁路安全运营带来较大风险，该文献同时验证了架设牵引网避雷线可保护牵引网系统不受直击雷影响。文献[3，4]基于经典击距理论计算高速铁路牵引网的引雷范围，得出当高架桥梁平均高度约15 m时，相应的接触网系统对地高度约为25 m的结论，此时接触网系统遭受雷击概率约为路基接触网概率的2倍，且遭受雷击风险等级也随之提高。由于高铁的线路密集度日趋增加，上跨桥情况增多，接触网高度随之增加，导致直击雷比感应雷更容易造成绝缘闪络。

对上述文献综合分析对比不难看出，研究接触网的雷击原理一般需要搭建EMTP模型，将电力系统中的实物进行模块化，引入雷电流后进行感应雷和反击雷的危害评估；另外一种主流方法是利用击距法分析直击雷对接触网的危害。本文主要讨论如何快速准确获取高铁接触网的直击雷跳闸率（跳闸次数），采用击距法进行分析，并融入雷击角度和风速值这两个影响因子，最后采用蒙特卡罗法对经典击距法进行改进，提升准确率。

1 搭建雷击几何模型计算接触网跳闸率

1.1 搭建雷击几何模型

雷电引向被研究物体的临界距离前，击距法无法准确预测雷击点[5]，雷电先导头部率先到达某一物体的击距范围内时，即向该物体放电。以电势为零的地面作为参考面，采用文献[4]的几何模型进行计算，导线的雷电击距RS为

地面的雷电击距RSG为

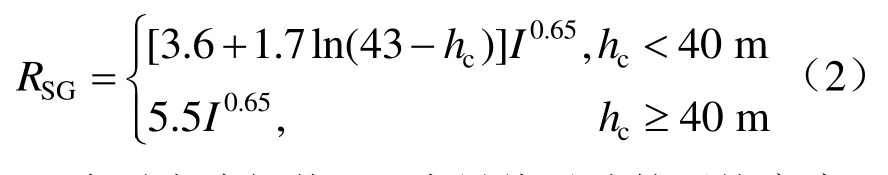
式中：I为雷电流幅值；hc为导线对地的平均高度。

通过式（1）、式（2）的击距计算式可以看出，牵引网导线与大地间的击距差随着牵引网导线高度的增加而有所增加，牵引网距离大地的导流通路增加，雷电流流向大地的占比减少，从而增加了牵引网遭受直击雷的风险。目前高速铁路的桥占比较高，其高度普遍高于建在地面上的普速铁路，因此遭受直击雷的概率大幅增加。

高铁牵引网一般将架空地线布置在正馈线上方，由此建立雷击T-F牵引网的电气几何模型，如图1所示。其中，1，1′为供列车取流的接触线；2，2′为架空地线；3，3′为正馈线。地面位于X轴，悬挂接触线的支柱位于Y轴，两轴交点设为原点O。图中C1、C2和C3分别为接触线、架空地线和正馈线的暴露弧（其半径均为r，圆心分别为P、M、N点），Y轴同C1的交点为A点，B点、C点和D点围成3个暴露弧的区域，以暴露弧的水平投影Dz1、Dz2、Dz3分别作为3点的暴露距离（单位：m）。当雷击位置处于Dz3点右侧时，过电压由感应雷引起，本文不作分析研究。

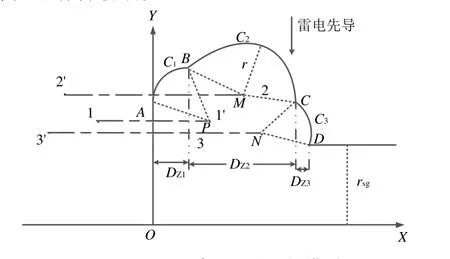
图1 雷击牵引网的几何模型

由图1可以得到A、B、C、D点的坐标计算式：

A(xa,ya)坐标计算式为

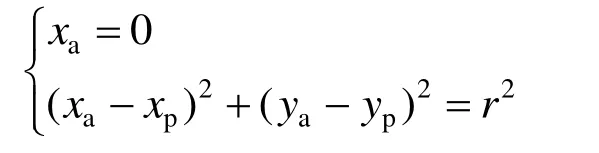
B(xb,yb)坐标计算式为

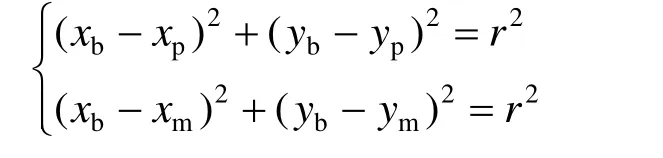
C(xc,yc)坐标计算式为

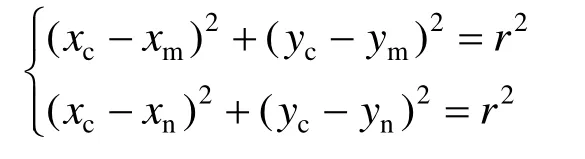
D(xd,yd)坐标计算式为

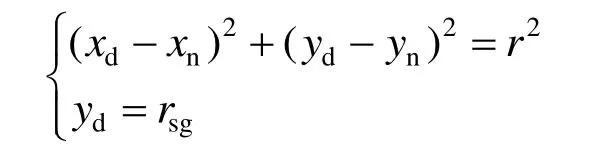
式中：(xp,yp)、(xm,ym)、(xn,yn)分别为P、M、N点的坐标。

如图1所示，地线完全位于接触线的击距范围外，接触线完全处于地线的保护范围以内，当接触线处于地线保护范围外时，接触线的最大绕击击距为rmax，接触线的最大绕击电流为Im1。

当雷击接触线或正馈线时，通过DDRTS仿真计算得到此时雷电流Ic= 3. 83 kA。

在雷电先导与大地垂直时，各类导线的暴露距离计算如下。

（1）接触线的暴露距离Dz1：

若Im1≥Ic，当Ic≤I≤Im1时，Dz1=xb-xa，否则，Dz1= 0。

（2）架空地线的暴露距离Dz2：

若Im1≤Ic，当I≥Ic时，Dz2=xc-xa；

若Im1＞Ic，。

（3）正馈线的暴露距离Dz3：

当xd≥xc时，Dz3=xd-xc；否则，Dz3= 0。

根据计算得到的Dz1、Dz2、Dz3，可以推出全段高速铁路高架桥段复线牵引网雷击跳闸面积为2×L1×Dz，其中：L1为线路长度，km；Dz为导线的暴露距离，m。则电气化铁路牵引网的直击雷跳闸次数(次/年)计算式为

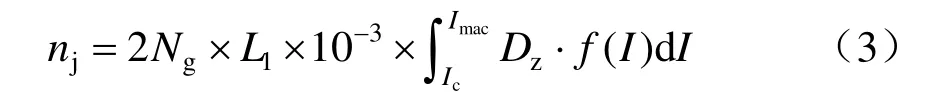
式中：f(I)为雷电流幅值的概率密度函数；Ng为落雷密度，次/(km2·年)，Ng=，Td为年雷暴日，参考GB/T50064—2014附录D的计算式，年雷暴日取40天[5]。

虽然图1模型的建立基础为目前普遍使用的牵引网结构，但是分析计算过程中各点所在位置的坐标均参与计算，各点之间的关系变换并不影响计算方法的使用。因此该计算过程并不局限于图1所示这一种模型，当分析其他结构的牵引网时，仍可采用该计算过程。

1.2 雷电流幅值的分布情况

雷电流幅值的概率分布是分析高速铁路牵引供电系统遭受直击雷跳闸过程的重要影响因素之一。IEEE雷电特性工作组评估输电线路时推荐的雷电流幅值的概率分布公式为

式中：P为电流幅值大于I的概率；I为雷电流的幅值，kA。

2 击距法模型的改进

2.1 考虑雷击入射角对击距法模型的改进

假设雷击入射时垂直于地面，即雷击入射角为0°，以接触线、架空地线和正馈线暴露弧在水平方向上的投影作为暴露距离Dz1、Dz2、Dz3，如图1所示[6]。而实际雷击入射通常不是垂直于地面，角度也并不是固定不变的，因此在改进牵引网的电气几何模型（击距模型）时，需要将雷击入射角ψ一同加入分析。

文献[7]在击距法分析中引入雷电入射角这一影响因素，重新定义导线的暴露距离（雷击入射的法平面作为参考平面，入射角在该平面的投影即为暴露弧的距离），代入式（3）求出在不同雷击入射角角度下的线路雷击跳闸次数。但由于该方法中线路与地面的屏蔽关系始终以雷电先导角度为0°为基础，而当雷电先导角度不为0°时，屏蔽关系将导致线路的暴露距离计算结果和入射角为0°时计算结果不同。本文分析雷击入射角不为0°时的情况，通过坐标变换改进击距法模型，以降低屏蔽关系发生改变时线路暴露距离的计算误差。

图2所示为考虑雷击入射角的电气几何模型。假设雷击入射角为ψ时，将直角坐标轴相应顺时针旋转ψ后，在新的X′ -Y'直角坐标系下，雷电先导向下与大地垂直时，雷电入射角保持0°，直角坐标系旋转后，坐标变换式如下：

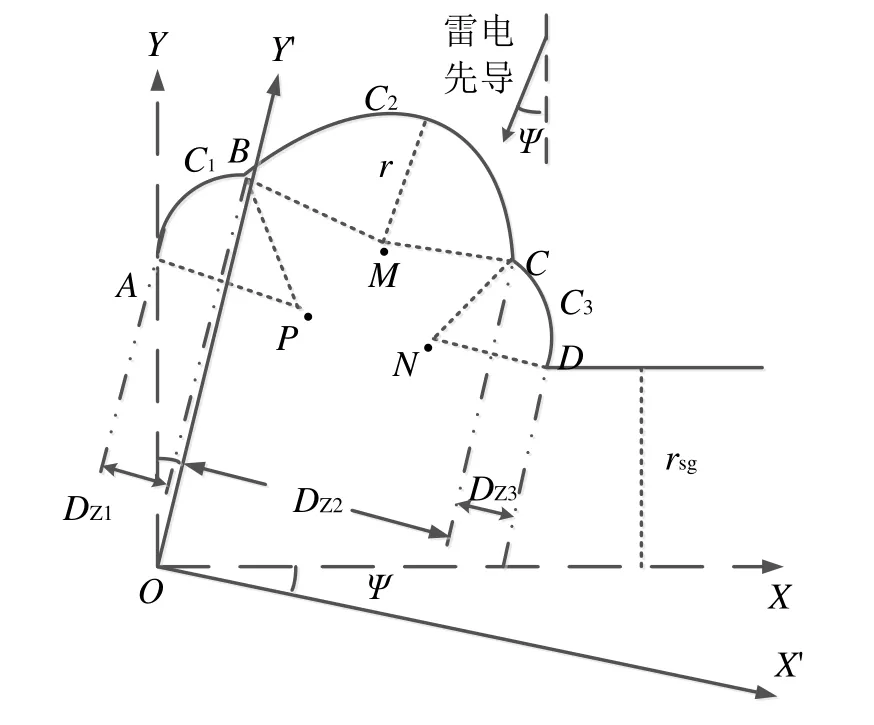
图2 考虑雷击入射角的电气几何模型

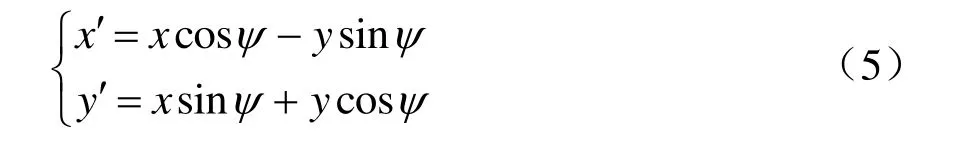
图1中P、M、N点坐标变换为新坐标系下的P′、M′、N′坐标。等式左侧变换后，接触线、架空地线和正馈线暴露弧投影的暴露距离 z1D′、z2D′、计算方法与雷电入射角为0°时相同。

根据文献[7]，入射角的概率分布可以表示为

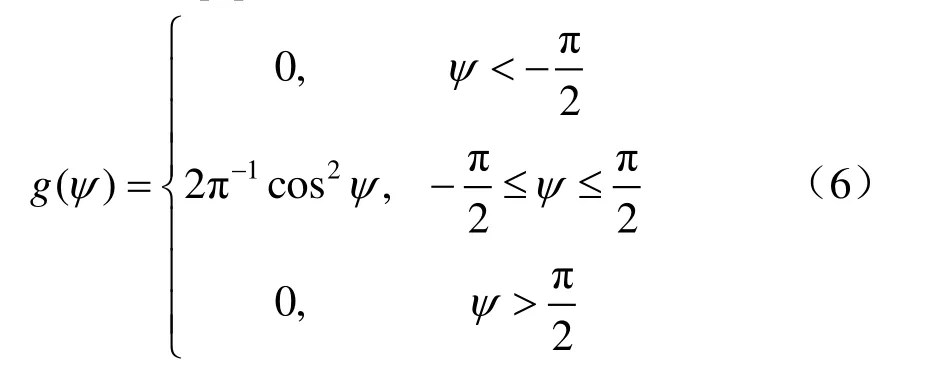
由地面击距公式可知，雷击入射角只需考虑（-90°，90°）范围内的变化情况，且该范围内的g(ψ)函数对ψ的正负取值轴对称，因此只需考虑入射角在（0，90°）范围内的变化情况。入射角在（0，90°）范围内，接触网的雷击跳闸次数可表示为

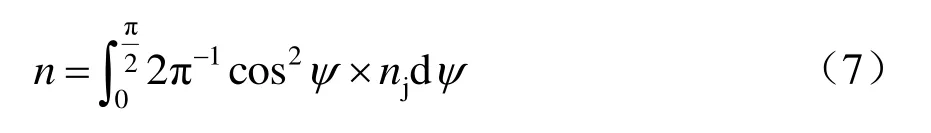
2.2 考虑风速对电气几何模型的改进

2.2.1 风速对牵引网的影响

大风时常伴随雷击发生，同时大风会引起牵引网导线及绝缘子串的摇摆，从而造成风偏角，此时牵引网导线弧垂最低点对地高度以及绝缘子串保护角度也随之增大，造成牵引网的引雷概率提高，即大幅增加了牵引网的绕击率。列车运行过程中会对牵引网产生一定的振荡，形成风速，其中高速铁路运行速度在250～300 km/h时，可以对应17级大风。

文献[8]举例500 kV输电线路在风速小于5 m/s时，风速引起输电线路导线和绝缘子串的风偏摇摆角很小，对线路雷电绕击率影响可忽略不计；但当风速大于5 m/s时，风速引起输电线路导线和绝缘子串的风偏摇摆角会随之增大，造成线路雷电绕击率大幅提高。因此，将风速纳入模型搭建过程，继续对击距法模型进行改进，可对雷击牵引网的状态进行更加切合实际的模拟。

2.2.2 电气几何模型（击距模型）的改进

假设风速为v时，导线与横担垂直方向的风偏摇摆角为ξ，绝缘子串与横担垂直方向的风偏摇摆角为φ，其计算式为

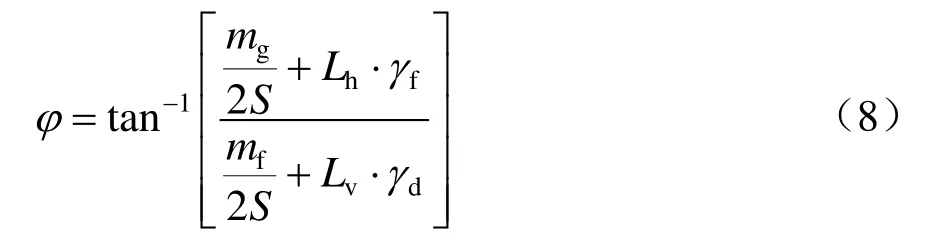
式中：Lh、Lv分别为该跨导线的水平档距与垂直档距，m；γd、γf分别为导线的自重比载和水平风比载，kg/(m·mm2)；mf、mg分别为绝缘子串重量和水平风荷载，kg；S为导线的总截面积，mm2。

计入导线分裂间距的影响时，计算式为

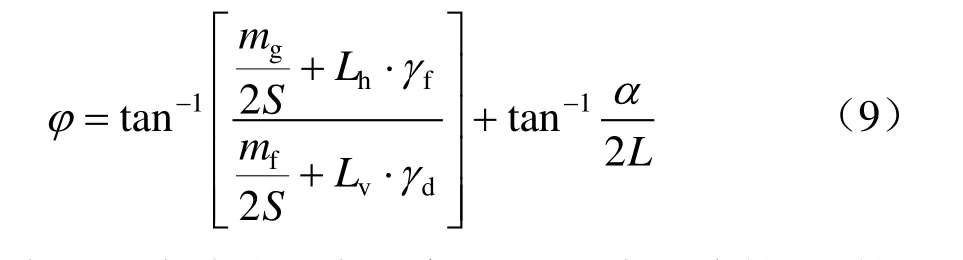
式中：L为绝缘子串长度，m；α为导线的分裂间距，m。

导线风偏角由式（10）确认，g1为垂直方向的自重荷载，g4为水平方向风荷载。

以接触线及架空地线为例，计及风速影响时，架空地线和接触线的坐标 MX′，PX′，MY′，PY′与静止状态时的架空地线和接触线的坐标XM，Xp，YM，Yp的关系如下：

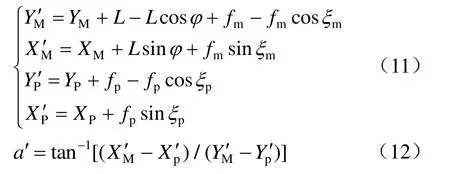
式中：a′为风偏保护角；fm、fp分别为架空地线和接触线的弧垂；ξm、ξp分别为架空地线和接触线的风偏角。

风速可认为服从双参数韦布尔分布[9]，根据双参数韦布尔分布公式，风速v的概率密度函数为

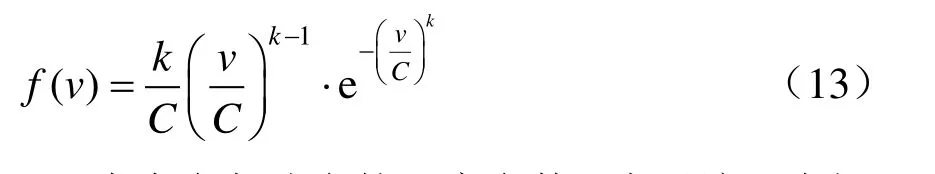
式中：C为韦布尔分布的尺度参数，表示该风电场的平均风速，m/s，通常取值为5；k为韦布尔分布的形状参数，表示分布曲线的峰值状态（无量纲），通常取值为2。

基于击距法模型得到的牵引网雷击跳闸次数计算式（3），再引入风速的概率密度函数，得到改进后的牵引网直击雷跳闸次数的计算式为

3 雷击牵引网的随机过程分析

3.1 蒙特卡罗法模拟流程

根据蒙特卡罗法算法原理，随机参数的计算方法如下：

根据式（4），依据图3所示的流程进行雷电随机情况模拟。根据文献[10]中的结论，将雷电流幅值设置在7～40 kA范围内。

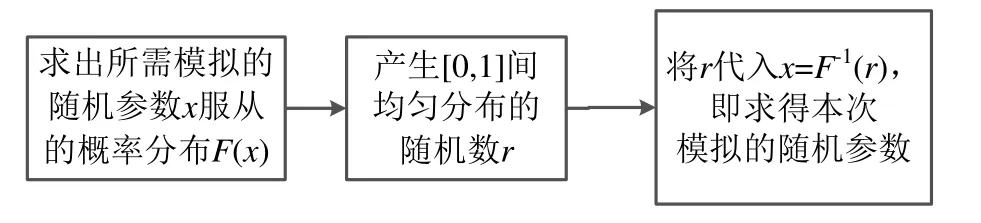
图3 蒙特卡罗法流程

3.2 牵引网雷击跳闸次数的算式简化

在计算牵引网的雷击跳闸次数时，对随机参数模拟后，将牵引网直击雷跳闸次数函数作为目标函数，利用蒙特卡罗法计算多重积分[11]，将计算目标函数转化为求算术平均值的方式作为其近似值，则跳闸次数计算式近似为 式中：N为模拟随机过程次数；A为多重积分所在区域的体积；f(ψ)为入射角的概率分布密度函数。

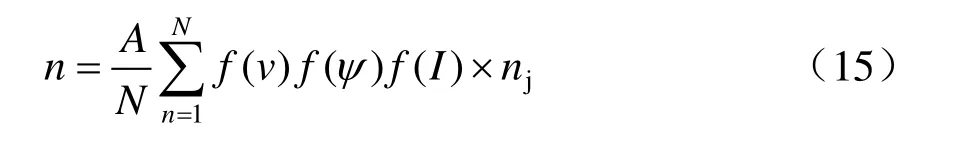
3.3 实例计算

某高速铁路支柱的结构型式见图4，图中AF为正馈线，PW为保护线，JQ为加强线。图4为接触网常见结构模型，本文不讨论带加强线的影响。

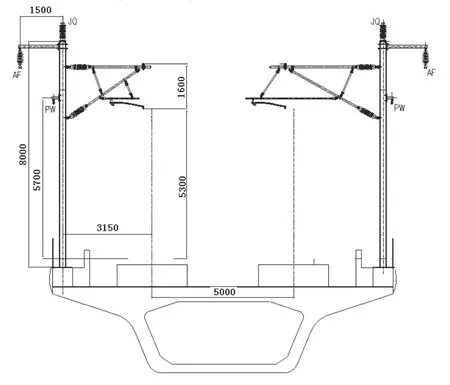
图4 支柱结构（单位：mm）

根据上文中改进击距法模型，并考虑雷击入射角度及风速的影响，建立符合算例结构的击距法模型，模拟3种导线分别在风速为0～5、5～10、10～15 m/s区间时，雷击入射角在[0，45°]和[45°，90°]范围内的雷击跳闸次数。

模拟计算结果如图5～图7所示。可以看出，雷击跳闸次数（跳闸率）与风速成正比。由图6可知，雷击入射角角度变化对正馈线雷击跳闸率产生影响，但不能起到重要作用。综上可知，雷击入射角度对3种导线的跳闸率会产生不同的影响，其中对接触线和架空地线的影响较大，对正馈线的影响较小，且与牵引供电线路架设的位置有关。

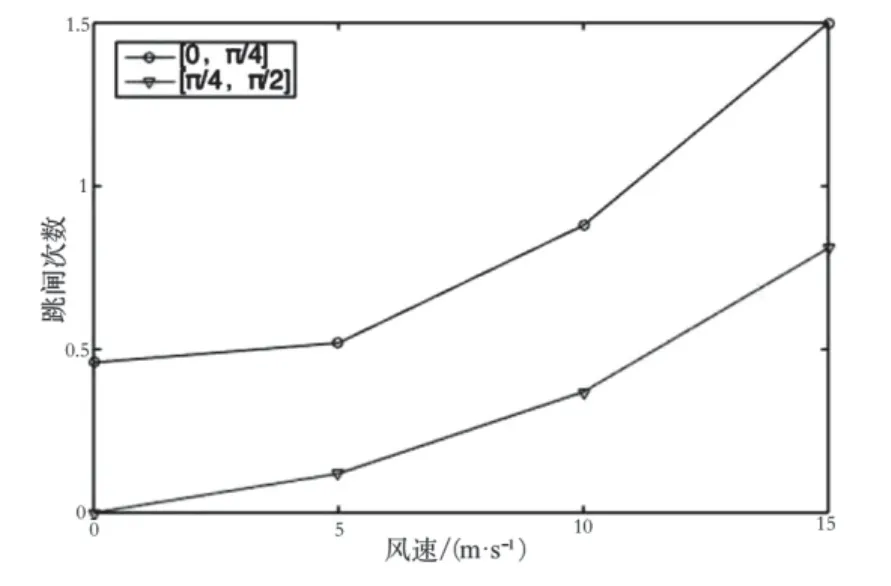
图5 接触线跳闸情况

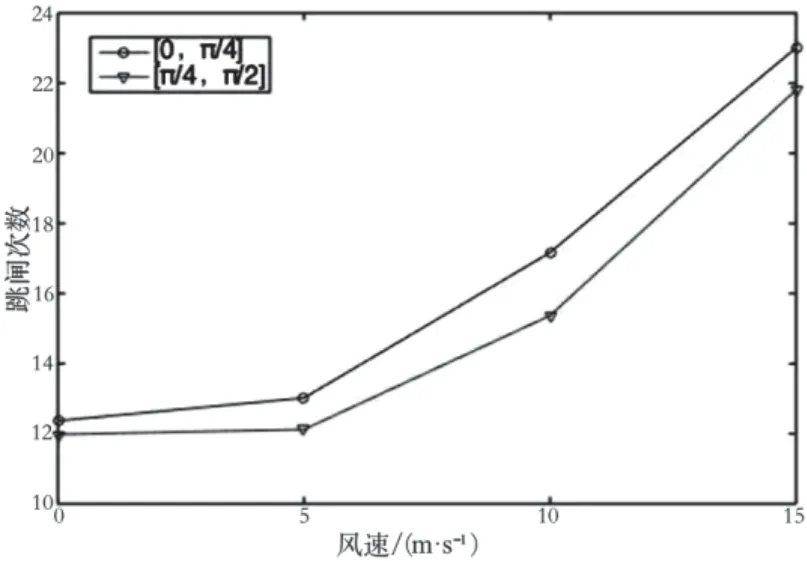
图6 正馈线跳闸情况

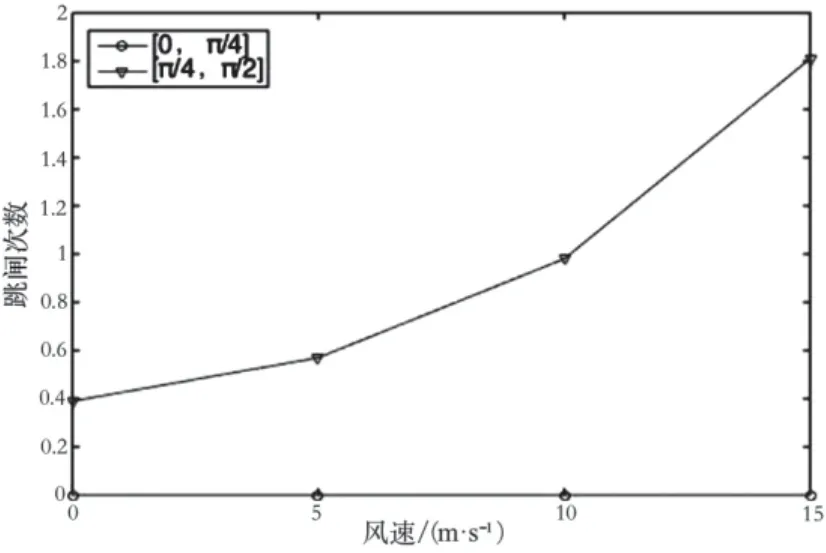
图7 架空地线的跳闸情况

此外，在该牵引网结构中，当保护地线位置较低时，雷电易被屏蔽，其跳闸次数计算结果较小。而正馈线位置较高时，引雷范围变大，可由此导致较高的跳闸率。

4 结论

本文主要分析雷击高速铁路牵引网的跳闸率，首先将击距法模型加以改进，再将风速、雷击入射角和雷电流幅值3个因素考虑进跳闸率计算式中，最后通过蒙特卡罗法模拟得到牵引网的直击雷跳闸率的简化计算方法。

模型中设置桥梁高度为30 m，以100个锚段长度为基础，通过电力系统动态仿真软件DDRTS的仿真计算结果表明：在图4的模型数据下，接触线、正馈线的雷击跳闸率均与风速成正比，表现为当风速增大到原来的2倍时，雷电绕击率会增大1倍以上；当入射角在[0，45°]区间范围内时，地线的绕击率基本为0，且雷击入射角的影响程度与牵引网线路架设的位置有关。实际工程中，架空地线设置在杆顶时可以有效降低接触线的绕击次数。