人寿保险额影响因素的多元回归分析
赵金兰 高丽英
(山西省财政税务专科学校,山西 太原 030024)
人寿保险额与从业经理的年平均收入及风险偏好度影响着人寿保险业的健康发展。近年来,学术界已有学者对相关影响因素进行研究,并经验式地粗略推导出一些影响因素的相关变化趋势,对从业经理从事保险业有一定的指导意义。但现有研究并未给出较为准确的研判结论,导致该行业从业经理受个人偏好的影响,有观望的、有退出的,都不同程度影响了行业的可持续发展。本文利用定量分析方法中最常见的多元回归分析法,通过数据间的客观数量规律,建立人寿保险额与从业经理的年平均收入及风险偏好度的多元非线性回归模型。此模型将有助于推进将对该行业的发展研究提升到较为精准的高度,并能有效指导从业经理理性规避偏好、稳定收入,保持保险行业的健康发展。
一、基本假设
假设1:人寿保险与年平均收入、风险偏好度存在相关性。
假设2:数据的记录是客观的。
二、模型建立与求解
在建立人寿保险额与从业经理年平均收入、风险偏好度的关系之前,需做如下符号约定:X1、X2是自变量,分别表示年平均收入、风险偏好度;Y是因变量,表示人寿保险额;ε表示随机误差项,是随机变量;R2表示决定系数,等于回归平方和(能够由X1或X2解释的部分)除以总平方和(Y的总变差),其值在0~1之间。决定系数有两个意义:第一个意义表示拟合效果,当R2越接近1,拟合效果越好,当R2越接近0,拟合效果越差;第二个意义表示因变量Y的总变差中能够由自变量X1或X2解释的比例。
在回归分析中,一元线性回归是多元线性回归的基础,而非线性回归是多元线性回归的拓展。在下列模型中,先从一元线性回归开始,然后到二元线性回归,最后提升到多元非线性回归。
模型一:利用Python一元线性回归探讨人寿保险额Y随单个因素变化规律并建立模型。
Y=β0+β1Xi+ε,ε~N(0,δ),i=1,2
(1)
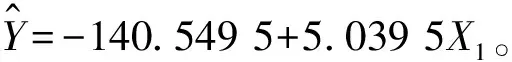
一元线性回归模型的假定只是我们自己的假定,X1与Y是否真的存在线性关系,即斜率β1是否真的不为零,需要做检验。检验的办法有t检验和F检验。在一元统计分析中,这两个检验是等价的。下面以F检验为例,进行假设检验。
第一步,提出假设:原假设H0:β1=0 (X1与Y的线性关系不成立,表示X1不需要进入模型,要从模型中去掉);备选假设H1:β1≠0(X1与Y的线性关系成立,X1需要进入模型)。

第三步,计算检验统计量的实现值及p值,如表1所示。
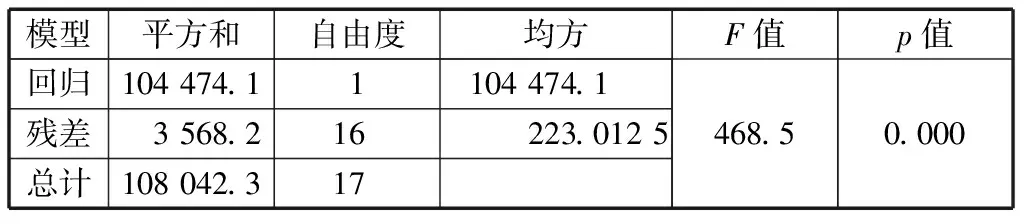
表1 方差分析表
其中,均方是平方和除以自由度,F值即为F统计量的实现值,是两均方的比值。

p值是F大于F实现值的概率,p={F>468.5}=0,因为p值小于0.05,所以认为X1与Y的线性关系是显著的,说明回归方程是显著的。
同样,对人寿保险额与风险偏好度做一元线性回归,Python运行结果为:β0=38.743 5,β1=13.521 8。由于R2=0.153,说明模型拟合效果不理想,F=2.885,因为p=0.109>0.05,说明人寿保险额与风险偏好度没有明显的线性关系。
在模型一的讨论中,人寿保险额与风险偏好度没有明显的线性关系,故一元线性回归模型不能反应人寿保险额与风险偏好度之间的关系,说明人寿保险额与多个因素相互关联,应由多个自变量的最优组合共同预测或估计因变量将更加有效,更符合实际。
模型二:通过模型一的讨论,尝试利用Python和多元线性回归分析讨论人寿保险额与年平均收入及风险偏好度之间的关系,建立人寿保险额与年平均收入及风险偏好度的多元线性回归模型。
Y=β0+β1X1+β2X2+ε,ε~N(0,δ)
(2)
对人寿保险额与年平均收入及风险偏好度利用参数的最小二乘估计做二元线性回归,Python运行结果为:β0=-158.767 6,β1=4.843 4,β2=5.201 4。同样,X1及X2的系数β1和β2是否都不为0,需要用t检验,不能用F检验。在多元统计分析中,这两个检验不同:单个回归系数用t检验;整体显著性系数用F检验。单个回归系数t检验过程比较复杂,可以参考多元回归分析教程。由Python运行结果可知,在单个回归系数β1和β2的t检验中,p值都等于0,也就是都小于0.05,所以认为X1及X2与Y的线性关系是显著的,说明回归方程是显著的。在F检验中,R2=0.988,决定系数R2比一元回归有所增加,说明模型拟合比一元回归也有所提高。F=623.6,F值增加了,且p=left{F>623.6 ight}=0,说明显著性也有所提高。
为了进一步弄清楚从业经理的年平均收入和人寿保险额之间是否存在二元关系,对模型二进行修改。
模型三:通过对模型一、模型二不断深化的讨论,增加上自变量X1的平方项,建立一个多元非线性回归模型。
Y=β0+β1X1+β2X2+β11X12+ε,ε~N(0,δ)
(3)
把式(3)中X12看作一个变量,仍然是多元线性回归问题,Python运行结果为:β0=-62.348 7,β1=0.839 6,β2=5.684 6,β11=0.037 1,p值都小于0.05,说明从业经理的年平均收入、风险偏好度和年平均收入的二次项与人寿保险的关系都是显著的。由R2=0.999 6可知,模型拟合有所提高。F=110 70,F值增加了不少,且p=0<0.05,说明显著性也有很大提高。
模型四:在模型三的基础上加上自变量X1,X2的平方项,再建立一个多元非线性回归模型。
Y=β0+β1X1+β2X2+β11X12+β21X22+ε,ε~N(0,δ)
(4)
把式(4)中X12,X22分别看作一个变量,仍然是多元线性回归问题。Python运行结果为:β0=-60.910 4,β1=0.930 3,β2=4.452 9,β11=0.035 9,β21=0.115 9,β21对应的p值等于0.347,大于0.05,且β21的置信区间为[-0.141, 0.373],包含零点,说明从业经理的风险偏好度的二次项本身对他们投资的人寿保险额没有显著影响。其它参数的p值都小于0.05,且它们的置信区间不包含零点。R2=0.999 6,决定系数R2的值与模型三的几乎相等,F=827 4,F值有所下降,虽然p=0<0.05,但显著性降低了。
模型五:在模型四的基础上加上自变量的交叉项,建立一个带有交叉项的多元非线性回归模型。
Y=β0+β1X1+β2X2+β11X12+β21X22+β12X1X2+ε,ε~N(0,δ)
(5)
Python运行结果为:β0=-65.385 6,β1=1.017 2,β2=5.217 1,β11=0.035 8,β21=0.166 2,β12=-0.019 6,β21和β12对应的p值分别等于0.192和0.186,都大于0.05,且β21和β12的置信区间分别为[-0.096, 0.428]和[-0.050, 0.011],都包含零点,回归不显著,说明除从业经理的风险偏好度的二次项本身对他们投资的人寿保险额没有显著影响外,还说明年平均收入和风险偏好度对人寿保险额无交互效应。其它参数的p值都小于0.05,且它们的置信区间不包含零点。R2=0.999 7,决定系数R2的值几乎不变,但F=7 110,F值又有所下降,说明显著性又降低了。
三、结论
经过分析对比上述模型可知,模型三最理想,表明只有从业经理的年平均收入及其二次项和风险偏好度本身对他们投保的人寿保险额有显著影响。研究人员可以根据从业经理未来的年平均收入及其风险偏好度,对从业经理未来投保的人寿保险额进行预测。同时,只要从业经理的年平均收入及其风险偏好度变化不大,他们投保的人寿保险额就比较稳定,这有助于行业健康、平稳地发展。
四、模型改进
本文按照我国某城市18位35~44岁从业经理的年平均收入、风险偏好度和人寿保险额的数据信息所建的模型只能较好地反映从业经理当年的规律,还有更多的提升空间。为了进一步提高模型的准确性和使用性,可以增加统计人数和影响因素,建立一个人数和影响因素较多的多元回归模型。

