一种描述磁流变弹性体滞回特性的分数阶导数改进Bouc-Wen模型
王 鹏,杨绍普,刘永强,赵义伟,王翠艳
1) 石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043 2) 石家庄铁道大学交通运输学院,石家庄 050043 3) 石家庄铁道大学机械工程学院,石家庄 050043
磁流变弹性体(Magnetorheological elastomers,MRE)是一种新型的磁敏智能材料,由弹性体基体、磁性粒子和添加剂组成,具有良好的磁流变效应. 与磁流变液相比,MRE具有稳定性好、响应快、无沉降、无泄漏等特点,在调谐阻尼器、节点衬套、变刚度悬架等领域具有良好的应用前景[1-2].长期以来,许多学者都致力于MRE的研究,对其制备、性能测试和性能改善进行了系统的研究[3-4].
目前,磁流变弹性力学特性的研究主要从微观和宏观两个方面进行. 微观本构模型是基于磁偶极子理论提出的,主要是为了解释磁流变效应产生的机理,以及磁致模量与各因素之间的关系.微观本构模型有磁偶极子模型[5]、链状模型[6]、柱模型[7]、网格模型[8]等. 基于磁偶极子理论的微观模型解释了磁流变效应产生的原因,但不能全面描述MRE在磁场中的力学行为. 此外,基于磁偶极子理论的物理模型结构往往过于复杂,不便于工程应用.
为使磁流变弹性体应用于工程实际,还需要可以描述其宏观力学行为的模型. 宏观力学模型应综合考虑外加磁场、激励幅值以及加载频率等对MRE力学性能的影响[9]. 黏弹性参数模型广泛用于MRE力学特性的预测. Li等[10]提出了四参数线性黏弹性模型预测MRE的力学特性. 该模型可以反映激励频率对磁流变弹性体力学性能的影响,但对于MRE非线性滞回特性的描述不够准确. 一些学者认为大应变下MRE滞回曲线的平行四边形特征是由弹性基体与磁性颗粒之间发生摩擦引起的,故采用库伦摩擦模型描述此种现象[11].Chen在黏弹性参数模型基础上提出了带库伦摩擦的线性黏弹性模型[12]. Blom将弹性模型和边界面模型结合,提出了一种新的磁敏(Magneto-sensitive,MS)橡胶非线性本构模型[13]. 由于库伦摩擦元件的存在使得上述模型的滞回曲线具备了平行四边形的特征,但不能准确地反映加载过程中切线模量渐变特性.
与整数阶黏弹性模型相比,分数阶模型的优势在于能以更少的参数和更高的精度来描述MRE的频率依赖性和磁致黏弹性[14-15]. 此外,黏弹性材料的力学特性与加载过程密切相关,而分数导数具有时间记忆功能,更适合描述有历史依赖过程的物理现象[16]. Xu依据基体黏弹性和磁致黏弹性,采用分数阶导数形式,提出了磁致黏弹性参数模型[17]. Wang建立了分数阶的非线性本构模型. 研究表明,分数阶导数单元可以实现更少的参数和更高的精度来描述频率相关性[18]. 孔凡采用谐波平衡法研究了简谐激励下滞回分数阶系统的稳态响应. 结果表明,分数阶数和稳态位移幅值的关系依赖于系统,分数阶导数模型能以较少的参数模拟力-位移关系的频率依赖性[19]. Wang等[20]鉴于MRE的剪切模量对磁场强度、加载幅值和频率的敏感性,建立了含分数阶微分单元的黏弹性模型. 结果表明上述分数阶黏弹性模型能够准确表征磁流变弹性体的频率依赖性和磁致黏弹性.
Bouc-Wen模型已广泛用于描述场相关的非线性滞回系统和其他复杂动态特性. Dominguez等[21]把磁流变阻尼器的励磁电流作为变量引入到Bouc-Wen模型,使得模型能够考虑不同电流强度对磁流变阻尼器力学特性的影响. Yang[22]首次采用Bouc-Wen模型用于模拟MRE隔振器的力学特性. 研究表明,Bouc-Wen模型能有效模拟MRE非线性黏弹区的滞回特性,但不能准确反映滞回曲线对频率的依赖性. 许多学者不断对Bouc-Wen模型进行修正,赵义伟等[23]针对Bouc-Wen模型在非识别激励工况下模拟的阻尼力与实际阻尼力误差较大问题,提出了一种描述减振器滞回特性的改进模型. Xu等[24]在Bouc-Wen模型基础上,同时考虑磁流变液温升效应和惯性效应,提出了带质量元素的温度唯象模型. Wang等[25]考虑了MRE的非线性、频率依赖性,提出了基于Bouc-Wen的MRE非线性本构模型. 上述Bouc-Wen模型能够模拟MRE的应力应变的非线性特性,但由于Bouc-Wen滞回算子在正弦荷载作用下的滞回曲线与加载频率无关,Bouc-Wen模型仅由弹簧和阻尼元件构成的Kelvin模型不能准确地表征MRE的磁致黏弹性和频率依赖性. 因此需要对Bouc-Wen模型进一步改进.
综上可知,上述模型在描述磁流变弹性体的力学行为时既具有一定的独特性,又表现出某些局限性. Bouc-Wen模型通用性好,能够很好地模拟大应变荷载下的非线性滞回特征,但不能准确预测MRE的磁致黏弹性和频率依赖性. 而分数阶导数模型却能以更少的参数和更高的精度来描述这一特性. 此外,分数阶导数具有记忆性功能,更适合描述MRE的黏弹性在加载过程中表现出的历史依赖性. 为了准确表征大范围应变幅值、激励频率和磁场下MRE的力学行为. 本文在Bouc-Wen模型的基础上,将黏弹性分数阶导引入到MRE的应力应变关系中,提出一种描述磁流变弹性体滞回特性的分数阶导数改进Bouc-Wen模型. 通过对剪切模式下测得的应力应变实验数据进行拟合,实现了模型参数的识别,验证了模型的有效性.
1 MRE力学特性实验分析
1.1 制备及性能试验
选用天然橡胶(Natural rubber, NR)、羰基铁粉(Carbonyl iron particles, CIP)和添加剂作为原材料,通过塑练、混炼、硫化等工艺制备了不同CIP质量分数(60%、80%)的各向同性和各向异性MRE,分别标记为CIP80%各向同性、CIP80%各向异性、CIP60%各向同性、CIP60%各向异性. CIP由江苏天一超细金属粉末有限公司购买,平均粒径5.5 μm,使用的添加剂主要有硬脂酸(Stearic Acid, SA)、氧化锌 (ZnO)、促进剂 (CZ)、防老剂 (RD)、防老剂(4010NA)、古马隆树脂 (Coumarone resin)、硫磺(S),天然橡胶和添加剂均由衡水中铁建工程橡胶有限责任公司提供. MRE的成分配比如表1所示.所用的设备有:CF-2L型密炼机(东莞市昶丰机械科技有限公司生产)、RL-6型开炼机(佰弘机械有限公司生产)、M-2000-AN型硫化仪(高铁检测仪器有限公司生产)、XLB-25型平板硫化机(邢台维斯特机械有限公司生产)等,MRE制备流程如图1所示.
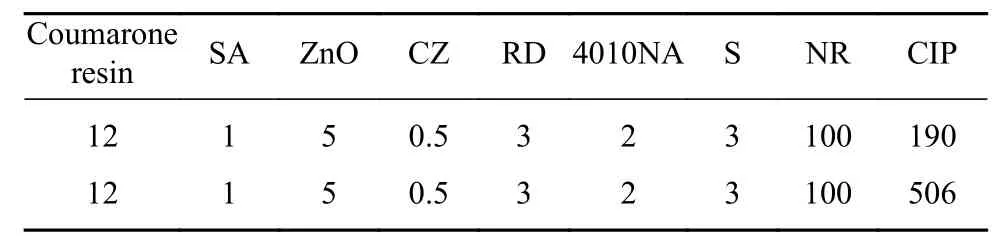
表1 MRE的成分配比Table 1 Composition of MRE g
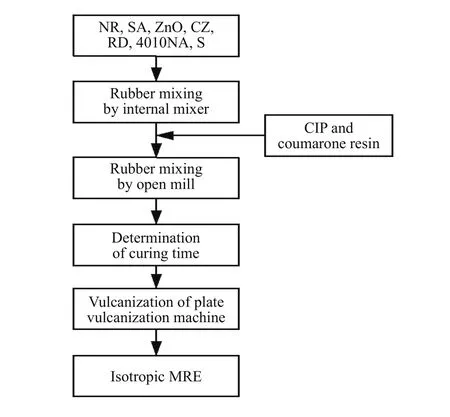
图1 MRE制备实验流程Fig.1 Experimental process of MRE preparation
通过扫描电子显微镜(Scanning electron microscope, SEM)观察MRE的截面形貌,观察前对样品进行表面喷金处理. 图2为MRE的截面形貌图,图中所示呈分散相的白色球形颗粒为CIP,连续相的黑色部分为天然橡胶基体.
由图2可知,MRE 4种样品的CIP颗粒表面被天然橡胶包裹且浸润性良好,颗粒与橡胶基体之间存在一些桥接结构,说明颗粒与基体的界面结合能力比较强. 各向同性MRE的CIP随机均匀分布在橡胶基体中,而各向异性MRE的基体中有许多直线状沟壑,CIP沿着硫化时施加的取向磁场的方向形成链状结构,与各向同性MRE的截面形貌明显不同.

图2 MRE 的截面形貌. (a)CIP60% 各向同性;(b)CIP80% 各向同性;(c)CIP60% 各向异性;(d)CIP80% 各向异性Fig.2 Cross section of MRE: (a) CIP60% isotropic; (b) CIP80% isotropic; (c) CIP60% anisotropic; (d) CIP80% anisotropy
采用奥地利安东帕公司生产的旋转流变仪(Physica MCR 301)对MRE进行动态性能试验. 图3为旋转流变仪、试件及测试示意图,其中试件为直径20 mm,厚度1 mm的MRE圆片. 测试时,首先将试件放置于下平台的中心,随后上部转子向下运动直至与试件上表面接触,并施加法向力(3 N)使试件与上下极板紧密贴合,防止试件发生滑动.旋转流变仪通过改变线圈电流实现在平行板系统上施加不同的磁场,上部转子按照设定程序施加平行于试件的旋转剪切应变激励,并由内部精密传感器测定试件反馈的应力,经过仪器控制软件计算得到所需结果. 在振荡剪切测试模式下,每个正弦应变加载周期内软件可记录257个应力应变数据点,根据这些数据点可绘制每个正弦应变加载周期内的应力应变曲线.
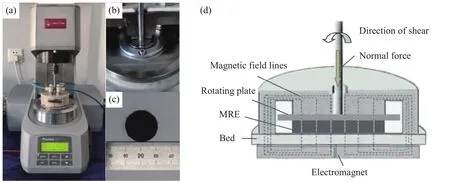
图3 (a,b)旋转流变仪;(c)MRE 试件;(d)测试示意图Fig.3 (a, b) Rotary rheometer; (c) MRE specimen; (d) schematic of the measuring system
选用振荡剪切模式,在不同应变幅值、频率和磁场下对MRE的动态黏弹性进行扫描测试. 另外,对MRE加载正弦应变激励,测试其在不同应变幅值、频率和磁场下的应力响应.
1.2 MRE力学特性分析
佩恩效应是MRE重要力学特性之一,表现为储能模量随着应变幅值的增加而急剧下降[3]. 图4为磁感应强度234 mT,频率1 Hz时,MRE的储能模量和损耗模量随应变幅值的变化曲线.
由图4可知,MRE的储能模量变化趋势相同,在一个较小的应变范围内保持不变,该应变范围称为MRE的线性黏弹区[4];当应变幅值继续增大,储能模量快速减小,呈现明显的佩恩效应. 随着应变幅值的增大,CIP80%的MRE损耗模量先保持不变后不断减小,而CIP60%的MRE损耗模量先小幅增加随后减小. 另外,CIP80%的MRE的储能模量开始出现下降时对应的应变幅值明显小于CIP60%的MRE,说明CIP80%的MRE的线性黏弹区较小,原因是羰基铁粉含量增加会降低橡胶基体的交联密度,使基体分子链稳定性变弱,相同应变下使储能模量更小.
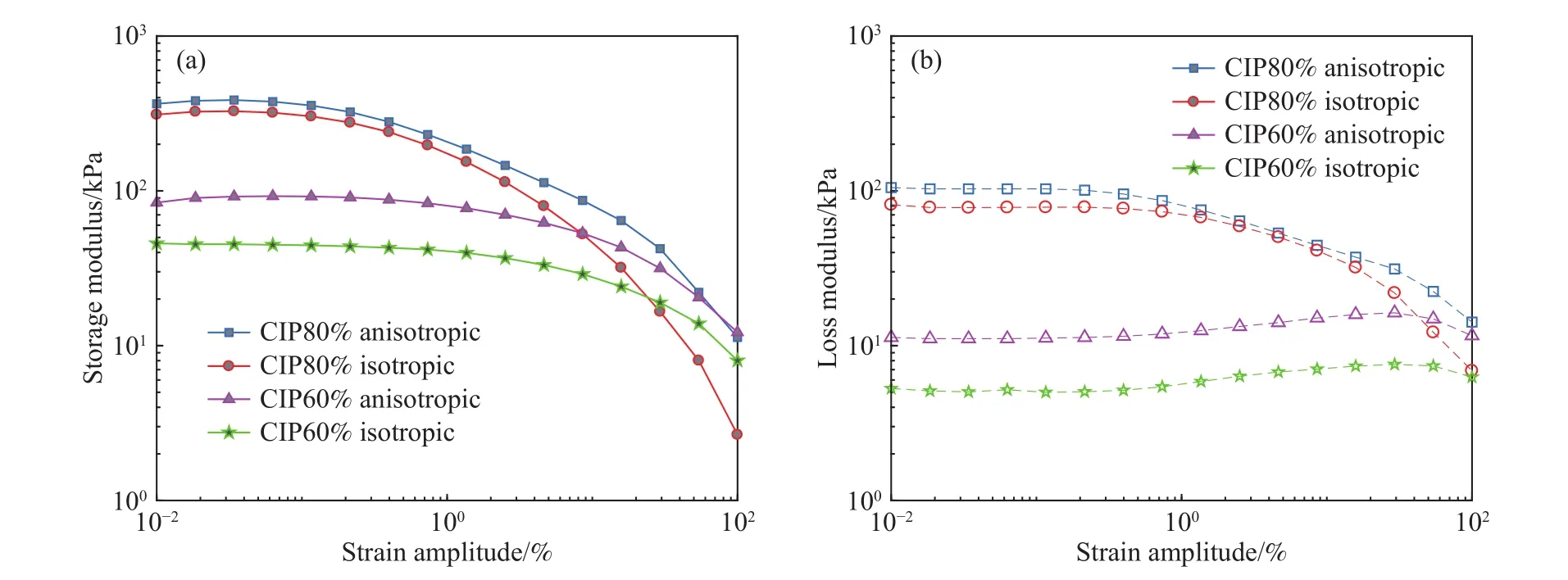
图4 MRE的储能和损耗模量随应变幅值的变化曲线. (a)储能模量;(b)损耗模量Fig.4 Storage modulus (a) and loss modulus (b) curves of MRE with strain amplitude
分析应变频率对MRE动态黏弹性的影响.图5显示了应变幅值0.05%时,不同磁感应强度B下,MRE的储存模量和损耗模量随应变频率的变化曲线.
由图5可知,MRE的储能模量和损耗模量随着应变频率增加而增大,因为当频率增加时,橡胶基体中分子链的应变跟不上应力的变化速度,这会造成分子链的纠缠,从而使CIP与基体间相互作用增强,使MRE的储能模量与损耗模量变大,可见储能模量和损耗模量都具有频变特性. 同时,随着磁感应强度增大,储能模量和损耗模量增加,反映了MRE的磁流变效应. 当频率和磁场相同时,CIP80%各向异性的储能模量和损耗模量最大,CIP60%各向同性的储能模量和损耗模量最小.
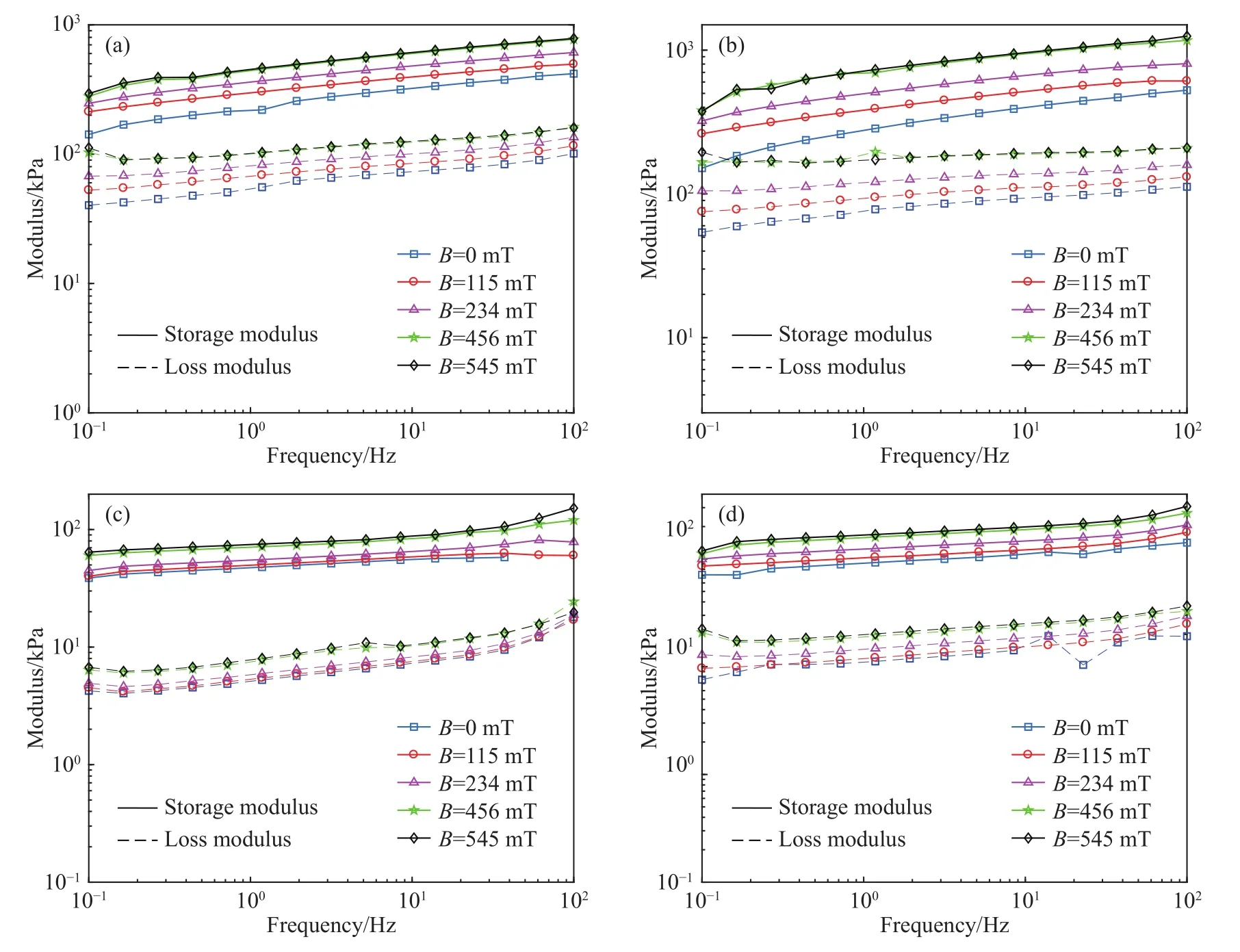
图5 MRE的储能和损耗模量随应变频率的变化曲线. (a)CIP80%各向同性;(b)CIP80%各向异性;(c)CIP60%各向同性;(d)CIP60%各向异性Fig.5 Storage and loss modulus curves of MRE with strain frequency: (a) CIP80% isotropic; (b) CIP80% anisotropic; (c) CIP60% isotropic; (d) CIP60%anisotropic
分析磁场对MRE动态黏弹性的影响. 图6为应变幅值0.05%,频率1 Hz时,MRE的储能模量和损耗模量随磁感应强度的变化曲线.
由图6可知,MRE的储能模量、损耗模量随着磁感应强度的增加而增大,磁流变效应明显. 磁感应强度为0 mT (零场)时,4种样品的储能模量由高到低分别为:193、174、85和 50 kPa,损耗模量由高到低分别为:57、44、10和 6 kPa,说明 CIP质量分数的增加使MRE零场模量增加,各向异性MRE零场模量高于各向同性,即CIP链状结构排列比其均匀分布具有更高的零场模量. 磁感应强度545 mT时,储能模量由高到低分别为:529、364、144和72 kPa,损耗模量由高到低分别为:182、113、20和10 kPa,其中CIP80%各向异性的最大储能模量是零场储能模量的2.7倍,最大损耗模量是零场损耗模量的3.2倍.
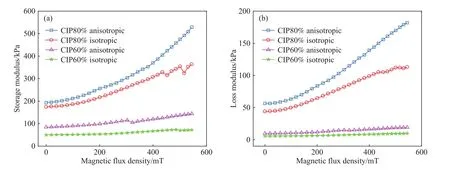
图6 MRE储能和损耗模量随磁感应强度的变化曲线. (a)储能模量;(b)损耗模量Fig.6 Storage modulus (a) and loss modulus (b) of MRE with magnetic flux density
需要指出的是MRE的磁流变效应随着应变幅值增加呈减小趋势. 因此,当应变幅值增加时制备的MRE的最大磁流变效应会有所降低. 为使橡胶基MRE在大应变工程应用中具有良好的磁流变效应,开展进一步提升橡胶基MRE磁流变效应的研究仍是必要的.
2 MRE本构模型
2.1 改进Bouc-Wen模型
Bouc-Wen滞回单元最早由Bouc和Wen提出,该模型采用非线性微分方程来描述磁滞特性,由两条光滑的曲线组成,精度较高,具有很强的灵活性,是一种经典的描述滞回曲线的模型. Yang等[22]首次将Bouc-Wen模型用于拟合MRE隔振器的力-位移关系,该模型由Bouc-Wen滞回单元、弹簧单元和黏滞阻尼单元并联组成. 控制方程为:
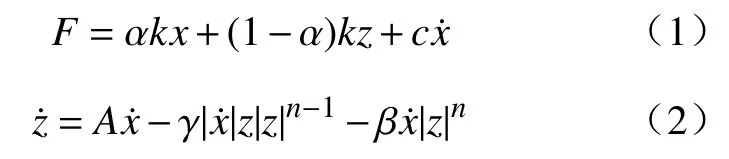
式中,F为模型输出力,分别为位移和速度,k、c分别为刚度和阻尼系数,参数z为中间变量,是z关于时间的一阶导数,α介于0到1之间,表征模型的线性程度,A、n、β、γ是量纲一参数,共同决定了滞回曲线的形状和大小.
分数阶导数能很好地模拟系统响应的黏弹特性,在黏弹性材料的建模中备受关注. 黏弹性材料的力学特性与时间相关,介于理想弹性体和理想黏性体之间,具有记忆性功能. 采用分数阶导数能够用较少的参数来准确地描述黏弹性材料的力学特性,并且适用于较宽的频率范围. 因此,将MRE复杂的形变恢复力用等效的黏弹性阻尼元件表示,把分数阶导数引入到MRE的应力应变关系中,提出引入分数阶导数黏滞特性的改进Bouc-Wen模型(如图7). 模型的控制方程为:
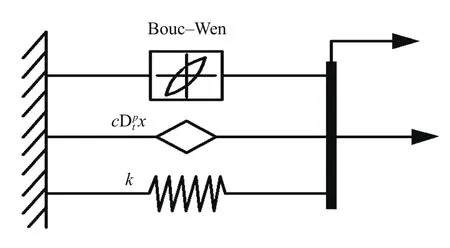
图7 改进Bouc-Wen模型Fig.7 Modified Bouc-Wen model
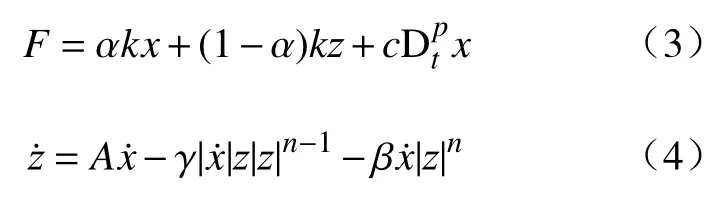
式中,p为分数阶导数阶次,其值介于0~1.为应变x关于时间t的p阶导数,其他参数含义同Bouc-Wen模型.
2.2 分数阶导数项计算
分数阶导数的定义有多种形式,本文采用Caputo型定义来描述:
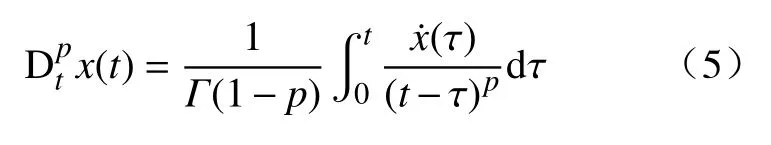
式中, Γ (z)为Gamma函数,满足:
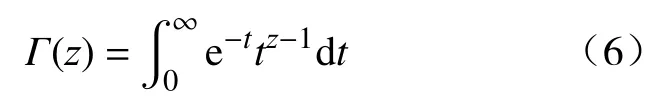
设MRE性能试验时施加的剪切应变为:

其中,xm为应变幅值,ω为角频率,φ为相位角.
根据文献[26]对分数阶导数项化简,可得:
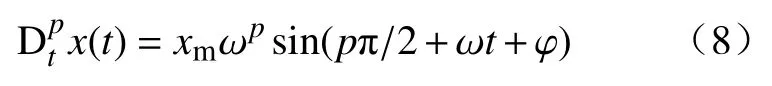
分数阶导数的求解常用的算法有:近似解析法、数值解法、滤波器算法,本文采用Oustaloup滤波器算法进行近似计算[27-28],基本思想是在选定的频率段(ωb,ωh)内做分数阶算子sp的近似替换,ωb,ωh分别为滤波器拟合频率段的上下限. 根据该思想构造Oustaloup滤波器:

式中,N为滤波器的阶次. 滤波器的零点和极点ωi分别为:

设x(t) 是滤波器的输入信号,则输出信号近似等于例如当分数阶算子为s0.5,选定的频率段范围为 0.001~1000 rad·s-1,当 Oustaloup 滤波器阶次分别取5、7和9时,得到的频响曲线如图8所示. 由图8可知滤波器阶次N=9时,该算法在选定的频率段内所得结果与真实值非常接近.

图8 频率响应曲线. (a)幅频;(b)相频Fig.8 Frequency response curves: (a) amplitude-frequency; (b) phasefrequency
3 MRE模型验证
3.1 参数识别算法
在诸多的优化算法中,粒子群算法(Particle swarm optimization, PSO)具有较好的寻优能力,尤其针对复杂的工程问题,能够迅速找到近似解. 假设在D维的搜索空间中,有M个粒子构成一个群体X,当前的迭代次数为λ,粒子i当前位置Xi,飞行速度Vi,粒子当前最优位置qi,粒子群的当前最优位置g. 每个粒子的位置就是一个潜在的解,代入目标函数L计算适应值,根据适应值的大小衡量解的优劣. 第i个粒子最优位置更新:
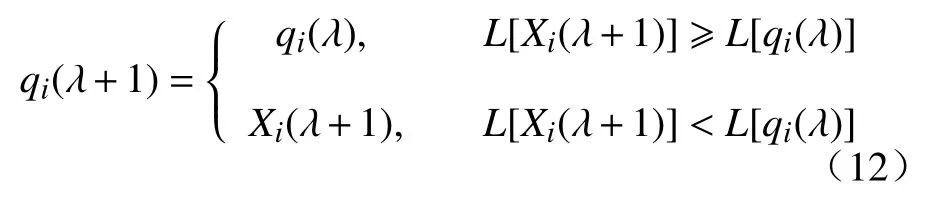
粒子群当前最优位置由下式确定:
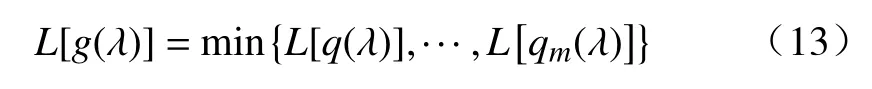
粒子在搜索空间中的速度更新公式:

粒子在搜索空间中的位置更新公式:
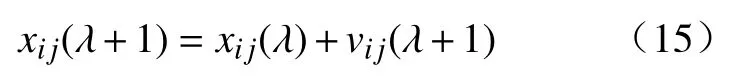
其中,i= [1,2,···,M],j= [1,2,···,D];η为惯性权重;d1和d2是加速常数;r1和r2是 (0, 1) 内的随机数.设定粒子的速度区间(vmin,vmax),位置范围(xmin,xmax),如果超出范围则取边界值.
粒子群优化算法具有很好的优化能力,但局部搜索性能较差,导致求解结果存在较大的偏差.而遗传算法(Genetic algorithm, GA)具有出色的局部搜索能力,但优化过程耗时且对种群初始化敏感. 本文将GA和PSO算法相结合[29],各取所长,用于MRE力学模型的参数识别. 将Spencer提出的误差计算公式作为参数识别的目标函数L[30],公式如下:
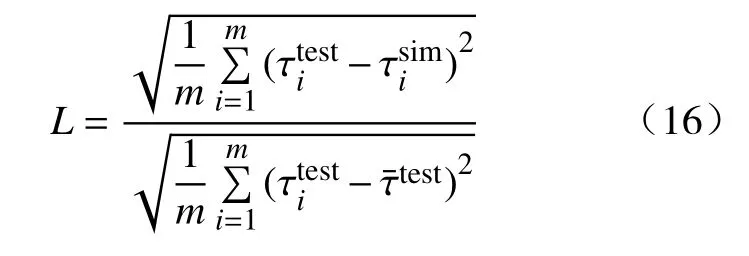
根据改进Bouc-Wen模型的控制方程在Simulink软件中搭建仿真模型,如图9所示,图中模块表示积分,实现到z的积分运算.x0表示位移x的初值. MRE力学模型的参数识别过程即目标函数最小值的优化过程,流程图如图10所示.
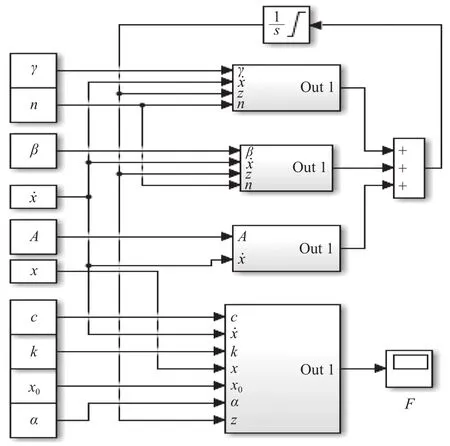
图9 Simulink建立的改进Bouc-Wen模型Fig.9 Modified Bouc-Wen model in Simulink
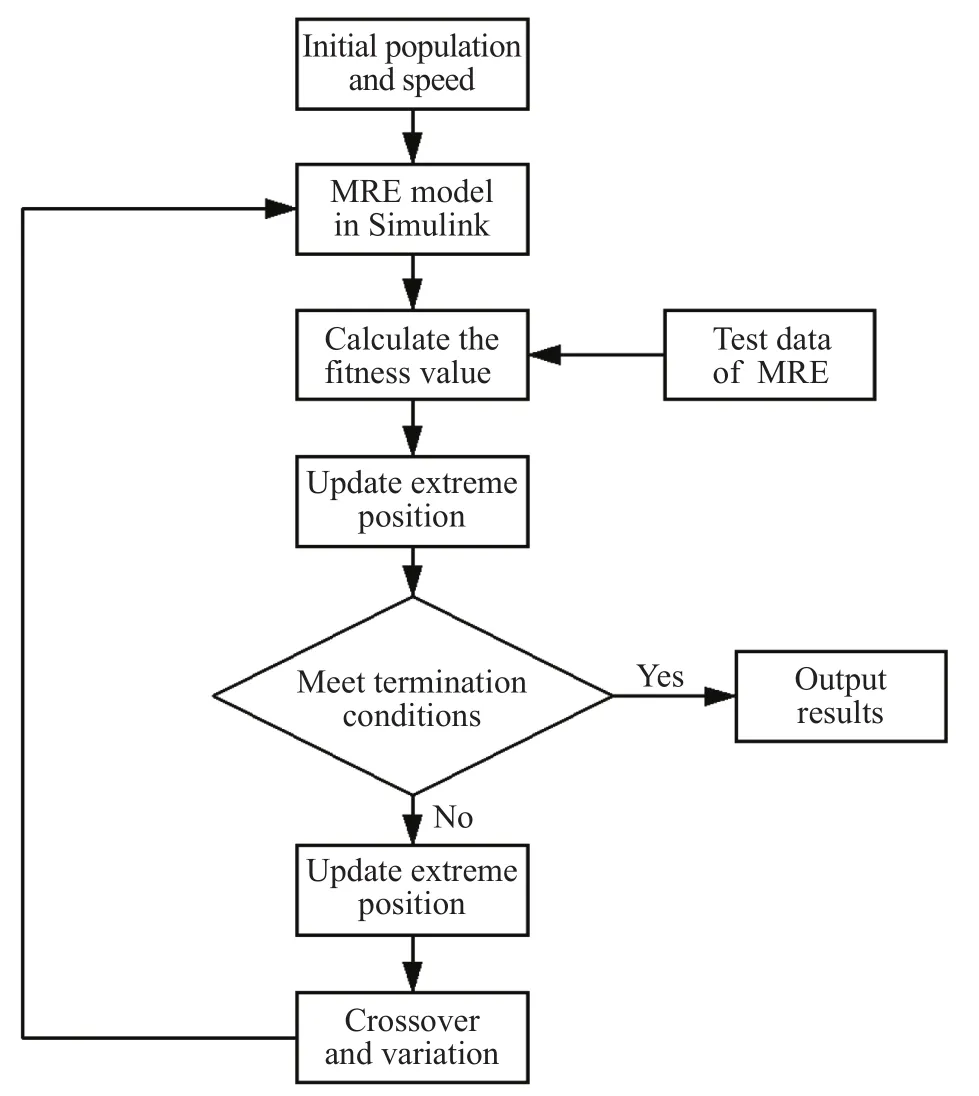
图10 基于GA-PSO算法的参数识别流程图Fig.10 Parameter identification based on GA-PSO algorithm
3.2 不同工况下模型验证
本节参数识别时选用的试验数据均为CIP80%各向同性的MRE在正弦剪切应变加载下得到的应力应变试验数据. 利用GA-PSO算法对MRE本构模型的参数进行辨识,验证模型的有效性,设置惯性权重η=1,加速常数d1=d2=3.5,粒子数M=36,迭代次数400,染色体编码长度8,交叉概率0.7,变异概率0.3.
(1) 不同应变幅值工况下的模型验证.
当磁感应强度为0 mT,应变频率为1 Hz时,选用不同应变幅值工况的试验数据(1.36%、2.51%、4.64%、8.57%、15.8%、29.3%),对 Bouc-Wen模型和改进Bouc-Wen模型的参数进行识别,得到的仿真数据和试验数据对比如图11所示.
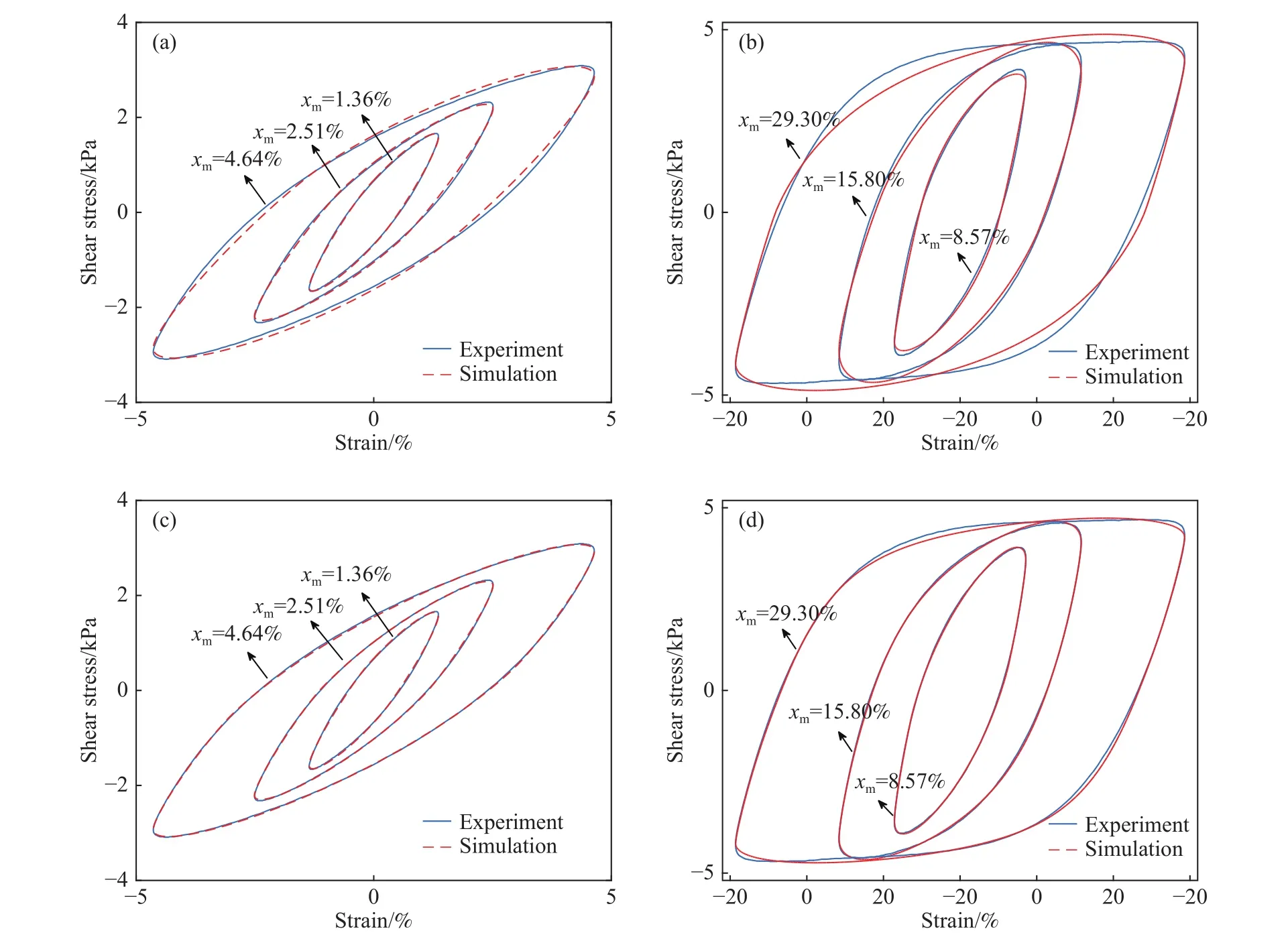
图11 不同幅值下的仿真与试验数据对比. (a, b)Bouc-Wen 模型;(c, d) 改进 Bouc-Wen 模型Fig.11 Comparison of simulation and experimental data under different amplitudes: (a, b) Bouc-Wen model; (c, d) modified Bouc-Wen model
由图11可知,Bouc-Wen模型在小应变幅值时拟合效果较好,在大应变幅值下能近似模拟试验数据滞回曲线的平行四边形特征. 但随着应变幅值增大,Bouc-Wen模型仿真数据与试验数据误差逐渐增大,当应变幅值为29.3%时,仿真和试验滞回曲线存在明显差异. 而改进Bouc-Wen模型在不同应变幅值下的拟合效果较Bouc-Wen模型明显提升,当应变幅值小于15.8%时,仿真数据和试验数据得到的滞回曲线几乎完全重合,即便当幅值为29.3%时,数据吻合度也较高,说明改进模型能够准确地描述MRE的滞回特性.
(2) 不同频率工况下的模型验证.
当磁感应强度为405 mT,应变幅值为0.40%时,选用不同应变频率工况的试验数据(0.5、1、3和 5 Hz),对 Bouc-Wen模型和改进Bouc-Wen模型的参数进行识别,得到的仿真数据和试验数据对比如图12所示.
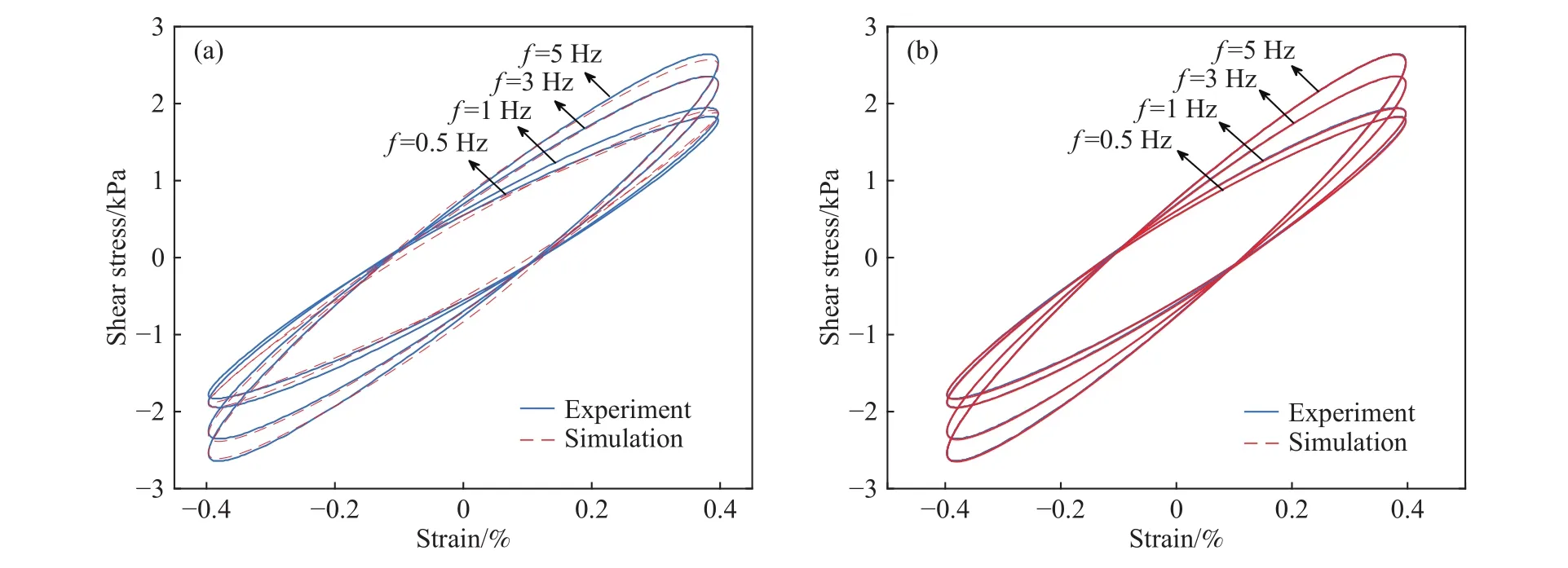
图12 不同频率下的仿真与试验数据对比. (a)Bouc-Wen模型;(b)改进Bouc-Wen模型Fig.12 Comparison of simulation and test data under different frequencies: (a) Bouc-Wen model; (b) modified Bouc-Wen model
由图12可知,Bouc-Wen模型在应变频率0.5和1 Hz时拟合误差较大,不能有效辨识滞回曲线随频率的变化规律. 对比可见,改进Bouc-Wen模型在不同应变频率下的仿真数据与试验数据的拟合效果均好于Bouc-Wen模型,在应变频率0.5和1 Hz时拟合精度明显提高. 说明改进模型可以准确的反映应变频率对MRE力学性能的影响.
(3) 不同磁场工况下的模型验证.
当应变幅值为2.51%,应变频率为1 Hz时,选用不同磁场工况的试验数据(115、234、405、456和545 mT,对应的线圈电流依次为1、2、3、4和5 A),对Bouc-Wen模型和改进Bouc-Wen模型的参数进行识别,得到的仿真数据和试验数据对比如图13所示.
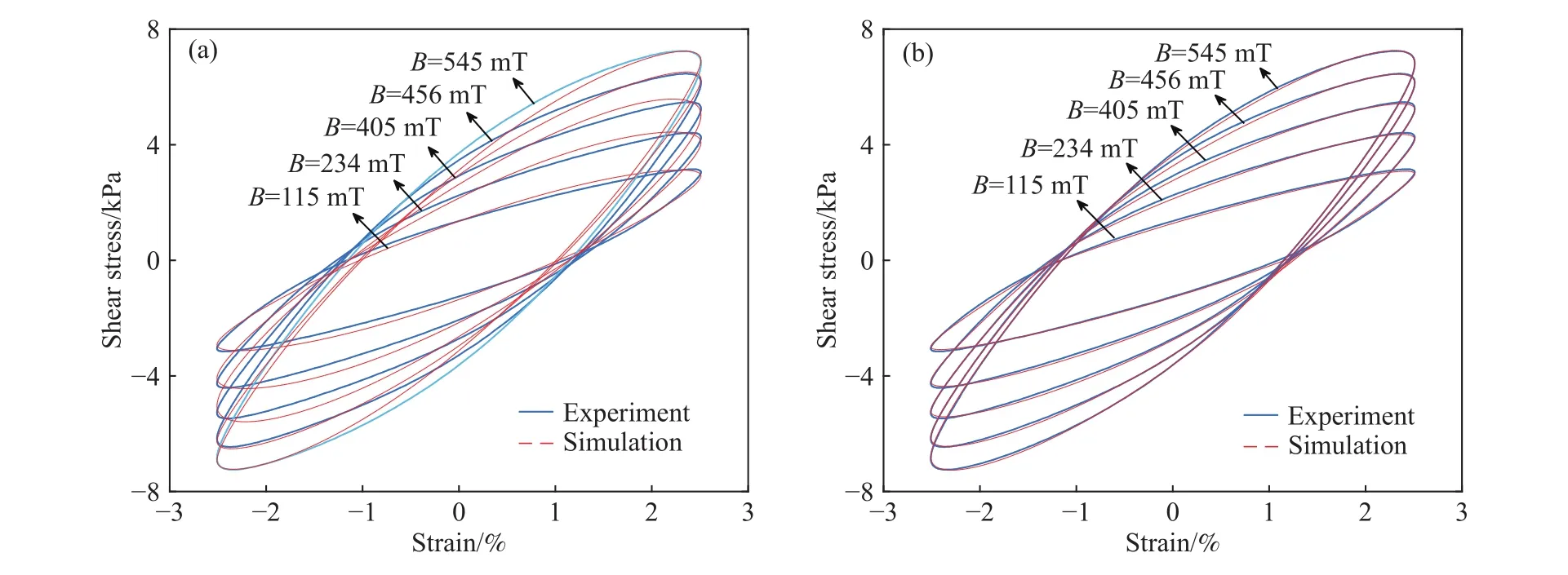
图13 不同磁场下的仿真与试验数据对比. (a)Bouc-Wen模型;(b)改进Bouc-Wen模型Fig.13 Comparison of simulation and test data under different magnetic flux densities: (a) Bouc-Wen model; (b) modified Bouc-Wen model
由图13可知,改进Bouc-Wen模型在不同磁场工况下的仿真数据与试验数据具有较高的吻合度,仿真和试验的滞回曲线几乎重合,拟合精度较Bouc-Wen模型明显提高. 说明改进模型可以准确反映磁场对MRE力学性能的影响.
本节各工况2种MRE模型的参数识别结果如表2、表3所示. 由表中数据可知,在磁感应强度456 mT,应变频率1 Hz,幅值为2.51%的试验工况下,Bouc-Wen模型的仿真数据与试验数据的吻合率为93.44%,为所有工况中最低;而此工况下改进Bouc-Wen模型的数据吻合率为99.41%,拟合精度提高了6%. 其他试验工况下,改进Bouc-Wen模型的仿真数据与试验数据的吻合率均高于Bouc-Wen模型,说明改进后的模型拟合精度提高,可以更加准确地表征MRE的力学特性.

表2 Bouc-Wen模型识别结果及吻合率Table 2 Identified values and fitness values of the Bouc-Wen model
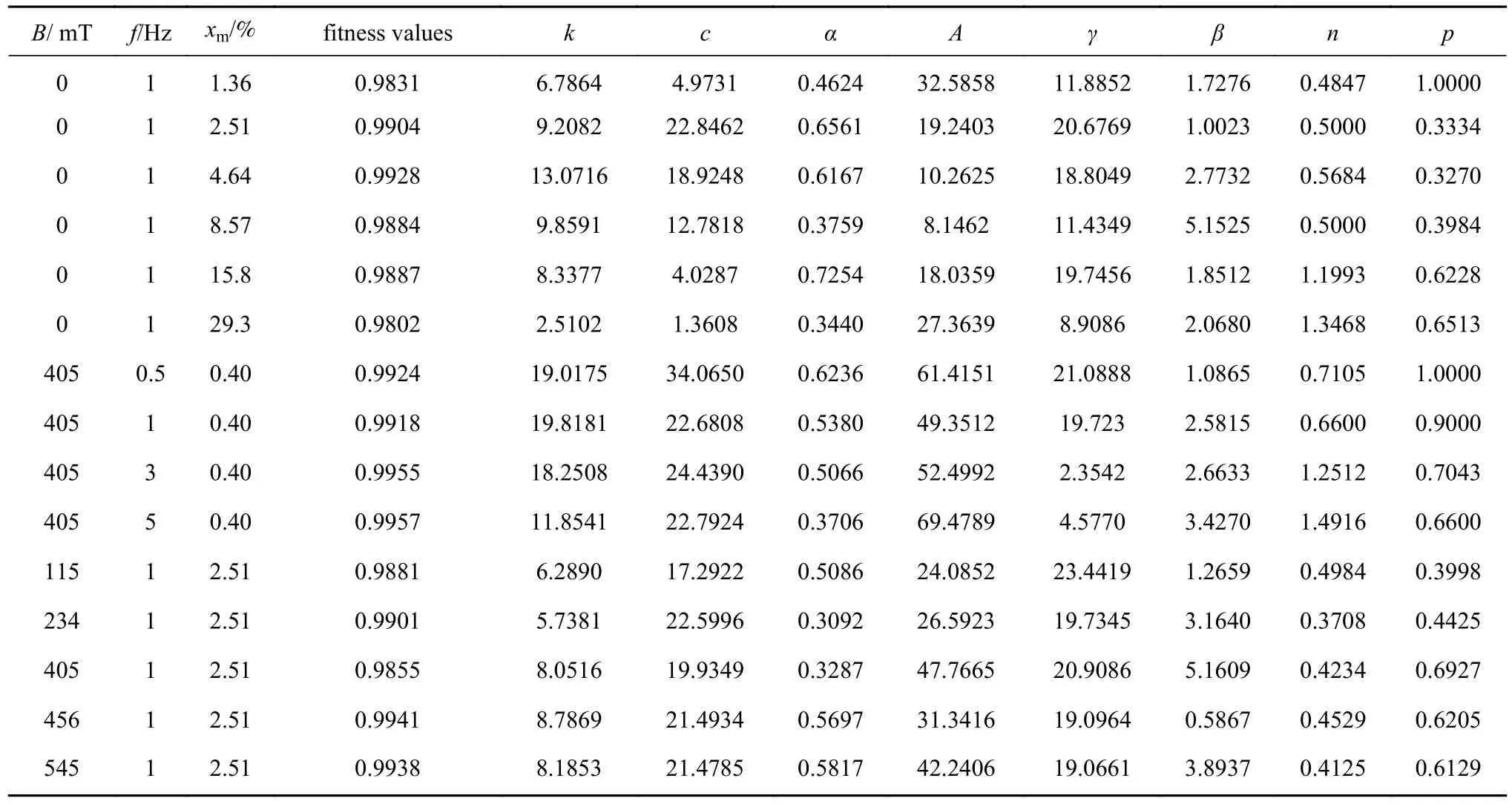
表3 改进Bouc-Wen模型识别结果及吻合率Table 3 Identified values and fitness values of the modified Bouc-Wen model
3.3 模型参数规律分析
由上面分析可知,表3中参数结果验证了改进Bouc-Wen模型在模拟MRE力学特性的有效性. 识别结果为全局最优解,具有拟合精度高,拟合效果好的优势. 根据表3可得模型参数随着应变幅值、磁感应强度的变化趋势,如图14所示. 从图中可以发现参数变化具有一定的随机性.
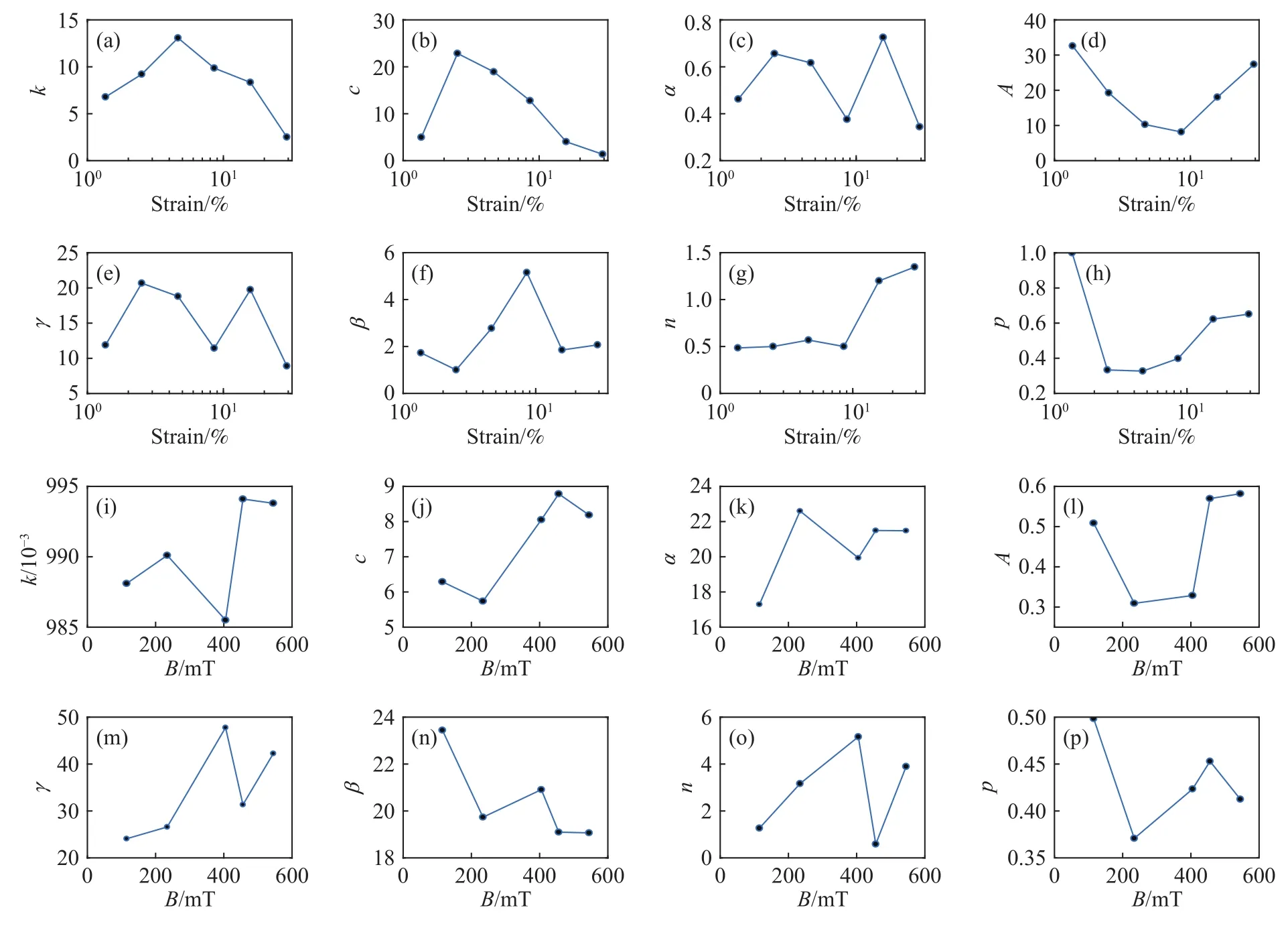
图14 各参数的变化趋势. (a~h)不同应变幅值下;(i~p)不同磁感应强度下Fig.14 Change trends of parameters under different strain amplitudes (a-h) and under different magnetic flux densities (i-p)
为了探究模型参数在不同加载条件下的变化规律,对改进Bouc-Wen模型进一步分析.
当应变频率和磁场相同时,将应变幅值1.36%工况得到的模型参数识别结果用于预测其他幅值2.51%、4.64%、8.57%、15.8%、29.3%的工况,发现模型仿真数据与试验数据存在较大拟合误差;同样将其他幅值工况得到的参数用于预测幅值1.36%工况时,仿真数据和试验数据吻合度较低,曲线存在较大拟合差异,说明改进Bouc-Wen模型的各参数与加载幅值存在耦合关系.
对图13中不同磁感应强度下的MRE滞回曲线进一步分析. 可以发现滞回曲线的形状基本保持不变,可近似看做滞回曲线形状不随磁场改变而改变. 而滞回曲线的形状由参数A、γ、β、n共同调控,所以可进一步假设参数A、γ、β、n受外加磁场影响较小,此处不再考虑其与磁场之间的耦合关系. 而磁场强度增加时,MRE的储能模量和损耗模量明显变大,说明表征弹性模量的参数k和表征黏性阻尼的参数c与磁场之间存在耦合关系.
由此可见改进模型参数能有效模拟MRE的力学特性,同时模型参数和应变幅值、磁场大小之间存在部分耦合关系. 为使磁流变弹性体应用于工程实际,利用MRE的磁流变效应实现变刚度和变阻尼的半主动控制,在后期的工作中构造函数关系来量化模型参数与影响因素之间的耦合关系,是一项很有意义的研究内容.
4 结论
(1)各向同性与异性MRE截面形貌明显不同.CIP与橡胶基体之间存在桥接结构,各向同性MRE中CIP呈现随机均匀分布,各向异性MRE中CIP沿磁场方向排列成链状结构.
(2)各向同性与异性MRE动态黏弹性变化规律一致,受到幅值、频率和磁场的影响. 储能和损耗模量随着应变幅值(0~100%)增大先不变后减小,随着频率(0~100 Hz)增大而增大,随着磁感应强度(0~545 mT)增加而增加.
(3)提出了分数阶导数的改进Bouc-Wen模型,该模型能够准确表征MRE的力学特性,拟合精度较Bouc-Wen模型明显提升,各工况的吻合率均高于98%,模型在较宽的应变幅值、频率、和磁场范围内是准确的.

