流态化的往昔寻觅及未来启示

王荘，吕潇，邵媛媛，祝京旭

（1天津大学化工学院，天津化学化工协同创新中心，天津 300072；2加拿大西安大略大学颗粒技术研究中心，加拿大安大略省伦敦 N6A 5B9）

引 言

流态化(fluidization)即是固体通过与气体或液体接触而转变为流体状态的操作。流态化是化工学科的一个分支，是一门现代科学，1950年Brown首次将“fluidization”作为一个独立的单元操作收录于化工教科书《Unit Operations》中[1]。其实，早在15、16世纪，中西方就有关于劳动人民使用流态化技术进行生活和生产的记载。16世纪宋应星[2]所著的我国古代百科全书《天工开物》中，就生动而形象地记载了扬簸、淘洗及选矿等过程（图1），是我国最早有关流态化技术应用的记录。第四卷记载了古人使用风车和扬簸法去除谷物中的杂物，将扬起的颗粒在流态化状态下风选，吹走较轻的“秕”，收集较重的谷物。第十四卷记载了用水淘洗铁砂，去除较轻的杂质，收集铁矿的流态化分选过程。16世纪Agricola的专著《De Re Metallica》则是西方最早记录流态化技术应用的书籍[3-4]。书中记载了当时的采矿、选矿和冶炼等过程。其中的一张木刻图（图2）描绘了工人利用筛子在盛满水的木桶中进行跳汰选矿：将矿粒置于不同粗细的筛中，在水中上下移动筛子，使固体颗粒流态化，让密度大的金属矿粒下沉，密度小的脉石上漂，再用刮板将脉石刮走[3]。这些未赋予“科学术语”的生活、生产技术可以说是流态化技术的雏形。

图2 《De Re Metallica》所记载的跳汰选矿过程[3-4]Fig.2 The process of jigging beneficiation recorded in“De Re Metallica”[3-4]

进入20世纪后，固体颗粒(particles)在石油、化工、能源、材料、环保等领域被广泛使用，赋予固体颗粒流动特性是增加工业生产效率的优选手段[5-7]。金涌[8]详细描述了颗粒间的相互作用，指出颗粒间的内摩擦力远大于流体的内摩擦力从而导致了颗粒和流体行为的差异，即消除颗粒间的内摩擦力会赋予颗粒流体特性。因此，流态化技术就是将固体颗粒悬浮于流体中使颗粒分离、消除颗粒间的内摩擦力，使之产生流化特性。固体颗粒被流体悬浮而具有一定的流体行为特性，这就是流态化现象。流态化技术的目的就是为了强化颗粒和流体之间的接触和传递过程，同时方便颗粒的批量输送。随着作用于颗粒的流体流速增加，流态化现象将历经低速浓相流态化(dense phase fluidization)、高速稀相流态化(dilute phase fluidization)，最后形成稀相输送(dilute phase transport)。除流速不同形成的不同流态化流型外，还有由于流体和颗粒密度差不同而形成的不同流态化现象，即以液固系统为代表的散式流态化(particulate fluidization)和以气固系统为代表的聚式流态化(aggregative fluidization)[9]。

流态化技术除了广泛地应用于化工与能源工程外，还用于干燥[10]、吸附[11]、喷涂[12]等物理操作。流态化的研究领域主要集中在颗粒流动特性[13-14]、流态化分类[15-16]、流化床结构[17-18]和传质[19-20]、传热[21-22]等。流态化技术的发展，从第一台流化床气化炉的出现至今刚好100年。流化床(fluidized bed)有许多优点，如超大的相间接触面积、高效的传热传质、温度均匀的床层、颗粒容纳量大且容易操控、较宽泛的运行条件等。这些优点使流化床在许多工业领域得到了广泛应用，在工业一线发挥着重要作用，为人类的经济社会发展贡献了重要力量。不断发展的流化床，具有高效节能的潜力，是代替高能耗、高污染的传统化工反应器的重要选择，是实现节能减排，达到“碳中和”目标的强力助推剂。长期以来，流态化工业应用的迫切需求促使了流态化理论的发展，伴随着流态化理论和技术的进步，涌现出许多著名学者及其研究成果，这些成果构成了流态化这座“高楼大厦”。迄今为止，流态化文献资料数量巨大，正如Davidson等在《Fluidization》专著中写道“一辈子也读不完”[23]。梳理前人的研究思路并揭示其规律和方法学，能够更好地、更加深入地探索流态化世界，了解流态化的历史和发展路径。

本文以中西方几位流态化先驱者的研究成果简单概括流态化的早期发展历史，通过对流态化发展过程中早期的开拓思路及一些突出贡献的梳理来循迹流态化的发展，以提炼出科学思想和揭示科研发展的规律，并联系现实展现给即将进入流态化领域的“未来百年读者”，同时也为流态化资深学者提供新的思考与借鉴，期望能助力科学发展。

1 流态化的早期工业应用

第二次工业革命后，经历本质性变革的工业社会快速发展，科学理论和技术也不断进步。在这一时期，流态化技术开始被引入工业生产中，早期的工业应用主要有煤的气化和石油的催化裂化。煤的气化对流态化技术的工业应用起了最重要的引领作用，而石油的催化裂化则是大型流态化技术应用的基础。关于流态化早期的工业应用，Kunii等[24]、郭慕孙等[3,25]、金涌[8]已经有了详细的总结。

Winkler[26]用于粉煤气化的气-固流化床(gassolid fluidized bed)可以说是近代流态化技术工业应用的开端。如图3(a)所示，煤颗粒位于炉膛下部，气体由下方孔道吹入使煤流化，增强了气固接触。1925年，第一座采用Winkler气化工艺的商业化工厂建于德国的BASF公司。尽管Winkler气化炉效率较低，但是在第二次世界大战期间，德国成功利用Winkler气化炉气化活性高的劣质褐煤来制取供给战争和生产的燃料。此后德国和日本相继建立了许多相似的装置，生产合成化学工业的原料气。1927年，德国开发了气液固三相流化床(gas-liquidsolid three-phase fluidized bed)反应器，以褐煤为原料生产机动车燃料油[27]。Winkler炉不仅用于煤的气化，还用于生产低值煤气和制造合成氨、甲醇和氢气[28]。图3(b)为典型的Winkler煤气发生炉。1956年，我国采用苏联设计和改进的Winkler炉来生产合成氨[3]。

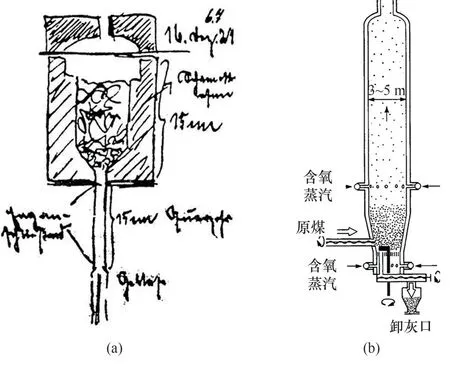
图3 Winkler煤气化炉手稿(a)及典型的Winkler煤气化炉(b)（改绘自文献[24]）Fig.3 The original manuscript of Winkler gasifier(a)，typical Winkler gasifier(b)(adapted from Ref.[24])

石油催化裂化中流态化技术的应用主要由美国石油公司及相关研究机构开发。关于这部分的历史沿革，陈俊武等[29]、Squires等[30]和Jahnig等[31]均有详细的论述，在此仅做简要的概述。20世纪初，原油蒸馏回收汽油产率低下的问题困扰着商业界和学术界，随着二次世界大战的爆发，寻找更有效的高质量汽油增产途径成为热点。1936年，Houdry开发出固定床(fixed bed)催化裂化装置。在进一步革新之后，Socony Vacuum公司率先建立起移动床(moving bed)催化裂化工业装置，形成了TCC工艺(thermofor catalytic cracking)。流化床催化裂化首先从细粉催化开始，1934年Imperial Oil公司发现生产润滑油的废白土有催化裂化作用。1938年，Standard Oil of New Jersey公司采用有蛇管反应器的粉料催化剂工艺线路，其顾问麻省理工学院(MIT)的Lewis教授认为竖管更好。于是Lewis、Chambers以及Gilliland等采用竖管进行了研究，发现竖管可以顺利地实现催化剂颗粒循环，并依此建立起一个上流式催化裂化装置，这就是流态化催化裂化(fluid catalytic cracking,FCC)的 开 始[24]。如 图4所 示，1942年第一个流态化催化裂化装置ModelⅠ型投产。随后，大量改进的流态化催化裂化装置问世。20世纪60年代，我国建立了第一个流态化催化裂化工厂，在再生器的改进和设计方面做了大量工作[25,29]。

图4 ModelⅠ型催化裂化装置（改绘自文献[24]）Fig.4 Model Type I catalytic cracking unit(adapted from Ref.[24])

基于上述工业应用和基础理论的发展，流化床凭借其温度均一的优异性能，成功应用于高放热反应的工业生产中，如萘或邻二甲苯制苯二甲酸、丁烯氧化制顺酐、丙烯氨氧化制丙烯腈等[24]。与此同时，流态化技术在非催化反应中也得到了应用，如1947年Dorr-Oliver公司建立了第一个砷黄铁矿焙烧装置，随后1952年采用硫铁矿焙烧炉生产SO2，Dorr-Oliver公司还在1948年采用流态化技术进行粉料干燥[24]。我国于1955年开始试验流态化焙烧黄铁矿，1957年南京化学工业公司永利宁厂建设了我国第一座大规模使用黄铁矿生产SO2和H2SO4的流态化焙烧炉。另外，一些物理过程也开始采用流态化技术，如萃取、矿石的浸取与洗涤等。流态化技术早期的工业应用进程是步履维艰的，甚至很多时候基本没有理论的指导，研究者们仅凭着少数的经验一点点进行尝试探索，而放大过程存在诸多问题也成了研究者们推广使用流态化技术的困难之一。回顾过往，正是这些早期的工业应用推动了流态化理论和技术的进步。

2 流态化的初期理论研究

2.1 流态化思想的起源与反思

有关流态化研究的许多经典文献目前难以找寻，如今再想详细梳理出清晰的发展脉络已不大可能。然而，前人的重要研究成果和他们的思路方法依然指引着后辈学者。本文从几位早期代表性人物的工作入手，尽量尝试还原流态化早期的研究工作以期帮助梳理发展思路。流态化的早期理论研究，先是以Lewis、Elgin等为代表的学者们，称之为“美国派”，他们使用了以单颗粒流动为主线的“概括式”研究方式；然后是称之为“英国派”的以Toomey、Rowe、Davidson等为代表的学者们，他们以气固分相为特征开发出气固流化系统理论的“区域式”研究方式；同时还有以流化状态为切入点提出散式与聚式分类的Wilhelm和Kwauk（郭慕孙）和以床层压降(pressure drop)、床层膨胀(bed expansion)等为着眼点提出流态化基本方程的Ergun、Richardson-Zaki等。他们的重要研究成果共同推动了流态化这门科学快速向前发展。

总之，流态化是一种物理状态，其现象和机理是复杂与多重的，因此在操作和理论分析上具有多样性。作为一个后起的化工分支，流态化主要是一门经验科学，很多科学原理常常会用含糊的经验来进行分析和解释；许多模型和方程均有使用条件限制，且多为经验性的，弱于科学推理。然而，也正是流态化的复杂性与多样性才支撑起了这座具有广阔研究方向的“大厦”。流态化的基石是两相流动(two-phase flow)，而两相流动有其特有的多样性（亦称多重性），为了展示其本质差别，在图5中描述了单相和两相流经过圆管中两个相同几何形状孔道的现象。在单相流中，因为两个孔道前后压差相等，所以两个孔道内部的流况一定完全相同；在两相流中，因为“浓颗粒+低气速”与“稀颗粒+高气速”可能产生相同的压差，会导致两个孔道中流况的多样性。

图5 单相和两相流流况示意(多相流体系的流动多样性)Fig.5 Flow diagrams of single-phase and two-phase flow(multiplicity in multiphase flow systems)

通过观察流态化的多样性，Kwauk等[9]将固体流态化区分为两种典型表现形式，即散式流态化和聚式流态化。图6(a)描绘了典型的散式流态化现象：颗粒均匀膨胀分散在流体中，为均匀流态化(homogeneous fluidization)。传统的液固系统属于散式流态化，最接近于理想流态化。20世纪80年代，有学者发现用低气速流化较轻颗粒时也会出现散式流态化现象[32-34]。图6(b)描绘了典型的聚式流态化现象：部分气体聚集形成不连续的气泡(bubbles)通过颗粒床层，为鼓泡流态化(bubbling fluidization)。传统的气固系统属于聚式流态化，而聚式体系中不连续的气泡对化学反应会产生不良影响，导致气固接触及反应效率降低，亦影响传质和传热。学者们着重研究了气泡的形成与长大规律，建立了两相理论和气泡模型。20世纪70年代，Yerushalmi等[35]提出了如图6(c)所示的快速流态化(fast fluidization)：高气速时气体形成连续相，颗粒聚集形成一个个颗粒团簇(clusters)，为循环流态化(circulating fluidization)。循环流化床中气体是连续相，因而形成了无气泡气固接触，特别适用于高速反应，是工业中常使用的流态化技术之一。继续提高流体流速，流态化则进入如图6(d)所示的稀相输送状态：在高速输送状态下，颗粒聚团被打碎，单颗粒均匀分散在床层内并随流体一起流动，此时系统又重新回到了均匀流态化状态。沿用Kwauk等的思路，将后两种状态分别称为高气速下的“聚式”与“散式”流态化，如图6(c)、(d)所示。综合而言，从相间受力角度分析，由浮力主导的图6(a)和由曳力主导的图6(d)均促成均匀的散式流态化。而在浮力和曳力交互作用下的图6(b)、(c)则形成不均匀的聚式流态化。虽然这两种不均匀分布状态不利于相间接触，但也正是由于不均匀状态造成的多样性，才扩展了流态化的操作空间，催生了多种流态化反应器的发明与应用。

图6 典型流态化现象Fig.6 Typical fluidization phenomenon

“美国派”Lewis和Elgin的研究没有考虑流况的多样性，而是将液固和气固系统均笼统地当作均匀流态化来考虑[36-37]。他们忽略了微观流况的多样性，认为只要在宏观上表现出一致状态，微观流况就可以被认为是均一的。如Elgin等[37-38]在考虑空隙率时认为，只要滑移速度(slip velocity)相等则空隙率就相等。从今天的视角回顾，Lewis和Elgin的研究可以被归为液固散式流态化，主要依据单颗粒的受力分析来解释流态化理论及液固体系的流型转变，开创了流态化理论的先河。与此同时，在未能对散式和聚式做区分前，特别是未能具体研究聚式流化的局部多样性之前，他们亦将这种研究思路应用到气固体系中，开展了一些卓有成效的研究[39-42]，并有效地推动了一些工业过程的发展，例如催化裂化装置的设计与改进[3,24,31]。他们是采用了“拟散式”方法来处理气固体系，虽然对细节有所忽略，但还是对促进早期流态化理论的发展做出了很大的贡献[36-37]。

稍后兴起的“英国派”Toomey等[43]和Davidson等[44]则有机会深入考虑流况的多样性。他们从不同的微观角度对流况进行分相考虑，通过测量局部流动现象特别是气泡现象，考察了气固流化床局部和整体情况的差异性。通过观察气泡行为，Toomey等[43]发现气固流化床中的流动现象并不是像之前认为的均相流态化，而是会出现一个个清晰的气泡，形成独立的气泡相(bubble phase)，因此提出了两相理论模型。Rowe等[45-47]和Davidson等[44]则通过对气泡进行更深入的独立研究，明确了单气泡行为，从而对后辈学者进一步研究流化床中气泡相行为起到引领作用。由此确定的流动模型对流态化理论的发展做出了重要贡献，也为工业流化床反应器的设计和强化提供了重要的理论基础。

2.2 对流态化的早期理解

20世纪40年代，流化颗粒的使用发展迅速，特别是用于石油的催化裂化。Lewis等[36]提到当时的研究者们所研究探讨的一些其他的化学操作，如液态碳氢化合物的合成、邻苯二甲酸酐的生产、煤的气化、燃烧和碳氢化合物的部分氧化。为了更好地设计这种新型的反应单元，必须清楚了解使流化装置获得满意运行的必要因素。麻省理工学院在流态化的早期发展过程中起到了非常重要的作用[36,39]，许多基础问题的研究也从这里开始，可以说麻省理工学院是流态化研究的起始点之一。许多研究人员参与其中，如Lewis、Gilliland等。正如之前介绍的，Lewis等的研究是在解决石油催化裂化的问题基础上开展的。虽然他们的工作在1938年就开始了，但出于保密的原因，直到1949年这些成果才陆续正式发表[36,39-42,48-50]。

1940年前后，Lewis的学生们对流化颗粒的特性做了许多研究，但是由于时间久远，他们的硕士论文和部分文献的原文已经无从考证。然而，仍然可以从Lewis等[36]的总结中挖掘他们的部分研究要点。他们使用空气、氢气和二氧化碳作为流化气来流化黏土，与其他研究者得到了流态化早期研究的一些基本结论如下。

（1）流化床由固定床状态转变而来，当流速大于临界速度时，固体颗粒被悬浮而进入流化状态[51-52]。

（2）流化状态下的压降等于颗粒的质量：

流体流经固体床层时，当流速达到足以使流体的摩擦力承托起颗粒，而不再由分布板或者颗粒间接触来支持的临界值，这时候床层的压降就近似等于单位床层截面中颗粒的质量[36,38,51-54]。压降和空隙率、流速等有一定的关系，Ergun方程即为主要代表[52]。由此还可以确定由固定床向流化床转变的临界速度[55]。

（3）滑移速度，即平均表观气体速度减去平均固体速度：相对独立于气体速度或颗粒进料速率和气体密度，是空隙率的唯一函数[36]。滑移速度相等，则空隙率相等[37-38]。

（4）根据固体颗粒在液体和气体中流态化现象的不同，流态化可分为聚式（不均匀）和散式（均匀）两种类型[9]。Walker早期提出的关于颗粒密度和气体黏度对流化状态有影响的结论也被证实[9,36,53]。

（5）流化时床层的膨胀（空隙率）和流速之间存在一定的关系，根据流速可以确定床层的膨胀情况，随着流速的增加，床层的膨胀（空隙率）也增加[9,36,51-52,54]。

（6）流化床可以较容易地获得均匀的传质和传热，但是存在返混现象[39,48-49]。从化学反应的观点来看，气固混合的程度是相当重要的，尤其是在催化反应中。流化床层有非常高的混合程度，因而传质、传热均匀。如Lewis利用粉状碳来减少局部过热，成功地利用该技术研究了碳还原二氧化碳[40,50]、甲烷和氧化铜反应[41]。

（7）液-固流化系统中不同尺寸颗粒会分级，细粒从较大颗粒的空隙中被移到床层顶部[56]。

2.3 流态化类型

理想的流化状态是固体颗粒间的距离随着流体流速的增加而均匀增加，以保持颗粒在流体中的均匀分布。所有的颗粒都能够和流体均等接触，这对化学反应和物理操作都非常有利。均匀的流化使得系统拥有均匀的传质、传热及流体停留时间，这时的流化质量(fluidization quality)被认为最高。但实际上，流化床总不能达到这样的状态。

流态化系统可分为液固流态化、气固流态化和气液固三相流态化。液固流态化中颗粒均匀分散，系统较为稳定；而气固流化系统在低速下气体聚集成气泡的形式穿过床层，高速下颗粒聚集形成颗粒团悬浮于气流中。针对这些现象，1948年，Wilhelm等[9]提出“散式”和“聚式”两种不同类型的流态化现象。液固流化系统中，由于流体和固体颗粒间的密度差小，颗粒均匀分散悬浮，接近理想流化状态，多属于散式流态化。而气固流化系统中，气体和颗粒的状态呈现多样性，形成气泡或颗粒团，处于高度非均匀和不稳定状态，属于聚式流态化。三相流态化兼有散式和聚式的特征。

当然，并不是所有液固系统都是散式的，也不是所有气固系统都是聚式的。决定性因素是流体和固体之间的密度差，然后是黏度、颗粒特性、操作条件等。如Wilhelm等[9]用水流化密度很大的铅颗粒，观察到了液固流化床中有大液泡形成，呈现聚式现象。Geldart A类颗粒在气速小于最小鼓泡速度时，处于较为均匀状态，属于散式流态化[32-34]。Varadi等[57]在1500～2200kPa下用密度增加了20倍的空气流化260μm的砂子，也观察到了散式现象。

Wilhelm等[9]给出了一个使用Froude数的简单判据来区分散式和聚式流态化。Romero等[58]将Reynolds数和Froude数组合，形成比Froude数单独使用更好的判据[58]。

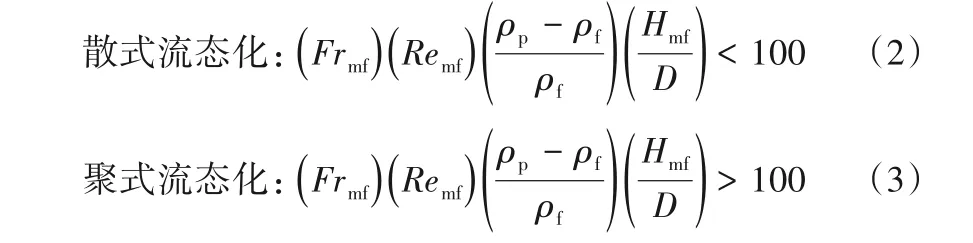
通过对流化类型的区分，可以判断流化的均匀性或流化质量。Geldart还通过粒径和颗粒与流体的密度差的乘积来衡量气固流化质量，将颗粒按照可能的流态化类型区分开来[59]。

3 散式流态化的早期发展

3.1 理想流态化和广义理论的启发

两相的连续逆流接触通常在某些类型的垂直塔中进行，这些塔的工作机理至关重要。Elgin等[60]在早期研究了填料塔、喷淋塔的理论和应用，这些成果为液固流化系统的研究奠定了坚实的基础。众所周知，流体流过管道和填充的固体颗粒时会产生压降；固体颗粒的不规则堆积使堆积层有空隙，空隙所占堆积层的比例即为空隙率，也可以看成空气占堆积层的体积率，所以固体所占比例为1减去空隙率，称为固相含率。前人的研究表明，相与相之间可能有某种联系，最后可以将压降、空隙率（相含率）及流体速度形成一般关联。在流态化过程中，颗粒床层随着流体速度的增加而膨胀，从完全填充状态的最小空隙率到理想完全膨胀时的100%空隙率。Elgin提出在流化区域中，决定流化程度或空隙率的是重力和摩擦阻力[38]。

经典流态化是指在流化床中，颗粒虽然在不断运动，但是系统并没有颗粒进出，无净流动。在对液固系统长期探索后，Elgin认为涉及悬浮在流体中的颗粒、液滴或气泡及多种操作可以归类为流动系统，如液-液萃取塔、细颗粒流化催化床、筛板塔、气力输送和喷雾干燥等[37]。Elgin对早期流态化理论做出了许多贡献，他扩展了流态化，包括底部有约束和自由无约束及有无颗粒净流动的系统，可以称他为一位集大成者。1957年，Elgin等[37]对垂直移动流化系统进行了较为全面的概括及对理论发展的思考，以颗粒和流体相对于彼此和包含容器壁的相对运动方向为基础，提出了垂直流化系统的可能类型。理想系统被定义为用不可压缩流体流化无孔刚性球体的系统。

滑移速度是所有类型系统的基本变量，滑移速度等于流体速度减去颗粒速度。即：

图7为Elgin提出的垂直流化系统的可能类型，规定向上流动为正，向下流动为负，ρd＞ρf。

对于给定的流体-颗粒系统，任一形式的流化系统在滑移速度值相同时将具有相同的空隙率ε或相同的固相含率εs=1-ε[37-38]。因此，无论哪种操作方式，固相含率和滑移速度的关系可表示为(1-ε)=ϕ(Vs)，如图8所示。

根据滑移速度公式推导可得：

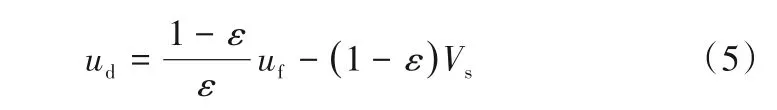
根据式（5）提出了固相含率εs=1-ε时表观固体速度ud与表观流体速度uf的示意图(图9)，对应于图7的流化系统类型。以固相含率εs=1-ε和表观流速uf为基础，Elgin编制了广义流态化图(图10)，指出了各种垂直流化系统之间的关系和极限，此图可用于预测和比较所有理想垂直流态化系统的运行力学和特性[37]。可以认为图10是图8、图9的结合，表1列出了关于不同操作区域的说明，和图7、图10对应。

表1 流态化系统的广义图说明Table1 Description of generalized graph of fluidization system

图7 理想垂直流化系统类型Fig.7 Type of ideal vertical fluidization system

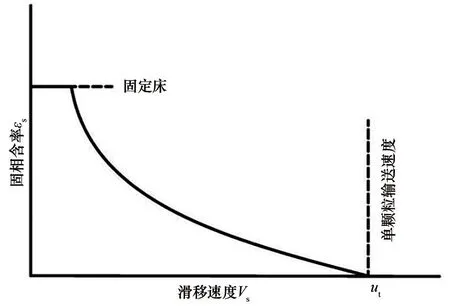
图8 固相含率εs与滑移速度Vs的典型关系（改绘自文献[37]）Fig.8 Schematic representation of holdup εs vs the slip velocity Vs(adapted from Ref.[37])

图9 固相含率为εs时表观固体速度ud与表观流体速度uf的示意图（改绘自文献[37]）Fig.9 Schematic diagram of superficial particle velocity ud vs superficial fluid velocity uf at constant values of the holdup εs(adapted from Ref.[37])

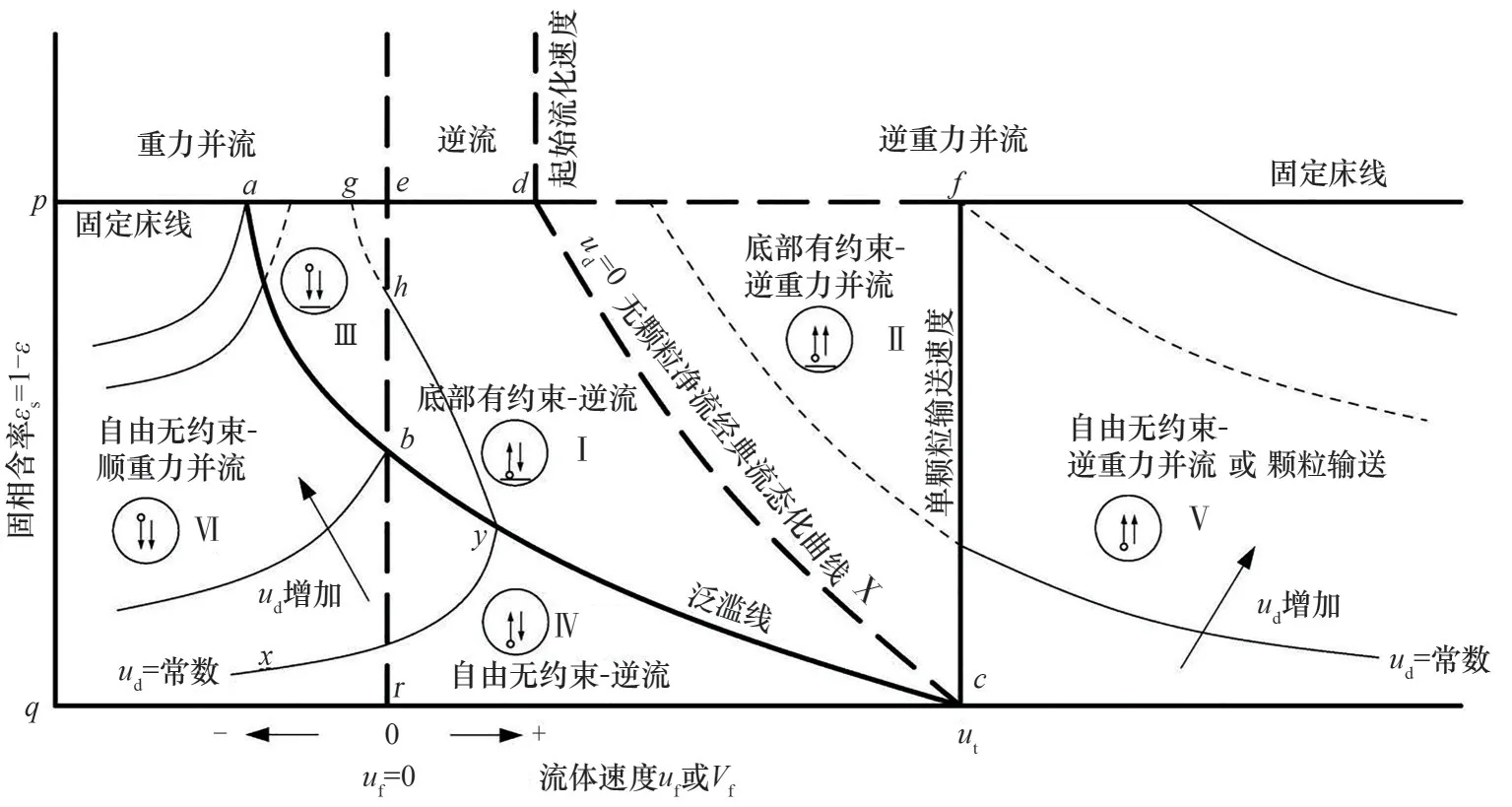
图10 流态化系统的广义操作图（改绘自文献[37]）Fig.10 The operation systems generalized graph for fluidization system(adapted from Ref.[37])

随后，Elgin等[37,61-64]对其提出的垂直移动流态化系统广义理论进行了验证，这些工作形成了对流态化系统进行扩展的重要系列，称之为早期的广义流态化理论。1959年，Price等[61]证明了自由逆流、底部约束无进料或间歇流化的相含率-滑移速度关系是一致的，这支持了在任何垂直流化系统的相含率和滑移速度之间存在一个基本关系的假设。Struve等[62]检验了广义理论分析在逆重力并流系统的适用性，支持了液固系统逆重力并流基本假设的正确性。逆重力并流的实验数据与操作图很好地吻合。如果固体有机械支撑，并且在柱底控制固体流量，则流体速度小于单颗粒输送速度的逆重力并流区域可以稳定运行。可以将该理论应用于复合并流逆重力流态化系统的行为预测。1960年，Elgin等[63]将先前对理想流态化系统的研究扩展到一个不太理想的系统——混合粒径的间歇流态化系统，以确定适用于单一粒径的原理是否仍然有效。在此之前，广义理论只被理想系统证明了，理想预测方法能合理地表示混合粒度的间歇-膨胀曲线。1961年，Quinn等[64]研究了重力并流，为重力并流流态化广义特性的预测奠定了基础。对于重力并流和间歇流化，滑移速度都是相含率的唯一函数，利用间歇流化曲线可以准确地预测重力并流的相含率和极限操作条件。

3.2 散式流态化膨胀和R-Z方程

采用流体和悬浮固体颗粒之间发生相对运动的系统在化工领域中很常见，有必要对其潜在特性有更深入的了解。早期的流态化理论研究对液固流化系统关注较多，液固流态化大多处于理想的流化状态[9,37]。对于均匀颗粒组成的液固流态化系统，只要流体流速保持在颗粒的终端速度以下，就能维持均匀的散式流态化，床层具有平稳膨胀的特性。许多研究者从流体和悬浮颗粒的相对运动扩展到液固流化系统，因为这两者有本质上相似的行为[54]。

液固流化系统中，如图11(a)所示，固定床阶段（颗粒静止），流体缓慢向上通过床层，穿过空隙，流速增加，空隙率不变；在此阶段继续增加流速，颗粒将重新定位，并达到最松散状态；如图11(b)所示，开始流化，颗粒被流体单独支撑，床层膨胀，空隙率增加，颗粒均匀地分散在流体中；如图11(c)所示，流体速度达到单颗粒自由沉降速度（终端速度），颗粒将处于输送状态。在流化阶段增加流速就会使床层发生膨胀，刚达到输送状态时流速和单颗粒自由沉降速度（单颗粒终端速度）近似相等。因此，可以看出液固系统中流速和空隙率存在一定的关系。

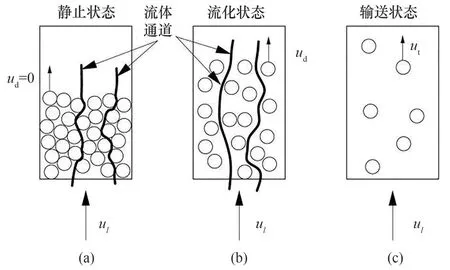
图11 散式流态化系统流动和膨胀示意图Fig.11 Schematic diagram of flow and expansion of particulate fluidization system

大量研究表明，在流态化阶段，流速和颗粒终端速度近似满足：

但是，实际的关系为：

受到壁面摩擦和颗粒间的相互影响，α总小于1，且不为常数。许多研究者想获得关于式(7)的一般表示，但是没有成功。Kwauk等[9]认为散式流态化颗粒的空隙率和修正的Reynolds数（流速）存在一定的关系，但是空隙率与其他变量之间并没有简单的关系。对于单一球形颗粒，空隙率和修正的Reynolds数（流速）有近似的直线关系[36]，流速和终端速度的关系可表示为[56]：

然而，以上研究并没有得到关于床层空隙率的较好一般关系式。1954年，Richardson等[54]对沉降和液固流化系统进行了总结和分析，坚持考虑沉降和流化的理论相似性，在理论推导中得到一些简单的包含多参数的函数关系。经过实验获得大量数据，将lgul和lgε作图，获得线性关系。更完美的是，沉降和流化的结果可以用同一直线相关联。科学不是偶然的，但科学的成就往往是辛苦工作后的偶然发现。由此，Richardson等[54]获得了一个完美的关系式：

式中的ui近似等于颗粒的自由沉降速度，但是发现颗粒直径与床直径比会略微影响该值。Richardson等在因次分析中发现，n是d/D和Ret的函数。另外，式(9)可以看作是Lewis提出当空隙率等于1时单个粒子的自由沉降速度，因此k为单位常数。由式(9)可以求得液固流化床的床层空隙率，并得到床层膨胀情况[54]。

因此，在实践中将理想化和实际情况达成妥协，得到了均匀球形颗粒的ui和n的关系，经过修正后，形成目前所使用的R-Z方程[65-66]：

其中

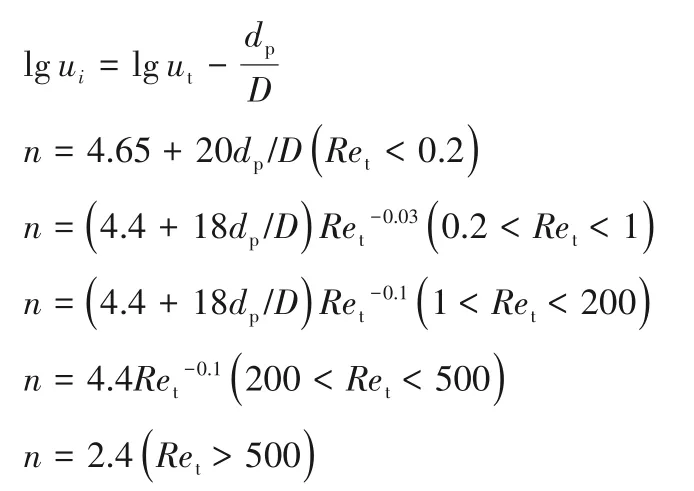
虽然R-Z方程没有理论依据，但是该方程是对液固流态化研究做出的迄今为止仍是最重要的贡献，提出了能够关联液固流化床中表观液速和床层空隙率的非常简单的经验公式。R-Z方程对于液固流化床模型的建立和反应过程的计算等具有重要意义。1989年，Richardsion等[67]将大小均匀的球形颗粒在液固系统流化和沉降过程中所观察到的速度与空隙率的关系与已发表的实验结果进行了比较，结果发现1954年给出的经验式能够完美应用于均匀液固系统，无须迭代程序，且其适用条件几乎涵盖了化学工程师感兴趣的全部范围。另外，由于某些气固流态化系统也能形成平稳的膨胀，多数学者认为空隙度和流速的关系与液固系统形式相同，但指数n可能更高，与液固系统并不完全一致。

3.3 广义流态化

经典流态化具有固定的颗粒床层，只考虑流体流速，没有颗粒的进出。在实际过程中，大多系统都存在颗粒和流体同时有进有出的情况。基于此，在原经典流态化系统中扩展出广义流态化的概念，来描述存在流动方向的多样性和有无颗粒净流动的综合流态化系统。正如前文所述，Elgin等[68]卓有成效的工作推动了广义流态化理论的发展，将该理论应用于萃取操作也获得了成功。这一时期，许多学者都曾提出将散式流态化的理论应用于广义流态化中[37,69-73]，奠定了广义流态化理论的发展基础，但是无法进行量化计算。Elgin等关于广义流态化理论的思路可以总结为：以广义流态化颗粒与流体的相对速度（即滑移速度）代替经典流态化的流速，流态化系统的压降和流速及空隙率和流速等变量间的关系依然成立。

郭慕孙等[74-76]在对垂直系统中均匀球体和流体运动的研究中，对流态化研究工作已有的成就进行了综合、归纳和改进，形成了广义流态化体系。包括三个部分：①经典流态化以及相关的固定床及颗粒沉降；②广义流态化；③加速度下颗粒和颗粒群的运动。

早在1948年Wilhelm等[9]对经典流态化的研究得出散式流态化中颗粒空隙率与流速的关系：

而后，Richardson等[54]提出的散式流态化床层膨胀公式：

滑移速度为：

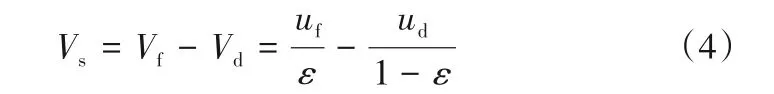
相对于空管的滑移速度：

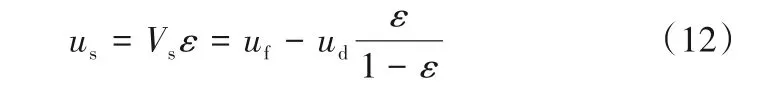
根据上述总结的广义流态化规律，将us替换成式（10）R-Z方程中的ul得：

则

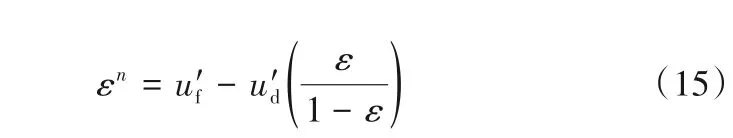
式(15)包含整个广义流态化的定量分析，即颗粒有进有出的散式流态化系统，适用于图7总结的各种操作类型以及后续发展的部分新操作。郭慕孙等[74]根据广义流态化理论编制了实用图表，可以快速计算出十种不同的广义流态化系统中的变量间的定量关系，并给出了应用情况，具体可参见文献。

在对散式流态化的研究中，Elgin为广义流态化的发展做了很好的铺垫，郭慕孙承前启后，在包容的思想下，使之能够量化计算。这一时期的“广义流态化理论”有两层意思，即流动方向的多样性和颗粒有无净流。

4 聚式流态化的早期发展

聚式流态化的概念是基于具有多样性的气固流化床所提出的，典型的聚式流态化如图6(b)所示。发生聚式流态化时，通入床层的超过最小流态化所需要的“超量”气体，会以气泡的形式通过颗粒层。小气泡先在分布板上形成，然后在不断上升的过程中发生聚并，最后在床层上界面处破裂。气泡尾涡会夹带一部分颗粒上行至床层上部，同时形成部分颗粒沿床壁及其他无气泡处下降的返混现象。相对于“美国派”的“概括式”研究方式，“英国派”Toomey、Rowe、Davidson等深入考虑了流况的多样性。他们从不同的微观角度对流况进行分相考虑，观察气泡行为，形成的流动模型对流态化理论的发展做出了重要贡献。

4.1 聚式流态化的“拟散式处理”

20世纪40年代，在石油催化裂化工业发展的迫切需求下，Lewis等[36]采用了散式流态化的理论，对气固流态化系统做了拟散式处理，并取得了初步的成功。他们通过研究玻璃珠颗粒在气固流化床反应器中的流动特性，得到如下结论：（1）尽管颗粒不同会带来微小差异，气固系统压降仍基本等于单位床层截面的固体质量；（2）大颗粒的滑移速度和理论预测的自由落体速度基本相等，细颗粒的滑移速度高于理论预测速度；（3）低气速时，空隙率很小，与固定床的空隙率基本一致，而随着速度的增加，空隙率增加。除此之外，Gilliland等[39]通过气体示踪法研究流化床中的气体返混，发现在大高径比的小型气固流化床反应器中，气体返混造成的反应速率变化可以忽略，因而可以直接采用平推流模型来处理流化床中的反应。但这样的方式如果用于大型反应器，将会由于较大的气体扩散，导致很大的误差。Deemter等[77]认为不能简单地忽略气体返混，需要在平推流模型的基础上叠加一个与流动方向相反的气体轴向扩散项，用气体涡流扩散系数E定量表征气体扩散的程度。上述研究均忽略了气泡现象，认为气固流态化和液固流态化本质类似，气固两相混合均匀，床层中的颗粒跟随气体运动，并伴随有一定的滑移。将上述研究归结于聚式流态化的“拟散式处理”。“拟散式处理方法”为处理早期聚式流态化问题提供了一种有效的解决途径，但由于聚式流态化的不均匀性，无法使用R-Z方程预测聚式系统的空隙率，使得该方法具有较大局限性。究其根本，是因为聚式系统流况具有多样性，如果简单地将气固流化床内部看作平推流，忽略局部细节，只采用散式流态化的模型对气固流化床流况进行笼统地均一化处理，不足以挖掘出聚式系统的流动规律，更不利于流化床反应器的设计应用。

4.2 聚式流态化的流动模型

如图12(a)所示，通入床层中超过最小流态化的“超量”气体，以气泡的形式通过颗粒层，这部分构成气泡的气体体积流量可以被认为是流化床的“可见流量”，用Gb表示。通过计算一定时间内穿过任一横截面的每一个气泡的体积，将这些单个气泡体积进行加和后，再除以观测时间即可确定Gb。

图12 气固鼓泡流化床的水平截面示意图（改绘自文献[78]）(a)，两相理论模型(改绘自文献[43])(b)Fig.12 Schematic diagram of a horizontal section through a bubbling fluidized bed(adapted from Ref.[78])(a)，the model of the two-phase theory(adapted from Ref.[43])(b)

“美国派”的“拟散式”处理没有考虑上述气泡现象，因此无法准确描述气固流化床内部的实际流况。之后兴起的“英国派”，以Toomey等[43]和Davidson等[44]为代表，采用全新的研究理论和流动模型，深入考虑了微观流况的多样性，从不同的角度对流况进行分相考虑，通过测量局部流动现象，明确了聚式流态化的局部和整体流动机理。图12(b)所示是Toomey等[43]于1952年提出的两相理论模型，该模型适用于描述含气泡的聚式体系。Toomey等认为不能将气固流化床内看成统一的一相，而应该简化为两相，一相由固体颗粒和少部分粒隙气体组成，固体颗粒间隙被速度为最小流化速度Umf的气体填充，被统一称为颗粒相(particulate phase)，也可称为密相(dense phase)；另一相为纯气相，由“超量”气体形成的许多个小气泡构成，气泡的体积流量可用式(16)表示：

气泡的体积流量Gb等于床层中气体的总体积流量G(G=UgA)减去密相中粒隙气体的体积流量Gd(Gd=UmfA)。但实际上，只有少部分的“超量”气体会形成气泡，大部分的“超量”气体都直接穿过气泡，因形成穿流而损失，所以气泡体积流率Gb一般小于(Ug-Umf)A。

为了更准确地计算气泡体积流量Gb，学者们提出了许多基于两相理论的衍生模型。这些模型主要被归纳为两类，一类是n型改进两相理论[78]，另一类是含有经验参数Y的改进两相理论[79]。n型改进两相理论在简单两相理论模型的基础上多引入了一个特征参数n，附加项nUmfεˉb用于表示不可见气体穿流量：

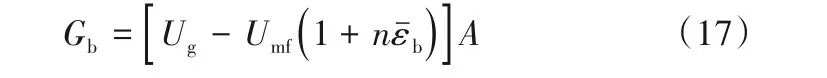
另一类引入经验型修正系数Y的改进两相理论为：

式(18)直接将两相理论中的(Ug-Umf)修正为Y(Ug-Umf)。因为高速粒隙气流和气泡穿流的存在，气泡体积流率Gb一般小于超量气体流率，因此通常Y≤1；当Y为1时，式(18)简化为Toomey和Davidson提出的两相理论模型。通过查阅Y与Ar的关系图可以得到Y的具体数值[80]或者通过含Y的经验公式，直接计算出Y[81]。这一类含修正参数Y的改进两相理论模型，公式简单，适应力强，可根据实际生产情况灵活地修正参数，因此被广泛采用。

聚式体系因气泡的存在而与散式体系有根本差别。聚式体系的流动行为几乎都可以通过气泡行为来解释，因此，Davidson等[44]对于气泡做了许多的细致的理论研究和计算。通过类比气液体系，Davidson等采用伯努利方程计算出了单个气泡相对于流化床层的上升速度Ubr为：

De为气泡在全床平均当量直径，可以采用最常用的Darton公式[82]计算得到。由于操作气速Ug通常高于最小流化速度Umf，因而单气泡的绝对上升速度Ub表达为：

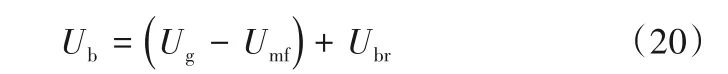
气泡在床内上升时会发生聚并，因此气泡群的上升，情况要更为复杂，Orcutt等[83]也在他们的研究报道中给出了相关的计算方法。

气泡相的存在造成气固流化床与液固流化床的床层膨胀现象有所区别，气固聚式流化床的床层膨胀由密相颗粒膨胀和气泡相的体积Vb组成，可以借由两相理论模型和Davidson等有关气泡行为的计算公式，得到床层膨胀高度Hf。

Toomey等[43]提出的两相理论模型及其衍生的流动模型，对聚式流态化流况做出了本质性的概括。Davidson等[82]则在两相理论模型的基础上对气泡做了许多的细致的理论研究和计算，通过计算气泡大小、气泡速度等来实现对床层膨胀高度的预测。在这些流动模型和理论方法的指导下，20世纪60年代前后的工业界已经能够成功设计大型气固鼓泡流化床反应器用于催化裂化过程。但实际的气固催化裂化装置中存在复杂的气固混合和化学反应，很多研究者对工业级鼓泡流化床中的气固混合情况进行了实验测定和研究，并根据实验结果做了模型分析。

聚式流态化由于气泡的存在而与液固散式流态化的混合机制存在本质不同。对于液固散式流态化，床层中颗粒间距随着液体流速的增加而增大，从而加强了液固轴向混合。但是对于气固聚式流态化，因为气泡的扰动，强化了气固混合，创造了较为均匀的床层温度。同时，也因气泡的存在，增加了气体短路，降低了气固接触效率，扩大了反应停留时间分布。通过气体示踪法，May[84]认为气固流化床反应器中，气泡相中的气体流型为活塞流，密相中的气体流型为活塞流模型和轴向扩散模型的叠加，并且密相中气体与固体的轴向扩散系数相等。然而，对于工业级气固流化床反应器，不能仅简单地将气泡相和密相看成两个平行反应。气泡相中虽然含有大量的反应气，但因为只含有少量的固体催化剂颗粒，所以会造成产率接近100%，选择性接近0；反之，对密相来说，产率接近0，选择性接近100%。为此，van Deemter[85]发展了May提出的密相气体扩散模型，不再采用May提出的密相中气体的轴向扩散系数与固体的轴向扩散系数相等的假定，而是认为气泡相气体和密相气体之间存在相间传质[图13(a)]。

在分析工业大型流化床的气固混合情况时，van Deemter模型不仅借助气体涡流扩散常数E较为准确地描述了密相气体混合机制，而且涉及气固催化裂化反应的气体相间传质，但van Deemter模型很大程度上依赖于稳态和瞬时气体混合实验，没有把握实际规律，不能从根本上对反应器放大、数据预测、反应速率计算等起到指导作用。为了探究相间传质规律，给出科学可靠的理论计算方法，Kunii等[86]提出了一种更完备的流动模型，只需要用单个气泡的当量直径De这一个特征参数即能实现对床层气泡相特征和气体相间传质情况的准确描述。物理模型如图13(b)所示，包括如下几点：（1）沿用Toomey等两相理论模型中密相处于最小流化状态、超量气体以气泡的形式通过床层的假定；（2）认为床层中的气泡均为有尾涡的有晕气泡，且气泡大小均一，用当量直径De表示；虽然通常在床层中的气泡大小是不均匀的，底部气泡小，顶部气泡大，但在含有内构件的工业级流化床中，因气泡的聚并和破裂处于动态过程，因此可以将气泡大小看作均一；（3）气泡上升过程中不断变大，挤压周围密相的固体颗粒，导致床层部分固体颗粒向下运动；固体颗粒向下运动的同时，会夹带部分气体也向下运动，造成气固返混现象；（4）气泡在密相中不断上升的同时，气泡、气泡晕和密相之间不断发生气体交换。

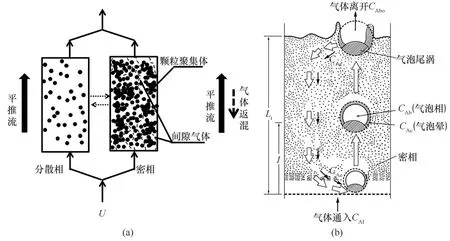
图13 van Deemter气体扩散模型(a)，Kunii-Levenspiel模型的气体和固体流动特征（改绘自文献[86]）(b)Fig.13 The schematic diagram of van Deemter gas diffusion model(a)，gas and solid flow characteristics in the Kunii-Levenspiel model(adapted from Ref.[86])(b)

和两相理论模型一样，Kunii等的模型中，通入气固流化床中的气体一部分用于密相床层膨胀，成为密相的粒隙气体，另一部分成为气泡相。

通过对任一床层截面进行固体物料衡算可以得到密相中的固体下降速度Us：

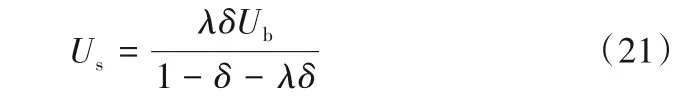
其中，λ是气泡尾涡中的颗粒含量。通过Us又可计算出密相中气体的上升速度Ue：

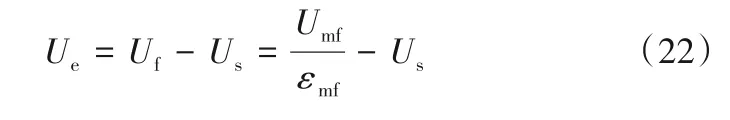
Kunii等的模型还用气体相间传质系数定量地描述了气泡相和密相间的气体交换情况，相间传质在气泡、气泡晕和密相间以二阶串联方式进行。即气泡相中气泡中的气体和气泡晕之间的转移以及气泡晕和密相中气体间的转移。根据气泡的单位体积，将气泡与气泡晕的交换系数，气泡晕与密相的交换系数以及总交换系数定义为：

对于单气泡的气泡与气泡晕之间的气体传质是由“分子扩散”和“强制对流”两部分控制，对于气泡晕和密相之间的气体传质仅由“分子扩散”控制。然后，在Davidson等给出的计算气泡速度、气泡穿流气体体积等的公式基础上最后可以得到总传质系数Kbe为：

Kunii等通过唯一的参数De实现了较完备的模型建立，尤其给出了用于定量计算气体相间传质系数的方法，可以说特征参数De的确定至关重要，但De受物系种类、设备尺寸和操作条件等多方面的影响，一般只能通过实验进行测定，不能通过理论计算得到，因此该模型仍有改进空间。

5 从固定床到流态化

流态化的流体力学行为可以认为是固定床向高流速的延伸。气流从底部引入固定床时，遵循固定床的特性，压降首先随流速增加而增加，床层不膨胀，空隙率不变；当流速足以使压力梯度等于单位体积固体的浮力时，床层处于临界流态化，进一步增加流速会使床层膨胀，空隙率增加，压降保持基本恒定，床层开始具有流体的特性；然后继续增大气体流量，床层变得完全流化，固体处于循环或混合状态。

5.1 固定床压降

许多的理论和经验关联式可以用于计算流体流经固定床的压降。最基本的思想是根据空隙率和床层高度得到流体经过的路程长度，再通过伯努利方程推导可得流体通过颗粒床层的压降。如图14所示，如果将颗粒间的缝隙看作是通道，那么流体的通路就可以用许多弯曲的管路来代替，称之为流路模型[87]。在直圆管的基础上修正，可以得到这些管路的压降。

图14 流体通过颗粒床层的流路模型图Fig.14 Flow path model diagram of fluid passing through the particles bed

直圆管压降根据Hagen-Poiseuille公式：

引入颗粒床层当量半径：

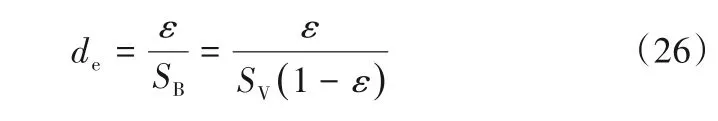
对管长修正，可得Kozeny-Carman方程[88]：

另外，Burke-Plummer还提出了适用于湍流的方程[89]。Leva[90]也曾提出用通过空管的流动来得到压降公式。基于以上，Ergun集成了一种经验性综合关联式，适用性较强，这里主要以他的研究思路来还原早期的学者们对于固定床压降的探索之路。Ergun的研究主要集中在煤炭领域，利用流化床研究非均相反应的动力学，因为流化床易于实现温度控制，这一特点使其非常适用于强放热反应。因此，必须了解标准的流化状态以及实现流化所需要的条件。研究流体流动规律，可以描述从零流速到流化时所需要的流动条件，这也是流态化研究的首要领域，以区别于其他单元操作。1949年，Ergun等[51]尝试建立了固定床压降与质量流量的一般关系式：

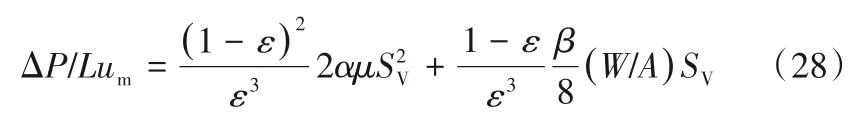
他们发现黏性效应和动力效应在压降计算中必不可少，固定床中压力梯度与表观流速之比是流体质量流量的线性函数，线性关系的常数包括颗粒比表面积、空隙率和流体黏度。同时，摩擦因数隐含地包含空隙率，而不是通常认为的仅是Re的函数。这些常数可用于预测压力梯度达到床层单位体积固体浮力后，随着气体流量的增加，床层膨胀的程度[51]。

许多学者期望找到一个一般方程将能量损失（压降）和流体的分子间力、黏性力、动力、静力等关联起来。基于前人的总结，影响因素可以考虑为：（1）流体的速度；（2）流体的黏度和密度；（3）填充物的紧密性和取向；（4）颗粒的尺寸、形状和表面。Ergun采用了破碎的多孔固体，而不是前人研究的理想条件。

Reynolds[91]第一个计算了流体运动的摩擦带来的阻力：

ΔP/L=aU+bρU2（29）

Kozeny[92]在压降计算中引入黏性，Ergun[52]总结了Blake采用动能项，同时使用摩擦变量来补偿黏性造成的能量损失的方法。可以想象当流体速度非常小时，几乎没有动能损失，黏性力主导了能量损失。根据泊肃叶方程和达西定律可得：

ΔP/L=a′μU+bρU2(a′=a/μ) （30）

方程的第一项代表黏性能量损失，第二项代表动能损失。

为准确反应压降情况，Blake提出了两个无量纲数群[52]：

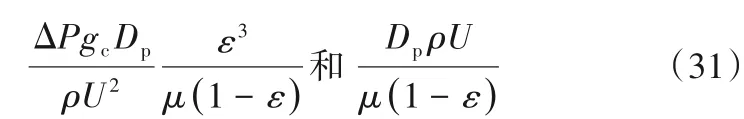
前者可以看作是修正的摩擦因数，后者可以看成修正的Reynolds数。这印证了之前的推论，压降不是某个单一数群的函数。许多研究者没有得出实用的压降表达式是因为没有考虑到压降是同时由动力和黏性的能量损失造成的。

Carman[88]在Kozeny方程的基础上，在低流速提出式(32)代表黏性造成的能量损失。

在高流速时，根据改进的Burke-Plummer湍流方程[89]式(33)代表动量损失。

Ergun将6～20种不同堆积密度的颗粒填充形成单一系统，因而产生了不同的空隙率。同时，注入气体后形成最松散的堆积以确保床层均匀，规避颗粒的紧密性和取向问题[51]。根据上述分析，并考虑颗粒的表面形态，将当量直径引入式(28)中可得：

其中，k1=72α，k2=3/4β。

Ergun使用多种气体和不规则固体，在多达640次实验后，得到k1=150，k2=1.75 。变换形式得到：

固定床的压降是黏性能量损失和动量损失之和，方程右边第一项可以看成是黏性能量损失，第二项可以看成是动量损失[52]。1953年，Ergun将这个方程应用于高炉中获得了成功[93]。可以这样认为，R-Z方程前阶段（未膨胀）的床层情况可以用固定床的压降来表示。如图11(a)所示，固定床阶段颗粒是连续相，空隙率不变，R-Z方程不适用，而Ergun方程可以从压降角度来表示流动情况；如图11(b)所示，床层膨胀后，颗粒逐渐分离，Ergun方程不再那么准确，R-Z方程则可以计算散式系统床层膨胀程度。本文作者祝京旭曾与Epstein讨论过此现象，当时Epstein根据经验总结推测Ergun方程可能适用于计算固定床和在散式流态化初期阶段空隙率小于0.7 时的流化床膨胀程度。

5.2 最小流态化速度（临界流态化）

在固定床中，流速增加，流体流过固定床层的阻力将不断增加，直到床层压降等于单位床层截面积上的颗粒质量。由于流体流动带给颗粒的曳力平衡了颗粒的重力，颗粒开始悬浮，进入流化状态。相应的流体速度即临界流态化速度或最小流态化速度umf。最小流态化速度是流化床过程分析和设计中的一个重要变量，可以通过实验或者目视法等来确定。理想流化和实际流化过程的压降-流速曲线存在微小区别，但是为了设计和理论分析，预测最小流态化速度就具有重要意义了。

如果将颗粒球形度引入Ergun方程进行修正，并与临界流化时压降关系：

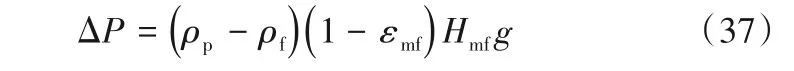
联立可得：

这个方程即是求解最小流态化速度的一般方程。1965年，Narsimhan[94]提出了一种最小流态化速度的广义表达式，在一定条件下结果较准确。1966年，Wen等[95]为检验Narsimhan所提出的表达式适用性，借鉴了Ergun[52]的思路，推导出固定床压降表达式，第一个注意到[55,95]：

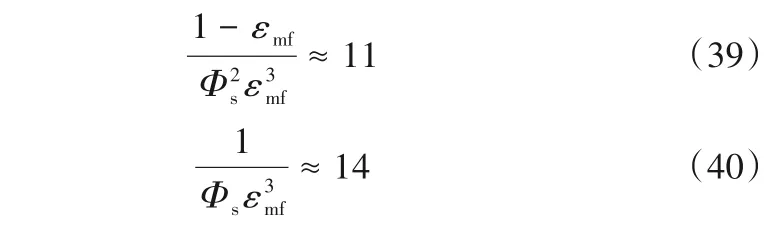
式(39)、式(40)在不同颗粒下保持近似恒定。因此得出最小流态化速度的表达式：

其中，C1=33.7 ，C2=0.0408 。

将数位研究者的数据用式(41)验证，284个数据点的相关性比Narsimhan提出的表达式好，且更简单、精确。将式(41)作图可以方便快速地估计最小流态化速度。虽然不是百分之百完美，但是在不断地探索中，依然找到了一个能够广泛适用的表达式。这也是在流态化研究中常遇到的问题，需要在妥协中，寻求折中的方式来解决问题。

如果Re＜20（层流），方程还可以简化为：

Re＞1000（湍流）：

式(42)、式(43)是既适用于气固又适用于液固的通用公式。研究者们提出了许多上述公式的修正式和其他类型的关联式，如Geldart等提出了细颗粒的适用式[34]。到目前为止，有超过100个经验或半经验方程被提出预测最小流态化速度，常见的最小流态化速度关联式可参考文献[96]。

6 回顾与展望

流态化科学与技术的发展迎来了第一个百年，过去的历史可谓百家争鸣又殊途同归。回望百年，流态化的发展阶段可分为：前半时期以液固散式流态化和以低速气固聚式流态化（鼓泡流化床）为主的初期理论发展及早期工业应用阶段，后半时期扩展到以高速流态化及气液固三相流态化为代表的流态化形态多样性与数模化及工业应用繁荣发展阶段。回顾历史，能够有助于在科学实践中寻找经验和教训；展望未来，能够指明发展的方向。

6.1 流态化早期探索

流态化前50年的历史已经在前文进行了回顾。Winkler的气化炉开启了流态化近代研究的先河，然后是基于石油催化裂化等工业研究而奠定的一些基础理论。Ergun和Richardson-Zaki分别从压降和床层膨胀来研究流化床的流动特性；Elgin等为代表的“早期美派”研究者扩展了散式流态化，在一定高度上将其统一，建立了广义流态化理论，为流态化后50年的快速流态化、湍动流态化(turbulent fluidization)、下行床(downer)和逆向流化床(inverse fluidized bed)等发展提供了很好的理论指导。“美国派”Lewis等提出的“拟散式处理”方法，虽然对早期工业应用做出了实用的理论贡献，但因无法采用RZ方程预测聚式系统的空隙率，具有很大局限性。“英国派”Toomey和Johnstone将气泡单独分相考虑，提出的两相理论模型较为准确地描述了低速聚式流态化流况。在此基础上，Rowe和Davidson等通过对单气泡行为的理论研究，成功地预测出床层膨胀高度及基本流动状态，为流态化反应模型奠定了基础。基于含有实际化学反应的气固催化裂化反应器，van Deemter模型引入气体涡流扩散系数E，通过实验结果描述了相间气体传质情况。后来的Kunii-Levenspiel模型采用单一特征参数（气泡直径De），通过计算相间气体传质系数，为工业级气固流化床反应器中化学反应的预测提供了理论依据。

6.2 流态化蓬勃发展

鼓泡床属于聚式流态化，以气体聚集形成气泡为主要特征，颗粒相是连续相。而流态化后50年兴起的快速流态化，以颗粒聚团为主要特征，气体是连续相，颗粒聚团成为分散相。快速流态化被称之为“反向”聚式流态化，同样处于高度不均匀分布状态，且颗粒聚团内外的反应状态也不同，因而降低了系统的运行效率。然而，聚式系统也有其好处，操作气速可以大大超过其终端速度，处理量较大。如FCC的提升管反应器操作气速在10m/s之上，而其颗粒终端速度仅为0.2m/s，50倍的操作条件使FCC在众多反应器中脱颖而出。

虽然快速流态化实现了无气泡气固接触，但是颗粒聚团现象让快速流态化仍具有聚式流态化的缺点。在工业实践中，人们发现在鼓泡流态化与快速流态化之间还存在一个过渡区域，称为湍动流态化。湍动流态化处于相转移状态，气泡和颗粒团簇都处于生成和消失的临界状态（不断聚并和破碎），实现了聚式和散式的“动态”归一化，可以被认为是一种更理想的气固接触。因此，湍动流态化受到了极大的关注。工业反应器也逐渐从20世纪五六十年代的鼓泡流化床大量过度到湍动流化床，实现了高效和均一的传热、传质以及良好的气固接触。

传统的液固流态化系统采用的是密度大于1的颗粒，而新型的逆流化床则将密度小于1的低密度颗粒使用在液固系统中。逆流化床液体向下运动，如果液速过小，流体对颗粒的曳力加上颗粒的重力不足以平衡颗粒的浮力，则颗粒向上流动，即位于图9所示的Elgin提出的“不可操作区”（现在来看，该区域存在可以操作的流化系统）；若液速较大，流体对颗粒的曳力加上颗粒的重力大于颗粒的浮力，则颗粒向下流动，即位于图9的“并流向下区”。逆流化床因其低能耗、易再启动等优点，近年来受到了较多关注。

早期的广义流态化在流体流向维度和颗粒净流维度将流态化系统统一，新型逆流化床的出现带来了新的思考，因而考虑引入固体颗粒密度作为另一维度来扩展广义流态化理论。从固体颗粒的相对密度入手，如果假定密度低于流体的颗粒所带来的固相含率为负值，则图10可扩展为图15，在其下部扩展出了“浮力流态化”区域。如图15所示，区域Ⅶ+Ⅷ即为在原广义流态化基础上扩展出的低密度操作区域，并据此来考察其流动特性。其中，区域Ⅶ可以认为是对应于前面讨论的逆流态化（浮力流态化）操作区域，即通过向下流动的流体，来悬浮流化低密度颗粒，形成逆向流化床。而区域Ⅷ则为“顺浮力流态化”，由向上流动的流体所产生的曳力，协同低密度颗粒的自身浮力，来共同推动颗粒顺浮力方向流动，反向类比于气固下行床的并流操作状态。通过以上讨论可以看出，成功地为广义流态化代入了第三层含义，即除了流动方向的多样性和颗粒有无净流之外，又将颗粒相对密度融入到了广义流态化理论中。

图15 广义流态化系统扩展示意图Fig.15 Schematic diagram of extended generalized fluidization system

另外，三相流化床也快速发展起来。三相流态化是气、液、固三相共存的流动体系，可以看作是由液固流化系统通入适量气体而形成的。它兼有散式和聚式的特征，强化了相间接触和传热、传质效率，近年来广泛用于石油化工、生物、环境等领域。从纯流态化理论角度，这里所说的三相床仅限于液体为连续相的操作状态，而将以气体为连续相的三相操作归属于从气液体系扩展而成的“气液搅拌流”(churn-turbulent flow)操作系统。

20世纪后期，伴随着计算机技术的迅速发展及数值计算方法研究的不断深入，计算流体力学(computational fluid dynamics，CFD)逐渐在石油化工中得到应用，被广泛应用于剖析流化床内复杂多相流非线性特征，为研究流化床中气固流动特征提供了一种新的高效途径。流态化技术的研究开始进入实验、理论和计算机模拟互为补充、共同提升的阶段，复杂的多相流动可以利用计算流体力学进行比较准确的量化描述[25,97]。目前，采用CFD软件进行数值模拟的方法主要有欧拉和拉格朗日法。同时，随着测量技术的提升，CFD软件和测量技术的结合使得对多相流的计算更为准确。另外，流化床反应器的工业放大过程，存在大尺寸气泡生成的缺点，导致传质效率降低，生产能力下降。因此，流化床反应器放大技术的关键是克服不均匀性。利用CFD软件模拟技术结合传质模型可以较为准确地分析反应器放大后的多相传质行为，并进行优化，指导流化床反应器的开发，是流化床工业放大和生产的有力支撑[98]。尽管CFD多相流模拟为流化床的开发和放大提供了新的手段，但是由于对复杂的流体动力学认识的不足，如对流化床边壁效应缺乏定量描述，在CFD模拟时找不到合适的边界条件，影响了流化床的设计、放大[99]。同时，为了计算效率，模拟时对流化床中粒子、流体的受力和运动行为存在着过度简化，如流体与颗粒间曳力模型选取的不合理，导致出现了和实际流化床流动行为差异明显[100]。CFD对流态化系统流动的模拟还有待提升，相关情况可参见文献[101-103]。

建立在流化床煤气化、石油催化裂化技术和流态化理论的快速发展基础上，流态化技术在后50年广泛应用于工业生产中。在石油化工领域中，流态化催化裂化技术不断革新，取得了重大进展。在化工领域，流态化技术广泛应用于合成工业来生产许多重要的化工原料。例如，丙烯腈是一种用来制备染料、合成树脂、原料药、聚丙烯腈、丁腈橡胶等的重要化工原料。然而早期的工业化生产，是在氯化亚铜的稀盐酸溶液中催化氢氰酸和乙炔反应制备丙烯腈。虽然催化法生产过程简单、收率高，但副反应多，反应物氢氰酸毒性也较大。基于此，20世纪60年代美国Sohio公司首次采用流化床反应器，将氨氧化丙烯制丙烯腈工艺商业化[104]。因该反应过程放热强烈，使得具有极佳传热效率的流化床反应器因占据独特的优势而一度垄断市场。常用的流化床催化反应器多为湍动流化床反应器（虽然学术界对鼓泡床的研究很多，但因其较大的返混，实际工业应用并不多见）。自从丙烯氨氧化制备丙烯腈工艺路径面世以来，针对湍动流化床反应器，借由聚式流态化的两相理论[105]，研究者们不断地开发出更具普适及实用性的模型，用以更准确描述流化床反应器内部的反应规律。

能源领域也是流态化技术的重要应用之一。流化床燃烧技术一直以来备受科研人员关注，近年来更是开发出许多大型流化床锅炉技术[106-109]。另外，煤化工技术因推动清洁生产而得以快速发展。流化床煤气化技术较为成熟，大型工业化装置相继建立[110]，实现了煤炭资源的有效利用，更为节能减排贡献了巨大的力量。煤化工新概念、新技术也带动了下游产业的蓬勃发展，诸如甲醇制烯烃技术，也采用了流态化技术[111]。低碳烯烃如乙烯、丙烯是石油有机化工的重要原料之一，尤其乙烯的产量是用来衡量一个国家石油化学工业发展水平的重要指标之一。甲醇制烯烃是一条重要的烯烃制备路径：高温条件下，甲醇气体在分子筛催化剂的作用下，可以生成乙烯或丙烯。但因甲醇制烯烃是强放热反应[112-113]，催化剂容易积炭失活，所以如果采用固定床反应器，热量无法及时移除，只能采用中间冷却的多段绝热固定床反应器，如鲁奇公司就基于这种反应器成功开发了具有高选择性的甲醇制丙烯工艺(MTP)[114-115]。但因为流化床反应器传热均匀，目前更为常用的还是流化床反应器，如Mobil工艺[116]、UOP/Hydro工艺[117]和中科院大连化物所开发的以二甲醚作为中间产物的DMTO工艺[118]等。

6.3 流态化技术推动节能减排

流化床在许多工业领域的应用，亦促进了产业结构的调整，为实现节能减排和清洁生产贡献了力量。化工既能够产生能源，也会消耗大量的能源。石油化工工业可以从石油中提炼汽油，煤工业可以制煤气，这些工业为社会的建设和发展提供了大量的能源及工业原料。然而，化工行业对能源的消耗巨大，与此同时能源浪费也很严重，因技术落后导致能源利用率低的情况普遍存在。另外，化工行业的污染问题也很突出，亟需解决。近年来，为响应化工行业节能减排的号召，许多单位开发了节能减排的新技术，并取得了较好的经济效益和社会效益。流化床技术的应用正是典型的代表，这里以三个例子来说明流态化技术具有高效节能和减少污染排放的潜力[109,119]。

锅炉是常见的工业设备，但是传统锅炉燃烧不彻底，燃烧效率非常低，造成了燃料和热能的浪费，还排放了大量的污染物。流化床燃烧是流态化技术重要的应用方向，能够利用的燃料范围很广，因此得到了广泛地使用[107-109,119]。新型的循环流化床锅炉可以将烟气中的煤粉收集，重新送入燃烧室，燃烧效率远高于普通锅炉，节约了大量的能源[120]。传统锅炉在燃烧时没有进行脱硫处理，含硫污染物的排放量较大，是空气中含硫污染物的主要来源。循环流化床锅炉在煤炭燃烧中同时进行脱硫处理，通过掺入氧化钙，大大减少了二氧化硫的生成和排放。同时，循环流化床燃烧迅速，燃烧温度较低，一般在850～900℃，容易在燃烧时对NOx类污染物的生成进行控制，而且还由于床料沿炉膛高度对NOx的破坏，因此NOx的排放量很低，实现了减排的目的[121]。循环流化床燃烧技术具有高效、节能、低污染、煤种适应性广等特点，已成为燃烧项目技术改造的优选之一。

煤炭气化是煤清洁高效利用的首选技术，大量应用于合成工业。煤气化技术主要有固定床、流化床和气流床等技术。我国早期的煤气化技术主要以常压间歇式固定床技术为主，该技术的碳有效气化率和CO的选择性低，气化组分成分复杂，需要冷凝提纯，因此能耗高、产率低[122]。同时，该技术使用的原料无烟块煤价格高、产生的三废排放量大、污水中含有焦油和酚类等有机物，造成处理成本高、经济效益差，技术升级受到制约，所以固定床技术不易实现大型化生产。而流化床煤气化生产的煤气较为洁净，减少了污染排放。另外，流化床造气流程比固定床简单，气化强度比固定床大、煤种适应性强[123]。循环流化床粉煤气化炉生产能力大、操作维修简单、环境污染低、综合经济效益好[119]。因此，循环流化床粉煤气化技术对推动高效、清洁的煤利用技术具有重要意义。

催化转化是化学工业的重要过程之一，其中顺酐的生产具有代表性。顺酐是重要的有机化工原料和精细化工产品，应用范围极其广泛。目前，工业化生产顺酐的路线逐渐从苯法过渡到正丁烷法。正丁烷选择性氧化制顺酐有固定床、流化床、循环流化床等多种技术[124]。固定床技术较为成熟，但是该技术投资费用高，建设和运行复杂；因床层热点温度难以控制，反应热移除也存在困难；又因受到正丁烷爆炸极限的限制而必须处理过剩空气而导致生产能力降低[125-126]。流化床技术由于催化剂颗粒处于良好的运动中，因此该技术传热效率高，近似于等温操作，避免了局部过热。而苯、正丁烷制顺酐是强放热反应，所以具有超强传热功能的流化床反应器比固定床反应器更适用。流化床技术生产顺酐克服了固定床能耗高的缺点，后续发展的循环流化床技术可以使催化剂单独再生，反应温度低、副产物少，显著提高了反应的选择性。

虽然流化床技术仍然存在一些弊端和瓶颈，但是从长远来看，流化床技术具有相间接触好、传热传质效率高、床层温度均匀、操作范围广、能耗低、可以强化化学反应等优点，是代替高能耗、高污染的传统化工反应器如固定床、回转窑等的重要选择。

6.4 流态化未来启发

从理论角度来看，气固流态化的散式化研究将是未来流态化的重要发展方向。散式流态化一般见于液固系统，颗粒均匀分散于液体中，无气泡和颗粒聚团，相间接触良好，具有均匀和高效的传质、传热以及较高的化学反应速率等优点。聚式流态化常见于气固系统，床层处于不均匀状态，低速下气体聚集形成气泡，高速下颗粒聚集形成颗粒团簇，进而降低了床层整体的传热、传质和化学反应速率。然而，快速流态化系统宽泛的操作条件亦为工业应用带来一些特有的优势，如可以极大地增加处理量。同期发展的湍动床，事实上尝试了将散式和聚式流态化融合为一体，在一定程度上实现了气固流化床层的均匀性。另外，随着超细粉应用的兴起，人们在积极寻找有效流化超细粉方式的同时，还发现了其明显的散式特征，或成为未来流态化发展的新节点。因此，未来50年，流态化研究的重点之一就是推动气固流态化的散式化，研究如何通过改变颗粒和流体的特性来减少气泡和颗粒聚团等聚式特征。

第一，可以采用超细颗粒获得较好的散式流态化行为。相对于B类颗粒既小且轻的Geldart A类颗粒，有较好的流化质量，并可以在低气速下实现散式流态化。由此推论，更小且轻的C类超细颗粒，势必应有更好的流化质量，及更多的散式流态化倾向。然而由于其强大的颗粒间作用力，C类颗粒难于被正常流化。近年来，本研究组通过纳米调制克服粒间力，释放出了C类颗粒的“流化潜力”，不仅能够让超细颗粒正常流化，而且还发现了其明显的散式流化特征：流化时所产生的气泡既少又小，并且形成很大的床层膨胀。极大的床层膨胀与更少的气泡，均说明有更多的流化气体进入了颗粒相，因而偏近于散式流态化。未来需要进一步研究超细颗粒的流化现象，从机理上揭示其具有散式流态化特征的原因，从而有效地利用此优势，开发出更多的实际工业应用。

第二，可以采用超临界流体，实现聚式的散式化，及散式与聚式的归一化。超临界流体是通过改变流化介质的密度来实现散式化。超临界流体的黏度，特别是密度明显增加，因而对颗粒的曳力和浮力也大幅度增加，这样有利于均匀流态化，使气固原本具有的聚式流化状态向散式靠近。加大流化床反应器的压力，同样会增加气体的密度与黏度，亦能促成气固流态化的散式化。

第三，可以将大小颗粒混合流化。极小的细微颗粒易于与气体形成同质的准流体，增加了有效流体密度，减少颗粒与流体的密度差，从而可以使聚式向散式靠近，实现气固流态化的散式化。

从工业实践角度来看，流态化技术在工业应用上的主要发展方向还是提高效率、减少能耗，可以考虑的手段有加强相间接触、强化传质传热和反应过程。许多化学反应过程放热强烈（如氨氧化丙烯生产丙烯腈），所以具有极佳传热效率的流化床反应器将成为优先考虑。鼓泡床返混较大，因此湍动床，特别是快速床在化学反应工业的应用将会是重要发展的方向。另外，在上述展望的理论取得实质进展之后，可以考虑进一步利用散式流态化的优良特性开发出更多的实际工业应用，以满足更高效、节能和安全的工业需求。从目前工业反应器所面临的弊端来看，今后更多的多相反应，同样可能会用到流态化技术。一些比较特殊的反应体系，也可以利用流态化的多样性、灵活性，取得进一步的开发。如多级（“快慢”或者“慢快”）反应，大量颗粒可以被输送，同时也会产生不同的状态，不同的需求阶段可以采用不同的流化状态来实现最适宜的处理效果，现有的流态化技术在干燥过程中的应用就是较好的例子。

目前，我国工业正处于产业结构和布局的大调整时期，工业技术人员将淘汰落后产能以实现节能减排和清洁生产。流态化技术以其突出的优点，正可以推动工业的变革。响应国家号召的碳达峰和碳中和目标，流态化将会贡献巨大的力量，在下一个百年更加繁荣发展。

符号说明

A——空塔的截面积，m2

Ar——阿基米德数

a，a′，b——公式系数

CAb,CAc,CAe——分别为气泡、气泡晕和密相中气体组分A的浓度，mol/m3

D——流化床直径，m

De——气泡的特征尺寸，m

Dp——颗粒有效直径，Dp=6/SV，m

dp，de——分别为颗粒直径、当量半径，m

E——气体涡流扩散常数，m/s

Frmf——Froude数，u2mf/(gdp)

G——流体的质量流速，kg/(m·s)

Gb——气泡的体积流率，m3/s

Gd——浓相中粒隙气的体积流率，m3/s

g,gc——重力加速度，m/s2

H——床高，m

Hf——得到床层膨胀高度，m

Hmf——初始流化条件下的床层高度，m

K，k1,k2，α，β——无量纲系数

Kbc——基于单位气泡体积的气泡与气泡晕之间的交换系数，s-1

Kbe——基于单位气泡体积的气泡和密相气体之间的总传质系数，s-1

Kce——基于单位气泡体积的气泡晕与密相气体之间的交换系数，s-1

L——流化床长度，m

l——距离分布板的垂直距离，m

NAb——气体传质通量，g/(mol·m2)

n——n型两相理论模型中的特征参数

ΔP——床层压降，Pa

Remf——初始流化条件下的Reynolds数，dpρfumf/μ

Ret——对应于颗粒终端速度下的颗粒Reynolds数，dpρfut/μf

SB——颗粒表面积，m2

SV——颗粒体积等球体表面积，m2

t——气泡上升时间，s

U——空床的表观流体速度，m/s

Ub——单个气泡的绝对上升速度，m/s

Ubr——单个气泡相对于流化床层的上升速度，m/s

Ue——密相中气体的上升速度，m/s

Ug——操作气速，m/s

Um——平均压力下的表观流体速度，m/s

Umf——最小流化速度，m/s

Us——密相中颗粒的下降速度，m/s

u——流体速度，m/s

ud——颗粒净平均表观速度，m/s

u′d——对比颗粒的表观速度，u′d=ud/ut

uf，ul——分别为表观流体速度、表观液体速度，m/s

u′f——对比流体的表观速度，u′f=uf/ut

ui——R-Z方程中的常数，m/s

um——平均压力下的表观气速，m/s

umf——初始流化速度，m/s

us——表观滑移速度，m/s

ut——单颗粒终端速度，m/s

Vb——气泡相的体积，m3

Vd，Vf——分别为颗粒速度、流体速度，m/s

Vs——滑移速度，m/s

W——流体的质量流量，kg/s

Y——Y型两相理论模型中的经验参数

δ——流化床中气泡相含率

ε——空隙率

εˉb——床层中的平均气泡相含率

εmf——初始流化状态下的床层空隙率

εs——固相含率

λ——气泡尾涡中的颗粒含量

μ——流体黏度，Pa·s

ρ,ρf——流体密度，kg/m3

ρp,ρd——颗粒密度，kg/m3

Φs——颗粒球形度