基于不同水层海水温度的阿根廷滑柔鱼栖息地模型构建
刘赫威,余为,2,3,4*,陈新军,2,3,4,朱文斌
(1.上海海洋大学 海洋科学学院, 上海 201306;2.国家远洋渔业工程技术研究中心, 上海 201306;3.大洋渔业资源可持续开发教育部重点实验室,上海 201306;4.农业农村部大洋渔业开发重点实验室,农业农村部大洋渔业资源环境科学观测实验站,上海 201306; 5.浙江省海洋水产研究所,浙江 舟山 316021)
阿根廷滑柔鱼Illexargentinus是广泛分布在西南大西洋的重要经济头足类[1-2],其中,栖息在公海海域的南部巴塔哥尼亚种群(south Patagonic stock, SPS)是中国渔船的重要捕捞对象[3],研究表明,海洋环境因素变化可能是造成短生命周期的阿根廷滑柔鱼产量波动的主要原因[4]。有学者探究了海表面温度[5]、叶绿素a浓度[6]和海面高度[7-8]等环境因素对阿根廷滑柔鱼资源及渔场的影响,结果表明,基于这些环境因素的栖息地模型可以较好地预测阿根廷滑柔鱼资源丰度的变化。然而,在探究环境因素对阿根廷滑柔鱼的影响时,研究者大多只考虑海表层温度等海洋表面环境因子,而对不同水层海水温度的研究较少。
阿根廷滑柔鱼栖息水层具有明显的季节性变化特征,冬季栖息水层的深度较深且温度较低,夏季则栖息在较浅较暖的水层[9],其栖息水层与海洋环境有关[10]。阿根廷滑柔鱼渔场的分布主要受马尔维纳斯寒流(Malvinas current,MC)与巴西暖流(Brazil current,BC)的影响[11],其产卵活动发生在两海流共同影响的辐合带,而摄食活动则发生在来自南方温度较低的马尔维纳斯寒流[7,12]。马尔维纳斯寒流靠近南美洲大陆架的西支,有时被称为巴塔哥尼亚洋流[13],在100~200 m等深线之间流过大陆架,把亚南极的富营养冷水向北传送[14]。有研究表明,在巴塔哥尼亚大陆架附近,水深50 m是阿根廷滑柔鱼资源丰度明显的分界水层[15]。对阿根廷-乌拉圭共同渔业区(Argentine-Uruguayan common fishing zone,AUCFZ)的调查发现,阿根廷滑柔鱼垂直洄游的水深最深可达280 m,但通常都出现在200 m等深线以内[8]。刘赫威等[10]证实了表层到195 m水深温度对阿根廷滑柔鱼资源丰度的影响,但并未得出不同水层温度与渔场分布的具体关系。
栖息地适宜指数(habitat suitability index,HSI)模型最早由美国地理调查局国家湿地研究中心鱼类与野生生物署(Division of Ecological Services U.S.Fish and Wildlife Service Department of the Interior)于1980年提出,被用来描述野生动物对周围栖息地环境的适应程度[16]。近年来,HSI模型的理论与方法已逐渐应用到渔业资源变动及渔场分布的研究中[17]。阿根廷滑柔鱼作为短生命周期的头足类,对环境极为敏感且温度对其渔场与资源的影响最为显著[13]。为此,本研究中基于50、100、200 m不同水层海水温度建立了综合HSI模型,并据此研究了西南大西洋公海渔场阿根廷滑柔鱼主要捕捞季节1—4月的栖息地变化情况,以期提升阿根廷滑柔鱼渔场的模型预测性能,增加阿根廷滑柔鱼的渔情预报的准确性。
1 材料与方法
1.1 材料
本研究中阿根廷滑柔鱼的捕捞数据来自上海海洋大学中国远洋渔业数据中心,时间尺度为月,空间分辨率为0.5°×0.5°,数据采集时间为2013—2017年。研究分析的阿根廷滑柔鱼渔场主要分布在41°~49°S、55°~61°W的阿根廷及马尔维纳斯群岛专属经济区外的公海海域。
环境数据为阿根廷滑柔鱼渔场水深50、100、200 m的海水温度数据,来自亚太数据研究中心(http://apdrc.soest.hawaii.edu/las_ofes/v6/dataset? catitem=71),时间尺度为月,单位为℃,空间分辨率为0.5°×0.5°。
1.2 方法
1.2.1 单因子的适宜性指数(suitability index,SI)模型的建立 采用2013—2016年数据进行模型的构建,并用2017年数据对模型进行验证。定义经纬度0.5°×0.5°为一个渔区,将作业天数定义为捕捞努力量,将每个渔区内的环境数据与渔业数据进行匹配。依据频率分布法,将不同深度的海水水温按照区间进行划分,将捕捞努力量作为计算适应性指数的指标[18-19],即假定在每一经纬度相对应的月份中最高捕捞努力量为西南大西洋阿根廷滑柔鱼资源分布最多的海域,SI值为1;捕捞努力量为0时,则认为是阿根廷滑柔鱼资源分布最少的区域,SI值为0[20-21]。根据指标建立SI模型,其计算公式为
SI=Eeffort/max(Eeffort)。
(1)
其中:Eeffort为指特定时间内不同水温区间的累计捕捞努力量(d);max(Eeffort)为指特定时间内不同水温区间累计捕捞努力量的最大值(d)。假设SI与水温的关系符合正态分布,将SI与不同深度的海水温度作为输入值进行拟合,其拟合公式为
SIT=exp[a(T-b)2]。
(2)
其中:a、b为应用最小二乘法估计的模型参数,使观测值与预测值的残差最小;T为不同深度的海水温度(℃);SIT为0~1。
1.2.2 综合HSI模型的构建 在已建立好的SI模型基础上,赋予不同水层水温以不同的权重(权重设置方案见表1)[22],综合50、100、200 m水深的SI模型建立HSI模型,HSI值计算公式为

表1 不同水层水温的不同权重方案Tab.1 Different scenarios for the weights of sea water temperature at different depths
HSI=k50 m×SI50 m+k100 m×SI100 m+k200 m×SI200 m。
(3)
其中:k50 m、k100 m、k200 m分别为50、100、200 m水深水温SI值的权重;SI50 m、SI100 m、SI200 m分别为50、100、200 m水深水温SI值。
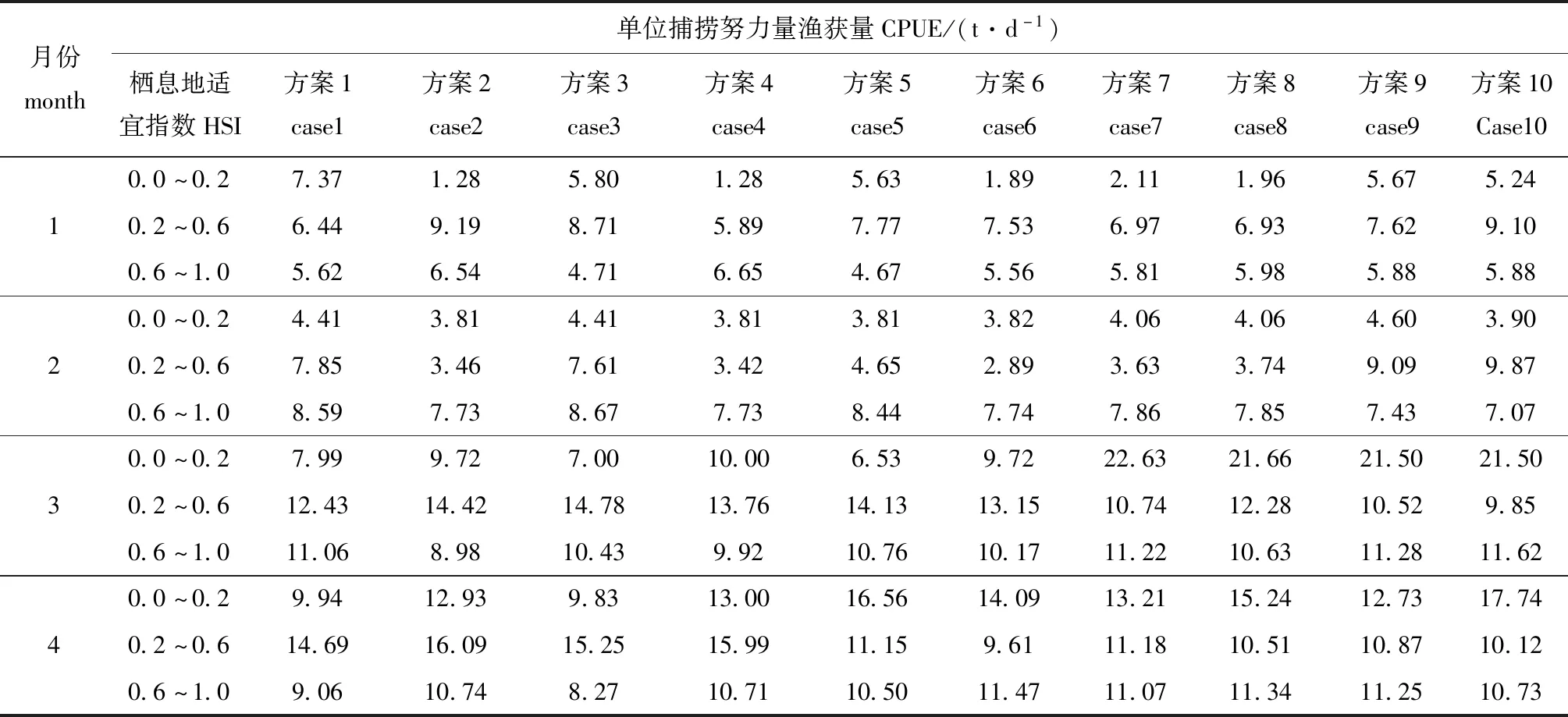
1.2.3 HSI最优模型的筛选 根据上述建立的不同权重下的HSI模型,分别计算2013—2016年1—4月的HSI值,其范围为0~1。将HSI≤0.2、0.2 CPUE=∑Ccatch/∑Eeffort。 (4) 其中:Ccatch为产量(t);Eeffort为捕捞努力量(d)。 在10种权重方案中,综合比较每个方案的产量、捕捞努力量所占比例和CPUE值,当HSI值为0.6~1.0时产量、捕捞努力量所占比例越高,模型预测性能就越好;当HSI值为0~0.2、0.2~0.6、0.6~1.0时的CPUE值呈递增趋势且HSI值为0.6~1.0时的CPUE值越高,模型预测性能越好,通过选取最优方案得到综合HSI模型。 1.2.4 模型验证 采用2017年数据对模型进行验证,将2017年数据带入综合HSI模型,计算3种类型栖息地的产量占比、捕捞努力量占比、CPUE值。基于得到的综合HSI模型,分别绘制2013—2016年1—4月份及2017年1—4月份的HSI空间分布图,并与捕捞努力量的分布叠加,验证模型的预测精度。 根据频率分布法及公式(1)、(2)进行拟合得到的拟合曲线如图1所示,计算得到1—4月不同水层的适应性指数模型公式如表2所示。 表2 SI模型拟合公式Tab.2 Fitting formula of SI models 图1 不同水层1—4月SI拟合曲线Fig.1 Fitted SI curves of water temperature at different depths from January to April 根据10种权重方案预测HSI模型得到的2013—2016年1—4月的产量、捕捞努力量、CPUE值如表3、表4所示。综合对比各个方案中HSI值为0.6~1.0时产量、捕捞努力量所占比例及CPUE值,结果表明,方案4为最优权重方案,即基于方案4权重的HSI模型为最优HSI模型,对应50、100、200 m的SI值权重比例为0.1∶0.1∶0.8,其中200 m水深水温所占比重最高。 表3 2013—2016年不同权重栖息地模型预测的HSI各区间内对应的产量和捕捞努力量比例Tab.3 Percentage of catch and effort under different HSI class interval sourced from different weighting model from 2013 to 2016 表4 2013—2016年不同权重栖息地模型预测的HSI各区间内对应的CPUE值Tab.4 CPUE under different HSI class intervals sourced from different weighting model from 2013 to 2016 使用2017年数据对综合HSI模型进行验证。将2017年的渔业数据与环境数据带入基于权重方案4的综合HSI模型,汇总不同HSI区间内的产量、捕捞努力量及CPUE值,结果如表5所示。从表5可见:1—4月在HSI值区间为0.6~1.0的产量与捕捞努力量比例均超过50%,2月与4月均超过90%;在2月与3月,CPUE值在HSI值区间为0~0.2、0.2~0.6、0.6~1.0时符合递增趋势。模型建立的2013—2016年(图2)与预测的2017年(图3)捕捞努力量大部分集中在HSI值高的区域。说明综合HSI模型可以较好地评估和预测西南大西洋阿根廷滑柔鱼的栖息地情况,且200 m水深水温SI值在模型中所占比重最大,说明该水深水温对阿根廷滑柔鱼栖息地的影响最大。 表5 2017年综合HSI模型预测结果Tab.5 Forecast results of comprehensive HSI model in 2017 图2 2013—2016年HSI及捕捞努力量空间分布图Fig.2 Spatial distribution of HSI and effort from 2013 to 2016 图3 2017年HSI及作业位置空间分布图(白色圆圈表示作业位置)Fig.3 Spatial distribution of HSI and fishing location in 2017(the white circle indicates the fishing location) 本研究中,基于2013—2016年的渔业数据与不同水层水温数据建立了综合HSI模型,并用2017年的数据对模型的预测精度进行了验证,根据HSI与捕捞努力量的空间分布图可知,综合HSI模型的构建与验证结果良好。HSI可用于描述物种与其栖息地的关系[25],基于不同环境因子建立的HSI模型已被广泛应用于渔场状况的探测及预报[26]。在捕捞努力量、产量、CPUE 3个指示渔业捕捞状况的因子中,捕捞努力量是更好的表征资源分布的指标[27-29],因此,本研究中将捕捞努力量数据作为计算初始SI值的渔业数据。使用捕捞努力量单一因子作为指标与综合两种或两种以上因子计算初始SI值相比[3,30],突出了捕捞渔船作业位置的重要性,但缺少了与产量的结合。本研究中在建立HSI综合模型时缺少产量因子的输入可能是导致结果中CPUE预测效果较差的原因之一。在综合HSI模型建立结果与2017年的预测结果中,以捕捞努力量作为指标时,2—4月的结果较好,适宜栖息地的捕捞努力量占比较高,且均在70%以上;1月结果较差,分布在适宜栖息地的捕捞努力量相对较低。其原因可能有3方面:一是,与2—4月相比,1月的总捕捞努力量较少;二是,在捕捞季节开始时,捕捞努力量较分散;三是,1月是阿根廷滑柔鱼的栖息水层从浅水层向深水层转移的过渡时期[9]等。 在本研究的HSI分布图(图2和图3)中,除本研究区域即西南大西洋公海渔场外,马尔维纳斯群岛专属经济区内的HSI值也相对较高。这表明,马尔维纳斯群岛周围海域的环境可能也对阿根廷滑柔鱼渔场的形成有利,但由于缺少海域内的相关渔业数据,故难以对结果进行验证。分析并验证马尔维纳斯群岛周围海域渔场形成与渔业资源的关系可能会使本研究结果更科学。 海表面温度、叶绿素a浓度、海表面高度等常被用作构建HSI模型的环境因子,但包括阿根廷滑柔鱼在内的大部分海洋生物在整个生命周期中会进行水平洄游和昼夜垂直洄游,并栖息于不同的水层[8, 31],而基于表层环境因子的HSI模型难以准确描述栖息环境与生物间的关系。本研究中,根据阿根廷滑柔鱼栖息的水层[9]与其他学者研究的结果[10],选择50、100、200 m 3个不同水层的水温作为构建模型的环境因子,探究了不同水层水温对阿根廷滑柔鱼渔场及资源的影响。在影响阿根廷滑柔鱼渔场的表层环境因子中,海表面温度及海表面高度等因子对阿根廷滑柔鱼资源的影响同样重要,通常可以作为寻找中心渔场的指标[3-4,7]。在本研究中综合HSI模型建立中,若在模型中加入其他重要的表层环境因子可能会得到更科学的研究结果。在以往关于阿根廷滑柔鱼的研究中,将表层环境因子与不同水层水温相结合探究其对物种影响的研究较少,但在将HSI模型应用于同为大洋性头足类柔鱼Ommastrephesbartrammi的研究中,采用1999—2004年8—10月的海表面温度、海表面盐度、海表面高度异常和叶绿素a浓度4种表层环境因子建立模型后, 2005年基于捕捞努力量的预测结果表明,HSI≥0.6的区域面积占渔场总面积的65.17%[32];在相同的时间,基于海表面温度、0~50 m水温垂直结构、200 m水深水温和300 m水深水温建立的HSI模型基于捕捞努力量的预测结果为82.5%[17]。这表明,在模型中加入不同水层水温相较于仅有表层环境因子的模拟结果更准确。本研究中,除1月预测结果较差外,2—4月基于捕捞努力量的预测结果均高于70%,且2月与4月高于90%,表明预测结果良好。因此,今后应基于阿根廷滑柔鱼个体建立动力学模型,模拟其完整生命周期并研究其在不同生命阶段对其影响较大的环境因子,或将最大熵模型[7]与HSI模型结合,采用最大熵模型筛选出用于构建HSI模型的关键环境因子,可能会使得到的综合HSI模型能更好地描述栖息地环境与生物的关系。 阿根廷滑柔鱼是具有垂直洄游行为的大洋性经济头足类[8],水温垂直结构会对其资源量与渔场分布产生影响。水温垂直结构一般包括不同水层温度与水层深度[17],因此,在研究水温垂直结构对渔业资源的影响时,常用不同水层水温差值与深度差值的比值(水温梯度为△T/△D)表示水温垂直结构的变化[17,33-34]。本研究中,基于不同水层温度建立了综合HSI模型,主要是研究温度对渔场形成的影响,因此,在模型中虽未考虑水层深度,但如果将水温梯度作为环境因子加入综合HSI模型的建立中,可能会得到更科学的结果。本研究表明,在50、100、200 m水深水温中,200 m水深水温对阿根廷滑柔鱼栖息地的影响最为重要。阿根廷滑柔鱼渔场分布与200 m水深的重要关系可能与温跃层有关[35],对西南大西洋阿根廷北部的巴塔哥尼亚海湾的研究表明,春季和秋季温跃层的形成、破裂及随后的空间异质性对海洋生物的影响明显[36]。若渔业资源栖息在温跃层以上,则其较难穿过温跃层进入较深的水层,从而容易在温跃层以上形成渔场;若栖息在温跃层以下,通过灯光等诱捕手段较难使渔业资源穿过温跃层上浮,可能会导致渔获量降低[37]。因此,温跃层上下界深度作为水温垂直结构对渔场的形成有重要影响。目前,对于在西南大西洋阿根廷滑柔鱼公海渔场区域内温跃层位置的季节变化与年际变化研究较少,对于温跃层位置与200 m水深的关系还需进一步探究。此外,阿根廷滑柔鱼饵料生物的分布也可能与其栖息水层及水层温度有关。阿根廷滑柔鱼渔场分布与温跃层及饵料生物的关系还需进一步探究。 阿根廷滑柔鱼渔场分布在马尔维纳斯寒流与巴西暖流的寒暖流交汇处[10],寒暖流交汇会形成温度线锋,不同水深的线锋位置也是水温垂直结构的一部分[38]。温度线锋及周围形成的涡旋会使周围渔业资源的密集度较高[39]。本研究中主要研究了不同水层海水温度对阿根廷滑柔鱼渔场的影响并基于水层温度建立HSI模型,未考虑不同水层温度线锋位置变化对模型及渔场的影响,包括HSI模型中若考虑温度线锋等其他因素与不同水层温度的综合影响,可能会得到更科学的结果。因此,研究阿根廷滑柔鱼栖息地对不同水层温度变化的响应及其之间的协同变动关系,可以为该种类资源的合理开发和管理提供科学支撑。 1)基于不同水层海水温度建立的HSI模型可以精确描述并预测西南大西洋公海渔场阿根廷滑柔鱼的渔场分布。 2)根据综合HSI模型的筛选结果,在50、100、200 m 3个水层中,200 m水深海水温度对阿根廷滑柔鱼渔场的影响最大。2 结果与分析
2.1 综合HSI模型建立
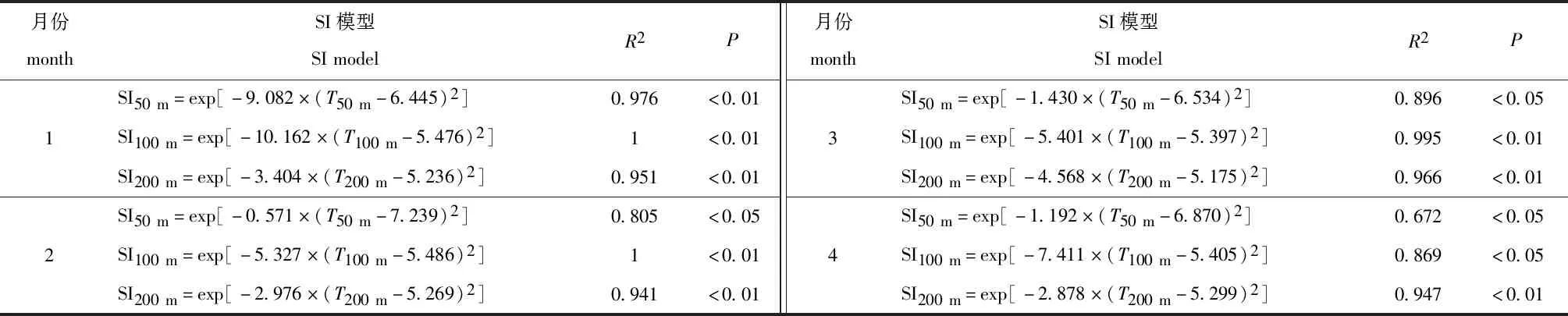


2.2 综合HSI模型的验证



3 讨论
3.1 综合HSI模型的建立
3.2 HSI模型中环境因子的选取
3.3 水温垂直结构对渔业资源的影响
4 结论

