CG-01高速风洞弹箭模型动稳定性导数实验系统设计

薛栋，刘金，王欢，尹晋涛，江春茂，袁先士

(1.西安现代控制技术研究所，陕西 西安 710065；2.中国航天空气动力技术研究院，北京 100074)

0 引言

动稳定性导数(简称动导数)是飞行器气动力/力矩系数对无量纲旋转角速度或姿态角变化率的导数，是飞机、导弹等飞行器设计导航系统和控制系统以及对飞行器进行动态品质分析所必需的重要原始数据[1-2]。以往，高机动性战斗机等军用航空飞行器对动导数实验需求较多，要求也更高，而弹箭类兵器对动导数实验需求较少，一般采用工程经验公式给出估算值。近年来，随着弹箭兵器向着精确制导化、高度智能化、打击远程化方向发展，新一代弹箭兵器的气动设计对动稳定特性的精确预测也提出了较高的要求[3-4]。

由于军事用途和作战形式的差异，相比于飞机类航空飞行器，弹箭兵器具有以下独特的气动特性：

1)弹箭兵器多采用旋转飞行方案。制导炮弹、远程火箭弹、高速动能弹、末敏子弹等弹箭兵器通过绕自身纵轴旋转，使其可用一个控制通道完成俯仰和偏航方向控制，而且旋转飞行还可消除推力偏心、质量偏心、气动偏心等不利影响，可提高弹箭兵器射击精度，减少弹丸空间散布[5-6]。旋转模型动导数参数如何预测，旋转弹动稳定性与不旋转弹有多大差异，成为旋转弹箭兵器动态气动特性评估需要解决的重要问题之一。

2)弹箭兵器多数具有较大的长细比。防空导弹、简易制导火箭、潜射导弹等，多为小口径、细长体外形。这类飞行器进行俯仰动导数风洞实验时模型弹尾尺寸较小，模型俯仰振动过程中尾部易与支杆发生接触，因此需研制新型的俯仰振动实验装置以解决此类模型难以开展俯仰动导数实验的难题。

3)弹箭兵器飞行速域跨度较大。弹箭兵器从发射、助推、平飞、攻击各个阶段，覆盖亚声速、跨声速、超声速，甚至达到高超声速，飞行马赫数跨度较大，这对弹箭动导数实验机构提出了更高的要求，进行高速风洞实验时运动机构要能承担高马赫数下的冲击载荷，机构运动要可靠稳定，信号干扰小。

4)弹箭兵器通常具有较小气动阻尼力矩。由于弹箭兵器升力面和操纵面一般较小，相应的气动阻尼力矩也较小，这对动导数测量系统提出了很大的挑战。需要精心匹配动态天平载荷、减少实验装置体积、降低非接触干扰、合理设计滤波方式等，通过多种手段提高测量精准度，降低动态实验不确定度。

风洞实验是获取动导数参数的重要手段之一。针对弹箭兵器气动特点以及项目研发需求，专门为CG-01高速风洞研制了一套动导数实验系统，该系统包含3个不同的实验装置(中小长细比(L/d<15，L为弹长，d为弹径)模型实验装置、大长细比(L/d≥15)模型俯仰振动实验装置和旋转弹模型实验装置)、控制子系统、数据采集子系统和数据处理子系统。

1 系统结构及原理分析

1.1 实验装置

实验装置是动导数系统最为关键的组成部分，主要由激励系统、运动转换机构、测量装置等组成。

1.1.1 中小长细比模型实验装置

中小长细比模型实验装置采用强迫振动法在某一自由度下模拟飞行器刚体运动模态，实现模型滚转、俯仰和偏航运动。滚转振动装置如图1所示，电机经减速器和联轴器驱动偏心轴转动，偏心轴驱动摆动筒带动传动轴绕中心轴线滚转振动，五分量测力天平和角位移测量元件分别测量运动过程中的动态载荷和滚转振动角位移。俯仰和偏航振动实验装置结构原理相同，如图2所示，传动轴一端设计有偏心凸轮，将电机的连续旋转运动转化为往复运动，驱动天平和模型简谐振动。

图1 滚转振动实验装置

图2 俯仰/偏航振动实验装置

1.1.2 大长细比模型俯仰振动实验装置

高速风洞俯仰振动实验装置其运动转换机构通常布置在模型内部[7-11]，模型相对固定支杆存在相对运动，这就要求模型尾部与支杆之间要预留足够的间隙，模型长细比越大，其间隙就越大，常规俯仰振动实验装置(如图 2所示)不太适用于小口径、细长体模型实验。为此采用尾部强迫振动方式，将运动转换机构设计于支杆尾部，激励系统驱动模型和支杆作为整体俯仰振动，支杆和模型之间不存在相对运动，如此可最大限度的减少模型内壁与支杆之间的间隙。以600 mm弹长的模型、20 mm杆径的天平计算，常规俯仰振动实验装置至少需保证40 mm的弹径，而尾振动方式弹径可减少至26 mm，即模型长细比可由15提升至23.

大长细比模型俯仰振动实验装置(简称尾振动装置)如图3所示。通过偏心轴带动滑块沿弧形滑轨上下往复运动，从而带动支杆和模型实现俯仰振动。在设计天平、支杆和模型的尺寸时综合考虑，保证天平的校准中心和模型的质心位于弧形滑轨的圆心处，即确保动导数实验天平校心、模型质心、俯仰转心三心重合，以减少实验过程中的惯性力，同时避免力矩转换带来数据修正误差，从而提高实验数据质量。

动导数计算需要获取力信号和角位移信号之间的相位差，因此角位移的精确测量至关重要。相比于常规的天平-弹性铰链动导数装置，尾振动装置角位移测量元件设计于支杆尾端，外形如图4所示，通过惠斯通电桥实现角位移→拉/压应变→电压的物理信号转变。图5所示为无风状态下测量的俯仰力矩Mz与角位移θ，Mz与θ具有较高的同步测量精度，相位差小于0.2°，曲线符合标准的正弦变化规律。

图4 角位移测量元件

图5 俯仰力矩Mz与角位移θ时序图

1.1.3 旋转弹模型实验装置

当前，国内各大风洞建立和运行的均为模型单自由度运动的动导数实验系统，关于模型旋转状态下动导数的实验测量以及旋转对动导数的影响至今鲜有研究报道。目前旋转弹气动评估的惯常做法仍然是通过计算流体力学(CFD)模拟或风洞实验给出不旋转模型的定常气动参数和动导数，以此建立气动数据库，作为旋转弹静态和动态气动性能评估的依据[5, 8-11]。为了在风洞中模拟旋转弹真实运动状态，测量旋转条件下的动导数，研制了针对旋转弹的动导数实验装置。

旋转弹动导数实验装置是在中小长细比模型动导数实验装置的基础上增加强迫模型旋转的驱动装置，从而实现模型自旋与往复振动的耦合。旋转模型及驱动装置如图6所示，主要由旋转弹模型、驱动装置和天平保护锥套构成。旋转弹模型进行不同自由度实验时，仅需将旋转模型及驱动装置装配于图1或图2所示的实验装置上即可实现“滚转振动+自旋”、“偏航振动+自旋”和“俯仰振动+自旋”的耦合运动。旋转弹模型动导数实验流程如图7所示，通过高速风洞实验测试，旋转弹模型实验装置在低马赫数下模型自旋频率能够达到16 Hz，受限于电机扭矩以及滚转阻尼作用，该装置目前具备开展中低转速、低马赫数下的动导数实验。

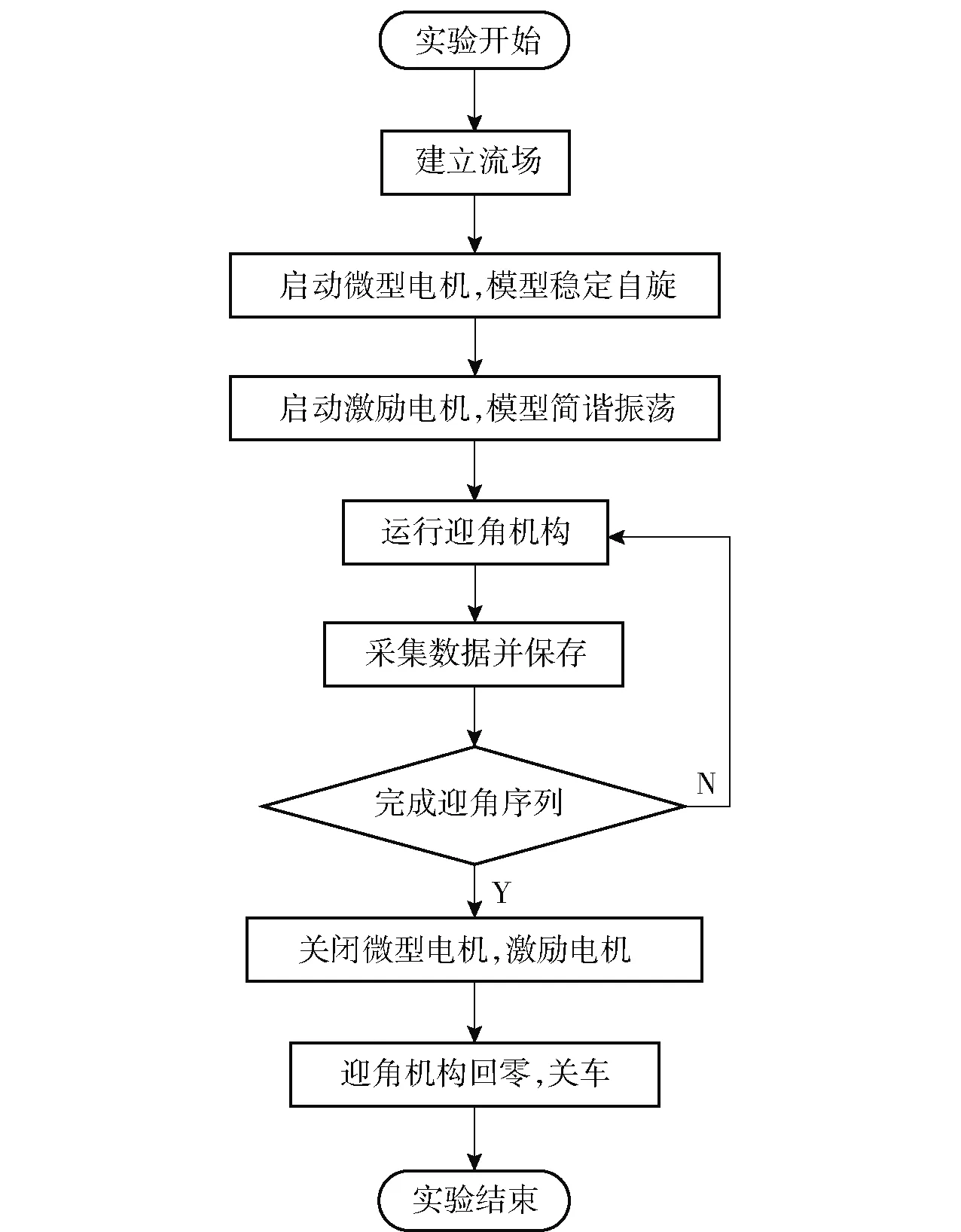
图7 旋转弹模型动导数实验流程图

1.2 控制系统

控制系统以德国Beckhoff的EtherCAT现场总线技术为核心，通过EtherNet工业以太网实现主控计算机与嵌入式PC双向通讯，通过BK系列总线耦合器实现嵌入式PC与伺服控制器之间的连接。现场控制单元是Beckhoff嵌入式PC可编程控制器CX9020和过程接口单元(I/O模块)，执行单元是伺服驱动器和伺服电机。控制系统组成图如图 8所示。

图8 控制系统组成

1.3 数据采集系统

数据采集系统采用美国NI公司的基于PXIe总线的模块化仪器，通过PXIe-4331应变采集板卡实现天平力和振动角位移的信号采集，该系统具有高可靠性、易用性和灵活性等特点。

数据采集和分析软件采用Labview软件进行开发。Labview能够高效地与PXIe/PXI硬件兼容使用，适用于数据采集及仪器控制。动导数数据采集与分析软件主界面如图9所示，该软件具备参数设置、信号滤波、信号采集与记录、图像实时显示等功能。

图9 数据采集与分析软件主界面

1.4 数据处理系统

实验数据处理系统的功能是将数据采集系统采集的动态天平力和角位移信号进行数据处理，通过数字滤波、互相关等数学方法获得模型简谐运动过程中的动态力、力矩和角位移等物理量，最终获得组合导数、交叉导数和交叉耦合导数等参数。整个实验数据处理的流程如图10所示。风洞吹风过程中获得的动导数包含了气动阻尼导数和机械阻尼导数，应在吹风前或吹风后测量机械阻尼导数，总阻尼导数扣除机械阻尼导数获得所需的气动阻尼导数。

图10 实验数据处理流程

2 系统实验及结果分析

2.1 Basic Finner模型

为验证动导数实验系统的正确性和适用性，需进行标模实验。最为广泛使用的弹箭标模为Basic Finner模型，该标模最早是作为炮弹、炸弹和制导兵器的风洞和弹道靶实验模型，后来逐步发展成为弹箭气动力静态实验、动导实验和旋转特性实验等风洞实验标准模型[12-13]。

Basic Finner模型基本型为一个尖锥形头部、圆柱形弹身并带有4个矩形尾翼的外形，如图11所示，图中所标尺寸为无量纲尺寸，参考长度为弹径，CG为质心位置。

图11 Basic Finner外形图

2.2 CG-01高速风洞

动导数标模实验在兵器203所CG-01高速风洞中进行。该风洞是一座直流暂冲式亚声速、跨声速、超声速三声速风洞，实验段截面尺寸为0.6 m×0.6 m，实验迎角α范围-10°～25°，该风洞具有较宽的马赫数模拟范围(Ma为0.3～4.0)、较高的马赫数控制精度(0.4≤Ma≤1.0，σMa≤0.002，σMa为马赫数均方根误差; 1.0

2.3 中小长细比模型实验结果

中小长细比模型在CG-01高速风洞进行了滚转、偏航和俯仰动导数实验，中小长细比动导数模型长细比为1∶10，弹径d为40 mm.马赫数分别为0.6、0.9、1.2和2.0，迎角分别为0°、5°和10°，每一个马赫数进行了3次重复性实验以考察实验系统测量精度。滚转动导数实验振动频率为12 Hz，振幅为3°左右；俯仰/偏航振动频率为10 Hz，振幅为1°左右。每个状态点采样时间为4 s，采集频率5 000 Hz，低通滤波截止频率30 Hz.

图12中3张图分别展示了滚转振动过程中滚转力矩Mx与滚转振动角γ时序图、Mx频谱图和迟滞环，实验状态Ma=1.2、α=0°.由于气动阻尼的存在，滚转振动角位移与滚转力矩之间存在一定的相位差，图12中根据滚转力矩识别出来的主频与机构振动频率非常接近，滚转振动迟滞环为逆时针旋转，阻尼导数为负，起正阻尼作用，滚转方向运动是动态稳定的。图13和图14分别为偏航方向和俯仰方向动导数实验测量结果。

图12 滚转动导数实验中Basic Finner模型滚转力矩Mx与滚转振动角位移γ变化规律

图13 偏航动导数实验中Basic Finner模型偏航力矩My与偏航振动角位移ψ变化规律

图14 俯仰动导数实验中Basic Finner模型俯仰力矩Mz与俯仰振动角位移θ变化规律

在迎角较小的情况下，Basic Finner模型气动力矩的迟滞效应主要是由于4片尾舵在模型运动过程中诱导的当地气动角度不同所致。以俯仰振动为例，俯仰力矩的迟滞主要来自于2片水平尾舵上诱导迎角的变化。在模型上仰和下俯过程中，水平尾舵分别受到气流上洗和下洗的诱导作用，上仰运动过程中的实际有效迎角比瞬时迎角大，而下俯运动与上仰运动正好相反，从而在整个俯仰振动过程中Mz-θ图像呈现出具有一定环幅的迟滞环[8, 14-16]。

表1给出了3次重复性动导数实验测量的滚转、偏航和俯仰阻尼导数最大相对偏差，最大相对偏差定义为3次实验数据中偏离平均值最大的量占平均值的比例，最大相对偏差的大小能够直接反映出动导数实验系统测量结果的精度水平。从表1中数据可知，滚转动导数测量精度较高，偏航和俯仰方向次之。不同迎角和马赫数下，精度指标波动较大，精度水平随马赫数和迎角未展现出较为明显的规律变化。

表1 不同马赫数和迎角下3次重复性实验力矩阻尼导数最大相对偏差

图15 滚转阻尼导数数据对比(α=0°)

图16 俯仰阻尼导数数据对比(α=0°)

2.4 大长细比模型实验结果

大长细比模型在CG-01高速风洞中进行了俯仰动导数实验，大长细比动导数模型采用加长的Basic Finner模型，弹翼和弹头尺寸相对弹径的比例不变，将弹身尺寸增长，全弹长细比增大至1∶15，弹径设计为35 mm.俯仰振动频率为8 Hz，振幅1°左右。

考虑到大长细比模型动导数实验采用尾部强迫振动的方式，技术成熟度较低，仅在Ma=0.6条件下进行了实验，迎角分别为0°和5°，表 2给出了3次重复性实验俯仰阻尼导数的数值。从表中2数据可以看出，0°迎角的实验精度要比5°迎角的高，俯仰阻尼导数随迎角有增大的趋势。

表2 大长细比模型3次重复性实验俯仰阻尼导数

2.5 旋转弹模型实验结果

旋转弹模型在CG-01高速风洞中进行了俯仰动导数实验，旋转弹模型仍为标准的Basic Finner标模，由于模型内部布置有旋转驱动装置，模型弹径为55 mm.俯仰振动频率8 Hz，模型低速自转频率为6 Hz.

考虑到旋转弹实验装置系首次进行高速风洞实验，而且模型内部结构和运动形式较为复杂，气动载荷较大，仅在Ma=0.6条件下进行了实验，第1次实验迎角只进行了0°，第2次到第4次实验迎角增大到5°.表 3给出了4次重复性实验俯仰阻尼导数的数值，俯仰阻尼导数随迎角有增大的趋势。

表3 旋转弹模型4次重复性实验俯仰阻尼导数

2.6 实验结果不确定度讨论

动导数实验由于复杂的运动机构和流场的非定常特性，实验数据的不确定度要普遍高于静态实验。不确定度是对实验数据可信度的评价，其基本内容是实验数据的精度和准度。

实验结果的精度反映了同一实验系统多次重复性测量的离散水平，是衡量一个实验系统最基本也是最重要的性能指标[7-9]。Basic Finner标模的滚转、偏航和俯仰重复性实验结果表明：实验数据精度最好的是滚转动导数，其最大相对偏差在5%以内；偏航方向和俯仰方向次之，其最大偏差在10%左右。这样的精度水平目前是足以满足工程型号项目对动导数实验的要求[7-9]。

实验结果的准度反映了实验系统测量数据与真实值的偏差。由于雷诺数、减缩频率、模型支撑方式和风洞干扰形式的不同，不同风洞实验结果对比会出现一定程度的差异，在个别马赫数和迎角下有时差异还很大，这些由于实验系统误差造成的数据结果的差异是正常合理的，不同风洞实验数据的对比仅能作为一种相互验证的手段。

3 结论

针对弹箭模型气动特点，在CG-01高速风洞建立了中小长细比模型、大长细比模型和旋转弹模型动导数实验系统，特别是对旋转弹和大长细比弹箭模型的动导数实验装置以及实验方法进行了有益的探索和尝试。得到主要结论如下：

1)采用传统强迫振动方法的中小长细比模型动导数实验系统，无论实验精度、准度方面均有一定的保证，可满足常规弹箭兵器对于动稳定性实验的需求。

2)研制的针对小口径、细长体模型的俯仰动导数实验装置，采用尾部强迫振动方式解决了高速风洞模型缩比后弹体内径过小造成的模型安装布置困难，建立了大长细比模型动导数实验能力，后续正在开展更高马赫数和迎角下的验证实验。

3)研制的针对旋转弹模型的动导数实验装置，实现了模型自旋与往复振动的耦合，可开展旋转运动状态下动导数测量实验，后续计划开展旋转运动与不旋转对比实验，以及旋转运动对模型动导数参数影响特性的研究工作。

参考文献(References)

[1] 李周复.风洞实验手册[M].北京: 航空工业出版社, 2015.

LI Z F.Handbook of wind tunnel test[M].Beijing: Aviation Industry Press, 2015.(in Chinese)

[2] 李周复.风洞特种试验技术[M].北京: 航空工业出版社, 2010.

LI Z F.Wind tunnel special test techniques[M].Beijing: Aviation Industry Press, 2015.(in Chinese)

[3] 唐志共, 许晓斌, 杨彦广, 等.高超声速风洞气动力实验技术进展[J].航空学报, 2015, 36(1): 86-97.

TANG Z G, XU X B, YANG Y G, et al.Research progress on hypersonic wind tunnel aerodynamic testing techniques[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 86-97.(in Chinese)

[4] 程厚梅.风洞实验干扰与修正[M].北京: 国防工业出版社, 2003.

CHENG H M.Interference and correction on wind tunnel testing[M].Beijing: National Defense Industry Press, 2003.(in Chinese)

[5] 徐文熙, 吴甲生.大长径比旋转弹俯仰动导数风洞实验技术[J].北京理工大学学报(自然科学版), 1989, 34(2):63-67.

XU W X, WU J S.Wind tunnel experimental technique for the pitching dynamic derivative of a spinning projectile having high fineness ratio[J].Transactions of Beijing Institute of Technology, 1989, 34(2):63-67.(in Chinese)

[6] 刘周, 谢立军, 杨云军, 等.弹丸旋转空气动力效应非定常数值模拟[J].航空学报, 2016, 37(5):1401-1410.

LIU Z, XIE L J, YANG Y J, et al.Unsteady numerical simulation of aerodynamics effect of a spinning projectile[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(5):1401-1410.(in Chinese)

[7] 潘金柱, 张杰, 才义, 等.高速风洞动导数试验精准度提升研究[J].空气动力学学报, 2016, 34(5):606-610.

PAN J Z, ZHANG J, CAI Y, et al.Investigation on the high-speed wind tunnel dynamic derivative test accuracy promotion[J].Acta Aerodynamica Sinica, 2016, 34(5):606-610.(in Chinese)

[8] 卜忱, 杜希奇, 王学俭.飞行器纵向阻尼动导数直接测量实验研究[J].实验流体力学, 2005,19(1): 31-34.

BU C, DU X Q, WANG X J.Investigation of longitudinal damping derivative of aircraft by direct measurement tests[J].Journal of Experiments in Fluid Mechanics, 2005, 19(1): 31-34.(in Chinese)

[9] 赵忠良, 任斌, 黄叙辉, 等.跨超、高超声速风洞模型动导数实验技术研究[J].航空学报, 2000, 21(1):52-55.

ZHAO Z L, REN B, HUANG X H, et al.Investigation on model dynamic stability derivatives test techniques in trans-, super-, hypersonic wind tunnels[J].Acta Aeronautica et Astronautica Sinica, 2000, 21(1):52-55.(in Chinese)

[10] 杜希奇, 卜忱, 于彦泽, 等.低速风洞旋转流场下滚转振荡动导数实验技术研究[J].实验流体力学, 2005, 19(4):46-48,55.

DU X Q, BU C, YU Y Z, et al.Investigation of roll oscillation dynamical stability derivative in rotation flow field[J].Journal of Experiments in Fluid Mechanics, 2005, 19(4):46-48, 55.(in Chinese)

[11] 陶福兴, 赵养正, 程玉庆, 等.CG-01风洞直接阻尼导数试验技术[J].弹箭与制导学报, 2008, 28(6):193-196.

TAO F X, ZHAO Y Z, CHENG Y Q, et al.Technique of direct damping derivative measurement in CG-01 wind tunnel[J].Journal of Projectiles, Rockets, Missiles and Guidance, 2008, 28(6):193-196.(in Chinese)

[12] XI K, YAN C, HUANG Y.Coupled CFD/RBD modeling for a Basic Finner projectile with control[J].Acta Aerodynamica Sinica, 2016, 34(2):182-189.

[13] MAKEICH G S，KRYUKOV I A.Aerodynamics and flight dynamics simulation of Basic Finner supersonic flight in aeroballistic experiment[J].Journal of Physics: Conference Series, 2018, 1009:012009-.

[14] 席柯, 阎超, 黄宇.俯仰阻尼导数分量的CFD数值模拟[J].北京航空航天大学学报, 2015, 41(2): 222-227.

XI K, YAN C, HUANG Y, et al.Numerical simulation of individual components of pitch-damping coefficient sum[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(2): 222-227.(in Chinese)

[15] 周瑞兴, 上官云信, 高永卫, 等.导弹高速动态空气动力特性[J].应用力学学报, 2002, 19(1): 31-34.

ZHOU R X, SHANGGUAN Y X, GAO Y W, et al.High speed dynamic aerodynamical characteristics of missiles[J].Chinese Journal of Applied Mechanics, 2002, 19(1): 31-34.(in Chinese)

[16] 赵养正, 蒋胜矩, 党明利, 等.旋转弹体及减旋片滚转阻尼数值模拟[J].兵工学报, 2015, 36(7):1176-1180.

ZHAO Y Z, JIANG S J, DANG M L, et al.Roll damping simulation of missile body and anti-rotation flaps[J].Acta Armamentarii, 2015, 36(7):1176-1180.(in Chinese)

[17] PARK S H，KIM Y，KWON J H.Prediction of damping coefficients using the unsteady Euler equations[J].Journal of Spacecraft and Rockets, 2003, 40(3):356-362.

[18] BHAGWANDIN V A，SAHU J.Numerical prediction of pitch damping stability derivatives for finned projectiles[J].Journal of Spacecraft & Rockets, 2011, 51(5):1603-1618.