噪声环境下基于蒲丰距离的依概率多峰优化算法
王 霞 王耀民 施心陵 高 莲 李 鹏
实际优化问题往往存在着多个全局最优解及其他有价值的局部最优解,我们不仅需要找到全局最优解,还需要找到局部最优解进行辅助决策,这类优化问题称为多峰搜索(Multi-peak searching)或多峰优化(Multimodal optimization) 问题[1].此外,实际优化问题总是受到各种随机噪声的影响.在噪声环境下求解多峰优化问题不仅要求算法能在噪声干扰下寻找真实的极值点位置,而且希望算法能提供备选的多个优化方案.噪声的分布往往符合一定的概率关系,因此噪声环境下的多峰优化问题是一个依概率求解极值点的问题.其中包含的噪声环境下的寻优问题[2](Noisy optimization)和多峰优化问题在科学和工程领域中有理论和实际意义.噪声优化算法的研究可以为机器人[3−5]、智能控制与决策[6−9]、信号识别与测量[10−11]、智能制造[12]等存在噪声干扰的工程优化问题提供优化解决方案.
在噪声优化算法的依概率问题研究方面,一些学者研究了噪声优化算法的概率模型,如Nakama[13]和李军华等[14]研究了噪声环境下遗传算法的 Markov模型.Ma 等[15]使用Markov 模型分析了噪声对生物地理优化算法(Biogeography-based optimization,BBO)的影响.Beyer 等[16]对自适应进化策略(Self-adaptive evolution strategy,ES)的鲁棒优化模型进行了稳态分析.但是算法求解优化结果的依概率关系尚无相关研究.也有一些学者在研究中涉及到了优化算法的依概率问题,但都是针对无噪声环境下的优化算法,例如蚁群优化算法[17](Ant colony optimization,ACO)基于信息素指导依概率为子代个体构建解,从而将信息素的分布理解为一种特殊的概率分布.李宝磊等[18]证明了所提出的多元优化算法以概率1 收敛于全局最优解.董易等[19]证明了所提出的斐波那契树优化算法以概率1 收敛于全局最优解.针对噪声环境下多峰优化算法的依概率问题尚缺乏相关研究.对于噪声优化算法的依概率特性研究非常重要,它可以评估算法搜索优化问题全部极值点的能力,衡量算法的优化效率,同时为算法性能的改进和提升指明方向.
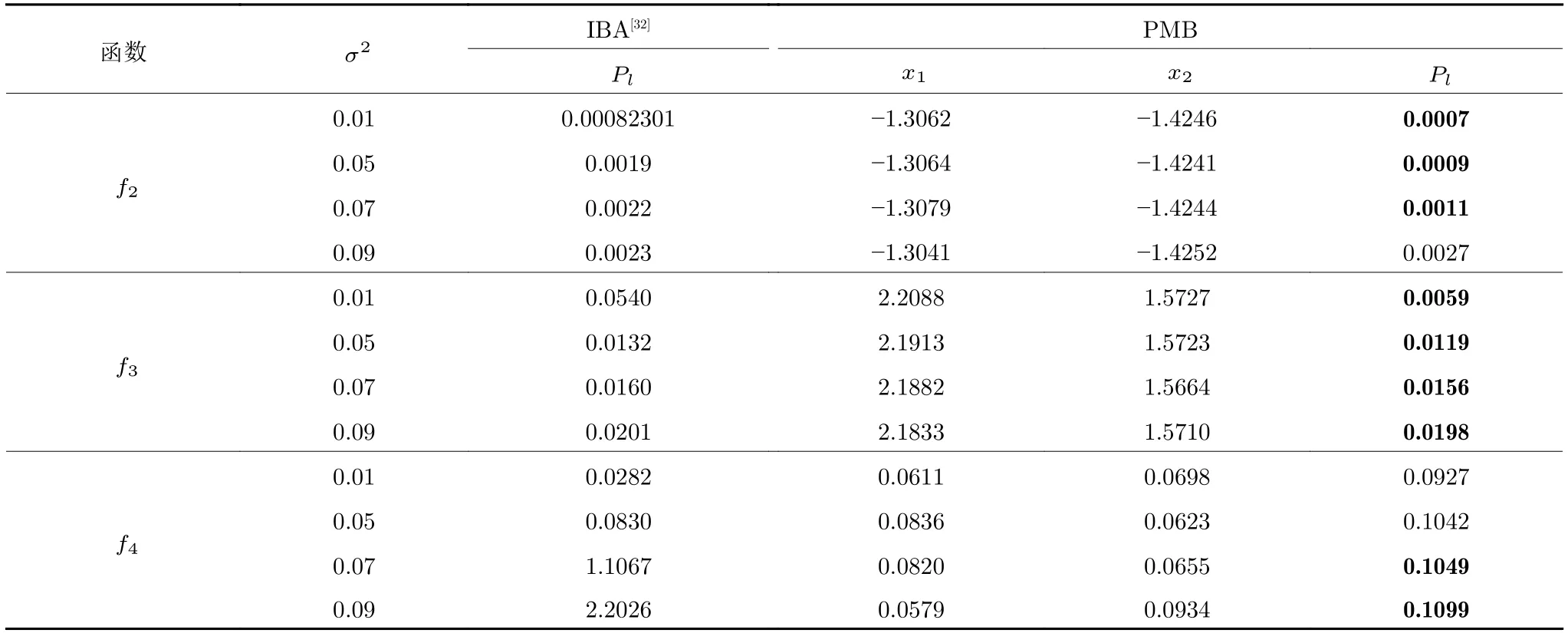
在噪声环境下多极值点寻优问题的研究方面,元启发式算法作为解决确定性优化问题的一种主流方法,其在噪声环境中的优化性能受到了越来越多的关注.李军华、黎明等[14,20−22]分析了噪声对遗传算法的影响以及正态随机噪声对适应度评价的影响机理,提出了多次评价一次采样的动态适应度评价方法.许多学者通过将假设检验(Hypothesis test,HT)、最优计算量分配(Optimal computing budget allocation,OCBA)技术、反向学习法、自动学习机(Learning automata,LAs)、重采样、聚类算法、加权搜索中心等多种策略引入粒子群优化算法(Particle swarm optimization,PSO)中[23−29],以提高算法的鲁棒性.这些优化算法能够在噪声环境中找到接近全局最优的极值点,但都没有求解其他极值点.在多峰优化问题的研究中,许多多峰函数优化算法[1,30−31]能搜索到多峰函数的多个极值点.但大部分算法只针对确定性环境,并未考虑噪声环境下的多峰优化问题.Jamil 等[32]对蝙蝠算法(Bat algorithm)进行了改进,使其适用于无噪声环境和有噪声环境,将其应用到多峰函数优化问题中,可以找到多峰函数的多个全局极值点.然而遗憾的是,文中并未讨论多个局部极值点的情况,且极值点的坐标并未明确给出.尽可能多的搜索局部极值点能为生产实际提供更多样化的优化方案.此外,为了提供明确的优化方案,实验结果应给出极值点的适应度值和对应的解,以便为实际应用提供明确的决策变量[33].
蒲丰投针问题是一个几何概率问题.它是法国科学家蒲丰(Buffon)在1777 年的论著 《或然性算术试验》 中提出的.蒲丰投针原理反映了几何概率的特征及处理方法,衍生出了蒙特卡洛(Monte-Carlo)方法.其概率规律在探矿、近似计算中得到广泛应用,但在优化算法中的应用尚无相关研究.在噪声环境中通过随机方式探索多峰函数的极值点与蒲丰投针问题具有相似的概率解释.本文将蒲丰推导得到的定概率原理应用于噪声环境下的多极值点寻优问题,从概率的角度出发,提出了噪声环境下基于蒲丰距离的依概率多峰优化算法(Probabilistic multimodal optimization algorithm based on the Button distance,PMB),推导证明了蒲丰距离和极值分辨度共同依概率决定算法的峰值检测率.依据蒲丰距离划分全局搜索空间,并在局部范围内利用改进的斐波那契法进行局部寻优,针对多维函数,采取多级划分策略,从而提高求解精度和算法效率.通过算法依概率收敛特性实验,验证了PMB算法在噪声环境下能够依固定概率找到多个极值点;通过设置不同的噪声强度与蒲丰距离进行实验,分析了噪声强度与蒲丰距离对算法求解结果的影响;通过对比噪声环境下的改进蝙蝠算法,表明了PMB 算法具有很好的多极值点寻优特性和定位精准性;通过对比PSO 算法在多维函数上的表现,证明了PMB 算法在噪声环境下对多维函数寻优的有效性.
第1 节对噪声环境下的多峰优化问题进行数学描述,并说明评价指标.第2 节详细描述了本文提出的PMB算法的基本原理和理论推导.第3 节是论文的仿真实验与结果分析,用以验证算法的有效性.第4 节给出结论和将来的研究方向.
1 问题描述及评价指标
1.1 问题描述
在受到加性噪声干扰的情况下,多峰函数的适应度值可描述为:
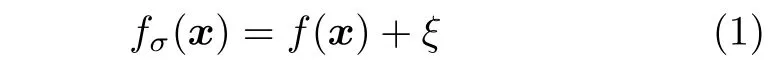
式中,fσ(x) 是受到噪声干扰后的函数值,f(x) 是未受噪声干扰的函数值.设 R 为实数集,S⊆R 称为搜索空间,即变量的可行解范围,x=(x1,x2,···,xd)∈S为d维实变量.xi ∈[ai,bi],i=1,2,···,d,其中ai和bi分别是第i维变量的取值上边界和下边界.由于高斯型噪声在自然和工程系统中普遍存在[34],因此考虑ξ为服从高斯分布的随机变量,ξ~N(µ,σ2) ,噪声的强度由方差σ2决定.以极小值优化为例,设x∗∈S,若存在δ>0 为任意独立的无穷小值,使得

则称x∗为f(x) 在S上的局部最优解,f(x∗) 为局部最优值.噪声环境下多峰函数优化问题可描述为:在一定强度的噪声干扰下,根据受噪声干扰的函数值fσ(x) ,尽可能多的定位f(x) 的多个极值点,即找到f(x) 的多个最优值及其最优解.
为全文描述方便,给出极值深井和极值分辨度的定义:
假设d维函数f(x) 包含m个极小值点(m ≥1),其中第i个极小值点为Mi(xMi,f(xMi)),其中,xMi=(xMi1,xMi2,···xMid) .在第k维坐标上,与Mi左右相邻的两个极大值点分别为Bk(xB,f(xB))和Ck(xC,f(xC)) .Bk和Ck的第k维坐标分别为xBk和xCk.
定义 1.在第k维坐标上,由Bk(xB,f(xB)) 和Ck(xC,f(xC)) 及函数f(x) 在该维平面上投影的曲线所确定的范围形如开口向上的深井,称此范围为该极值点在第k维坐标平面上的极值深井.
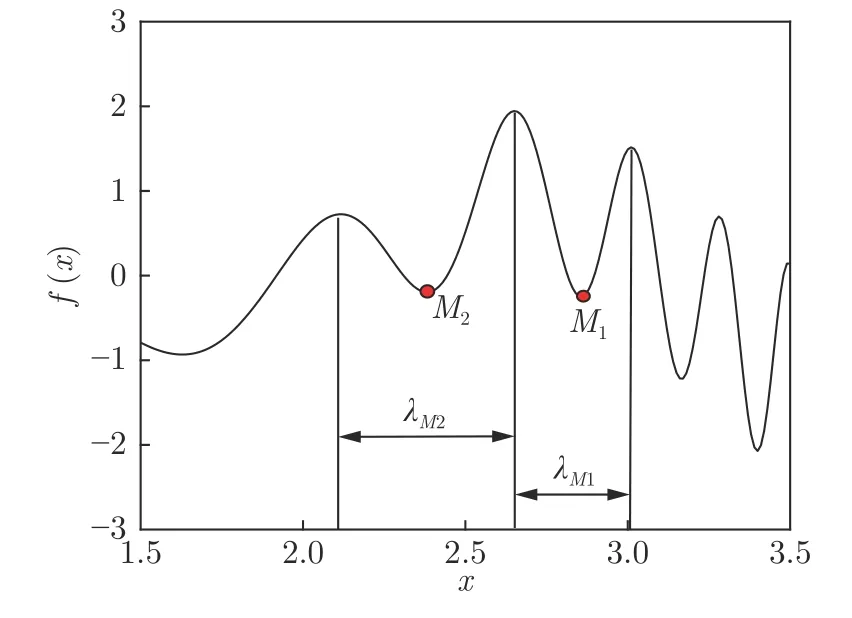
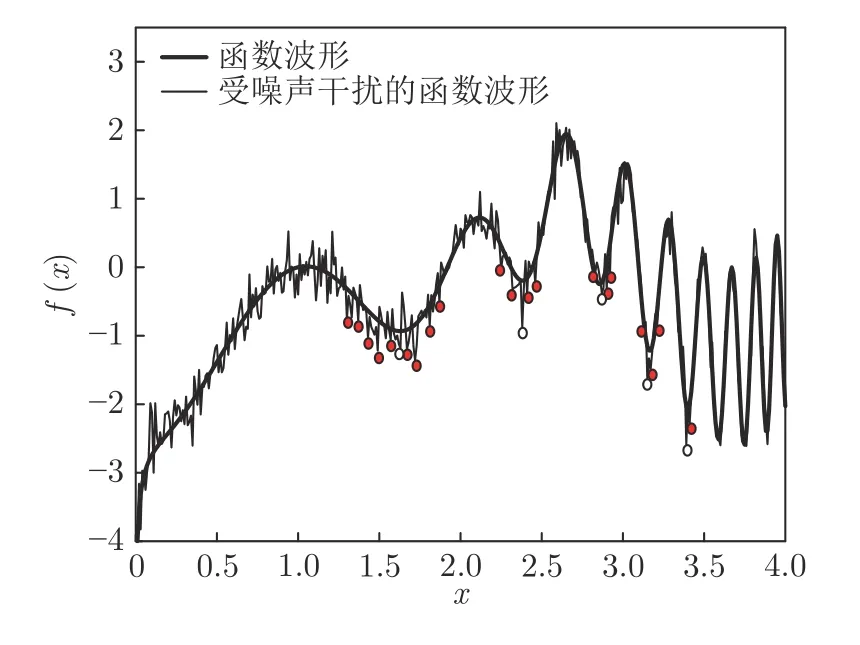
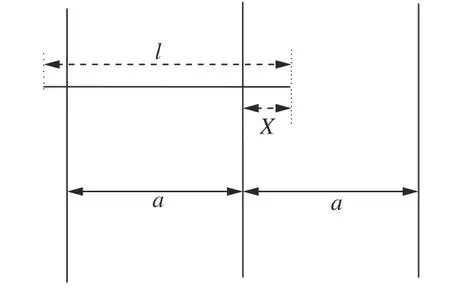
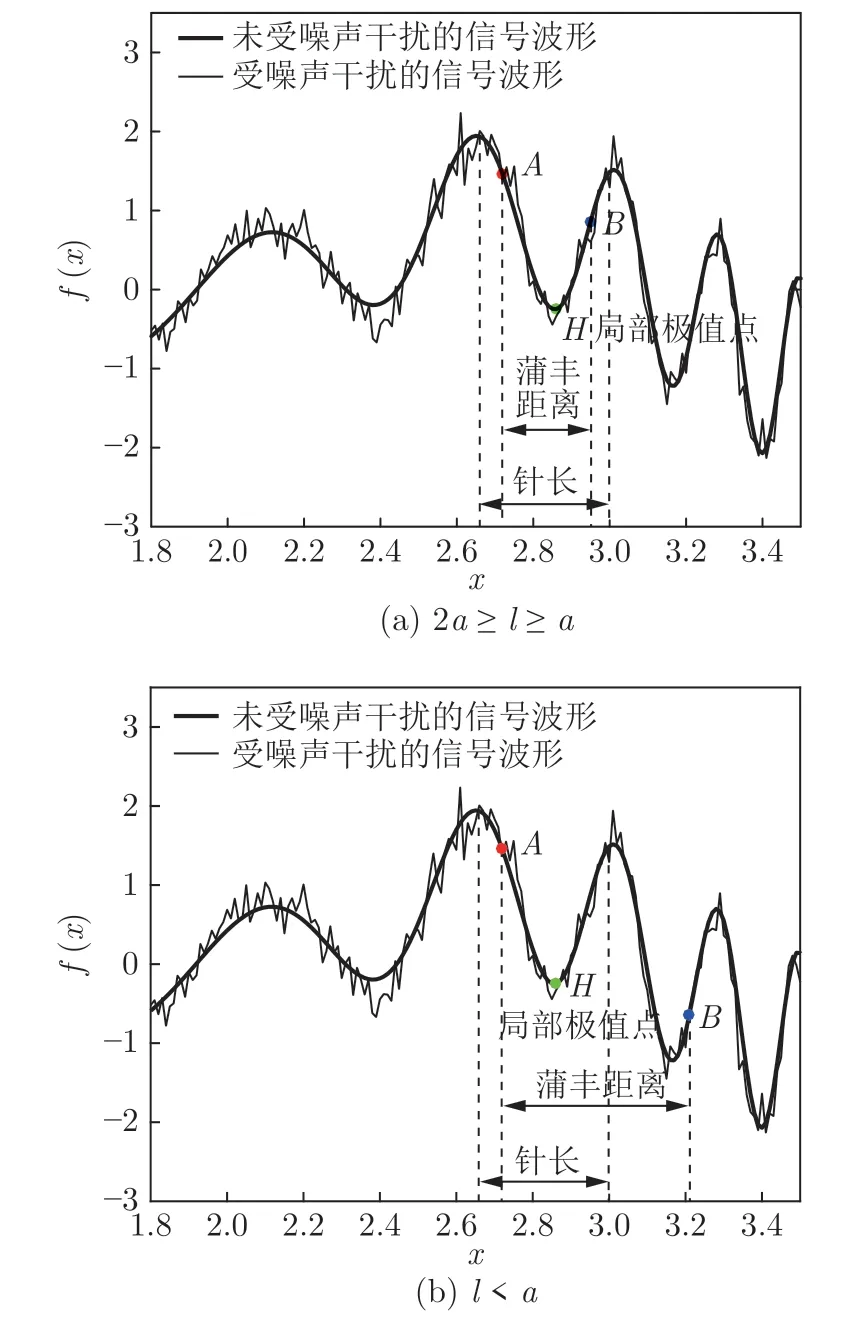
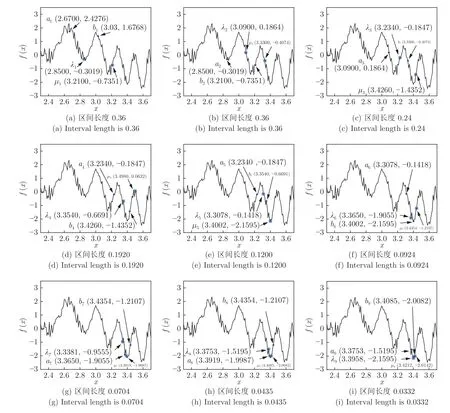
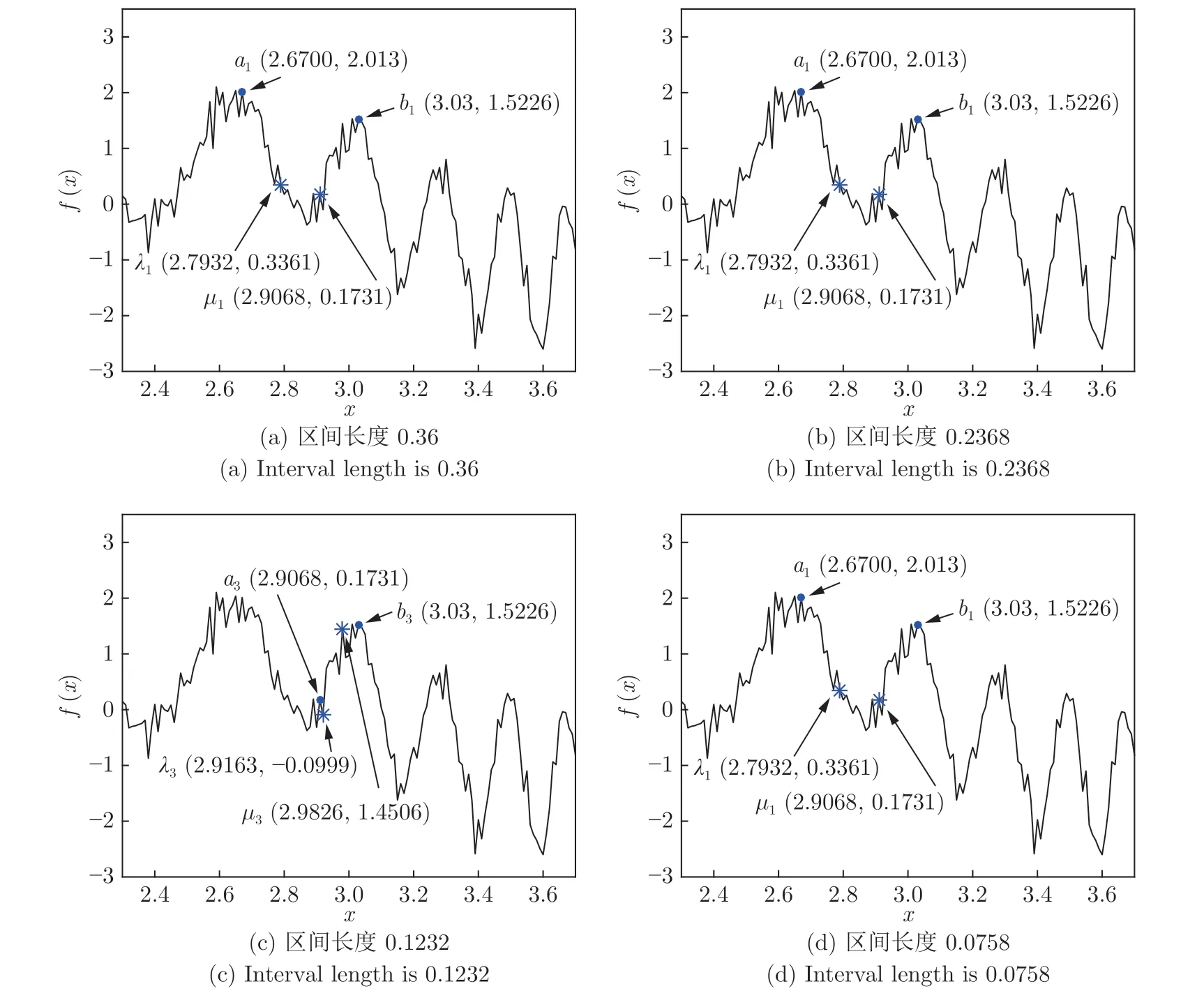
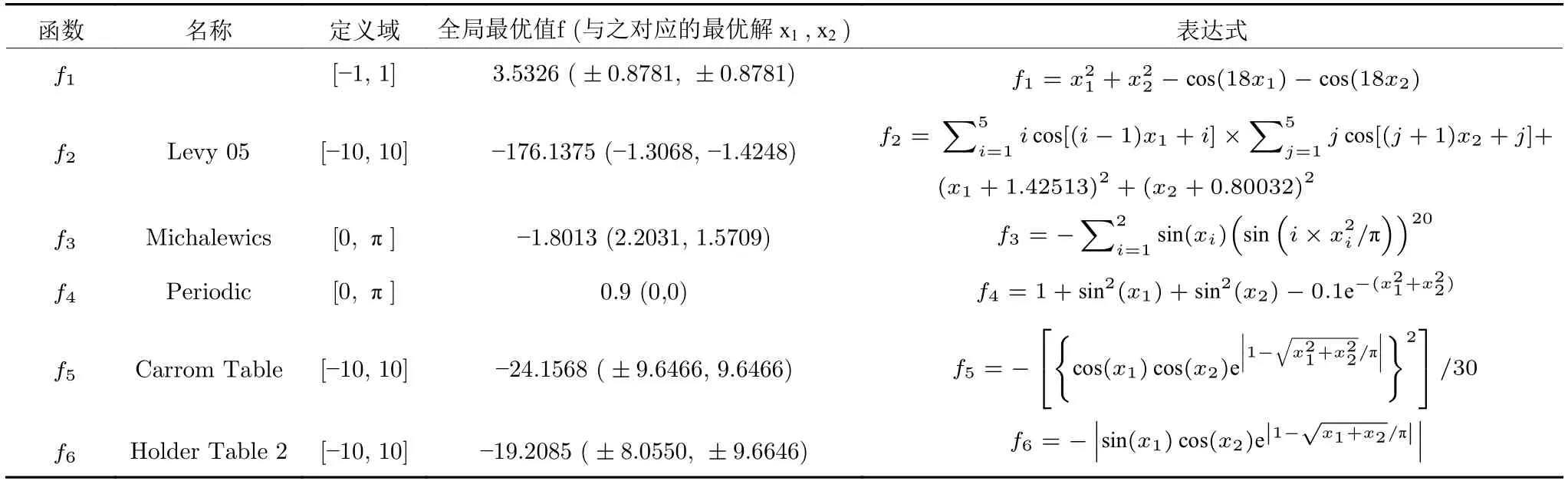
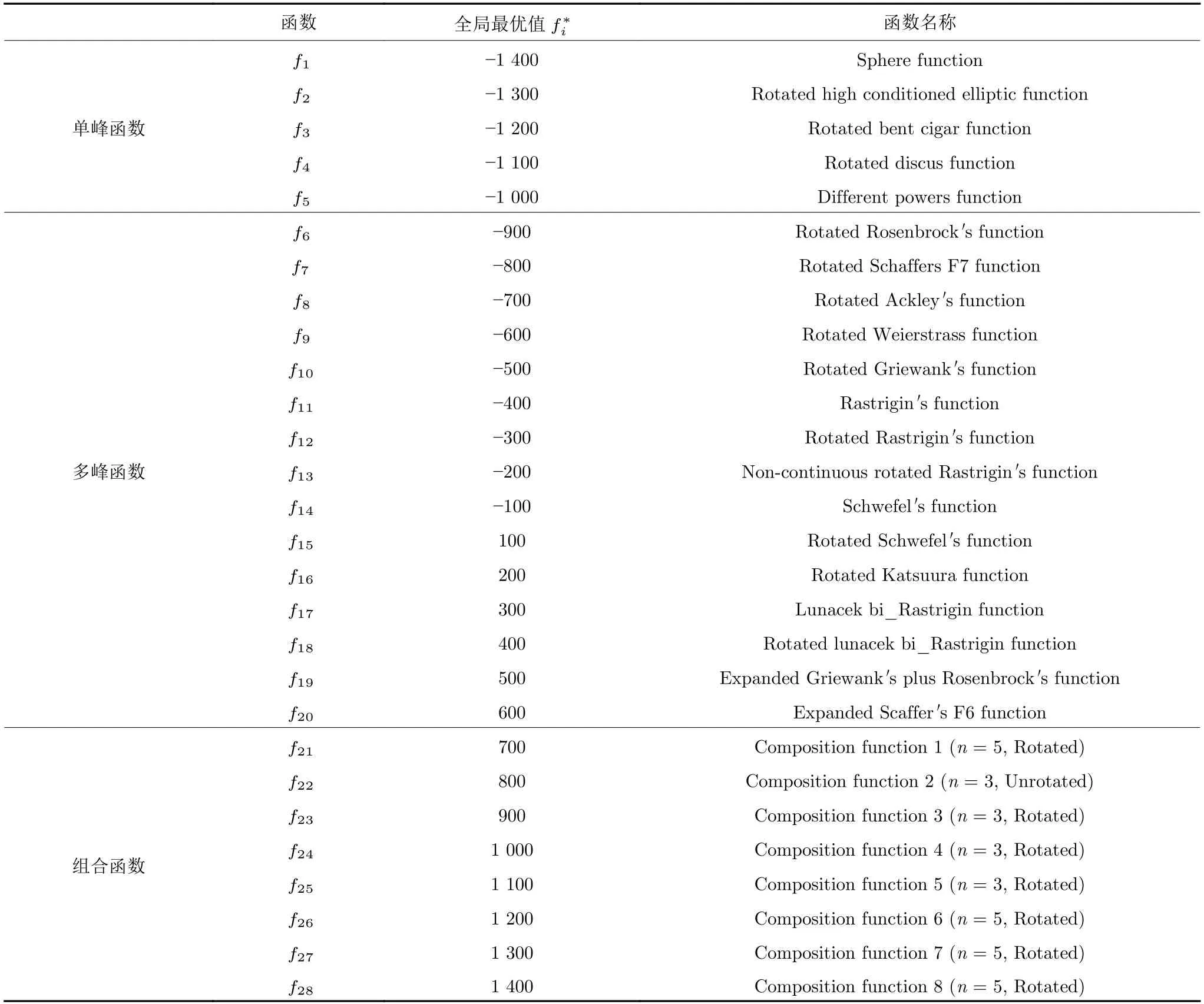
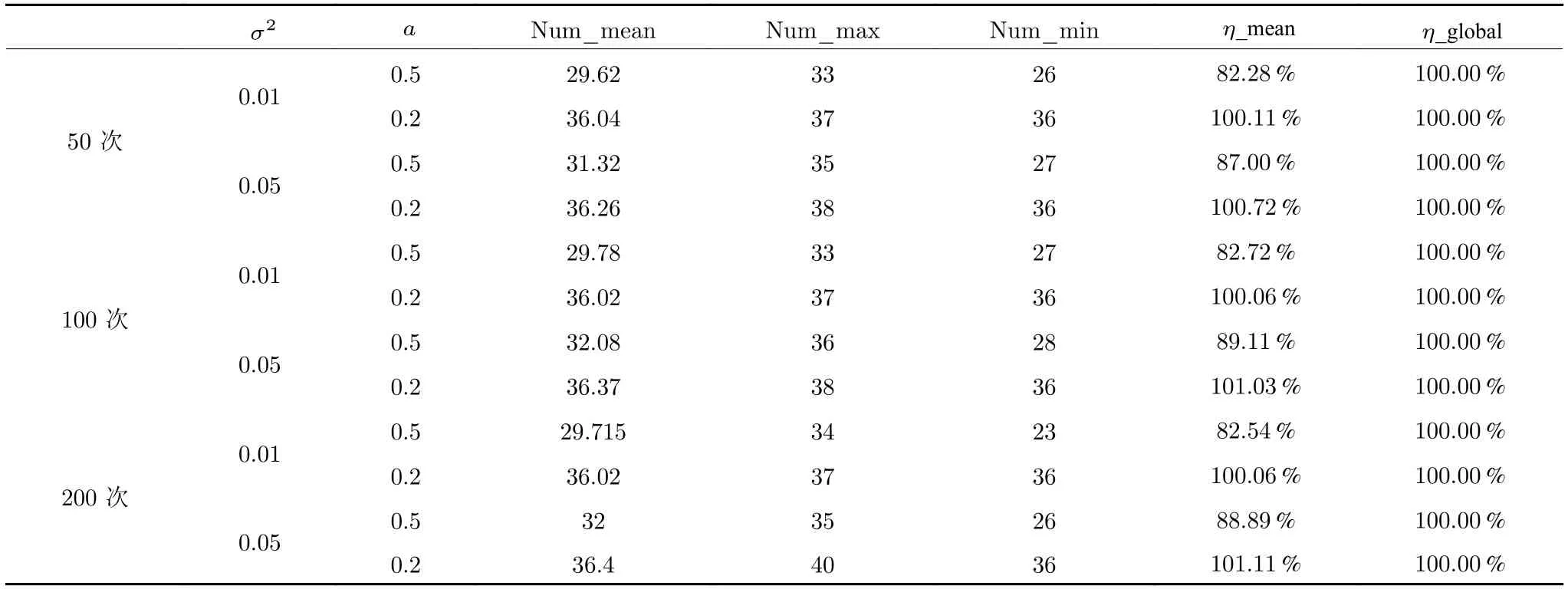
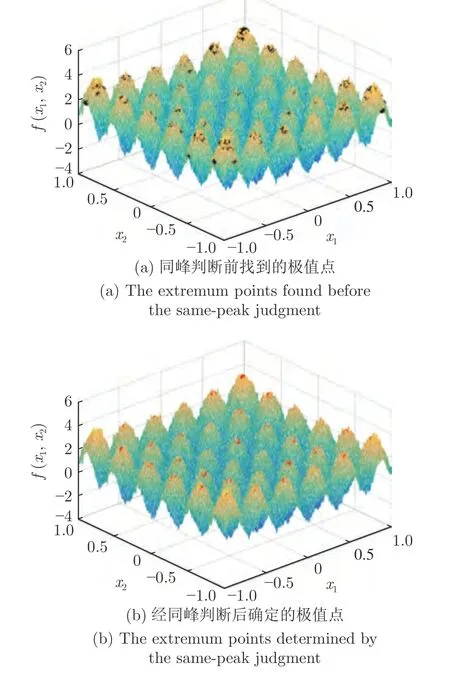
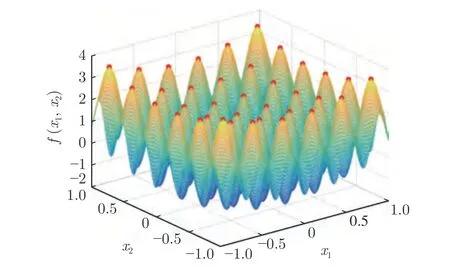
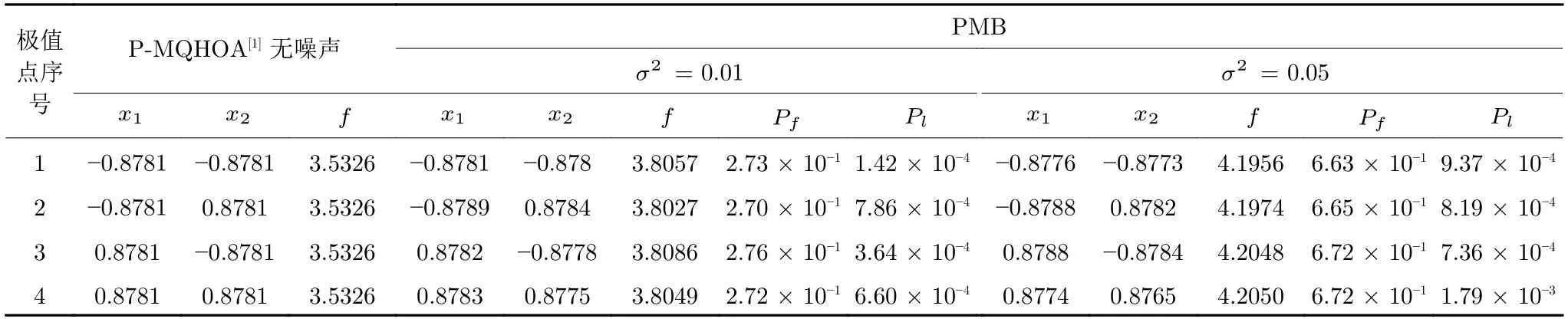
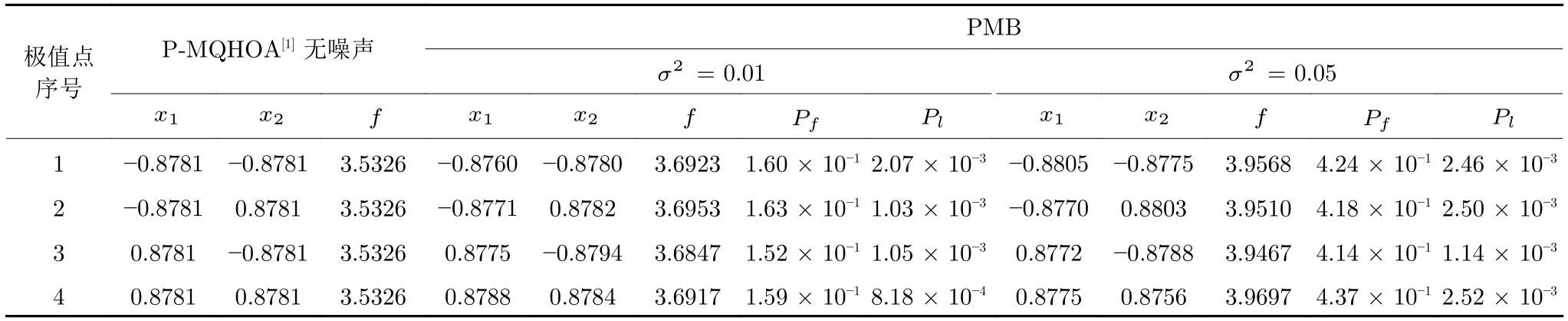
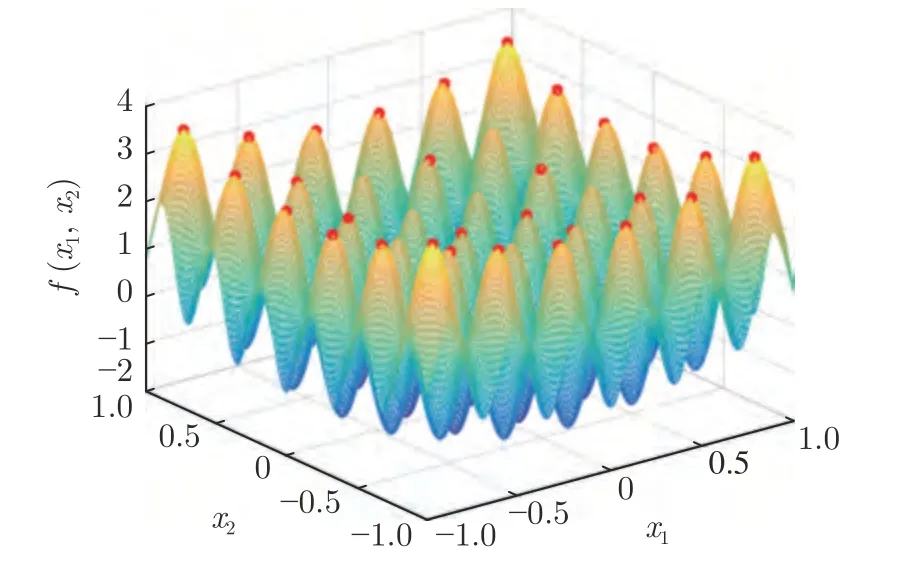
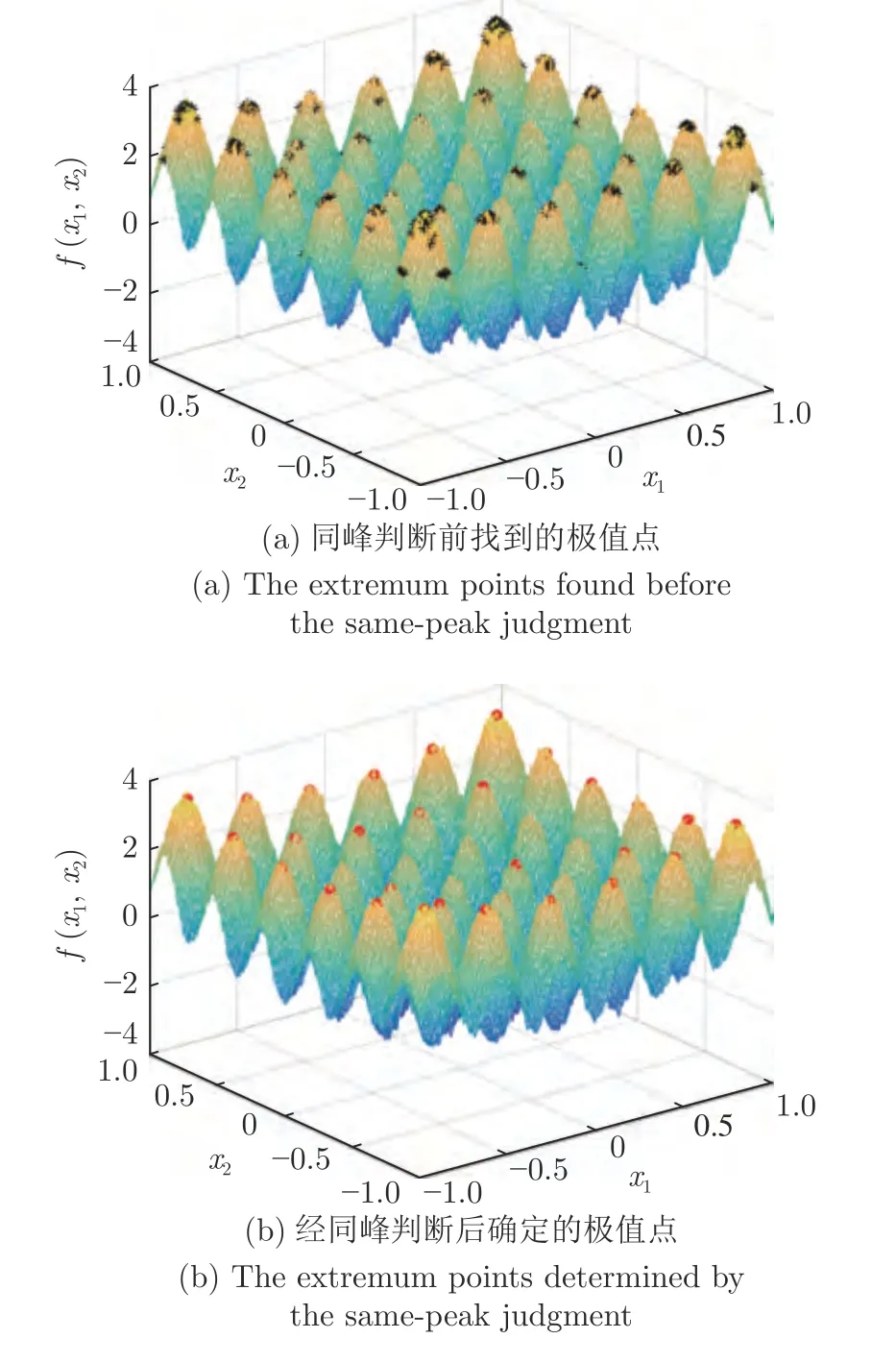
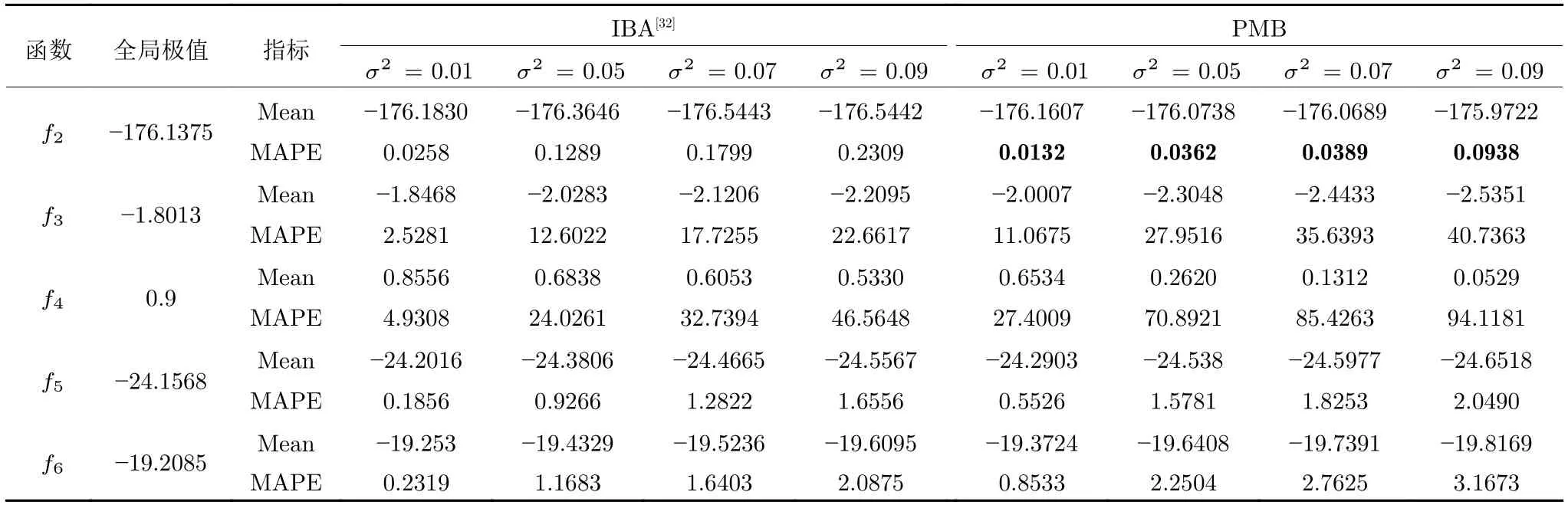
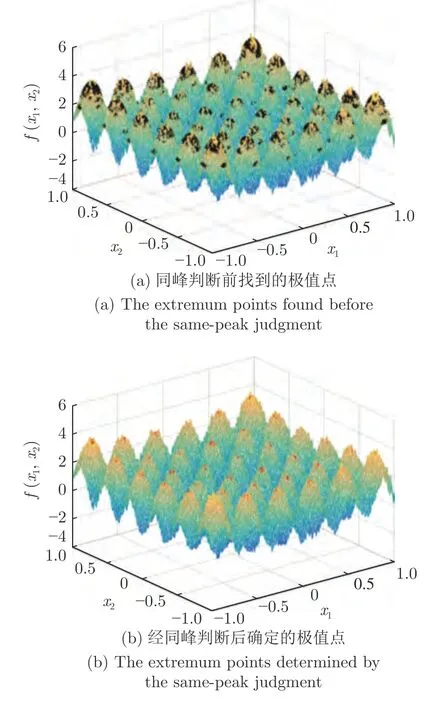
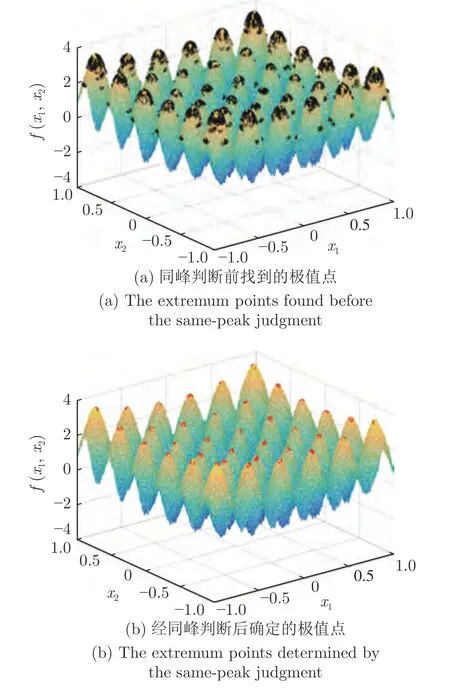
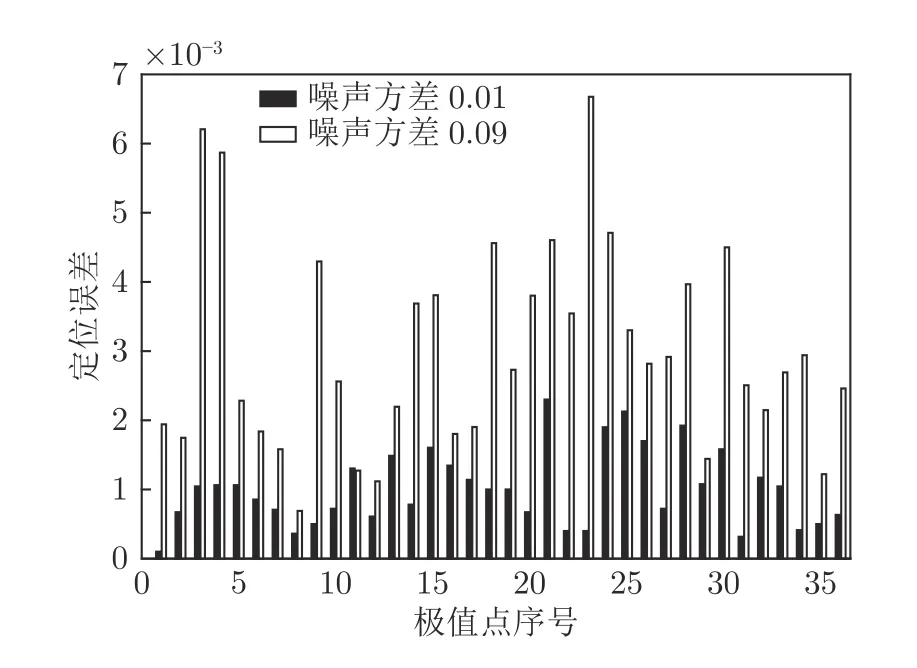
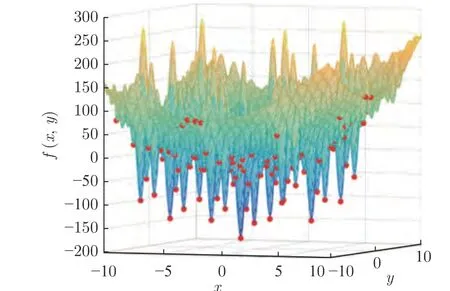
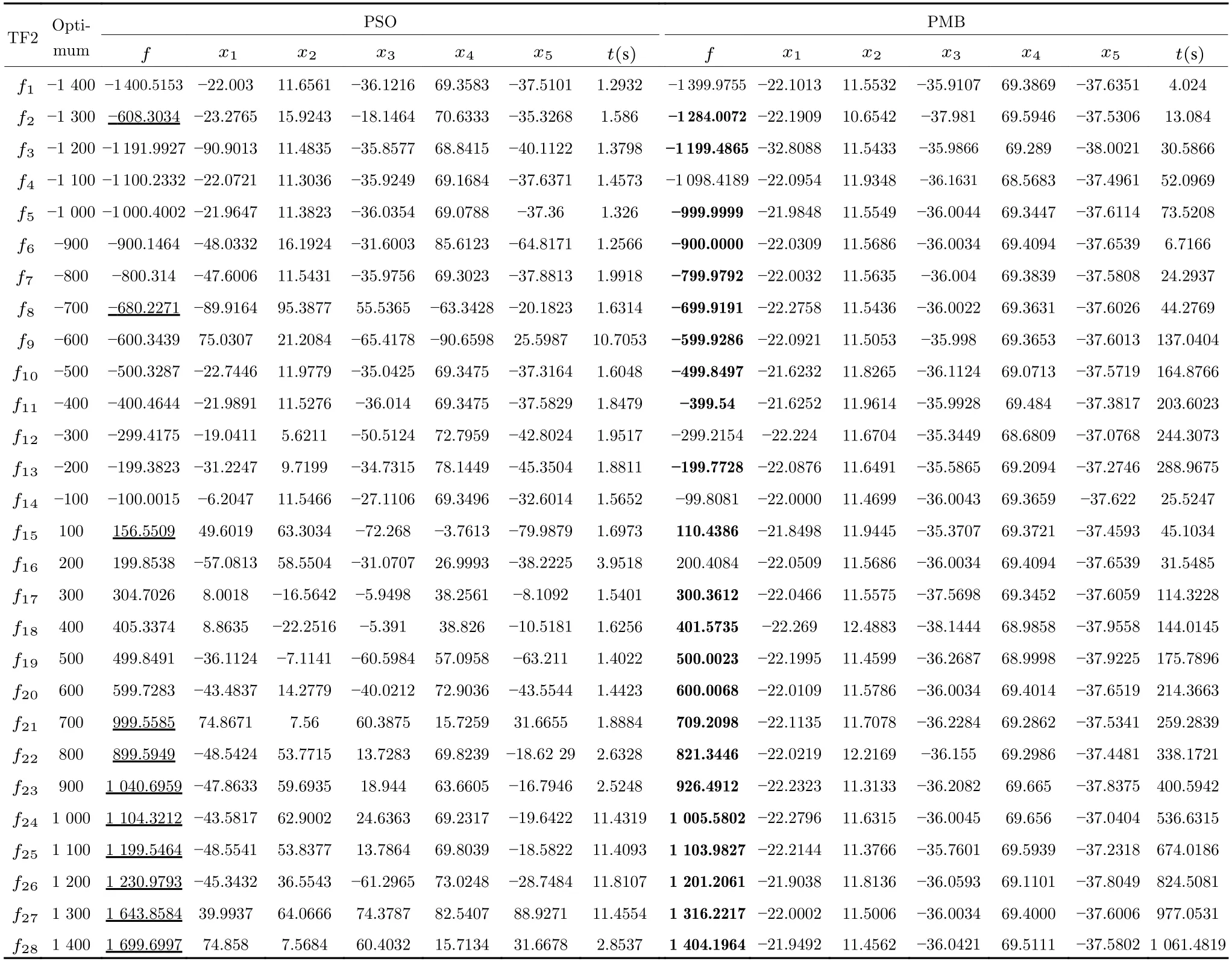
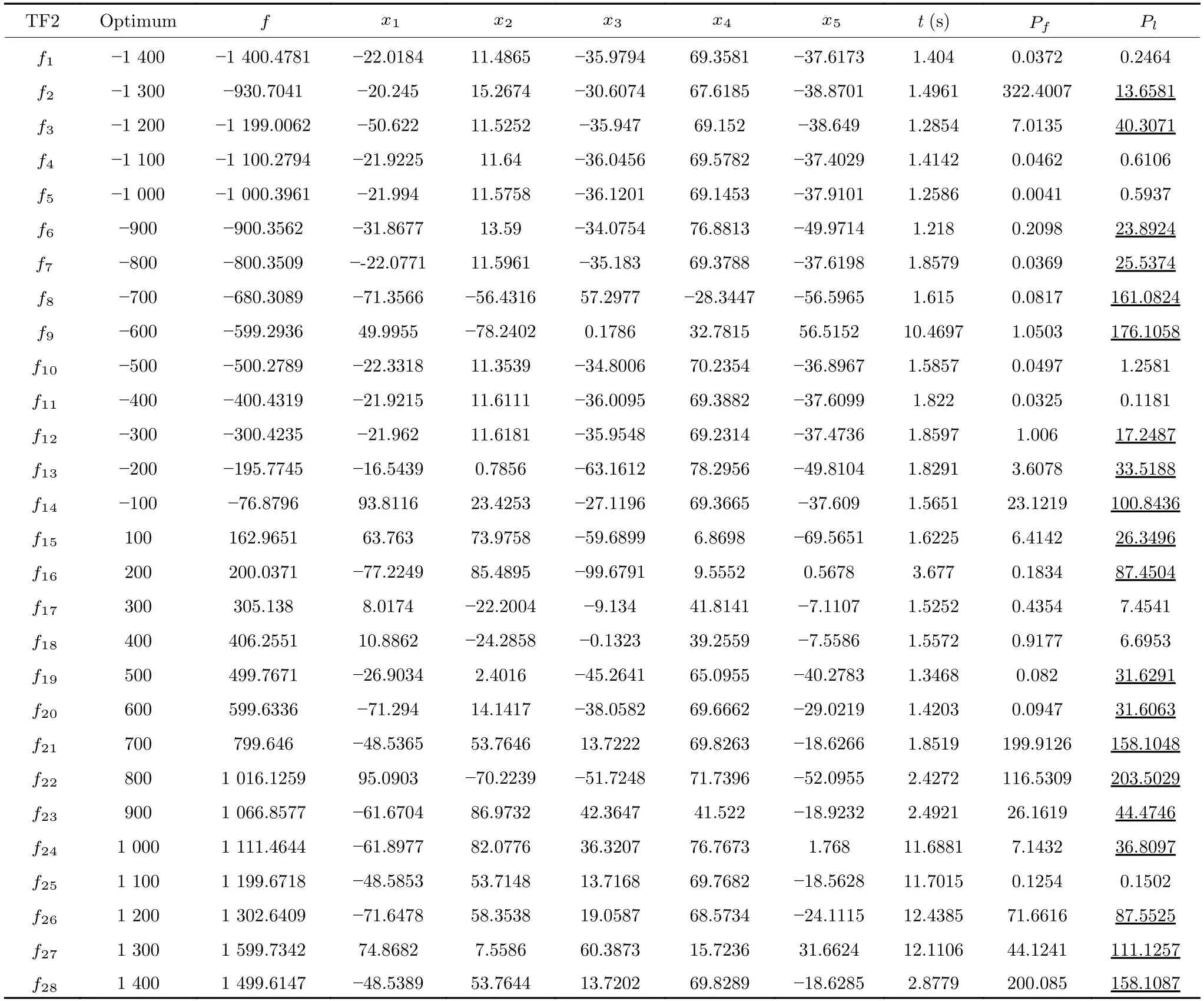
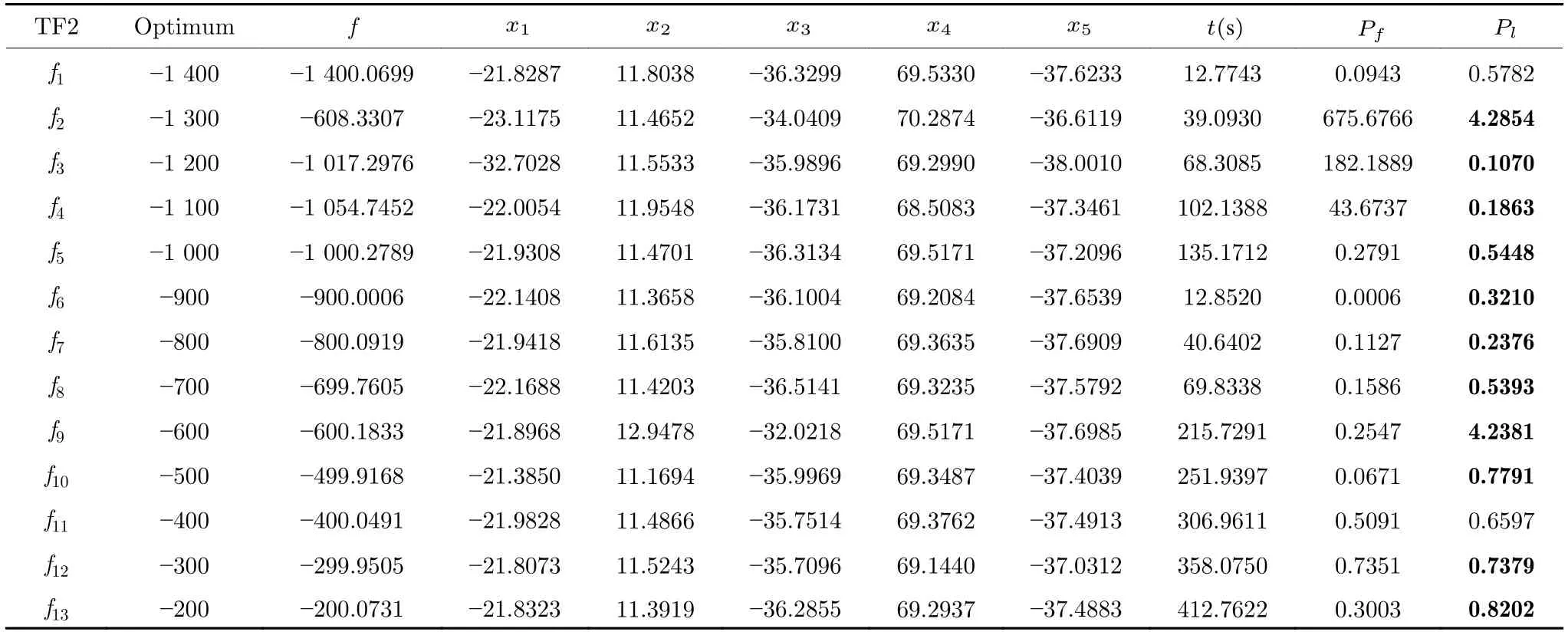
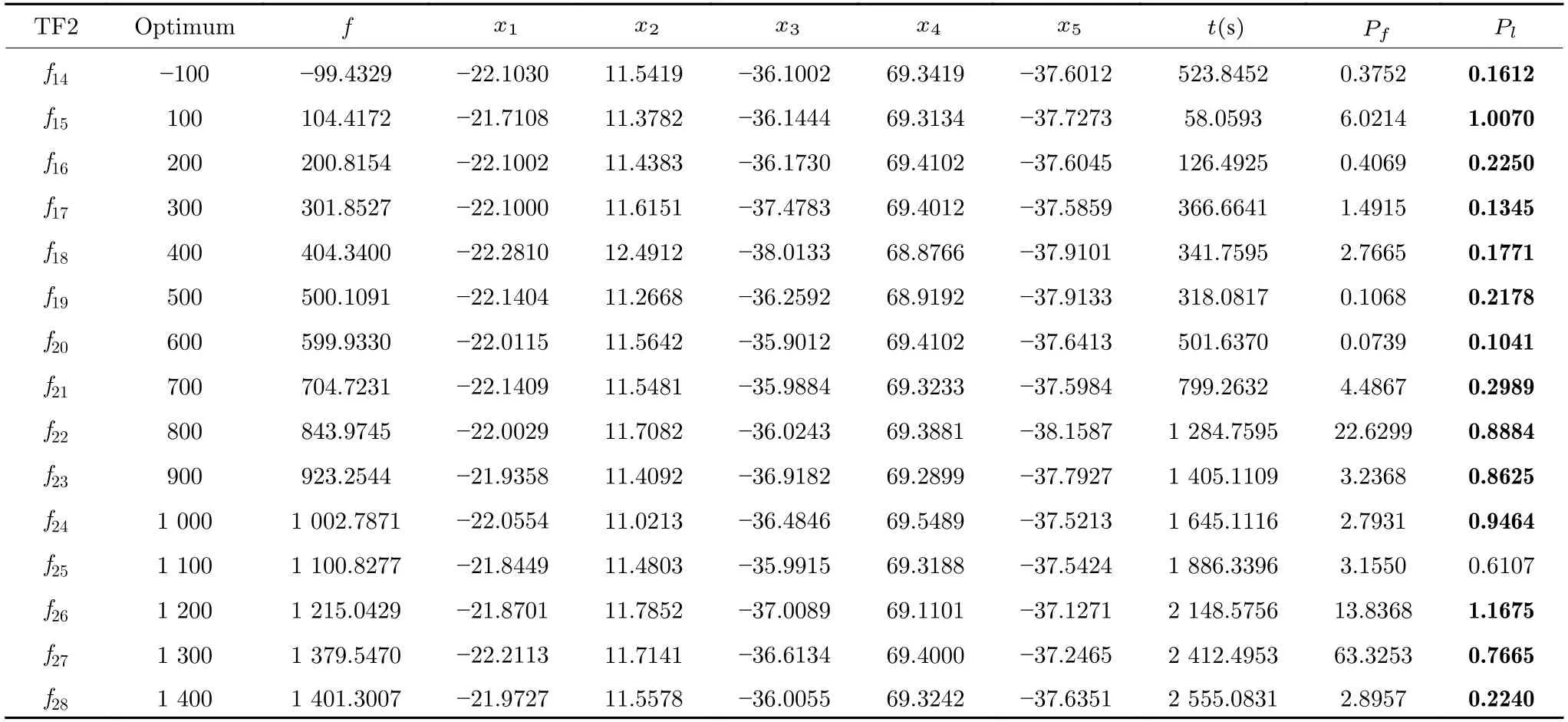
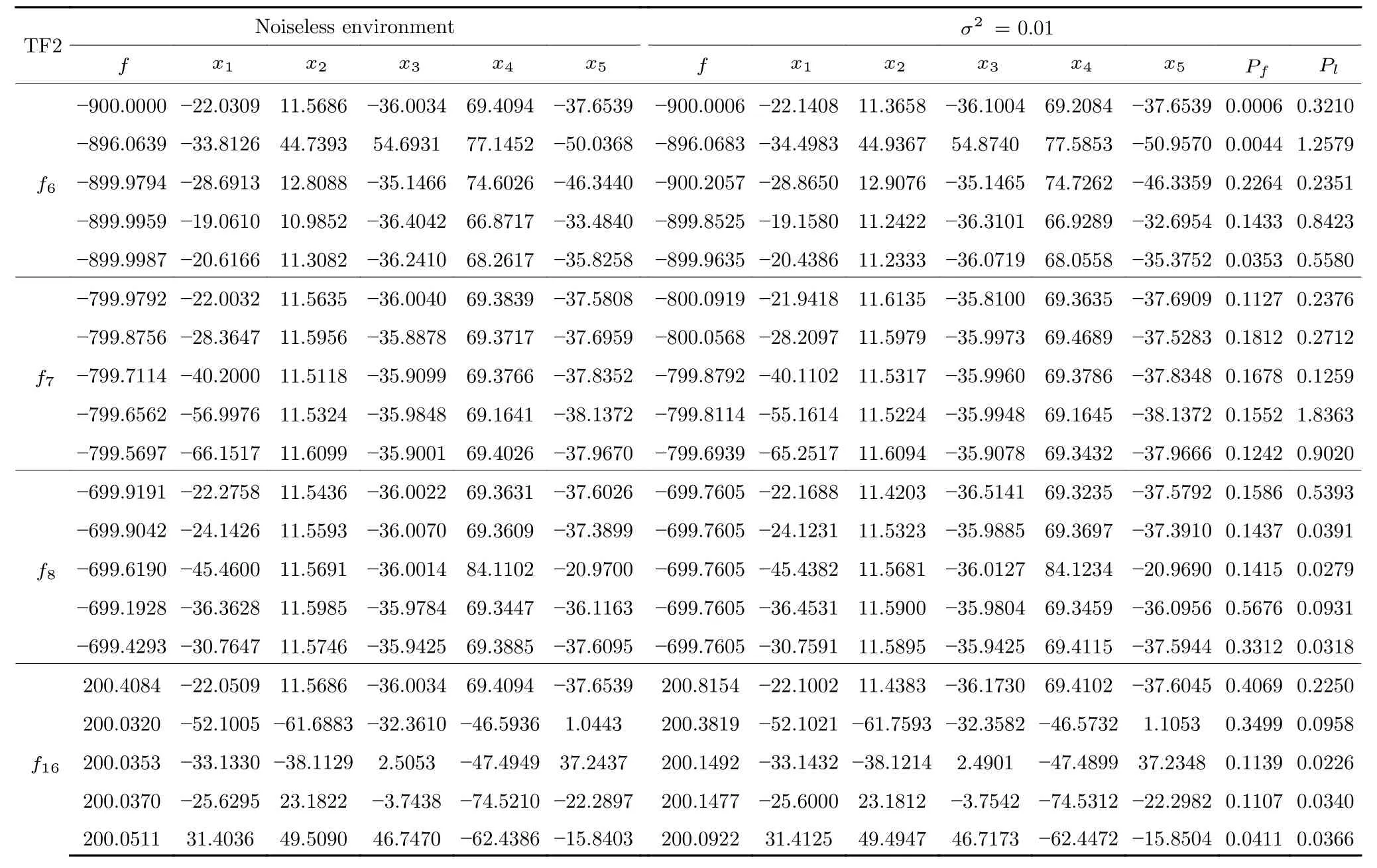
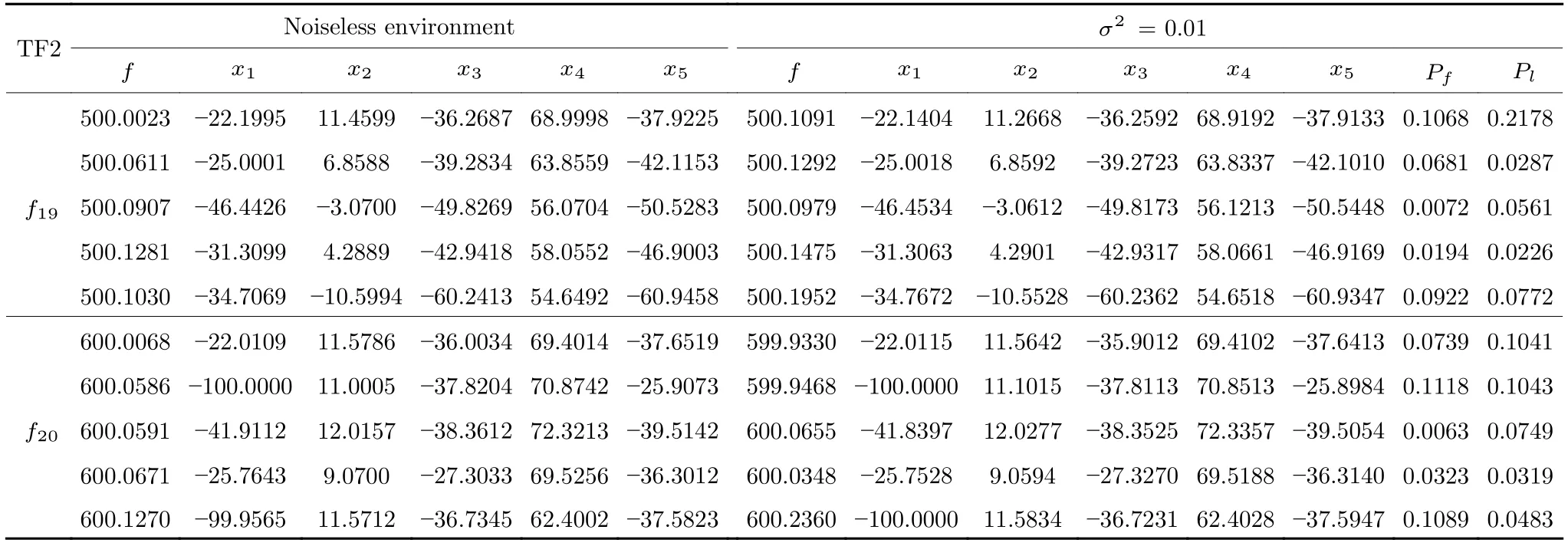
定义 2.Bk(xB,f(xB)) 和Ck(xC,f(xC)) 的第k维坐标之差的绝对值记为λMi_k=|xBk −xCk|,称为极小值点Mi在第k维坐标平面上的极值深井的井口宽度.λMi=min1 称为该函数的极值分辨度. 以一维函数为例,如图1 所示,极值点M1的极值 分辨 度λM1小 于极值 点M2的极 值 分辨度λM2.当决策变量受到外界不确定因素产生的噪声影响时,函数适应度值总是不可避免地产生波动,如果产生的波动较小,则认为解的抗噪声性能较强,如果目标函数波动的很厉害则说明解的抗噪声性能较差.从图1 可以看出点M1和M2都是函数的局部极小值点,其函数适应度值相差不大.假设决策变量受到干扰产生相同程度偏移,点M2的适应度值的变化将比点M1的变化更小,从而点M2的抗噪声性能优于点M1. 图1 极值分辨度Fig.1 Extreme value resolution 从上面的例子和分析可以看出,极值分辨度越低,即该极值点所在深井的井口宽度越小,则该极值点的抗噪声性能越差.工程应用时要根据实际要求的误差允许范围确定极值分辨度.例如,误差允许范围是0.05,若极值分辨度小于0.05,通过优化算法将找出井口宽度小于0.05 的极值点,这样的点在受到噪声干扰时,若决策变量的偏移量达到0.05,虽然没有超过误差允许范围,但适应度值已经由极小值偏移到了极大值,偏移程度较严重,极有可能对工程设计造成不良后果.因此,选取的极值分辨度需大于误差允许范围. 优化问题是工程领域普遍存在且需要解决的问题[35],涉及到的研究领域繁多,除了优化方法的依概率问题、噪声优化问题和多峰优化问题,还包括全局优化问题[36−37]、局部收敛精度提高问题[37]、高维优化问题[38]、算法收敛速度问题[39]、多目标优化问题[40−41]、多目标鲁棒优化问题[42]等.针对不同的研究领域,都有相应的评价指标.本文主要研究噪声环境下的多峰优化问题,在这类问题的优化求解中,不仅要尽可能多地求出优化问题的全局极值点和局部极值点,而且要求出每个极值点的d维变量取值,因此定义噪声环境下的峰值检测率、峰值误差和定位误差,并将它们作为评价噪声环境下算法性能的指标. 定义 3.假设d维函数f(x) 包含m个极值点(m ≥1) ,算法求得m∗个极值点,则 称为算法求解极值点的峰值检测率. 称为该算法求解极值点的峰值误差. 称为该算法求解极值点的定位误差. 在噪声环境下的多峰优化求解问题中,噪声干扰使得函数波形发生波动,由此引入若干局部极值点,如图2 中的实心点.噪声环境下多峰优化的目的是要找到函数的真实极值点位置,即图2 中的空心点.为此,可以根据工程需求对搜索空间进行合理均匀划分,在划分的多个局部区域内进行单极值点搜索,从而保留下多个极值点,最后利用合适的同峰判别方法区分异峰极值点,合并同峰极值点. 图2 函数波形与极值点Fig.2 Function waveform and extremum points 在此过程中,需要解决两个问题:1)划分搜索空间的依据;2)局部区域搜索时如何尽可能地避开实心点(噪声引起的局部最优)的干扰. 本文从概率的角度出发,将蒲丰投针问题中的几何概率规律引入解空间划分问题,提出了噪声环境下基于蒲丰距离的依概率多峰优化算法.首先基于蒲丰投针原理提出蒲丰距离,推导并证明了蒲丰距离与峰值检测率的关系.在此基础上,依据蒲丰距离对全局区域进行探索,得到多个探索点.在多个探索点之间进行局部寻优,可以保留下多个极值点.其次,在局部寻优阶段,为减小算法陷入噪声引起的局部最优的发生概率,利用区域伸缩准则改进斐波那契法,提高了算法在真实最优解邻域附近的收敛能力,削弱了噪声的影响. 18 世纪,法国数学家蒲丰(Buffon,1707~1788)提出的 “投针问题”,记载于蒲丰1777 年出版的著作中:“在平面上画有一组间距为a的平行线,将一根长度为l(l ≤a) 的针任意掷在这个平面上,求此针与平行线中任一条相交的概率.”如图3所示.蒲丰最早设计了投针试验.这一方法的步骤是: 图3 蒲丰投针实验设计图Fig.3 Experimental design of Buffon needles 1) 在白纸上画数条间距为a的平行线. 2) 取长度为l(l ≤a) 的针,随机地向画有平行直线的纸上掷n次,观察针与直线相交的次数. 3)计算针与直线相交的概率. 由于向桌面投针是随机的,所以用二维随机变量 (X,Φ) 来确定它在桌上的具体位置.设X表示针的中点到平行线的距离,Φ 表示针与平行线的夹角,则当X 则针与直线相交的概率为 若对多峰函数的求解空间进行等间隔采样,每对相邻的采样点可以确定一个局部范围.若采样间隔设置合理,使得在此局部范围内函数只包含唯一一个局部极值点,则在此范围内进行单极值寻优即可找出函数的局部极值点.通过采样得到的多对相邻采样点,可以找到函数的多个局部极值点.为实现等间隔采样,将求解域在每一维上以固定长度划分,划分的等间隔平行线与函数的若干个交点即为采样点,相邻采样点在第k(1 定理 1.设a为采样平行线间距,以函数的极值分辨度为固定针长l,若 2a ≥l ≥a,则针同时与两条平行线相交的概率为 若l≤a,则针同时与两条平行线相交的概率为P2=0 . 证明.以二维平面为例,用二维随机变量(X,Φ)来确定针在平面上的具体位置.设X表示针的端点到平行线的距离,如图4 所示.X在 ( 0,a) 范围内服从均匀分布,由此可以写出X的概率密度函数 图4 式(9)证明示意图Fig.4 Diagram to prove (9) Φ表示针与平行线的夹角,根据极值分辨度的定义,可知针与平行线始终为垂直方向,Φ =π/2,故当 0 若l≤a,则针同时与两条平行线相交的概率为P2=0 . 定理 2.设a为采样平行线间距,以函数的极值分辨度为固定针长l,若 2a ≥l ≥a,则针只与一条平行线相交的概率为 若l≤a,则针只与一条平行线相交的概率为 若l≥2a,则针只与一条平行线相交的概率为P5=0. 证明.以二维平面为例,用二维随机变量(X,Φ)来确定针在平面上的具体位置.设X表示针的端点到平行线的距离,在 ( 0,a) 范围内服从均匀分布,由此可以写出X的概率密度函数为式(10)所示.Φ 表示针与平行线的夹角,因此根据极值分辨度的定义,可知针与平行线始终为垂直方向,Φ =π/2 .若2a ≥l ≥a,当l−a 若l≤a,当 0 若l≥2a,则针与一条平行线相交的概率为P5=0. □ 定理 3.在噪声环境下,对于由两条平行线确定的局部范围内的极值点,若针同时与两条平行线相交,则找到该极值点的概率为P6=1−Pξ,若针只与其中一条平行线相交,则找到该极值点的概率为P7=1−Pγ −Pξ. 证明.根据算法的基本原理和极值分辨度的定义,若针同时与两条平行线相交,说明由两条平行线确定的两个采样点包含在局部极值点所在的深井范围内,即两个采样点确定的范围内只包含唯一一个极值点,在此局部范围内进行单极值点寻优,无噪声环境下算法将以概率1 找到该极值点,在噪声环境下,该区域内将出现若干噪声引起的极值点,若以概率Pξ出现函数值低于该极值点函数值的点,则算法将保留函数值更低的点,故找到该极值点的概率为P6=1−Pξ. 若针只与一条平行线相交,则在三条平行线确定的范围内,除去此针长l的确定的范围,其余(2a −l) 的范围内,若以概率Pγ出现函数值更低的极值点,或以概率Pξ出现函数值更低的噪声波动点,则算法将留取函数值更低的点,故P7=1−Pγ −Pξ. 综上可得如下推论: 推论 1.设a为采样平行线间距,称为蒲丰距离,以函数的极值分辨度为固定针长l,若2a ≥l ≥a,则算法找到极值分辨度最小的极值点的概率为 若l 以一维函数为例,图5 (a)和5 (b)所示分别是2a ≥l ≥a和l 图5 蒲丰距离与针长的关系示意图Fig.5 Diagram of the relationship between Buffon distance and needle length 对比式(16)和(17)可以看出,在函数的极值分辨度l既定的情况下,蒲丰距离a越小,算法找到所有极值点的概率也就越大,反之则遗漏的极值点将会越多.然而,a取值过小则会带来数据量急剧增加,延长了算法的运算时间,因此,要根据工程需要来设定a的值,例如,当a=(1/2)l时,算法找到极值分辨度最小的极值点的概率为 1−Pξ,仅受噪声引起的局部极值点的影响,若在无噪声环境下,则此概率为1,即当蒲丰距离为针长的一半时,算法以概率1 找到极值分辨度最小的极值点,这一结论与采样定理相符. 推论 2.设a为采样平行线间距,以函数的极值分辨度为固定针长l.对于全局极值点,由于Pγ=0,故 对比式(16)与(18)以及(17)与(19)可知,算法找到全局极值点的概率大于找到局部极值点的概率,因此算法具有较好的全局极值点优化性能. 对于无约束优化问题,斐波那契法是求解一维单峰函数的最优策略[43].将斐波那契法的变量维数从一维扩展到多维,可以解决多维函数优化问题[43].斐波那契策略通过按比例压缩搜索区间令区间内的试探点不断逼近最优解.斐波那契法中需要用到斐波那契数列,其通项递推公式为: 斐波那契数列中相邻两项之比形成的数列收敛于黄金分割数[44],即 PMB 算法在进行局部搜索时,为使算法能够跳出噪声引入的局部最优,算法的搜索范围不能只局限于初始的局部范围,而应适当扩展,探索周围邻域内是否有更优点.如有更优点,则搜索区域应该适当扩展,向更优点偏移.可以利用试探点引导区域向优化点方向移动.同时,为使算法收敛,搜索区域还需进行压缩.随着迭代次数的增加,区域最终将收敛于可接受的精度范围内.为此提出区域伸缩准则,定义如下: 对于由任意两点A(xA,f(xA))和B(xB,f(xB))确定的区域边界,若f(xA) 点C(xC,f(xC)) 用来试探新扩展的区域中是否存在更优的点,然后再以比例β对区间进行压缩,压缩率β根据对扩展点C(xC,f(xC)) 的试探情况进行设置.若f(xA)>f(xB) ,则选取点B(xB,f(xB))为中心,做类似扩展和压缩操作. 利用区域伸缩准则改进斐波那契法,得到算法步骤如下: 步骤 1.选定初始区间 [a1,b1] 及求解精度ε>0,令k=1 ,若f(a1)>f(b1) 转步骤2,否则转步骤3; 步骤 2.计算 若f(µk) 步骤 3.计算 若f(λk) 步骤 4.置 若|bk+1−ak+1|≤ε,转步骤7,否则令k=k+1,转步骤2; 步骤 5.置 若|bk+1−ak+1|≤ε,转步骤7,否则令k=k+1,转步骤2; 步骤 6.置 若|bk+1−ak+1|≤ε,转步骤7,否则令k=k+1,转步骤2; 步骤 7.停止计算,取极小值点的坐标为1/2|bk+1−ak+1|. 由算法执行步骤可以看出,初始搜索区间由[a1,b1]界定,但后续的搜索范围并不仅仅局限于[a1,b1],而是向周围邻域进行了适当的扩展,探索周围是否还存在更优的点.虽然每次都对区间进行了扩展,但是每次计算结束时都根据探索的结果对区间进行压缩,根据选取的扩展点不同,第k次计算后的区域压缩率为β1或β2, 由斐波那契数列的特点,可知 可见,算法的搜索区间在逐渐缩小,最后可以收敛到设定的精度范围内. 为了对比改进前的斐波那契法与改进后的斐波那契法,以受噪声干扰的一维函数为例,图6 的9个子图展示了改进的斐波那契法的区域伸缩过程,图7 的4 个子图展示了改进前的斐波那契法的区域收缩过程.其中实线波形是受噪声干扰的函数波形,点‘·’ 表示区域边界点ai和bi,点‘∗’代表试探点λi和µi.图6(a)表示局部搜索的初始区间由[a1,b1]=[2.6700,3.0300] 确定.由于f(a1)>f(b1),根据式(24)可以得到式(33): 由于f(µ1) 通过比较图6 中的 9 个子图,我们可以观察到改进后的斐波那契法的搜索区间可以扩展到具有更优解的邻域,而不是初始时的局部范围.而从图6可以看到,传统的斐波那契法的搜索区间始终限制在初始的局部范围内.此外,从图7 中可以看出,斐波那契法在第4 次迭代时区间长度就压缩到了0.0758,而改进后的斐波那契法在第7 次迭代时区间长度才压缩到0.0704,说明引入了区域伸缩准则的斐波那契法每次迭代都遵循先扩展再压缩的规则,因此区域压缩和算法收敛的速度比改进前的斐波那契法下降了,但是改进后的算法可以搜索到初始区间附近邻域范围内的极小值点,提高了算法在函数真实最优解邻域附近的收敛能力,避免其陷入噪声引入的局部最优. 图6 改进的斐波那契法的区域伸缩过程Fig.6 The process of regional scaling of the improved Fibonacci method 图7 斐波那契法的区域收缩过程Fig.7 The process of regional shrink of the Fibonacci method 步骤 1.初始化设置.根据实际需求的极值分辨度确定蒲丰距离a和求解精度ε. 步骤 2.在全局范围内以蒲丰距离a进行等间隔采样,得到采样点集合S={A1,A2,···,Ak}. 步骤 3.以采样点集合S中的相邻点作为初始区间的两个端点,在局部范围内利用区域伸缩的斐波那契法进行单极值点寻优,可以得到k−1 个极值点{E1,E2,···,Ek−1}. 步骤 4.利用改进型插点法[45]对得到的极值点进行同峰判断. 步骤 5.利用归并方法[1]将同峰的极值点进行合并,并取这些点中的最大(最小)值最为最终解. 为了提高PMB 算法的求解精度,同时也为了提高算法在多维函数上的优化效率,可以采用多级划分策略.对于N级划分策略,首先依据蒲丰距离对全局区域进行划分,得到多个探索点,在多个探索点之间进行局部寻优,可以保留下第一级的多个极值点.对第一级的极值点的极值大小进行比较后,选取一定数量的较优极值点,对它们所在的区域仍然依据蒲丰距离进行下一级划分,得到多个探索点,在多个探索点之间再进行局部寻优,从而得到第二级的多个极值点.依此类推,直到划分到第N级.对第N级得到的极值点,利用改进型插点法[45]进行同峰判断,再利用归并方法[1]将同峰的极值点进行合并,并取这些点中的最大(最小)值最为最终解. 以图8 (a)所示的二维平面为例,首先在每一维上进行等距离划分,可以得到若干交点,即为第一级的采样点,如图8 (a)中的实心交点所示.每一维上划分的间隔距离可以相同,也可以不同,一般情况下设置为每一维上的划分间隔都是相同的,特殊情况除外.如图8 (a)所示,虽然两个维度上的范围尺度不同,但不影响对它们进行等距离的划分.然后每个实心交点与其相邻的点之间进行局部寻优,得到若干第一级极值点.以图8 (a)中点A为例,它将分别与点B、C、D、E之间进行局部寻优.在第二级划分时,若选中了A和D局部寻优得到的极值点,则将对A和D两点所在的公共区域进行第二级划分,得到第二级的采样点,如图8 (b)所示.可以证明,若n维变量空间的每一维划分为m段区间,则在每一维上可以得到m+1 个采样点.所有采样点经局部寻优后将得到m×(m+1)×2(2×n−3)个极值点.以三维变量空间为例,假设每一维的长度域为[−100,100],第一级若取蒲丰距离a1=5,则每一维可得到m1=40 段区间和41 个采样点.所有采样点经局部寻优后将得到m1×(m1+1)×2(2×n−3)=40×41×23=13120个第一级极值点.从第一级极值点中选出部分较优极值点,对它们所在的区域依据蒲丰距离a2=0.1 进行下一级划分,对于其中一个子区域而言,其每一维的长度域为5,按照a2=0.1 划分,每一维可以得到m2=50 段区间和51 个采样点,从而每个区间可以得到m2×(m2+1)×2(2×n−3)=50×51×23=20400个第二级极值点,之后执行类似操作,直到达到指定的划分等级. 图8 PMB 算法的多级划分策略Fig.8 The multilevel partition strategy of PMB algorithm 从上述过程可以看出,初始时每一维的长度域为200,经过第一级划分后,每一维的长度域为5,经过第二级划分后,每一维的长度域为0.1,若第二级只选取1 个最优区域进行划分,则需要局部寻优的次数为13120+20400=33520.若不采取多级划分策略,直接对初始时长度域以a2=0.1的蒲丰距离进行划分,则m=2000,需要局部寻优的次数为m×(m+1)×2(2×n−3)=2000×2001×23=32016000.可见采取多级划分策略可以省去很多计算时间,这在多维函数的优化问题上优势更为明显.此外,多级划分策略不仅在同级区域内横向可并行执行,不同级区域也可纵向并行执行,计算过程不会相互干涉. 为了验证本文所提出的PMB 算法的寻优结果与蒲丰距离之间的依概率关系,研究噪声和蒲丰距离对PMB 算法寻优结果的影响,验证PMB 算法在噪声环境下的多极值点寻优能力,以及研究PMB算法在噪声环境下对多维函数寻优的有效性,本文选用两组基准测试函数研究PMB 算法的上述性能.第一组测试函数来自文献[1]和文献[32],如表1所示.这6 个测试函数都是多峰函数,不仅有一到多个全局极值点,还有若干局部极值点,其中,除f2,f3和f4只有唯一一个全局极值点,其他函数均有多个全局极值点.第二组测试函数是文献[46]中给出的CEC2013 推荐基准函数,如表2 所示.其中,f1~f5是单峰函数,f6~f20是多峰函数,f21~f28是组合函数.CEC2013 被视为黑盒问题,并且不允许使用问题的显式方程[46]. 表1 测试函数集1 (TF1)Table 1 Test function set 1 (TF1) 表2 测试函数集2 (TF2) (维度为5)Table 2 Test function set 2 (TF2) (Dimension is 5) 通过第3.2 节的理论推导可知,PMB 算法的寻优结果与蒲丰距离之间存在依概率关系.当蒲丰距离a与针长l满足 2a ≥l ≥a时,算法找到极值分辨度最小的极值点的概率满足式(16),当l≤a时,概率关系满足式(17).为了验证上述依概率关系,在本节实验中分别取两种不同的蒲丰距离l≤a和2a ≥l ≥a,观察PMB 算法的寻优结果并进行讨论.为了确定针长,参考文献[1]所得到的结果及本文定义2 可知,TF1 中的f1的极值分辨度大约为0.38,即针长l≈0.38 .分别取蒲丰距离a=0.5 (即l≤a)和a=0.2 (即 2a ≥l ≥a) 两种情况,求解精度ε=0.01,验证本文所提PMB 算法在无噪声环境和不同噪声环境下对TF1 中的f1中的所有极值点求解结果的依概率特性. 参照文献[32]中的噪声环境设置参数,分别取噪声方差σ2=0.01 和σ2=0.05,重复独立 实验50 次、100 次和200 次,PMB 算法求得的优化数值结果列于表3 中.表中σ2表示噪声方差,a表示蒲丰距离,Num_mean 表示算法平均搜索到的极值点数,Num_min 和Num_max 分别表示算法在重复实验中搜索到的极值点个数的最小值和最大值,η_mean 表示平均峰值检测率,η_global 表示全局极值点检测率.从表3 中可以看出: 表3 针对TF1 中的 f1 取不同蒲丰距离时PMB 算法在不同噪声环境下的优化结果Table 3 Optimization results of PMB algorithm for f1 of TF1 in different noise environments with different Buffon distances 当蒲丰距离a=0.2 时,即满足2a ≥l ≥a时,可得出如下结论: 1)在σ2=0.01 和σ2=0.05 的噪声环境下,重复独立实验50 次、100 次和200 次,PMB 算法都能找到所有极值点,η_mean 为100 %以上.重复独立实验中算法每次最少都能确保找到全部36 个极值点. 2)σ2=0.01 时算法最多能找到37 个极值点,σ2=0.05 算法最多能找到38 至40 个极值点,且σ2=0.05 时的η_mean 略高于σ2=0.01 时的η_mean,出现了η_mean 的值超出100 %的情况.这是由于噪声的干扰引入了众多的局部极值,使得算法找到的极值点数超出了原函数的极值点数.可以看出,随着噪声强度的增大,这种干扰越明显,噪声引入的局部极值点数越多. 3)在σ2=0.01 和σ2=0.05 的噪声环境下,重复独立实验50 次、100 次和200 次,PMB 算法都能找到所有全局极值点,η_global 都能达到100 %. 当蒲丰距离a=0.5 时,即满足l≤a时,有如下结论: 1)在σ2=0.01 的噪声环境下,重复独立实验50 次、100 次和200 次,PMB 算法的η_mean 都是82 %左右. 2)在σ2=0.05 的噪声环境下,重复独立实验50 次、100 次和200 次,PMB 算法的η_mean 都为88 %左右. 3)由于噪声干扰会引入局部极值点,因此当噪声强度增强时,PMB 算法的η_mean 有所增加. 4)在σ2=0.01 和σ2=0.05 的噪声环境下,重复独立实验50 次、100 次和200 次,PMB 算法都能找到所有全局极值点,η_global 都能达到100 %. 综上可知: 1)在相同的噪声环境下,PMB 算法的平均峰值检测率是一个固定概率,取决于算法的蒲丰距离a.对于TF1 中的f1,当 2a ≥l ≥a时,平均峰值检测率可达到100 %,当l≤a时,平均峰值检测率约为80 %以上.这一结果映证了推论1,即算法依固定概率找到函数的多个极值点. 2)在不同噪声环境下取不同蒲丰距离时,PMB算法都能找到TF1 中的f1的所有全局极值点.这一结果映证了推论2,即算法找到全局极值点的概率高于找到局部极值点的概率.表明PMB 算法具有较好的全局极值点优化性能. 3)噪声强度对峰值检测率有一定程度的影响.由于噪声干扰会引入局部极值点,因此当噪声强度增强时,PMB 算法的平均峰值检测率也会有所增加,其中包含了少数几个噪声引入的局部极值点. 首先定量分析噪声强度和蒲丰距离对PMB 算法求解结果的影响.分别取a=0.2 和a=0.5,求解精度ε=0.01 ,参照文献[32],分别设置σ2=0.01和σ2=0.05,PMB 算法对TF1 中的f1的一次寻优结果分别绘于图9~图14 中,其中,图11~图14的(a) 图呈现的是算法在同峰判断前找到的极值点,(b)图呈现的是算法经同峰判断后确定的极值点. 图11 σ2 =0.05,a =0.5 时PMB 算法对TF1 中的f1的寻优结果Fig.11 Optimization results for f1 of TF1 by PMB algorithm in noise environment with σ2 =0.05 and a=0.5 从图9~图14 中可以看出,算法求得的极值点个数受蒲丰距离的影响较为明显.蒲丰距离越小,PMB 算法找到的极值点越多,a=0.2 时可以找到全部极值点,a=0.5 时,PMB 算法不能找到全部极值点,个别局部极值点会被遗漏,但仍然可以找到所有全局极值点. 图9 a =0.2 时无噪声环境下PMB 算法对TF1 中的f1的寻优结果Fig.9 Optimization results for f1 of TF1 by PMB algorithm in noiseless environment with a =0.2 为进行定性分析,以全局极值点为例,将PMB算法求解TF1 中的f1得到的全局极值点的数值结果分别列于表4 和表5 中. 表4 a =0.2 时PMB 算法针对TF1 中的 f1 在不同噪声环境下的全局极值点优化数值结果Table 4 Numerical results of global extremum points for f1 of TF1 searched by PMB algorithm with a =0.2 under different noise environments 表5 a =0.5 时PMB 算法针对TF1 中的 f1 在不同噪声环境下的全局极值点优化数值结果Table 5 Numerical results of global extremum points for f1 of TF1 searched by PMB algorithm with a =0.5 under different noise environments 从表4 和表5 中可以看到,算法求解的定位误差和峰值误差同时受到蒲丰距离与噪声强度的影响.在蒲丰距离相同的情况下,随着噪声强度的增加,全局极值点的峰值误差Pf和定位误差Pl也随之增加.在噪声强度相同的情况下,蒲丰距离越小,全局极值点的定位误差Pl越小,定位精度越好. 除了全局极值点,PMB 算法还能求得多个局部极值点.取a=0.2,PMB 算法在σ2=0.01 和σ2=0.09 的噪声环境中的100 次独立重复实验结果列于表6 中. 从表6 中可以看出,当a=0.2 时PMB 算法可以找到TF1 中的f1的全部极值点.对比文献[1]的数值结果,可以验证PMB 算法在噪声环境下定位所有极值点的正确性.依据文献[1]的数值结果计算得到PMB 算法定位每个极值点的定位误差,绘于图15 中. 表6 P-MQHOA[1]算法与 a =0.2 时的PMB 算法针对TF1 中的 f1 在不同环境下的所有极值点求解结果对比Table 6 Comparison of total-extremum points for f1 of TF1 searched by P-MQHOA[1] algorithm and PMB algorithm with a =0.2 under different noise environments 从图15 中可以看出,随着噪声强度的增加,各个极值点的定位误差都随之增加.综上可知: 图10 a =0.5 时无噪声环境下PMB 算法对TF1 中的f1的寻优结果Fig.10 Optimization results for f 1 of TF1 by PMB algorithm in noiseless environment with a =0.5 1)蒲丰距离的大小会对PMB 算法找到极值点的个数以及求解极值点的定位精度产生主要影响.蒲丰距离越小,算法的全极值点寻优性能就越好,遗漏的极值点越少,峰值检测率越高,同时定位准确度越高. 2)噪声强度也会对PMB 算法的峰值检测率和求解极值点的定位精度产生影响.噪声强度的增加使得极值点的峰值误差Pf和定位误差Pl都随之增加,同时会引入更多的局部最优,使得峰值检测率增加. 本节实验选用文献[32]中的5 个测试函数,即表1 中TF1 函数f2~f6,检验本文所提PMB 算法在不同噪声环境下对不同函数的多极值点寻优能力,并与文献[32]提出的改进蝙蝠算法(Improved bat algorithm,IBA)进行对比分析. 图12 σ2 =0.01,a =0.5 时PMB 算法对TF1 中的f1的寻优结果Fig.12 Optimization results for f1 of TF1 by PMB algorithm in noise environment with σ2 =0.01 and a=0.5 参照文献[32] 的噪声环境设置,分别在σ2=0.01、σ2=0.05、σ2=0.07 和σ2=0.09 的噪声环境中利用PMB 算法对TF1 函数f2~f6进行优化求解,重复独立实验100 次,求解精度ε=0.01,优化数值结果列于表7 中.表中Mean 表示100 次重复独立实验得到的全局极值点的适应度平均值,MAPE 表示适应度平均值相对百分比误差. 从表7 中看到,全局极值点的适应度值受噪声的影响非常明显,随着噪声强度的增加,MAPE 随之增大.从TF1 中f2的寻优结果上可以看到,本文所提出的PMB 算法可以得到比IBA 算法更低的MAPE,而在其他函数上,PMB 算法的MAPE 高于IBA 算法,但依然呈现出平均相对百分比误差随着噪声强度的增加而增大的规律. 表7 PMB 算法对TF1 中的 f 2~f6 在不同噪声环境下的全局极值点优化数值结果Table 7 Numerical results of global extremum points for function f 2~f6 of TF1searched by PMB algorithm under different noise environments 图13 σ2 =0.05,a =0.2 时PMB 算法对TF1 中的f1的寻优结果Fig.13 Optimization results for f1 of TF1 by PMB algorithm in noise environment with σ2 =0.05 and a=0.2 图14 σ2 =0.01,a =0.2 时PMB 算法对TF1 中的f1的寻优结果Fig.14 Optimization results for f1 of TF1 by PMB algorithm in noise environment with σ2 =0.01 and a=0.2 图15 a =0.2,PMB 算法在不同噪声环境下对TF1 中的 f1 求解所有极值点的定位误差Fig.15 Positioning errors of total-extremum points for f1 of TF1 searched by PMB algorithm with a =0.2 under different noise environments 尽管在TF1 中f3~f6上PMB 算法得到的MAPE 更高,但是在噪声环境下衡量算法的优化性能应该更关注算法的定位误差指标.在无噪声环境下,衡量算法的寻优性能往往通过考察算法求得的全局极值点的适应度值与真实适应度值的误差来得到,例如,函数f2在无噪声情况下的全局极值点是−176.1375 (−1.3068,−1.4248),如果算法找到的极值点的适应度值近似为 −176.1375,则通常认为算法已经找到了全局极值点,同时也证明了算法的全局优化性能较好.而在噪声环境下,点 (−1.3068,−1.4248)处的函数值将发生变化,偏离原来的函数值 −176.1375,因此,衡量算法在噪声环境下优化求解性能的指标不应是找到函数值为 −176.1375 的点,这样的点极有可能已经不是原函数的全局极值点,算法优化求解的目的应该是力图找到(−1.3068,−1.4248)这个点,因为它才是原函数的全局极值点位置.因此,在噪声环境下,求解极值点的坐标显得尤为重要,它是判断算法是否能够找到全局极值点的有力依据,而定位误差则反映了算法定位全局极值点的精确度. PMB 算法在不同噪声环境下求解TF1 中f2~f5得到的全局极值点的定位误差分别列于表8和表9 中. 从表8 和表9 中可以看到,PMB 算法求出了每个极值点对应的坐标值,明确了全局极值点的位置,可以直观地与无噪声时的真实极值点位置做对比,从而证明PMB 算法在噪声环境下定位全局极值点的准确性.而文献[32]只给出了IBA 算法求解全局极值点的Pl结果,并未给出具体的坐标值. 表8 PMB 算法对TF1 中 f 2~f4 在不同噪声环境下得到的全局极值点的定位误差Table 8 Positioning errors of global extremum points for function f 2~f4 of TF1 searched by PMB algorithm under different noise environments 表9 PMB 算法对TF1 中的 f 5~f6 在不同噪声环境下的全局极值点优化数值结果Table 9 Numerical results of global extremum points for function f 5~f6 of TF1searched by PMB algorithm under different noise environments 同时,对比两种算法得到的Pl值可以看到,除了4 个极值点(f2在σ2=0.09 时、f4在σ2=0.01和σ2=0.05 时、f6的第3 个极值点在σ2=0.09时)外,PMB 算法在不同噪声环境下求解TF1 中f2~f5得到的全局极值点的定位误差均小于IBA算法得到的结果.即PMB 算法在不同噪声环境下对TF1 中f2~f5的全局极值点定位比IBA 算法更为精确. 此外,文献[32]的IBA 算法只给出了TF1 中f2~f5的全局极值点求解结果,对其他局部极值点并未讨论.而PMB 算法运行一次即可得到全部极值点和多个局部极值点.以TF1 中f2为例,取蒲丰距离a=1 时,PMB 算法运行一次得到的优化结果如图16 所示. 从图16 中可以看出,TF1 的f2是一个多峰函数,其在σ2=0.05 的噪声环境下出现了无穷多的噪声峰值点,PMB 算法有效的找到了它的1 个全局极值点及170 个局部极值点.综上可知: 图16 a =1,σ2 =0.05,PMB 算法对TF1 中f2的寻优结果Fig.16 Optimization results for f2 of TF1 by PMB algorithm in noise environment with σ2 =0.05 and a=1 1) PMB 算法在噪声环境下可以一次性得到极值点的适应度值和对应坐标,可以为生产实际提供明确的决策变量. 2) PMB 算法求解的极值点位置精度总体高于IBA 算法. 3) PMB 算法不仅能够求得噪声环境下的全局极值点位置,还能得到多个局部极值点的位置,为生产实际提供更多的备选方案. 本节实验选用文献[46]中给出的CEC2013 推荐基准函数,即表2 中的函数f1~f28,检验PMB算法在噪声环境下对多维函数寻优的有效性,并与PSO 算法进行对比分析.为了检验PMB 算法和PSO 算法在噪声环境中寻优的准确性,首先给出了无噪声环境下的优化结果,然后与噪声环境下的优化结果进行了比较.实验中改进的斐波那契法的求解精度ε设置为1 × 10−5,针对CEC2013 的5 维测试函数采用5 级划分策略. 1) 无噪声环境下的比较 PMB 算法和 PSO 算法在无噪声环境下对TF2 测试函数进行寻优,获得的优化结果列于表10中,其中t是完成一次实验的时间. 从表10 中可以得出以下结论: 表10 PMB 算法和PSO 算法对TF2 在无噪声环境下得到的全局极值点Table 10 Global extremum points of TF2 obtained by PMB algorithm and PSO algorithm in noiseless environment a)从函数值的角度来看,PMB 对 24 个测试函数得到的函数最小值更接近这些函数的全局最小值,精度高于PSO.PMB 得到的这24 个测试函数的数值结果已在表中用粗体标示出.PSO 仅在4 个函数上得到的极值比PMB 更接近函数的全局最小值,在其他24 个函数上陷入了局部最优.且PSO在单峰函数f2、多峰函数f8~f15和组合函数f21~f28上得到的极值点的适应度值偏离函数的全局最小值较大,在表中已用下划线标示出.其中,在函数f2上的偏离值为691.6966.这说明PSO 算法很容易陷入局部最优,而PMB 算法具有很好的全局寻优性能,不容易陷入局部最优. b)对比两个算法运行的时间t可以看出,为了跳出局部最优和保留多个极值点,PMB 算法需要花费比PSO 算法更多的计算时间. 2)σ2=0.01 的噪声环境下比较 PMB 算法和 PSO 算法在σ2=0.01 的噪声环境下对TF2 测试函数进行寻优,获得的优化结果分别列于表11 和表12 中. 对比表11 和表12 中可以得出以下结论: 表11 PSO 算法对TF2 在 σ2 =0.01 的噪声环境下得到的全局极值点Table 11 Global extremum points of TF2 obtained by PSO algorithm in noise environment of σ2 =0.01 表12 PMB 算法对TF2 在 σ2 =0.01 的噪声环境下得到的全局极值点Table 12 Global extremum points of TF2 obtained by PMB algorithm in noise environment of σ2 =0.01 表12 PMB 算法对TF2 在 σ2 =0.01 的噪声环境下得到的全局极值点 (续表)Table 12 Global extremum points of TF2 obtained by PMB algorithm in noise environment of σ2 =0.01 (continued) a) 通过比较Pl的数值结果,可以看出 PMB在25 个测试函数上得到的极值点的Pl小于PSO,这25 个数值结果已在表11 中用粗体标示出.这表明PMB 在噪声环境和无噪声环境下获得的极点位置偏差很小,说明PMB 算法具有良好的稳定性和抗噪性能.然而,PSO 在噪声环境中获得的结果与在无噪声环境中获得的结果差距较大,其中在20个测试函数上的Pl值超过了10,在表11 中已经用下划线标示出.这表明PSO 的稳定性差,这使得它易受噪声干扰,抗噪性能较差. b)对比两个算法的运行时间t可以看出,在噪声环境中,PMB 需要花费更多的时间来跳出由噪声引起的局部最优.PSO 的收敛速度在噪声的影响下也会减慢,但往往会收敛到噪声引起的局部最优. 3) 多极值点寻优结果 PMB 算法可以在噪声环境中实现多极值点优化.对于多峰函数f6,f7,f8,f16,f19和f20,PMB 算法得到的多个极值点的数值结果列于表13中.由于篇幅有限,每个函数只列出 5 个极值点的数值结果. 从表13 中可以看出,PMB 算法可以在无噪声环境和噪声环境中找到多峰函数的多个极值点,说明PMB 算法可以在噪声环境中实现多维、多峰函数的多极值点优化. 表13 PMB 算法对TF2 中部分函数在无噪声环境和 σ2 =0.01 的噪声环境下的多极值点优化结果Table 13 Optimization results of multiple extremum points for some functions of TF2 obtained by PMB algorithm in noiseless environment and noise environment of σ2 =0.01 表13 PMB 算法对TF2 中部分函数在无噪声环境和 σ2 =0.01 的噪声环境下的多极值点优化结果 (续表)Table 13 Optimization results of multiple extremum points for some functions of TF2 obtained by PMB algorithm in noiseless environment and noise environment of σ2 =0.01 (continued) 综上可知: a) PMB 算法可以在无噪声和噪声环境中准确定位测试函数的真正全局极值点,反映了PMB 算法良好的稳定性和抗噪性能.PSO 算法在无噪声环境中容易陷入局部最优,而在噪声环境中容易陷入由噪声引起的局部最优.因此,PSO 算法的稳定性和抗噪性能较差. b)PSO 算法运行一次只能获得一个极值点,而PMB 算法运行一次可以获得多个极值点.表明PMB 算法可以在噪声环境下找到多维、多峰函数的多个全局和局部极值点. c)为了跳出局部最优和保留多个极值点,PMB算法需要花费比 PSO 算法更多的计算时间.PSO的收敛速度在噪声的影响下也会减慢,但它更容易收敛到局部极值点. 针对噪声环境下的多极值点寻优,本文采用一种定概率的方法来解决这类随机优化问题.从蒲丰投针的定概率原理出发,提出了噪声环境下基于蒲丰距离的依概率多峰优化算法(PMB).理论推导证明了蒲丰距离和极值分辨度依概率影响算法的峰值检测率.验证了在不同的噪声条件下,PMB 算法依概率收敛到函数的多个极值点,且算法找到全局极值点概率高于找到局部极值点的概率;验证了蒲丰距离影响PMB 算法的全极值点寻优性能和求解极值点的定位精度,噪声强度影响算法的峰值检测率和定位精度;对比噪声环境下的改进蝙蝠算法,PMB 算法具有更好的极值点定位精度和较好的多极值点寻优特性;对比PSO 算法在5 维CEC2013测试函数集上的表现,PMB 算法具有更好的多维函数寻优能力、抗噪声性能和多极值点寻优性能.从而使得PMB 算法能在生产实际中提供更准确的决策变量和更多的优化方案.噪声环境下的依概率优化算法的理论和应用研究刚刚起步,作者后续工作将进一步研究提高PMB 算法对高维问题的处理效率.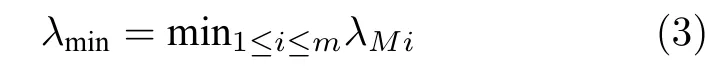
1.2 评价指标


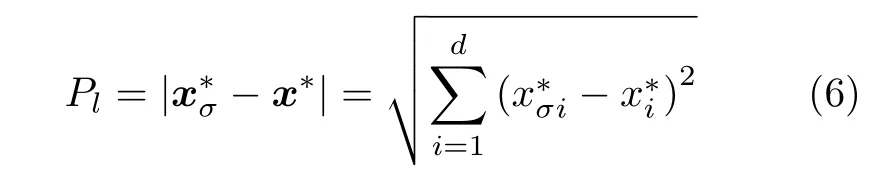
2 噪声环境下基于蒲丰距离的依概率多峰优化算法
2.1 算法基本原理
2.2 蒲丰投针原理与蒲丰距离


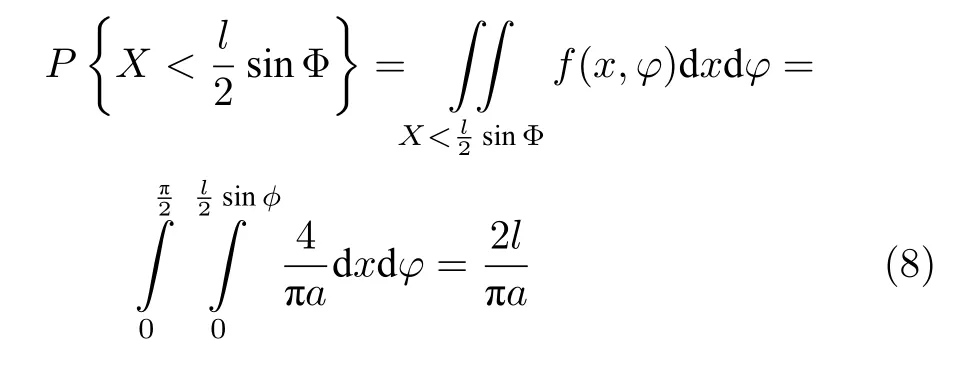
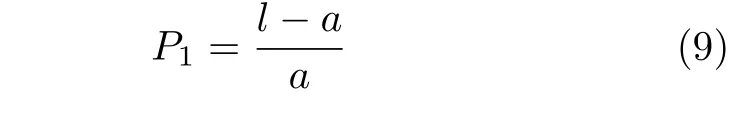

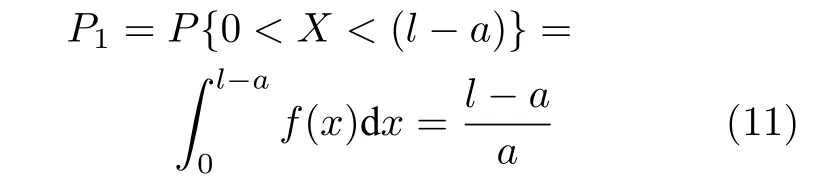
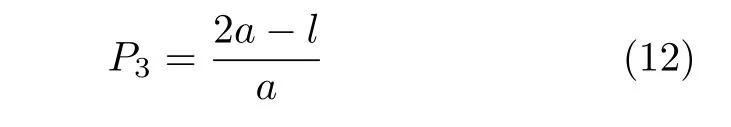

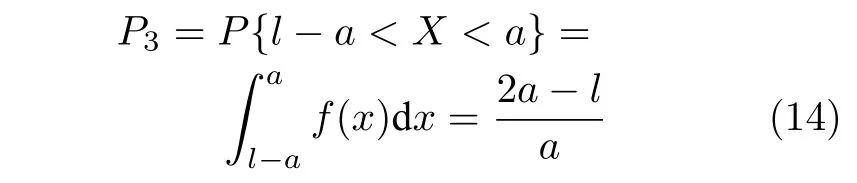

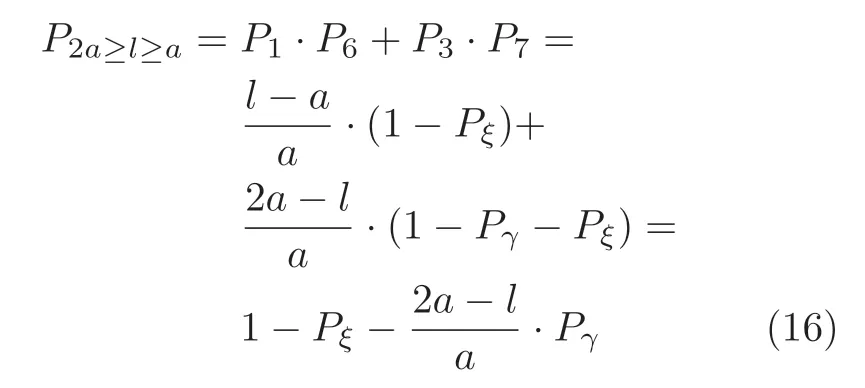
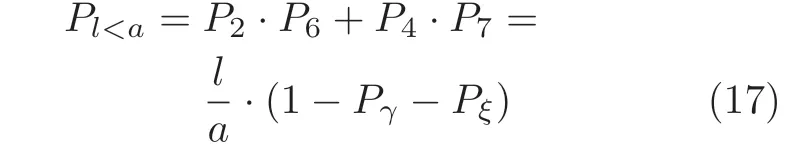
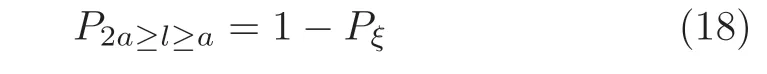
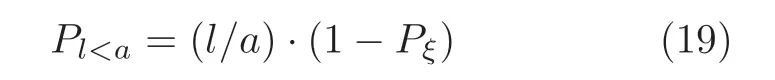
2.3 改进的斐波那契法
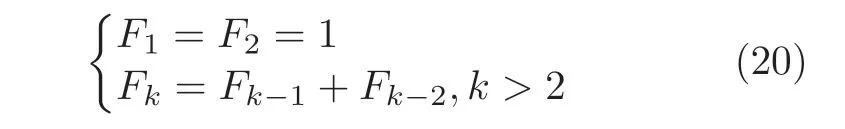

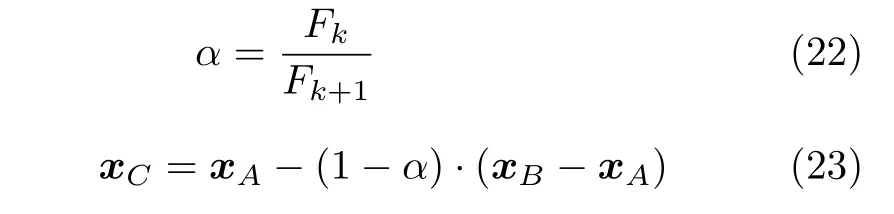

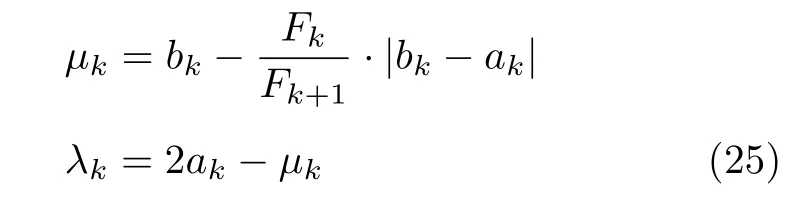
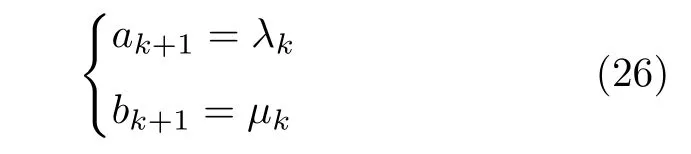
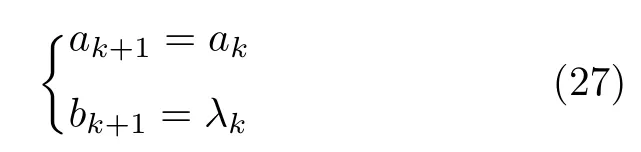

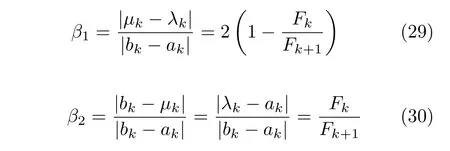

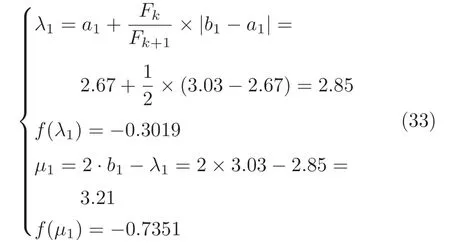
2.4 PMB 算法流程
2.5 PMB 算法的多级划分策略

3 实验仿真与分析
3.1 实验设计与测试函数
3.2 PMB 算法依概率收敛特性验证
3.3 噪声强度与蒲丰距离对PMB 算法寻优结果的影响

3.4 PMB 算法在不同噪声环境下的多极值点寻优能力

3.5 PMB 算法在CEC2013 测试函数上与PSO算法的对比
4 结论

