基于多参数灵敏度分析与遗传优化的铁水质量无模型自适应控制

温亮 周平

高炉是钢铁制造最主要的大型冶金反应器之一.如图1 所示,整个高炉炼铁系统分为高炉本体、给料系统、热风系统、煤粉喷吹系统、高炉煤气处理系统及出铁系统等几个子系统.高炉炼铁是一个持续不中断的过程,在整个流程中,铁矿石、焦炭、溶剂按一定比例和布料制度分批次逐层从高炉顶部经由旋转溜槽装载到炉喉中.同时,煤粉由喷枪喷入高炉风口,冷空气、氧气在热风炉中加热到约1200°C 左右后经由风口鼓入高炉炉腹部分.上部调剂加入的焦炭在风口前经过燃烧产生大量高温煤气,煤气不断向上运动,与下降的炉料相遇,发生一系列复杂的物理化学反应,将铁从铁矿石中还原出来.上升的高炉煤气最终从炉顶回收,经过重力除尘、余压发电等环节回收再利用.下降的炉料经过加热、还原、熔化等物理化学变化,最终生成液态的生铁和炉渣,并且分别从铁口和渣口排出[1−4].

图1 高炉工艺流程示意图Fig.1 Diagram of BF ironmaking process

高炉炼铁生产的主要目的是持续、稳定、高效、低能耗地生产铁水,为后续转炉炼钢等下游工序提供优质铁水.因此,对整个高炉炼铁过程的优化控制通常可以等价于对高炉生产最终产品— 铁水质量的控制.目前,铁水质量的好坏通常由两大参数来表征,分别为铁水温度(Molten iron temperature,MIT)和铁水硅含量([Si]).其中MIT 是反映铁水物理热的重要指标,MIT 高有利于后续转炉炼钢的稳定操作和自动控制,铁水温度过低会影响铁元素氧化过程和熔池的温升速度,不利于成渣和去除杂质,容易发生喷溅.我国炼钢规范规定转炉炼钢入炉铁水的温度应大于1250°C,并且要相对稳定.考虑到铁水在运输和待装过程中损失的热量,质量优良的铁水温度应控制在1480°C～1530°C 为宜.此外,[Si]是反映铁水化学热的重要指标.铁水[Si] 高,渣量增加,有利于去除铁水中的有害物质磷、硫.[Si] 高还会增加转炉热源,提高废钢比.但[Si] 过高会使生铁变硬变脆,收得率降低且容易引起喷溅.另外,[Si]高使渣中SiO 含量过高,影响石灰的渣化速度,延长吹炼时间,同时也会加剧对炉衬的冲蚀.通常,质量合格的铁水[Si] 应控制在0.5%～0.7%[1−5].

高炉炼铁是一个多相、多场耦合严重的强非线性时变动态过程,机理不清,数学模型难以建立,或者建立的模型由于理想假设条件太多而难以实际应用[1−2].因此,传统基于模型的控制器设计策略很难应用于高炉多元铁水质量控制,而仅依赖于系统输入输出数据的数据驱动建模与控制方法就显示了诸多优越性.到目前为止,基于数据驱动的方法针对多元铁水质量的建模已经有了大量的研究成果,例如文献[6] 中的多信息融合时间序列神经网络模型,文献[2]、[7−8] 的随机权神经网络模型,文献[9−10]的支持向量机模型,文献[1]、[11] 的子空间模型等,但是却鲜有关于高炉炼铁过程直接数据驱动控制的相关研究成果和文献报道.

目前,直接数据驱动控制已受到学术界和控制工程界越来越广泛的关注,发展了多种数据驱动控制方法和技术,例如无模型自适应控制(Model free adaptive control,MFAC)[12]、懒惰学习控制[13]、虚拟参考反馈整定(Virtual reference feedback tuning,VRFT)[14]、迭代反馈整定(Iterative feedback tuning,IFT)[15]、去伪控制(Unfalsified control,UC)[16]、基于相关性分析的控制器整定(Correlation-based controller tuning,CbT)[17]等.总的来说,这些数据驱动方法大体可分为两类,第一类是控制器结构确定,控制器参数利用输入输出测量数据离线整定的数据驱动控制方法[18],比如VRFT、CbT、UC 等.高炉内部严酷的冶炼环境决定了基于工业高炉系统数据实验的不可实现性,而高炉冶炼过程中复杂的动态特性又使得很难从理论上确定一个合适的控制器结构,因此,这种控制方法并不适用于高炉多元铁水质量的控制.另一类数据驱动控制方法则假设控制器结构不确定[18],这种控制方法的一个典型代表就是MFAC.该方法由北京交通大学的侯忠生教授在文献[19] 中针对单输入单输出离散时间非线性系统首次提出,其后在文献[20] 中拓展到了多输入多输出动态系统.该方法针对离散时间非线性系统使用了一种新的动态线性化方法及一个称为伪雅可比矩阵的新概念,在闭环系统的每个动态工作点处建立一个等价的动态线性化数据模型,然后基于此等价的虚拟数据模型设计控制器[21].因此,鉴于高炉冶炼系统机理模型难以建立,可将MFAC 方法作为该研究领域的一条新的思路.

综上,本文针对复杂高炉炼铁过程多元铁水质量难以采用常规方法进行控制的难题,综合采用基于紧格式动态线性化(CFDL) 的无模型自适应控制方法(CFDL-MFAC)、递推子空间模型辨识方法、多参数灵敏度分析技术以及遗传算法优化技术,研究高炉炼铁过程多元铁水质量的无模型自适应控制问题.首先,针对高炉铁水质量参数控制系统建立CFDL-MFAC 控制器.然后,为了对控制器的诸多关键参数进行优化和整定,基于实际高炉工业数据建立多元铁水质量的递推子空间动态模型,并用建立好的CFDL-MFAC 控制器和多元铁水质量递推子空间动态模型进行蒙特卡罗(Monte Carlo) 模拟实验.根据实验结果,集成采用多参数灵敏度分析(Multi-parameter sensitivity analysis,MPSA) 和参数遗传优化(Genetic algorithm,GA) 技术离线整定控制器参数.最后,基于实际工业现场运行数据进行工业实验和比较分析.

1 控制策略

高炉冶炼过程为连续的强非线性时变动态过程,高炉内部伴有高温、粉尘、强噪声等常规检测设备所惧怕的问题,因此反应状态不清,机理研究难以进行.其状态信息主要来源于丰富的外围检测设备及黑箱状态下各项操作参数设定对应的铁水质量参数化验记录.这些数量庞大的历史数据被业内人士认为应当包含着一些尚未发现的高炉知识,有必要进行深入研究与挖掘.由此,本文以高炉历史数据为出发点,提出如图2 所示整体采用CFDL-MFAC 数据驱动在线控制与控制器参数MPSA-GA 离线整定的控制策略.

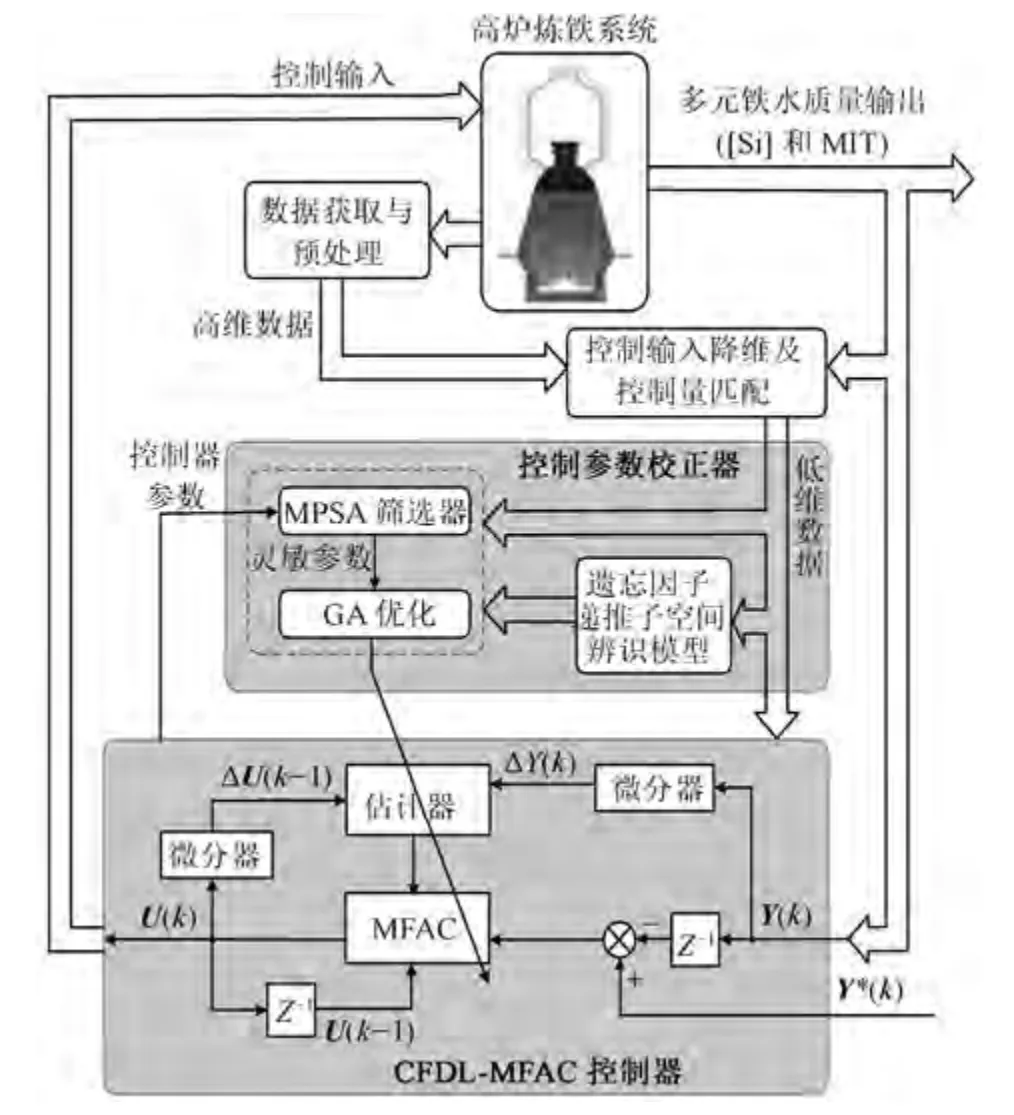
图2 CFDL-MFAC 控制策略Fig.2 Control strategy of CFDL-MFAC

1) 首先,采用典型相关性分析(Canonical correlation analysis,CCA)、相关性分析(Correlation analysis,CA)、MPSA 相结合的方法从所有高炉主体参数中选出对MIQ (Molten iron quality) 参数影响最大的可控变量作为建模与控制的输入变量,并采用灰色关联分析的方法对控制量与铁水质量指标之间的主要对应关系进行匹配;

2) 采用基于遗忘因子的递推子空间辨识方法建立铁水质量参数动态模型,并依据此模型建立参数整定所需的优化模型;

3) 依据基于紧格式动态线性化的无模型自适应控制(Compact form dynamic linearization-Model free adaptive control,CFDL-MFAC) 方法建立多元铁水质量的数据驱动控制器,并用此数据驱动控制器来控制建立的递推子空间数据模型,从而进行针对控制参数的Monte Carlo 实验;

4) 针对高炉炼铁过程铁水[Si] 与MIT 的控制难题,所提数据驱动控制根据Monte Carlo 实验结果,采用MPSA 方法分析各个控制器参数的灵敏度,选出灵敏参数;

5) 以递推子空间数据模型为指标,依据遗传算法的思想整定灵敏参数,以此提高控制器的控制性能;

6) 用参数整定后的CFDL-MFAC 控制器在线控制高炉多元铁水质量,以此适应高炉炼铁过程的慢时变特性,使高炉顺行,铁水输出质量稳定.

2 控制算法

由图2 可知,CFDL-MFAC 控制器和控制参数整定模块为本文所提控制策略中最主要的两个部分,因此本节将围绕这两部分进行展开.第2.1 节将依据高炉炼铁系统的具体特性给出CFDL-MFAC 控制器的设计过程,第2.2 节将依据第2.1 节中给出的CFDL-MFAC 控制算法设计相应的参数整定算法.

2.1 CFDL-MFAC 数据驱动控制算法

采用如下多输入多输出(Multiple input multiple output,MIMO) 离散时间非线性方程来描述高炉铁水生产过程:

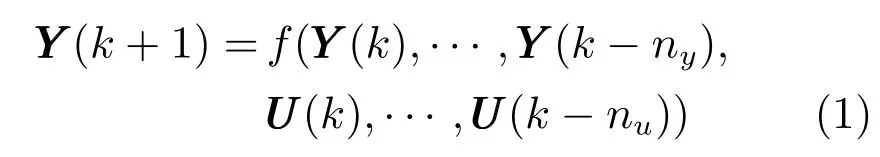
式中:UUU(k)∈Rm,YYY(k)∈Rn分别表示k时刻系统的m维控制输入和n维多元铁水质量输出;nu,ny为表征系统阶次的未知正整数;f(·) 为未知非线性映射函数.在这里,n维多元铁水质量输出指[Si]和MIT 两个铁水质量指标,m维控制输入指从高炉主体参数中选出的对多元铁水质量输出影响最大的几个控制输入变量,将在第3 节数据实验时具体给出.

针对上述系统的无模型自适应控制器设计过程如下:

1) 紧格式动态线性化:为了便于铁水质量数据驱动自适应控制律的设计,在每个动态运行工作点建立一个等价线性化动态模型.根据文献[21] 提出的无模型自适应控制(MFAC) 理论,此等价线性化模型的建立需要系统满足如下两条假设条件.

假设1[21].系统对应的非线性映射函数f(·) 对系统控制量在系统输入阶次nu范围内各个时刻的分量UUU(k),···,UUU(k −nu) 存在连续偏导数.

假设2[21].系统满足广义Lipschitz 条件,即在任意两个时刻k1,k2(k1,k2≥0 且k1k2),当UUU(k1)/UUU(k2) 时,系统输入与系统输出之间满足

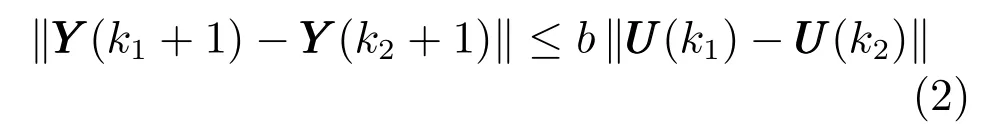
式中,b>0 是一个常数.

上述假设仅是对于一般非线性系统的典型约束,由于多元铁水质量控制系统亦满足能量守恒,有界输入定会产生有界输出.具体来说,[Si] 存在一个确定的上界100%和下界0%,在煤粉、焦炭及热风的供应量范围内,MIT 也不会无限升高,所以,在任意两个时刻,一定能够通过计算获得[Si]、MIT 变化量与高炉本体主要控制参数变化量之间的有界系数,因此可认为高炉系统满足假设1 和假设2,由此可给出如下引理.

引理1[20].任意时刻k,若有‖ΔU(k)‖=‖UUU(k)−UUU(k −1)‖/=0,则一定能够找到一个时变参数矩阵Φc(k)∈Rn×m,使得系统(1) 可转化为如下紧格式动态线性化(CFDL) 模型:

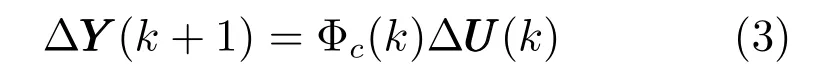
且对任意时刻,Φc(k) 是有界的,称Φc(k) 为伪雅可比矩阵(Pseudo Jacobian matrix,PJM).

2) 控制量求解:取准则函数如下:

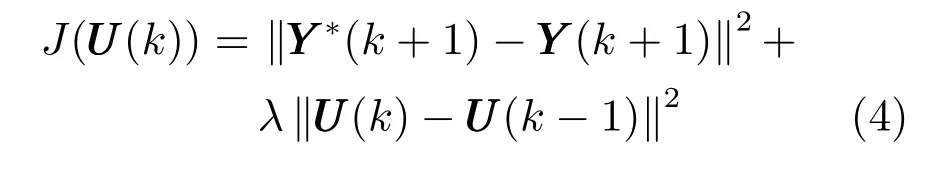
式中,第1 项的引入是为了使多元铁水质量输出能够跟踪设定的参考轨迹,其中YYY ∗(k+1) 是k+1 时刻期望输出值;第2 项的引入是考虑到高炉本体控制参数喷煤量、富氧流量等的变化均需要过渡时间,不能突变,过大的控制量变化难以短时间实现,为此弱化控制增量,减轻执行机构负担;λ >0 是控制增量惩罚项的权重因子.

将式(3) 代入式(4),并对UUU(k) 求偏导,令其为零,得

由于算法(5)中包含矩阵求逆运算,当系统输入输出维数很大时,求逆运算非常耗时,不利于实际应用,将式(6) 替代式(5) 从而避免矩阵求逆运算.

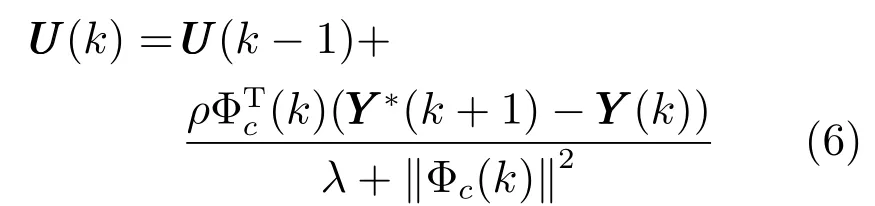
式中,ρ ∈(0,1] 是为了使控制算法更具一般性而加入的步长因子.

3) 伪雅可比矩阵估计算法:由于多元铁水质量控制系统模型未知,因此,式(6) 中伪雅可比矩阵Φc(k) 无法得知,需要对其进行在线估计.考虑如下估计准则函数:

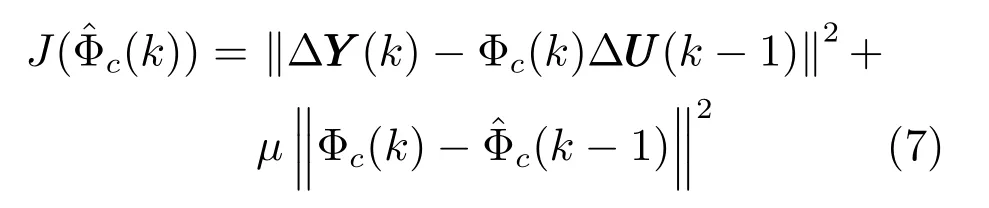
式中,µ>0 是权重因子:为Φc(k −1) 的估计值.极小化准则函数,可得PJM 的估计算法如式(8) 所示.同样,为避免矩阵求逆运算,将上式替换为如式(9) 所示形式.

式中,η ∈(0,2] 为引入的步长因子,作用与式(7) 中的ρ相同.

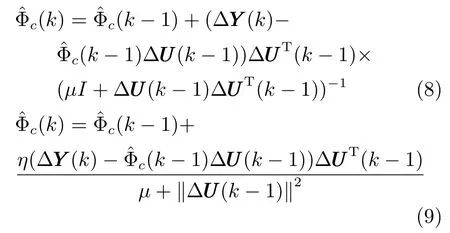
4) 算法重置机制:由于高炉多元铁水质量参数每次出铁仅能获得一组数据,因此采样间隔时间较长,参数时变程度较大.为了使PJM 估计算法能够更好地对时变参数进行跟踪,引入如下算法重置机制:

上述中,式(6)、(9)、(10) 即为CFDL-MFAC控制器的基本结构框架,该控制器结构框架的确定完全依据基于紧格式动态线性化的多输入多输出无模型自适应控制方法,因此文献[20] 中给出的稳定性数学证明在本文中依然成立.

2.2 基于多参数灵敏度分析和遗传优化(MPSAGA)的(CFDL-MFAC)参数整定方法

由上述第2.1 节可知,CFDL-MFAC 控制器有7 个固定的控制参数(λ,µ,ρ,η,α,b1,b2) 和m×n个伪雅可比矩阵初值.若假定控制器输入输出维度均为2 维(即m=n=2),则CFDL-MFAC 控制器将包含4 个伪雅可比矩阵初值(φ11,φ12,φ21,φ22),共11 个可调变量.这些控制参数及伪雅可比矩阵初值会严重限制控制器的控制性能.同时,由于MFAC方法在高炉多元铁水质量控制中没有实际应用,缺乏相应的经验取值,其他系统应用中采用的参数在高炉系统中并不适用,因此需要引入优化算法来对控制器参数进行整定.但由于参数较多,全部优化相当于在一个11 维的参数空间中寻找一个全局最优解,时间成本较大,且通过实验发现部分参数的取值对控制结果的影响较小甚至可以忽略不计,因此考虑对各个参数进行灵敏度分析.

常用于参数灵敏度分析的方法有直接求导法、因子扰动法等.直接求导法的思路是根据灵敏度的含义,直接对系统参数进行求导[22−23],这种方法适用于能写出明确表达式的系统,对高炉铁水质量控制系统并不适用.因子扰动法[24]的思路是指变化一个参数的数值,其他参数保持不变,以输出变量与输入变量的比值为指标,单独分析每个参数的灵敏度,然后综合所有分析结果.显然,这种方法忽略了参数之间的相关性,只是一种局部的分析方法.本文采用多参数灵敏度分析方法[25]来分析参数的灵敏度,多参数灵敏度分析基于Monte Carlo 实验进行.Monte Carlo 实验是以概率统计理论为基础,依据大数定律(样本均值替代总体均值),利用电子计算机数字模拟技术,解决一些很难直接用数学运算求解或用其他方法不能解决的复杂问题的一种近似计算方法[26].Monte Carlo 实验同时变化所有参数的取值,多次运行控制器,相比于因子扰动法中只改变单个参数的取值,能够更真实、全面地模拟实际物理过程,包含了参数之间的相关性.多参数灵敏度分析综合考虑多次运行结果,同时给出所有参数的灵敏度,灵敏度不是由输出变化值与参数变化值的比值来描述,而是依据定义的目标函数,将多次运行结果按给定指标进行分类,分别绘制累计频率曲线,依据统计学的原理来判断[27].

本节基于MPSA 和GA 技术,提出一种CFDLMFAC 数据驱动控制器参数整定方法.首先采用递推子空间辨识方法建立高炉多元铁水质量局部动态模型,然后依据此模型建立离线参数优化模型,采用MPSA 技术通过该模型来对CFDL-MFAC 控制器的参数及伪雅可比矩阵初值的相对重要性做出统计评价,然后基于遗传优化技术设计适用于高炉铁水质量控制系统的优化流程,以该流程来对MPSA 分析后灵敏度高、对控制器性能影响较大的参数及初值进行整定,其余参数及初值在其限定范围内选取适当的值.

2.2.1 多元铁水质量动态模型的建立

采用MPSA 方法分析参数灵敏度和遗传参数优化均需要进行大量试验获取测试性输入输出数据,包括随机产生控制变量加载在高炉炼铁系统,以获取相应的铁水质量指标输出.由于高炉操作存在的危险性,这些试验操作无法在真实高炉系统上来完成.为此,本文结合文献[28] 中的基于遗忘因子的递推子空间辨识方法建立高炉多元铁水质量系统的动态模型,该动态模型是由高炉离线输入输出数据推导出的一系列子空间模型参数组.

对于式(1) 表述的高炉炼铁系统,假设在k时刻,多元铁水质量输出可由过去时刻的系统输入输出信息和当前时刻控制量输入推算出来,其关系为

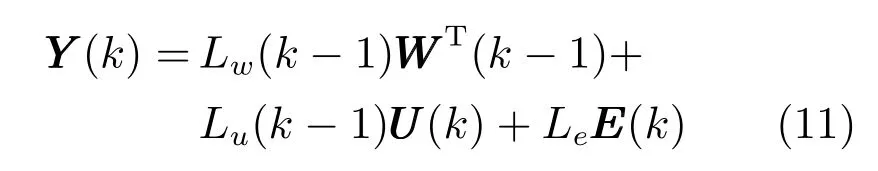
式 中,WWW(k −1)=[YYY(k −1)T,UUUT(k −1)],Lw、Lu、Le分别为状态子空间矩阵、确定输入的子空间矩阵和随机输入的子空间矩阵,EEE(k) 为零均值白噪声向量.则当k →∞时,当前时刻输出预测为

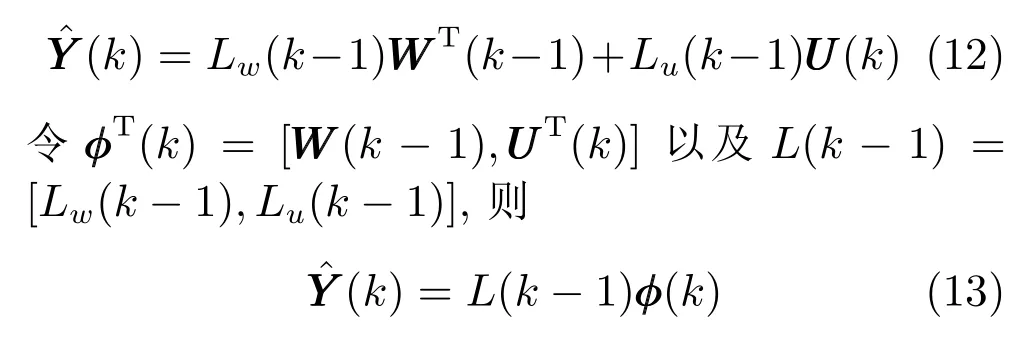
系数矩阵参数集L={L(1),L(2),···,L(k),···,L(Z)},k=1,···,Z即为所需求解的多元铁水质量动态模型,其中Z为动态模型采样时间长度.每一组参数L(k) 可以通过求解如下最小二乘问题来获得:

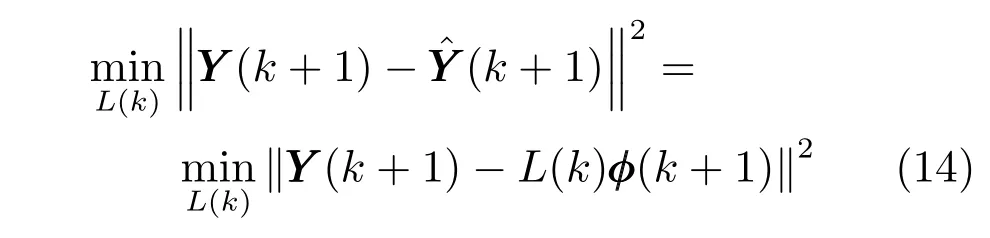
引入递推最小二乘法来求解上述问题,递推方法如式(15)～(17):

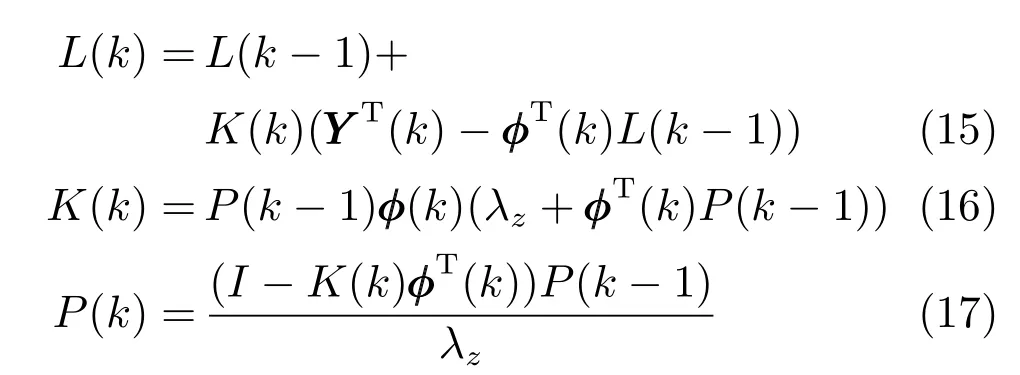
式中,K(k) 是增益矩阵,P(k) 是协方差矩阵,λz为遗忘因子.

2.2.2 CFDL-MFAC 参数优化问题描述

控制器参数整定的主要目的是获取一组较优的控制器参数以提高控制器性能.若以控制器控制前述的多元铁水质量动态模型跟踪输出参考曲线T个采样周期的累计均方误差为控制器性能衡量指标,则CFDL-MFAC 控制器参数优化问题可用如式(18) 所示优化模型来描述:

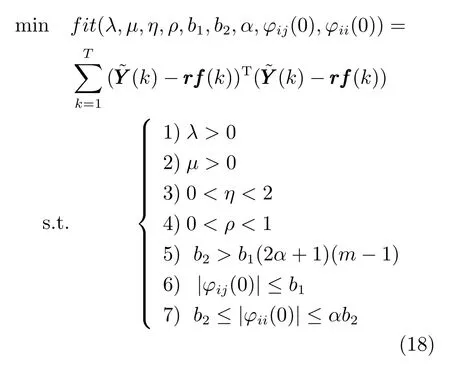
式中,i=1,···,m,j=1,···,n,j/=i;约束5)～7) 的引入是为了保证伪雅可比矩阵初值满足严格对角占优条件;为在k时刻控制器输出控制量UUU(k) 作用下多元铁水质量动态模型的输出向量,可由式(13) 计算得到;rf为输出参考曲线,因为真实高炉系统的铁水质量输出期望值的变化通常为阶跃变化,因此将其定义为一个多次跳变的分段函数,以此使优化后的参数对系统设定值跳变具有较好的适应性.

由式(18) 可知,该参数优化问题为一个含有非线性不等式约束的混合约束优化问题,为了便于优化算法的设计计算,采用惩罚法来松弛式中的各项约束.当参数集不满足任意一项约束时,为目标函数值加上高额惩罚,使该参数集无法成为最优参数集,由此将原混合约束优化问题转化为如下无约束优化问题:

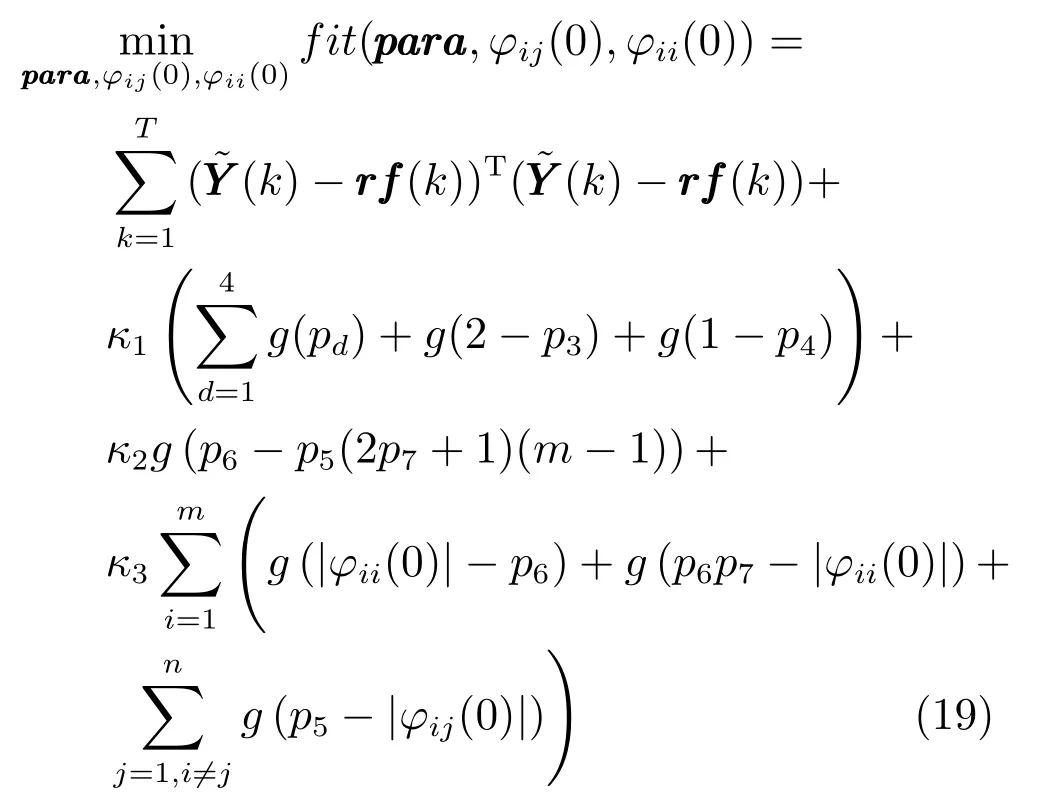
式中:para=[p1,···,p7]=[λ,µ,η,ρ,b1,b2,α]为控制参数向量;κ1,κ2和κ3分别为对应约束1)、4)、5)、6) 和7) 的惩罚因子,一般选取为一个相对正常适应度值较大的数值;g(·) 为如式(20) 的分段函数.

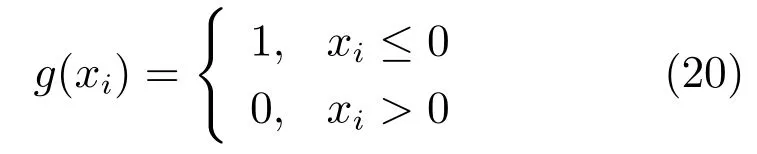
2.2.3 基 于 MPSA 与 改 进 GA 的 CFDLMFAC 数据驱动控制器参数整定

针对式(19) 的无约束优化问题,结合改进的遗传算法及多参数灵敏度分析[23]技术,提出CFDLMFAC 数据驱动控制器的参数整定方法,如下所示:

1)基于Monte Carlo 实验的控制器多参数灵敏度分析:根据高炉过程实验经验,在满足式(19) 的约束条件下设置每个控制参数的取值范围.在每个参数限定的取值范围内,生成N个服从均匀分布的独立随机数,构成N组随机分布的参数集.应用生成的N个参数集,分别运行控制器,根据下式计算损失函数值:

依据损失函数值的大小,将N个参数集分为两组,分别为损失函数值“可接受的” 参数集和损失函数值“不可接受的” 参数集;分类准则依据制定的“主观指标”,即将N个损失函数值按大小排序,选取后50%分位点处的损失函数值作为“主观指标”,如果损失函数值大于“主观指标”,那么该参数组被分类为“不可接受的” 参数组;反之,如果损失函数值小于“主观指标”,那么对应的参数组被分类为“可接受的” 参数组.

对每个参数,比较“可接受” 的参数集和“不可接受” 的参数集两组中参数值的分布情况.如果两组分布形式相同,则表明该参数不灵敏;反之,则表明该参数较灵敏.若一组参数中不同数值的个数为Nv,则其中第j(1≤j ≤Nv) 个参数值对应的累计频率Cfj的计算方法如式(22) 所示

式中vi为第i个数值出现的频次.

对每个参数,绘制累计频率曲线,并根据式(23)计算累计频率曲线的分离程度(Degree of separation,DS):

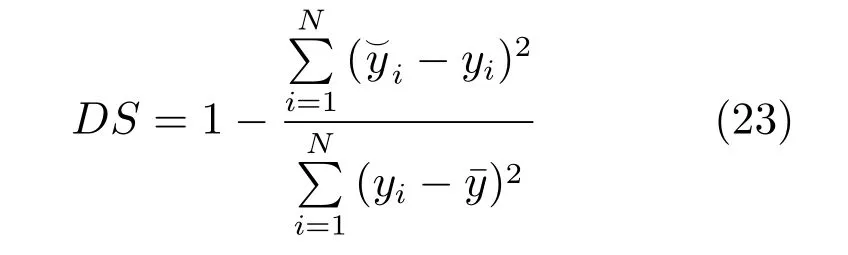
式中,和yi分别是相应参数“可接受” 和“不可接受” 参数组对应累计频率数值,是相应参数“可接受” 参数组对应累计频率数值的平均值.DS 的取值范围介于0 和1 之间.参数越灵敏,DS 越接近于1,参数越不灵敏,DS 越接近于0.

根据计算的分离程度数值,筛选出累计频率曲线分离程度较大的s个灵敏参数x1,···,xs.另外,为每个判定为不灵敏的参数在其约束范围内取定一个合理的值,一般取为取值范围的中位数或0.

2) 基于大规模变异与精英局部搜索的灵敏度参数遗传优化:以全部灵敏参数x1,···,xs作为问题变量进行参数染色体的编码,鉴于经MPSA筛选后的灵敏参数数量较少,计算压力较轻,可以选择精度更高,能使遗传算法收敛速度更快的实数编码方式来对问题变量进行编码[29−30].因此,每条染色体由s个浮点数作为基因串联组成,用ccc=[x1,···,xs] 表示,种群为r条染色体构成的基因组Popu=

基因重组与基因变异:采用单点交叉方式对基因进行重组,交叉方式为从父代基因种群中无放回地随机抽取一对染色体,以一定概率gj决定是否对该对染色体进行重组,或结果判定为真,则随机产生一个截断的位置loc ∈[1,s],将该对染色体从s处截断,交换[loc,s] 部分的基因,从而产生一对子代染色体,重复该项操作直至父代种群中所有个体均被遍历为止.该项操作可以等价为将父代种群两两配对进行交配,因此要求父代种群规模r为一个偶数;对基因重组后产生的每个子代以一个很小的概率gb判定是否进行变异操作,若判定结果为真,则随机选取该染色体的某一位基因xb进行变异,变异算子采用[31] 中的实值变异算子,变异运算如式(24) 所示:

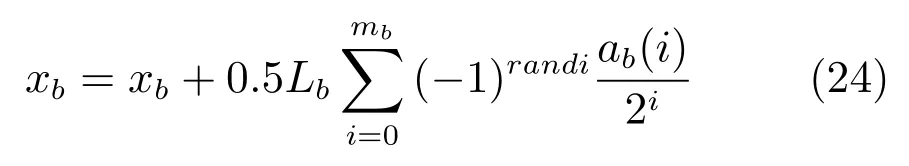
式中,Lb为对应xb灵敏参数的取值范围;randi为随机产生的任意正整数;mb为变异算子二进制意义下的精度,且ab(i) 以1/mb的概率取值为1,否则取值为0.

大规模变异:考虑到该参数优化问题是一个局部最优解较多的问题,为了增强算法的搜索能力,提出大规模变异的遗传操作,对种群最优个体适应度进行监控,若30 代种群最优适应度没有较为明显的改进,且未达到系统控制精度要求,则将父代和进行基因重组与变异后的子代集中到一起,以一个较大的概率值gs对新种群中的每个个体判定是否变异,若某个染色体对应的判定结果为真,则在1 至s范围内随机产生若干个地址,对每个地址对应的基因进行变异操作.可见,由于变异概率很大,该项遗传操作在一定程度上退化为了随机搜索,在很大程度上脱离了父代基因的束缚,提高了搜索能力.大规模变异算法伪代码如下所示,该算法时间复杂度为O(r+ra).

精英局部搜索:考虑到最优个体附近必存在局部最优解,为了提高算法搜索到局部最优解的速度,提出了精英局部搜索操作,即对适应度值最小的染色体的每一个基因以变异算子绝对值的幅度进行加减操作生成2s个子代并入种群.精英局部搜索算法的伪代码如下所示,该算法时间复杂度为O(s).

子代筛选:对产生的各个子代染色体进行反归一化并用式(21) 计算适应度值,与父代放在一起进行比较,筛选出新一代种群.同样考虑到该优化问题易陷入局部优解,子代的筛选机制可以采用Metropolis 准则[32],但所有子代种群个体均用Metropolis 准则筛选会严重降低计算效率,为此,取一个折中方案,仅子代中的半数个体采用Metropolis 准则筛选.具体筛选机制为,直接将种群所有个体中适应度值最小的r/2 个个体选出归入新一代种群,再从剩余的个体中每次无放回地随机抽取两个个体,对其利用Metropolis 准则判别选择哪个个体进入新一代,直至选够r/2 个个体为止.子代筛选算法的伪代码如下所示,该算法时间复杂度为O(rn×T).

重复上述操作直至算法收敛或控制精度满足要求抑或是达到最大迭代次数ge.所提控制器参数整定算法的伪代码如下所示.由于进化过程中临时种群的染色体个数rn要远小于最大遗传代数及Monte Carlo 实验次数,并且因为提前终止条件的存在,一般不会达到最大遗传代数,因此该算法时间复杂度主要取决于Monte Carlo 实验次数设定值.当设定的Monte Carlo 实验次数远大于遗传算法最大遗传代数时,该算法的时间复杂度为O(N ×T),而较为一般的情况下,该算法的时间复杂度介于O((N+rn)×T) 与O((N+ge×rn)×T) 之间,仅在第一轮遗传即满足控制精度要求的条件下算法时间复杂度为O((N+rn)×T).

3 工业数据试验

基于柳钢2#高炉现场数据库收集到的2015 年5 月1 日到2015 年5 月23 日共552 组高炉实际生产数据进行工业数据试验.本节内容安排如下:第3.1 节给出CFDL-MFAC 数据驱动控制器维度的确定方法及结果;第3.2 节为所提数据驱动控制器参数优化整定的过程及结果;第3.3 节给出采用参数整定后的控制器进行设定值跟踪数据试验及抗干扰控制数据试验的铁水质量控制结果.

3.1 CFDL-MFAC 数据驱动控制器维度确定及控制量匹配

对于CFDL-MFAC 方法,因为控制目标变量确定为多元铁水质量指标中的[Si] 和MIT,因此控制器输出维度确定为2 维,只需要确定控制器的输入维度.

基于高炉现场可用传感器,对高炉铁水质量参数有影响的可测变量包括:热风温度、热风压力、压差、富氧率、富氧流量、透气性、炉腹煤气指数、鼓风动能、鼓风湿度、冷风流量、顶压风量比、送风比、阻力系数、设定喷煤量、理论燃烧温度、标准风速、实际风速、顶压.这些变量部分之间存在较强相关性,信息冗余较为严重,而且如果全部选为控制器输入,控制器维度过高,计算量大,不适用于在线控制,为此引入文献[28] 中基于典型相关性分析(CCA)与相关性分析(CA) 相结合的数据降维方法对控制变量进行初步筛选,并依据MPSA 结果与控制实验结果对控制变量进行二次筛选,具体流程如下:

a) 对从高炉历史生产数据运用CCA 的方法计算出高炉主体参数与铁水质量参数之间的全部典型变量以及对应的典型相关系数;

b) 对各典型变量的典型相关系数进行显著性检验,舍弃掉相关程度不显著的典型变量;

c) 比较剩余铁水质量参数的典型变量与各个高炉主体参数之间的系数,保留绝对值较大的几个对应的高炉本体参数;

d) 对步骤c) 中保留下来的高炉本体参数进行相关性分析,在相关性达到80%以上的变量中,选取可控的参数变量予以保留;

e) 将步骤d) 中保留下来的可控变量全部用作控制变量,用MPSA 分析控制器伪雅可比矩阵初值的灵敏度,若某个控制变量对应所有铁水质量输出的伪雅可比矩阵初值均不灵敏,则分别进行保留该控制变量和去除该控制变量的设定值跟踪在线控制实验,比较两组实验的跟踪效果及累计跟踪均方根误差,若去除控制变量后的跟踪效果与保留变量下的跟踪效果相近且累积跟踪均方根误差没有明显增大,则认为该控制变量对控制器的贡献度较小,删除该控制变量.

经过步骤a)～d) 的筛选,4 个可控变量被予以保留,分别为冷风流量、压差、富氧流量和设定喷煤量.其中冷风流量、富氧流量在步骤e) 的分析中发现其在控制器中对应的伪雅可比矩阵初值经灵敏度分析均不灵敏,且对控制效果影响较小,因此舍弃掉这两个变量.为此,最终控制输入选取为压差和设定喷煤量,控制器输入维度m确定为2.

为了保证伪雅可比矩阵矩阵为严格对角占优矩阵,需要保证第一个控制量u1与第1 个铁水质量参数[Si] 的相关性、第二个控制量u2与第2 个铁水质量参数MIT 的相关性要强于u1与MIT、u2与[Si]之间的相关性.为此,采用灰色关联分析方法[33]分析了输入输出之间的关联度,结果如表1 所示.

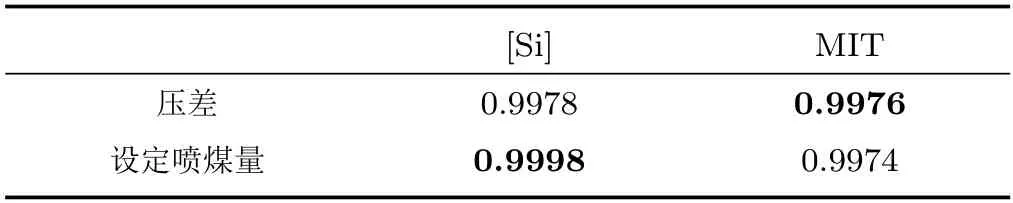
表1 输入输出灰色关联系数Table 1 Grey correlation coefficients between input and output

由表1 容易看出压差与MIT 的关联性相对更高,设定喷煤量与[Si] 的关联性相对更高,为此将设定喷煤量作为u1,将压差作为u2.

3.2 控制器参数灵敏度分析及灵敏参数遗传优化整定

高炉炼铁过程铁水质量CFDL-MFAC 数据驱动控制器需要进行灵敏度分析的控制参数及参数含义如表2 中第1 列、第2 列所示,其设定取值范围如第3、4 列所示:

Monte Carlo 模拟运行次数设定为N=5000,各参数的累计频率曲线对比如表2 中第7 列所示,其中“虚线” 累计频率分布曲线代表“不可接受”的情况,“实线” 累计频率分布曲线表示“可接受”的情况,两条曲线的分离程度越大,表示该参数的灵敏度越大.用式(23)计算“可接受”情形的累计频率曲线与“不可接受” 情形的累计频率曲线的分离程度DS,如表2 第5 列所示.可以看出,λ,µ,η,α,b1,b2的DS 值均大于0.9,非常不灵敏,因此舍弃掉,只优化相对灵敏的参数ρ和4 个伪雅可比矩阵初值φ11,φ12,φ21,φ22.

表2 CFDL-MFAC 参数表Table 2 Parameters of CFDL-MFAC

采用所提改进遗传算法进行灵敏参数优化时,惩罚因子κ1,κ2,κ3均设定为20,参数优化设定及收敛过程分别如表3 和图3 所示,最终控制器参数设置如表2 中第6 列所示.为了使图像较为清晰,在图3 中仅绘至改进遗传算法的收敛代数,基础遗传操作是指交叉变异操作,改进遗传算法在基础遗传算法的基础上增加了大规模变异操作和精英局部搜索操作,改进后的算法在进化了157 代后收敛至1.4877 并退出循环,而基础遗传算法在达到最大遗传代数时仍未收敛,适应度值为1.6249,将改进算法157 代中每一代最优个体的来源通过四种不同的符号标记了出来,并对四种来源进行统计分析,绘制了如图4 所示的饼状图,其中69 次迭代的最优个体来源于父代成员是由于在此次进化中三种遗传操作均为找到更优的个体.由图4 可以看出,新引入的大规模变异及精英局部搜索操作为算法收敛过程中提供了很大占比的最优个体,加快了算法的收敛过程,提高了算法的搜索能力,因此该两项遗传操作的提出具有一定的理论意义及应用价值.

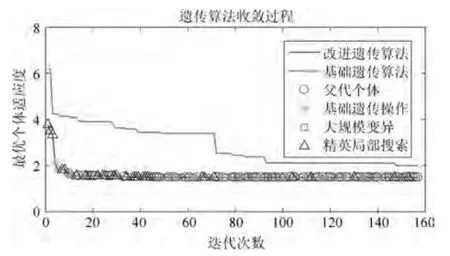
图3 遗传算法最优个体收敛过程Fig.3 Optimal individual convergence process of GA

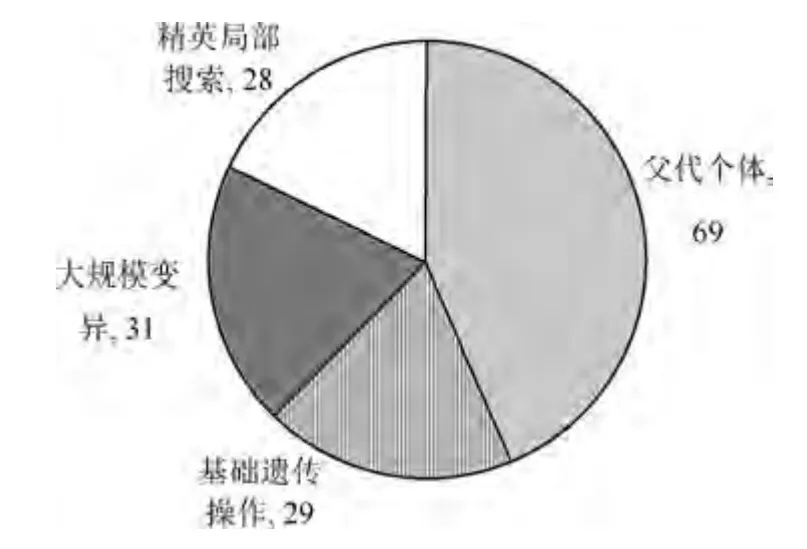
图4 最优个体来源统计图Fig.4 Optimal individual source statistics

表3 GA 参数设定Table 3 Set value of GA parameters

3.3 在线控制实验

CFDL-MFAC 数据驱动控制器参数优化整定后,进行两组多元铁水质量参数的在线控制实验,一组为方波扰动下的设定值跟踪实验,另一组为正弦扰动下的设定值跟踪实验.为了更加直观地展示所提控制策略的控制效果,两组实验均与文献[28] 中所提基于递推子空间辨识的数据驱动预测控制(Data-driven predictive control based on recursive subspace identification,RSMI-DPC) 方法进行对比.结合本文第3.2 节中所提的基于遗忘因子的多元铁水质量递推子空间动态模型建立方法,利用柳钢2# 高炉实际运行数据来建立高炉铁水质量输出系统作为被控对象,选取任意三个时刻的动态模型参数如下:

观察上述3 组参数可以发现,参数随着时间的推移在缓慢变化,能够较为充分地反映出高炉系统的慢时变动态特性.

为了模拟真实高炉系统,在动态模型预测出的高炉输出信号上人为加入均值为0,方差为0.02 的伪随机数来模拟传感器信号采集混入的高斯白噪声.本文测试了控制系统对阶跃信号的跟踪能力,设定铁水硅含量y1初始设定值为0.45,铁水温度y2初始设定值为1490°C;在k=60 时刻给予y1设定值+0.2%的阶跃跳变信号;在k=90 时刻给予y2设定值+30°C 的阶跃跳变信号.分别针对方波扰动和正弦扰动进行抗干扰性能测试,在跟踪上述阶跃信号的基础上分别加入幅值为0.07%、频率为0.01的方波负载扰动和幅值为7°C、角频率为0.01π的正弦负载扰动,观察控制器能否保持稳定并平稳地由一个动态工作点过渡到另一个动态工作点,两组测试结果及伪雅可比矩阵变化曲线分别如图5 和图6 所示.由于过程扰动一般与输出量数值幅度不相同,为了能够较为清晰地反映出过程外部扰动下设定值跟踪曲线的变化趋势,将外部扰动曲线的数值加上历史数据均值,即[Si] 含量扰动曲线数值加上0.53%,MIT 扰动曲线数值加上1510°C,并与设定值跟踪曲线绘制在同一张图上.

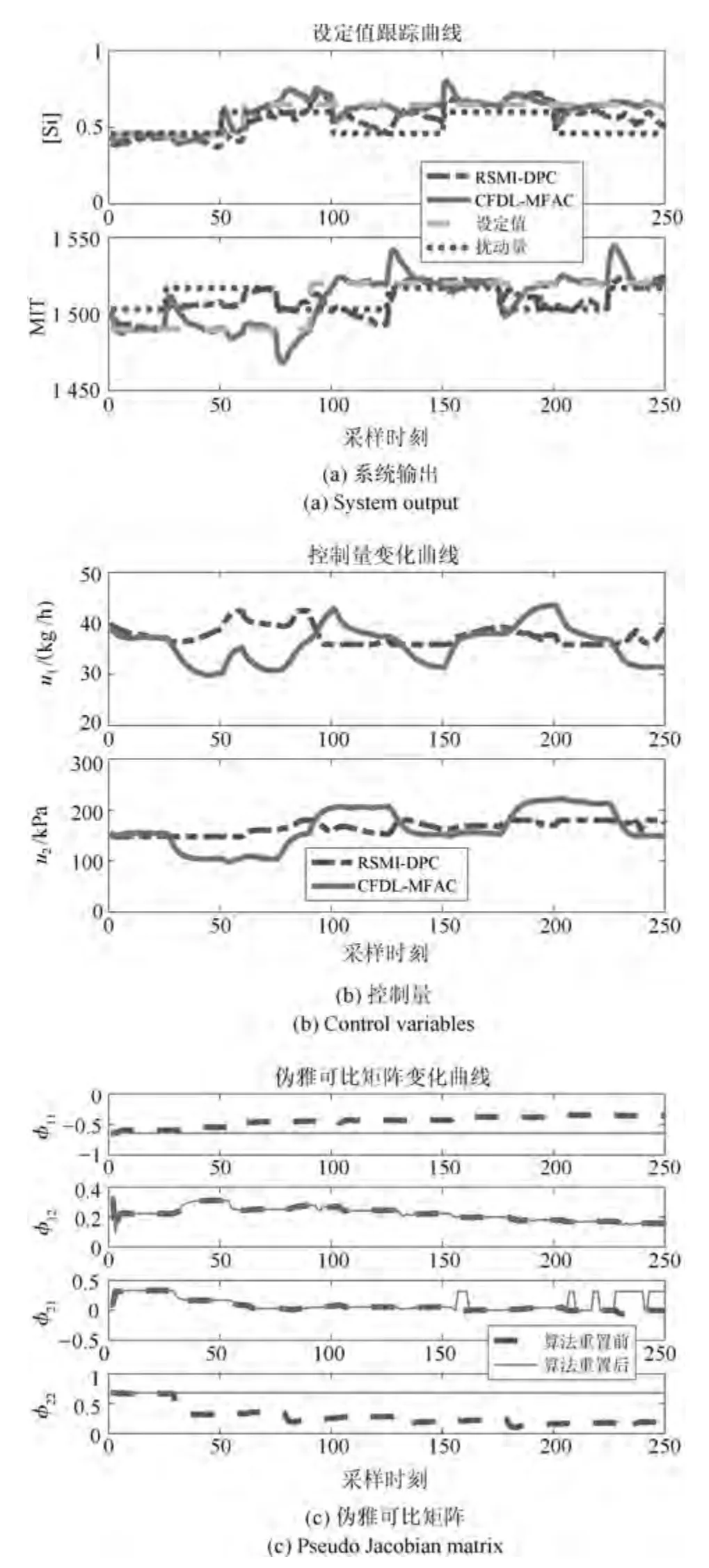
图5 方波干扰测试Fig.5 Square wave disturbance test

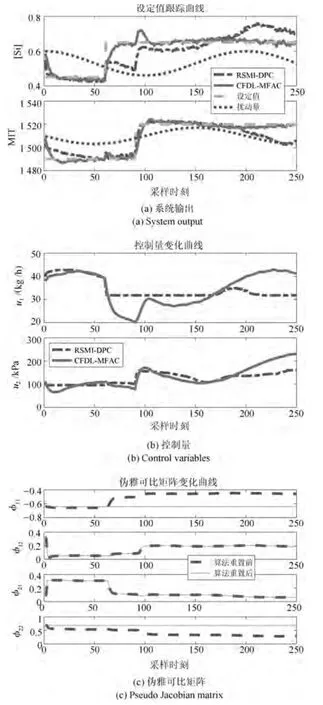
图6 正弦干扰测试Fig.6 Sinusoidal disturbance test

从图5 和图6 可以看出,对比文献[28] RSMIDPC 方法控制下的铁水质量指标在方波扰动下始终在相应设定值附近浮动,很难收敛到设定值.在正弦扰动下,RSMI-DPC 方法无法使得实际铁水质量输出较好地跟踪设定值,始终存在较大的控制误差,而所提基于MPSA 以及改进遗传优化的CFDLMFAC 方法控制下铁水质量指标在方波干扰切换的瞬间会有较大幅度的跟踪误差,但是控制误差能够逐渐收敛,始终跟随设定值的变化趋势,并且受低频正弦扰动的影响很小,始终保持着稳定跟踪.此外,表4 给出了两种控制方法更新一次控制量的平均运行时间和两类外部干扰下的铁水质量设定值跟踪均方根误差(Root-mean-square error,RMSE).从表中可以看出,所提改进CFDL-MFAC 方法不仅设定跟踪误差要比文献[28] 所提RSMI-DPC 方法小很多,计算速度也要快出3 个数量级.即所提方法具有快速、准确和稳定的在线控制性能.

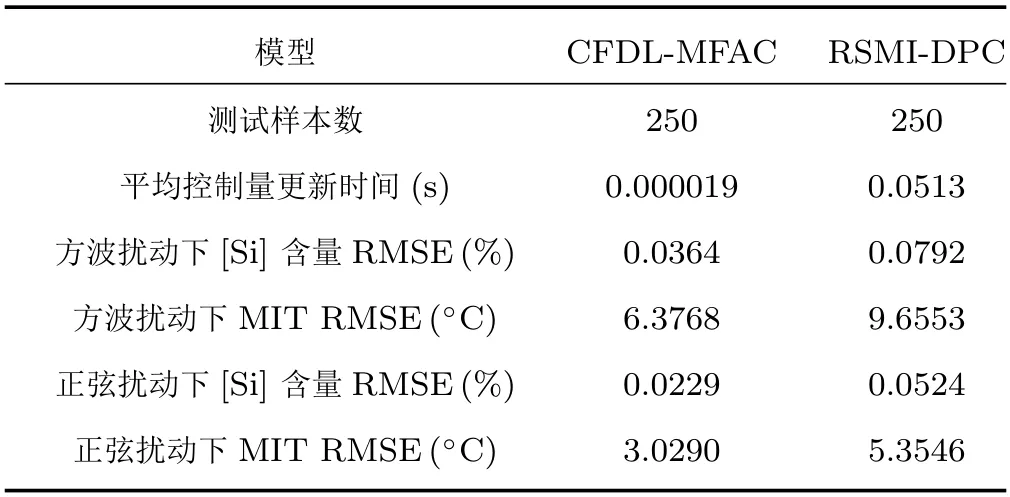
表4 控制器性能对比Table 4 Control performance comparision

4 结论

针对难以采用常规基于模型的方法进行高炉多元铁水质量建模与控制的难题,改进和完善基于紧格式动态线性化的无模型自适应控制(CFDLMFAC) 方法,提出一种基于多参数灵敏度分析与大规模变异与精英局部搜索遗传优化的CFDLMFAC 直接数据驱动控制方法.通过多参数灵敏度分析方法分析了CFDL -MFAC 控制器众多关键参数的灵敏度,并根据遗传算法的思想设计了灵敏参数校正算法,同时在基本遗传算法的基础上增加了大规模变异和精英局部搜索的遗传操作.基于实际工业数据的实验结果表明,所提出的改进遗传操作提高了优化算法的搜索能力及收敛速度.用该方法整定了控制器的参数,使其适应工程实际需求,并利用实际工业高炉数据进行了数据实验,与已有文献的RSMI-DPC 方法进行对比.结果表明所提改进CFDL-MFAC 直接数据驱动控制方法不仅能够达到很好铁水质量控制性能,而且优于RSMI-DPC方法,尤其在在线控制的运算速度、抗干扰性能以及设定值跟踪等方面,有着显著优势.