结构冲击动力学进展（2010－2020）*

余同希，朱 凌，许 骏

（1.香港科技大学机械与航空航天工程系，香港 九龙；2.武汉理工大学船海与能源动力工程学院船舶、海洋与结构工程系，湖北 武汉 430063；3.北卡罗来纳大学夏洛特分校机械工程与工程科学系，美国 北卡罗来纳州 夏洛特 28223）

现代经济的迅速发展和新兴技术的推广应用，对工程结构的安全运行提出了前所未有的挑战。高速行驶的车辆、高速列车、各种飞行器和航天器，都必须应对碰撞事故或紧急着陆；核电站、化工厂、船舶和海洋平台的设计需要考虑到恶劣工作条件下的安全性；武器装备和防护结构可能要经受更恶劣的服役环境；日常生活中不可或缺的各种电子产品需要在坠落和撞击后仍然保持可靠；从事体育运动的人们要求佩戴更可靠的安全防护装备。如此种种来自工程设计和日常生活的大量需求，召唤世界各国的科学家和工程师更努力地去理解在冲击和爆炸作用下各类结构的变形、坍塌、破损和失效等动力行为，通过建立理论模型、改进数值模拟技术及积累实验数据来探索结构动力行为的规律和预报方法，进而谋求在设计中增强结构的耐撞性、冲击防护能力和能量吸收能力。上述工程背景和科学问题，大体上勾勒出了当代结构冲击动力学的研究范畴。

在这样的大背景下，全世界每年发表的关于结构冲击动力学的期刊论文有数百篇之多，还有众多的国际会议与之相关。在期刊方面，除广大读者熟知的《国际冲击工程学报》（International Journal of Impact Engineering）外，在International Journal of Mechanical Sciences,International Journal of Solids and Structures,Thin-Walled Structures,Composite Structures,Engineering Structures等力学和结构刊物上也散见不少相关的论文。在国内，《爆炸与冲击》多年来为结构冲击动力学论文提供了一个可依托的发表平台。鉴于文献的分散性，定期作出一些综合、分析和评述显然有益于推动研究工作；但同时由于文献浩如烟海，也不可能巨细无遗地加以收纳。

本文在时间区间上侧重于评述2010－2020 这十来年发表的文献，同时注意到研究的传承性，需要时也会引述此前发表的奠基性和前驱性工作。对于2000－2010 年期间的结构冲击动力学文献及相关的前期工作，可以参考Qiu 等2011 年发表在《应用力学评论》（Applied Mechanics Reviews）上的综述文章（文献[1]），以及朱建士等2010 年发表在《力学进展》上的综述文章（文献[2]）；前者侧重于结构冲击动力学的进展，后者介绍材料本构关系、损伤破坏、冲击相变、射流等，所以二者有很好的互补性。此外，先后出版或再版的关于结构冲击动力学的专著（文献[3-5]），包含了相关学科的基础知识和发展脉络，也具有参考价值。

需要说明的是，结构冲击动力学学科主要关心的是在撞击、爆炸等强动载荷下结构发生弹塑性大变形和失效的动态行为，而不考虑在超高速撞击或超强冲击波作用下材料因高温、高压和超高速变形而发生的绝热剪切、相变、裂纹高速传播、破碎、熔融、流动等行为。在这些极端条件下，原先的结构已经完全失去作为结构的物理意义，关注的重点将转移到极端条件下的材料行为，从而属于材料动力学的研究范畴。那么，结构冲击动力学的动载的范围应该如何界定？我们可以参照一个无量纲的损伤数（damage number，或称Johnson number[6]），即ρv2/Y加以衡量，其中ρ 为材料的密度，v为冲击速度，Y为平均流动应力。Johnson[6]指出：当损伤数ρv2/Y处于10−3～10−2量级时，结构的动态行为主要表现为弹塑性大变形。考虑到民用工程领域常用的结构材料（如钢、铝、工程塑料等）以及绝大多数动态加载场景，如交通运载工具的碰撞、物体坠落、容器和管道事故、体育运动等（相当于冲击速度范围为5～30 m/s 的中低速冲击），这时的损伤数ρv2/Y对应于弹塑性大变形的结构动态行为，因而本文综述的文献也主要属于这个范围。

本文在内容选取上首先着眼于结构冲击动力学的基本科学问题，以金属板的冲击动力响应为示例展现理论概念、模型和工具的发展（本文第1 节和第2 节），然后综述典型薄壁结构件的冲击动力行为（第3 节）和运动结构物对固壁的撞击（第4 节）。同时，关注到近十多年来轻质材料（如多胞材料、3D 打印的超材料等）和以它们为芯层的轻质结构的大量涌现，以及对生物材料和仿生结构的日益增长的兴趣，对这些材料和结构的冲击动力学行为的研究构成了本文的第5 节和第6 节。

由于可能涉及的文献很多，依照上述综述框架，很明显有不少同结构冲击动力学相近和相关的论题可能会被割爱。例如，因篇幅和范围所限，本文的评述没有包括结构受到强动载荷后早期的应力波传播和可能引起的层裂，以及侵彻、穿透等终点弹道行为；没有涉及动态断裂、破碎等失效分析；对多种多样的复合材料结构的冲击动力响应及失效也未能更全面地覆盖。有一些专题可以借助于相关的评述。例如，材料和结构的能量吸收是近20 年的热门话题，但其中很多论文并不涉及动态加载的情形，有兴趣的读者可以参考综述文章（文献[7]）和专著（文献[8]）。又如，关于航空结构的冲击动力学研究十分活跃，可以参考文献[9-10]；关于增强混凝土结构的冲击动力行为的研究，则有一篇新近发表的综述文章（文献[11]）可供查阅。与结构冲击动力学相关的实验技术和计算方法，已形成自身的专门领域，请读者参考相关的刊物或书籍。

1 结构在爆炸与冲击下的动力塑性响应

1.1 饱和冲量现象与饱和分析方法

研究结构在爆炸与冲击下的塑性动力响应，评估结构的承载能力，是核电站、船舶与海洋平台、大型桥梁、航空航天、汽车等工程领域长期以来重点关注的课题；脉冲载荷是爆炸冲击中常见的载荷形式，研究结构物在脉冲载荷下的塑性动力响应具有重要的工程和科学意义。

自20 世纪50 年代开始，学者们对结构在脉冲载荷下的塑性动力响应行为开展了大量研究，然而早期研究大都只限于结构的小变形。Symonds 等[12]在1958 年进行了开拓性的研究：对于横向压力脉冲载荷作用下两端受约束的梁，当中点挠度达到或超过梁的厚度时，考虑轴向约束得到的最终挠度会比简单梁小变形理论的预测值小得多。Komarov 等[13]基于刚塑性小挠度理论得到了动态载荷下板的最终挠度的上下限值，但当最大挠度超过板厚的2 倍时，与实验值有显著的偏差。许多实验都表明，当横向挠度达到或超过梁或板的厚度量级时，膜力将起非常重要的作用，甚至能主导结构的变形行为。在工程中，受爆炸和冲击作用的板的挠度可能达到其厚度的十几倍或更多，因此进行大挠度分析必须考虑膜力的影响。

对于结构塑性动力响应的理论求解，多年来使用较广泛的是Martin 等[14]最先提出的模态近似分析法。1989 年，Nurick 等[15-16]对薄板受脉冲载荷的理论和实验方法进行了综述和对比分析，为理论分析和工程设计提供了简单的近似解法。2014 年，Jones[17]基于大量文献调研，对强动载荷下板结构的动态响应进行总结，给出了圆板、方板、矩形板在质量块撞击、压力脉冲、初速度脉冲和爆炸载荷下的理论分析方法，为进一步发展理论方法以解决应变率敏感材料板的动力响应问题奠定了基础。

然而，先前大部分的研究工作都是针对脉冲载荷持续时间较短的情形，对于脉冲载荷作用时间较长的情形（如舱室内爆），饱和冲量现象将成为制约结构动力响应的重要因素之一。Jones[3]早就注意到，在持续时间相对较长的砰击载荷作用下，矩形板的变形将在脉冲载荷结束之前停止；当无量纲矩形脉冲载荷的持续时间等于某一定值时，矩形板即已达到最大变形，不再增长[18]。Shen 等[19]还发现，对于持续时间较长的矩形脉冲载荷作用下的固支梁，无量纲最大挠度并不会随时间一直增大，而是趋于一个定值。

Zhao 等[20-21]随后将该现象定义为“饱和冲量”现象，作为板在塑性动力响应过程中的一种特性：当板受到强烈的横向压力脉冲载荷时会产生较大的变形，而大变形诱发的膜力又增强了板的承载能力；因此，一块板在持续时间足够长的矩形压力脉冲作用下，只有脉冲的早期部分对最大和最终变形有影响，其后的加载脉冲不会进一步增加板的挠度。饱和冲量的概念随后被拓展到了理想刚塑性的简支圆板、简支和固支方板以及圆柱壳[21]，矩形脉冲载荷下不同结构的饱和参数如表1 所示。表1 中 λ=p/py为无量纲载荷幅值；W0/H为结构的挠度与板厚之比为无量纲饱和冲量，µ 为面积质量；为单位宽度塑性极限弯矩；N0=σ0H为单位宽度塑性极限轴力；L为梁长度或方板边长的一半；R为圆板或圆柱壳的半径。表中对应结构的无量纲饱和时间对于矩形脉冲载荷，当载荷持续时间大于饱和时间时，就会发生饱和冲量现象。应该注意，饱和冲量不仅限于矩形脉冲载荷，饱和冲量的概念也不仅限于上述结构[22]。Zhao 等[20-21]提出的“饱和冲量”概念对应于理想刚塑性结构的最大变形，未考虑弹性影响。稍后，Zhu 等[23]基于弹塑性数值分析方法，首次提出了分别对应于最大变形和最终变形的2 种饱和冲量，以及临界脉冲时长为饱和时间，从而将饱和分析从刚塑性结构推广到了更广泛的弹塑性结构。

表1 矩形脉冲载荷下不同结构的饱和参数Table 1 Saturation parameters for different structures under rectangular pulse loading

1.2 结构塑性大变形情况下的饱和分析

基于上述刚塑性和弹塑性饱和冲量现象的概念，席丰等采用数值方法分析了脉冲载荷作用下简支圆板的动力响应，指出饱和冲量现象同样存在于高载范围内的脉冲加载情况[24]，也存在于脉冲载荷作用下发生塑性变形的钢梁之中[25]，且该现象的发生依赖于载荷强度和作用时间2 个必要参数。

近几年，武汉理工大学朱凌研究组与余同希、陈发良等合作[26-34]对饱和冲量课题开展了更广泛而系统的研究，不仅将饱和冲量的刚塑性理论方法扩展到了矩形板及高载范围的脉冲载荷，还详细分析了不同脉冲形状、边界条件、应变率效应等因素的影响。

1.2.1 基于模态近似技术的刚塑性理论分析方法

在Zhao 等的开创性研究[20-22]的基础上，结合Jones 对脉冲载荷下刚塑性板的研究[35]，Zhu 等[26]明确指出，板的塑性变形的停止时间tf正是饱和时间tsat，这为饱和脉冲等效技术奠定了基础；Bai 等[27]提出板的饱和时间和饱和冲量并不直接受边界条件的控制，而是由变形模态决定；白雪玉等[28]还发现在矩形脉冲载荷作用下矩形板变形的饱和时间是一个与脉冲幅值无关的量，仅取决于结构的材料和几何参数，这与文献[22]针对脉冲加载的方板给出的结论一致。

1.2.2 考虑瞬态响应阶段的刚塑性理论分析方法

当外加的动载较强（即通常所说的高载情形）时，结构动力响应的早期存在以移行铰为特征的瞬态响应阶段。Bai 等[29]考虑了瞬态响应，对线性上升-指数衰减（linear rise-exponential decay,LRED）的脉冲载荷作用下的刚塑性方板进行了饱和分析，发现此时方板的响应有3 种类型，如图1 所示：（1）Ⅰ型，方板内部的移行铰线在脉冲的线性上升段相遇，板的响应亦在脉冲的线性上升段停止；（2）Ⅱ型，方板内部的移行铰线在脉冲的线性上升段相遇，板的响应则持续到脉冲的指数衰减段才停止；（3）Ⅲ型，方板内部的移行铰线在脉冲的指数衰减段相遇，板的响应也在这一阶段停止。

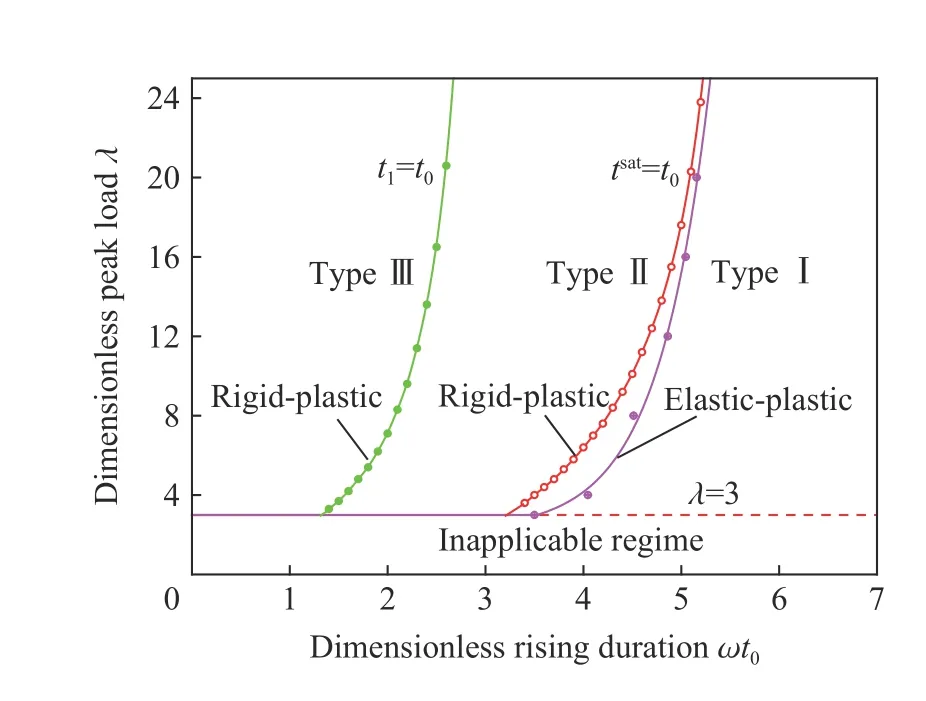
图1 理想刚塑性固支方板在LRED 脉冲载荷作用下的响应区域划分图[29]Fig.1 Response map for a fully clamped rigid-perfectly plastic square plate subjected to an LRED pressure pulse[29]

对比模态解可知，包含瞬态阶段的完全解与模态解在饱和挠度上差别很小，但前者求得的饱和冲量大于后者的结果。因此，如果在工程问题中主要只关注结构的最大变形，用求解较易的模态解代替复杂的完全解是合理的[29]。

1.2.3 膜力因子法与饱和分析的结合

瞬态响应阶段对结构的变形历史预测有影响，同时采用正方形近屈服面以简化分析也会给塑性大变形的计算带来误差。Symonds 等[12]虽然同时考虑了上述2 种因素，但求解过程非常复杂，难以应用于其他工程结构。在研究刚塑性梁的碰撞问题时，Yu 等[36]提出了表征轴力对能量耗散贡献的膜力因子，铺设了同时考虑准确屈服面和瞬态阶段求得大挠度响应的通途。由此开创的膜力因子法概念清晰，减少了人为假设，同一般求取刚塑性完全解的方法相比大大减少了分析计算量，结果与实验吻合良好。为了探讨该方法的理论基础和应用，余同希和陈发良利用膜力因子法对圆板[37]、正多边形板[38]和矩形板[39]的塑性动力响应进行了分析求解。之后，一些学者[40-43]参照余同希等的研究，进一步推广了膜力因子法的应用。Qin 等[44-46]将膜力因子法从金属单板扩展到了多胞夹芯结构的研究中，考虑芯层的特点建立了新的屈服准则，并分析了夹芯结构在冲击载荷下的塑性大变形响应。

膜力因子法能够系统地计入膜力对结构承载能力的贡献。膜力因子是计及弯矩与轴力效应时的能量耗散率同只计及弯矩效应时的能量耗散率之比，即fn=Jmn/Jm，膜力因子可以写作梁或板挠度的函数fn=ψ(δ)，其表达式的推导细节可参见文献[30]。

Tian 等[30-31]将膜力因子法与饱和分析结合，研究了脉冲载荷作用下的刚塑性梁和板，在考虑准确屈服面的基础上分析了结构的瞬态响应和塑性铰的移行规律，得到了比模态法更精确的结果（见图2），并且给出了对高载矩形脉冲载荷适用的固支梁和方板的饱和冲量和饱和挠度的计算公式。

图2 膜力因子法与饱和分析结合得到的方板在脉冲载荷下的塑性动力响应[30-31]Fig.2 Dynamic plastic response of square plates under pulse loading analysed by the combination of the membrane factor method (MFM) and the saturation analysis (SA)[30-31]

1.2.4 尺度效应、材料性质、应变率与应变硬化效应对饱和冲量现象的影响

为了阐明尺度效应、材料性质、应变率与应变硬化效应等对饱和冲量现象的影响，Zhu 等[32]采用弹塑性分析方法分别计算了几何相似的固支方板和加筋板的挠度-时间历程，发现无量纲饱和参量与板的边长与厚度之比有关，而同板的绝对尺寸无关。He 等[33]研究了不同屈服强度和板的尺寸对饱和参量的影响，得到了参数之间的比值关系。对于爆炸与冲击产生的强动载荷，材料应变率和应变硬化效应也会对结果产生显著的影响，Zhu 等[34]在饱和冲量的分析中提出了由应变率敏感性加强因子n1和应变硬化加强因子n2共同确定的广义加强因子n，将应变率敏感性和应变硬化的联合加强作用予以量化。

1.3 脉冲等效技术

工程实际中的脉冲形状通常十分复杂，经过理想化的、用解析式表示的脉冲载荷形状与实际载荷形状常常不完全吻合，致使得到的解析公式偏离实际问题的解；对于近场爆炸等复杂脉冲载荷，甚至很难用简单的解析式表达。

早在1953 年，Symonds[47]以中心受脉冲载荷的无限长梁为例，研究了脉冲形状对结构最终变形的影响。之后，Hodge[48]指出Symonds[47]的结论仅适用于载荷远大于结构的屈服极限载荷的情形，否则会造成极大的误差。

Youngdahl[49]在20 世纪70 年代初提出了一种半经验方法，用等效冲量Ie和等效载荷pe来近似地消除脉冲形状对结构响应的影响。这个等效的矩形脉冲的参数由下式决定：

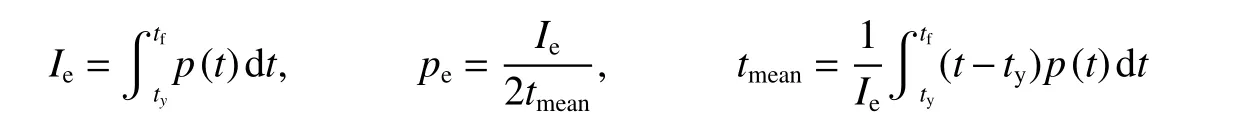
式中：p(t)为脉冲载荷，ty和tf分别为结构塑性变形开始和结束的时刻。等效脉冲Ie的表达式表明，首先要对外加的脉冲“掐头去尾”，只保留中间的有效部分，相当于图3 的阴影部分；然后，找出这部分面积的重心的时间坐标tmean，应用上述关于pe的公式使得tmean也保持为等效矩形脉冲的重心。因此，上面给出的一套公式就得到了Youngdahl[49]意义下的等效矩形脉冲。

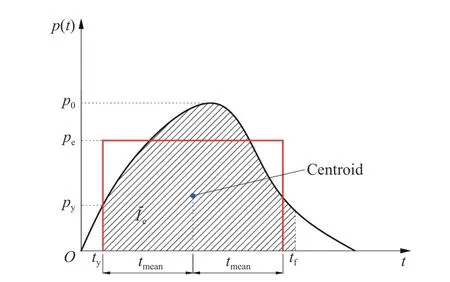
图3 任意形状脉冲的Youngdahl 等效技术[49]Fig.3 Demonstration of Youngdahl equivalent method for a pulse of arbitrary shape[49]

Youngdahl 的脉冲等效技术存在一个薄弱环节，这就是：虽然结构塑性变形的开始时刻ty不难根据p=py确定，但是从理论上却很难确定塑性变形的终止时刻tf。为实用的需要，Youngdahl[49]建议采用下述经验公式来估计tf：

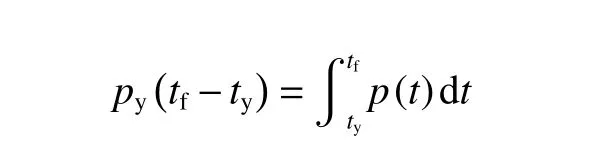
这一缺陷使得Youngdahl 的脉冲等效方法限于一种半经验的技术，尽管这并没有妨碍它在过去几十年里被广泛采用来简化实际工程分析。

Zhu 等[50]检验了在均布脉冲载荷作用下的简支梁、简支圆板和圆柱壳经历小变形动力响应时的临界载荷，证实用Youngdahl 等效技术计算得到的不同形状脉冲的临界载荷曲线结果相差在5%以内。Li 等[51]进一步检验了Youngdahl 等效技术对单自由度模型的适用性，并通过刚塑性界限定理给出了Youngdahl 等效技术的一种理论诠释。

以上工作表明Youngdahl 提出的经验公式可以在小变形预测中找到支持，但是无法说明它是否适用于持续时间较长的脉冲载荷下的结构塑性大变形。近几年，Zhu 等[26]、Bai 等[29]基于饱和冲量的研究，提出了物理意义更明确、计算结果更准确的解析的饱和等效方法，用饱和时间tsat代替Youngdahl 公式中的tf，区分出脉冲载荷中的有效部分，再利用Youngdahl 技术中的“重心相同”原则获得等效的矩形脉冲载荷。

图4 以线性衰减脉冲为例，绘制了不同等效方法的示意图。Zhu 等[26]、Bai 等[29]对比了全脉冲等效、Youngdahl 等效和饱和等效这3 种等效方法在饱和区的刚塑性理论结果，证实了饱和等效方法在合理性、准确性和适用性方面均优于先前的2 种方法。

图4 3 种脉冲等效技术的对比（图中 λ 为载荷比）[26]Fig.4 Comparison of three equivalent methods (EMs) with λ being the loading ratio[26]

朱凌等[52]在刚塑性理论框架下，将饱和分析和脉冲等效技术结合起来，验证了舱室内爆超压下饱和冲量现象的普遍存在性；运用饱和脉冲等效技术（见图5(a)），并考虑应变率效应，所得结果与数值模拟结果的误差小于10%（见图5(b)）。这表明，将饱和冲量分析方法与脉冲等效技术结合起来，可以更准确地预报结构的塑性动力响应，在结构抗冲击设计时显著提高非线性数值计算的效率。

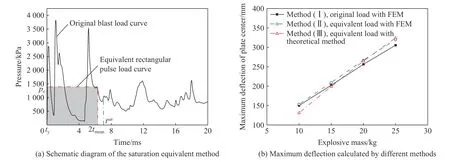
图5 基于饱和分析的脉冲等效技术在舱室内爆中的应用[52]Fig.5 Application of the saturation equivalent method in cabin explosion[52]

2 结构在爆炸与冲击下的失效和重复受载

2.1 结构在强动载荷下的失效

结构失效通常是指由于结构发生严重变形、破裂或由于结构承载能力剧烈降低而使结构不能发挥其原有功能的状况[53]。在引言界定的动载（中低速冲击与碰撞）范围内，结构的失效过程一般可分为微观或细观的损伤、零部件失效、整体失效3 个层次。研究结构在强动载荷下的塑性动力失效，需要研究结构在强动载荷作用下由变形增大、损伤积累直到部分或整体失效的全过程，侧重其终极阶段；其工程意义及复杂性是显而易见的[54]。考虑到工程中最常用的结构是由简单结构元件构成的，简单构件的失效模式以及对失效模式的预测具有普遍意义。因此，本节中仅针对梁、板、壳等简单构件在强动载荷下的主要失效模式及其预测模拟方法予以概述。

1973 年，Menkes 等[55]基于受均布冲击载荷作用的固支铝合金梁的系列试验，首次提出了梁的3 种失效模式：模式Ⅰ，非弹性大变形；模式Ⅱ，固定端拉伸撕裂；模式Ⅲ，支座处剪切破断。此后，不少学者对常见工程构件（如梁、薄板、圆柱壳、夹层及复合材料结构等）在强动载荷下的塑性动力失效进行了大量研究，包括失效模式、失效准则、与材料参数的关联性等，相关的总结分析可参见文献[53-54]。

均匀加载下的板也会出现类似梁的3 种失效模式[55]。针对实验中板发生拉伸撕裂前的塑性变形是否会出现瞬时的“平台”问题，Zhu[56]采用光学试验方法，成功得到了固支方板的瞬态塑性大变形模态，为固支板的破坏模态研究提供了瞬时模态的实验信息，并用自编程序对铝板和钢板的塑性大变形行为进行了数值模拟，获得了一致的结果。根据支座处的颈缩情况，Nurick 等[57]将梁的3 种失效模式扩展到板。其中模式Ⅰ细分为3 个子模式，分别为：Ⅰ*，无颈缩；Ⅰa，部分颈缩；Ⅰb，全部颈缩。模式Ⅱ细分为：Ⅱ*，支座部分拉伸破坏，板中心挠度随冲量增加而增大；Ⅱa，伴随板中心挠度随冲量增加而增大，支座处完全撕裂；Ⅱb，伴随板中心挠度随冲量增加而减小，支座处完全拉伸撕裂[58]。

平板局部加载时[59]，受载荷作用的区域局部挠曲明显，并且随着冲量的增加,将依次出现颈缩环、冲碟和花瓣型破口。Jacob 等[60]在前人的研究基础上分别对均布和局部爆炸载荷下板的失效模式进行了总结，并考虑爆距的影响，建立了低碳钢固支圆板失效模式Ⅰ的挠厚比经验公式。

针对加筋板的失效，Yuen 等[61]对于4 种加筋布置方式（单加筋、平行双加筋、十字形加筋和双十字形加筋）下的固支矩形板进行了均布爆炸加载实验和数值模拟，并与相同尺寸的平板进行了比较。结果表明，加筋数量和布置方式对模式Ⅰ的变形模态影响很小，但对中心挠度有较大影响；对模式Ⅱ的撕裂位置和数量有较大影响，且加筋交叉处可能发生颈缩断裂。Langdon 等[62]对文献[61]所述的4 种加筋板进行了局部加载实验和数值模拟。结果表明，随着冲量的增加，加筋板的失效过程依次表现为：局部鼓包，板格在加筋侧面处发生颈缩，部分撕裂，完全撕裂形成花瓣型破口和加筋撕裂。Zhao 等[63]通过实验和数值方法研究了加筋板在约束爆炸下的动态塑性大变形，结果表明外部加筋板的承载能力要强于内部加筋板；此外，由于约束爆炸下准静态超压的存在，可以看到该实验中发生了饱和冲量现象。牟金磊等[64]进行了加筋板水下爆炸实验，结果表明，改变爆距会改变脉冲载荷冲量，因而改变加筋板的变形模态。Bonorchis 等[65]则研究了局部爆炸冲击载荷作用下加筋高度（即刚度）和加筋焊接方式对加筋板失效的影响。

最近，一些学者针对板的失效研究提出了几个分析模型，Yuan 等[66]研究了固支矩形板在均匀冲量作用下的变形和破坏，给出了对应于变形模式之间过渡的临界速度的分析预测。对失效模式Ⅰ，Jones[17]分析了在强动载荷下板的动力响应的大量研究成果，在刚塑性假设框架下，提出了一个用于预测板中心永久变形的理论模型。Micallef 等[67]考虑横向剪力和旋转惯量的影响，提出了局部爆炸载荷下简支圆板动态塑性响应的分析模型，可用于计算板的最终变形。Mehreganian 等[68]还在文献[67]的基础上进行了扩展与修改，将其推广于局部爆炸载荷下的简支厚方板塑性动力响应的分析，并就载荷参数及板厚对最终变形的影响进行了参数分析。Aune 等[69]用数值方法研究了铝板及钢板在强动载荷下的非弹性响应，对板的失效模式Ⅱ中的边界处的部分撕裂和全部撕裂进行了模拟，结果与实验结果一致。Yuan 等[70]基于能量密度失效准则提出了能涵盖强动载荷下板的3 种失效模式的理论模型，然后将针对低碳钢方形板的计算结果同数值模拟结果和实验结果进行对比，结果吻合较好。此外，纪冲等[71]研究了薄壁圆柱壳中心部位受侧向爆炸载荷冲击下的动力响应，通过爆炸实验得到了非接触爆炸和接触爆炸条件下圆柱壳的变形破坏特征，并建立三维实体模型对实验过程进行数值模拟，结果与实验吻合较好。

除了上述相关研究外，对失效模式的模拟及预测方法的研究也十分重要。其中，对于结构起裂或破口位置的预测，目前主要采用实验与数值模拟相结合的研究方法，材料模型及失效准则是研究中的关键及难点。结构的失效与材料的失效密切相关，一般应考虑应变率、应变硬化、温度效应等。一些学者研究了失效准则及其应用[72-81]，为使用方便，一般采用不考虑应变状态的等效塑性应变失效准则，但金属材料的失效与应力状态有关[72]。当结构承受冲击载荷作用时，材料往往会经历大变形，使得应变硬化、应变率效应及温度软化效应不能忽略。基于此考虑，Johnson 等[73]不仅提出了Johnson-Cook (JC)本构模型，还提出了相应的JC 延性失效准则（经验型），综合考虑应变硬化、应变率效应及温度软化效应。Zhu 等[74]引入了金属成形领域的成形极限曲线（forming limit diagram,FLD）和断裂成形极限曲线（fracture forming limit diagram,FFLD）作为板材断裂失效准则，预测了船体板碰撞时颈缩断裂的起点。由于等效塑性应变失效准则可较好地模拟以拉伸失效为主的模式Ⅰ和模式Ⅱ，但模式Ⅱ-Ⅲ和模式Ⅲ的模拟效果不甚理想，Rudrapatna 等[75]提出了剪应力失效和拉伸应变-剪应力关联失效准则，模拟金属薄板和加筋板在爆炸冲击载荷下的失效模式Ⅲ（剪切失效）和模式Ⅱ-Ⅲ（介于模式Ⅱ与模式Ⅲ之间的拉剪关联失效）。Bao 等[76]研究发现JC 失效准则的应力三轴度表达式在剪切、压缩等低应力三轴度区间的误差较大，他们在进行了大量的铝合金破坏实验后，以应力三轴度为自变量将临界断裂失效应变分为3 个区间：韧性断裂破坏、剪切破坏和混合断裂破坏，提出了与材料失效破坏情况更接近的B-W (Bao-Wierzbicki)准则。Bai 等[77]提出利用应力三轴度和Lode 参数共同表征应力状态，对JC 失效准则中低应力三轴度区间不准确的情况进行了改进，提出了MMC (modified Mohr-Coulomb)准则。

最近，Storheim 等[78]基于幂律塑性材料模型和Bressan-Williams-Hill (BWH)准则，结合初始颈缩后的损伤模型，提出了一个可用于快速预测粗网格壳单元失效的模型，尤其适用于冲击载荷下的海上结构物；Yang 等[79]进行了6 种不同试样的双轴拉伸实验，建立了高强度钢的双轴损伤演化模型，提出了修正的BWH 失效准则，提高了在高应变比下模拟的准确性；考虑到Gurson-Tvergaard-Needleman (GTN)损伤模型[82]对孔洞聚集型断裂模拟较好，但不能准确预测低应力三轴度下的失效，且仅适于低应变率工况，Wang 等[80]对其进行了改进，并与Johnson-Cook 材料本构模型[73]结合使用，对一系列模型实验（准静态拉伸实验、高速拉伸实验、落锤冲击实验）进行了数值模拟，得到的结构损伤模拟结果与实验结果较一致。Moriello 等[81]采用基于应力三轴度修正的Mohr-Coulomb 断裂准则[77]，结合拉伸和剪切实验校准的材料参数，对脉冲载荷下简支和固支方板的失效模式（见图6）进行了有限元模拟，得到的中心变形、裂纹长度、拉伸位移等结果与实验结果吻合较好。但是，目前结构失效预测并没有形成统一的标准，仍需要对现有失效准则进行适用性和准确性评估，提出更广泛适用的失效准则。

图6 脉冲载荷下固支方板的失效模式[81]Fig.6 Failure modes of fully-constrained square plates under impulsive loadings[81]

2.2 压力-冲量图

压力-冲量（p-I）曲线图是目前广为采纳的评定爆炸破坏的方法，也是描述结构抗爆特性最科学有效的方法，最早应用于二战时期爆炸载荷下房屋和人员的安全评估[83]。p-I图中的每条曲线都描述了一定程度的结构损伤，为了更好地评估结构的安全性，研究人员们运用多种方法建立和确定p-I图。

爆炸载荷下p-I曲线的传统确定方法通常分为3 种[84]，试验法最精确但花费最大，解析法大多使用矩形或三角形等形式较为简单的爆炸荷载模型，数值法由数值模拟得到构件的动态响应超压冲量数值组合点，再对各点进行曲线拟合。试验法在经费方面及爆炸试验安全性要求方面受限制较多[85-86]，试验结果数量较少，不足以形成完整的p-I图，而且试验试件的材料参数对试验结果的影响也很大[87-88]。因此，用试验法构造p-I图的结果较少，但试验法的缺陷也推动了解析法和数值法在建立p-I图中的发展。基于解析法，汪维[89]利用剪切和弯曲相互耦合的等效单自由度简化模型提出了确定钢筋混凝土构件p-I曲线的方法，并通过数值计算和数据拟合给出了不同破坏模式及荷载形状情况下的p-I曲线经验公式。师吉浩等[90]基于最大破裂应变准则分析不同类型防爆墙的破坏模式，构建了p-I曲线统一方程，再根据p-I曲线参数影响性分析，考虑应变率效应及局部响应效应，确定了不同防爆墙p-I曲线的预测经验公式。丁阳等[91]通过对数据的回归分析，将二维拓展到压力-冲量-时间的三维空间中，绘制出了三维的p-I-t图。基于数值法，陈赟等[92]研究了装药质量和作用距离变化对作用在靶板上的超压与冲量的影响，得到了能够反映爆炸冲击波下靶板不同损伤等级的p-I图；李天华[84]根据钢筋混凝土板在爆炸载荷下不同损伤程度的动态响应数值试算，绘制了对应于损伤等级分界点的超压冲量组合点，从而得到了p-I曲线。

压力脉冲载荷的形状会影响结构的动态响应，进而影响p-I图。早年Symonds[47]认为脉冲载荷下结构的最终变形仅取决于冲量I和峰值载荷pmax，且由pmax和I确定的变形量与实测值误差仅为15%。但对于加载载荷并非远大于屈服载荷的情况，脉冲形状也对结构的变形和损伤评估很重要。Hodge[48]认为仅用pmax和I描述脉冲载荷得到的结果误差很大；Abrahamson 等[93]用单一的p-I特征曲线去预估任意形状的临界载荷曲线，显示其误差可能高达40%。Youngdahl[49]用有效冲量Ie和有效载荷pe来描述，以消除脉冲形状对p-I曲线的影响，得到了理想刚塑性的单自由度模型解。Zhu 等[50]结合了Youngdahl[49]和Abrahamson 等[93]的方法，将误差降低至5%，建立的p-I特征曲线可认为不受脉冲形状的影响。Li 等[51,94]基于上述工作，将p-I曲线图进一步延伸到了理想弹塑性模型解上；而Fallah 等[95]将其进一步拓展，提出了无需实验和大量数值模拟工作的p-I图建立流程，适用于大多数抗爆级别的防爆屏障能力评估。Dragos 等[96]根据对多个双线性脉冲载荷的分析，按照等效脉冲载荷的概念构造了解析方程，排除脉冲形状的影响建立了标准化的p-I曲线，随后加以改进并应用于爆炸载荷作用下的柱状钢体结构[97]。白雪玉[28]用刚塑性理论分析方法预测了固支方板在矩形脉冲载荷作用下的拉伸失效p-I曲线，结合能够消除脉冲形状影响的饱和等效方法，用矩形脉冲载荷的拉伸失效p-I曲线预测了爆炸载荷下固支方板的动态行为，绘制了可为工程设计提供参考的p-I曲线图，如图7所示。

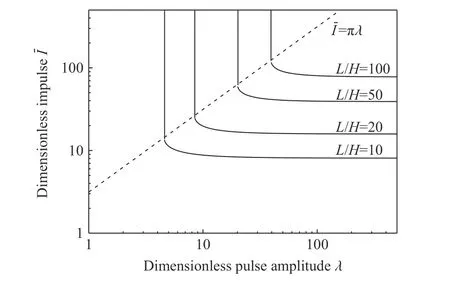
图7 矩形脉冲载荷作用下的固支方板拉伸失效p-I（超压-冲量）图[28]Fig.7p-I diagram on tensile failure of fully clamped square plates under rectangular pulse loading[28]

近年来，学者们将能量法应用到了p-I图的建立中。Tsai 等[98-99]基于能量解确立了载荷-冲量关系，进而得到基于能量法的p-I图，并将基于能量法得到的p-I图进一步延伸应用[100]。陈俊杰等[101]在能量法的基础上，考虑阻尼的影响对理想弹塑性模型的p-I曲线渐近线方程进行求解，给出了p-I曲线动态区的拟合公式，提出构件阻尼比的提高有助于提高构件的抗爆性能。潘建军等[102]运用能量法，综合考虑了阻尼比、轴向力和高温效应的影响，构建了基于等效单自由度模型的钢管RPC(reactive powder concrete)柱抗爆p-I曲线，对于阻尼比和p-I图得出了与陈俊杰等[101]类似的结论。Shi[103]用能量法结构响应图谱得到了三角形爆炸载荷下单自由度弹性系统的p-I图，并提出合理利用中间变量参数有助于建立压力和冲量之间的一一对应关系，p-I图也可以反过来验证能量法的有效性。

此外，不同的失效模式也在p-I图的建立中进行讨论。典型的p-I图一般用简化的单自由度模型来描述，先前的很多研究工作中，p-I图中的区域划分由结构的最大变形量或容许损伤量来确定，即基于结构最大变形准则建立p-I图[94]。但最大变形准则通常假定结构只发生非弹性大变形，即Menkes 等[55]在1973 年提出的3 种失效模式中的第1 种。汪维等[104]用弯曲与剪切相互耦合的单自由度模型方法确定了钢筋混凝土板在爆炸载荷下的p-I图，图中给出了失效模式对应的区域，用以确定钢筋混凝土板的失效模式。Yu 等[105-106]基于欧拉梁理论，针对爆炸载荷下的钢筋混凝土梁柱，提出了一种适用于弹塑性模型的无量纲解析方法，利用该方法计算所得数据确定了不同失效模式下的p-I图。Yuan 等[107]采用全固支延展性梁的模型确立的p-I图囊括了3 种失效模式，并将饱和冲量等结构响应特性参数补充到p-I图中（见图8），为爆炸载荷下工程结构的设计和评估提供了更详尽的定量指引。

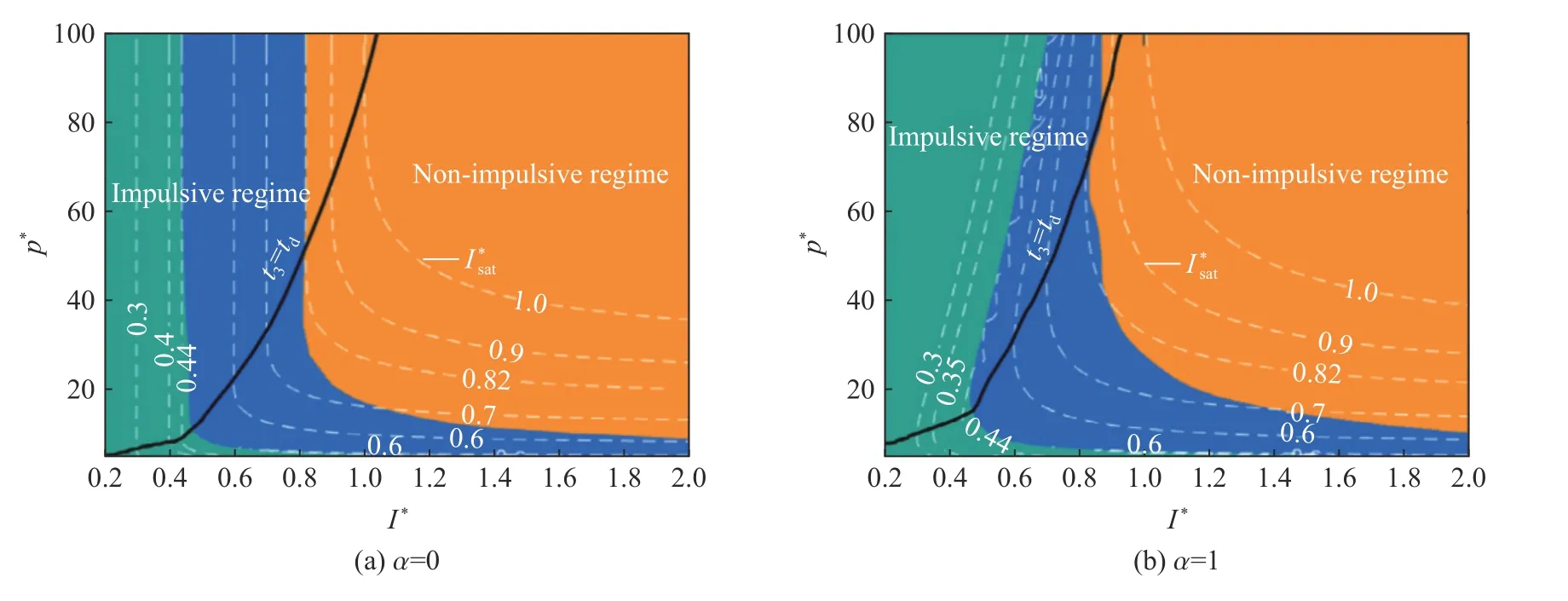
图8 无量纲饱和冲量叠加在载荷参数空间上的等值线[107]Fig.8 Contours of non-dimensional saturated impulse superimposed on the loading parameters space[107]

对于更多关于p-I图的参考信息，可参见Chernin 等[108]对过去70 多年的p-I图建立方法及相关发展进行的归纳总结，文中分门别类地讨论了p-I图的建立推演方法，给出了现有的p-I公式。

2.3 结构在重复冲击下的塑性大变形

2.3.1 结构在重复脉冲载荷作用下的塑性大变形

船舶与海洋工程结构在营运过程中经常遭受反复脉冲载荷的作用，如波浪对海洋平台、船体艏部和尾部的砰击作用等。基于这一工程现象，Jones[18]于1973 年针对反复砰击载荷作用下的理想刚塑性结构首次提出了“伪安定”的概念，当脉冲载荷作用下的结构达到伪安定状态后，在后续相同的动载荷作用下结构将不会产生新的塑性变形。Yuhara[109]在1975 年根据船艏模型入水冲击试验结果证实了伪安定现象的存在。Shen 等[19]基于刚塑性假定，对承受反复矩形脉冲载荷作用下梁和板等刚塑性结构发生伪安定的条件作了理论论证，证实了伪安定现象的存在，且认为其充分必要条件是：结构在第一次脉冲载荷作用下的最终变形W1小于同等峰值的静态载荷作用下变形值Wsm。然而，Stoffel[110]在圆板受到反复脉冲载荷的实验研究中发现了另一种伪安定现象的产生条件，即当脉冲载荷持续时间足够长时，圆板的最终变形将大于同等峰值的准静态载荷施加后的变形值Wsm，当变形后的板再次受到相同脉冲载荷的作用时，板的最终变形会逐渐增大，但将逐渐趋近某一常数，如图9 所示。Stoffel[111]建立了相关的力学模型对该特殊情形进行研究，分析表明：前期实验中发现的伪安定现象是由材料的弹性特性引起的，由于刚塑性模型中忽略了弹性特性，因此未能考虑后一种伪安定现象。为了研究弹性效应对结构塑性动力响应的影响，Shin 等[112]实验研究了平板在反复砰击载荷作用下的塑性变形累积问题。

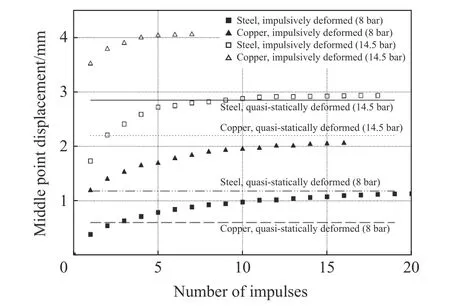
图9 脉冲和准静态加载下钢/铜板中心点变形量与脉冲载荷作用次数的关系[110]Fig.9 Variation of the midpoint displacement of steel and copper plates with the number of loading impulses[110]

除反复砰击载荷外，基于工程上的需求，反复爆炸载荷下的结构响应机理也在研究探讨当中。Henchie 等[113]利用实验和数值方法研究了圆形钢板在多次均匀爆炸载荷作用下的塑性动力响应问题，研究结果表明：实验板表现为较大的非弹性变形，且在夹紧边界处变薄甚至出现撕裂现象；但随着爆炸载荷次数的增加，中点挠度增量逐渐减小，边界和中心区域的维氏硬度增加。Kumar 等[114]利用有限元软件ABAQUS 模拟了多次爆炸载荷作用下半埋设结构的动力响应，主要讨论爆炸量、应变率以及结构加强筋的设置对结构抗爆性能的影响。Zhou 等[115]对不同壁厚的金属圆柱壳进行了单次和二次爆炸试验，讨论了二次爆炸载荷、隔爆距离和壁厚对圆柱壳结构变形和损伤的影响，结果表明：相同爆炸载荷作用下受第一次爆炸冲击的变形圆柱壳较未受损圆柱壳能够吸收更多的能量，且防爆距离和壁厚对二次爆炸作用下圆柱壳结构的破坏模式和能量分布有显著影响。Yuen 等[116]在实验中通过改变炸药与四边形板的相对角度及炸药量研究了爆炸载荷作用方向对四边形板塑性动力响应的影响，并基于数值模拟方法分析了不同实验工况下爆炸载荷的分布特性。Cheng等[117]研究了不同壁厚及间距的充液圆柱壳复合结构在反复爆炸载荷作用下的动力响应和结构损伤，主要讨论了壁厚和隔爆距离对结构抗爆性能的影响，确定了隔爆厚度和临界隔爆距离。Rezasefat 等[118]利用数值方法研究了反复爆炸载荷下由钢或铝材料组合制成的单层和多层圆形板结构的抗冲击性能和动态塑性响应。Ziya-Shamami 等[119]采用实验方法研究了单层和多层金属板在5 次均匀爆炸载荷作用下的塑性响应，主要讨论了结构参数的变化对结构抗冲击性能的影响。

2.3.2 结构在刚性块重复冲击下的塑性大变形

反复碰撞载荷作用下工程结构塑性大变形问题给结构营运安全带来了巨大的挑战。早在1990 年，Zhu[120]针对海洋平台的重复碰撞实际问题，对矩形板遭受刚性块重复碰撞问题，进行了较系统的理论、实验和数值模拟研究，较好地总结了重复碰撞载荷下矩形板塑性动力响应的力学机理。此后，工程结构构件遭受刚性块重复撞击的问题被广泛讨论与研究，其结构形式主要包括板[121-125]、梁[126-128]、桁架[129]和加筋板[130]，如图10 所示。由上述的理论、数值模拟和实验研究结果发现，反复碰撞载荷下梁、板、板架和加筋板等结构构件的动态行为呈现以下规律：随着刚性质量块碰撞次数的增加，结构的塑性变形不断累积增加，但增加的趋势逐渐变缓；同时，碰撞力逐渐变大，碰撞时长逐渐变小，回弹速度逐渐增大；此外，结构的卸载刚度逐渐增大，如图11 所示。

图10 结构遭受刚性质块反复碰撞实验Fig.10 Repeated impact experiments of structures impinged by a rigid indenter

工程结构在刚性块重复撞击下会产生较大的累积塑性大变形。Zhu 等[121]基于刚塑性理论方法，对四周固支的矩形板受到刚性楔形块重复碰撞进行研究，提出了重复碰撞下结构最终塑性变形的刚塑性解析公式。Huang 等[122]基于不同能量的质量块撞击固支圆板和方板的重复碰撞实验，得到了结构的弹性能与塑性挠度之间的关系式。Jones[123]和Truong 等[129]考虑到材料的弹性能对结构塑性动力响应预测的影响，基于实验结果提出了反复碰撞载荷下结构塑性变形的半解析刚塑性修正公式。Zhu 等[130]基于前期工作，将板的重复碰撞问题拓展到加筋板，考虑材料的应变硬化、应变率敏感效应等真实特性，基于刚塑性理论方法提出了加筋板在质量块重复撞击下的解析公式。最近，Hao 等[131]基于弹塑性模型，研究了矩形截面梁在小球撞击下的应变率效应，提出了一种分析球-梁碰撞瞬态响应的解析-数值模型，并探讨了冲击条件对接触持续时间和恢复系数的影响。

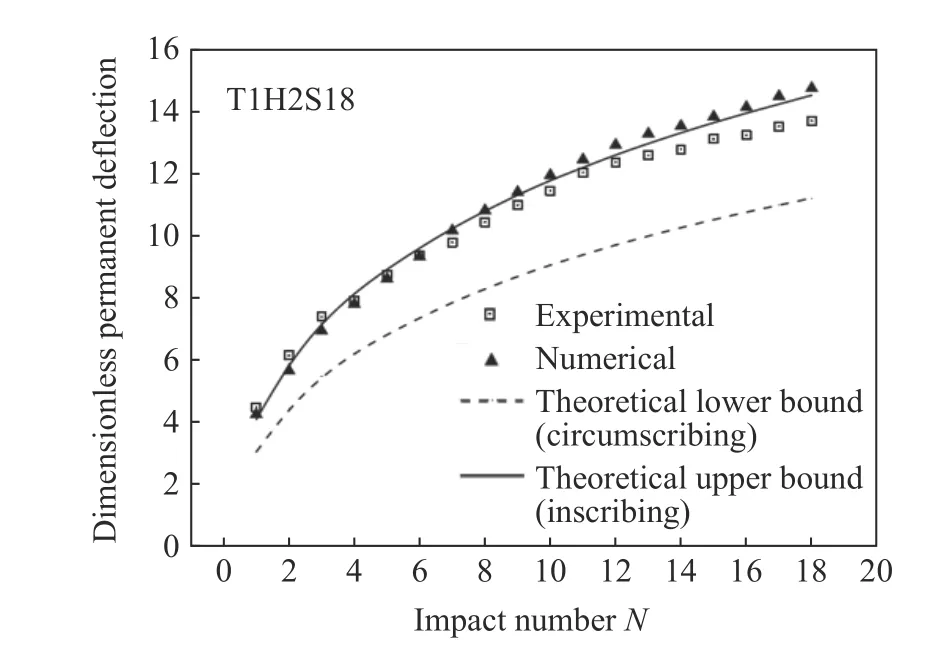
图11(a) 板塑性变形的刚塑性理论方法对比结果[130]Fig.11(a) Comparison of plastic deformation obtained from different methods[130]

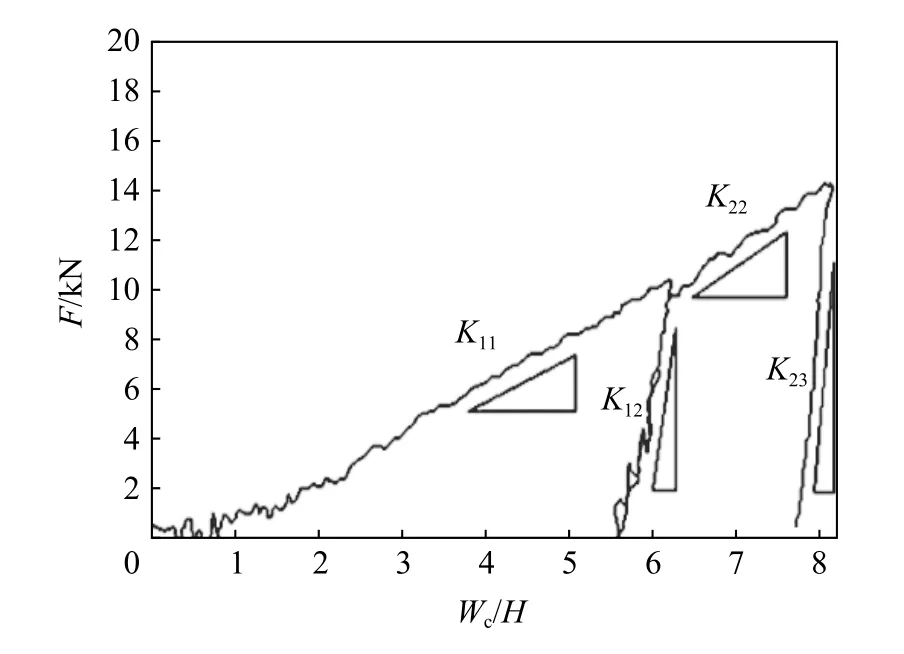
图11(b) 反复碰撞载荷下刚度变形特性[124]Fig.11(b) Variation of stiffness under repeated impact loading[124]

针对一些极端环境下结构遭受重复碰撞的问题，一些学者开始研究低温环境下重复碰撞载荷作用下的塑性动力响应。Cho 等[126]和Truong等[129]分别开展了常温和低温环境下梁、桁架以及泡沫铝金属夹层板的重复碰撞下的动态响应实验研究，研究中考虑了低温、应变硬化以及应变率对重复碰撞下结构动态响应的影响，如图12所示。

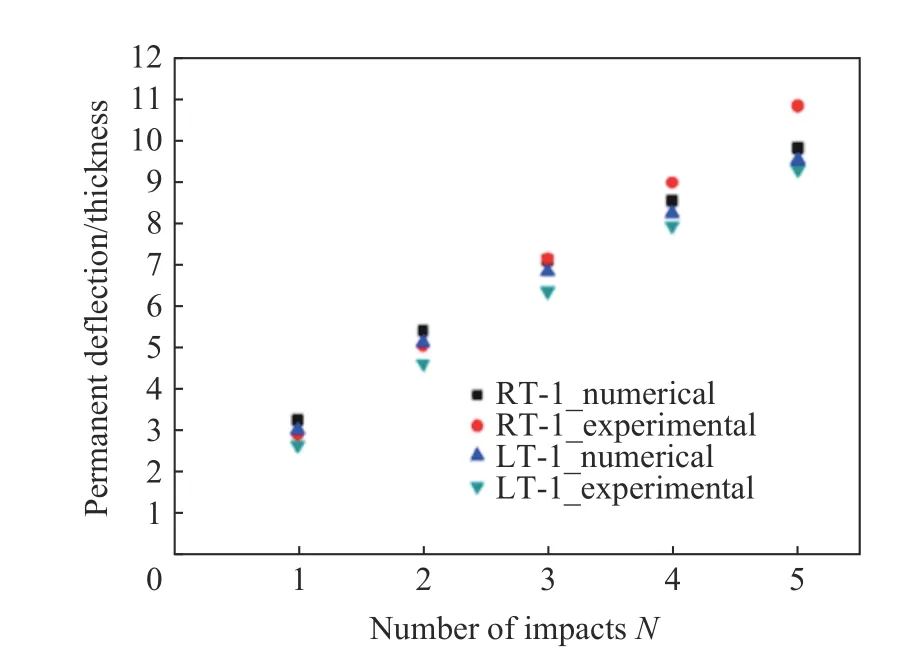
图12 室温和低温环境下结构永久变形值随碰撞次数的变化关系[126]Fig.12 Relationship of permanent deformation at room and low temperatures versus the number of impacts[126]

然而，针对重复碰撞载荷下的结构响应问题，伪安定现象是否发生仍处于探讨之中。目前，针对刚性块重复碰撞下结构的伪安定现象的发生判据只作了定性分析，而重复碰撞下结构的伪安定现象发生时冲击能量临界判据为多少仍然是需要探讨的难点问题。Zhu 等[121，130]对楔形冲头重复撞击固支矩形板和加筋板进行了模型实验、刚塑性理论分析和弹塑性数值模拟，结果表明：随着碰撞次数的增加，板的塑性变形一直保持着增大的趋势，伪安定现象没有出现。Huang 等[122]采用不同能量的质量块撞击固支圆板和方板进行重复碰撞实验，结果表明：随着塑性变形的增大，每次碰撞下板的弹性能在增大，吸收的塑性能在减小；当碰撞次数达到一定量且碰撞能量小于板能够储存的最大弹性能时，船体板的挠度将不会继续增大，即出现伪安定现象[128]。Jones[123]回顾了Zhu 等[121，130]和Huang 等[122]的工作，指出在实际工程案例中碰撞能量一般会大于结构最大弹性能，反复碰撞载荷下结构塑性变形能仍将继续增加，伪安定现象很难出现。新近，He 等[132]报道了他们对低碳钢梁和铝合金梁进行的落锤低能量重复冲击实验，发现在反复撞击过程中，梁的最终塑性变形达到一个稳定值，梁结构出现了伪安定现象。

3 薄壁结构件在冲击和爆炸作用下的动力行为

薄壁结构件具有很高的强度对质量之比值，在车辆和飞行器结构中应用极为广泛；同时，薄壁结构件容易发生大变形，从而较好地吸收冲击能量，适合用于冲击和爆炸的防护结构。

3.1 圆环、嵌套和串列

3.1.1 圆环和嵌套的圆环组

作为一种最简单的薄壁结构元件，薄壁圆环自20 世纪50 年代起就已经吸引了学者们的注意，对它们的准静态大变形行为和冲击响应都开展了大量实验研究和理论分析，其中与冲击行为有关的经典结果见文献[133-134]，而刚塑性理论模型均以包含固定和移动塑性铰的机动场为分析对象。近年来新的研究报道不多，文献[135]报道了用楔形块撞击圆环的实验。

拓展圆环的能量吸收能力和抗冲击能力的一个可能途径是在圆环中间填充泡沫等轻质材料。对此，准静态的研究很多，也有文献报道了相关的冲击实验及分析，例如文献[136]。另一个可能途径是采用相互嵌套的薄圆环组（见图13），用以提高横向的抗冲击能力，近几年已有很多研究[137-142]，而相关的理论模型大都是在单个圆环的四铰或多铰模型的基础上加以扩展。理论模型和数值模拟都表明，由于间歇式的内部接触，嵌套的薄圆环组具有阶梯状的力-位移关系，这使得人们能够根据设计要求来选取圆环的数目和尺寸，从而获得比较理想的抗冲击能力和能量吸收能力。

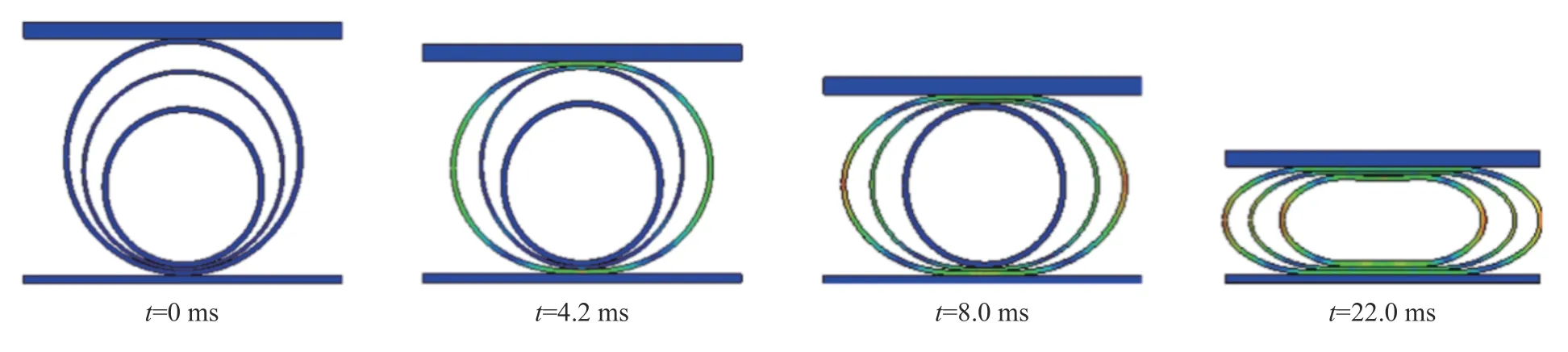
图13 嵌套的薄圆环组承受横向冲击后的变形形态[137]Fig.13 Deformed configurations of a nested ring under transverse impact[137]

3.1.2 圆环和其他胞元的串列

早在20 世纪80 年代，Reid 等[143-145]就对圆环串列进行了系统的研究，并建立了压缩变形在串列中传播的模型。进入21 世纪后，Gao 等[146-147]、Yu 等[148]、Liu 等[149]、Gao 等[150]和Shim 等[151]将有关研究扩展到由其他形状的胞元构成的一维串列，揭示了动态变形的传播特性与胞元形状的关联性。例如图14显示的以弯折薄板为单元的一维串列[146-147]，每个单元都是一个典型的Ⅱ型结构，它的力-位移曲线在峰值后有显著下降，因而其串列的动态行为也与圆环串列[149]有显著不同。尽管一维串列很难直接付诸应用，但是对它们的研究可以揭示不同胞元构型和材料特性对胞元链的波传播特征及动态行为的影响，因而成为研究二维或三维多胞材料动态行为的实验场和预演场。

图14 在轴向冲击下的折板胞元的串列[147]Fig.14 A chain of pre-bent plates under axial impact[147]

近年来发现，当胞元材料具有渐减硬化（即应变硬化曲线对上方呈凹形）的特性时，多种构型的胞元串列可以引导应力波由压缩波向拉伸波转化，甚至产生冲击波。将串列改成离散单元的系统时，由于单元之间的力和位移依据接触规律来传递，更可以产生复杂的动力学现象，例如观察到孤立波的传播，相关的描述参见本文的5.2 节。

3.2 受轴向冲击的圆柱壳

由于其理论和实用意义，弹塑性圆管/圆柱壳承受轴向冲击的问题多年来一直受到很大的关注。在早期工作[152-154]的基础上，Karagiozova 等的一系列研究[155-159]揭示了2 类屈曲（即动态屈曲和渐进屈曲）各自的形成和发展机理，以及应力波、材料惯性等因素对动态屈曲过程的影响。相关的工作还有不少，例如文献[160-161]。可以发现，弹塑性圆管/圆柱壳受到轴向冲击后，应力波的传播和结构的动态屈曲这2 个力学现象互相耦合，是实验中观察到的复杂现象的根源；而随之发生的壳体大变形中，几何形状的变化又同动态过程的惯性效应纠缠在一起，形成比准静态大变形更为复杂的响应模式。

Rajabiehfard 等[162]报道了对圆柱壳施加轴向冲击的2 种加载方式：用气炮发射的子弹直接撞击圆柱壳，和圆柱壳以一定速度撞击到固壁。实验发现，总能量吸收和皱褶半波长与加载方式无关，并与理论分析符合良好；但峰值力和柱壳的屈曲形状则与加载方式及撞击速度有关。Kuleyin 等[163]采用数值模拟研究了有内压的圆柱壳受轴向冲击时压力波在轴向和径向的传播，实验结果也显示有内压的圆管受撞击后的大变形褶皱更规则（见图15，图15(b) 所示的圆管内充气，初始有0.4 MPa 的内压，撞击过程中内压由压力控制器控制），这同准静态的实验观察[164]是一致的。对嵌套或多胞的圆管的轴向冲击行为也有不少新的报道，典型的如Zhang 等[165]的报道。

图15 受到30 m/s 子弹撞击后的圆管[163]Fig.15 Circular tubes after impact by a bullet traveling at 30 m/s[163]

3.3 承受横向冲击或爆炸的管梁和圆管

3.3.1 圆管梁在横向冲击载荷下的大变形

管梁（即截面呈管状的梁）在建筑、能源和海洋工程中有广泛应用，但由于管梁在大变形过程中会发生截面的畸变，反过来会影响截面的承载能力，因此对管梁动态大变形的分析难度很大。以Bambach[166]和Jama 等[167]的实验结果为依据，Karagiozova 等对方形和圆形的管梁在远场爆炸载荷作用下的动力大变形提出了理论模型[168-169]，在模型中，管梁的动力响应由总体变形（类似于实心梁，大变形诱导出的轴力用膜力因子法处理）和局部变形（考虑管截面形状的畸变）2 部分构成，并考虑二者的相互作用（局部变形的截面的承载能力降低），较好地解释了实验结果。圆管梁的受载情况和截面的畸变模式如图16 所示[169-170]，图16(b)显示截面变形模式，总变形包括总体挠度w和局部位移δ。

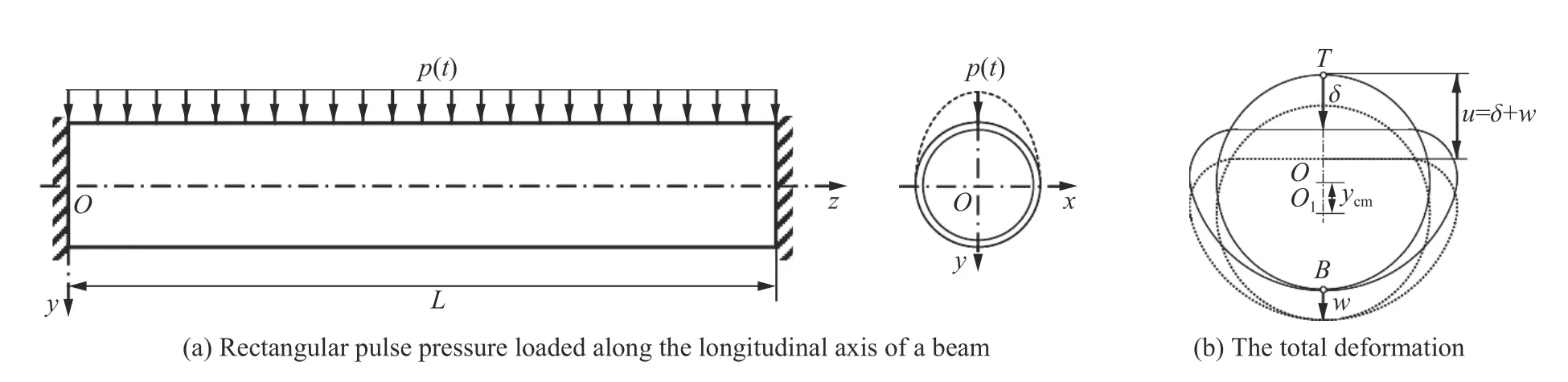
图16 圆管梁承受横向均布矩形压力脉冲及其截面的畸变模式[169-170]Fig.16 A beam of circular tubular cross-section subjected to transverse pressure as rectangular pulse as well as its cross-section distortion mode[169-170]

最近，Karagiozova[170]在先前提出的大变形模型[169]的基础上，研究了圆管梁在均布矩形压力脉冲作用下可能出现脉冲饱和现象的条件，率先将本文第1 节中阐述的饱和冲量的概念和分析方法拓展到非实心截面梁的动态响应分析。

Li 等[171]利用图17 所示的实验装置开展了不锈钢短圆管横向承受爆炸的实验，并进行了数值模拟；基于实验观察到的圆管塑性大变形模式的演变，提出了一个近似理论模型。纪冲等[71]、陈勇等[172]、宋克健等[173]、余洋等[174]也报道过关于爆炸加载下圆管或方管的动态响应的研究。

图17 对圆管施加横向爆炸载荷的实验装置[171]Fig.17 Experimental setup for a circular tube subjected to explosion in its lateral direction[171]

3.3.2 受横向撞击的圆管梁和充液管道

以输油输水的管道受到车辆、船舶或坠落物品的撞击为工程背景，Jones 等[175]较早就开展过具有内压的管道的横向冲击实验。Zeinoddini 等[176]对预加轴力的钢管受横向冲击的情况作了数值模拟。稍后，Kristoffersen 等[177]开展了一系列空心的和充水的钢管的横向冲击实验。近几年，圆管梁受到带有不同形状（楔形、半球形、圆柱形等）冲头的刚性块的横向撞击实验陆续有所报道，如文献[178-181]。Lu等[182-183]对于充液圆管受到横向冲击的研究包含了流固耦合的数值模拟。

除管状结构外，拉伸蒙皮在横向强动载荷下的动力响应可能出现几何上的不稳定性，对此，Ren 等[184-185]进行了初步理论分析。

3.4 承受撞击的薄壁球壳和薄壁球

对柱壳以外的薄壁壳体一直研究较少，原因之一是试件的制作相当困难，同时在工程结构中的应用也相对较少。Gupta 等[186-187]对金属球冠进行落锤加载实验是较早的尝试。路国运等[188]、Yang 等[189]、Zhang 等[190]发表了相关课题的实验工作；刘文祥等[191]则研究了爆炸下球壳变形空间周期分布的理论计算方法。

Ruan 等[192]首先通过实验注意到乒乓球的材料性质十分接近理想弹塑性，而且国际标准的比赛用球的规格十分严谨，由此开创了采用乒乓球作为试件研究球壳的压溃和撞击响应的先河。接着，Dong 等[193]使用Hopkinson 杆对乒乓球施加动态脉冲，研究了球壳和球壳串列的动态变形特性。Zhang 等[194]通过对乒乓球撞击区域进行高速摄像，研究了球壳的局部动态屈曲过程，并与准静态的局部变形过程进行了对比。

在以上实验工作的基础上，Karagiozova 等[195]提出了球冠在冲击载荷下的刚塑性理论模型，假定球冠的塑性变形只发生在压扁和翻转的局部区域，成功地揭示了球冠在准静态和动态受载时局部区域的变形剖面以及力-位移关系的差异。如图18(a)所示，动态翻转屈曲似乎来得较迟，翻转之后也没有准静态情形凹陷得那么深；而如图18(b)显示的力-位移关系上动态曲线与准静态曲线的差异，主要归因于撞击区被加速的惯性效应，撞击速度增大时这种差异也增大。Li 等[196]报道了撞击实验，同时在理论模型中考虑了局部剪切变形（见图19）。

图18(a) 准静态加载和动态加载下球冠变形剖面的比较[195]Fig.18(a) Deformed profiles of a spherical shell under quasi-static and dynamic loadings[195]

图18(b) 加载速度为30 m/s 时力随位移的变化[195]Fig.18(b) Variation of the force with the displacement under the loading speed of 30 m/s[195]

图19 考虑局部剪切变形区的球冠动态变形模型[196]Fig.19 Dynamic deformation model of a spherical shell with local shear region being considered[196]

此外，类似于3.1 节中介绍的对相互嵌套的薄圆环组的研究，Hu 等[197]也借助数值模拟预测了嵌套的圆球组的冲击行为。由于试件制作困难，并没有开展相应的实验。对于外廓接近球面的网壳在冲击或爆炸下的动力响应，参见文献[198-200]。

3.5 经受坠落和内爆的容器

在石油化工以及运输工业中，带有封头的圆柱形容器和球形容器都有十分广泛的应用。容器内部通常用于充填液体或气体，有些液体或气体在剧烈撞击下容易发生爆炸和燃烧，造成重大事故。此外，在反恐中暂存和引爆疑似爆炸物的安全壳也必须具备良好可靠的抗内爆的能力。因此，坠落和内爆都是防范容器发生危险事故所需要考虑的场景。

Dong 等[201-202]、Chen 等[203]对球形安全容器受到内爆的情形作了系统的研究。目的相类似的工作在南非开普敦大学和中国的一些高校也有所开展[204-209]。基于平均剪应力的屈服准则，Chen 等[210]分析和预测了圆柱形容器在内压下发生动态爆裂的压力。

相对而言，对含液容器的坠落的研究比较少，已见到发表的有文献[211-212]。

4 运动的物体和结构物对固壁的撞击和反弹

4.1 实心球体对固壁或厚板的撞击和回弹

弹性球体对固壁或弹性板的撞击和回弹很早就受到研究者的注意，不少早期文献报道了钢珠坠落到钢板后回弹的实验。至今经常被引用的重要工作包括文献[213-216]，这些工作假定碰撞是完全弹性的，分析了撞击发生后弹性波的传播和携带的能量。1997 年以来，Thornton[217]和Wu 等[218-219]的一系列工作详细分析了弹塑性球撞击后的回弹行为和能量耗散。Vu-Quoc 等[220-221]和Zhang 等[222]对弹性碰撞和弹塑性碰撞的情形，分别利用Hertz 理论和Stronge 提出的碰撞模型[223]进行了分析，对碰撞接触时间、接触力、接触位移等给出了解析的结果。

Stronge[224]在更为普适的框架下对球之间的撞击作了系统的阐述，其中对恢复系数(coefficient of restitution,COR，e) 给出了3 种定义方法，即：运动学定义、动力学定义和能量定义。对小球撞击固壁的情形采用运动学定义时，恢复系数是小球回弹的速度vr与初始速度v0之比，即e=vr/v0。

另一项有特色的工作来自Minamoto 等[225-226]，他们采用摆锤和气枪作为动力源加速2 个直径25.4 mm的钢球，两球相撞的相对速度范围分别为＜3 m/s 和10～20 m/s。如图20(a)和图20(b)所示，分别画出了两球的接触时间tc和恢复系数e随撞击速度vi的变化，可以通过数值拟合分别表示为：

他们的研究也显示，对于钢球，即使是低速碰撞也不应忽略材料的应变率效应，这可以从图20(b)中实验结果与有限元模拟的比较得到证实。

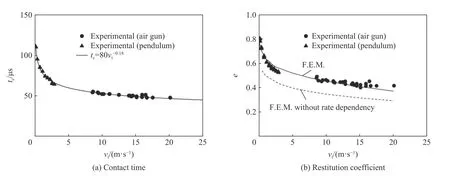
图20 撞击接触时间和恢复系数随撞击速度的变化[226]Fig.20 Contact time and restitution coefficient varying with impact velocity[226]

作为一个最简化的飞射物体向固壁的撞击模型，理想弹性球对理想弹塑性半空间的撞击以及两球相撞的问题近年来仍然被反复地用不同方法加以研究，例如文献[227-230]。Müller等[231]、Böttcher等[232]、Boettcher 等[233]对刚球与厚板的撞击中弹性波引起的能量损失进行了细致的分析，其中着重讨论和改进了Hunter 的经典结果[214]。

也许值得一提的还有，Parra 等[234]讨论了在用摆锤撞击玻璃板的实验（见图21）中有多少能量有效地传递给了靶板，也是对撞击过程中能量损失的分析。显然，这项研究可以应用到路人头部撞击到橱窗或隔墙的玻璃板的事故分析。

图21 摆锤撞击玻璃板[234]Fig.21 A glass panel impacted by a pendulum[234]

4.2 运动的结构物对固壁或另一结构物的撞击

如果说4.1 节介绍的实心球撞击半空间或厚板的研究主要源自理论上的兴趣，那么工程和生活实际中大量发生的是另一类情形的撞击。汽车、高铁、船舶、飞行器、航天器等运动的结构物在碰撞事故或紧急着陆时都要经历对固壁或另一结构物的撞击；在生活中，手机和各种便携式电子用品的跌落十分常见；各种球类运动更是离不开薄壁球体对地面、墙面或台面的撞击和反弹。这类问题与带有支撑的结构承受撞击或给定脉冲的传统动力学问题不同，也与实心球的撞击不同。在运动结构物对另一结构物或固壁的撞击问题中，撞击物的质量和初始速度是已知的，但撞击过程中能量转化十分复杂，结构物通常会发生非弹性大变形并因此耗散掉大部分输入动能，同时一部分输入能量将转化为弹性变形和振动，还有一部分能量则被结构发生反弹时的总体动能带走。由于能量的具体分配既取决于撞击中结构物自身的质量和弹塑性特性，又依赖于撞击速度，因此结构物的动态变形和反弹行为有很大的变化范围和探索空间。

在2001—2010 的10 年间，Yu 等[235]、Yang 等[236]、Ruan 等[237-241]和Yang 等[242]共同开拓了“2 个可变形的结构之间的撞击”这一新研究领域。典型的撞击场景包括平动的自由梁、转动的梁、运动的圆环、弹簧-质量系统等运动结构物对具有固定支承的梁的撞击；在分析方法上，尝试和比较了刚塑性完全解、模态解、数值模拟和实验。分析表明，在2 个可变形的结构发生撞击时，刚度较弱的一方终将吸收大部分撞击动能；撞击速度很高时，局部变形及相应的能量吸收尤为显著。

4.3 薄壁圆环对固壁的撞击和反弹

Bao 等[243]采用数值模拟和理论分析相结合的方法，研究了运动中的薄壁圆环沿其直径方向以初速度v0撞击到一个固壁上的情形。假定圆环材料是弹-理想塑性的，那么圆环的动态变形和反弹行为由3 个无量纲参数决定，即：（1）无量纲壁厚 η ≡h/R，其中h和R分别为圆环的壁厚和半径；（2）无量纲撞击速度v≡v0/vy，其中vy≡Y/(Eρ)1/2为材料的屈服速度，Y、E和ρ 分别为圆环材料的屈服应力、杨氏模量和密度；（3）材料的屈服应变 εy=Y/E=vy/c，其中c=(E/ρ)1/2为弹性纵波的波速。

采用ABAQUS 数值模拟的结果表明：当圆环的撞击速度很低时，撞击后圆环的变形完全是弹性的，它与固壁的接触时间可以解析地得到。撞击速度升高时，圆环中明显出现塑性变形，先是呈现为四铰模式，后来转化为五铰模式（见图22），它们都同圆环准静态受压时的大变形模式不同。分析也表明，撞击延续的时间以及反弹速度都与撞击速度相关，当撞击速度等于材料屈服速度的2～3 倍时，反弹发生时圆环的质心的速度vr达到最大，为材料屈服速度vy的50%～60%。

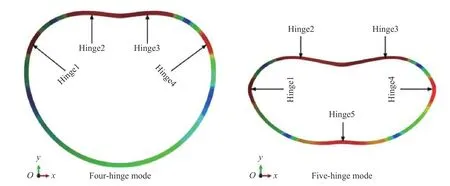
图22 圆环撞击固壁后的动态变形模式[243]Fig.22 Dynamic deformation modes of a circular ring after it impinged onto a rigid wall[243]

在4.1 节中已经提到恢复系数COR 从运动学上可以定义为e=vr/v0。对于圆环撞击问题，v0仍是初始撞击速度，但vr表示的是圆环反弹时它的质心的速度，而不是撞击点的瞬时速度。Bao 等[243]报道的结果表明，尽管具体数值结果受到圆环的几何和材料参数的轻微影响，恢复系数随撞击速度的变化都具备以下共同特征（见图23(b)）：（1）恢复系数COR 随撞击速度的升高而降低；（2）当撞击速度很低，圆环只发生弹性变形时，恢复系数约为0.78；（3）当撞击速度约等于屈服速度时，恢复系数降低的斜率突然放缓。为什么圆环低速撞击时恢复系数并不趋近于1，而是约为0.78？李凤云等[244]和Wang 等[245]对此作了探索。

为了验证数值模拟和理论分析的结果，Xu 等[246]对70 个铝合金圆环试件进行了撞击实验，材料的屈服速度vy约为23 m/s，圆环冲击速度范围为15～110 m/s，实验在分离式Hopkinson 压杆系统上进行，实验得到的圆环大变形形状以及撞击力随位移的变化都同数值模拟结果符合较好，反弹速度和恢复系数的变化趋势如图23 所示。实验和数值模拟也都证实，h/R的值或Y/E的值变化时，对恢复系数COR 的影响都并不大。

图23 圆环对固壁的撞击实验结果和数值模拟结果的比较[246]Fig.23 Comparisons of experiments and numerical simulations for a circular ring impinging onto a rigid wall[246]

4.4 薄壁球对固壁的撞击和反弹

对于薄壁圆球在集中力和平板压力作用下的准静态变形已有很多研究，表明其变形过程包含以下3 个阶段：（1）在一个逐步扩大的扁平的圆形区域内发生接触；（2）接触区向着球内部发生翻转屈曲，形成接触环；（3）随着位移的增大，翻转区扩大并产生环向的皱曲。相应的力学机理也已有一些解释，但由于金属薄壁圆球试件加工困难，动态实验研究长期未能进行。

Zhang 等[247]采用图24 所示的装置，将乒乓球加速到10～40 m/s 后撞击到一块有机玻璃厚板上。乒乓球的材料为赛璐珞，外直径约为40 mm，壁厚约0.38 mm，质量为2.6 g。实验采用高速相机摄取了撞击区内接触环的演变图像。测出的撞击时间约为0.8 ms，与撞击速度基本无关；在撞击情况下，翻转屈曲时接触圆半径比准静态情况下要大。

图24 乒乓球撞击厚板的实验装置[247]Fig.24 Experimental setup for a ping-pong ball impinging onto a thick plate[247]

Bao 等[248]对薄壁圆球撞击固壁进行了详细的数值模拟，其中的3 个无量纲参数与前述圆环撞击问题相似，参数范围为1/250 ≤h/R≤ 1/20,0.2 ≤v0/vy≤ 5.0。结果表明：（1）当撞击速度很低（v0/vy≤ 0.1）时，薄壁球的变形是完全弹性的，这时可以解析地给出力和位移随时间变化的关系，得到薄壁球与固壁的接触时长为7.2R3/2h−1/2/c，其中c为应力波（纵波）的波速，与撞击速度无关，因而乒乓球的撞击时长为0.8 s，这同Yu 等[235]的实测值十分吻合；（2）随着薄壁球的撞击速度升高，撞击点附近变得扁平，进而发生局部屈曲并伴有多次撞击的现象，同时接触时长增大而恢复系数减小；（3）当薄壁球的撞击速度接近材料的屈服速度时，撞击区形成非轴对称（带褶皱）的翻转屈曲，恢复系数进一步下降。图25 所示为不同撞击速度（速度由左向右递增）产生的撞击区的顶视图。

图25 不同撞击速度（速度由左向右递增）产生的撞击区的顶视图[248]Fig.25 Top-views of the collided region after collision at various velocities (the velocity increased from the left to the right)[248]

研究揭示了薄壁球撞击后的变形呈现高度局部化，除撞击区外球面几乎没有变形，这与圆环撞击后发生的整体性变形（图22）有很大不同。对于薄壁球撞击，发现球的最大反弹速度只有屈服速度的1/4，而恢复系数随初始撞击速度的变化规律同圆环撞击大体相似。

在球类运动中，控制球对固壁的撞击和回弹是运动员必须掌握的基本技术。针对特定种类的运动用球，Cross[249-253]做过系统的测量和分析，Hubbard 等[254]也做过很好的理论研究。

4.5 运动的直杆和直梁发生弹性撞击后的反弹

根据弹性波理论，长为L的直杆以一定初速度沿轴向撞击到一个刚性壁后，撞击产生的一维压缩应力波以波速c从撞击端传到远端（自由端），反射成拉伸波再传回撞击端并造成分离和反弹。整个撞击过程的持续时间为2L/c；由于没有能量损耗，恢复系数必定等于1.0。此过程中应力波传播的详细描述可以参见有关书籍，例如文献[5]。

Zhao 等[255]讨论了撞击直杆具有非均匀截面的情形，解释了反复撞击现象。Lundberg 等[256]阐述了如果撞击杆内预加弹性波，撞击后的恢复系数可能大于1.0。Gheadnia 等[257]则针对直杆对平面的斜撞击研究了恢复系数。

Wang 等[258]从弹性振动的角度重新审视了这类问题。他们假设运动中的直杆撞击到一个无质量的理想线性弹簧上（见图26(a)），在保持接触的期间按照约束运动、在非接触期间按照自由运动，分别建立结构的振动微分方程，并用经典的模态叠加法求解。对于多次接触和分离，必须反复应用不同的解并加以衔接，同时还要确保模态叠加中的级数的截断精度。计算和分析的主要目标是确定恢复系数（COR）和无量纲的反弹时间（non-dimensional rebounding time,NRT）对弹簧与杆间的刚度比的依赖关系。图26(b) 中的代表刚度比，AAS 是一种近似解析解。从图26(b) 看到，当刚度比在1～10 之间时，COR 可以比1.0 略小，这是同简化的一维应力波解有所不同的。

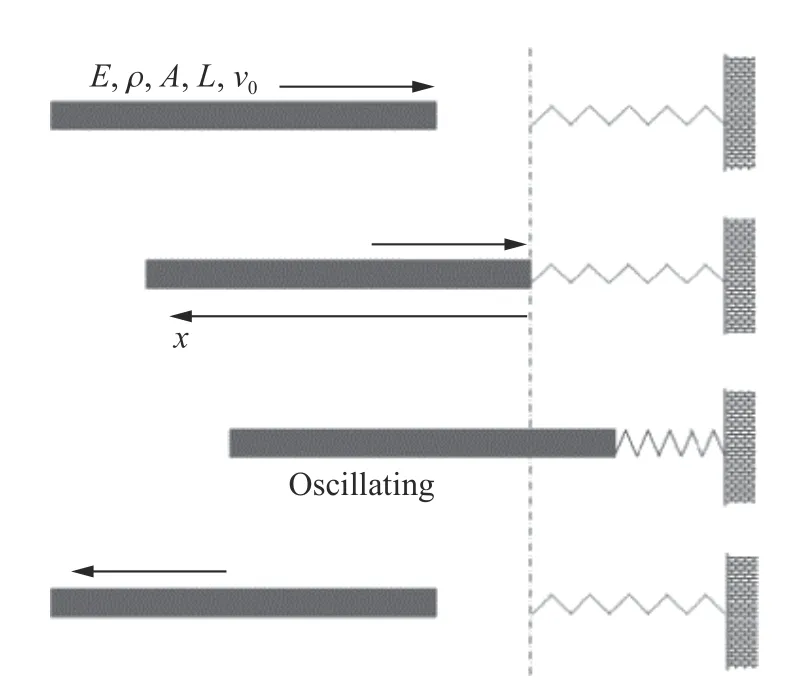
图26(a) 直杆对线弹簧的撞击与反弹[258]Fig.26(a) Collision and rebounding of a straight rod on a linear spring[258]

图26(b) 恢复系数（COR）和无量纲的反弹时间（NRT）随刚度比 的变化[258]Fig.26(b) Coefficient of restitution (COR) and non-dimensional rebounding time (NRT) varying with the rigidity ratio [258]

Wang 等[258]运用类似的方法，还分析了直梁对一个或2 个无质量的理想线性弹簧的撞击和反弹过程（见图27），得到了恢复系数COR 和无量纲的反弹时间（NRT）对弹簧与梁间的刚度比的依赖关系。

图27 梁对理想弹簧的横向撞击[258]Fig.27 Collision of beams onto ideally elastic springs[258]

4.6 恢复系数极小的一个案例

在理论力学课程讲解动量守恒定理时，通常都会以2 个小球的对心碰撞作为典型案例，并且认为完全弹性碰撞的恢复系数一定等于1.0，其理论依据是在弹性变形过程中不会造成系统总能量的损失。但是这个论断其实仅对刚性小球间的低速碰撞近似成立，因为即使小球是理想弹性体，考虑到撞击激发的弹性波和随之而来的弹性振动都会携带一些能量，小球撞击前的动能不可能全无缺失地保持为反弹后小球刚体运动的动能。当撞击的一方或双方都可能因弹性变形而储存可观的变形能时，即使所有的变形都确实在弹性范围之内，按照碰撞前后速度之比定义的恢复系数(COR)都必然会小于1.0。4.3 节的圆环撞击及4.5 节的杆和梁的撞击都提供了弹性撞击产生的恢复系数小于1.0 的证例。

弹性碰撞可能导致多小的恢复系数？因为削减总体刚体运动的动能（以质心的速度为代表）的主要因素是弹性振动，Ruan 等[259]尝试利用一个二自由度模型来检验这个问题。如图28(a)所示，这个模型包含2 个质点（质量分别为m1和m2）和2 个弹簧（弹簧系数分别为k1和k2）。k1弹簧代表接触行为，具有线性的力与位移关系；k2弹簧则将2 个质点连接在一起。撞击发生前2 个质点以相同速度v0运动。令α ≡m2/m1和β≡k2/k1分别表示质量比和弹簧系数比，这2 个无量纲数控制着系统的行为；而系统动力行为的唯一的无量纲标志量是恢复系数（COR），即反弹发生时质点组的质心的平动速度与v0之比。

图28(a) 二自由度质量-弹簧系统[259]Fig.28(a) A two-degree-of-freedom mass-spring system[259]

Ruan 等[259]对这个二自由度系统的动力学方程进行求解，在不同弹簧刚度比β ≡k2/k1下分别得到了恢复系数COR 随质量比α ≡m2/m1的变化（见图28(b)）。值得注意的是，COR 随α 变化的曲线呈现许多个尖锐的极小值。例如，图中黑线代表 β=0 的情形，相应于接触弹簧极为刚硬（弹簧系数k1趋于无穷大），这时恢复系数（COR）的极小值0.178 在α=0.697 出现。粗略地说，当m2≈0.7m1时，系统质心的反弹速度仅为撞击速度的18%，因而在发生反弹后系统质心的平动所携带的动能仅为初始撞击动能的3%左右。余下的97%都转换为k2弹簧的变形能和系统的弹性振动的“局部”动能，且这二者之间可以不断相互转化。由一个极其简单的动力学模型发现如此低的恢复系数，具有重要的理论意义和潜在的应用价值。

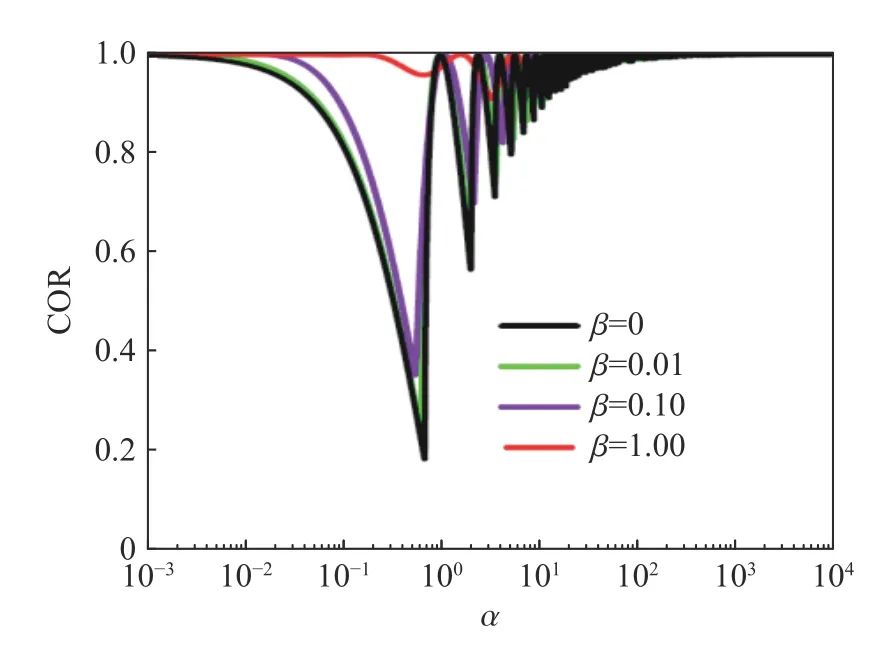
图28(b) 恢复系数随质量比的变化[259]Fig.28(b) COR varying with the mass ratio[259]

弹性振动对撞击和反弹行为的影响也引起了物理学家的重视。例如：理想气体可以想象成一个由许多物质点组成的系统，相互之间存在着类似于弹簧的相互作用力。如果在撞击发生之前物质点已经存在热振动，在碰撞发生后这种振动的“局部”动能可以部分地转化为质点组的平动动能，因而表观上出现恢复系数COR 大于1.0 的怪异行为[230,260-261]。

在4.1 节提到的Müller 等的工作[231]中，报道了他们完成的钢球坠落在玻璃板上的反复弹跳实验，自动记录钢球在每次撞击前后的高度，进而计算每次撞击的恢复系数；对数千次撞击与反弹的实验作出大数据分析，发现COR 对撞击速度的依赖曲线呈现阶梯式的变化，而阶梯的宽度和高度同玻璃板的振动频率和幅度一致。这项研究展现了COR 与弹性振动之间的高度关联性。

5 轻质材料和轻质结构在冲击下的动态响应

5.1 多胞材料的动态响应

5.1.1 蜂窝材料的动态响应

多胞材料的动态响应研究对汽车、航空轻量化意义重大[262-263]。其中，蜂窝材料是规则分布的二维多胞材料，其胞元截面以六角形为主，也可以是三角形、长方形、圆形等[264]。六角形蜂窝材料的几何参数及压溃时的典型载荷-位移曲线如图29[265]所示。曲线可分为线弹性段、平台段和压实段3 个阶段。当加载方向不同时，蜂窝材料的变形机制存在显著差异。

图29 六角形蜂窝材料[265]Fig.29 Hexagonal honeycomb materials[265]

面内加载时，在线弹性段，蜂窝材料胞壁发生小挠度弯曲。达到临界应力后，胞壁失效进入平台段。失效机制包括弹性屈曲、塑性破坏或脆性断裂。随后，胞元被完全压溃，胞壁相互接触，进入压实阶段，载荷急剧增加。压实应变和平台应力是衡量蜂窝材料动态响应的重要参数。压实应变的理论值与蜂窝材料密度的定量关系为 εd=1−ρ∗/ρs[266]，式中 ρ∗为多胞材料的表观密度，ρs为胞壁材料固体密度[267]。压实应变的实验值略小于理论值，可通过添加经验系数来估算实际压实应变[268]。随着加载速度变化，蜂窝材料整体在面内压溃过程中也存在不同的变形模式（见图30）[269]。当速度较低时，可在蜂窝材料中观察到X 形局部变形带[270-271]。当速度较高时，可观察到垂直于加载方向的I 形变形带。而中等速度压溃时，可观察到过渡模式，即V 形变形带。不同模式之间的转换由胞元的几何参数决定。Ruan 等[269]给出了六角形蜂窝临界速度的经验公式。其中，X 模式转换到V 模式的临界压溃速度约为14 m/s，而V 模式转换到I 模式的临界压溃速度与正相关。对于非均匀蜂窝材料，例如屈服强度[272]或密度[273]梯度变化，其变形模式与均匀蜂窝材料不同，且随着梯度方向的不同而改变。

图30 蜂窝材料面内压缩变形模式[269]Fig.30 Deformation modes of honeycombs under in-plane crushing[269]

蜂窝材料面外加载的应力-应变曲线形式上与面内加载类似。针对弹性屈曲导致的平台应力，Gibson 等[274]给出了平台应力与胞元几何参数的关系。针对塑性坍塌，Wierzbicki[275]参照薄壁方管的经典轴向压溃模型，考虑单元的拉伸和弯曲变形，对渐进破坏过程中的塑性区进行能量分析，从而获得平均压溃应力。Zhang 等[276-277]通过实验和有限元分析研究了X 形和Y 形等单元的动态响应，发现Wierzbicki 的经典直角单元模型[278]不能准确预测存在锐角和钝角的单元性能；因此，基于不同单元的变形模式提出了改进模型，并准确预测了Rhombic 和Kagome 等蜂窝的平均压溃力[279]。此外，Hu 等[280]基于Alexander 圆管压溃模型[281]给出了圆形蜂窝材料的面外压溃应力 σ3=(C1/K)(h/d)n1Y，其中K与蜂窝材料中圆形胞元的堆积形式有关，C1和n1均为常数，d为圆形胞元直径，Y为蜂窝胞壁材料的屈服应力。

由于蜂窝材料的应力-应变曲线呈现对上方凹陷的形状，当碰撞速度较高时，蜂窝材料中会产生塑性波的汇聚[282-283]。Reid 等[282]假设达到压实应变前的应力-应变关系为理想刚塑性，将塑性冲击波理论应用于蜂窝材料的动态响应分析，给出：

式中：σp为准静态加载下的平台应力，σD为动态压溃应力，ρ0为冲击波到达前的密度为压实应变。这里将蜂窝材料理想化为连续介质，由准静态加载到冲击波加载所增加的应力值(σD−σp)与初速度v0的平方成正比。Hu 等[284-286]则从蜂窝结构的角度出发，得出与上述公式完全一致的动力增强项，而且解析地获得了压实应变与蜂窝几何参数的关系。此外，考虑到胞壁材料可能存在应变率效应，Tao 等[287-288]通过在冲击波理论中引入Cowper-Symonds 模型得到了应变率相关的冲击波理论。后续研究表明，该理论也适用于非均匀蜂窝材料[289]。

随着3D 打印技术的不断发展，新型蜂窝材料的设计和制备存在更多可能。因此，研究人员从结构设计的角度出发，通过实验、理论、数值模拟等方法研究了各类新型蜂窝材料的动态响应[290-291]。例如：Qiao 等[292]在六角形蜂窝材料中引入多层级的概念，并基于不同的变形模式计算其面内动态压溃应力。Chen 等[293]则研究了冲击载荷下双层连拱形结构的动态响应。在摆锤冲击实验中，双层连拱形试样的背板均出现塑性变形，并且可以观察到对角折痕、局部变形以及固定端处的颈缩现象。Meng 等[294]讨论了组合铝蜂窝受爆炸冲击的动态响应，并建立了一个半经验公式来描述2 个层叠蜂窝的压缩深度。Hatami 等[295]通过实验和数值模拟讨论了金属网状结构的动态响应及其几何参数的影响，并且利用能量方法建立了理论模型。此外，负泊松比材料作为新型蜂窝材料的代表，具有优于传统蜂窝材料的抗冲击性能[296]。Zhang 等[297]通过有限元模拟探究了几何参数对内凹蜂窝材料动态响应的影响，并发现低速加载时内凹蜂窝材料的变形机制与传统六角形蜂窝材料类似。Baertsch 等[298]在内凹结构中引入梯度变化的刚度，从而获得了更优异的能量吸收特性。Qiao 等[299]则基于胞元的微结构变形建立了双箭头拉胀蜂窝材料受低速和高速冲击时压溃应力的理论模型。Gao 等[300]通过实验和有限元模拟探究了手性拉胀结构受面内冲击时的动态响应。

5.1.2 泡沫材料的动态响应

泡沫材料是由多面体胞元组成的三维多胞材料，胞元类型为三棱柱、四棱柱、六棱柱等。根据胞元间是否相通，泡沫材料可分为开孔泡沫和闭孔泡沫，其相对密度分别为是由胞元几何决定的常数[271]。泡沫材料的响应与蜂窝材料类似，Deshpande 等[301]建立了各向同性的本构模型来描述金属泡沫材料的应力-应变关系。对于开孔泡沫的弹性屈曲变形，Gibson 等[274]通过分析理想胞元的欧拉屈曲载荷得到平台应力对于闭孔泡沫，估算平台应力时须考虑胞元中空气的压缩，因此这里 Δp为闭孔泡沫胞元内初始压力与大气压力差。发生塑性坍塌时，开孔泡沫仅考虑塑性弯曲，平台应力为σp/Ys=0.3(ρ∗/ρs)3/2；而闭孔泡沫须同时考虑胞元棱边的弯曲和胞壁的拉伸。

假设泡沫材料的母材为理想刚塑性材料，可应用前述塑性冲击波理论得到动态平台应力。Tan 等[302]通过研究泡沫铝材料的动态响应，在塑性冲击波理论的基础上提出了改进模型。该模型考虑了材料的弹性性能，且理论结果与实验和数值模拟相符[303]。Harrigan 等[304]在模型中同时考虑了材料的弹性和塑性性能。Zheng 等[305]则通过在冲击波理论中引入线性硬化描述了泡沫材料不同的变形模式，并基于刚性-塑性硬化模型(R-PH)分析了多胞材料抗冲击牺牲层行为[306-307]。Kader 等[308]通过实验和数值模拟探究了闭孔铝蜂窝泡沫中的应力波传播和变形机制，发现应力波传播的最短路径与泡沫材料的拓扑结构密切相关。此外，Liao 等[309]和Zheng 等[310]先后建立了二维和三维Voronoi 模型，从而更好地理解泡沫材料的变形机制。同时，Li 等[311]利用Voronoi 模型讨论了冲击速度、相对密度、胞元不规则程度、胞壁材料的率相关特性等关键参数对泡沫材料动态响应的影响。结果表明，与冲击波理论相比，Voronoi 模型能更准确地描述闭孔泡沫的动态响应。

与传统泡沫材料相比，具有功能梯度的泡沫材料通常表现出更优异的能量吸收和抗冲击特性。例如：密度梯度变化的泡沫材料具有平稳上升的平台应力[312]。Gupta[313]讨论了胞元厚度梯度变化时泡沫材料的响应。结果表明，可以通过梯度控制泡沫材料的模量、强度以及能量吸收性能。Zeng 等[314]通过准静态和霍普金森压杆探究了密度/强度梯度变化对泡沫材料抗冲击性能的影响，发现梯度方向对冲击防护效果影响显著。此外，Shen 等[315]通过研究梯度泡沫杆在轴向冲击下的动态行为，首次从理论上提出了双冲击波模式，即同一冲击可以在冲击端和支撑端同时产生冲击波。随后，Shen 等又讨论了不同的梯度对泡沫杆变形模式和能量吸收特性的影响[316]，并通过实验验证了双冲击波模式的存在[317]。

5.1.3 点阵/格栅材料的动态响应

点阵材料（也称格栅材料）是由结点和连接结点的杆件单元组成的具有有序细观结构的多胞材料[318]，通常具有体密度小、比表面积大、比刚度高、比强度高等优势[319]。在动态载荷作用下，点阵材料会发生塑性屈曲和结构动态失稳等，具有良好的缓冲吸能特性[320]。

按照点阵材料承载形式的差异，可将点阵材料分为弯曲主导型和拉伸主导型结构。理论分析表明，设计三维拉伸主导型结构的充分条件为b−3j+6≥0，这里b和j分别为杆件单元数量和结点数[321]。Qiu等[322-323]分析对比了典型的弯曲主导型和拉伸主导型点阵材料的准静态和动态力学特性。他们发现，相比于弯曲主导型结构，拉伸主导型结构的动态力学特性更出色。2001 年，Deshpande 等[324]提出了具有面心立方堆积（FCC）特性的八角点阵材料（见图31(a)）并分析了其宏观力学特性。此后，学者们持续探讨各类点阵材料的宏观力学特性，常见点阵材料类型包括锥形（见图31(b)）、体心立方堆积（BCC）（见图31(c)[325]）、Kagome、Kelvin 及全三角形等[326-327]，其中图31(d)和(e)分别为锥形点阵材料和BCC 点阵材料的典型应力-应变曲线[328-329]。

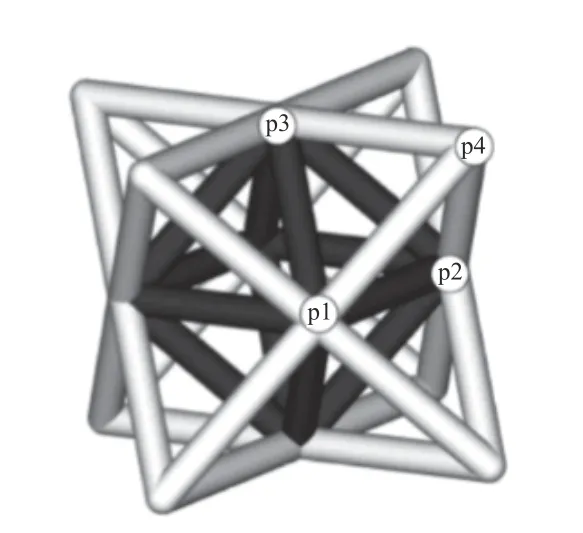
图31(a) 八角点阵材料[324]Fig.31(a) Octet-truss lattice[324]

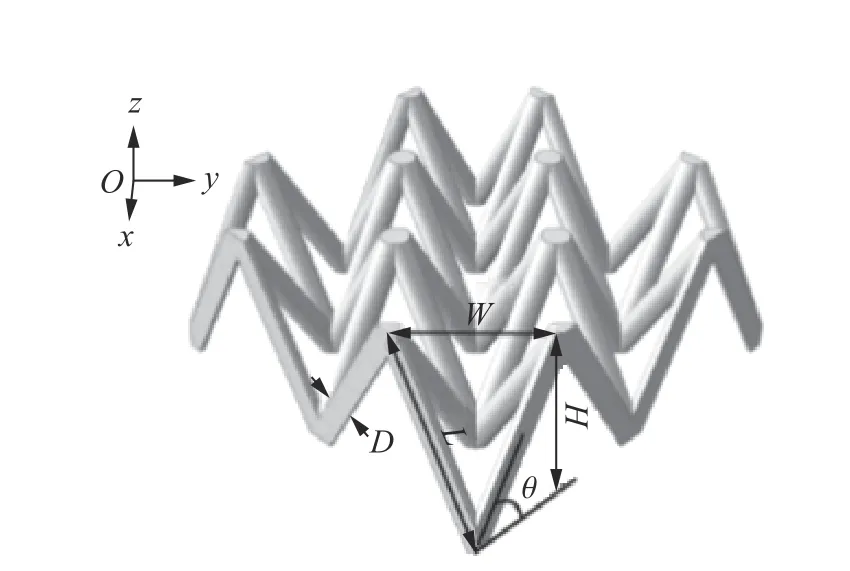
图31(b) 锥形点阵材料[328]Fig.31(b) Pyramidal lattice[328]

图31(c) 体心立方堆积(BCC)点阵材料[325]Fig.31(c) Body-centered cubic (BCC) lattice[325]

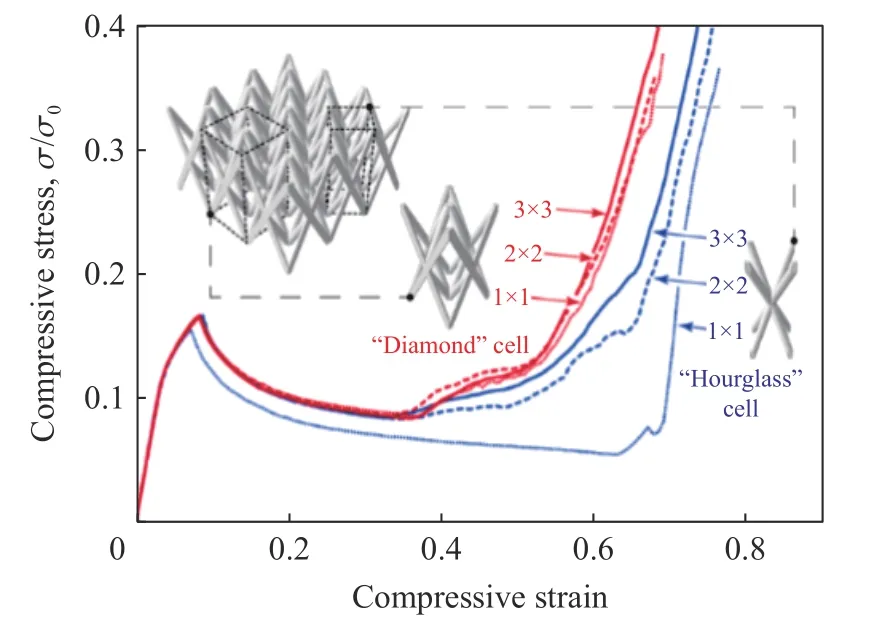
图31(d) 具有不同胞元的锥形点阵材料应力-应变曲线(相对密度0.2)[328]Fig.31(d) Stress-strain curves of pyramidal lattice with different unit cells (relative density 0.2)[328]

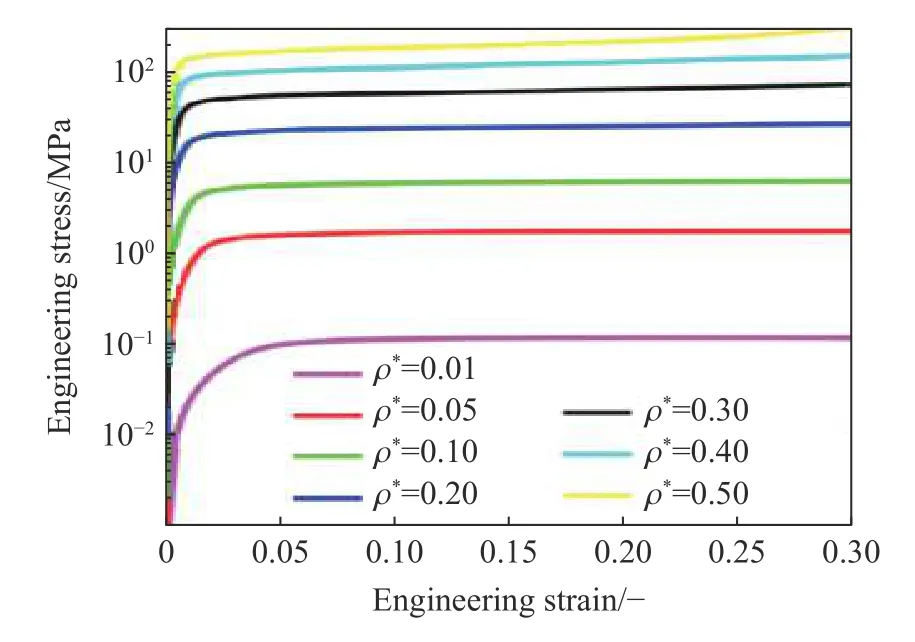
图31(e) 当相对密度变化时，BCC 点阵材料应力-应变曲线[329]Fig.31(e) Stress-strain curves of BCC lattice as the variation of relative density[329]

针对动态力学特性，Ozdemir 等[330]通过霍普金森压杆实验探究了立方点阵、钻石型点阵和内凹型立方点阵的动态响应。结果表明，点阵材料可以及时分散冲击载荷从而降低峰值应力。Tancogne-Dejean 等[331]则通过有限元模拟和实验研究了相对密度和杆件单元截面对动态响应的影响。他们发现，若相对密度大于30%，不锈钢八角点阵材料的宏观应力-应变曲线趋于稳定，并且其比吸能显著高于传统多胞材料。

得益于先进的3D 打印技术，点阵材料的研究从宏观发展至微观和纳观尺度[335-336]。Schaedler 等[337]设计并制备出空心杆件管壁厚度为100～500 nm 的金属微点阵材料。实验结果表明，这种金属微点阵材料压缩至50%应变后仍然能恢复初始形状，并且能量吸收性能与弹性材料相当。Zhang 等[338]则发展了制备热解碳纳米点阵材料的方法，得到了具有低密度（＜1.0 g/cm3）、高强度（GPa 级别，接近理论值）和良好变形能力（＞10%）的纳米点阵材料。虽然表面效应对纳米点阵材料的强度和刚度几乎没有影响[339]，但点阵材料杆件结点处的应力集中会严重影响其性能。为了改善点阵材料的结点性能并提升其动态力学行为，学者们提出了一种由光滑薄壳组成的新型微点阵材料（shellular material，见图32）[340-341]。由于不受结点性能影响，即使相对密度较低，它们也具备优于传统点阵材料的高强度、高刚度和高比吸能等特性。Chen 等[342]对比了相对密度相近的传统BCC 点阵材料（见图33(a)）与shellular material（见图33(b)）的压溃特性，发现shellular material 的比吸能几乎是传统BCC 点阵材料的4 倍（见图33(c)）。

图32 典型shellular material[340]Fig.32 Typical shellular material[340]

图33 传统点阵材料与shellular material 压溃时应力-应变曲线对比[342]Fig.33 Comparison of the stress-strain curves under crushing between traditional lattice material and shellular material[342]

5.2 超材料的动态响应

5.2.1 声子晶体和声学超材料的应力波响应

20 世纪90 年代，Kushwaha 等[343]首次提出声子晶体的概念。声子晶体是具有不同弹性常数和质量密度的材料组成的周期性结构，并存在弹性波能带结构和带隙。在带隙所覆盖的频率范围内，弹性波无法传播。声子晶体中带隙的产生源于Bragg 散射，且波长与晶格常数相当。最典型的一维声子晶体为周期性层状结构（见图34(a)）[344]。声学超材料作为声子晶体的发展，通常包含基体和共振单元（见图34(b)）。它们一般也具有周期性结构，但其带隙的形成不依赖于周期性，而是基于局域共振原理[345]。因此，声学超材料所调控波长可高出晶格常数几个数量级（见图34(c)）[346]。近年来，声子晶体和声学超材料的研究蓬勃发展，读者可以参考相关综述[347-349]。

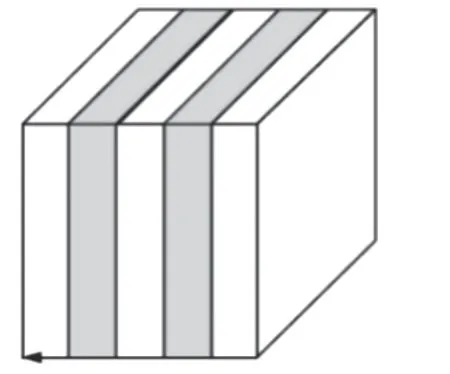
图34(a) 周期性层状结构[344]Fig.34(a) 1D periodic structure[344]

图34(b) 典型共振单元[345]Fig.34(b) The basic unit cell of a locally resonant sonic crystal[345]

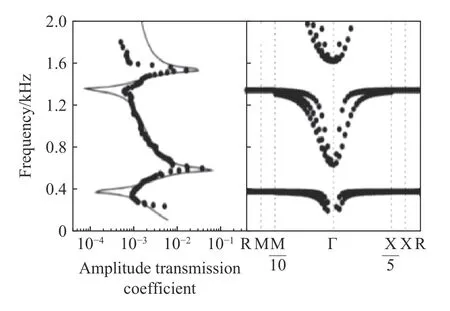
图34(c) 声学超材料能带结构图[345]Fig.34(c) Transmission characteristics of a sonic crystal[345]

声学超材料可以用质量-弹簧模型描述[350]。由于弹性波波速，当有效弹性常数和有效质量密度为一正一负时，弹性波不能传播[351]。此类超材料的局限性在于带隙较窄，且主要集中于内部质量的局部共振频率附近。为了满足实际应用较宽的带隙和频率范围需求，可采用以下2 种设计策略。

第1 种策略是设计多层或梯度变化的共振单元（被动策略）。例如：Tan 等[350]提出了双共振单元，即在基本共振单元的基础上增加中间层。结果表明，双共振单元的带隙和频率范围均显著增宽[352]。随后，Xu 等[353]设计了多层级共振单元，进一步拓宽带隙影响范围。此外，在基本共振单元或多层级共振单元上增加阻尼项也可显著提升弹性波衰减的效率[354-355]。第2 种策略是设计可调节/自适应共振单元（主动策略）。Airoldi 等[356]利用压电材料设计了新型声学超材料。通过外部电路调节材料的机械阻抗，最终获得可调控的带隙。后续研究表明，对压电材料的形式、外部电路等进行改进可使超材料更加符合冲击防护的应用需求[357]。Ning 等[358]则通过给超材料施加压缩载荷使其产生变形，从而实现对弹性波带隙的机械调控。

5.2.2 颗粒晶体应力波的传播与调控

颗粒材料能有效起到冲击防护作用。1983 年，Nesterenko[359]首次提出了颗粒晶体的概念。颗粒晶体通常由紧密有序排列且相互接触的弹性颗粒组成（见图35(a)[360]）。相邻颗粒之间的接触关系满足赫兹接触定律，即F=Aδ3/2，其中F和 δ分别为接触力和变形，A为与颗粒几何、材料相关的参数。在此基础上，Daraio 课题组探究了应力波在不同颗粒链中的传播，讨论了颗粒形状（例如空心球[361]、椭球[362]和圆柱[363]）和材料（例如铝[364]、PTFE[365]和尼龙[366]）对应力波传播的影响。随后，他们将一维颗粒链的相关研究手段和结论推广至二维及三维[367-368]。事实上，传统颗粒晶体的研究主要关注厘米级的弹性颗粒，他们则搭建了微观实验观测平台，从而针对应力波在微米级不锈钢颗粒链中的传播进行了充分讨论[369]。

图35(a) 一维颗粒晶体的基本构型[360]Fig.35(a) The basic configuration of 1D granular crystal [360]

实验研究表明，颗粒晶体可以支持衰减的应力波，因而在冲击防护领域具有重要应用价值。应力波衰减的主要原因包括颗粒与导轨间的摩擦[370]、颗粒材料的黏弹性[371]、颗粒的塑性变形[372]、流体介质的黏性阻力[373]以及应力波传播过程中颗粒的转动[374]等。其中，颗粒的塑性变形会引起应力波传播过程中幅值迅速降低[375]。而当颗粒晶体被置于流体介质中时，介质的黏度不同可能导致波的形状发生变化[373]。

Kim 等[376]研究了空心椭圆环颗粒晶体的动态响应，其颗粒呈现应变软化特性，即颗粒之间的接触关系满足幂接触定律且指数小于1。此时颗粒晶体可将受到冲击而产生的脉冲转化为后倾的稀疏波波前和振荡的波尾（见图35(b)），因而不依赖于材料阻尼或塑性实现缓冲。后续研究表明，该结论适用于其他具有应变软化特性的颗粒晶体[377]。基于考虑横向惯性修正的Rayleigh-Love 波动方程，彭克锋等[378]提出了柱壳链受冲击时弹性波传播的简化模型，并分析了弹性波弥散机理。结果表明，当存在横向惯性时，应变最大处波速随着泊松比和惯性半径的增大而降低。Zhang 等研究了一维球形[379]和柱形[377]颗粒晶体中应力波的传播与调控机制，并将相关理论推广至一维复合颗粒链[380]。通过实验研究，Yin 等在一维错配空心球链中观察到应力波幅值的衰减[381]。进一步地，为了实现了应力波的定量调控，相继提出了实心圆柱及柱壳链中颗粒质量、刚度以及几何错配的耦合衰减策略[382]。更多关于应力波在颗粒晶体中的传播与调控可参考相关综述[375,383-386]。

图35(b) 空心椭圆环颗粒晶体中应力波的衰减[376]Fig.35(b) Stress wave attenuation in a 1D granular crystal composed of elliptical rings[376]

5.3 复合材料和结构的动力响应

先进复合材料具有高比强/刚度和优异的抗冲击性能，被广泛应用于航空、轨道交通、船舶及汽车等冲击防护领域[387]。对于复合材料动态行为的研究，已有不少综述可作参考，例如文献[388-390]；本节主要介绍复合材料夹层结构和复合材料薄壁管。

5.3.1 复合材料夹层结构动态行为

复合材料夹层结构通常由表层的层合板和芯层材料组成。芯层材料主要包括前述的蜂窝材料、泡沫材料、点阵材料以及生物材料（例如竹子[391]）等。受到动态加载时，外部能量通过层合板的弯曲、拉伸和断裂以及芯层材料的压溃而耗散，从而获得良好的抗冲击特性。复合材料夹层板的动态行为与冲击能量直接相关。当冲击速度较低时，变形模式以塑性变形为主（见图36(a)），表层与芯层可能发生分层[392]。在高速冲击下，由于应力波的产生、传播与反射，可在多个表面导致屈曲，层合板表现出穿孔、撕裂等复杂的动态失效（见图36(b)），且层合板内部脱层现象显著[393]。通过分析压缩和剪切区域的尺寸和穿孔处的挠度，可以粗略估计期间耗散的能量[271]。

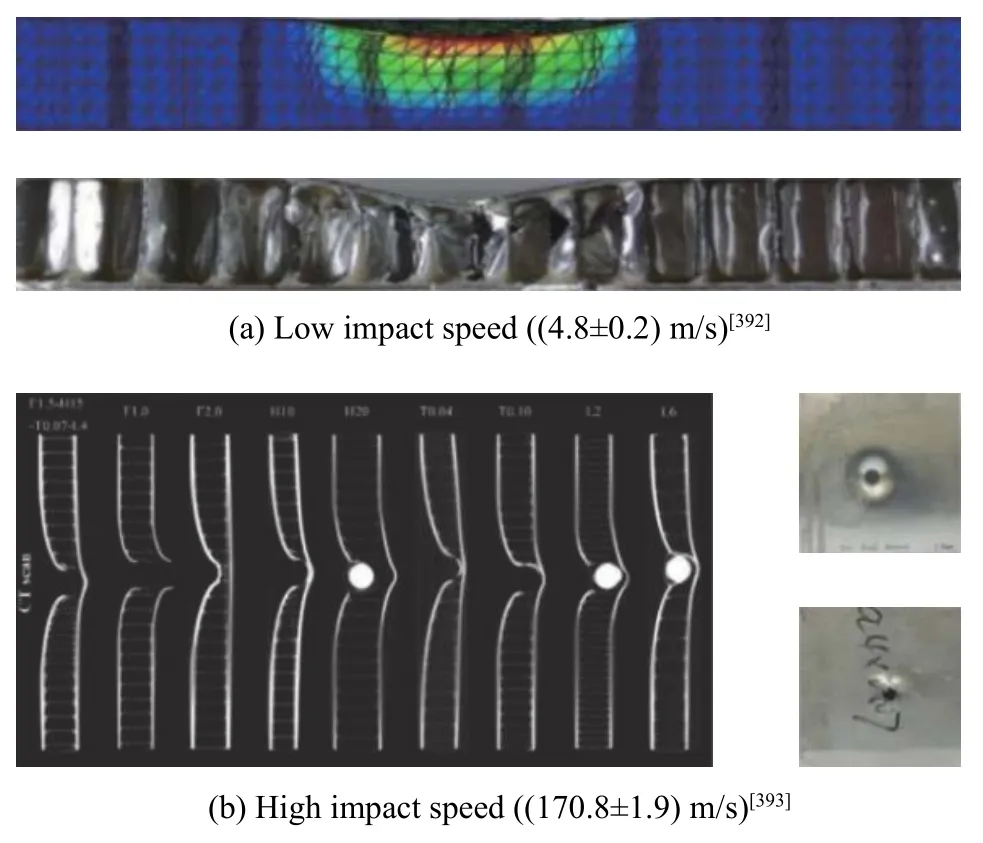
图36 复合材料夹层板在低速((4.8±0.2) m/s)[392]和高速((170.8±1.9) m/s)[393]冲击下的动态响应Fig.36 Dynamic responses of sandwich structures under a low impact speed ((4.8±0.2) m/s)[392] and high impact speed ((170.8±1.9) m/s)[393]

对于复合材料夹层结构的低速冲击，Foo 等[394]和Qin 等[395]分别建立了复合材料夹层板和夹层梁的理论模型。这些模型利用了能量和动量守恒定律，并假设全局和局部变形相互独立。随后，Xiang 等、Zhang 等和Wang 等通过实验、数值模拟和理论分析探究了芯层材料（例如梯度分布的泡沫芯层[396]）、面板材料（例如纤维-金属层合板[397]）和构型（例如波纹夹层板[398]、多层夹芯板[399]和非对称夹层[400]）等因素对夹层结构动态响应的影响。Crupi 等[401]建立了简化的理论模型来描述复合材料夹层结构的不同失效机制。Liu 等提出了剪滞模型用以描述复合材料黏性基体对能量耗散的影响[402-403]。Tan 等[404]通过落锤实验研究了低速冲击下冲击能量对夹层结构动态响应的影响，并给出了临界冲击能量。Sun 等[405]结合有限元模拟和实验讨论了几何参数对夹层结构失效机制的影响。Zhou 等[406]研究了两层钢板中间留有空隙层的情形，并且讨论了如何分配两板的厚度及空隙的厚度对横向冲击的防护最有利。Ha 等[407]详细归纳了不同波纹形结构（包括管、板、梁、蜂窝以及夹层结构等）的抗冲击和能量吸收特性。此外，Huang 等通过研究PVC 泡沫夹层结构[408]和铝波纹板夹层结构[409]发现，复合材料夹层结构在水下受到冲击时的变形机制与在空气中差异显著，并且在冲击速度相同时，复合材料夹层结构在水下的抗冲击性能更佳。Chen 等[410]通过实验探究了面板构型和芯层材料对夹层结构水下爆炸响应的影响。考虑载荷的不同施加方式，Wang 等[411]、Teich 等[412]和Ghoshal 等[413]建立了流固耦合模型，描述一维空气介质中爆炸载荷下的结构响应。

考虑到实际应用中存在多次冲击的工况，Rezasefat 等[118]对比了单层和多层金属板受到局部重复冲击加载时的动态响应。结果表明，双层板混合构型（背面为薄钢板，前面为厚铝板）的抗冲击性能最优。随后，Ziya-Shamami 等[119]利用弹道摆锤对单层及多层圆形金属板进行至多5 次均匀重复加载，并探究了质量、层状构型、厚度以及间距等对结构动态响应的影响。其中，由厚铝板和薄钢板组成的三层板混合构型在5 次重复加载中性能最佳。Wang 等[414]开展了编织复合材料试件落锤重复冲击实验和数值研究，分析了编织复合材料试件的损伤形态，预测了编织复合材料结构的碰撞峰值力和吸收能量水平。Guo 等[415-416]开展了大量泡沫铝金属夹芯板重复冲击实验和数值模拟，研究了夹芯板重复冲击动态响应，分析了重复冲击加卸载过程、夹芯板刚度变化、变形破坏以及能量吸收情况，如图37(a)～(b)所示。Wu 等[417]通过重复冲击实验和数值模拟研究了编织复合材料管在重复横向低速冲击下的损伤行为和破坏模式，评估了冲击能量和冲击位置对冲击响应的影响。Zhou 等[418]利用数值方法研究了重复低速冲击下交叉复合层压板的动态力学响应和损伤扩展。Zhang 等[419]开展了蜂窝铝金属夹芯板重复冲击实验和数值模拟，研究了蜂窝铝夹芯板在重复冲击载荷下的塑性动态力学行为和能量吸收特性。此外，Zhu等[420]实验研究了常温和低温环境中泡沫铝金属夹层板在重复碰撞下的动态响应，结果表明，低温环境下结构的最终累积永久变形值比室温下的结构永久变形值小，如图37(c)所示。

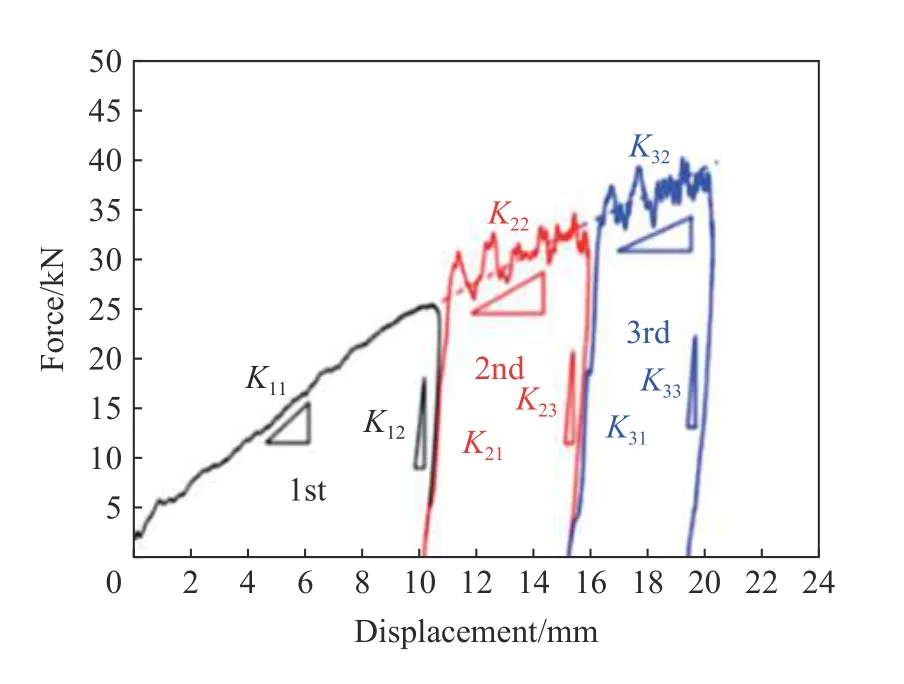
图37(a) 泡沫金属夹芯板重复加卸载过程[415]Fig.37(a) Repeated impacts of aluminum foam sandwich plates[415]

图37(b) 泡沫金属夹芯板破坏模式[415]Fig.37(b) Repeated impact induced damage in aluminum foam sandwich plates[415]

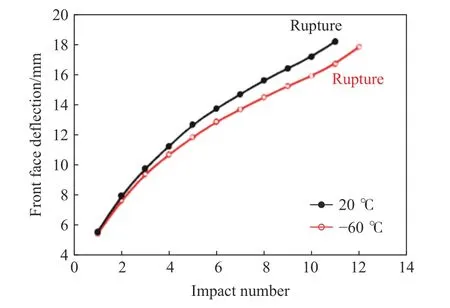
图37(c) 上面板的塑性变形值随碰撞次数的变化关系[420]Fig.37(c) Relationship between front face deflection and impact number[420]

5.3.2 复合材料薄壁管的动态响应及破坏

复合材料薄壁管多由纤维增强树脂基复合材料制成。薄壁管的整体失效模式主要包括欧拉屈曲、环绕薄壁管的中部断裂以及渐进式压溃等[421]。其中，薄壁管中部断裂通常由剪切失效造成，发生中部断裂后，轴力迅速降低，压溃过程中吸收能量较少[422]。发生渐进式压溃时，复合材料薄壁管常出现散射或碎裂现象。碎裂时轴向和周向发生初始碎裂，进而导致管壁内侧压缩屈曲、外侧拉伸断裂。这一现象随着压溃过程不断重复直至薄壁管截面完全压溃，最终在压溃区形成许多碎片（见图38(a)）[423]。散射则指基体材料阻止了裂纹的增长且出现大量断裂纤维，因而在压溃前沿产生大量开裂（见图38(b)～(c)）[424]。这2 种模式的产生由复合材料薄壁管轴向和周向的失效强度等因素共同决定。

图38 复合材料薄壁管渐进式压溃常见失效模式Fig.38 Progressive crushing of composite tubes

为了得到复合材料薄壁管的平均压溃力，可将其压溃模式进行简化。Gupta 等[425]指出，复合材料薄壁管压溃过程中的能量耗散主要包括基体轴向开裂吸收的能量、材料向内/向外弯曲变形吸收的能量、环向纤维拉伸吸收的能量以及摩擦耗能。同时，Hanefi 等[426]基于Alexander 模型建立了简化模型来描述复合材料包裹金属管的静态响应。Song 等[427]则将Cowper-Symonds 引入该模型中，从而考虑材料的应变率效应并得到动态压溃应力。此外，实验表明叠层顺序对复合材料薄壁管的动态响应影响显著[428]。Mirzaei等[429]建立了考虑各层纤维取向的理论模型。传统圆管模型将复合材料薄壁看作正交各向异性的单层材料，而该模型考虑了每一层复合材料的力学响应，其轴向和环向的强度均由Tsai-Hill 失效准则计算得到。

除了圆形管件，方形、锥形以及穹状复合材料薄壁管也具有优异的能量吸收特性。Mamalis 等[430]从宏观和微观的角度探究了不同厚度和高度的复合材料方管在准静态和动态加载下的力学响应，并基于圆管压溃模型建立了相似的方管理论模型。针对锥形薄壁管，Boria 等[431]进行能量分析时引入了锥形管的关键几何参数，从而得到了改进模型。当锥角为0°时，该模型可退化为圆管模型。由于复合材料薄壁管的变形过程和失效机制复杂、影响因素众多，难以获得某些理论模型中所需参数的准确值。同时，考虑到多数复合材料为脆性材料，Hussein 等[432]提出了基于实验观测结果的理论模型。该模型考虑的耗散能类型包括裂纹扩展、横向剪切以及摩擦力，为复合材料薄壁管的动态行为建模提供了新思路。

6 生物及仿生材料的动态响应

面对不同的生存环境，自然界的生物进化出形态各异的材料/结构体系，从而能够抵御外部冲击载荷、实现自我防护。通过学习这些独特的生物材料，可以设计出性能优异的人工结构。对于动物的抗冲击策略及其仿生机理，邢运等[433]已作了详细归纳。此外，Lazarus 等[434]和Ha 等[435]分别总结了与仿生材料的抗冲击和能量吸收相关的研究。因此，本节仅介绍典型生物材料的抗冲击分析及仿生结构设计。

6.1 典型生物材料的抗冲击分析

6.1.1 典型动物材料的抗冲击分析

（1）)甲虫前翅

甲虫前翅是最具代表性的抗冲击生物材料之一。它们既要辅助甲虫飞行，也须保护甲虫免受天敌伤害[436]。早在19 世纪末，Comstock 等[437]便指出甲虫前翅具有柱状芯层的截面形状（见图39(a)）。事实上，甲虫前翅是一种天然层状复合材料，其中前翅蛋白质是基体材料，几丁质是增强纤维[438]。

Xiang 等[441]通过实验观察发现甲虫前翅的内外层边缘具有空心孔状结构，其直径为18～33 µm，因而甲虫前翅一般具有轻质且强韧的性能。为了进一步理解甲虫前翅力学性能和微观结构间的关系，Lomakin 等[442]通过静态和动态实验研究了Tribolium和Tenebrio前翅的力学性能（例如硬度、杨氏模量等），并探究了含水量对其性能的影响。此外，Chen 等[443]利用扫描电子显微镜观察了雄性甲虫前翅的层状截面，发现纤维体积率以及层状截面的形状与前翅的位置密切相关，并且纤维在层状结构中具有错综交联的网状结构，可以有效地提升材料整体强度。同时，网状结构中存在不规则的蜂窝和管状结构，且管状结构主要集中于蜂窝胞元的交点及胞壁处（见图39(b)）。这种混杂多胞结构具有良好的抗冲击特性[444]。

图39 甲虫前翅微观结构[439-440]Fig.39 Microstructures of beetle forewings[439-440]

（2）)螳螂虾

螳螂虾的趾肢击打时能够产生高达1 500 N的载荷，其加载速度和加速度分别可达23 m/s和10 000g[445]，而其趾肢无任何损伤。这种抗高应变率冲击的性能与其趾肢结构直接相关。研究表明，螳螂虾的趾肢是多区域、多层级的复合结构[446]。其中，周期性区域为主要吸能区，通常为螺旋层状复合结构[447-448](见图40)。

Weaver 等[449]指出，螳螂虾趾肢的螺旋结构主要由结晶羟基磷灰石、无定形的磷酸钙和碳酸盐以及纤维状几丁质复合而成。受到冲击载荷时，该螺旋复合结构可以通过偏转和扭曲微裂纹的扩展来耗散能量[450]。此外，Huang 等[451]进一步研究了高应变率（～104s−1）对螳螂虾趾肢的影响，发现其趾肢表面包含一种耐冲击的纳米颗粒涂层，该涂层由紧密堆积的羟基磷灰石双连续纳米颗粒（～65 nm）与有机基质结合而成（见图41）。当受到高应变率冲击载荷时，纳米颗粒发生旋转和平移，而纳米晶格网络在低角度晶界处发生破裂，从而产生位错和非晶化现象。同时，互相贯穿的有机网络还能提供额外的增韧效果并产生大量的耗散。因此，螳螂虾趾肢的独特结构对于抗高应变率冲击的结构设计有所启发。

图40(a) 螳螂虾趾肢的螺旋层状复合结构[449]和(b)结构断面的扫描电子显微镜图片[449]Fig.40(a) Illustration of a 3D helicoid[449] and (b) SEM figure of the chitin fibril helicoidal structural motif on dactyl clubs[449]

图41 趾肢表面纳米颗粒涂层的(a)扫描电子显微镜和(b)透射电子显微镜图片[451]Fig.41 Nanoparticle coating on the dactyl club of mantis shrimps (a) SEM and (b) TEM images[451]

（3）)啄木鸟

啄木鸟啄木时频率和速度分别可达20 Hz 和7 m/s，而加速度甚至达到1 200g，即便如此，其大脑也不会产生损伤或脑震荡[452]。Wang 等[453]指出，啄木鸟的抗冲击特性与材料结构密切相关，主要包含3 点：（1）头部（主要是头骨）的宏观及微观结构；（2）头部具有板状非均匀的舌骨结构[454]；（3）上下喙的长度差异。此外，啄木鸟喙的多层级结构在冲击防护中也起到了关键作用。Lee 等[455]通过实验研究发现，啄木鸟的喙在宏观尺度上包含3 层结构，即最外层的嘴鞘层、泡沫状的中间层以及最内侧的骨头层。这里，每一层的面积比率沿啄木鸟喙长度方向不断变化，形成功能梯度结构，从而有效增强其抗冲击性能。同时，纳观尺度上，角蛋白间存在缝线一样的波浪形间隙，能够容纳局部剪切变形[456]。

为了分析啄木鸟啄木过程的动态响应，Liu 等[457]利用压电力传感器和高速摄像机分别记录了啄木过程中的脉冲曲线和动态响应，并建立了啄木鸟头部模型模拟啄木过程。结果表明，啄木鸟的颈部约束在冲击过程中的影响可以忽略。Jung 等[458]通过微型计算机断层成像以及纳米压痕等实验发现啄木鸟舌骨中致密坚硬的区域被多孔材料所包围，能够有效地耗散啄木过程中地冲击能量。随后，他们针对3D 打印的啄木鸟头骨进行了落锤实验并对冲击过程中应力波传播路线进行了分析[459]，发现啄木过程中啄木鸟头骨能够有效防止应力波向大脑方向传播。

6.1.2 典型植物材料的抗冲击分析

（1）)木材

木材是一种天然的多胞材料，具有显著的各向异性和良好的能量吸收特性[460]。它属于闭孔泡沫型多胞材料，具有3 个正交平面（见图42(a)），即径向（R）、轴向（L）和切向（T）。木材的各向异性由材料和几何因素共同决定，其中细长的胞元主要沿轴向分布，因而木材在轴向的力学性能更加优异。同时，受木材生长的影响，年轮的形成使得径向和切向的力学性能也存在一定差异。木材受到径/切向压缩时，应力-应变曲线与传统多胞材料相似（见图42(b)），而受轴向压缩时，由于杆状纤维屈曲，曲线存在一个初始峰值[271]（见图42(c)）。

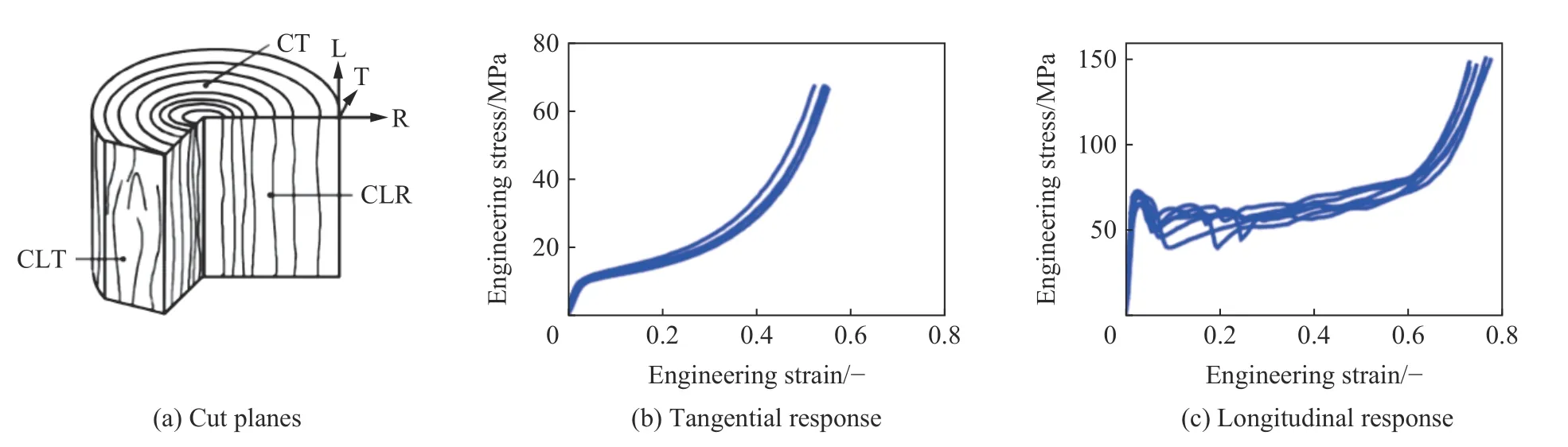
图42 山毛榉树干正交平面示意图以及在0.001 s−1 应变率下山毛榉样品的切向和轴向压缩曲线[462]Fig.42 Cut planes of the trunk tree and tangential and longitudinal responses of beech samples at the strain rate of 0.001 s−1[462]

木材具有应变率相关的特性[461]。Reid 等[282]通过准静态和动态实验全面探究了木材的动力行为，并首次提出了后来在泡沫动力学中广为采纳的冲击波理论模型。Wouts 等[462-463]研究了0.001～600 s−1应变率下云杉木和山毛榉木材的力学特性，发现木材的率相关特性与加载方向密切相关，并且木材的密度不同会影响其能量吸收及抗冲击特性。Hepworth 等[464]指出，即使密度相近，微观结构差异也会导致木材之间性能相差甚远。随后，Matsushita 等[465]通过准静态压缩和落锤实验研究了8 种不同木材的动态响应，并利用扫描电子显微镜观察冲击后的试样。结果表明，密度较大的木材具有更优异的抗冲击性能。同时，由较小细胞束组成的射髓（rays）能够有效阻止裂纹的扩展，并在一定程度上增强木材径向的冲击防护能力。

（2）)柚子皮

为了传播与繁衍，柚子果皮对种子的保护至关重要，其冲击防护机制与微观结构具有内在联系。成熟的柚子一般为1～2 kg，最大质量可达6 kg[466]，而柚子树最高为15 m 左右[467]。因此，柚子成熟落地时，需要耗散的动能可达882 J。为此，Fischer 等[468]对柚子进行了不同高度的自由落体实验。结果表明，当柚子从10 m 的高度下落至水泥地，柚子表面没有出现明显的外部损伤。从生物学的角度出发，柚子种子的主要传播载体是动物（例如蝙蝠、猴子和熊）[469]。若柚子成熟下落后出现外部损伤现象，则真菌和细菌会进入果实，它们与传播载体为竞争关系，会严重降低种子的传播和发芽几率。Thielen 等[470]通过实验观察不同破坏程度的柚子中产生霉菌的时间，进一步验证了柚子皮抗冲击性能的重要生物价值。

柚子皮一般为2～3 cm 厚，可以分为外果皮、中果皮（柚子皮主要组成部分）和内果皮。通过扫描电子显微镜观测发现，柚子皮呈现多孔结构[471]，其中分布着致密的维管束结构（见图43(a)），并且从外果皮到内果皮孔隙率先迅速增加，然后缓慢降低（见图43(b)）[472]。梯度分布的多孔结构通常具有良好的能量吸收特性。此外，Thielen 等[473]发现柚子皮中维管束结构在抗冲击中起到了关键作用。Wang 等[472]则指出维管束的体积率是柚子皮受到压缩载荷后应变分布的重要影响因素。与柚子皮的研究相近，Ha 等[474]通过实验研究了榴莲外壳对撞击的保护作用。他们发现，榴莲外壳上刺的数量为影响其能量吸收性能的关键参数。

图43 柚子皮微观结构Fig.43 Microstructures of pomelo peel

（3）)椰子壳

椰子壳的重要生物价值是在椰子成熟落地受到冲击载荷时保护种子，同时还须防止人类或其他动物在不借助现代工具的情况下破坏椰子[475-476]。因此，椰子壳通常兼具高强度、高韧度和良好的抗冲击特性。根据产地不同，椰子壳厚度一般为1～5 cm[477]，并且从外至内可分为3 部分，即外果皮、中果皮和内果皮。其中外果皮类似皮肤，中果皮是纤维状复合结构，内果皮则质地较硬。

Nguyen 等[478]通过实验研究了椰子壳中果皮的能量吸收特性，发现其具有各向异性的力学特性，并且在纵向纤维方向表现最优。随后，Lu 等[479]进行了椰子自由跌落实验，并通过理论分析指出椰子壳纤维分布与抗冲击性能之间的关系。Schmier 等[480]指出，椰子为多尺度结构，从器官尺度到分子尺度一共可分为8 个层级。Gludovatz 等[475]探究了椰子壳多尺度结构与其优异力学性能之间的关系，发现椰子壳材料的纳观结构会随着加载而变化，例如，部分椰子壳纤维素晶体结构的（002）平面在拉伸实验中会发生明显变形。此外，椰子壳的抗冲击性能随椰子的年龄增加而得到改善。因此，学者们利用椰子壳纤维制成新型混凝土材料[481-482]或三明治复合结构[483]。与传统混凝土材料相比，它们不仅环保、性价比高，还具有优异的抗冲击性能。

6.2 仿生材料抗冲击结构设计

6.2.1 多胞结构

（1）)混杂型多胞结构

基于甲虫前翅的网状结构，Xiang 等[484]通过将圆管嵌入六角形蜂窝材料内部以及胞元棱边的方法设计了2 种仿生蜂窝材料。结果表明，嵌入蜂窝胞元棱边的仿生蜂窝材料表现更佳，其比吸能比传统六角形蜂窝材料高出35.97%。随后，Hao 等[444]比较了不同圆管嵌入位置（蜂窝材料的胞元结点和棱边等，见图44）的区别，发现圆管同时嵌入胞元结点和棱边时，抗冲击性能最优。此外，Ha 等[485]基于啄木鸟喙设计了波浪形蜂窝材料（见图45），即六角形蜂窝材料的胞元棱边模仿了角蛋白间的波浪形缝线结构。受到冲击加载时，波浪形蜂窝材料的变形模式主要包括完整褶皱模式、过渡型屈曲模式以及全局屈曲模式。与传统蜂窝材料相比，波浪形蜂窝材料在褶皱处产生扭转变形，从而在压溃过程中形成更多塑性铰（见图46）。通过参数分析，他们进一步讨论了波幅、波峰数量和胞壁厚度等关键参数对波浪形蜂窝材料抗冲击性能的影响。

图44 甲虫前翅启发得到的蜂窝材料[444]Fig.44 Bionic honeycombs inspired by the internal structure of elytra[444]

图45 啄木鸟喙角蛋白间的波浪形缝线结构[455]和波浪形蜂窝材料胞元示意图Fig.45 A cross-section view of a wavy suture line on woodpeckers’ beaks[455] and the unit cell of a wavy honeycomb

图46 面外加载时，波浪形蜂窝材料的变形模式[485]Fig.46 The deformation mode of the wavy honeycomb under out-of-plane crushing[485]

（2）)多层级多胞结构

受柚子中果皮维管束结构的启发，Zhang 等[265]设计并制备了多层级蜂窝材料（见图47(a)）。结果表明，多层级蜂窝材料中各层级的厚度比不同会导致不同的变形模式。因此，他们针对不同变形模式分别建立了面内和面外压溃强度的理论模型。Tsang 等[486]通过模仿骨骼肌的多层级结构设计了仿生多层级管状材料（见图47(b)），其抗冲击性能随层级的增加而增强，例如，第3 层级的仿生管状材料抗冲击特性和能量吸收特性可分别提高258%和172%。

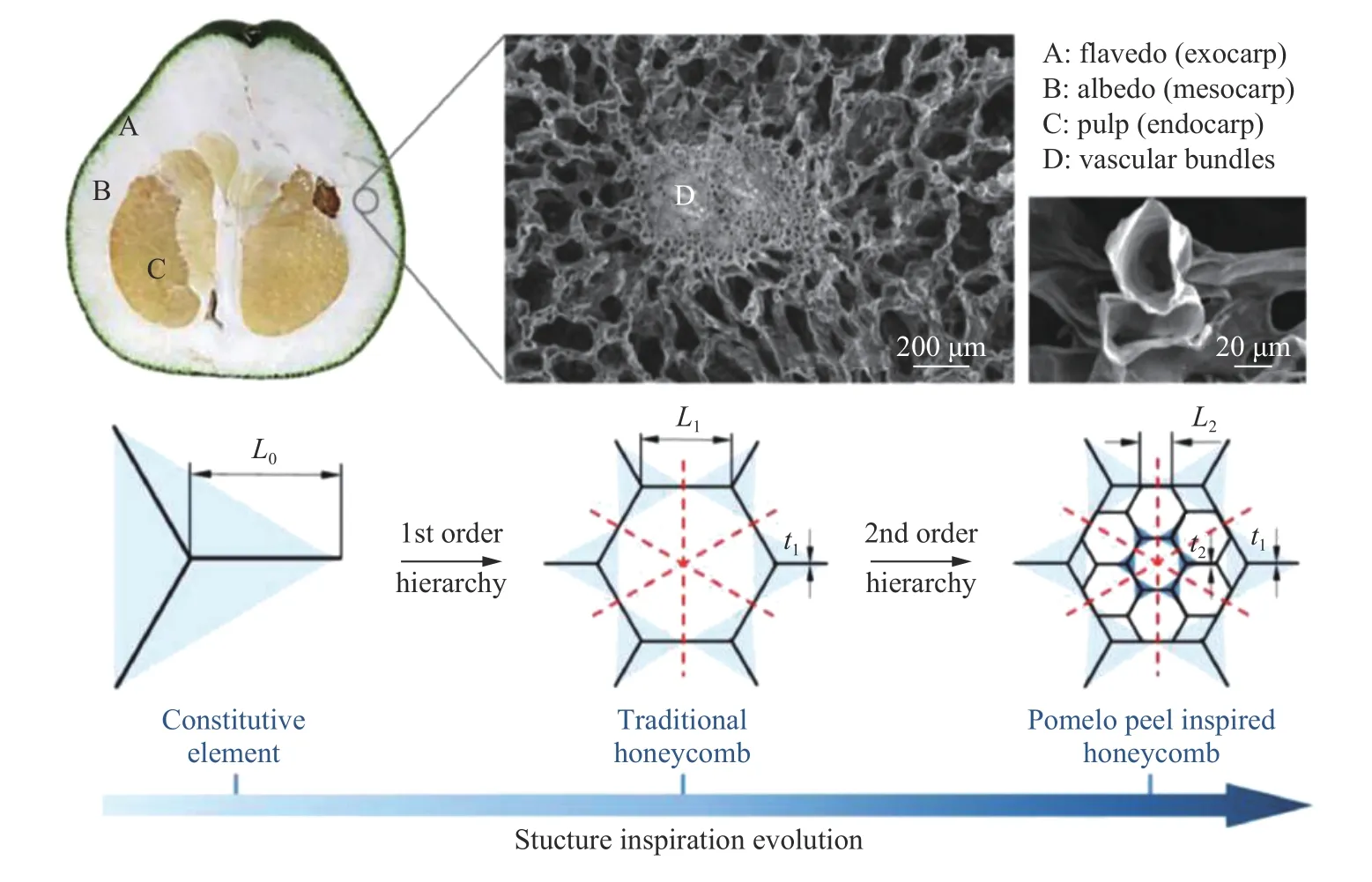
图47(a) 柚子皮微观结构启发得到的多层级蜂窝材料[265]Fig.47(a) Hierarchical honeycombs inspired by the microstructures of pomelo peel[265]

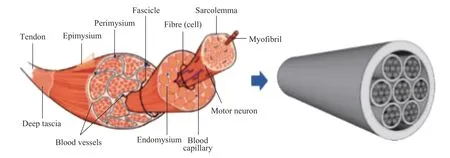
图47(b) 骨骼肌启发的多层级管状材料[486]Fig.47(b) Muscle-inspired hierarchical structure[486]

以上多层级仿生材料均为自相似结构，即胞元微观结构在各个层级保持一致。Zhang 等[487]通过理论分析指出，虽然自相似多层级材料能够有效改善材料的韧性，但同时也会牺牲材料的刚度。因此，Chen 等[488]提出了各层级间微观结构不同的多层级蜂窝材料，从而全面提高了材料的力学性能。此外，Haldar等[489]则基于棕榈木的多层级微观结构设计了仿生复合材料夹层结构，在泡沫材料中加入碳棒作为增强相，制成夹层结构的芯层材料。实验结果表明，其强度和比体积吸能与传统复合材料夹层结构相比分别增加了10 倍和14 倍。王海任等[490]基于王莲叶脉结构设计了一种双向梯度仿生夹芯结构，该结构具有良好的抗爆性能。结果表明，双向梯度的设计可以有效降低后面板挠度，并获得更优异的能量吸收特性。

6.2.2 螺旋结构

通过模仿螳螂虾趾肢吸能区的螺旋复合层状结构可以设计基于纤维增强的仿生螺旋复合材料。Cheng 等[491]系统地研究了几何参数对于玻璃纤维增强的螺旋复合材料力学性能的影响。Zimmermann等[492]指出，由于层间偏角的存在，仿生螺旋复合材料能够根据不同的加载工况调整各层位置。当层间偏角较小时，仿生螺旋复合材料受面内加载呈现各向同性[493]。

此后，Grunenfelder 等[494]通过实验和有限元模拟研究了碳纤维增强的螺旋复合材料的动态响应。结果表明，螺旋结构可以有效防止复合材料厚度方向的失效，增强了复合材料的抗冲击性能。Ginzburg 等[495]则对比了仿生螺旋复合材料和传统复合材料在低速冲击下的动态响应（见图48），发现虽然仿生螺旋复合材料容易出现分层现象，但传统碳纤维增强复合材料穿孔现象较为严重，所以螺旋复合材料的抗冲击强度更高。Yin 等[496]通过在螺旋复合材料中增加孔洞模仿螳螂虾趾肢中几丁质与蛋白质的界面。实验表明，这些孔洞能够有效控制和扭曲裂纹的扩展，进而提高复合材料的韧性和抗冲击特性。随后，他们通过实验证明，双螺旋复合材料比单螺旋复合材料抗冲击性能更佳[497]，并且设计并制备了双相仿生复合材料，从而进一步提高其强度、刚度及比吸能等特性[498]。对于高速冲击，Liu 等[499]指出，仿生螺旋复合材料的失效机制主要为基体开裂（与准静态面外加载情况类似）伴随着各层前端的纤维失效。与传统正交铺层复合材料相比，纤维强度对仿生螺旋复合材料的动态性能影响较小。Abir 等[500]通过研究仿生螺旋复合材料的弹道性能发现，螺旋结构独特的变形和失效机制的综合效应使复合材料在完全穿透前能够吸收更多冲击能量，从而得到更高的弹道极限。

图48 传统复合材料与仿生螺旋复合材料示意图[495]Fig.48 Illustration of traditional composites and bio-inspired helicoidal composites[495]

7 小结与展望

结构冲击动力学具有广阔的工程应用背景，同时又蕴含了深刻的力学和物理规律。从1950 年至今的70 年里，基于刚塑性假设和对梁板壳的动力响应的分析，这门学科已经建立了系统的理论框架和方法，与实验测试技术和数值模拟手段相辅相成，为解决形形色色的实际问题提供了有力的工具。本文回顾了结构冲击动力学近十年左右的研究进展，通过强动载荷作用下典型结构动态行为的范例，揭示了概念、模型和方法的创新在推动学科发展中至关重要的作用。我们也看到，从工程与生活问题中提出的复杂加载（如非规则脉冲、重复冲击等）、复杂结构（如加筋板壳，夹层板壳、组合结构等）和复杂行为（如撞击后的反弹、应变率效应、多种失效模式等），都对这门学科的理论方法、实验手段和模拟技术提出了新的挑战，同时也为学科的持续发展提供了广阔的空间。

近年来多胞轻质材料、超材料和仿生结构异军突起，不但大大地拓展了结构冲击动力学的研究疆域，而且借助新的设计理念（例如梯度、多层级、负泊松比等）、制造技术和优化方法，使人们开始主动而有效地提高材料的能量吸收特性和结构的抗冲击能力。可以期待的是，动态加载技术、高精度非接触式测量、结构动态原位表征等方面的进步，以及新型材料的增材制造、仿生设计、梯度/层级设计等技术付诸实际应用，不仅有力地推动冲击动力学的学科前沿向细观和微观尺度延伸，而且使得在多尺度框架下，以更全面、深刻的视角研究材料-结构-性能的综合内在规律成为一个强大的新趋势。例如，在多尺度框架下探讨多物理场耦合（力-热-电）中的材料和结构的动态行为已成为一个新的热点。这些趋势为冲击动力学赋予新的生命力，必然会将这一领域的研究推向一个新的高度。

感谢北卡罗来纳大学夏洛特分校博士生张雯和武汉理工大学硕士生王佳月协助进行文献收集和编排工作。