气相爆轰波起爆与传播机理研究进展*

韩文虎，张 博，王 成

（1.北京理工大学爆炸科学与技术国家重点实验室，北京 100081；2.上海交通大学航空航天学院，上海 200240）

气相爆轰是在可燃气体爆炸反应传播过程中前导冲击波与化学反应强耦合、并且自持传播具有强间断的现象，波前介质经冲击波压缩至较高的温度和密度，从而能够在很小尺度内迅速发生化学反应，而释放的化学能量又反过来支持前导冲击波的传播[1]。爆轰是一种具有更高热效率的燃烧方式，不易对其进行控制，一旦失控会导致重大灾害事故发生；如能对其实现有效控制，使之成为可控爆轰，则在航空推进领域具有广泛的应用前景。因此，气相爆轰研究具有两方面的重要意义：首先，通过对可燃气体爆轰特征和规律的把握，为爆炸事故中如何防止爆轰波的形成或弱化已经形成的爆轰波提供依据，达到防止发生严重爆炸灾害的目的；然后，基于爆轰燃烧的热力推进特性，可研制爆轰推进动力装置，如脉冲爆轰发动机[2]、旋转爆轰发动机[3]、斜爆轰冲压推进技术[4]等，这些新概念爆轰推进手段具有明显的热力学特征方面的优势，成为吸气式高超声速飞行器推进技术研制的重要研究方向。另外，爆轰机理的研究在天文学方面也具有重要的应用，最近，Poludnenko 等[5]发现在某些形式的超新星和化学爆炸中，以亚声速爆燃传播的火焰会自发地演变成由超声速爆轰驱动的火焰，从而极大地增加了能量输出。

对于气相爆轰已开展了大量研究，可概括为2 类：第1 类倾向关注爆轰现象和物理机制，如Shepherd[6]、Ciccarelli 等[7]、Roy 等[8]、Oran 等[9]、Lee[1]、姜宗林等[10-11]、Zhang 等[12]、张博等[13]；第2 类更加关注爆轰推进理论与应用，如范宝春等[14]、王健平等[15]、王兵等[16]、Wolański[17]。这些文献对于人们认识爆轰的现象、机理以及应用起到了非常重要的作用。本文中将结合爆轰机理和应用研究，着重介绍爆轰波的起爆与传播在数值模拟和实验研究方面的最新进展，分析起爆与传播过程中的重要影响因素与理论模型，并对气相爆轰在起爆和传播方面进行概括和展望。

1 爆轰波起爆

爆轰起爆通常可由爆燃转爆轰触发，也可以通过直接起爆方式实现，通过研究这两种起爆方式，逐渐形成了热点起爆、湍流加速火焰转爆轰和直接起爆理论。热点起爆可认为是由化学反应主导的起爆方式，通常，热点存在于高压、高温、高非均匀场等环境，这种环境中气体的自着火时间特别短，反应特征时间尺度比流动特征时间小得多，流动对起爆的作用很小，由于梯度机理一般会自发起爆产生爆轰波，即热点起爆理论。湍流加速火焰转爆轰，是在流动与反应耦合驱动下火焰不断加速而发展到爆轰的过程，需要考虑层流或湍流燃烧对起爆的作用。直接起爆通常需要很强的点火源产生强激波，激波在传播过程中不仅诱导反应，同时也会产生复杂的流动，因此，直接起爆过程是流动和化学反应协同控制的过程。

1.1 典型爆轰起爆理论

1.1.1 热点起爆

目前关于爆燃转爆轰的诱发机理，普遍被接受的观点是爆轰的发展是源于湍流燃烧火焰或其前方热点的出现，根据Zel'dovich 梯度机理[18-24]，爆燃通过热点最终形成爆轰波。尽管爆燃转爆轰的模态有所不同，触发爆轰核(detonation bubble)的机理都可归结为热点自发起爆机理（梯度机理）。

自发起爆机理包括Zel'dovich 梯度起爆机理和Lee[1]的SWACER (shock wave amplification by coherent energy release)机理。热点中的温度不均匀性能够自发起爆产生爆轰，并在梯度中传播形成发展中的爆轰。然而，这种爆轰波在进入冷预混气体时会熄灭，原因可能是梯度的抵消作用[25-26]。爆轰波离开热点时的传播状态与热点外部环境中预混气体的反应活性密切相关，并且与初始温度、压力、燃料类型有关[27-29]。爆轰是否能够最终存活取决于一个特征参数χ～ τind/τe，该参数与诱导时间和反应时间密切相关。热点起爆过程是一个复杂的化学过程，与预混气体的点火延迟时间密切相关。Han 等[30]给出了点火延迟时间与温度梯度的斜率及自发起爆之间的关系（见图1）：增加初始温度会显著影响热点环境中的点火延迟时间，而对CJ 爆速的影响较小。在有温度梯度的区域，反应开始于最短的点火延迟时间，然后在诱导时间较长的相邻位置沿温度梯度自发进行，即自发反应波。自发反应波的速度[27,31-33]其中τind为诱导时间，usp(x) 依赖于温度梯度的斜率和诱导时间的温度梯度。一般情况下，自发波在一定温度下达到最小值，与当地声速的比较可作为临界起爆判据，可以写成：

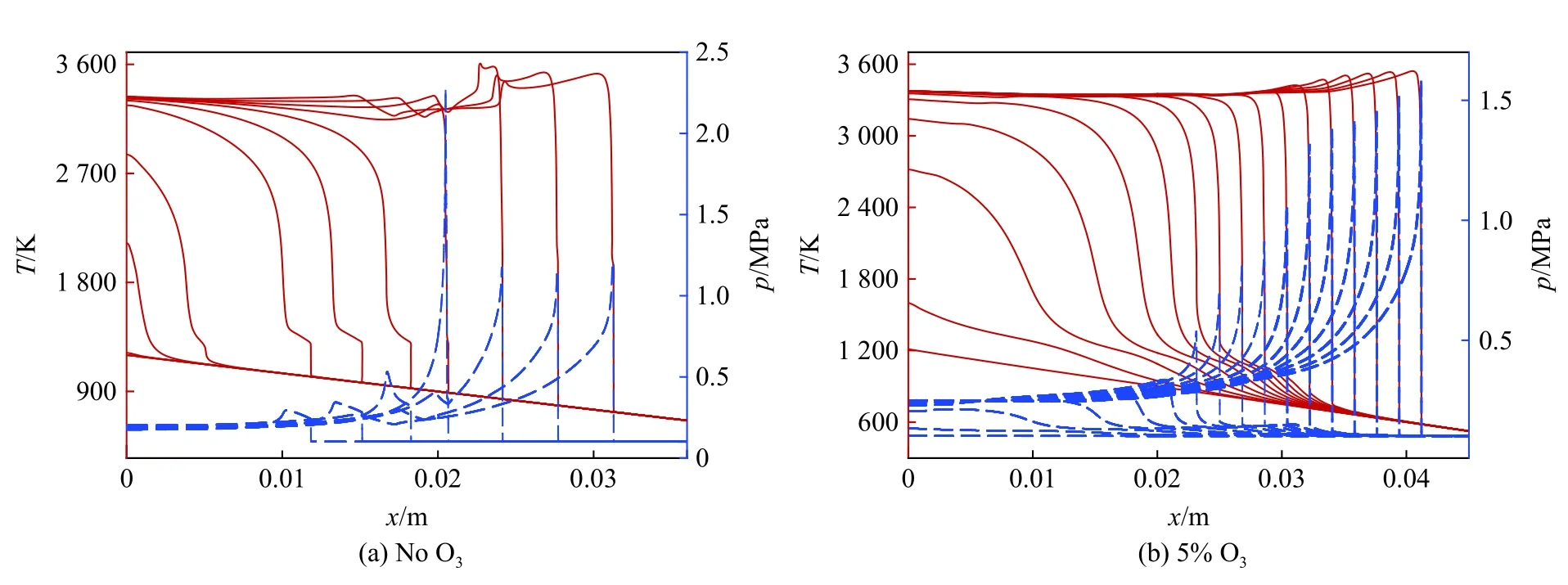
图1 自发起爆过程中压力和温度分布[30]Fig.1 Pressure and temperature profile in spontaneous initiation[30]

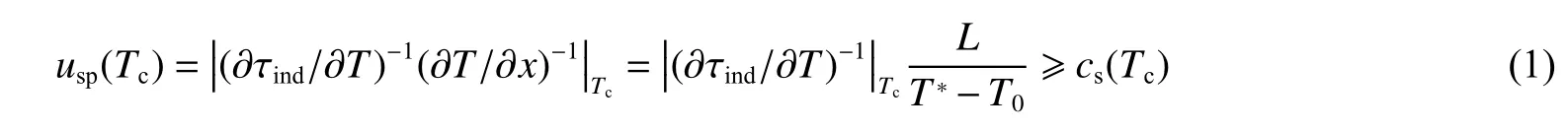
式中：cs（Tc）为对应于自发波速最小值对应的声速，Tc为临界初始温度，T*为沿梯度的最高温度，T0为均匀区域中的初始温度，L为梯度长度。

He 等[25，34]指出，冷的新鲜介质容易引起猝灭，T0时的冷均匀混合物中起爆的判据必须要求Tc＜T0。Han 等[30]发现，缩短诱导时间，沿温度梯度发展的爆轰波在进入冷态混合物时容易存活。因此，在爆轰不稳定性的控制下，从热点传播出来的爆轰，其熄灭与持续不是自发的，它与诱导时间密切相关。当爆轰进入冷预混气体时，随着诱导时间的缩短，脉动不稳定性减弱，如图2～3 所示。

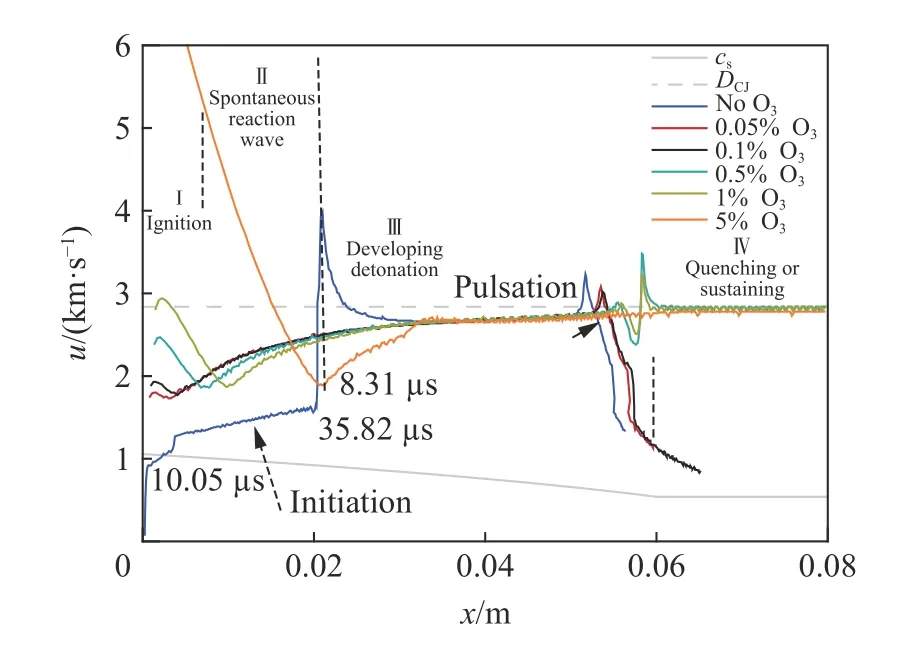
图2 自发波速度与传播距离的关系Fig.2 Speed of spontaneous wave as a function of distance

He 等[34]认为，温度梯度可能会阻止爆轰波在均匀新鲜混合物中的持续传播，然而，通过改变诱导时间，发现爆轰的猝灭与混合物相应的爆轰不稳定性相关。因此，如Radulescu 等[35]和Ng 等[36]所述，诱导时间可能是导致冷的混合物中爆轰猝灭的关键参数，这与稳定性因子密切相关。Radulescu 等[37]指出，在一维模拟中，强脉动不稳定性可以导致爆轰波的熄灭。对于一步反应模型，稳定性因子χ=(τind/τe)(Ea/RT)能够判定爆轰的不稳定性，其中Ea为活化能，R为气体常数；对于均匀的预混气体，缩短诱导时间τind使得稳定因子减小，导致爆轰趋于稳定。因此，发展中爆轰进入冷环境中可能存活。目前，对热点内部发展中爆轰存活的影响因素及机理的认识仍然不足，需要深入研究。

1.1.2 湍流加速火焰转爆轰

爆燃波到爆轰波的转变现象通过实验观测发现后[38-39]，学者们围绕这一现象开展了一系列研究。特别是Urtiew 等[20]通过实验研究，发现爆燃转爆轰包含2 个阶段：火焰的逐渐加速阶段和爆轰波的形成阶段。首先,低速火焰在一定条件下不断连续加速，并转变为高速的湍流火焰，但此时火焰速度仍然是低于声速的；然后在壁面上边界层内火焰发生失稳，在这些失稳区域或者在湍流火焰面附近能够产生局部爆炸。局部爆炸产生的更强的压缩波向外传播并使得化学反应速率增加，进而形成爆轰核。该工作对于研究爆燃转爆轰的机理具有重要的促进作用。

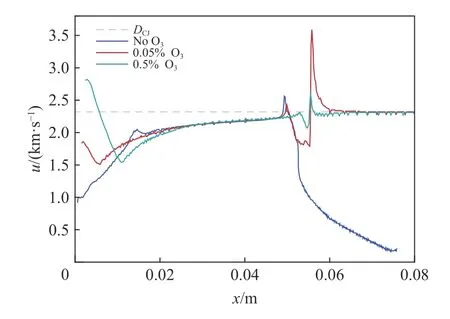
图3 反应波速度与传播距离的关系Fig.3 Speed of reaction wave as function of distance

热点起爆过程主要是由化学反应控制，流动作用起次要作用。由于热点通常是处于高温、高压环境中，自着火时间尺度与流动时间尺度相比非常小，起爆过程主要由快速化学反应控制，因此，热点起爆需要更详细和精确的反应机理描述。Han 等[40]研究表明，在宏观尺度管道中，预热后的边界层更早产生局部燃烧，进一步加速了湍流火焰，使前导压缩波逐渐放大，形成强烈激波，如图4 所示；然后，火焰前方和边界层中产生的冲击波积聚和反射，触发局部爆炸。当该爆炸波向前传播并与前导激波耦合时，形成一个过驱动爆轰，并最终演化为单头爆轰。在边界层中，反应速度加快，火焰温度升高，火焰阵面出现一些热点。当横波与壁面碰撞并从壁面反射后，增强的反射波放大了热点的快速放热并导致边界层中发生局部爆炸，如图5 所示。值得注意的是，Liberman 等[41]和Gamezo 等[42]研究了激波-边界相互作用在爆燃转爆轰中的作用，发现爆轰的发生与边界层中反应激波的分叉有关，他们首次引入激波来考察反射激波与入射激波产生的边界层的相互作用。事实上，激波是由不断加速的火焰产生的，由于湍流火焰产生的压力波相当复杂，因此，激波-火焰相互作用使人们认识到，激波对剪切涡层热点的热释放的放大以及局部爆炸的发生至关重要，需要更加深入研究爆轰起爆的内在机理（见图5）。

图4 宏观通道中爆燃到爆轰的转变和胞格爆轰Fig.4 Transition from deflagration to detonation and cellular detonation in macro-scale cannel

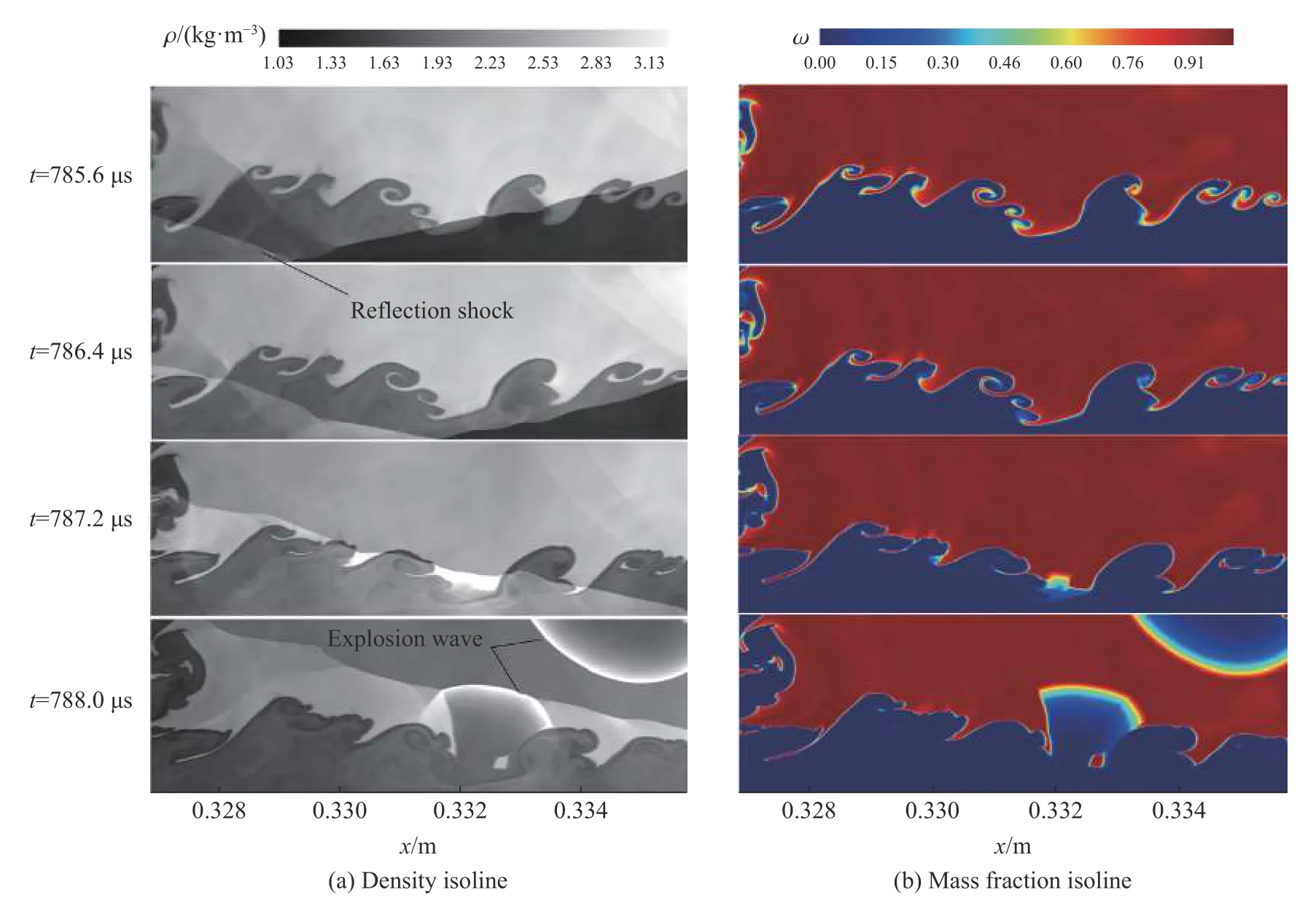
图5 边界层火焰结构与局部爆炸的形成Fig.5 Flame structures of boundary layer and formation of local explosion

在管道中，火焰加速通过拉伸、湍流、激波反射叠加等正反馈机制能够促进火焰加速，最终使爆燃转变为爆轰。在开放空间中，火焰面只能通过不断分裂以及湍流燃烧加速机制产生加速火焰，使火焰前方形成高温、高压环境的反馈机制，这种流动和反应耦合控制的加速机制是否能够将反应波加速到超声速爆轰波阶段目前仍然不确定，有待进一步研究。

1.1.3 爆轰直接起爆

爆轰的形成除了通过爆燃转爆轰途径，还可以通过高能量源直接爆炸形成，即直接起爆。爆轰直接起爆指的是爆轰瞬间形成而没有经历火焰加速的预爆轰阶段，所谓的“瞬间”是指起爆源在极短的时间内产生强爆炸波能量，并作用于混合气体而形成爆轰，而不是一般通过火焰加速而引起爆轰[43-44]。在可燃气体发生爆炸的事故中，绝大部分都是由于可燃物质燃烧转化为爆燃造成的。由于直接起爆需要点火源在瞬间产生足以引起爆轰的起爆能量，对起爆源点火能量要求比较苛刻，因此常被忽略，没有引起足够的重视。

Lafitte[45]、Zhang 等[46]最早利用直接起爆形成球形爆轰，随后，Zel'dovich 等[47]对直接起爆相关机理进行了系统研究，发现直接起爆的本质就是起爆源在瞬间产生足够强的能量所诱发。对给定的爆炸性混合气体，通过实验测定形成球形爆轰的最小起爆能量，是判断该混合物敏感性最直接和有效的方法[43-44]。

直接起爆可由多种起爆源瞬间起爆产生强爆炸波形成。Bull 等[48-49]和Alekseev 等[50]利用高能炸药点火研究了碳氢燃料与空气的直接起爆问题；Knystautas 等[51]、Lee 等[52]利用电火花点火，并与高能炸药点火和平面爆轰波诱导产生球形爆轰的点火能量分别进行了比较；Knystautas 等[51]、Zhang 等[53]分别通过理论和实验发现，只有最初1/4 周期的放电能量才真正作用于直接起爆；Matsui 等[54-55]对电火花点火中不同几何形状的电极及电极之间的不同间距对放电能量的影响进行了研究；Berets 等[56]对冲击波诱导爆轰做了比较系统的研究；Mooradian 等[57]用爆轰波替代冲击波诱导来研究直接起爆问题；Norrish 等[58-59]、Thrush[60]、Klimkin 等[61]、Kataoka 等[62]和Lee 等[63]研究了通过激光诱导的方法形成起爆；解立峰等[64]和姚干兵等[65]通过立式激波管对环氧丙烷（PO）、正己烷、癸烷分别与空气组成的混合气体进行了直接起爆。Zel'dovich 等[47]早期针对爆轰波研究曾提出理想的爆轰波具有稳定的一维ZND 结构，爆轰波如果能自持传播就必须满足：当爆炸波衰减为CJ 状态时，爆炸波的半径必须至少约为诱导区的长度。并提出直接起爆的临界起爆能（EC）与ZND 诱导区长度（ΔI）的3 次方成正比关系。对临界起爆能量的研究一直延续至今[62,64,66-70]。

1.2 研究爆轰起爆的重要因素

1.2.1 化学反应模型

在受限区域火焰会加速，并可能经历爆燃到爆轰的转变（deflagration to detonation transition，DDT）。反应混合物中局部小能量释放导致不同着火模式的基本机理和过程是燃烧物理学中最重要和最基本的问题之一。人们需要知道燃烧是如何开始的，瞬态能量沉积是如何影响从瞬态热能沉积的有限体积反应气体中传播出来的反应波（热点，不均匀自发引起的有微小时差的点火，进而传播的反应波）[7,9,32,42,71-74]。加速火焰导致热点的形成，热点可以通过Zel'dovich 梯度机制产生爆轰。为了证明这种方法的合理性，Kessler 等[72]认为：对于许多实际情况，不需要对化学途径的细节进行广泛描述，更重要的是要有一个精确的流体动力学模型与一个化学能释放模型相耦合，该模型能在正确的时间将释放的能量放在流动的正确位置。然而，由于简单化学反应模型确定的点火时间比详细化学模型计算的点火时间小几个数量级，无论流体动力学模型多么精确，都不可避免地在错误的时间将释放的能量放在错误的位置。还应注意，由简单反应模型给出的火焰速度-压力依赖性也与实验测量的不一致。因此，用简单反应模型研究爆轰起爆需要谨慎。

王成等[30,75]采用详细化学模型研究了热点起爆问题，结果表明，采用详细化学模型计算的自发反应波的演化与采用简化模型预测的结果有着本质的差异。首先，对于简单模型，反应在所有温度下都是放热反应，而详细反应链分支反应则从吸热诱导阶段开始，因此，简单模型预测的诱导时间比详细化学模型预测的小一个数量级。这意味着，用详细化学模型预测的热点起爆问题可能与简单模型预测的存在数量级的差别[76-77]。从简单模型模拟结果来看，Zel'dovich 梯度机制通常被认为是解释爆燃向爆轰转变的普遍机制，被认为是爆燃转爆轰研究的主流。Kuznetsov 等[78]通过实验证明，爆燃转爆轰之前，火焰附近的温度仍然很低（不超过550 K），无法自着火，表明梯度机理无法解释这一类爆轰起爆现象[41,79-82]。

（1）)单步、两步和四步反应模型

单步化学反应模型已被广泛应用于理论研究和数值模拟。Kessler 等[72]标定了一步Arrhenius 模型的参数，并模拟了通道中火焰加速和爆燃转爆轰过程。Westbrook 等[83]和Franzelli 等[84]通过修正经典两步模型开发了2S-CH4-BFER 反应模型，并证明了该模型对贫燃燃烧预测的有效性，为火焰结构和燃烧速度提供了准确的描述。Jones 等[85]开发的四步反应模型包括4 个描述链分支、链断裂和CO 氧化的全局反应。该四步反应模型虽然计算时间比一步反应模型稍长，但预测的产物温度和组分更准确。

（2）)简化反应模型与详细化学模型的比较

为了能够正确预测点火延迟时间，将简化模型的预测与Zambon 等[86]、Kazakov 等[87]开发的详细反应模型和Smooke[88]的模型进行了比较，验证了在不同压力、温度和当量比范围内与点火延迟时间和层流火焰速度相关的燃烧特性[89-91]，并与详细反应模型GRI 3.0 Mech[92]和实验数据进行了比较。虽然所有简化模型都能以令人满意的精度再现层流火焰的特性，由简化反应模型和其他简化模型预测的诱导时间大致接近，但与使用详细化学模型GRI 3.0 Mech 计算的值以及实验测量的点火延迟时间存在显著差异。

图6 显示了使用简化和详细化学反应模型计算的诱导时间与温度，以及使用GRI 3.0 Mech 计算的结果和一些最新实验结果[91,93]。可以看出，由详细化学反应模型预测的诱导时间与由GRI 3.0 Mech 预测的和由实验得到的结果非常吻合[91,93]。简化化学模型预测的诱导时间比详细化学模型预测的诱导时间短3 个数量级。用详细化学模型计算的同一温度梯度产生的自发波速与用简化模型计算的自发波速相差很大。

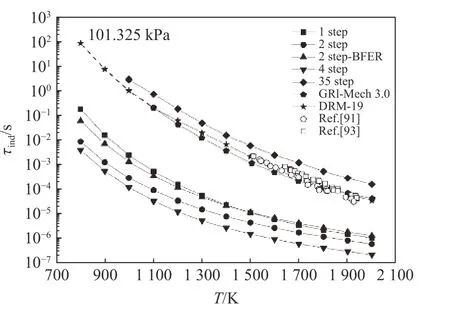
图6 当量甲烷-空气混合气体的诱导时间与温度的关系[27]Fig.6 Induction time vs.temperature for stoichiometric methane-air mixture[27]

从物理角度来看，用简化模型计算的诱导时间与用详细化学模型计算的诱导时间之间的差异，意味着简化模型校准对应的活化能仅为有效活化能的1/8～1/6。因此，某些简化反应模型预测的层流火焰速度-压力依赖性与用DRM-19 计算的以及实验测量的速度-压力依赖性存在很大的差异。图7 显示了简化模型和详细模型计算的层流火焰速度-压力依赖关系。

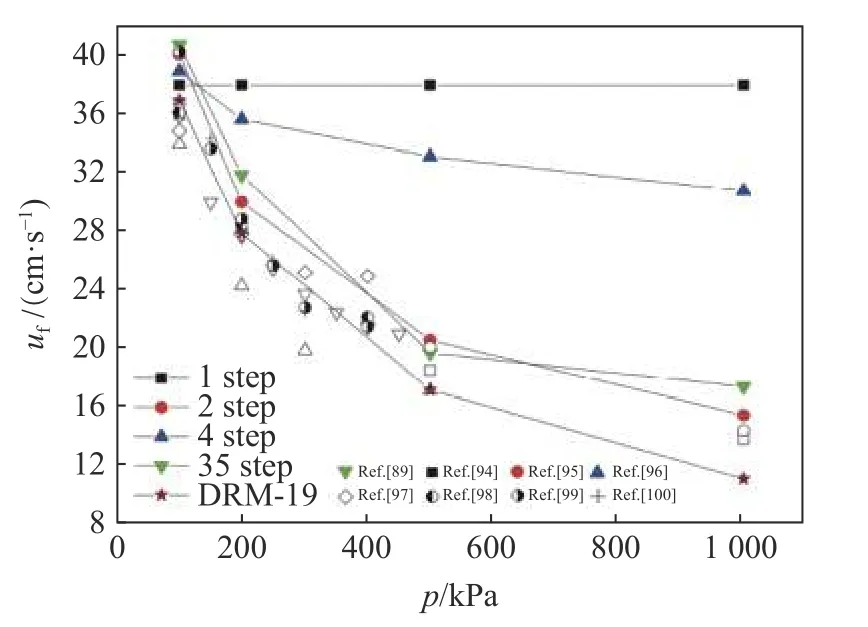
图7 层流火焰速度与压力函数关系[27]Fig.7 Laminar flame speed as a function of pressure[27]

（3）)不同反应模型下温度梯度起爆

化学反应模型能显著改变点火延迟时间，也将显著改变热点自发发起爆进程[75-76]。一般来说，温度梯度激发的自发波传播模式的分类与Liberman 等[76]所描述的高反应化学计量氢氧的模式相似。反应放热阶段产生的压力波演变为自持续爆轰波，而根据梯度陡度和热点外温度而产生熄爆现象。

图8（a）为一步化学模型下，温度梯度中爆轰的形成和猝灭过程。在这种模式下，反应区开始慢慢远离领先的激波，稀疏波向反应区传播，放热区与主导激波的间距增大；最后冲击波强度变弱，爆轰猝灭。图8（b）为较缓梯度下稳定爆轰的发展情况。

图8 爆轰形成过程中温度、压力波演化[27]Fig.8 Temperature and pressure profiles in initiation process[27]

如果初始温度梯度较陡，在压力波超过反应波的位置，反应阵面速度不足以维持激波后面流动中压力脉冲的同步放大。因此，压力波在反应波前面传播，反应波的速度降低。相反，对于较缓的梯度，稳定的CJ 爆轰能够持续。He 等[25,34]和Radulescu 等[35]首次研究了爆轰的熄灭现象他们指出，在给定温度条件下，CJ 爆轰自发形成的局部判据决定了临界温度梯度。He 等[34]用一种特殊形式的准稳态近似简单地解释了爆轰的熄灭。Liberman 等[76]对由温度梯度引发的反应波进行分类时，对应于由激波和反应区组成的稳态结构，认为该结构可能转化为沿温度梯度传播的爆轰。一般来说，由初始温度梯度引发的燃烧模式的分类，对于所有简化的一步、两步和四步化学模型都是非常相似的，如图9 所示。需要注意的是，虽然四步模型的诱导时间小于两步模型，并且在这两种情况下诱导时间都小于一步模型，但四步模型要求的热点临界尺寸与一步模型相同，两步模型要求的热点临界尺寸比一步模型要求的稍大。

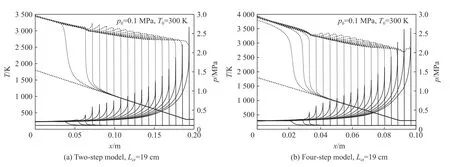
图9 温度、压力波演化[27]Fig.9 Temperature and pressure frofiles in initiation process[27]

温度梯度引起爆轰的临界热点尺寸的差异是由于其不仅取决于诱导时间，而且取决于决定自发波速度的dtin/dT。Liberman 等[76]指出，在高压下，诱导时间较小，爆轰起始所需的最小梯度陡度增加，然而，两步和四步模型计算起爆所需的最小梯度都是相同的。Wang 等[27]考虑了详细化学模型DRM-19 与两步模型和四步模型在高压下起爆过程，如图10～11 所示。

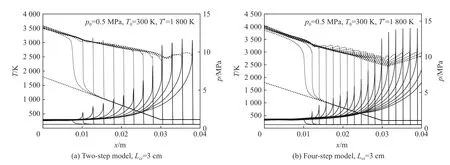
图10 温度、压力波演化[27]Fig.10 Temperature and pressure frofiles in initiation process[27]

在详细化学模型情况下，起始反应不发生放热，诱导阶段的气体动力扰动非常微弱。自发波由终止反应的时间尺度决定。因此，即使在足够缓的温度梯度下，自发波也会以超临界声速传播，对于详细的化学模型DRM-19，爆轰传出热点后无法持续传播，而简化模型即使在更陡的梯度下，发展中的爆轰也能够存活下来，如图11 所示。

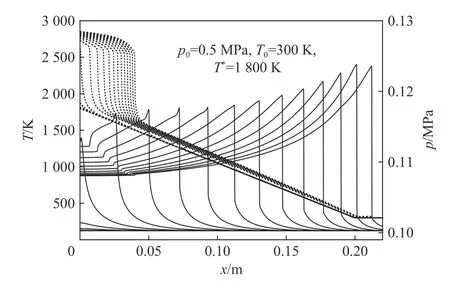
图11 温度、压力波演化：DRM-19 机理[27]Fig.11 Temperature and pressure frofiles in initiation process:DRM-19 mechanism[27]

总之，不同化学模型对初始温度梯度起爆的影响很大。对于简化的和详细的化学模型，温度梯度陡度（热点尺寸）和触发爆轰的热点外初始温度的要求有很大的不同。对于详细化学模型，温度梯度的大小和通过梯度机制引发爆轰的热点的大小比简化模型大几个数量级。随着压力的增加，爆轰所需的热点尺寸减小。然而，对于一个详细的化学模型，只有在热点以外的高温下才能形成稳定的爆轰，因此在梯度上发展的爆轰与在梯度端或热点以外发展的热爆轰之间存在竞争。因此，使用一步模型模拟火焰动力学，必须根据具体应用来选择合适的模型参数并需要对其进行标定。特别是对于非稳态过程，如点火、瞬态过程等，采用简化的化学模型会导致热点起爆的预测值误差较大，在爆燃转爆轰模拟中使用简化化学模型时，得出的结果需要谨慎对待。

1.2.2 爆轰稳定性对直接起爆的影响

对于接近临界起爆能的直接起爆，起爆能产生的过驱爆轰波先衰减为准稳态爆轰波，再衰减为稳态爆轰波，然后由于脉动不稳定性而迅速熄灭[101-102]。在理论上，存在一个临界起爆半径，而不存在广义的Chapman-Jouguet 解，Eckett 等[103]、Short 等[104-105]的研究给出了临界起源能，指出准稳态假设理论在直接起爆研究中具有局限性[104-105]。实验和数值模拟[106-109]也表明，规则和不规则胞格对起爆过程有不同的影响，对于低活化能规则胞格爆轰，起爆主要由激波压缩点火机制产生。然而，对于活化能较大的不规则胞格爆轰，局部化学速率敏感，阵面后存在未反应气囊[107,110-113]，导致起爆更加困难。图12(a)～(b)中显示了稳定爆轰由全局曲率引起的爆轰胞格不稳定对起爆的影响，表明胞格爆轰可以通过亚临界起爆路径成功起爆。图中lin为诱导长度，c0为未反应气体的声速，Es为无量纲起爆源能，r为半径。

图12(a) 胞状柱爆轰的最大压力历程[114]Fig.12(a) Maximum pressure history of cellular cylindrical detonation [114]

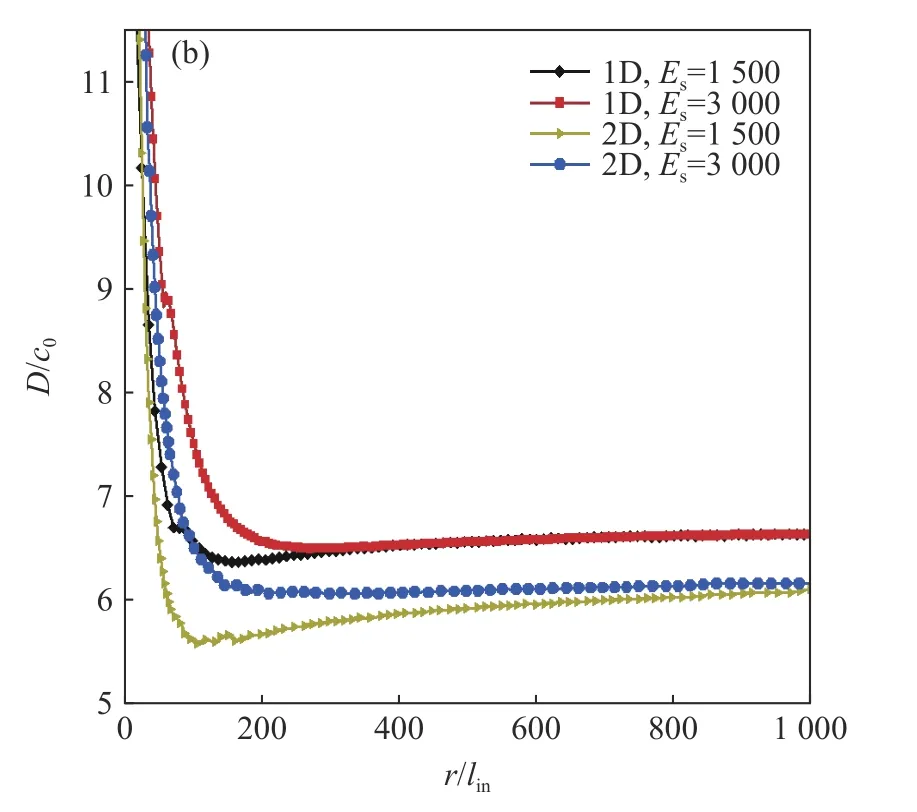
图12(b) 圆柱形爆轰平均速度[114]Fig.12(b) Average velocity of cylindrical detonation[114]

从图13（图中Ea为无量纲活化能）可以看出，对不稳定爆轰，要在自由空间中成功起爆胞格爆轰，很大程度上依赖于起爆能量[105]。当源能略有下降，爆轰在衰变到CJ 状态后，很可能无法实现自持传播。随着活化能的增大，这种依赖性会随着不稳定爆轰的增强而增大。实际上，当活化能较大时，小的源能量无法实现二维柱状爆轰的起爆，如图13(b)所示。当点火源能量足够大时，二维柱形爆轰成功起爆，爆轰能够自持传播，见图13(c)和图14。因此，在自由空间中，在极不稳定的情况下，通过亚临界起爆途径实现自持爆轰是极其困难的；相反，学者们更倾向于通过强起爆能量的直接起爆途径实现自持爆轰。

图13 圆柱爆轰的最大压力历程[114]Fig.13 Maximun pressure history of cylindrical detonation[114]

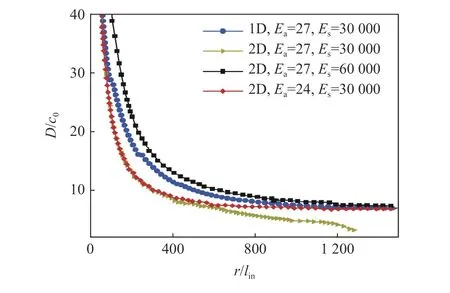
图14 圆柱形爆轰的平均速度[114]Fig.14 Average velocity of cylindrical detonation[114]

对于高度不稳定爆轰，初始形成的胞格爆轰无法维持，最终起爆熄灭导致起爆失败。爆轰熄灭机理如图15 所示。起爆熄灭的主要原因是曲率导致局部温度降低，近一步增加了等效活化能，使得爆轰不稳定性增强。对于单步反应，反应速率对后激波温度非常敏感。由于气流的分叉和波面的扩展，曲率效应显著降低了激波后温度，增加了反应的敏感性。由于活化能较高，前导激波衰减速率快，进一步延迟了爆轰阵面结构中气体激波的点火，从而导致更多未反应气体未在主反应层燃烧，进入滑移层[115]。相对弱的三波点和前导激波则无法直接起爆流入阵面的气体。爆轰全局结构拉伸，大块未反应气囊留在下游。前导激波与反应层解耦，反应放热无法支持前导激波传播，迅速衰减为惰性激波，最终熄灭导致起爆失败。

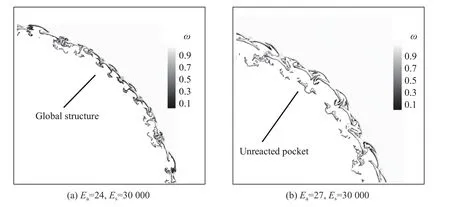
图15 胞状圆柱爆轰的锋面结构[114]Fig.15 Frontal structure of celluar cylindrical detonation[114]

Watt 等[102]模拟了二维圆柱形爆轰在自由空间中的起爆过程，给出了柱形爆轰起爆与不稳定之间的初步联系。然而，实验表明，高度不稳定的爆轰胞格对起爆具有积极作用，这与数值模拟预测的趋势相矛盾。Mazaheri 等[116]和Redulescu 等[117-118]的研究表明，对于高度不稳定的爆轰，数值模拟忽略了黏性扩散效应是导致这一矛盾的原因。然而，胞格不稳定性对爆轰起爆的影响没有形成定论，仍然需要进一步确定。

1.2.3 黏性扩散效应对直接起爆的影响

Maxwell 等[119]通过对通道中多维爆轰的大涡模拟表明，在局部条件下，未反应气囊从边界穿过表面湍流火焰的燃烧速率大约是层流燃烧速率的3～7 倍。如图16 所示，在爆轰胞格出现后，黏性Navier-Stokes (NS)系统得到的平均爆轰速度与欧拉方程得到的平均速度不同，特别是出现了大体积未反应气囊，考虑扩散得到的全局平均速度较大。然而，在扩散存在的情况下，改变未反应气囊的燃烧速率并不会改变起爆失败的结果。因此，自由空间中高度不稳定爆轰的失败可归结为横波的再放大机制的缺失。Radulescu 等[111]也指出，横波的再放大机制在不稳定爆轰在多孔壁管内传播的点火和传播机制中起着重要作用。Mazaheri 等[116]研究了通道中不规则爆轰未燃气囊的起源，并指出横波与壁面的碰撞对未反应气囊的形成和消耗至关重要。值得注意的是，在有限的空间中，由反射激波引起的再放大横波与未反应的气囊相互作用，大大提高了这种高度不稳定爆轰的生存能力[118]。而在自由空间中，没有约束相互作用的再放大机制，横波的强度完全取决于三波点的碰撞。此外，活化能高的爆轰比活化能低的爆轰具有更长的诱导区。因此，在自由空间中，当三波点和横波因起爆源能量不足而减弱时，三波点很难通过约束相互作用再次增强，不足以直接起爆进入爆轰阵面结构的气体。这也是爆轰在其速度略低于CJ 值时骤然速度亏损的原因。目前，黏性扩散效应对不稳定爆轰以及准爆轰的影响认识尚且不足，仍然需要深入研究。

图16 欧拉和NS 方程求得的爆轰平均速度[114]Fig.16 Average velocity of detonation obtained by Euler and NS equations[114]

通过比较不稳定爆轰在自由空间和密闭空间中的传播，发现在自由空间中，爆轰衰变到CJ 状态后，最终熄灭。而在受限空间内，通过反射横波的再放大作用，爆轰可以通过再起爆而存活下来，如图17 所示。因此，爆轰是否持续传播，很大程度上依赖于横波再放大和再生成机制。

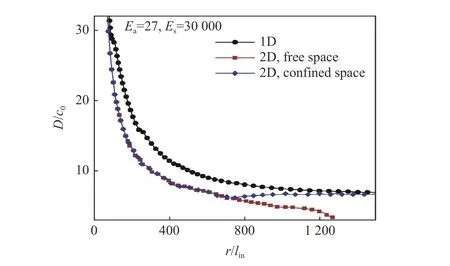
图17 自由空间和约束空间中爆轰平均速度[114]Fig.17 Average velocity of detonation in free and confined spaces[114]

总之，对高度不稳定爆轰在自由空间和封闭空间中的失效和再起爆机理的研究表明，在自由空间中，胞格不稳定性使平均二维速度相比一维速度低，导致成功起爆更困难。对于高度不稳定爆轰，其持续传播在很大程度上依赖于横向激波和三波点的再放大和再生机制。比较在自由空间和密闭空间中传播的2 种工况，发现爆轰在自由空间无法传播，但在密闭空间可以重新起爆并持续传播。然而，对于低激活能，由于没有未反应气囊，可以通过亚临界起爆路径成功起爆胞状柱形爆轰;与不稳定爆轰相比，在自由空间中传播对横波和三波点的衰减不敏感。

研究发现，无黏反应流在描述通道内爆轰结构方面存在局限性，对于弱不稳定爆轰，扩散在燃烧未反应气囊中的作用相对较弱，无黏体系和一步反应模型的计算结果是可信的。然而，对于高度不稳定爆轰，NS 体系的平均速度要高于欧拉方程的平均速度。通过与一步反应模型的爆轰结构和详细机理的比较，可以看出一步反应模型对一维爆轰结构有明显的改变，但在两种模型中均未观察到爆轰波前后方存在未反应物质。另一方面，在二维模拟中，由于全局曲率效应导致胞格爆轰局部反应速率降低[103，120-121]，导致出现局部未反应气囊。因此，目前模拟的爆轰胞格可能与详细模型的结果存在差别，有待进一步研究。

黏性扩散效应通常会使爆轰平均反应区厚度增加，比理想的Zel'dovich-von Neumann-Doring（ZND）模型给出的更厚，导致爆速亏损，而且黏性摩擦会增强爆轰不稳定性，进而使得爆轰起爆更容易失败[122]。在许多情况下，在开放的柱形或球形几何空间中，爆轰波阵面全局是弯曲的，曲率对爆轰起爆影响很大。因此，有必要评估爆轰脉动和胞格不稳定性与曲率之间的关联及其对起爆的影响机理。实验研究[121]也表明，圆柱形和球形爆轰波阵面具有胞格结构，以匹配爆轰阵面发散扩大引起的点火能量不足，因此，阵面的三波点需要不断分裂增加。由于曲率的发散作用，爆轰前导激波会减弱，从而导致后激波温度降低，这样相当于增加了等效的活化能，使得曲率大的区域爆轰变得更加不稳定。在高度不稳定爆轰阵面后，通常能够看到未反应气囊逃过激波压缩点火而留在下游，这使得平均声波面延迟达到，平均爆轰气动力厚度增加。因此，对于高度不稳定的研究，通常的反应区层流燃烧假设理论不能很好地预测这一类问题，因此，需要发展新的理论和湍流反应模型来研究这类爆轰现象。

2 爆轰波传播

爆轰波传播具有一维脉动[123]和多维胞格不稳定性，且反应区长度直接影响爆轰的稳定性。在传播过程中，爆轰胞格分裂机理源于爆轰的不稳定。一维不稳定传播呈现稳态：单周期模式、多周期脉动、混沌脉冲等。脉动不稳定边界通过一步反应模型的活化能可以确定[124]，而且可以由诱导长度和反应区长度决定的特征化参数表征[125]。Ng 等[36]还研究了链分支反应驱动的一维CJ 爆轰动力学，通过定义控制参数，提出了一维爆炸不稳定性的通用判据。Sharpe 等[126]通过一步全反应发现，对于高度不稳定的大活化能爆轰，经历了一系列熄爆再起爆，在爆轰波阵面后观察到大量未反应气囊，这些未反应气体的延迟反应改变了爆轰的不稳定性边界。如果化学反应对扰动敏感，由于气流中的扰动导致激波后气体点火时间不同，可能导致未反应气囊形成，正如Meyer 等[127]首次提出的其在后期的燃尽最终将导致反应区的不稳定性。这种脉冲不稳定模式取决于放热时间与诱导时间的比值，而其研究大多都是基于简单反应模型。因此，脉冲不稳定研究拓展到真实的详细化学模型将是该问题研究的发展方向。

2.1 爆轰传播的模拟结果

2.1.1 一维爆轰传播模态

图18 显示了不同氩稀释度混合物的典型一维爆轰模式，结果表明，在初始阶段出现的高频脉动是全局振荡的，然后在不同的情况下发展为不同的传播模式。这种脉动模式也在使用整体一步反应的模拟中观察到，其活化能接近中性不稳定边界，如图18（b）所示。脉动不稳定性从混沌模式逐渐变为单周期模式，再到稳定传播模式，类似于用Ea=27[1]和He 等[124]的一步反应获得的结果，如图18（c）所示。图中ps、pVN为激波压力和激波冯诺伊曼压力。

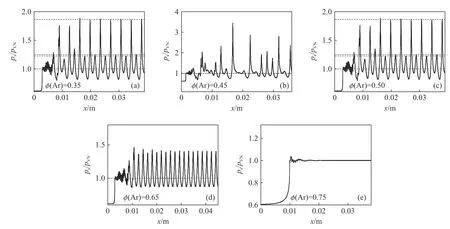
图18 不同氩稀释度的最大压力随距离的变化趋势Fig.18 Maximum pressure history of detonation for different Ar dilutions

3 种爆轰模式分别表现出稳定、周期和混沌行为，已通过详细的反应和改变混合物成分进行了鉴定，类似于Ng 等[36]和Sharpe 等[126]发现的爆轰模式。Clavin 等[123,128]的理论研究对于解释一维不稳定性的起源以及脉动不稳定性和细胞不稳定性之间的关系具有里程碑意义，证明了爆轰波ZND 结构的改变是引起一维脉动不稳定性的原因，因为扰动的作用改变了冲击气体中的点火延迟时间。此外，Ng 等[36]已经证明爆轰模式取决于爆轰结构，并且与诱导区和反应区的优势有关。

2.1.2 多维爆轰传播模态

多维爆轰传播呈现出多种模态，包括螺旋模式、矩形模式和角形模式等传播特征[129-131]。对于螺旋爆轰传播，螺纹间距大约是管道直径的3 倍，这也通过烟迹实验观测得以证实[132-133]。螺旋爆轰发生在窄管道中，当管道宽度足够大时，螺旋爆轰消失。Hanana 等[134]通过实验指出，在矩形管道中至少存在2 种类型的爆轰结构，即矩形和角形爆轰结构。矩形结构模式分为同步和不同步模式两种类型[135-137]。对于矩形爆轰结构，垂直于传播方向的正交波在4 个壁面上相互独立地移动，这些波是由三波线与壁面或三波线之间的碰撞产生的。壁面上的烟熏痕迹呈现出钻石形的胞格形状，同时，壁面上呈现出“拍波”特征。当三波线沿着对角线方向运动时，由垂直于对角线的三波线构成了爆轰阵面的角形结构，壁面上的“拍波”消失。Hanana 等[134]能够在实验中形成角形爆轰，证实了角形爆轰的存在[138-139]。

图19 中给出了螺旋爆轰在壁面上的最大压力历程和主螺旋轨迹。从图中可以清晰地看到螺旋爆轰在壁面上以顺时针方向传播的螺旋迹线。对于稳定的螺旋爆轰，在固壁上呈现出螺旋爆轰明显的“带状”特征[140-141]。

图19 壁面上的最大压力历程和主螺旋轨迹（爆轰波沿着 x 正向传播）Fig.19 Maximum pressure history and main spinning track of detonation (detonation wave propagates along x direction)

预测的螺距-直径比和文献[142]中实验测得的相近，且螺旋角与文献[143-146] 中的吻合。当管道宽度足够大时，横波能够充分发展，横波相互碰撞使得爆轰自持，没有必要通过降低横向模态维持爆轰传播，因此，爆轰可以保持矩形结构，如图20 所示。

图20 壁面上最大压力历程Fig.20 Maximum pressure history on walls

对于高度不稳定爆轰（活化能Ea=50.0、热释放Q=50.0、过驱因子f=1.2 ），初始时的对角爆轰模式随着时间的推移被破坏，阵面演化成螺旋模式的结构特征，表明爆轰由角形模式转变为螺旋模式，如图21 所示，图中t为无量纲时间。爆轰的不稳定性以及高横向模态到最低横向模态的转变是触发螺旋爆轰的主要原因。

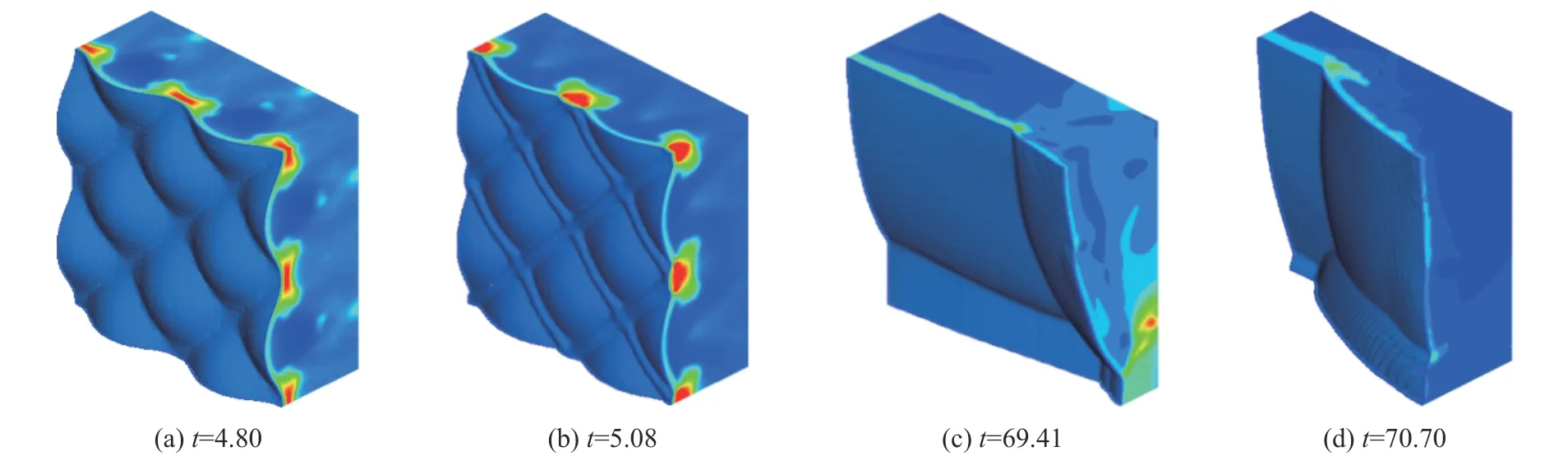
图21 不同时刻的爆轰阵面结构Fig.21 Detonation frontal structures at different times

图22 中给出了高度不稳定爆轰阵面结构的演化过程。从图中可以看出，爆轰阵面早期具有矩形结构特征。初期爆轰阵面仍然保持矩形结构，由于流动的高度不稳定导致爆轰阵面呈现复杂的三波线结构。随着时间的推移，爆轰由矩形模式转变为角形模式。随着阵面结构的不断演化，爆轰阵面显示出明显的螺旋结构特征。因此，最终能够触发螺旋爆轰。

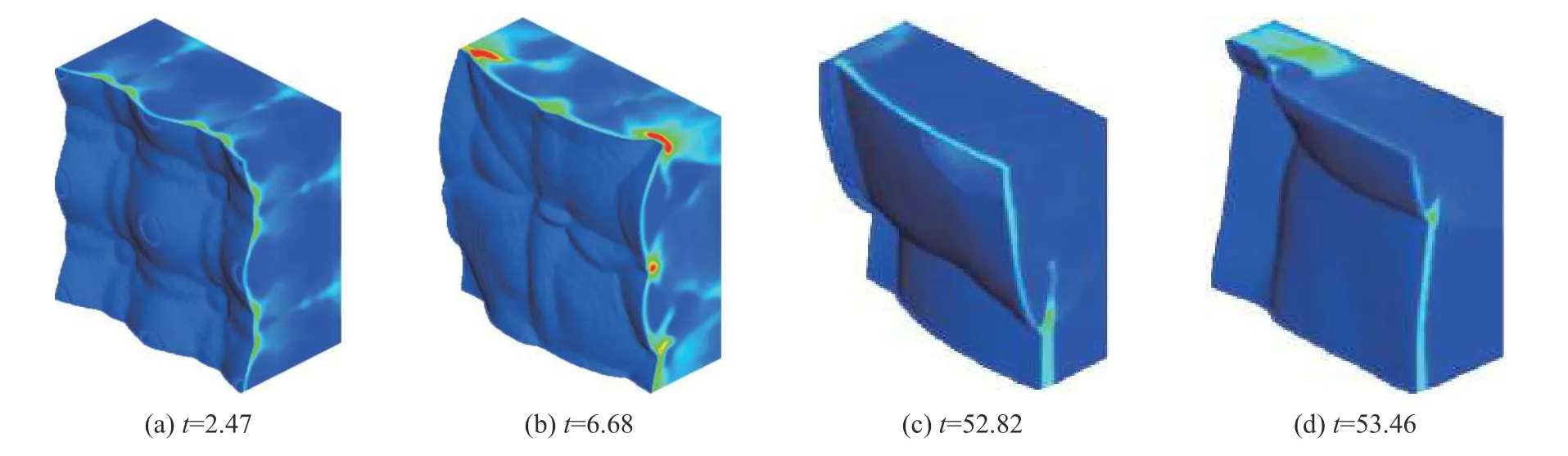
图22 不同时刻的阵面结构演化Fig.22 Detonation frontal structures at different times

对于轻度不稳定爆轰（活化能Ea=50.0、热释放Q=50.0、f=1.6 ），在开始阶段，爆轰以角形模式传播。随着时间的推移，爆轰阵面呈现出螺旋模式的结构特征，表明螺旋爆轰形成。图23 中显示了轻度不稳定爆轰在初始横向余弦扰动下的演化过程。初期局部过驱明显，爆轰阵面高度扭曲。随着爆轰的传播，爆轰的本质不稳定性导致三波线弯曲。尽管阵面扭曲，但仍然能够保持矩形结构，螺旋爆轰难以触发。可知当过驱因子f=1.6 时，初始的矩形扰动模式与角形扰动模式相比，螺旋爆轰较难触发。因此，螺旋爆轰的产生不仅与爆轰的不稳定性以及横向尺度有关，还依赖于初始扰动模式。

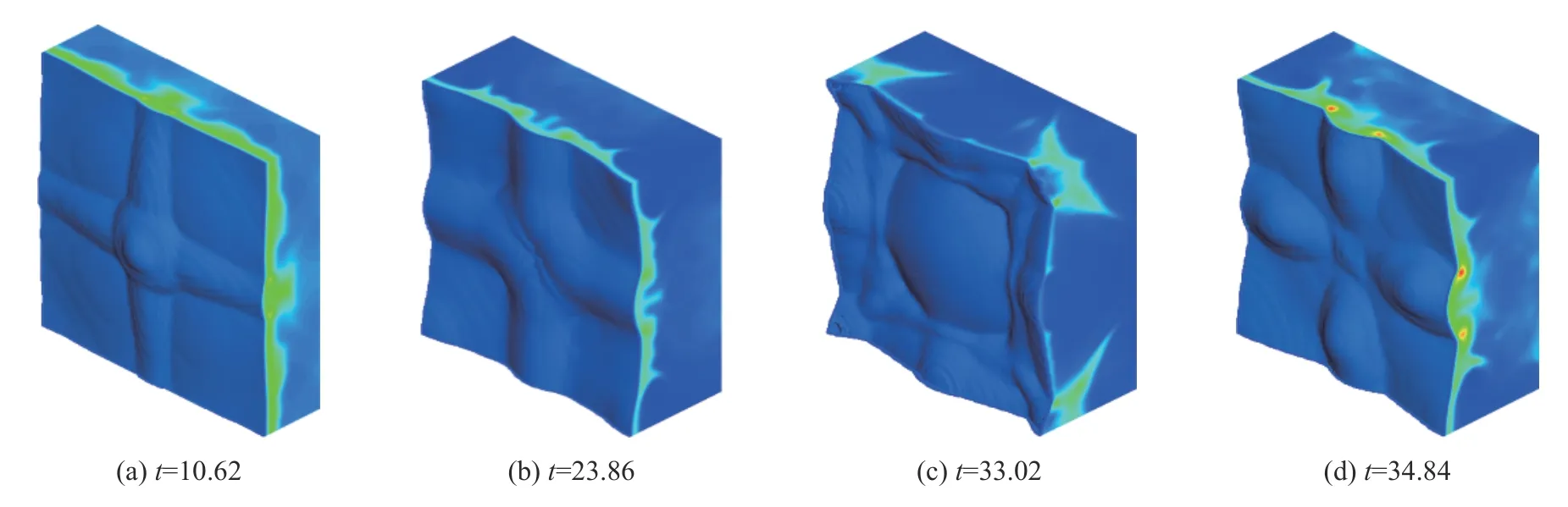
图23 不同时刻的阵面结构Fig.23 Detonation frontal structures at different times

2.2 爆轰胞格实验研究

在爆轰传播过程中，爆轰波阵面具有特殊的精细结构，而且大量实验研究已经清晰地观测到爆轰阵面结构特征[1]。Radulescu 等[37,117,147]、Ng 等[36,148]、Zhang 等[149]的研究表明，气相爆轰波的结构特征取决于混合物的物化属性，尤其是混合物经过高浓度（体积分数大于70%）氩气稀释之后，胞格结构呈现规则结构，而一般燃料/氧化剂混合物胞格结构都为不规则结构，主要原因是惰性气体的增加，极大提高了混合物的活化能，而爆轰不稳定性在很大程度上被抑制。因此，胞格结构规则的混合气体被称为稳态气体（stable mixture）；反之，胞格结构不规则的混合气体则被称为非稳态气体（unstable mixture）。

2.2.1 稳定爆轰胞格结构

使用80%Ar 稀释的理论配比的氢氧混合气体，在p0=20 kPa 时的胞格结构如图24 所示。由图片可见，爆轰波阵面略有弯曲，胞格结构排列较规则，大小基本一致，因此为稳定的胞格结构。

图24 2H2-O2-80%Ar 的爆轰胞格（p0=20 kPa）Fig.24 Detonation cell for 2H2-O2-80%Ar mixture (p0=20 kPa)

图25 是加州理工学院Pintgen 等[106]得到的2H2-O2-80%Ar 混合气体在初始压力p0=20 kPa 时的爆轰结构图。由图25（a）可见，爆轰波阵面较整齐，可观察到爆轰的三波结构，但亮度较弱。在图25（b）中可以清晰地见到呈“楔形”的OH 基团。通过图25（c）中的纹影和荧光叠加效果可知，剪切流始于波阵面交叉处，横波是已反应气体和未反应气体的分界，并形成了“楔形”的边界。

图25 2H2-O2-80%Ar 的爆轰结构[150]Fig.25 Detonation cellular structure in 2H2-O2-85%Ar mixture[150]

而用体积分数为85%的氩气稀释时，相同状态下氢氧混合气体的胞格结构如图26 所示。85%氩气稀释后的胞格比较规则，因此为稳定的胞格结构。在相同状态下爆轰结构如图27 所示。

图26 2H2-O2-85%Ar 爆轰胞格[151]（p0=20 kPa）Fig.26 Detonation cells in 2H2-O2-85%Ar mixture[151] (p0=20 kPa)

图27 2H2-O2-85%Ar 爆轰结构[150]Fig.27 Detonation cellular structure in 2H2-O2-85%Ar mixture[150]

从图27（a）中爆轰结构的纹影图可见，爆轰波波阵面非常齐整，基本位于同一垂直线，并能明显看出横波及三波点。图25（b）与图27（b）相比则有明显的区别，在图27（b）并未见OH 基团的“楔形”结构，而是比较平滑的圆弧形结构。

2.2.2 中度不稳定爆轰胞格结构

图28 是用72%氮气稀释理论配比的氢氧混合气体，初始压力p0=20 kPa。由胞格图片可知，此时的胞格明显不如85%或者80%氩气稀释的胞格整齐，大小也不规律。但每个胞格都具有独立结构，并没有发现胞格“子结构”，因此称为中度不稳定胞格结构。而通过图28（b）中的纹影图像可见，此时的爆轰波阵面出现弯曲。并观察到在波阵面之后约一个胞格长度的距离之内，密度梯度出现了小范围的变化。图28（c）中的PLIF 图像显示，反应区比用85%Ar 稀释时出现明显的歪曲现象。

图28 2H2-O2-72%N2 混合气体[151]Fig.28 Detonation cellular structure in 2H2-O2-72%N2 mixture[151]

2.2.3 高度不稳定爆轰胞格结构

体积分数为60%的氮气稀释的H2-N2O 的混合气体，在初始压力p0=20 kPa 时的胞格如图29（a）所示。胞格的规律性非常差，并且出现“子结构”现象，如要确定胞格尺寸则相对较困难，胞格尺寸的数据一般采用平均值和误差线。图29（b）中爆轰前导冲击波与图27（b）和图28（c）中的结构有明显的区别：用氩气或者氮气稀释的混合气体的爆轰前导冲击波为稍弯曲的结构，但图29（b）中的爆轰结构除了具有弯曲结构之外，由于小尺度的扰动，波前结构比较粗糙。紧接着波阵面之后的区域包含小尺度的密度波动，并持续约一个胞格尺寸的长度。图29（c）中的PLIF 图像也明显区别于图27 和图28 用氩气和氮气稀释的情况。在图28（c）中并没有看到明显的“楔形”结构，OH 结构非常粗糙，OH 基团并不具有连续性，在OH 主波阵面之后，高浓度区域和低浓度区域相互独立。

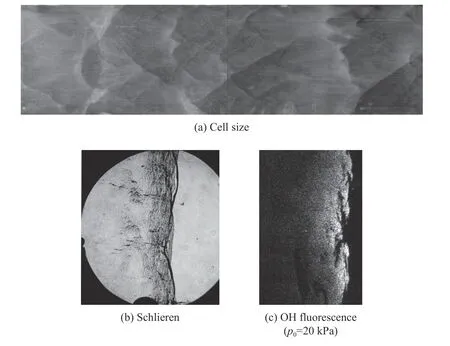
图29 H2-N2O-60%N2 混合气体[151]Fig.29 Detonation cellular structure in H2-N2O-60%N2 mixture[151]

2.2.4 近极限传播的爆轰波胞格结构

Zhang 等[152]、Gao 等[153]通过实验测量了多种混合气体接近爆轰波传播极限状态时的速度和胞格结构，获得的结论主要有：（1）爆轰在极限之内，其传播速度与CJ 爆轰速度较接近；（2）当通过降低初始压力来接近爆轰极限时，爆轰速度逐渐远离CJ 爆轰速度，这是由于初始压力降低时，爆轰诱导区长度增加，边界层扩散导致的能量损失增大（Fay[154]），爆轰的化学反应变缓而导致速度降低（Komadsu 等[155]）；（3）当初始压力一定时，管道直径的减小将导致爆轰速度降低，这主要是由于当管径变小时，管壁的边界层效应更加显著，因此极大降低了爆轰波速度；（4）随着初始压力的降低，爆轰波的胞格结构逐渐由多头结构（multi-headed detonation structure）发展为双头结构（double-headed）和单头螺旋结构（single-headed spinning），最终爆轰熄灭，爆轰波的结构消失。如图30 所示，CH4-2O2混合气体随着初始压力的降低，爆轰波结构逐渐依次出现上述3 种特征。

图30 不同初始压力下CH4-2O2 的胞格结构[156]Fig.30 Detonation cell size of CH4-2O2 mixture under different initial pressures[156]

2.3 近失效状态的爆轰波模式及理论预测模型

2.3.1 影响爆轰极限因素的多重性

气相爆轰波在接近传播极限时会出现复杂的非稳定传播现象，不少学者已针对这一现象开展了研究。张超等[157]揭示了微尺度下爆轰波的4 种传播模式和各自具有的不同特征。Wu 等[158-160]实验研究了管道尺寸和混气配比对在毫米级管道内爆轰波传播的影响，得到了多种火焰传播模式。近年来，学者们对爆轰极限的复杂机理也逐步开展了研究。Camargo 等[161]利用条纹相机捕捉爆轰波在管道内传播的图像，并研究了爆轰极限的波动模式，发现爆轰波接近极限状态时，其传播速度发生了明显的波动；Huang 等[162]对爆轰极限时出现的单头螺旋结构进行了分析；Wu 等[163]研究表明，当爆轰波接近极限状态时，单头螺旋结构能够广泛地存在于稳态和非稳态气体中；Gao 等[164]详细研究了驰振爆轰的结构以及速度变化规律；Wang 等[165]通过数值模拟揭示了爆轰波在不同宽度的管道中接近极限状态时的波系结构规律。波动模式、单头螺旋模式和驰振模式在以上的研究中都被用作爆轰极限的判断依据，在学术界缺乏定义爆轰极限的统一标准。

为了理解爆轰极限的复杂机理，一些学者对爆轰极限的影响因素进行了分析。例如，喻健良等[166-167]研究指出初始压力对爆轰极限具有显著的影响；夏昌敬等[168-169]研究并获得了初始条件、声学吸收壁、弯管尺寸、扩张管对爆轰波传播的影响规律；Yoshida 等[170]系统研究了管道直径对甲烷氧气混合气体爆轰极限的影响规律；Zhang 等[152,171-172]则对甲烷氧气混合物、氢气氧气混合物、甲烷氢气氧气混合物在不同混合浓度时的爆轰极限规律进行了初步研究。

Lee 等[173]研究了不同规格的圆管和环形管中爆轰波接近极限状态的速度亏损，并获得了d/λ（d为管道直径，λ 为胞格尺寸）与速度亏损的变化趋势。Lee 等[173]研究表明，在光滑管中，爆轰波传播速度的亏损达到15%vCJ时开始失效，但在粗糙管中，爆轰波传播速度亏损高达50%vCJ时仍然保持稳定自持传播。Jackson 等[174]对爆轰波在极度能量亏损条件下的传播模式以及波动频率开展了分析，发现了能量亏损与爆轰驰振模式的关联性。Ishii 等[175-176]研究了方形管道内爆轰波的传播和失效情况，发现爆轰极限与传播过程中的热损失有关。Gao 等[164,177]研究了几种典型稳态和非稳态气体的爆轰极限，发现了氩气稀释浓度对爆轰极限的影响规律。

目前研究所获知的爆轰极限的影响因素可概括为：混合气体初始热力学条件（包括初始压力、燃料混合浓度、惰性气体稀释浓度）、管道尺寸规格（圆管、环形管、内径大小）以及边界条件（如管壁粗糙度、能量损失）。而事实上，以上这些影响爆轰极限的复杂因素通常是相互耦合作用，仅考虑单一影响因素则很难把握爆轰极限的规律。

2.3.2 近极限爆轰波典型传播模式

Haloua 等[178]提出了爆轰波接近失效状态时出现的几种模式：稳定（stable）爆轰、波动（stuttering）爆轰、驰振（galloping）爆轰、单头螺旋（single-headed spinning）爆轰、低速爆轰和快速火焰。颜秉健等[179]对气相爆轰波近极限状态传播模式进行了详细研究，对于给定的预混气体与管道，实验中通过逐渐降低预混气在管道内的初始压力来获得爆轰极限的临界压力。临近极限状态下，爆轰波在管道内传播的速度波动逐渐增大，呈现6 种不同的传播模式：稳态、快速波动、结巴式、驰振式、低速以及失效模式（见图31，图中ū为平均爆轰速度）。对于特定组分气体，在某些特定压力下，会交替出现多种传播模式。对于活化能较低的混合气体C2H2+2.5O2+70%Ar 和C2H2+2.5O2+85%Ar，在其传播过程中速度波动较小，只存在稳态、快速及失效模式；而对于活化能较高的C2H2+5N2O、C3H8+5O2和CH4+2O2等3 种混合气，在其传播过程中速度存在较大波动，且随着初始压力的逐渐降低，依次出现6 种传播模式。管道尺寸影响爆轰在管道中的传播模式的形成及演变。CH4+2O2混合气体的非稳定性远大于C3H8+5O2和C2H2+5N2O 等2 种气体，且出现驰振爆轰的压力区间随着管径的增加而逐渐减小。在稳态、快速波动及结巴式传播模式下，对于活化能较低的气体，爆轰波具有规则的多头胞格结构；而对于活化能较高的气体，爆轰波胞格呈现出不规则、多头胞格结构，表明此类气体的稳定性较差。多头爆轰胞格尺寸随着初始压力的降低而逐渐增加。在驰振爆轰模式下，爆轰波出现单头螺旋爆轰，且在解耦处爆轰波胞格消失；当前驱冲击波与火焰面重新耦合时爆轰波发生过载，同时出现较小尺寸的胞格结构。在低速爆轰与失效模式下，爆轰波由多头胞格转变成单头螺旋爆轰，在失效和低速阶段爆轰波胞格完全消失直至管道末端。

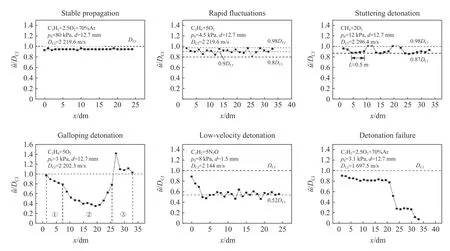
图31 爆轰波接近极限状态的多种传播模式Fig.31 Typical propagation modes near the detonation limits

2.3.3 爆轰极限预测模型

由于处于极限状态时爆轰波传播现象和机理极其复杂，并且爆轰极限的影响因素较多，因此对于爆轰极限的预测难度极大。Fay[154]考虑了边界层效应对爆轰波传播的影响，初步建立了预测爆轰极限的定量模型。爆轰波在管道中传播，如果速度亏损超过了临界值，爆轰波就会失效，即形成爆轰极限。Fay[154]提出的爆轰波在管道内传播时速度亏损的表达式如下：

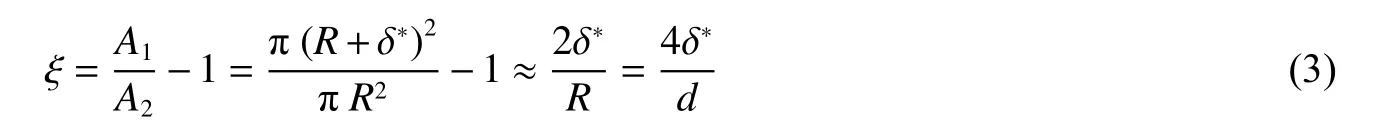
对于光滑内壁管道，Gooderum[180]通过实验研究得出边界层位移厚度为：

式中：x为爆轰波化学反应区长度，mm；µe为爆轰波化学反应区内预混气体的黏性系数，Pa·s；ρ0为反应前预混气体的密度，kg/m3；v为反应前预混气体的传播速度，m/s。对于在管道内传播的爆轰波，近些年相关学者[66-67，181-182]通过研究得出，爆轰波在管道内传播时，其化学反应区长度约为1.67 倍胞格尺寸，即x≈1.67λ，因此，采用此长度计算边界层位移厚度。对于化学反应区内预混气体黏度系数µe，其值等于CJ 平面温度下黏性系数并可通过相关物理化学手册获得。预混气体的密度ρ0为已知，而对于预混气体传播速度v，其值等于爆轰波在管道内传播的CJ 速度，即v=vCJ。在获得以上相关参数后，便可结合式（2）～（4）计算得到爆轰波在管道内传播时的速度亏损值。

通过与实验结果对比发现，Fay 模型[154]对于稳态气体具有较好的吻合性，而对于非稳态气体则与实验值差距较大，表明该模型并不能完全适用于所有可燃混合气体（见图32）。并且Fay 模型对于宏观尺度（～10 mm 量级）管道中的爆轰极限预测值与实验结果吻合较好，但对于微尺度管道，则实验值和预测结果之间的误差较大。这是由于Fay 模型采用的爆轰参数都是理论CJ（Chapman-Jouguet）值，但在微尺度管道中，爆轰波动量和能量的损耗导致模型中关键参量的实际值明显区别于理论CJ 值。如何建立可靠的爆轰极限预测模型是研究爆轰波传播规律的关键问题。只有综合考虑爆轰极限的关键影响因素及其相互耦合作用，确定多元混合燃料爆轰失效特征，建立适用于复杂工况下的爆轰极限等效表征参量，才能实现对爆轰极限的可靠预测，这也是目前研究的重点和难点问题。最近，Crane 等[183]把胞格尺寸分解为爆轰波结构中的诱导区和反应区长度，并提出λ=B(ΔI+ΔR)，其中B为常数，由拟合公式确定。在此基础上，Zhang 等[184]把Fay 模型中的爆轰波化学反应区长度x视为ZND 结构尺度的函数，即：

图32 爆轰极限Fay 模型与改进模型的对比Fig.32 Theoretical prediction models (Fay model and modified model)

式中：C为常数,α 为ΔI和ΔR之间的比例系数（α=ΔI/ΔR）。表1 中给出了CH4-2O2爆轰极限预测模型中的参数，表中气体热力学参数通过GASEQ[185]获得。

表1 CH4-2O2 爆轰极限预测模型中的参数Table 1 Parameters of prediction model for CH4-2O2

2.4 气相爆轰实验方法和数值模拟研究进展

在气相爆轰实验方面，爆轰的测试手段取得了长足的进步。自Oppenheim 等[18-19]、Urtiew 等[20]、Han 等[40]和Liberman 等[41]通过纹影技术清楚地观测到爆燃转爆轰的详细过程，纹影技术在爆轰波阵面结构的测试方面得到了广泛的应用。Lee 等[51]通过烟膜技术测试了爆轰胞格特征和胞格尺寸，建立了爆轰特征尺寸与诱导长度之间的定量关系。随着激光诱导荧光诊断技术在燃烧领域的广泛应用，近年来，Shepherd 等[6]、Pintgen 等[106,151]、Jackson 等[174]和Boeck 等[186]将这一技术应用于爆轰波阵面结构反应层中的关键自由OH 的分布特征研究，并结合纹影系统清楚地观测到了爆轰阵面激波-化学精细结构。然而，对于大分子燃料高度不稳定的爆轰阵面结构的化学精细结构以及更多组分结构的研究仍然缺乏，需要进一步发展宽光谱范围PLIF 测试技术。

在气相爆轰理论模型方面，CJ 理论和ZND 理论模型能够较好地预测爆轰速度和一维爆轰结构。然而，ZND 模型对于多维的爆轰胞格的复杂结构不适用。Lee[1]提出了气动力学厚度模型，认为能够将爆轰波阵面后流动中的任何非平衡效用的脉动都包含在这个厚度中。Radulescu 等[36-37,117-118,147]通过这一模型研究了高度不稳定爆轰的结构特征，并给出了爆轰平均结构概念，与稳态ZND 理论对比，发现平均爆轰厚度比稳态理论厚度大近100 倍。因此，他们认为对于这一类爆轰需要在爆轰结构中考虑湍流扩散效用。Han 等[187-114]通过数值模拟指出了忽略黏性扩散效用时，数值模拟对爆轰起爆的预测与实验相矛盾，并通过分析揭示了引起这一矛盾的根本原因。然而，针对爆轰气动力学厚度理论模型方面的研究仍然非常有限。这方面的研究将会产生丰硕的成果，也会对气相爆轰理论模型的研究起到重要的推动作用。

在爆轰数值计算方面，无论在计算数值格式、反应动力学模型还是简化反应模型等方面都取得了很大进步。大多数模拟的理论模型均忽略黏性扩散效用，采用Euler 方程描述爆轰传播动力学过程[188-189]时，通常认为爆轰阵面中的层流反应模型能够很好地预测反应层的点火过程。然而，当Radulescu 等[117]提出平均厚度概念后，发现胞格爆轰全局结构长度大大拉长，通常的层流燃烧假设不再适合预测爆轰速率，需要考虑黏性扩散效应。目前，发展适合描述高度不稳定爆轰阵面结构中小尺度湍流与反应相互作用的湍流燃烧模型，将是气相爆轰问题研究的新方向。

在气相爆轰数值算法方面，Einfeldt 等[190]、Linde 等[191]给出了低阶格式的保正性算法,但是低阶格式的收敛速度较慢,为得到较高的精度需要庞大的计算量。张涵信等[192-193]和沈孟育等[194]通过改善激波附近数值解行为的作用,构造了无波动、无自由参数的耗散差分格式，并在科学与工程领域得到了很好的应用。Zhang 等[195-196]提出了高阶RKDG 保正格式，得到了不破坏守恒性和稳定性并保持高精度的保正格式。Shen 等[197]发展了时空守恒型 CE/SE 算法、之后韦伟等[198]实现了CE/SE 算法在气相爆轰大规模数值模拟中的应用。总之，处理强间断数值震荡算法已经取得了长足的进步。然而，在气相爆轰大规模计算的加速算法方面仍然缺乏。发展高效、高保真的自适应网格细分方法和自适应简化反应加速算法成为目前气相爆轰大规模计算的研究方向。

3 结论与展望

对近年来气相爆轰起爆及传播领域的研究工作作了回顾和评述，结合作者近几年在这一领域的研究工作，着重回顾了爆轰起爆及传播数值模拟和理论预测等方面的研究进展。

总体来说，气相爆轰的研究在近些年取得了丰硕的成果，大量的研究都集中在爆轰微观结构方面，获得的爆轰阵面结构趋于精细化。然而，绝大部分理论都基于无黏欧拉方程和一步反应描述。这是由于大多研究问题都集中在小分子燃料，这对应于稳定或中度不稳定爆轰范畴，通常受黏性扩散效应的影响很小，而且爆轰结构很薄、反应速率非常快，基于简单反应的层流燃烧假设即可满足要求。

简化反应模型与详细机理预测诱导时间有量级上的差别，特别是一步反应很难体现压力对点火的影响，因此，很难精确预测爆轰结构自着火特征。特别是在模拟爆轰起爆问题时，起爆过程强烈依赖于反应机理。另外，对于一些燃料具有多阶段热释放特征，这些爆轰传播机理也需要详细化学模型来描述。因此，爆轰模拟需要从简单化学模型向复杂化学模型扩展，这也是气相爆轰研究发展的方向之一。

通常认为黏性扩散对具有规则结构的爆轰波影响很弱，然而在高度不稳定爆轰中，通常会在下游存在未反应气囊[161]，并且在燃烧产物和新鲜气体边界上的Richtmyer-Meshkov（R-M）和Kelvin-Helmholtz（K-H）不稳定性会产生小尺度漩涡，可以提高它们的燃烧速率[92]。对于高度不规则爆轰，下游未反应气囊的燃烧与扩散效应密切相关[161,168]。由于下游未反应气囊的存在导致爆轰全局结构长度大大拉长，通常的层流燃烧假设不再适用于预测爆轰速率，需要考虑黏性扩散效应，并且需要发展适合描述高度不稳定爆轰阵面结构中小尺度湍流与反应相互作用的湍流燃烧模型。

无黏理论模型不能正确预测高度不稳定爆轰的起爆以及未反应气囊的燃烧速率。对于需要考虑黏性扩散效应的高度不稳定爆轰，反应流NS 模型比欧拉模型预测更准确。另外，在具有高过驱爆轰传播时，黏性扩散的影响也需要考虑。当爆轰接近CJ 状态时，中度不稳定爆轰的NS 方程的结果与无黏预测结果几乎一致。然而，对脉动爆轰和胞格爆轰，尽管平均全局传播在CJ 状态，但存在明显的局部过驱效应和未反应气囊等特征，黏性扩散的影响需要考虑。特别是当反应流系统拓展到详细化学机理时，组分扩散效应对爆轰结构的影响更加重要。因此，研究高度不稳定爆轰问题时考虑黏性效应是爆轰领域研究的新方向。

实验方面，通过PLIF 激光诱导荧光技术结合纹影系统能够清楚地观测到爆轰阵面激波-化学精细结构。然而，目前大多数研究仅给出了OH 自由基的化学组分结构，对于大分子燃料高度不稳定的爆轰阵面结构的化学精细结构以及更多组分结构的研究仍然缺乏，需要进一步发展宽光谱范围的PLIF 测试技术。一些特殊的爆轰传播模式，即当爆轰近极限传播时，其传播模态维度需要降到最低以便能够自持传播，如螺旋模式等。然而，在一些特殊极限情况下，爆轰能够以极低的速度传播，却常常被认为是爆燃波而非爆轰传播。这种速度极低的爆轰的传播的可能性需要确认，其传播机理尚且不明确。

目前为止，爆轰波起爆和传播的研究都仅限于单组分燃料与氧气/空气混合气体，对于多元混合燃料研究较少。事实上，多元混合燃料在工业和军事上应用非常广泛，由于在多元混合燃料体系中，燃料种类的复杂性和各燃料热力学性能的差异较大，因此对气相混合燃料爆轰极限的动力学特性尚不完全清楚，针对燃料的不同物化属性，结合化学反应动力学，建立燃料混掺对爆轰起爆和传播特性的调节和激励技术，值得深入研究。