磁驱动平面准等熵加载装置、实验技术及应用研究新进展*

王桂吉，罗斌强，陈学秒，张旭平，种 涛，蔡进涛，谭福利，孙承纬

（中国工程物理研究院流体物理研究所，四川 绵阳 621999）

近20 年来，磁驱动准等熵压缩作为一种偏离Hugoniot 状态热力学路径加载实验技术，发展十分迅速，在材料动力学特性、武器物理、高能量密度物理、天体物理等学科领域应用广泛[1]。2012 年，孙承纬等[2]从磁驱动平面准等熵加载原理、数据处理方法、实验装置、磁驱动等熵压缩实验等方面全面综述了该技术自1998 年提出以来至2011 年10 多年间的研究进展，并就该技术的发展趋势作了分析和展望。

至当前，十年又过去了，该技术得到了进一步发展，应用更为广泛和深入。例如，加载装置方面，为更高效利用该技术研究高压、高温和高应变率等极端条件下材料的动态物理力学行为，国内外学者研制和建设了多台紧凑型大电流脉冲功率装置，如美国圣地亚国家实验室Thor[3]装置、中国工程物理研究院流体物理研究所的CQ-3[4]和CQ-7[5-6]装置；准等熵压缩实验数据处理方面，发展了特征线反演[7-9]、原位粒子速度处理的传递函数法[10]、磁驱动准等熵压缩实验的蒙特卡洛不确定评估技术[11]等方法，与之前发展的拉格朗日原位粒子速度近似法和反向积分法[12-14]等一起构成了准等熵压缩实验数据处理方法体系；磁驱动准等熵加载实验技术方面，发展了冲击-准等熵加载[15-16]、磁压剪联合加载[17-18]、小尺寸套筒柱面准等熵压缩[19]等新型实验技术，大大拓展了磁驱动准等熵加载技术的应用范围。利用相关装置和实验技术，国内外学者在极端条件下材料的高压状态方程[19-24]、强度与本构关系[10-11,25-27]、相变和相变动力学[28-32]等方面进行了深入研究。

为便于读者更好和全面了解磁驱动准等熵加载技术的研究进展和发展全貌，本文从加载装置、实验技术、数据处理方法和物理力学应用等方面就该技术近十年的研究新进展进行全面介绍，同时展望其发展趋势。

1 磁驱动平面准等熵加载装置

磁驱动平面准等熵加载的实验原理首先由美国圣地亚国家实验室的Asay 等[33]于1998 年在强脉冲功率装置Z 机器上实现，其原理是利用Z 装置产生的数MA 至20MA 大电流流经一对平行板条状铜或铝正负电极板，与其自身感应强磁场相互作用产生磁压力，作用于电极板内表面，实现对材料样品随时间光滑上升的准等熵加载。利用这种随时间光滑上升的磁压力，还可以实现宏观金属飞片的超高速发射。为更好发挥Z 装置的这种加载能力，将其应用于极端条件下材料的动力学行为研究，2002年始，圣地亚国家实验室结合磁驱动惯性约束聚变等科学目标牵引，对Z 装置进行了升级改造，改造后的Z 装置可产生百纳秒上升前沿、26 MA 幅值的脉冲大电流，可实现装置36 路的分时放电功能，有效调节其放电波形，电流上升前沿从100 ns～1 µs 可调[34-35]。基于Z 装置，在金属样品中，可以实现超过450 GPa 的平面准等熵加载[22]，超过1 TPa 的柱面准等熵压缩[19]。目前来讲，Z 装置是世界上加载能力最强的脉冲功率装置，但其规模也十分庞大，装置主体直径约33 m，运行和维护较为复杂。此后的数年，国内外学者研制和建设了系列加载压力数十至100 GPa 左右的紧凑型磁驱动准等熵加载装置，专门用于材料的磁驱动准等熵压缩和发射超高速飞片实验研究，例如：2003 年法国原子武器研究中心报道的GEPI 装置[36-37]、2007 年美国圣地亚和华盛顿州立大学建设的VELOCE 装置[38-39]和2010 年中国工程物理研究院流体物理研究所建设的CQ-4 装置[40]等，这些装置放电峰值电流为3～4 MA、上升前沿400～600 ns。

为实现100 GPa 至数百GPa 的更高加载压力、应用于危险物质动态力学性能研究等目标，近十年来，相关装置和技术仍然得到快速发展，主要的代表有中国工程物理研究院流体物理研究所的10 MA 大电流强脉冲功率装置[41-42]、CQ-3/7 装置[4-6,43]、美国圣地亚实验的Thor 装置[3,44]等。

2012 年，中国工程物理研究院流体物理研究所研制并建设了一套10 MA 大电流装置（如图1 所示），用于高能量密度物理、天体物理、材料动力学等方面科学研究[41-42]。该装置采用了“Marx 发生器+中间储能器+水介质形成线+水介质传输线+绝缘堆+真空磁绝缘传输线”的传统技术路线。10 MA大电流装置由24 个支路并联组成，包括Marx 发生器、水介质中间储能器、主同步开关、单同轴水介质脉冲形成线、输出开关、水介质传输线、绝缘堆、磁绝缘传输线等部件。24 个支路模块中每路Marx 发生器、水介质中间储能器、主同步开关、单同轴脉冲形成线部件具有独立结构，之后的所有水介质自击穿输出开关和三板传输线部件共用一个去离子水池，24 个支路模块通过绝缘堆和圆盘锥磁绝缘传输线并联汇聚后到传输至负载上。绝缘堆和圆盘锥磁绝缘传输线均为四层结构。

图1 10 MA 大电流装置三维效果图Fig.1 Three-dimentional effect of the 10 MA high current facility

10 MA 大电流装置直径约33 m，标称储能为7.2 MJ，具备同步放电和分时放电功能。同步放电模式下在负载中可获得峰值约8 MA、上升前沿约65 ns 的脉冲大电流，用于丝阵箍缩、动态黑腔辐射、小尺寸套筒内爆和高马赫数喷流等高能量密度物理和天体物理实验研究。利用电流波形调节技术，分时放电模式下在负载中可获得上升时间为300～700 ns、峰值为4～7 MA的中等脉宽大电流，主要用于极端条件下的材料动力学和发射超高速飞片的冲击动力学、高压物理等实验研究。利用该装置可以在中高阻抗样品上实现200 GPa 以上准等熵压力加载，发射宏观尺寸铝飞片速度可达20 km/s 以上的超高速度。图2 给出了10 MA 大电流装置的典型放电电流曲线。

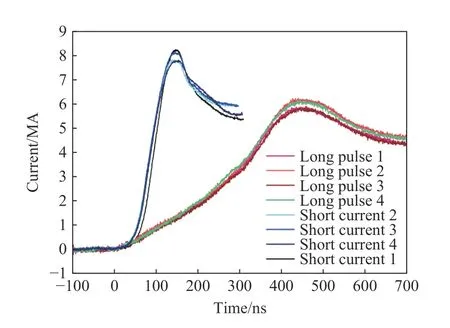
图2 10 MA 大电流装置的典型放电电流曲线Fig.2 Typical discharging current curves of 10 MA high current facility

紧凑型磁驱动准等熵加载装置方面，除实现更强的准等熵加载能力外，研制和建设这类装置的另一个目的是用于危险物质的动力学行为研究，因此在技术路线方面做了全新考虑。2012 年，中国工程物理研究院开始论证相关项目，于2015 年底研制和建设了一种电容器组储能、低阻抗电缆传输、低漏率防护靶室的紧凑型磁驱动准等熵加载装置CQ-3[4,43]，探索了此装置用于危险物质动力学行为研究的新途径及其可行性。2018 年研制建成了采用单极Marx 模块储能和电缆传输技术路线的CQ-7 装置[5-6]。与CQ-4装置不同，CQ-3 和CQ-7 采用了低阻抗高压电缆进行能量传输，传输线设计为同轴结构，特性阻抗不大于10 欧姆、可承受150 kV 高电压和200～300 kA 脉冲大电流。另外，CQ-7 在储能模式上做了新的设计，采用单级Marx 储能模块结构和双极性充电模式。

如图3 所示，为了实现CQ-3 靶室的高真空、低漏率设计要求，采用过渡转接方式，低漏率陶瓷转接电缆直接进入靶室，与靶室内的平行板电极连接。CQ-3 装置没有采用CQ-4 装置所采用的锐化电容器组和次级放电开关组进行放电波形调节，而是采用32 个电容器组-放电开关模块直接并联而成，32 个储能模块分为4 四组，由4 个高压脉冲发生器单独进行触发放电，通过分时放电功能进行放电波形的适当调节。由于CQ-3 装置属于技术探索型，因而装置的工作电压不大于85 kV，最大短路放电峰值电流约为3 MA、上升前沿400～800 ns 可调，图4 为其典型放电电流波形。

图3 CQ-3 装置Fig.3 CQ-3 device

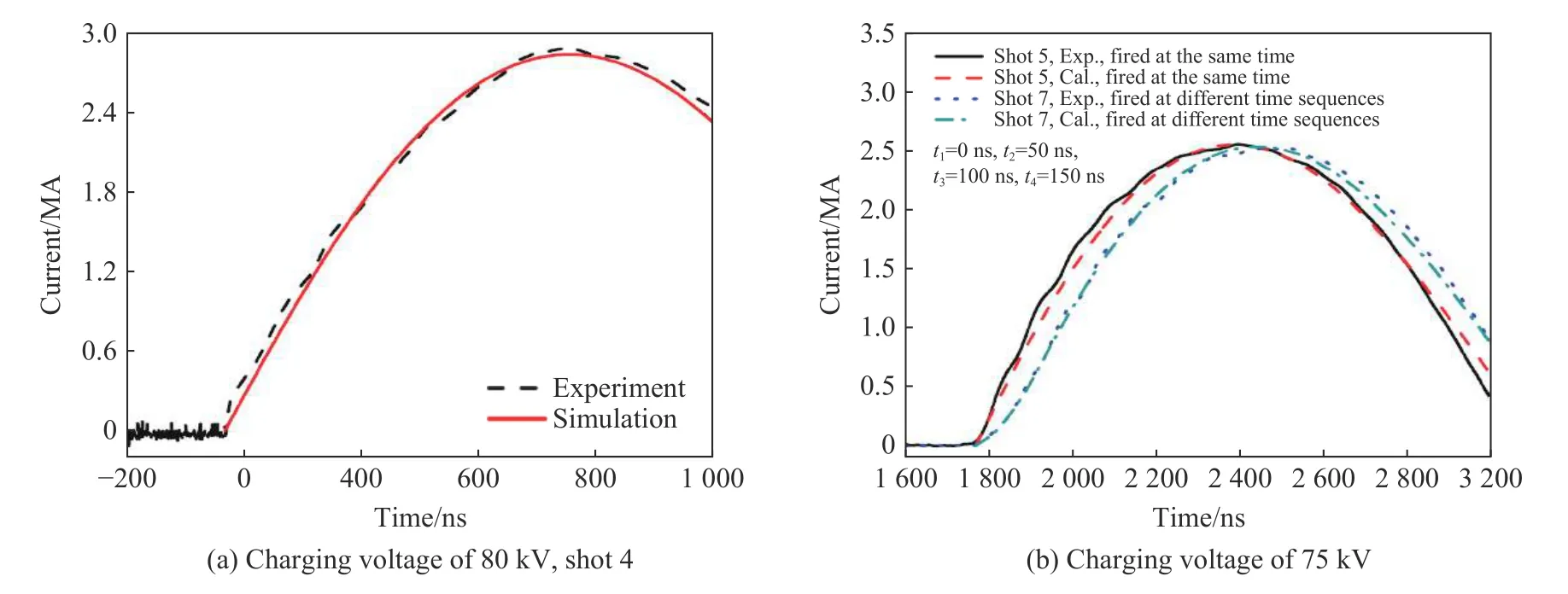
图4 CQ-3 装置直接短路时的典型放电电流曲线[3]Fig.4 Typical discharging current histories of CQ-3 in short circuits for programmed discharging[3]

CQ-7 装置的电参数设计指标为：短路峰值电流达到7 MA；上升时间为200～600 ns (10%～90%)之间可调；阻抗要满足物理应用开展平面准等熵压缩实验平板驱动电极低阻抗的特性要求。鉴于此，CQ-7装置采用了256 个双极性充电单级Marx 模块并联储能，256 根低阻抗高压同轴电缆并联进行能量传输，通过双层圆柱筒过渡转接成平板传输线至负载。装置放电开关通过16 路120 kV 高压脉冲触发器进行同时触发放电或分时放电。256 个单级Marx 储能模块每16 个分为一组，置于一个不锈钢油箱中，共计16 组；1 路高压脉冲触发16 个放电开关。图5 为CQ-7 装置的实物照片，图6 为其典型放电电流曲线。

图5 CQ-7 装置实物照片（左）和三维效果设计剖面图（右）Fig.5 Practical photo (left) and conceptual design (right) of CQ-7

图6 工作电压±50 kV 时CQ-7 装置的典型放电电流波形Fig.6 Typical current waveforms of CQ-7 at charging voltage of±50 kV for programmed discharging

2015 年，美国圣地亚国家实验室基于全电路阻抗匹配传输的设计理念提出了专门用于磁驱动等熵压缩材料动力学实验研究的紧凑型型脉冲功率装置Thor 的概念设计（如图7 所示）[3]。Thor 装置采用单极Marx（两个80 nF/100 kV 电容器和一只气体开关）作为储能模块，单模块参数为储能电容为40 nF、回路电感为240 nH、电阻为0.37 Ω、阻抗为3 Ω。每个模块连接3 根10 Ω 阻抗60 m 长的聚乙烯同轴电缆匹配传输，300 ns 电长度时间防止电压波反射，数百根电缆汇聚后直接驱动负载。根据储能模块个数不同，圣地亚国家实验室提出了Thor-96（96 个储能模块，每个模块3 根10 Ω 阻抗电缆）、Thor-144（144 个储能模块，每个模块两根5.42 Ω阻抗电缆）和Thor-288（288 个储能模块，每个模块一根3.55 Ω 阻抗电缆）三种建设方案，采用288 根电缆并联传输，电缆尺寸相同，不同之处在于拟通过改变电缆绝缘介质的介电系数来改变电缆阻抗。Thor-96、Thor-144、Thor-288 分别期望在1 cm 宽、2 cm 长的平行板条形负载上分别实现4.1、5.4 和6.9 MA 的强脉冲电流。目前基于普通聚乙烯电缆传输的Thor-96 已研制成功并应用于相关物理实验研究[44]。Thor 装置拟实现的另一个功能是通过波形调节技术，实现放电电流波形线性光滑上升和一定宽度平顶峰值特征，以保持样品准等熵加载后达到热力学平衡状态，如图8 所示。

图7 Thor 装置设计概念（左）及其Thor-96 模块装置（右）Fig.7 Conceptual design of Thor (left) and practical photo of Thor-96 (right)

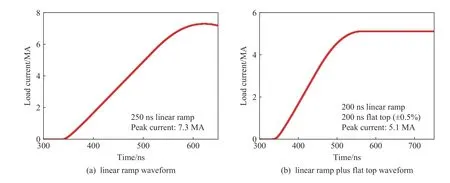
图8 Thor 装置可实现的放电电流波形Fig.8 Typical current waveforms achieved on Thor

表1 归纳了目前国际上用于材料动力学行为研究磁驱动准等熵压缩装置的技术参数、特点和应用范围等情况。

表1 磁驱动准等熵压缩装置及其技术参数一览表Table 1 Facilities of magnetically driven quasi-isentropic compression

2 磁驱动准等熵加载技术

自磁驱动准等熵加载技术提出以来，国内外学者基于各自的大电流脉冲功率装置，发展了多种用于材料动力学实验研究的加载技术，包括一维平面应变磁驱动准等熵压缩、磁驱动高速飞片一维平面应变冲击压缩、冲击-准等熵压缩、磁压剪联合加载以及小尺寸套筒准面内爆等。文献[2]就一维平面应变磁驱动准等熵压缩和磁驱动高速飞片一维平面应变冲击压缩技术的原理和加载特征进行了详细阐述。本文主要就近10 年发展起来的冲击-准等熵压缩、磁压剪联合加载、小尺寸套筒柱面内爆准等熵压缩等新实验技术进行介绍。

2.1 磁驱动冲击-准等熵加载

如图9 所示，静高压等温压缩线、冲击Hugoniot 线和等熵压缩线，只是覆盖了材料热力学相空间范围的一部分，要更全面和系统探索材料的物性，需要发展更多加载技术，以实现多热力学路径加载，在更宽广相空间范围内研究和探索物质的特性。结合磁驱动准等熵压缩和发射高速飞片的特点，国内外学者利用负载结构的巧妙设计，实现了磁驱动冲击-准等熵压缩的新热力学加载路径[15-16]，用于材料高温条件下的等熵压缩实验研究。

图10(a)是磁驱动冲击-准等熵压缩的原理示意图，电极基板在驱动电流作用下，以一定速度飞行一小间隙距离（通常小于1 mm）撞击靶样品，此时电极基板未发生断裂，后续电流持续准等熵加载作用于基板和样品，在样品中实现冲击-准等熵加载热力学路径。通过控制装置加载电流大小、电极基板飞行距离等参数，在样品中实现不同冲击和准等熵压力幅值的冲击-准等熵压缩，图10(b)给出了不同厚度Sn 样品冲击-准等熵加载条件下的样品/窗口界面粒子速度剖面[39]。

正如图9 所示，利用磁驱动冲击-准等熵加载技术，可以开展不同初始冲击Hugoniot 状态下材料的准等熵压缩特性研究，例如介于冲击绝热线和主等熵压缩线相空间范围内的材料固固多形相变及其动力学行为，位于材料熔化曲线及其以上范围内材料的液液相变、液固凝固相变及其动力学特性等，这些研究对深入认识极端条件下物质的特性具有重要科学意义。

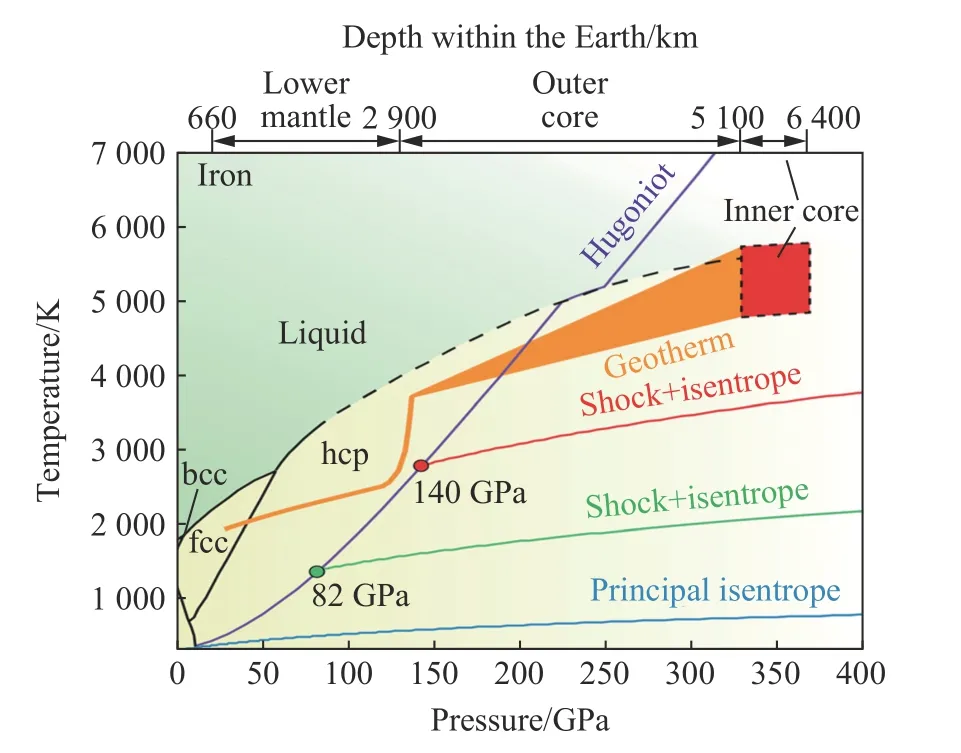
图9 铁的热力学相图[37]Fig.9 Thermodynamic phase diagram of Iron[37]

2.2 磁驱动压剪联合加载

动态载荷下材料的高压强度测量多采用双屈服面方法[10,45-46]或静水压比较法[47]，而磁驱动压-剪联合加载技术[17-18]为准等熵压缩下材料的高压强度研究开辟了新途径。该方法物理概念清晰、数据处理简单，在材料的动高压强度测量方面展示出很大的应用前景。磁驱动压-剪联合加载实验负载区的结构见图11。脉冲大电流J流过条形金属板回路时，在载流电极板之间的空腔中生成脉冲强磁场B。在负载区域再施加垂直于电极板表面的外部稳恒强磁场B0，载流导体将在相互垂直的磁场中承受轴向和切向的电磁力。轴向应力和切向应力同时从载流面位置向电极内部传播，两者具有相近的应力剖面。

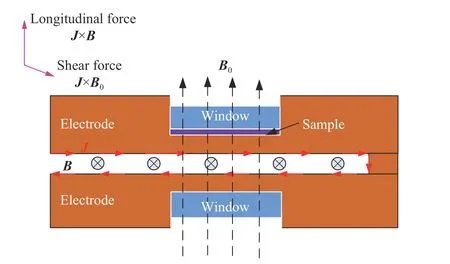
图11 磁驱动斜波压-剪联合加载示意Fig.11 Schematic of magnetically driven ramp wave pressure-shear loadings

在一维轴向应变（压缩）和一维切向应变（剪切）联合加载的情况下，材料的屈服强度Y可表示为纵向和横向两个偏应力Sxx和Sxy的函数，即

对磁驱动压-剪联合加载实验而言，剪切应力Sxy的加入将调整屈服面上的应力状态。当剪切应力Sxy增大到时，Sxx将减小到零，此时，轴向应力处于静水压状态。通过测量此状态下材料的剪切应力Sxy，即可获得σxx压力下材料的屈服强度。具体实验中一般通过测量高强度窗口的自由面横向速度来反推样品传入窗口的最大切应力。

磁驱动压剪联合加载测量技术提供了一种直接测量材料高压强度的方法，与双屈服面、静水压比较等方法不同，它不依赖于物理模型获取材料强度数据；与现有的基于飞片斜撞击压剪技术（压剪炮）相比，磁压剪联合加载类似于一种非接触加载，有效避免了较高速度下飞片发生更大角度倾斜的问题，为数十甚至百吉帕高压力下材料强度直接测量提供了可能。

2.3 磁驱动小尺寸套筒柱面准等熵压缩

磁驱动装置靶区由平面结构改为柱面结构时，流经套筒表面的大电流与其感生的强磁场相互作用并在套筒表面产生强大的洛伦兹力驱动套筒向轴心内聚运动，是一种增加加载压力的有效方式。磁驱动套筒柱面加载的原理如图12 所示，柱面等熵压缩的磁压力与加载电流关系如下：

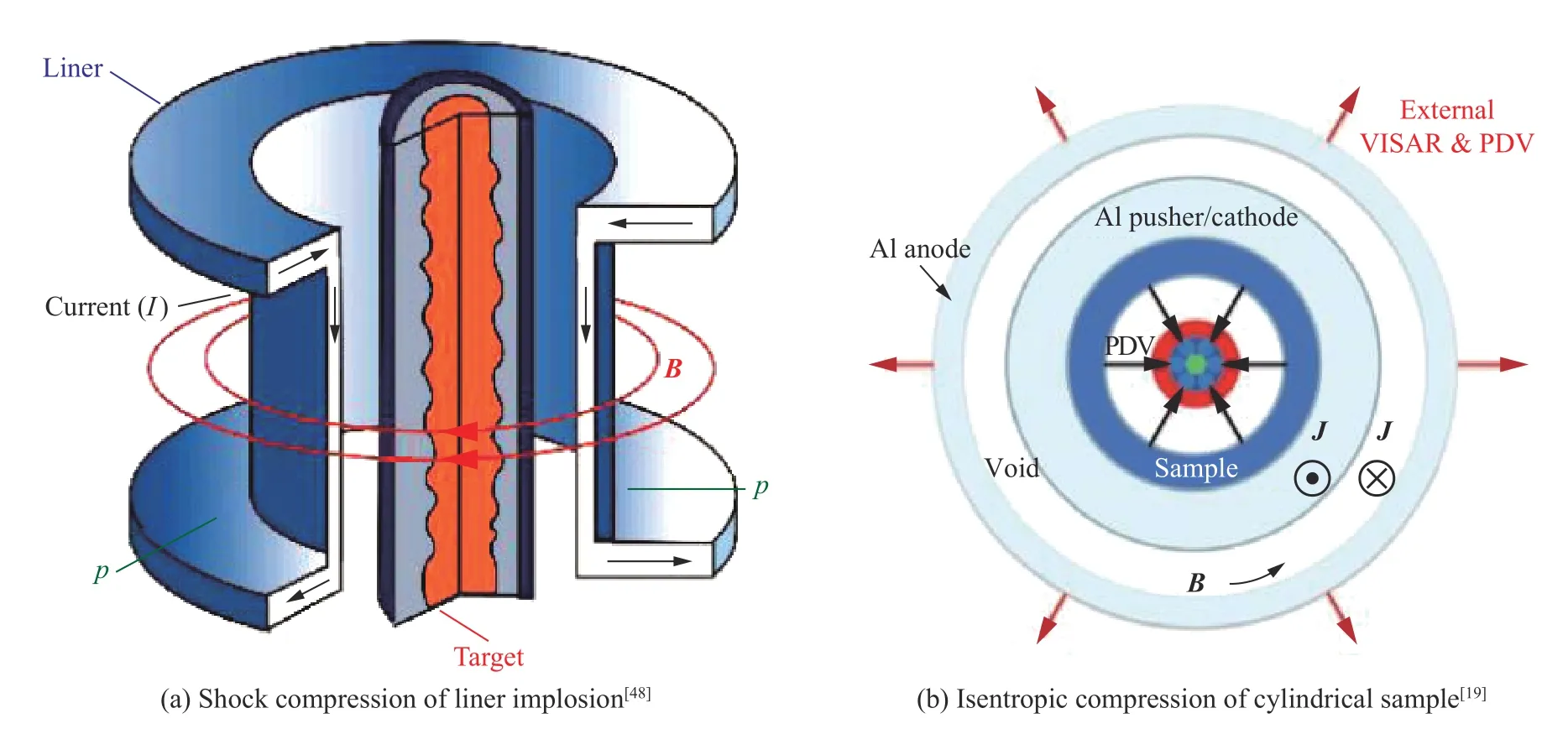
图12 磁驱动柱面套筒内爆加载示意图Fig.12 Schematic of magnetically driven liner implosion loading

式中：p为压力，µ0为真空磁导率，I为放电电流，R为套筒外半径。由于加载磁压力和放电电流的平方成正比，与套筒半径的平方成反比因此，因此相同电流条件下可在小尺寸套筒上可实现更高的加载压力和更高的内爆速度。

利用磁驱动小尺寸套筒对样品材料进行柱面等熵压缩时，由于电磁力加载下套筒的收缩将导致加载线电流密度增大从而提升加载压力，同时应力波的轴心汇聚传播使得加载压力进一步增强。但由于小尺寸、小面径比的套筒受更大的电流密度加载，容易造成套筒焦耳热烧蚀，加载面因焦耳热沉积导致材料强度的丧失和状态的变化，此时磁压力的加载易导致磁瑞利-泰勒（magneto Rayleigh-Taylor,MRT）流体不稳定的发生，影响套筒稳定性和加载效率。另外，短的加载上升沿在套筒内部易形成冲击波，导致套筒内部材料的冲击加热和熔化，加剧MRT 不稳定性对套筒内壁完整性的破坏。因此，实验时需采用合适的电流波形驱动套筒来避免冲击波形成，保持套筒大部分材料仍处于固体状态有利于抑制MRT 不稳定性的发展。

柱面准等熵加载由于非一维结构、加载压力波多次反射作用等特点，其实验测试、数据处理方法与平面准等熵实验有很大不同。目前可行的有2 种实验方法：第一种方法是测量准等熵压缩数据点，采用多幅单色X 射线背光照相测量准等熵压缩的样品靶，获得靶准等熵压缩后的X 射线图像，通过特定发展的反演数据处理方法导出压缩过程中材料的密度和压力，获得压缩材料的准等熵压缩数据点。采用背光照相方法除实验条件要求高外，因X 射线能量问题，应用于原子序数较大的材料非常受限；第二种方法是基于PDV (photonic Doppler velocimetry)测速技术状态方程测量方法获得准等熵压缩线（如图12(b)所示），通过测量实验加载电流，获得实验加载条件，采用PDV 测速获得实验套筒内爆速度，借助磁流体数值模拟计算，利用正反迭代数据处理方法获得材料的准等熵压缩线[19]。

3 磁驱动准等熵压缩实验数据处理方法

磁驱动准等熵压缩实验的实验数据为不同厚度样品（不同Lagrange 位置）的自由面或样品/窗口界面粒子速度，通过特殊的数据处理方法，可由速度曲线解读出材料的状态方程、高压强度、相变动力学和多相物态方程等信息。这些数据处理方法（程序）包括正向Lagrange 方法、反向积分方法[12-13]、反向特征线方法[7-9]、以及正向-反向迭代计算方法[20,28]等。文献[2]对正向Lagrange 方法和反向积分方法已做阐述，在此只对近些年新发展的数据处理方法作简要介绍。

3.1 传递函数方法

正向Lagrange 方法处理斜波压缩实验数据时，难点在于如何准确还原不同厚度样品的原位粒子速度。以自由面速度的一半作为样品中原位粒子速度时，Lagrange 方法处理得到的材料高压声速和等熵线的结果与实际值存在较大的差异。采用增量阻抗匹配[46]的方式对实验测量的样品/窗口界面速度进行还原时，难以考虑样品/窗口界面反射稀疏波对加载稀疏波的影响。2013 年，Brown 等[10]提出了传递函数方法（transfer function method,TFM）用以反演计算斜波压缩下台阶样品中的原位粒子速度。传递函数方法的数学思想为：假定数值计算可以准确的表征界面反射波与后续加载波的相互作用，采用数值计算给出界面速度和原位速度之间的映射关系，将该映射关系对实验测量的速度剖面进行反演，即可获得实验对应的原位速度。该方法自2013 年提出以来，在Sandia 实验室迅速获得广泛应用[10-11,20,25]。和自由面近似以及增量阻抗匹配方法相比，传递函数方法可以考虑界面反射波与后续加载波的相互作用，准确的将非简单波情形还原为简单波情形，尤其适合卸载波原位速度的计算。

传递函数方法的数据处理流程为：首先，采用数值计算获得样品/窗口界面的粒子速度剖面uwc(t)和相同位置的原位速度剖面uic(t)，要求计算的uwc(t) 尽可能地和实验测量的样品/窗口界面速度剖面uwe(t)一致；然后，寻找uwc(t)和uic(t)之间的传递函数f(t)，具体操作时可先将uwc(t)和uic(t)变换到频率域，给出Uwc(ω)和Uic(ω)，计算Uwc(ω)和Uic(ω)之间的关联函数F(ω)=Uic(ω)/Uwc(ω),再将F(ω)转换到时间域，即为uwc(t)和uic(t)之间的传递函数f(t)；最后，利用传递函数f(t)对实验测量的样品/窗口界面的粒子速度剖面uwe(t)做卷积，给出实验对应的原位粒子速度剖面uie(t)：

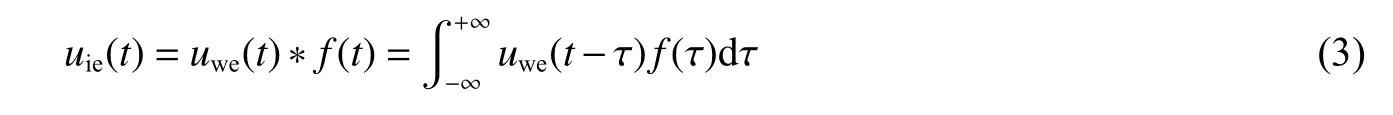
计算过程中可先计算频率域的实验原位速度以避开卷积的计算，再将Uie(ω)做傅里叶逆变换还原为实验对应的原位粒子速度剖面uie(t)。图13 给出了采用数值实验方法对传递函数方法进行考核的结果，传递函数方法可根据样品后界面加载-卸载速度波形反演出准确的原位粒子速度波形。

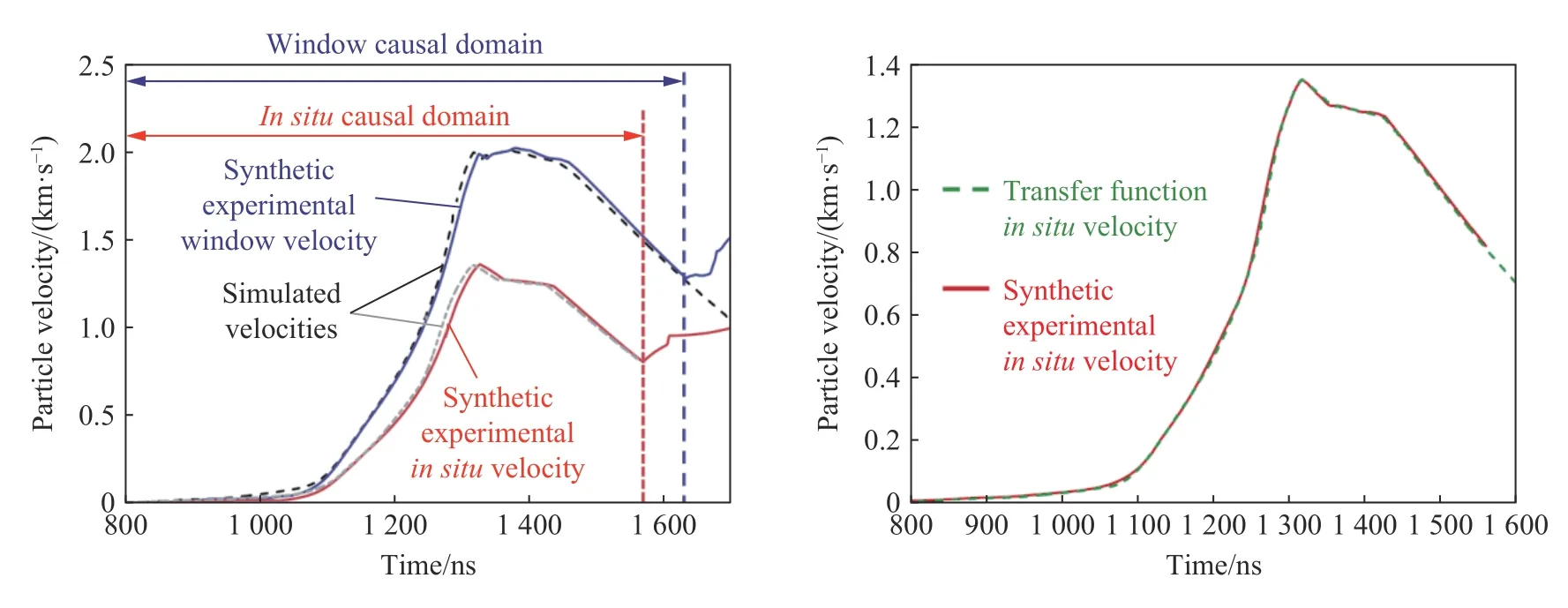
图13 传递函数方法的可靠性考核Fig.13 Reliability check of transfer function method for in-situ particle velocity

3.2 反向特征线方法

反向特征线方法主要通过分析样品内部入射波和后界面反射波的相互作用规律，沿特征线反演得到靠近加载面位置未受干扰的特征线上的信息，进而沿右行特征线得到样品内任意拉氏位置处的原位粒子速度，具有精度高、计算量小等特点。反向特征线方法处理准等熵压缩实验数据的流程为：首先对测量样品后界面速度和压力信息进行时间离散，假定材料声速，并根据特征线方程确定其左侧相邻点的位置和状态，以此逐级递推直至左行特征线到达加载面。由于不同厚度样品具有相同的加载压力边界，以此可作为约束条件对声速进行迭代优化，直至不同厚度样品的反向计算获得相同的加载边界，从而确定材料的声速。另一方面，由于第一条左行特征线的下方区域均为简单波区，因此也可由第一条左行特征线上的信息沿右行特征线推出材料任意拉氏位置处的原位粒子速度和应力等信息，再由式cL(u)=Δh/Δt(u)获得材料的声速曲线并将其代入下一轮的特征线计算，经过多次迭代计算直至声速曲线收敛并满足误差限后，可得到准等熵压缩下材料的声速曲线，进行积分可获得材料在准等熵压缩下压力-比容曲线。

在特征线方法的反向计算中，如果输入的速度曲线为台阶样品自由面速度，对速度曲线进行等增量离散可使声速的计算变得特别简单，且能保持足够的精度（如图14 所示）[49]。在此条件下，内部格点的原位粒子速度和应力状态的计算可简化为

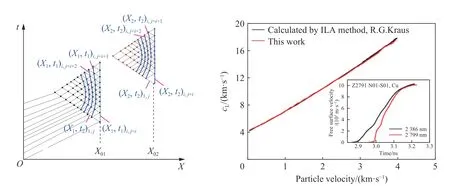
图14 基于特征线反演方法的声速直接计算原理和结果[49]Fig.14 The calculation principle and results of sound speed by inverse characteristics method[49]

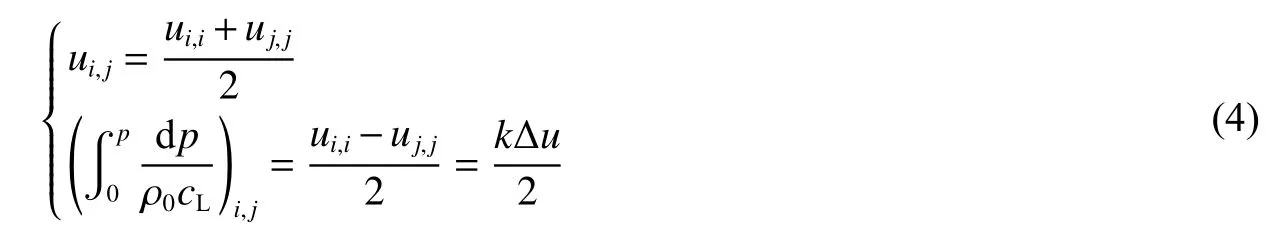
式中：ui,j为格点速度，Δu为速度离散的单位变化量，k为整数。从自由面位置向样品内部逐步推进，声速可直接从第一条左行特征线的(X,t)坐标计算给出。

3.3 反向-正向迭代计算方法

采用反向-正向迭代计算方法处理实验数据，可以较好地避免反积分和反向特征线方法因初猜值偏差过大造成的迭代不收敛或是多值收敛的问题，获得具有较高精度的实验数据，但具体的数据处理流程较为复杂。反向-正向迭代计算方法处理实验数据时，磁驱动加载实验一般设计为单样品加载。Knudson[50]和Davis 等[20]提出的单样品数据处理流程（如图15 所示）：(1) 同步测量电极板自由面速度和样品后界面速；(2) 根据实验测量的电极自由面速度，采用返积分方法计算电极加载界面压力历史并优化一维磁流体程序计算的A-K 间隙磁感应强度B；(3) 初猜样品声速和压力-比容关系，利用步骤(2)获得的加载边界计算电极/样品界面速度u*；(4) 利用计算的电极/样品界面速度和测量的样品后界面速度，利用迭代Lagrange 方法计算材料声速和压力-比容关系；(5) 利用计算获得的材料的声速和压力-比容关系，重新计算电极/样品界面速度u*；(6) 重复步骤(4)和(5)直至计算的材料响应收敛。采用类似的方法，种涛等[28]开展了磁驱动准等熵压缩下材料的相变过程研究。

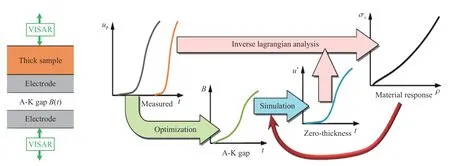
图15 正向-反向迭代计算流程图Fig.15 Flow chart of forward-backward iterative calculation

3.4 磁驱动准等熵压缩实验不确定度分析

磁驱动准等熵压缩实验结果的不确定度评估是开展精密物理实验的基础。罗斌强等[51]系统分析了影响磁驱动平面准等熵压缩实验结果的物理因素：基于Lagrange 数据处理方法分析了实验误差传递途径，获得了准等熵压缩下实验测量的材料高压声速和准等熵压缩线的相对误差评估公式；以反向积分方法为基础，采用数值实验的方法评估了基于反积分数据处理的实验结果不确定度，反向积分计算和正向Lagrange 分析的结果一致；分析得到磁驱动斜波压缩实验的声速标准相对不确定度小于1.5%（k=1，k为包含因子），应力不确定度小于2.5%（k=1）（图16），这表明磁驱动平面斜波压缩是一种可靠的精密物理实验技术。Brown 等[11]采用蒙特卡洛方法分析了磁驱动压缩下材料高压强度测量实验的不确定度，结果表明实验压力的不确定度为5%（k=2），材料高压强度的不确定度为9%～17%（k=2）。Brown 等[52]还发展了基于贝叶斯模型校正的动态实验材料物性参数的误差分析方法并运用于Z 装置上钽材料的等熵压缩实验，给出加载压力的实验不确定度约为5%（k=2）。

图16 磁驱动准等熵压缩实验测量LY12 铝的声速与应力应变曲线结果[51]Fig.16 Experimental results of LY12 under magnetically-driven quasi-isentropic compression[51]

4 磁驱动准等熵加载实验技术的物理力学应用

4.1 高压状态方程

磁驱动准等熵加载实验技术的发展，提供了一条有别于静高压等温压缩和冲击绝热压缩的新的加载途径，为材料高压状态方程的研究提供了新的手段。由于磁驱动准等熵压缩过程中材料温升较小，材料的压缩状态十分接近等熵压缩，因此高精度的磁驱动准等熵加载实验为特别适合于开展材料高压状态方程的模型验证和参数校核。自1999 年以来，Sandia 实验室在Z 装置上的一项重要工作就是开展材料准等熵压缩下的状态方程研究，目前在Z 装置上已将铝准等熵压缩至240 GPa[53]、铜压缩至450 GPa[22]、钽压缩至近400 GPa[20]，均超过了材料的冲击熔化线，获得了物质的高压缩度状态特性，为材料的状态方程数据库校核提供了重要参考。值得一提的是，2016 年Sandia 实验室在对LiF 的状态方程进行校核时发现，准等熵压缩实验结果和理论模型预测在高压下存在较大的差异（如图17 所示）[54]，通过对其理论模型的改进，新的计算结果和实验吻合很好，这充分验证了准等熵压缩实验作为精密物理实验在高压状态方程模型验证与校核方面的重要价值。Seagle 等[15]利用磁驱动冲击-斜波压缩复杂路径加载技术开展了LiF 状态方程的校核研究（见图18），获得了有价值的认识。

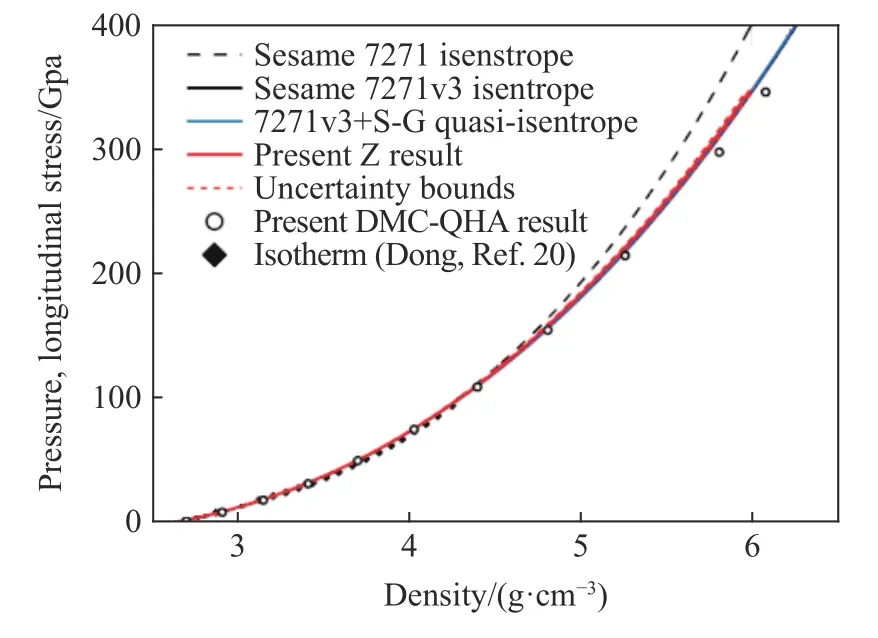
图17 准等熵压缩下LiF 的等熵压缩线[54]Fig.17 Isentrope of LiF under quai-isentropic compression[54]

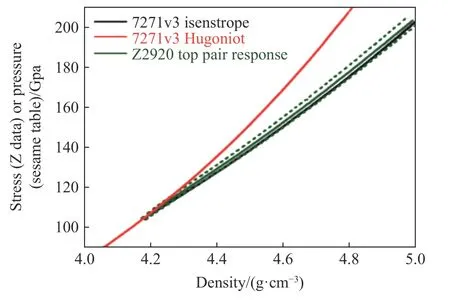
图18 准等熵压缩下LiF 状态方程的校核[15]Fig.18 Check of equation of state of LiF under quasi-isentropic compression[15]

国内由于装置的加载能力有限，因而更多的精力集中在发展实验技术和理论研究方面。莫建军等[55]以冲击Hugoniot 线为参考，推导了基于Grüneisen 物态方程形式的等熵压缩线方程，计算了以Hugoniot关系为基础的基于Appy 经验物态方程导出的等熵压缩线。Luo 等[56]以钽的实验等熵线和冲击Hugoniot 为基础，分析了Grüneisen 状态方程、Vinet 状态方程、Brich 状态方程、PUFF 状态方程和Tillotson 状态方程在等熵压缩状态下的适用性（如图19 所示）。孙承纬等[57]提出，准等熵压缩下实验测量的准等熵线实质为纵向应力线，扣除材料强度后才是准等熵压力，再扣除塑性耗散和黏性耗散等引起的不可逆热效应，剩下的才是纯粹的等熵压力。基于此思想，提出了“准”等熵、表观等熵和“净”等熵的概念，并指出把直接测量获得的准等熵线（即纵向应力线），配套以符合热力学第二定律的比内能线，发展为自洽、并有较高精度的基于Grüneisen 型物态方程的参考线。

图19 不同形式状态方程计算得到的等熵线与实验结果的比较[56]Fig.19 Comparison between calculated and experimental isentropes based on different equation of states[56]

4.2 材料的高压强度

准等熵压缩下材料内部的温度变化较小，因此准等熵压缩与冲击压缩实验配合有望对动高压加载下影响材料高压强度的温度效应和应变率效应作出关键性鉴别，从而提升动高压加载下材料剪切强度控制机理的认识，为材料高压本构方程模型修正和参数校核提供参考。Asay 等[45,58]和Vogler 等[46-47]将冲击实验中的双屈服面方法成功拓展至准等熵压缩情形，获得了令人耳目一新的结果。Asay 等[45]在实验研究中发现，在冲击压力超过40 GPa 时，采用气炮和磁驱动加载测得铝的高压强度已经具有明显的差异，并以此为基础开展了铝材料本构模型和参数的修正与校核。2013 年Brown 等[10]提出利用传递函数法来计算准等熵加载-卸载过程样品的原位粒子速度，从而大大提高了磁驱动强度实验中材料卸载声速和高压强度的实验精度，在Z 装置上获得了准等熵压缩下钽在250 GPa[11]、铍在110 GPa[25]压力下的强度数据，并以此为基础开展了SG、SGL、PTW 等多种本构方程的参数修正（图20，图21）。中国学者利用CQ-4 和10 MA 强流脉冲功率装置，实验研究了数十GPa 至近200 GPa 压力范围内LY12 铝[59]、无氧铜[60]和纯钽[61]等多种材料在磁驱动准等熵压缩下的高压强度。基于双屈服面方法，结合反积分方法和传递函数方法，建立了磁驱动准等熵压缩下材料强度测量的实验技术，开展了SG 本构模型的参数校核。

图20 准等熵压缩下钽的高压强度[11]Fig.20 High pressure strength of Tantalum under quasi-isentropic compression[11]

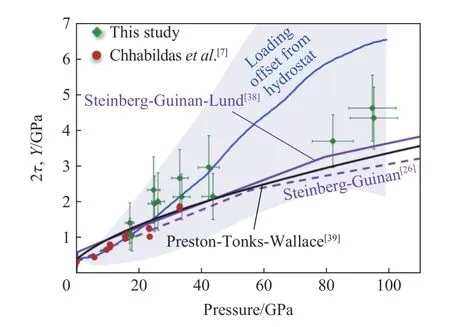
图21 准等熵压缩下铍的高压强度[25]Fig.21 High pressure strength of Beryllium under quasi-isentropic compression[25]

由于磁驱动准等熵压缩单次实验可获得一条从低压到高压的应力应变曲线，因此可利用静水压比较法获得加载过程中材料屈服强度的变化。Vogler 等[47]拓展了静水压比较法在等熵压缩实验中的应用，并考虑了塑性温升对材料强度计算的影响。罗斌强等[27]建议利用等温压缩线计算等熵线，因塑性耗散引起的热压力修正可表示为屈服强度的显式函数，和待求强度值一同求解。利用静水压比较法，Vogler 等[47]和罗斌强等[27]分别计算了准等熵压缩过程中6061-T6 铝（图22）和bcc 相铁的屈服强度（图23）。显然，利用静水压比较法可获得加载过程中材料的流动应力随加载压力的连续变化曲线，这一优点是双屈服面方法所不能比拟的，但该方法的不足是对实验准等熵线和理论等熵线的精度有较高的要求。

图22 静水压比较法计算铝的强度[47]Fig.22 Strength of Aluminum calculated by hydro-static pressure comparison[47]

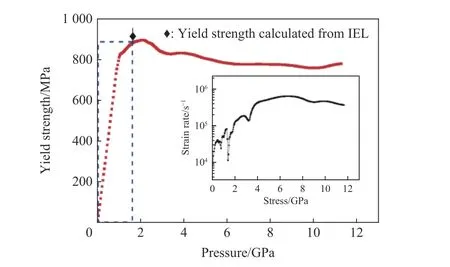
图23 静水压比较法计算纯铁的强度[27]Fig.23 Strength of Iron calculated by hydro-static pressure comparison[27]

4.3 未反应炸药的状态方程

爆轰过程的计算模型中，未反应固体炸药的完全物态方程对高压和高温下未反应固体炸药的压力、温度等热力学状态参量的描述精度，直接关系到炸药化学反应率模型和炸药产物状态方程的计算精度。作为典型的多组分非均质颗粒材料，未反应固体炸药的完全物态方程构建依赖于宽压力区间内炸药的动力学实验数据。利用磁驱动准等熵压缩下材料温升较小的特点开展固体炸药的动力学行为研究，可以大大拓宽未反应炸药的加载压力，获得宽压力范围内未反应炸药的状态方程参数。自Sandia实验室在Z 装置上建立磁驱动准等熵压缩加载实验技术以来，LLNL 实验室和SNL 实验室就有组织地对其武器用炸药进行了准等熵压缩实验研究[62-66]，将未反应固体炸药的加载压力拓展到20 GPa 以上，并在HMX 单晶中实现了50 GPa 的等熵加载压力[67]，改善了未反应固体炸药高压段实验数据缺乏的情况并补充了炸药响应数据库，使人们对未反应炸药的状态方程有了更直观的认识，实现了炸药的完全物态方程模型校核，为爆轰模拟计算提供了基础的物性参数。国内蔡进涛等[68-71]和种涛等[72]在CQ-4装置上开展了JO-9159、JOB-9003、JB-9014 等多种炸药及其组份的准等熵压缩实验研究，将未反应固体炸药的加载压力拓展到了近20 GPa 的压力范围（图24），获得了宽压力范围内多种未反应固体混合炸药的状态方程，并校核了一种率相关的粘弹性本构关系模型，较好地模拟了实验结果，扩展了未反应炸药粘弹性本构关系研究思路。利用准等熵加载波剖面光滑平缓、能有效展示波传播细节的优势，蔡进涛等[69-70]研究了多种炸药单晶例如RDX、CL-20 和粘接剂的相变动力学和黏弹塑性动力学问题，获得了一些新认识。

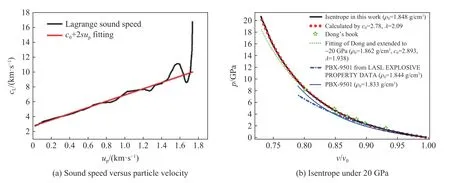
图24 准等熵压缩下PBX-59 样品的声速-粒子速度曲线和20GPa 内的准等熵压缩线[72]Fig.24 Sound velocity-particle velocity curvers PBX 59 explosive under quasi-isentropic compression and quasi-isentropic compression curves [72]

4.4 金属材料的相变

动高压下材料的相变具有典型的非平衡效应。相比于冲击压缩，磁驱动准等熵压缩的加载波阵面时间尺度展宽至数百纳秒，使得材料内部的相变演化有充足的时间达到亚稳态，非常适合于分析加载率对相变过程的影响。另一方面，磁驱动加载的单发实验多样品靶结构以及良好的加载一致性也有利于分析微细观结构对相变过程的影响。国外Z 装置上公开报道的关于材料相变的研究并不多，Asay 等[33]、Bastea 等[73]、Smith 等[74]利用磁驱动准等熵加载研究了铁α→ε 相变过程的加载率效应（图25[74]），Rigg 等[75]利用磁驱动准等熵加载研究了杂质含量对锆α→ω 相变过程的影响。国内种涛等[28-31,76]利用CQ-4 装置，通过调整加载应力波形上升沿和样品材料初始温度的方法，开展了纯铁、钛、锡、铋、锆等多种材料的相变过程研究：理论上，联合以Helmholtz 自由能为基础的多相状态方程和以Gibbs 自由能为基础的相变速率方程，开展了磁驱动斜波加载下金属材料相变过程的数值模拟研究；通过计算速度波形和实验测量的相变速度波形的比较，确定了斜波压缩下铁的相变驰豫时间在30 ns 左右，同时验证了不同的波阻抗边界对材料的相变过程具有明显的影响（图26）。

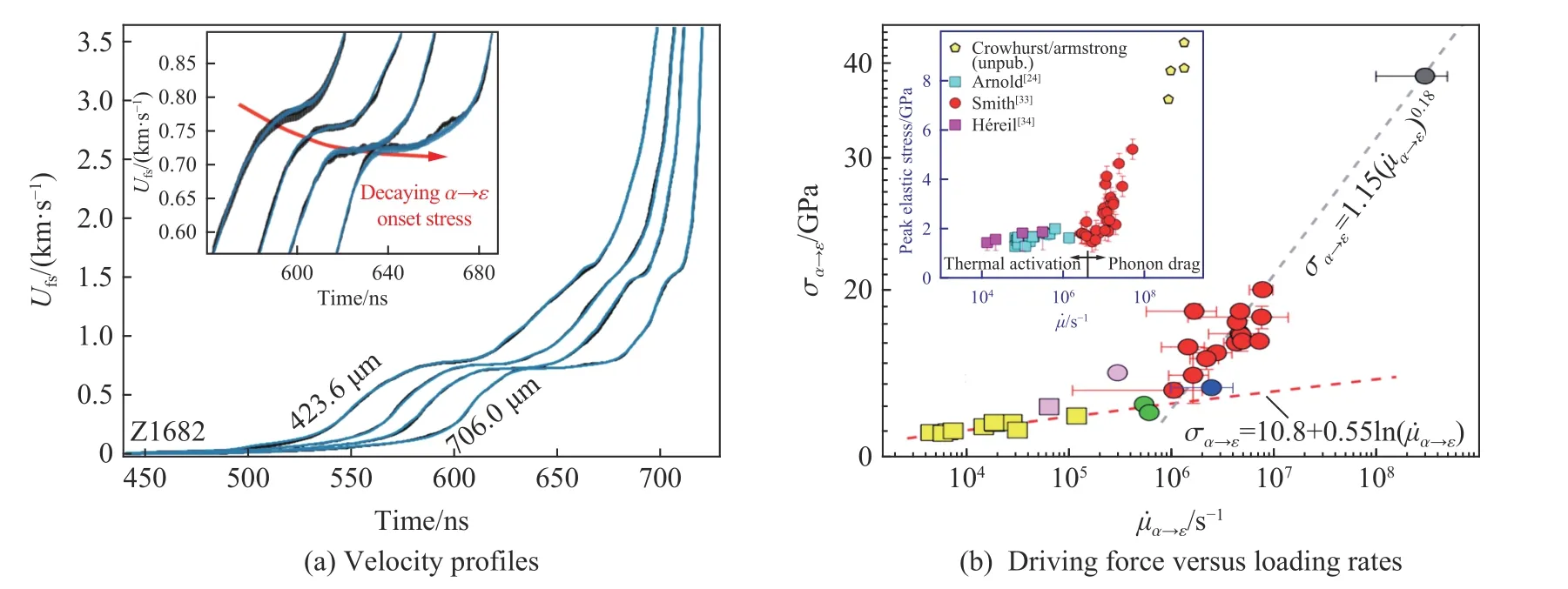
图25 准等熵压缩下铁的相变速度剖面和相变驱动力与加载率关系[74]Fig.25 Phase transition of iron under quasi-isentropic compression[74]

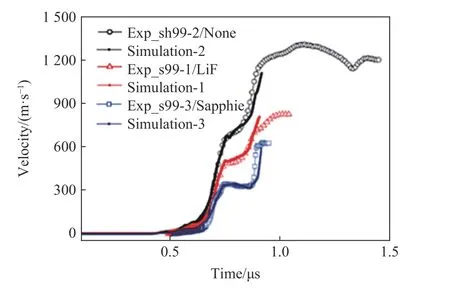
图26 不同窗口阻抗时铁的相变波形演化[28]Fig.26 Evolution of phase transition wave profiles of iron with different window impedance[28]

4.5 材料的冲击压缩

磁驱动加速飞片的优点是飞片加速时间短、运动距离小、飞片速度高且姿态可控。Sandia 实验室在Z 装置上利用磁驱动加载技术将25 mm×13 mm×1.0 mm 的铝飞片在数百纳秒、几毫米的距离内加速至45 km/s[77]，远超目前三级轻气炮的水平；并以此为基础开展了铍、铜[78]、石英[23,79]、水[80]、金刚石[81]等多种材料在300～2 000 GPa 冲击压缩下主Hugoniot 线与卸载线的测量，发现了材料在极端高压和高温条件下的诸多新物理性质，特别是Knudson 等[82]采用磁驱动冲击-斜波加载技术开展液氘的高压物性研究，在动高压加载下首次获得了液氘绝缘体-金属转变的反射率变化（图27）。国内利用磁流体动力学数值模拟的优化设计技术，在CQ 系列和10 MA 大电流装置上建立了磁驱动高飞片冲击压缩实验技术，实现了20 km/s 超高速度宏观尺寸金属飞片的发射；开展材料的冲击压缩实验研究，实验精度与传统轻气炮冲击压缩实验相当；利用磁驱动高速飞片冲击压缩实验技术，开展了无氧铜[83]、NiTi 合金[84]、聚苯乙烯[85]等多种材料的冲击Hugoniot 状态方程、层裂强度测量、塑性变形微结构演化和光学折射率、导电率等动力学和光学行为研究，例如：深入研究并获得了高应变率冲击压缩下近等原子比Ni52Ti48合金的初始屈服强度、50 GPa 压力范围状态方程等实验数据，在加载范围内未发现Ni52Ti48合金存在A-M 相变，为澄清其应力诱导相变学术争议提供了直接证据，校核的Johnson-Cook 本构模型参数能有效描述冲击和准等熵加载下NiTi 合金的动力学响应行为[84]。研究了应变率106s−1量级下聚苯乙烯初始屈服强度和其离解起始压力附近折射率的变化规律，建立了基于Helmholtz自由能模型聚苯乙烯的三项式完全物态方程，获得温度是聚苯乙烯的有效极化率、禁带宽度及驱动聚苯乙烯离解相变的主导因素等新认识[85-86]。

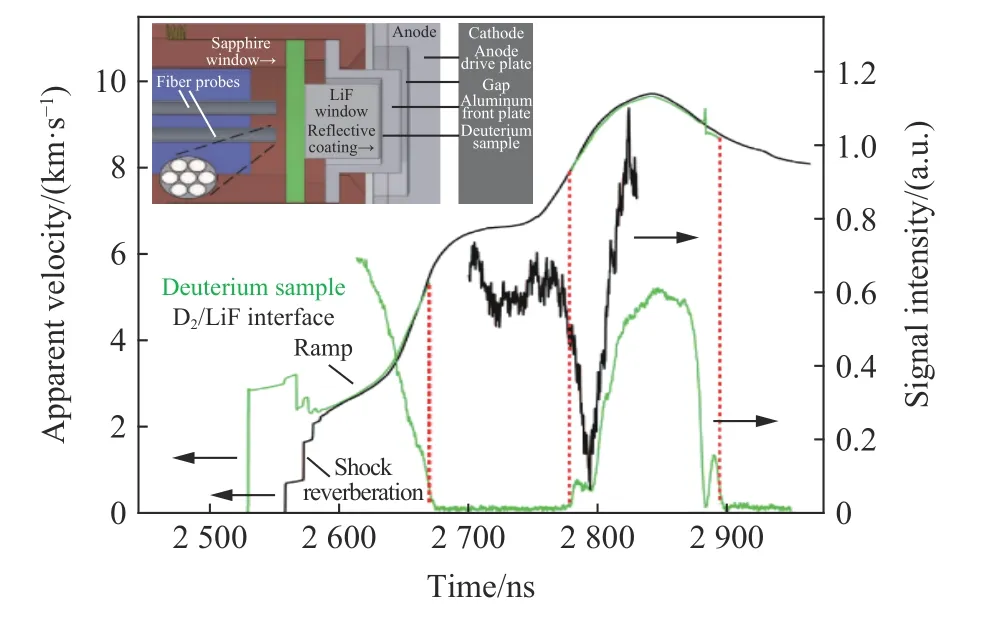
图27 冲击-斜波加载下液氘的反射率变化[82]Fig.27 Reflectivity of liquid deuterium under shock-ramp wave compression[82]

5 总结与展望

基于大电流装置的磁驱动准等熵加载技术涉及脉冲功率科学与技术、冲击动力学、计算力学、固体力学等多学科交叉与融合。近十年的发展现状显示，国内外在磁驱动准等熵加载装置、实验技术、数据处理方法以及物理力学应用研究方面均取得新进展。主要表现为：基于新设计思路和途径的专门装置孕育而生，装置加载能力不断得到加强；结合危险材料实验需求，特殊的安全防护技术得到发展；针对低、中、高阻抗材料的准等熵压缩实验设计需求，装置的放电波形调节能力越来越精细；发展和建立了冲击-准等熵加载、磁压剪联合加载、小尺寸套筒柱面等熵压缩等多种热力学加载新技术，用于探索物质更广泛相空间的响应特性；实验数据处理与解读方法精度更高，建立了处理材料复杂响应的特征线反演技术，获得了原位粒子速度的转换函数方法和正向-反向计算结合的数据处理方法等；研究获得了近500 GPa 压力范围内材料的等熵线和状态方程、1～2 TPa 压力范围内材料的冲击Hugoniot 线和精细状态方程、100～250 GPa 以上材料高压强度和本构关系以及材料的多相状态方程、相变动力学和塑性变形机制，等等。

展望未来，研制和建立加载能力达到数百GPa 甚至1 TPa 的磁驱动准等熵加载装置仍是一个重要追求目标，其中一个方向是进一步基于全电路阻抗匹配和低阻抗能量传输的技术路线，研发准等熵加载能力300～500 GPa 的紧凑型装置，并满足危险材料准等熵压缩实验的需求，这类装置采用模块化设计，结构紧凑，运行和维护效费比高，可实现的最大放电峰值电流为15～20 MA，例如美国圣地亚实验室提出的概念设计装置Neptune[87]、中国工程物理研究院流体物理研究所提出的CQ-15 装置等；另一个方向是基于新能源和惯性约束聚变的需求，研发和建设数十兆安大型强脉冲功率装置，在此装置上实现准等熵加载能力达1 TPa 及以上的实验研究需求，例如美国圣地亚实验室提出的Z300 和Z800 装置[88]、俄罗斯提出的“贝加尔”（Baikal）装置[89]，中国工程物理研究院流体物理研究所提出的50 MA 装置[90]等。

磁驱动准等熵压缩的一个显著特点是，其为过程加载，能有效识别加载过程中物质发生的弹塑性、相变、塑性变形和损伤演化等动力学现象。面对如此复杂的材料响应过程，准等熵压缩实验数据处理和解读至关重要，需要建立能反映这些复杂物理现象的物理模型，例如多相物态方程和相变动力学模型、基于位错、孪晶等微结构演化的多尺度模型和损伤演化模型等。这些模型的研究和建立，需要材料动态响应过程中的微观和介观尺度信息，因此研发能与同步辐射光源、X 射线自由电子激光等先进诊断光源结合的磁驱动准等熵加载装置也是一个重要的发展方向。

磁驱动准等熵压缩的另一个显著特点是加载过程中样品温升较低，以铝为例，流体动力学计算结果表明[91]，冲击和准等熵压缩至200 GPa，冲击压缩情况下铝的温度达到9 000 K 以上，而准等熵压缩情况下铝的温度不到1 000 K。目前超快动态加载下2 000 K 以内样品温度的精确测量仍未有效解决，是目前学术界的一个挑战和难点。而获取温度信息至关重要，它是研究材料完全物态方程的重要参量。

前面的分析表明，准等熵压缩实验对武器物理研究具有重要的科学意义和工程应用价值。因此，推动磁驱动准等熵压缩实验技术朝武器物理研究方向应用值得重视，相关技术值得发展。

磁驱动准等熵压缩技术是研究材料状态方程、变形、损伤、相变和化学反应等物理力学特性的重要手段，正如其首创者Asay 所说[92]，磁驱动准等熵压缩实验是冲击压缩和准静态等温压缩实验之间的重要桥梁,获得这种中间状态数据就可对各种物态方程理论作出关键性的鉴别，并可以探索更广泛的物态方程区域的材料物性。他认为磁驱动准等熵加载实现了冲击动力学界长期追求的目标，是开辟波结构技术研究新领域的革命性新能力。