最大度不大于5的图的2距离列表染色

李禄佳 孙明皓 孙 磊

( 山东师范大学数学与统计学院,250358,济南 )

1 引 言

在无线通讯网络信道分配问题中,将网络抽象为图建立数学模型,其中距离小于等于2的点对应的网络节点会有信道约束.这里所研究的信道分配问题是研究如何分配信道使满足信道约束的网络节点保持信道分离且使用最少的信道数目使整个网络的干扰达到最小或者没有干扰.通过建立数学模型,可将信道分配问题转化为在网络对应的图中给距离小于等于2的点分配不同颜色的2距离染色问题.如果每个网络节点有特定信道可选,就可将此问题进一步转化为图的2距离列表染色问题[1].

本文只研究无向有限简单图.d(v)表示顶点v在图G中的度数,若d(v)=k(或d(v)≥k,d(v)≤k),则称点v为一个k-点(或k+-点,或k--点).Δ(G)表示图G的最大度.l-段是路P=vx1x2…xlu,满足d(xi)=2，i=1,2,…,l,且d(u)≥3,d(v)≥3.悬挂边表示一个1-点与关联此点的一条边.

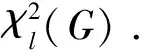
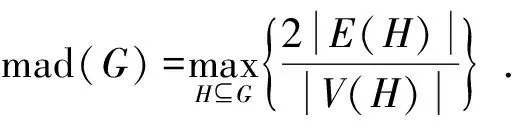
文中所出现的图,实心点表示此点的度数已知,白点表示此点的度数未知.

文中未加说明的符号和术语与文献[2]一致.

2 研究概况

关于图的2距离染色问题, Wegner从1977年开始研究,并在文献[3]中提出了如下猜想1.

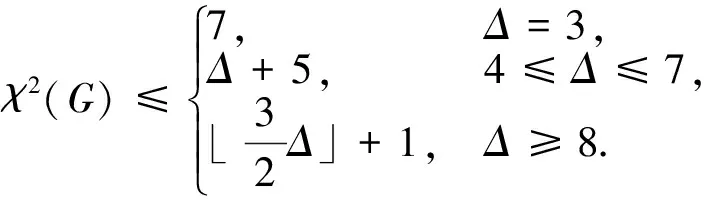
这个重要的猜想目前还没有得到完全证明.但部分结果已经得到证明，比如对于Δ=3的平面图, Thomassen在文献[4]中证明了上述猜想成立.目前对于图的2距离染色数的上界,有很多结论是关于平面图的, Molloy等人在文献[5]中证明了下面的定理1.

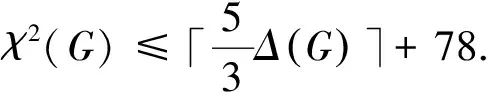
将研究对象限制到满足某种约束条件的图类中,比如对平面图的围长加以限制,会得到更好的对于平面图的2距离染色数的上界, Borodin等人在文献[6]中证明了下面的定理2.

定理2[6]给定g(G)≥6且Δ(G)≥18的平面图G,有χ2(G)≤Δ(G)+2.

随着研究的深入,人们不再局限于图的2距离染色,开始研究条件更加严苛的图的2距离列表染色.Borodin等人在文献[7]中将定理2的结果推广到2距离列表染色,得到了下面的定理3.

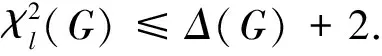
Bonamy等人在文献[8]中将定理3的结果做了改进,将最大度的条件放宽,得到了下面的定理4.

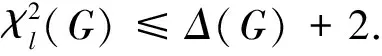
对于一般图的2距离染色问题,近年, Cranston等人研究了在最大度与最大平均度条件下的一般图的2距离染色问题,并在文献[1]中得到了下面的定理5.

定理5[1]对于图G,有如下结论成立：

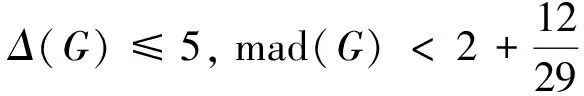
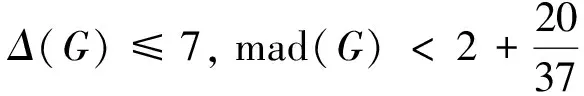
严晓燕在文献[9]中将定理5中的结果做了改进,得到了下面的定理6.

卜月华等人在文献[10]中进一步讨论了有最大平均度限制的最大度不大于5的一般图的2距离列表染色问题,并得到了下面的定理7.

定理7[10]对于图G,有如下结论成立:

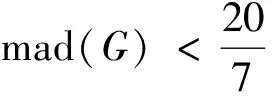
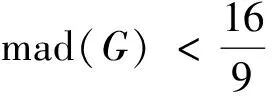
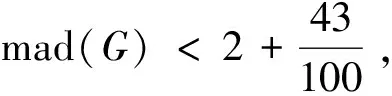
3 主要结果及证明

在前人研究的基础上，本文主要得到了下面的定理8.

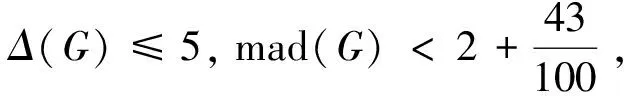
下面在3.1节中探讨最小反例的结构性质，在3.2节中给出定理8的完整证明.

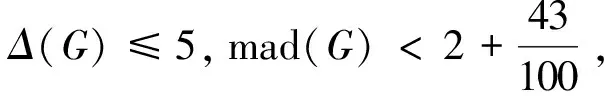
(C1) 4-段；

(C2) 一个端点为4--点的3-段；

(C3) 一个端点为3-点,另一个端点为4--点的2-段；

(C4) 当4|i时d(vi)=5,其它点d(vi)=2的4l-圈v1v2…v4l；

(C5) 当3|i时d(vi)=4,其它点d(vi)=2的3l-圈v1v2…v3l；

(C6) 由端点都是3-点的1-段组成的圈,且至少一个3-点关联另一个端点也是3-点的1-段(图1)；

图1 可约构型(C6)

(C7) 关联两条2-段(与点v相邻的2-点分别为点u1,u2)且相邻一个3--点(点u3)的3-点(点v).

(C8) 关联一条2-段和两条1-段且其中一条1-段的另一端点为4--点的3-点(图2)；

图2 可约构型(C8)

证在图G′即G-N[v]中,若d(wi)=3(i=1,2)且点wi(i=1,2)的邻点中有5-点,则对点wi(i=1,2)增加一条悬挂边.此时可使图G′满足每个5-点至少相邻一个3+-点并且|V(G′)|+|E(G′)|≤|V(G)|+|E(G)|-4-3+4<|V(G)|+|E(G)|.因为图G是极小反例,但图G′的点数加边数之和小于图G,所以可以将图G′进行染色.染色完成后,再将新增加的悬挂边去掉.接下来,在此基础上对图G进行染色.首先,点u1的可用色数至少为6-5=1,将点u1进行染色.之后,点u2的可用色数至少为6-4-1=1,将点u2进行染色.点v的可用色数至少为6-2-2-1=1,将点v进行染色.最后,点u3的可用色数至少为6-2-3=1,所以将点u3进行染色.此时,能够将图G染好.

由文献[1]中定理4的证明可知,每条3-段都可视为由它的一个端点发起,且每个5-点至多发起一条3-段.端点都是4-点的2-段都可视为由它的一个端点发起,且每个4-点至多发起一条2-段.端点是3-点的1-段都可视为由它的一个端点发起,且每个3-点至多发起一条1-段.

3.2定理8的证明

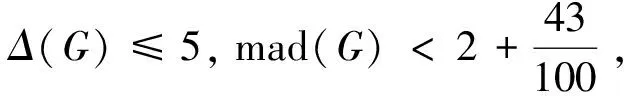
对于任意v∈V(G)构造初始权函数为ω(v)=d(v),可得

(1)

本文所提到的给l-段转权值,都是指给l-段上的所有2-点所转的权值总和.所转的权值总和之后会由段上的2-点均分.

定义权转移规则如下：

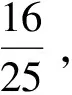
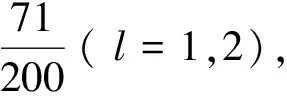
下面分4种类型检查每个顶点的新权值.

1)d(v)=5.由定理8的条件及(C1)知,5-点最多关联4条l-段(l=1,2,3),所以由(R1)得

2)d(v)=4.由(C1),(C2)知，4-点最多关联4条l-段(l=1,2),所以由(R2)得

3)d(v)=3.由(C7)知,点v最多关联两条2-段,考虑它关联2-段条数的下述3种情况.

① 点v关联两条2-段，由(C7)知，此时点v相邻一个4+-点.由(R3)得

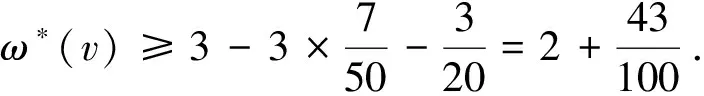
4)d(v)=2.对于2-点,考虑它在段上的下述3种情况.

① 2-点在3-段上.由(C2)知,每条3-段的端点都是5-点,且由一个端点发起,由(R1)得

② 2-点在2-段上. 由C3知,2-段的端点只有以下2种：一个端点是3-点,另一个端点是5-点或者都是4+-点.

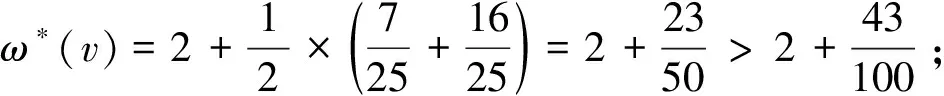
(2)

这与(1)式矛盾,从而定理8得证.