超临界二氧化碳射流破岩的热流固耦合机理

李木坤，王刚，程卫民，浦仕杰，倪红坚，时贤

（1. 山东科技大学安全与环境工程学院，山东青岛 266590；2. 中国石油青海油田公司采油一厂，青海格尔木 816499；3. 中国石油大学（华东）石油工程学院，山东青岛 266580）

0 引言

中国具有丰富的非常规油气资源，致密（页岩）油、致密气和页岩气的可采资源量分别占全球可采资源量的9.7%、5.7%和4.8%[1]。非常规油气储集层具有低孔隙度和渗透率，采用常规水基钻井液和压裂液会伤害储集层，而超临界二氧化碳（SC-CO2）不会伤害储集层，可作为非常规油气高效开采的无水钻井液和压裂液，以增加油气产量、节约水资源、节能减排，相关应用技术包括 SC-CO2射流钻井[2]和 SC-CO2喷射压裂[3]。

相比水基钻井液，SC-CO2黏度是纯水的十分之一以下，8 MPa、50 ℃下黏度为0.02 mPa·s，20 MPa、50 ℃下黏度为0.07 mPa·s，因而循环压耗低；避免了黏土膨胀和水锁效应，不会伤害储集层；密度对井口回压敏感，8 MPa、50 ℃下密度为 220 kg/m3；20 MPa、50 ℃下密度为785 kg/m3，更易达到欠平衡钻井条件[4]。相比氮气泡沫等钻井液，SC-CO2能达到与水相近的密度从而为井下马达提供足够的扭矩[5-6]。此外，在55～193 MPa喷射压差下，SC-CO2射流破碎花岗岩和页岩的门限压力分别是水射流的2/3和1/2[6]。上述特性使得采用SC-CO2射流破岩钻井具有较高钻井速度，且能够大幅降低钻井成本[6-9]。

相比水力喷射压裂，相同压力下SC-CO2喷射压裂可产生更大的射孔体积和孔底静压力，能够在更低的喷射压力下产生裂缝[3]，起裂压力是水力喷射的一半以下[10]；CO2在裂缝中流动发生温降而产生的温度应力有助于主裂缝周围复杂缝网的形成[11]，与 CO2接触时岩石强度降低[12]。SC-CO2喷射压裂尤其适合中国页岩气的开发，因为页岩渗透率和孔隙度低，黏土含量高，广泛分布在缺水区域，采用水基压裂液压裂采收率低[13]。采用SC-CO2作为压裂液，可以解决黏土水化膨胀和缺水问题，压裂液基本无残留因而不会伤害储集层渗透率；并且由于页岩对 CO2的强吸附性可置换出甲烷，同时实现CO2的地质埋存[14-16]。

目前国内外大量的实验研究证明 SC-CO2射流比水射流破岩优势大。Kolle等[6-7]通过实验证明SC-CO2射流的破碎岩石比能耗是水射流的一半以下；Tian、黄飞、杜玉昆和Wang等[5,17-19]发现SC-CO2射流下页岩呈网格状体积破碎，获得了喷距、射流温度、射流压力等对射流破岩的影响规律。SC-CO2黏度低、密度高，能够在孔隙和裂缝中快速传递压力，但对破岩机理缺乏进一步的量化研究；Li等[20-22]研究发现岩石受SC-CO2射流场冲击后表面出现了几十度的温降，射流强化传热下产生大的温度梯度和温度应力，基于此证明了更大的温度应力是 SC-CO2射流破岩优于水射流的关键因素，解释了SC-CO2射流比水射流破岩门限压力低、破岩面积大的机理。

射流破碎岩石是一个层层剥蚀和喷距增加的过程，射流压力和温度随喷距的变化决定了射流破岩门限压力、破岩面积和破岩深度，但现有关于温度应力对 SC-CO2射流破岩影响的研究主要是在定喷距下完成的[20-22]，缺乏射流场和岩石应力随喷距变化的探讨，无法充分解释 SC-CO2射流破岩深度比水射流更大以及岩石呈体积破碎的现象。因此，本文开展了不同喷距下SC-CO2、水和氮气射流破岩的流场和岩石应力对比研究，揭示SC-CO2射流破岩的热流固耦合机理，为SC-CO2射流钻井和 SC-CO2喷射压裂技术的发展和应用提供理论依据。

1 计算模型

1.1 物理模型和网格划分

基于室内实验装置[18]，建立了全尺寸物理模型（见图1）。喷距Dst为2～100 mm，岩心半径R3为50 mm，岩心长度D3为100 mm；喷嘴出口半径Rn为1 mm，喷嘴入口内径及外径R1，R2分别为6.5，11.5 mm，喷嘴喷孔前收缩面及喷孔长度D1，D2分别为100，10 mm。定义Dra为岩心表面某一点距射流中心的径向距离，Dver为岩心内部轴线上某一点距射流中心的垂向距离，Dra与喷嘴半径Rn的比值（Dra/Rn）为无因次半径，Dver与喷嘴出口直径ϕn的比值（Dver/ϕn）为无因次深度。为了更好地捕捉温度、速度和压力的波动，模型采用局部加密的笛卡尔网格划分（见图 2），网格平均质量达0.98（1表示质量最好）。

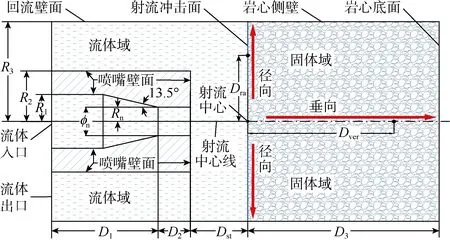
图1 物理模型二维结构示意图

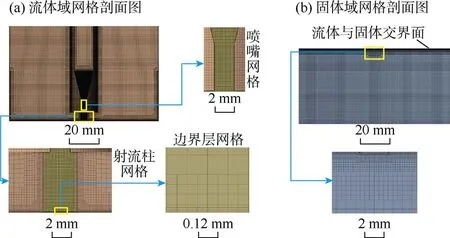
图2 网格划分

1.2 模拟假设

①流体与喷嘴壁面的换热量很少，流体流经喷嘴的过程可假设为绝热；②渗流对射流破岩的影响很小[23]，模拟中不考虑岩石的渗透性；③射流压差为60 MPa下岩石变形量小于多数岩石的表面粗糙度，忽略岩石变形对流场影响；④岩石内部热膨胀系数的不同和温度梯度是岩石热破裂的主要原因[24-27]，人为设置岩石非均质性会增加温度应力，假设岩石是均匀介质。

1.3 流体湍流方程和流体物性控制方程

通过力学软件 Fluent进行流场计算，采用软件提供的 Realizablek-ɛ湍流模型可有效地计算旋转剪切流、喷射和边界层流以及分离流动等[28-34]。采用美国国家标准与技术研究所（NIST）建议的隐式方程可以精确描述二氧化碳[35]、氮气[36]和水[37]的压力、温度、黏度和热导率等变化：

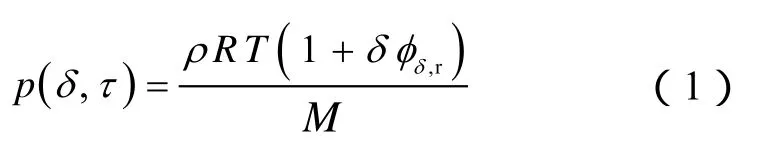
方程中比热容计算式如下：

二氧化碳和氮气的黏度方程如下[38-39]：

二氧化碳和氮气的热导率方程如下：

水的黏度和热导率方程如下[40]：

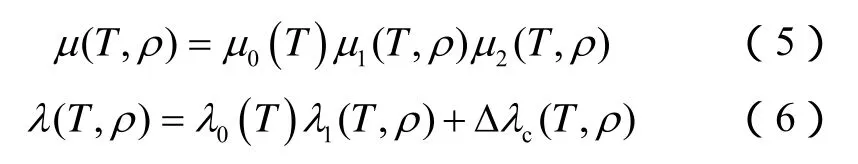
1.4 岩石本构关系及热传导方程

本文采用静弹性破坏理论，即认为岩石在射流下主要发生拉伸和剪切破坏。动态破岩过程主要包括岩石在射流下产生初始裂纹，射流通过水楔效应进一步扩展裂缝，最后碎裂的岩石被冲蚀。上述过程重复进行，喷距和破岩深度增加。

通过ANSYS中的Static structural模块进行应力计算，岩石力学和热传导的控制方程如下。

应力与应变关系为：

热传导方程为：

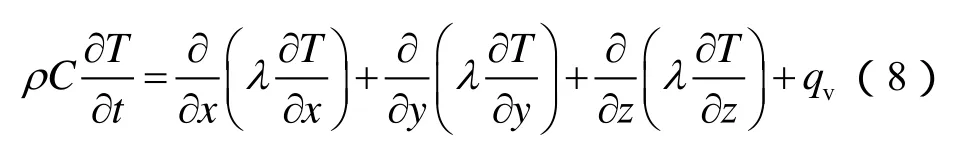
基于对岩石力学和热力学性质的调研[41-46]，确定了模拟中硬质岩石密度为 2.55×103kg/m3，比热容为1 kJ/（kg·K），热导率为1.8 W/（m·K），泊松比为0.15，弹性模量为 70 GPa，热膨胀系数为 15×10−6K−1。

1.5 边界条件

模拟中设置入口压力和温度边界条件以及出口压力边界条件（见图 3），喷嘴壁面设置为绝热条件，其他边界条件设置如（9）—（11）式所示。

图3 边界条件示意图

岩心侧壁和底部边界条件分别为：

流体与岩石交界面边界条件：

1.6 求解步骤

①设置流体入口和出口边界条件，不考虑流体与岩心间传热，计算稳态下的射流温度场和压力场；②考虑流体与岩心间传热，以步骤①中的流场为初始条件和时间零点，计算tj时岩心表面压力场和岩心内部温度场；③以步骤②中得到的岩心表面压力场和岩心内部温度场作为初始条件，对岩心底部边界设置零位移约束，对岩心侧面设置10 MPa的压力边界条件，计算tj时岩心的拉应力和剪应力。

2 模拟方法验证

2.1 流场计算方法验证

采用无因次喷距（Dst/ϕn）为2时的实验数据对流场模拟方法进行验证。测试中，通过测试盘上钻孔外接压力传感器直接测量压力，测试盘上钻孔保护罩内温度传感器间接测量温度；压力传感器放置在无因次半径（Dra/Rn）为0，8，16和24处，温度传感器放置在无因次半径为 8，16，24和 32处，实验条件为Tin=300.15 K，pin=30.3 MPa，Ta=287.95 K，pout=9.6 MPa。考虑射流时间对传热的影响，采用射流2 min后相对稳定的温度和压力数据平均值。基于实验中的测试盘结构和材料性质建立物理模型，计算得到了压力和温度的分布，图 4为模拟和实验测得的温度与压力分布对比。压力的平均误差在1%以下，温度的平均误差在2%以下，模拟计算值与实验测量值基本吻合，验证了流场计算方法的有效性。

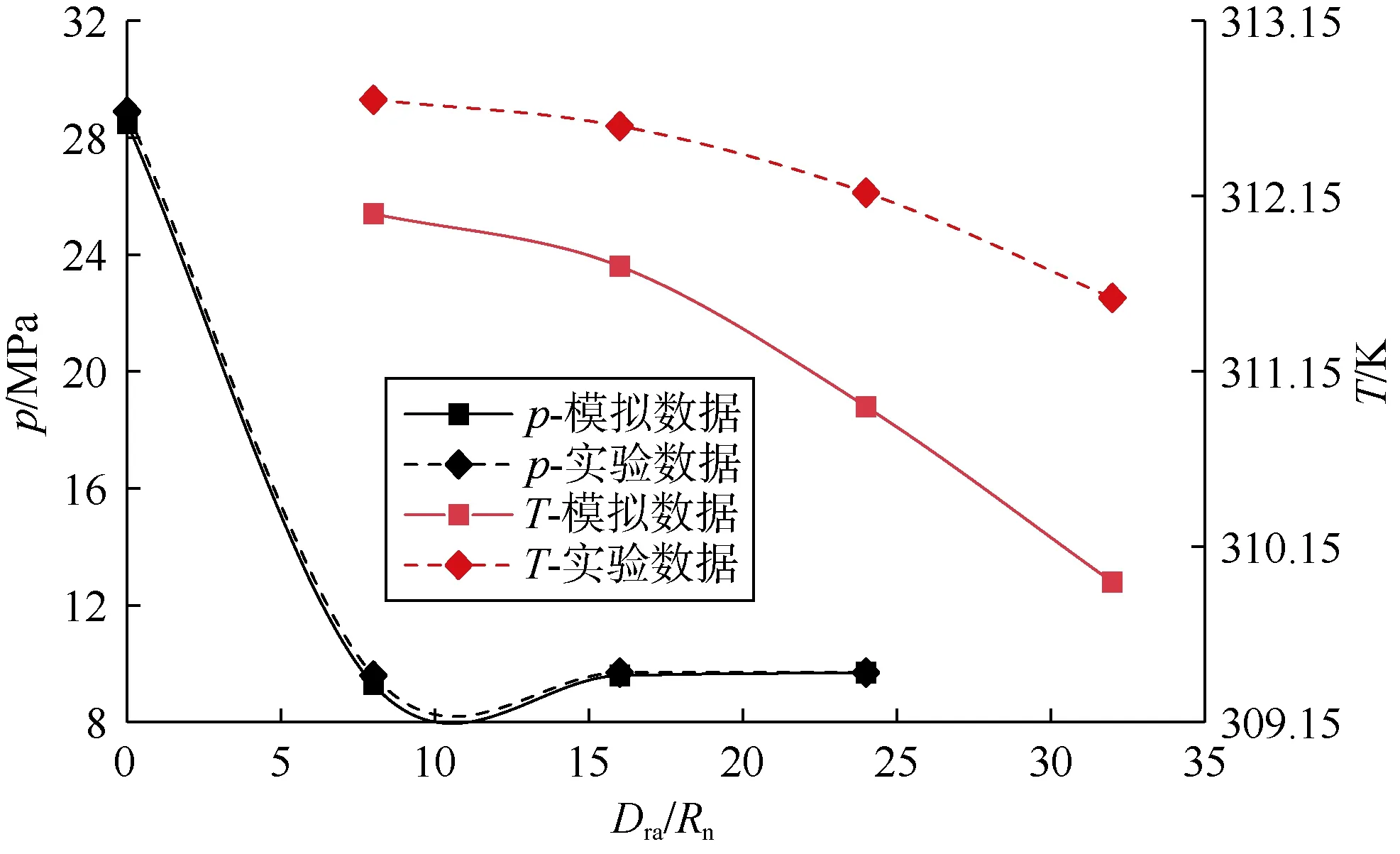
图4 模拟计算和实验测得的温度与压力分布对比

2.2 应力场计算方法验证

结合现有破岩实验数据[6,18]对应力场计算方法进行验证。SC-CO2射流有两个明显特征：同一压力下，SC-CO2射流破岩的面积和体积是水射流的2倍以上；SC-CO2射流破岩的门限压力pth是水射流的 66.7%以下。图5为计算得到的SC-CO2和水射流的应力分布对比，模拟条件为tj=1 s，pin=30 MPa，pout=10 MPa，Ta=343.15 K，Dst/ϕn=2。结果显示水射流的最大拉应力是 SC-CO2射流的 43%。假设岩石的抗拉强度是 15 MPa，根据图5中15 MPa等值线的分布，计算出水射流的破坏半径和破坏体积分别是SC-CO2射流的9%和17%，计算结果与实验结果基本吻合，验证了计算方法的有效性。

图5 27 ℃下水射流和70 ℃下SC-CO2射流作用下岩石应力云图

3 射流流场随喷距的变化

3.1 射流中岩心表面压力场随喷距的变化

由于激波影响[47]，氮气射流压力整体上小于水和SC-CO2射流压力；无因次喷距为10时SC-CO2射流压力比水射流的大，其他无因次喷距下两者无明显差别（见图 6）。定义射流中心线上岩心表面压力为pcen，无因次半径（Dra/Rn）在4以内时岩心表面压力与出口压力（pout）的平均压力差为Dp4。随着喷距增加，水和SC-CO2射流作用下的pcen减小，氮气射流作用下的pcen先增加后减小（见图 7a）；水、SC-CO2和氮气射流的Δp4均先增加后减小（见图7b）。基于应力分析可知射流最大压力决定最大拉应力，高压力作用范围决定着高应力区域的范围，因此pcen越大，喷嘴射流破岩门限压力越小；Δp4越大，破岩面积越大。因此，分别把pcen和Δp4作为破岩门限压力和破岩面积的评价标准。无因次喷距在 10～15时，SC-CO2射流相比水射流有更小的破岩门限压力，其他无因次喷距下两者区别不大；整体上看，SC-CO2射流与水射流的破岩面积相差不大，无法解释SC-CO2射流相比水射流在破岩上的优势。氮气射流的破岩面积比水和SC-CO2射流的都小，表明水和SC-CO2射流相比氮气射流在破岩上更有优势。

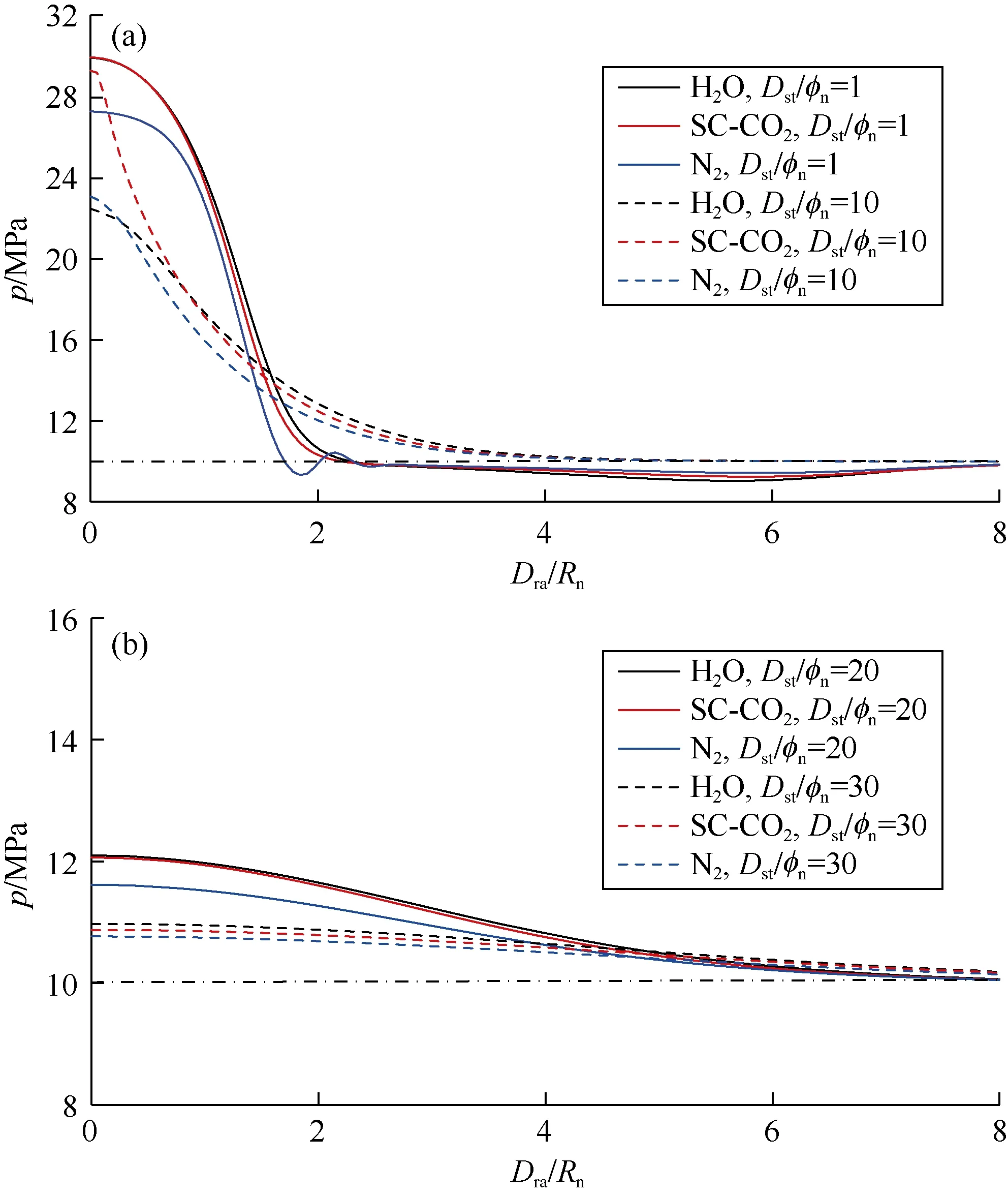
图6 岩心表面射流压力分布随无因次喷距的变化

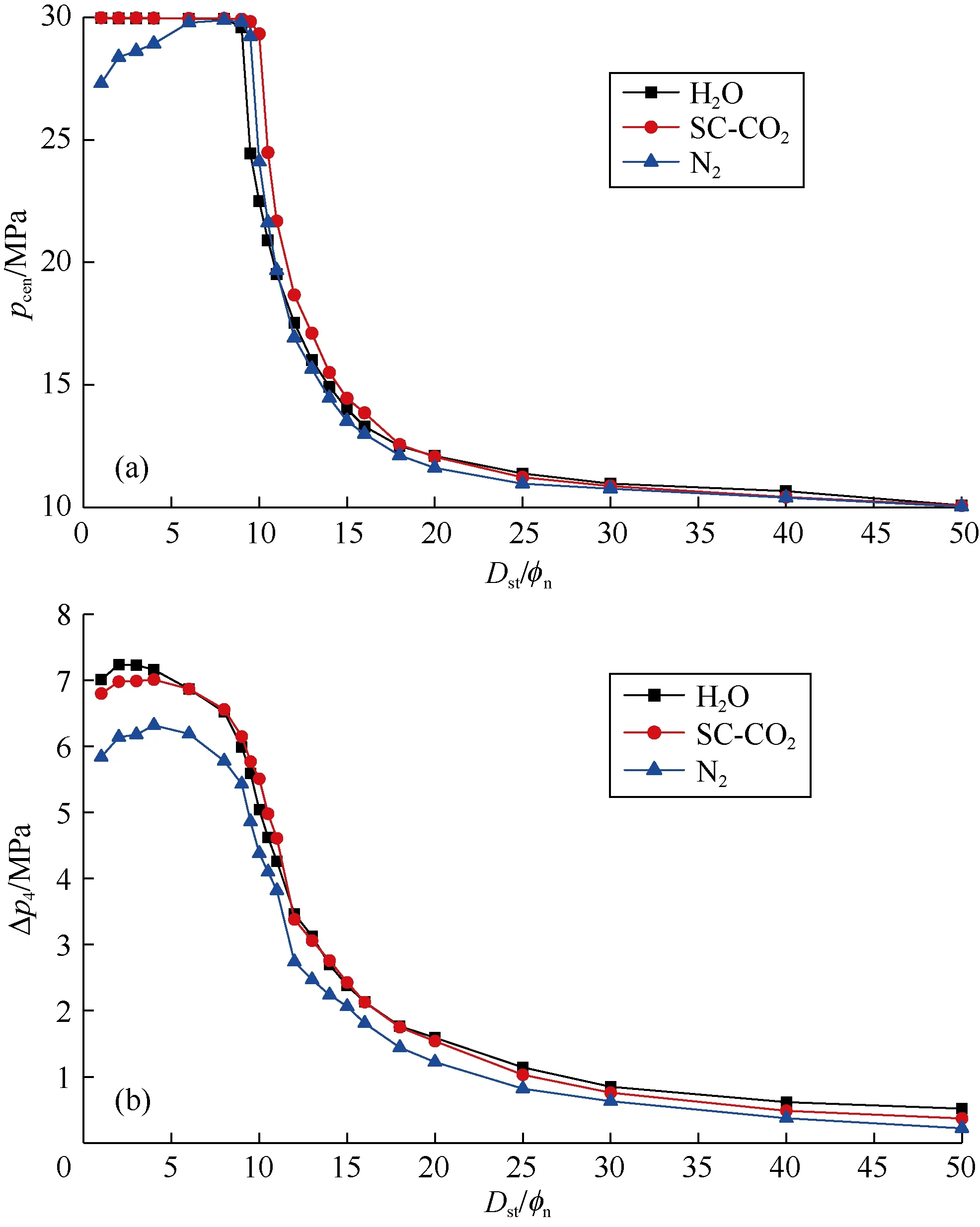
图7 岩心表面射流中心压力（a）和平均射流压力差（b）随无因次喷距的变化（pin=30 MPa，pout=10 MPa，Tin=Ta=343.15 K）

3.2 射流中岩心表面温度场随喷距变化

由图 8可以看出岩心表面温度分布随无因次喷距（Dst/ϕn）的变化，水射流对岩石起升温作用，SC-CO2和氮气射流对岩石起降温作用，SC-CO2射流造成的温差最大。现场钻井中流量是本算例的10倍以上，高流量会导致钻杆内流体与地层温度换热不充分，喷嘴入口流体温度小于地温，因此实际工况下水射流一般不会引起岩石表面温度的升高。射流压力主要作用于无因次半径为 2以内的区域，射流温差作用于整个岩心表面，影响范围是压力的20倍以上。

图8 岩心表面射流温度随无因次喷距的变化

定义射流中心线上岩心表面温度为Tcen，无因次半径（Dra/Rn）在4以内的岩心表面温度与环境温度的平均温差为ΔT4。图9为射流中心温度和平均射流温差随无因次喷距变化的曲线。受湍流发热和膨胀吸热的双重影响，射流温度随喷距的变化更加复杂。从整体趋势上看，SC-CO2射流下ΔT4随喷距增加而增加（绝对值增大），氮气射流下ΔT4先减小（绝对值减小）后增加，水射流下ΔT4小幅增加。在喷距（Dst/ϕn）大于10时，SC-CO2射流下ΔT4分别是水和氮气射流的5倍和2.5倍以上，而此时 SC-CO2、氮气和水的射流压力大幅降低。现有研究结果表明，射流温度的升高或降低都会增加岩石应力。因此，射流温差引起的热应力导致SC-CO2射流相比水和氮气射流在破岩面积和破岩深度上更有优势，这与定喷距下的实验结果一致[6-7]；随着喷距增加，SC-CO2射流温差对岩石应力的贡献增加。

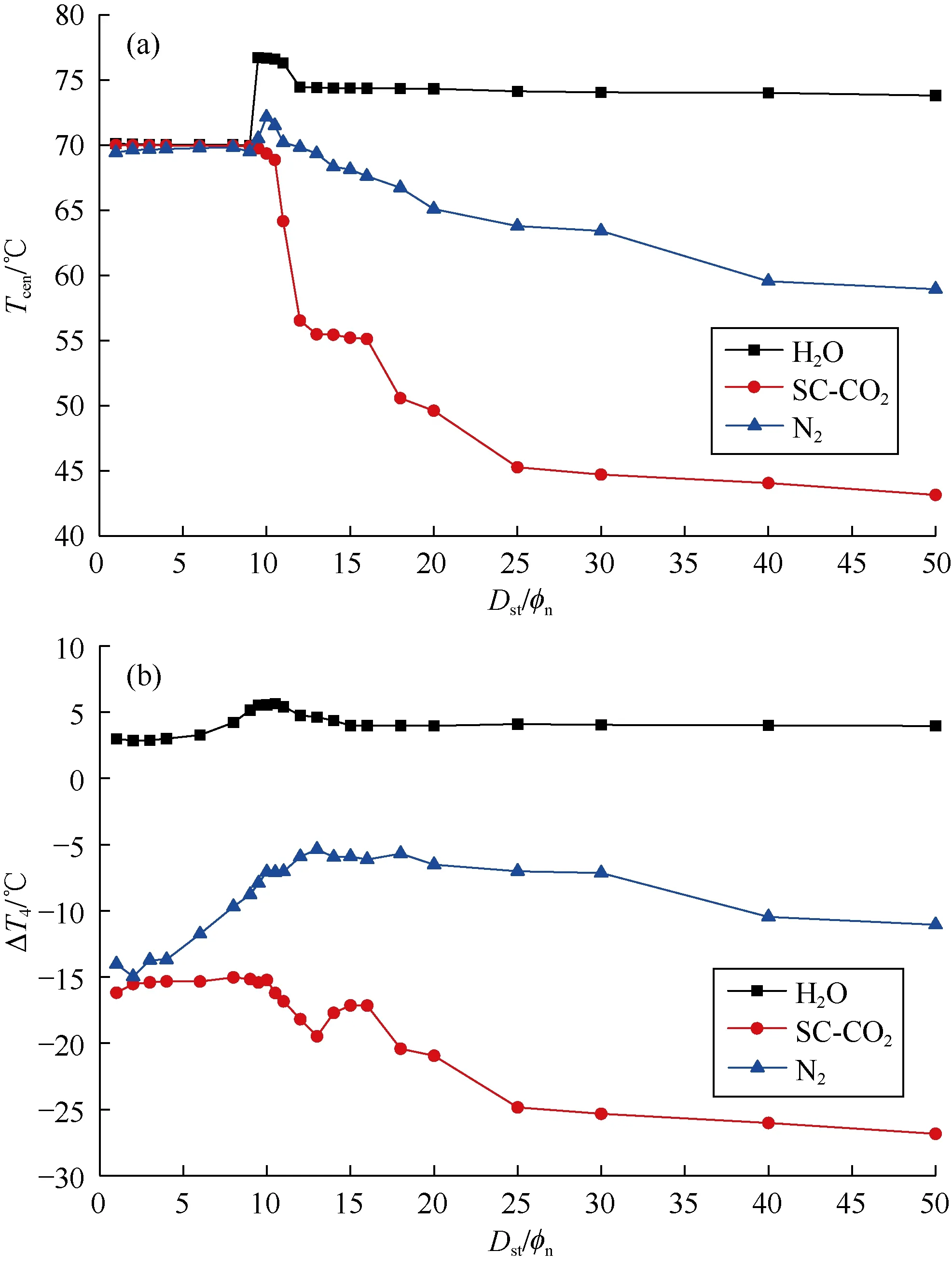
图9 岩心表面射流中心温度（a）和平均射流温差（b）随无因次喷距的变化（pin=30 MPa，pout=10 MPa，Tin=Ta=343.15 K）

4 射流下岩石应力场随喷距的变化

4.1 岩石应力分布随射流时间和喷距的变化

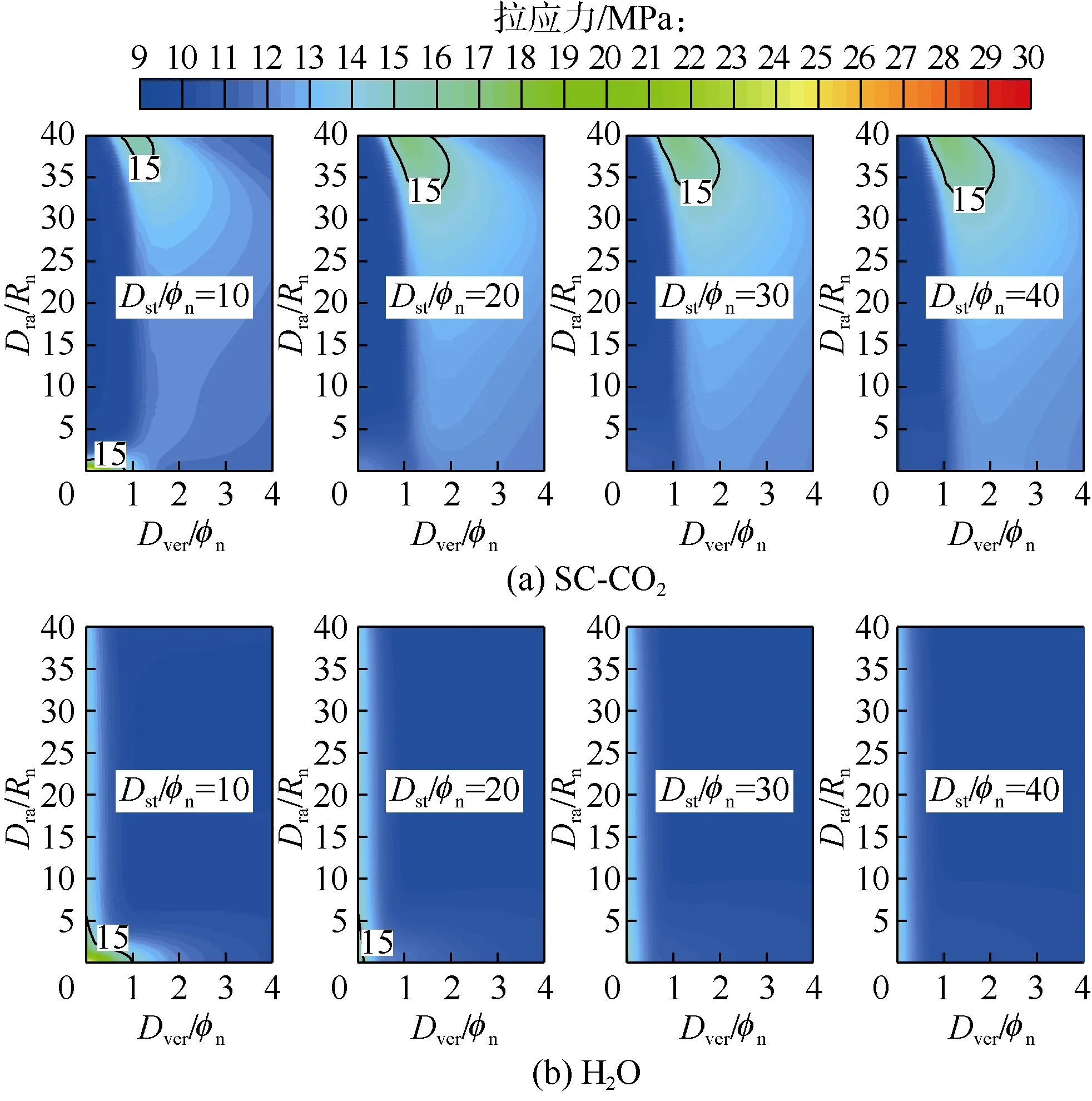
无因次喷距（Dst/ϕn）为10时，温度和压力耦合场下岩石应力随射流时间的变化如图10和图11所示。可以看出，射流时间增加，岩心表面（Dver/ϕn=0，00，0

图10 岩心表面和内部拉应力随射流时间的变化（pin=30 MPa，pout=10 MPa，Tin=Ta=343.15 K）

图11 岩心表面和内部剪应力随射流时间的变化（pin=30 MPa，pout=10 MPa，Tin=Ta=343.15 K）

根据射流时间为1 s和60 s的岩石应力分布（见图12、图13）分析喷距对射流下岩石应力影响。随着无因次喷距从20增加到40，SC-CO2和氮气射流作用下岩石内部的拉应力和剪应力增加，水射流下岩石表面的拉应力和剪应力减小，表明SC-CO2射流相对水射流的破岩优势增强。随着喷距增加，SC-CO2和氮气射流下的高应力区域从射流中心向附近的岩石表面及内部转移，而此时SC-CO2和氮气射流作用下的压力减小（见图7），温差增加（见图9），表明射流温度场对岩石应力的贡献增加。

图12 射流时间为1 s时岩石拉应力和剪应力随无因次喷距的变化（pin=30 MPa，pout=10 MPa，Tin=Ta=343.15 K）

图13 射流时间为60 s时岩石拉应力和剪应力随无因次喷距的变化（pin=30 MPa，pout=10 MPa，Tin=Ta=343.15 K）

4.2 射流温度应力对岩石应力影响分析

根据最大应力随喷距变化进一步分析温度应力对岩石应力的影响。从射流压力场下岩石应力随无因次喷距的变化（见图14）可以看出，无因次喷距为1～6时，水射流和 SC-CO2射流比氮气射流下的岩石应力大；无因次喷距为 11～15时，SC-CO2射流相比水射流产生更大岩石应力，但破岩优势较小，还不能充分解释SC-CO2射流破岩深度更大的原因。

图14 压力场下最大拉应力（a）和最大剪应力（b）随无因次喷距变化（pin=30 MPa，pout=10 MPa，Tin=Ta=343.15 K）

由射流压力-温度耦合场下岩石应力随无因次喷距的变化看出（见图15），相比氮气射流，水射流下岩石有更大的拉应力和更小的剪应力；由于岩石以拉伸破坏为主，整体上水射流比氮气射流更有破岩优势。SC-CO2射流相比水射流和氮气射流产生更大的岩石拉应力和剪应力，尤其在无因次喷距为 20～50时，SC-CO2射流的最大拉应力分别是水射流和氮气射流的1.3倍和1.5倍以上，最大剪应力分别是水射流和氮气射流的 6倍和 3倍以上，表明压力-温度耦合场下SC-CO2射流更易产生拉伸和剪切组合破坏。以15 MPa作为岩石的抗拉强度，则SC-CO2射流的有效破岩无因次喷距为50以上，水射流和氮气射流分别为30和13，表明温度应力是 SC-CO2射流比水射流破岩深度大的原因。

图15 压力-温度耦合场下最大拉应力（a）和最大剪应力（b）随无因次喷距变化（pin=30 MPa，pout=10 MPa，Tin=Ta=343.15 K）

对比压力场和压力-温度耦合场下最大拉应力和最大剪应力随无因次喷距的变化可以看出（见图 16、图17），射流温度场分别在无因次喷距为10和13时增大水和 SC-CO2射流的岩石拉应力，在无因次喷距为16左右时温度应力对岩石拉应力开始起主导作用，因此岩石拉应力随喷距的变化曲线可分为压力主导区和温度主导区两部分。射流温度场对剪应力与拉应力的影响差别较大。水射流作用下，无因次喷距小于13时，射流温度场使岩石剪应力降低；无因次喷距大于13时，射流温度场使岩石剪应力增大。SC-CO2射流的温度场对岩石剪应力起增强作用，其中最小增大倍数为2.3，剪应力主要由温度应力产生，随喷距的变化不存在压力主导区。

图16 压力场和压力-温度耦合场下最大拉应力随无因次喷距的变化（tj=1 s）

图17 压力场和压力-温度耦合场下最大剪应力随无因次喷距的变化（tj=1 s）

岩石的抗拉强度为15 MPa，从射流时间为1 s和60 s时拉伸破坏区域面积随无因次喷距的变化看出（见图 18、图 19），水射流主要对射流中心（坐标 0点）及附近的岩石产生破坏；随着射流时间增加，拉伸破坏区域面积减小，表明水射流主要以短时间内岩石表面层层剥蚀为破坏方式。SC-CO2射流不仅破坏射流中心及附近的岩石，还能破坏岩石内部区域；随着射流时间增加，内部拉伸破坏区域面积增大，表明SC-CO2射流作用下不仅存在短时间内岩石表面层层剥蚀破坏，而且伴随长时间的岩石内部体积破坏，从而比水射流的破岩效率更高。SC-CO2射流相比水射流有更大的破岩面积，无因次喷距为 10时可增加破岩面积 15倍以上，且随着喷距和射流时间增加，这一优势更加明显。

图18 SC-CO2和水射流破坏面积随无因次喷距的变化（tj=1 s）

图19 SC-CO2和水射流破坏面积随无因次喷距的变化（tj=60 s）

5 结论

随着喷距增加，氮气射流作用下岩石表面压力整体上小于水和SC-CO2射流作用下的压力；无因次喷距大于 10时，SC-CO2射流作用下的岩石表面平均温差分别约是氮气和水射流的2.5倍和5倍以上；与射流压力仅作用于岩石射流中心附近不同，SC-CO2射流温差作用于整个岩石表面。因此，SC-CO2射流相比水和氮气射流可以产生更大破岩面积和深度。温度应力是SC-CO2射流比水和氮气射流在破岩上更有优势的原因，喷距较小时射流压力起主要破岩作用，喷距较大时射流温差起主要破岩作用。相比水和氮气射流，SC-CO2射流下岩石拉伸和剪切破坏更严重，更易发生体积破坏，且破岩优势随喷距增加而增加。

在地面泵压受限的情况下，欠平衡钻井可产生更大的射流压差和温差；脉冲和钻头旋转射流也可通过高频脉动增加岩石表面的压力和温度梯度，这些措施均可提升SC-CO2射流的热流固耦合破岩效果。

符号注释：

C——岩石比热容，J/（kg·K）；Cp——等压比热容，J/（kg·K）；Dra——岩石表面某一点距射流中心的径向距离，mm；Dra/Rn——无因次半径；Dst——喷嘴与岩心表面距离，mm；Dst/ϕn——无因次喷距；Dver——岩石内部轴线上某一点距射流中心的垂向距离，mm；Dver/ϕn——无因次深度；D1——喷嘴喷孔前收缩面长度，mm；D2——喷嘴喷孔长度，mm；D3——岩心长度，mm；E——弹性模量，Pa；k——湍流动能，J；lR——岩石底面位移，m；M——相对分子质量，kg/mol；p——压力，Pa；pcen——射流中心线上岩石表面压力，MPa；pcon——岩石围压，Pa；pin——流体在喷嘴的入口压力，MPa；pL——界面流体压力，Pa；pout——流体出口压力，MPa；pth——射流破岩的门限压力，MPa；qv——热生成率，J/（m3·s）；R——气体常数，J/（mol·K）；R1——喷嘴入口内径，mm；R2——喷嘴入口外径，mm；R3——岩心半径，mm；Rn——喷嘴出口半径，mm；t——时间，s；tj——射流时间，s；T——温度，K；Ta——环境温度，K；Tcen——射流中心线上岩石表面温度，℃；Tin——入口温度，K；TL——界面流体温度，K；TR——界面岩石温度，K；T0——岩石初始温度，K；x，y，z——直角坐标轴3个方向；α——热膨胀系数，K−1；δ——密度与临界密度比值，无因次；Δp4——Dra/Rn为4以内时岩石表面压力与出口压力的平均压力差，MPa；ΔT4——Dra/Rn为4以内时岩石表面温度与环境温度的平均温度差，℃；Δλ——同温度下相对稀薄气体密度升高引起的热导率增加值，W/（m·K）；Δλc——临界点附近引起的热导率增加值，W/（m·K）；Δμ——同温度下相对稀薄气体由于密度升高引起的黏度增加值，Pa·s；Δμc——临界点附近引起的黏度增加值，Pa·s；ε——湍流动能发散率，无因次；εii——i方向应变，无因次；λ——热导率，W/（m·K）；λ0——某一温度下密度接近零时的极限热导率值，W/（m·K）；λ1——同温度下相对稀薄气体密度升高引起的热导率增加比例，无因次；μ——黏度，Pa·s；μ0——某一温度下密度接近零时的极限黏度值，Pa·s；μ1——同温度下相对稀薄气体密度升高引起的黏度增加比例，无因次；μ2——临界点附近引起的黏度增加比例，无因次；ν——泊松比，无因次；ρ——密度，kg/m3；σii，σjj，σkk——沿坐标轴 3 个方向的应力张量，Pa；σR——岩石表面正应力，Pa；σs,max——最大剪应力，MPa；σt,max——最大拉应力，MPa；τ——温度与临界温度比值，无因次；ϕn——喷嘴出口直径，mm；ϕδ,r——剩余亥姆霍兹自由能ϕr（δ，τ）的偏微分，无因次；ϕττ,o——理想亥姆霍兹自由能ϕo（δ，τ）的第二阶偏微分，无因次；ϕδτ,r，ϕδδ,r，ϕττ,r——剩余亥姆霍兹自由能ϕr（δ，τ）的第二阶偏微分，无因次。下标：r——剩余；o——理想。