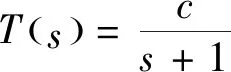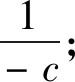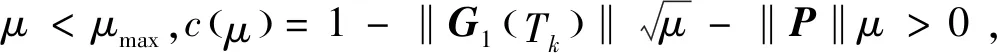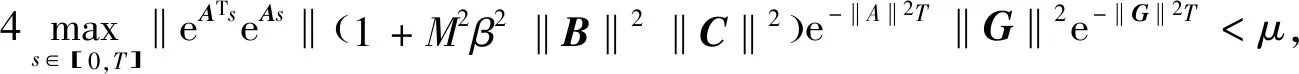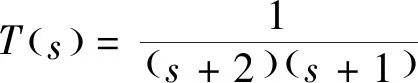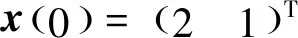具有第二类脉冲宽度调制随机系统的稳定性分析
兰德新,叶丽霞
(武夷学院数学与计算机学院,中国 武夷山 354300)
近年来,脉冲宽度调制被广泛地应用于电流控制、信号处理及神经网络等系统的许多领域中[1-7]。尤其是加入随机干扰的脉冲宽度调制反馈系统稳定性的研究,已受到许多学者的关注,文献[8-15]详细介绍脉冲宽度调制反馈系统稳定性理论的相关研究结果。文献[9]利用李雅普诺夫函数、随机分析法和广义积分算子不等式,研究了具有马尔科夫切换和时滞的随机微分方程的p方指数稳定性问题,文献[12]利用李雅普诺夫函数和伊藤积分,研究了一类具有第一类脉冲宽度调制的随机系统的全局指数稳定性问题并取得相关结果。目前,对于脉冲宽度调制反馈系统的稳定性研究大多涉及第一类脉冲宽度调制,对第二类脉冲宽度调制反馈系统研究的比较少。在文献[14]中,作者研究第二类脉冲宽度调制反馈系统的稳定性,并建立相应的理论结果,其结果显示第二类脉冲宽度调制反馈系统趋于平衡点的速度快于具有第一类脉冲宽度调制的反馈系统。
本文在文献[14]的基础上,加入随机干扰,利用李雅普诺夫函数,线性矩阵不等式和伊藤积分法,研究了具有第二类脉冲宽度调制的随机系统的p方指数稳定性问题,给出这类系统p方指数稳定性的充分条件,并通过合理选择脉冲宽度调制参数的最大上界,使该系统达到稳定。同时用两个具体实例说明这类系统具有更强的抗干扰能力且趋于平衡点的速度快于具有第一类脉冲宽度调制的随机系统。
1 预备知识
令(Ω,F,P)表示一概率空间,Rn表示n维欧氏空间,对∀x∈Rn,定义x∈Rn:Ω→X⊂Rn上的可测函数。令I表示一指标集,对∀t∈I,定义X(t)为(Ω,F,P)上的随机变量,则{x(t),t∈I}表示一随机过程。
考虑如下的随机系统,其流程如图1所示。
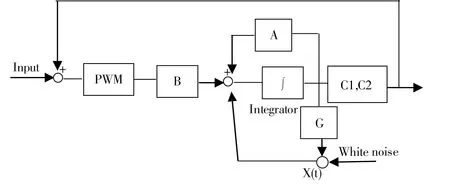
图1 随机系统的流程图Fig. 1 Block diagram of stochastic systems
定义随机系统的第二类脉冲宽度调制的输出函数为
(1)
其中e(t)=r(t)-y(t),r(t)表示激励输入,y(t) 表示系统输出,k=1,2,…,Tk表示脉冲宽度,sgn表示符号函数。定义脉冲宽度Tk和符号函数sgn为
(2)
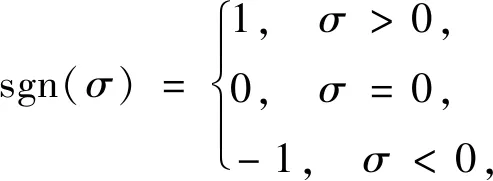
其中T为样本周期,M为脉冲的振幅,β为常数,若Tk不存在,则令Tk=T。
本文总假设r(t)≡0,记第二类脉冲宽度调制的脉冲宽度Tk在采样时刻kT取决于错误信号:
则具有第二类脉冲宽度调制的随机系统被描述为
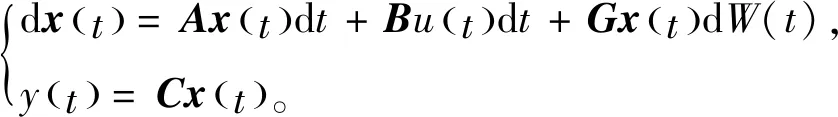
(3)
其中x∈Rn,y∈R,u∈R表示脉冲宽度调制的输出,A,B,C和G表示相同维数的矩阵,W(t)表示维纳过程。注意到x(t)=0是随机系统(3)的一个平衡点。
下面给出相关的定义和引理。
定义1[12]设{T,X,A,S}为一随机动力系统,记d是域X上的测度,M⊂A,t0∈T,a是初始状态,
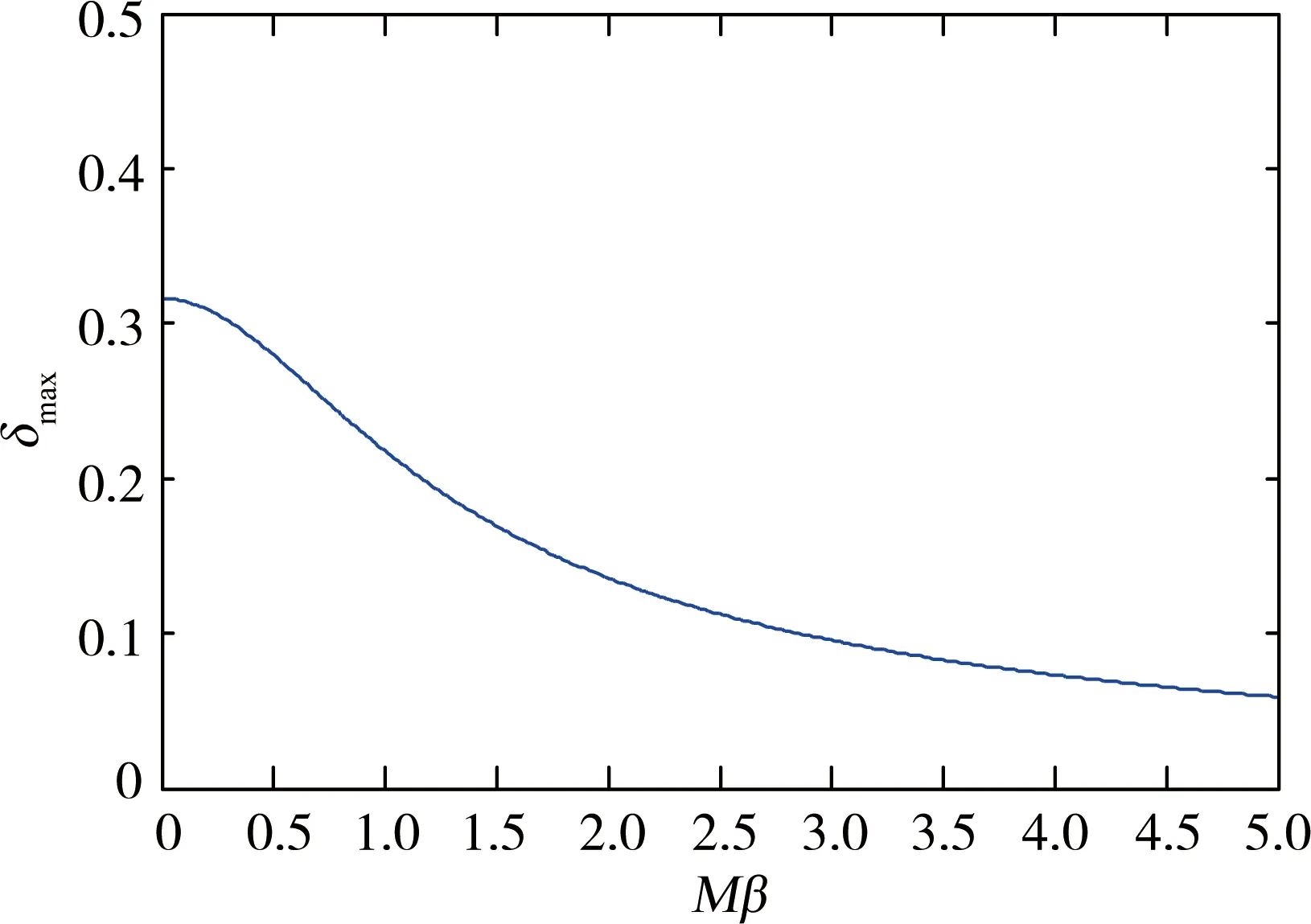
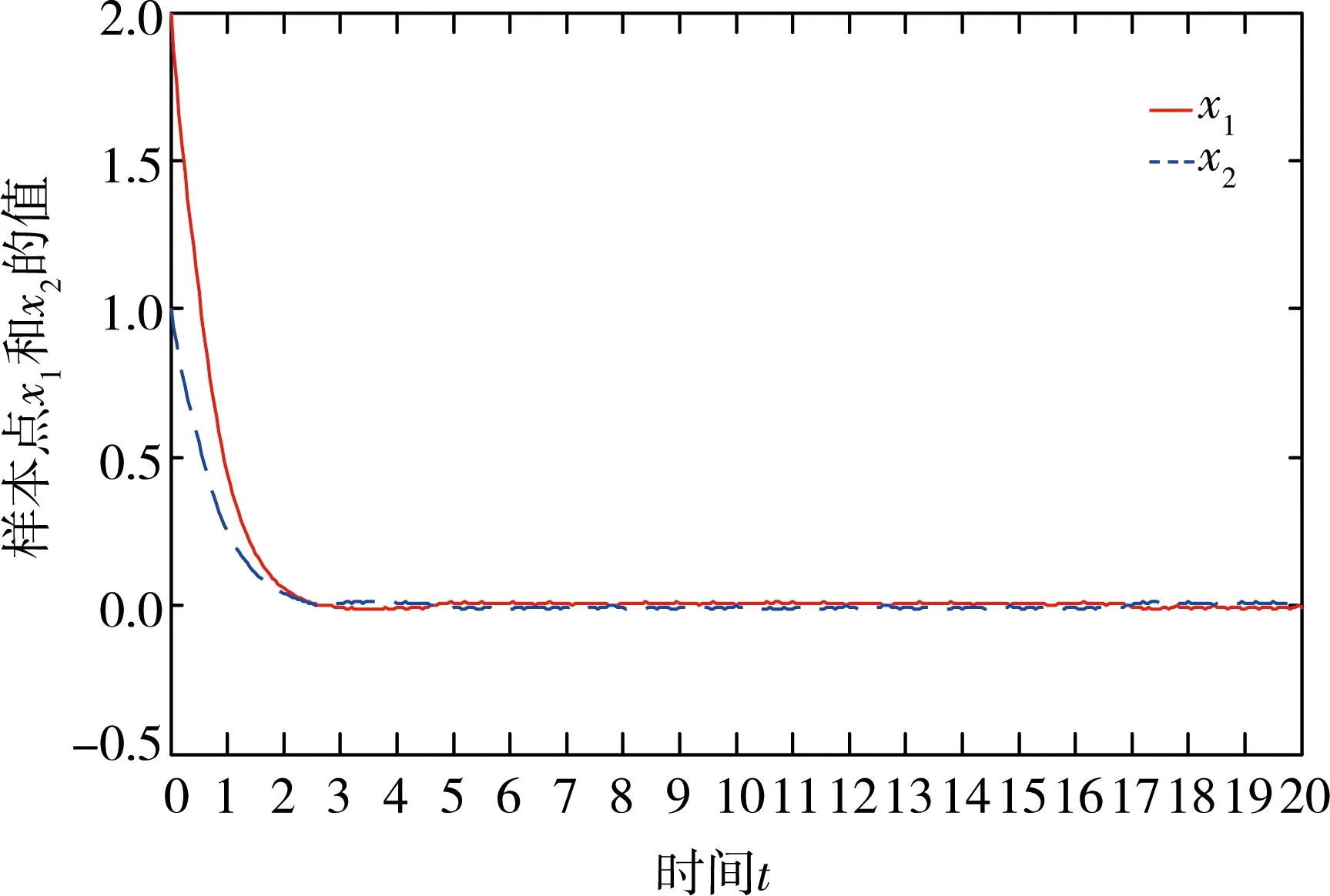
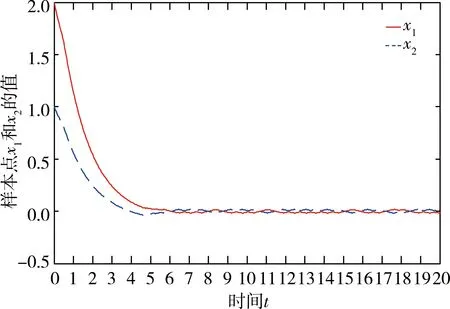
(1)如果对∀ε>0,∃δ=δ(t0,ε)和常数β>0,k>1,使得当d(a,M)<δ时,对∀x(·,·,a,t0)∈S都有E[d(x(t,ω,a,t0),M)p] (2)如果上述δ不依赖于t0,则称(S,M)是p方一致指数稳定的; (3)如果对∀ε>0,∃δ=δ(ε)>0,τ=τ(ε),使得对∀x(·,·,a,t0)∈S,∀t>t0+τ,当d(a,M)<δ时,有E[d(x(t,ω,a,t0),M)p] 引理1[13]假设W(t)是一维纳过程。如果φ(t,ω)是有界的初等函数,则 (4) 定理1 假设随机系统(3)中的矩阵A是赫兹稳定的,且满足下列条件: (1)-MβCB<1; 则随机系统(3)在平衡点xe=0处达到p(p∈Z+)方指数稳定。 先证明当p=2时,定理1结论成立。 首先由随机系统(3)的两边积分得 (5) 所以当t=kT+Tk时有 其中:Tk=β|Cx(kT+Tk)|, 因此 (6) 再由随机系统 (3)两边从sk-1到kT积分得 (7) 即 (8) [I+MβW(Tk)]Z(sk)=eATZ(sk-1)+h(sk)。 (9) 由条件Mβ满足-MβCB<1,可推得I+MβW(Tk)是正定矩阵,由此说明式(7)有意义。 其次,令二次李雅普诺夫函数V:Rn→R+,V(Z)=ZT(P-I)Z,其中正定矩阵P满足(P-I)是正定的和P=(e-AT)T(P-I)(e-AT)。 因此,当t∈[sk-1,sk]有 ∇E[V(x(t))]=E[V(Z(sk))]-E[V(Z(sk-1))]= E[ZT(sk)(P-I)Z(sk)]-E[ZT(sk-1)(P-I)Z(sk-1)]= E[ZT(sk)(-I-Mβ(PW(Tk)+WT(Tk)P)-M2β2WT(Tk)PW(Tk))Z(sk)]+ MβE[hT(sk)PW(Tk)Z(sk)+ZT(sk)WT(Tk)Ph(sk)]-E[hT(sk)Ph(sk)]。 (10) 记Φ(Tk,Mβ)=I+MβG1(Tk)+M2β2G2(Tk),G1(Tk)=WT(Tk)P+PW(Tk),G2(Tk)=WT(Tk)PW(Tk)。 则式(10)简化为 ∇E[V(x(t))]=-E[ZT(sk)Φ(Tk,Mβ)Z(sk)]+MβE[ZT(sk)WT(Tk)Ph(sk)+ hT(sk)PW(Tk)Z(sk)]+E[hT(sk)Ph(sk)], (11) 结合条件(1)中θMβ>0,可以得到Φ(Tk,Mβ)是正定矩阵。 接下来估计h(sk)。即证明对∀μ>0,存在δ>0,当‖G‖<δ时,有 E[‖h(sk)‖2]<μE[‖Z(sk)‖2]。 因为当t∈[sk-1,sk]时,得 (12) (13) 注意到 (14) 由引理1即得 而式(14)简化为 其中K0=I+M2β2‖B‖2‖C‖2。 再由Gronwall不等式得 E[‖x(t)‖2]≤4K0e-(‖A‖2+‖G‖2)TE[‖x(sk)‖2]。 (15) 因此 4K0K1e-(‖A‖2+‖G‖2)T‖G‖2E[‖x(sk)‖2]≤K‖G‖2e-‖G‖2TE[‖x(sk)‖2], (16) 结合条件(2)可以得到 E[‖h(sk)‖2]≤μE[‖Z(sk)‖2]。 (17) 又因为当t∈[sk-1,sk]可得 其中λm(·)和λM(·)分别为矩阵的最小特征值和最大特征值。即: (18) 注意到 V(x(0))=xT(0)(P-I)x(0)≤‖P-I‖‖x(0)‖2=‖P-I‖‖a‖2, 其中a=x(0)为初始值。 所以当t∈[0,s0]时,则E[V(s0)]≤E[V(x(0)]=‖P-I‖‖a‖2,当t∈[sk-1,sk]时,得到 (19) 注意到E[V(x(t))]≥λM(P-I)E[‖x(t)‖2],由此得到 (20) 因此,由定义1知当p=2时,随机系统(3)在平衡点xe=0处是均方一致稳定的。 接下来证明该随机系统(3)是p方指数稳定的。 令p=2q,q≥1,则 E[V(Z(sk))q]-E[V(Z(sk-1))q]= E[(V(Z(sk))-V(Z(sk-1)))V(Z(sk))q-1+…+V(Z(sk-1))q-1]≤ 所以 因此当t∈(sk-1,sk)时,可以得到 类似地,可以得到 因此由定义1知p为偶数时,随机系统(3)是p方指数稳定的。类似地,可以证明,当p为奇数时,该结论也是成立的。 所以,对于∀p∈Z+定理1成立。 注1 本文考虑随机系统的p方指数稳定,且该随机系统的解趋于平衡点的速度快于具有第一类脉冲宽度调制的随机系统。随机系统的解的变化情况在图3中显示。 推论1 假设A是赫兹稳定的,如果CB>0,且随机系统的输出y(t)与状态变量x(t)线性相关。则当干扰足够小,脉冲宽度调制参数Mβ的最大上界达到足够大时,随机系统(3)在平衡点xe=0处是p(p∈Z+)方指数稳定。 注2 当B是正向量,C是负向量,且Mβ上界足够小,则随机系统(3)将具有很强的抗干扰能力。 本文给出了一些数值例子,说明了本文的理论结果,并给出了推导结果的创新点。 因此,可以计算定理3.1中所涉及的量W(Tk),P,G1(Tk)和G2(Tk),经计算得 不妨设c=1,则Mβ∈(0,+∞)。 又因为δ<δmax, 所以 经计算得δmax=0.316。 下面应用Matlab软件作出图2,并用图2来描述‖G‖的最大上界的估计值δmax与Mβ之间的关系。从图2中可以看到δmax随Mβ的增大而减小,并且当状态变量远离原点直至Tk=T时,脉冲宽度调制的输出为+M或-M。因此,对给定的β,随着M的增加,允许确保系统p方指数稳定的最大干扰量δmax将减小,即如果随机系统(3)的干扰量增加(小于δmax),则可以通过减小M的值来保证该系统是p方指数稳定的,具体变化情况如图2所示。 图2 估计值δmax与Mβ之间的关系Fig. 2 Upper bounds for‖G‖whenMβ∈(0,+∞) 如果c=1,而Mβ∈(0,1),则计算得‖G‖∈(0,+∞),这说明具有第二类脉冲宽度调制的随机系统具有很强的抗干扰性。 图3 例2中的具有第二类脉冲宽度调制的随机系统的样本点Fig. 3 Sample response of PWM feedback system with type 2 in Example 2 图4 例2中的具有第二类脉冲宽度调制的随机系统的样本点Fig. 4 Sample response of PWM feedback system with type 1 in Example 2 从图3显示当时间t≥3时,该系统的通解将趋于平衡点。从图4显示当时间t≥5时,该系统的通解将趋于平衡点。虽然这两类随机系统的脉冲宽度调制参数的最大上界相近,但从图3和图4中可观察到具有第二类脉冲宽度调制的随机系统的通解趋于平衡点的速度快于具有第一类脉冲宽度调制的随机系统。 本文第一个实例考虑随机系统(3)状态空间为A=-1,B=1,C=c,周期为T=1,即一阶微分方程模型: 根据定理1的结论,计算出当该系统达到稳定时参数Mβ的取值范围,并用Matlab软件作出随机干扰系数‖G‖的最大上界的估计值δmax与Mβ之间的关系图,并分析它们之间的变化情况。本文第二个实例考虑随机系统(3)为二阶微分方程模型: 应用Matlab软件分别作出具有相同参数和相同初始值下的第一类脉冲宽度调制随机系统和第二类脉冲宽度调制随机系统的解的变化情况,有力说明第二类脉冲宽度调制随机系统具有强抗干扰和较快趋于平衡点的优势。2 主要结果
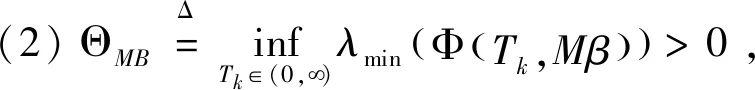
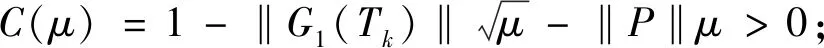
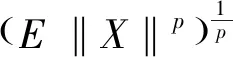
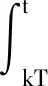
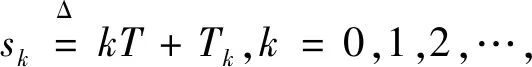
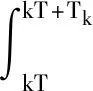
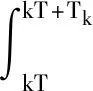
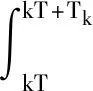
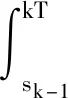
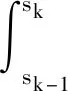
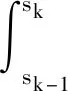
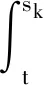
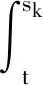
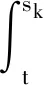
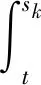
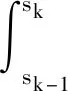
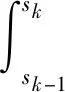
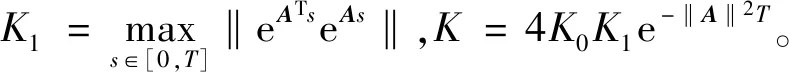
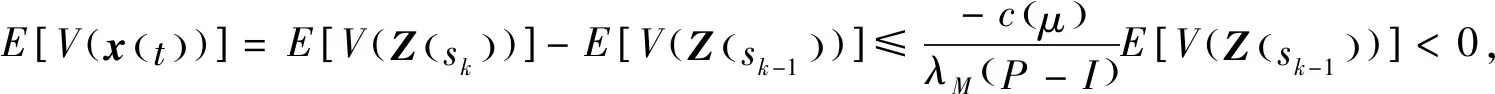
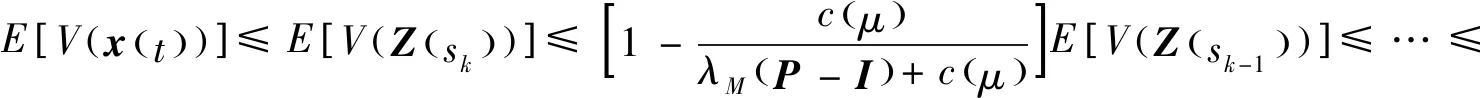
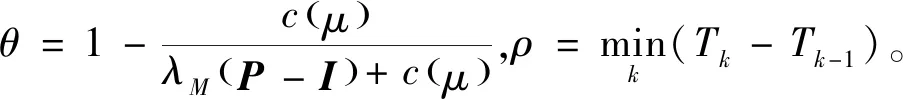
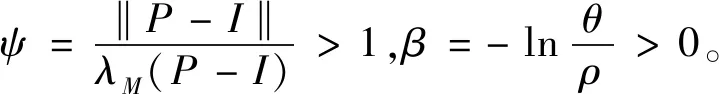
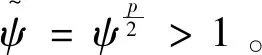
3 数值仿真