大型风电安装船环境载荷与运动响应分析

万家平，屠 艳，蔡 灵

（南通中远海运船务工程有限公司，江苏南通 226006）

0 引言

第3代自航自升式风电安装船可作为施工平台和运输平台，不仅具有运输航行、施工安装、人员居住、船体平台自动升降和动力定位等功能，还具有抗风浪能力强和工作效率高的特点。该船船型扁平，装备有超高起吊高度的重型起重机，带有4根桩腿和桩靴，可装运多达10台大功率风力发电机机舱、风叶和配套的塔筒等设备。由于风机安装船在风浪较大的海上风电场区域作业，所遭受到的风、浪、流环境荷载复杂，这些环境载荷直接影响到平台的设计和施工，关系到平台的稳定性，适航性和安全性。因此，对风机吊装平台进行水动力特性分析是非常必要的。本文结合船型特征和作业环境，基于三维势流理论，应用SESAM和ANSYS软件，对风电安装船进行环境载荷与动力响应的频域分析。

1 安装船载荷与运动响应计算理论依据

Denis-Pierson理论表明：浮体在不规则海浪中运动响应可以由单位规则波中的响应（传递函数）和海浪谱来确定，风机吊装平台的运动响应可通过计算传递函数和不规则波统计预报的谱分析进行计算。

规则波中船体运动与载荷计算广泛应用三维源汇理论，其基本假定为：1）船体运动及波浪均是微幅线性的；2）视水为无黏性流体；3）考虑绕射和辐射的影响。

建立包括船体及桩腿在内的平台整体频域运动方程：

式中：

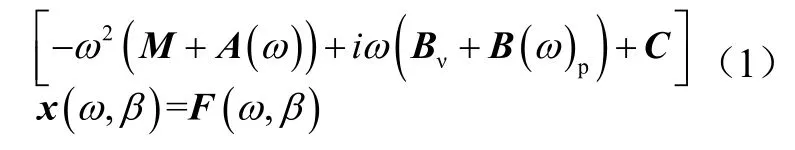
ω

为入射波角频率；

β

为入射波传播方向；

M

为浮体惯性矩阵；

A

(

ω

)为与频率有关的附加质量矩阵；

B

(

ω

)为与频率有关的辐射阻尼矩阵；

B

为与流体黏性有关的线性阻尼矩阵；

C

为静水回复刚度矩阵；

x

(

ω

,

β

)为浮体运动矩阵；

F

(

ω

,

β

)为波浪激励力矩阵，由作用在大尺度构件上的波浪激励力和作用在小尺度构件上的惯性力以及拖曳力组成。

波浪载荷采用绕射理论，对水动压力在船体湿表面上进行积分计算波浪载荷。本文采用波谱计算，按等效线性化方法对速度平方项进行处理：

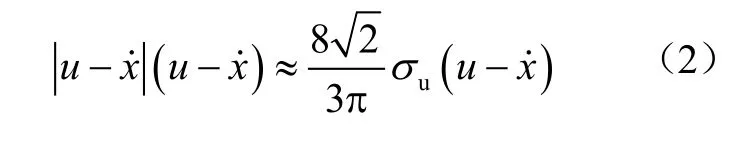
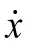
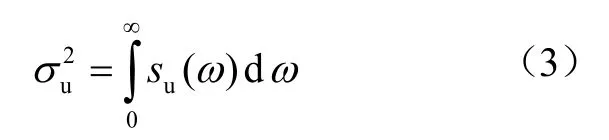
传递函数（RAO）是浮体在单位波幅的简谐波作用下的浮体响应。在简谐波作用下随时间而变化的响应函数可写为

式中：

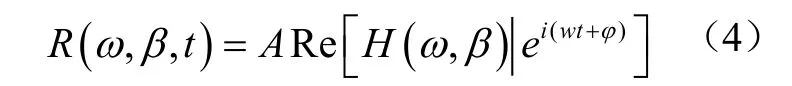
H

(

ω

,

β

)为传递函数。

结构的响应谱为

式中：

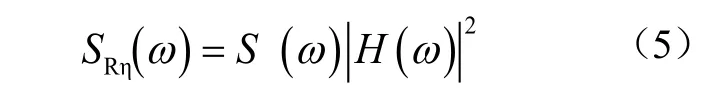
H

(

ω

)为传递函数；

S

(

ω

)为波谱。

2 环境载荷分析

本文取第3代自航自升式海上风机安装船为研究对象，其最大工作水深为40 m，是一种将自航运输、自升平台和起吊船等多种功能融为一体的新型船舶。安装船示意图和有限元模型分别见图1和图2，

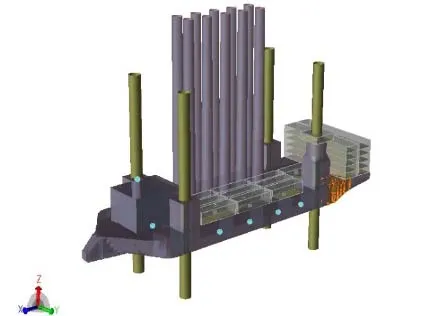
图1 安装船效果图

图2 安装船有限元模型

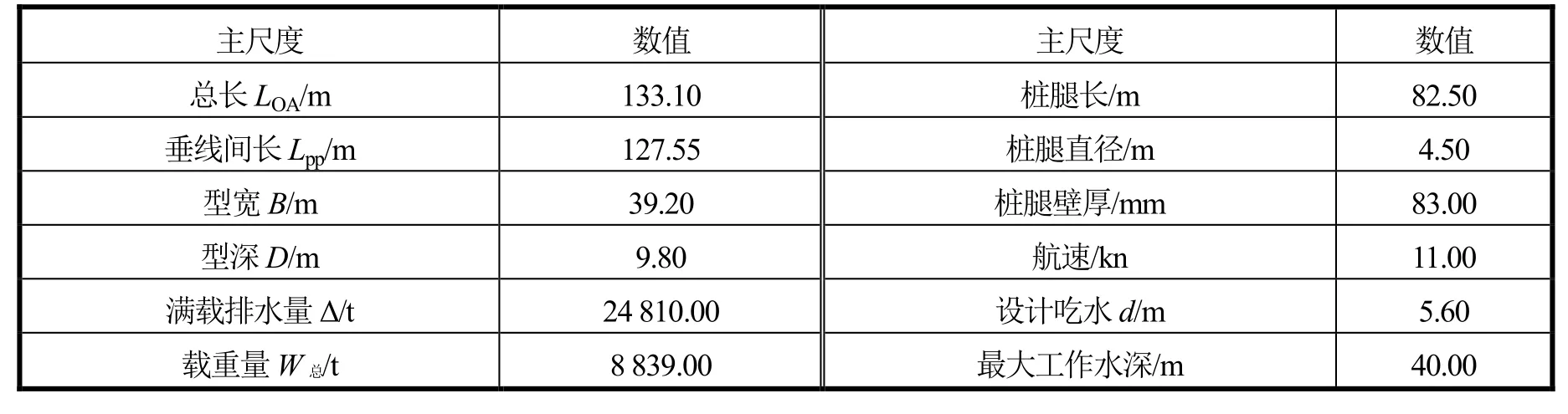
表1 安装船主尺度

JONSWAP谱是基于中等风况和有限风距情况测得的，其主要特点是考虑了有限风压的作用，且适用于不同成长阶段的风浪。根据实际环境和相关规范的要求，计算工况考虑JONSWAP谱的5级海况，风速为浦氏6级（13.5 m/s），有义波高2.5 m，波浪周期5 s。

3 三维面元模型计算

运用SESAM程序中的GeniE模块建立自升式风机安装船的水动力三维模型，包括湿表面模型和Morison模型。计算时坐标原点选在基线面，0站号，

x

方向指向艏部，

y

方向指向左舷，

z

方向竖直向上。

根据平台的特点，主船体（如主甲板、船底板、船体外板和舱壁等结构）选用板单元，桩腿选用梁单元（Pipe Section），桩腿与船体之间刚性连接，船体平台的三维面元模型和桩腿的Morison模型分别见图3和图4。

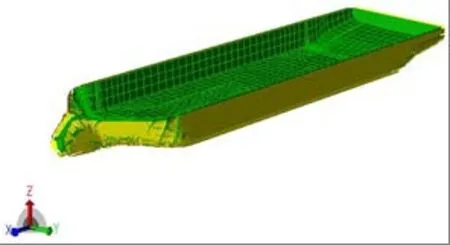
图3 船体平台三维面元模型

图4 桩腿的Morison模型

4 安装船漂浮到桩腿下放过程中的运动响应频域计算分析

考虑船体平台漂浮工况（零航速、桩腿回收入船体）和船体平台就位过程中桩腿下放不同深度的工况对船体运动响应进行计算。风机安装船体左右对称，浪向角取值范围为0°～180°，间隔为15°。波浪周期取值范围为2 s～22 s，间隔为1 s。采用JONSWAP谱模拟短期海况，谱峰因子取为 2，有义波高为2.5 m，周期为5 s。

4.1 船体平台零航速漂浮状态运动响应

自航自升式风电吊装船航行到风电场，在风电机组安装位置就位前及安装完成后，有较长时间处于漂浮状态（零航速、桩腿回收），现将该状态作为一种计算工况。

通过传递函数计算可得，在波浪周期为5 s～10 s时，垂荡运动幅值较大，在浪向角为0°、波浪周期6 s时，垂荡运动幅值达到极值；波浪周期大于10 s时，其运动逐渐趋向缓慢，幅值趋向于1.1 m。船体平台纵摇运动在波浪周期为5 s～10 s区域内幅值较大，在浪向角为15°、波浪周期为9 s时达到极值，而后随运动波浪周期增加幅值逐渐下降；浪向角为90°时，纵摇最小，最大值只有5.78×10m。不同浪向角对于平台的运动产生较大影响，浪向角对垂荡、纵摇和横摇的影响非常大。浪向角为0°时（迎浪），垂荡运动幅度在波浪周期 6 s时达到最大值3.43 m，浪向角150°时达到最小值9.06×10m。浪向角为15°时纵摇幅值最大，达到最大值3.43×10m，浪向角为90°（横浪）时纵摇最小为2.75×10m；浪向角为 90°（横浪）时横摇最大，达到最大值1.92×10m，浪向角为180°（随浪）时横摇最小，为8.93×10m。

4.2 桩腿下放近海底时船体平台运动响应分析

船体平台未插桩时仍属于漂浮状态，随着桩腿不断下放，船体平台的运动，可能使得桩腿与海底可能发生碰撞，甚至会导致桩腿和固桩架发生破坏。因此，研究自升式风机吊装平台桩腿下放接近海底时的运动响应，对于确定平台的触底力及触底安全校核具有重要的意义。

以工作水深25 m，桩腿下放24 m为研究工况，在SESAM软件后处理模块Postresp中对计算结果进行处理，得到平台6个自由度运动响应的传递函数（RAO）曲线。由传递函数计算可得，自升式平台的横摇、艏摇和纵摇运动都比较弱，可着重考虑纵荡、垂荡和横荡的影响。在波浪周期为6 s～8 s时，船体平台的垂荡运动比较剧烈。浪向角为0°（迎浪）时，运动幅度最大，在周期为6 s时达到最大值2.91 m；浪向角为150°时运动幅度最小，极小值为 0.645 m。船体平台纵荡运动的幅值随着波浪周期的加大不断加大，在浪向角为180°（随浪）时运动幅度最大；在周期为5 s出现极值0.285 m；周期为22 s传递函数达到最大值；浪向角为90°（横浪）时，运动幅度最小。船体平台的横荡运动幅值随着波浪周期的加大不断加大，在浪向角为 90°（横浪）时运动幅度最大；在周期为22 s时达到最大值；浪向角为0°（迎浪）时，运动幅度最小。

在波浪周期为6 s～8 s时，垂荡运动的运动幅值最大；在5级风浪，波频为7 s时实际垂荡幅值有可能会达到7.275 m。由于此时桩腿接近海底，如此大的运动幅值将导致桩腿触底，在桩腿下放操作时应该避开该波频风浪。自升式海上风机吊装平台在航行以及定位时，应该避开这些危险的浪向角以及波浪能集中的频率范围。

5 航行状态下平台在波浪上的载荷与运动响应计算

5.1 时域内的载荷与运动响应计算

平台在规定的航行状态下，

H

=8.4 m，

T

=13.5 s的海洋环境下，以12 kn（6.17 m/s）的服务航速航行，规则波应选取Stokes 5阶波。平台主体遭遇浪向角选取180°（迎浪）作为研究对象，时间间隔关系到计算的精确度以及计算的时间。本文根据Wasim所规定的经验值计算出时间间隔不得大于0.19 s，选择时间间隔为0.1 s，计算的时间长度取300 s。在短期范围内，各个自由度的运动不断处于交替往复的状态，都随着时间趋于稳定。由于在 6个自由度的运动模态中，垂荡、纵摇和横摇运动模态存在静水回复力（或力矩），垂荡、纵摇和横摇的运动比较稳定。垂荡运动值稳定在4.2 m左右，纵摇运动最大值-0.417°，横摇运动稳定在 6.3°左右。横荡和艏摇运动相对稳定，横荡运动最大值为9.843 5 m，艏摇运动最大值为-6.561°。

迎浪航行提高了有效频率，有可能使波激力较大的波浪频率范围接近或者达到船舶自振频率，进而产生共振，引起一系列的问题。图5～图16为6个自由度运动的速度以及加速度时历曲线。加速度对时间的变化最为敏感，运动值、速度以及加速度之间存在一定相位差。但是其运动频率整体上相差不大。

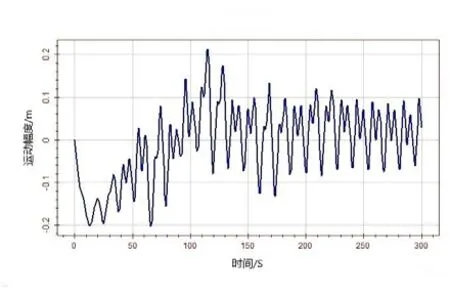
图5 纵荡运动速度时历

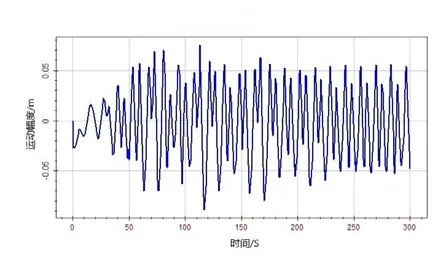
图6 纵荡运动加速度时历

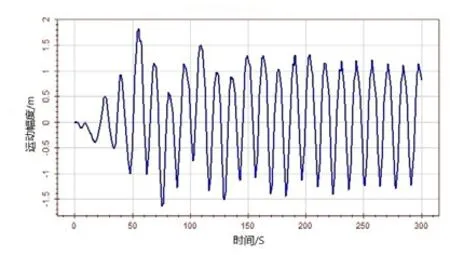
图7 横荡运动速度时历

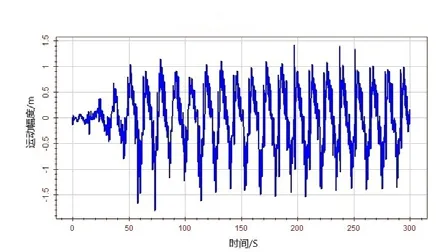
图8 横荡运动加速度时历

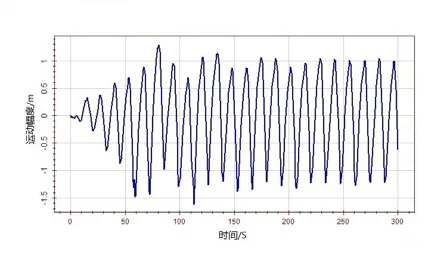
图9 艏摇运动速度时历

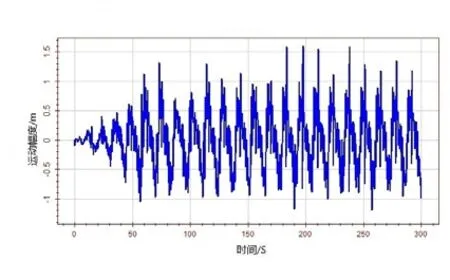
图10 艏摇运动加速度时历

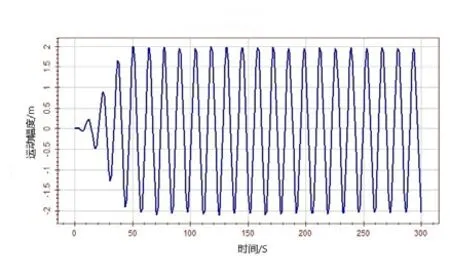
图11 垂荡运动速度时历

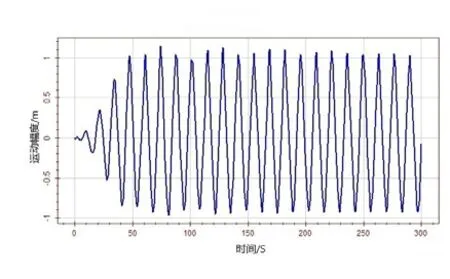
图12 垂荡运动加速度时历

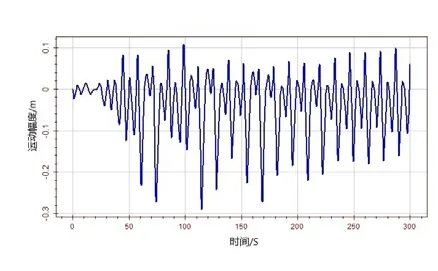
图13 纵摇运动速度时历

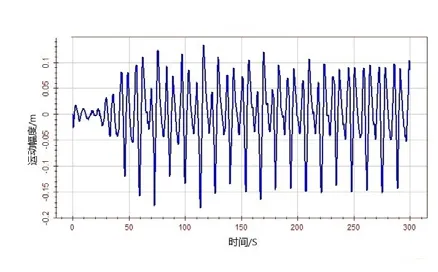
图14 纵摇运动加速度时历

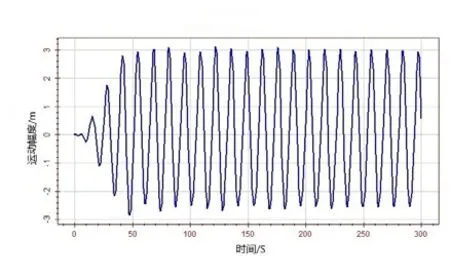
图15 横摇运动速度时历

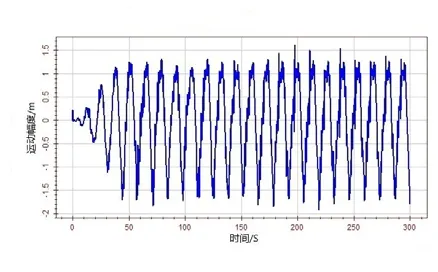
图16 横摇运动加速度时历

5.2 水深对平台运动响应的影响

选取无限水深（记为 WasimAcivity1）、150 m（记为 WasimAcivity2）以及 50 m（记为WasimAcivity3）水深3种工况来分析水深变化对平台6自由度运动响应的影响。由图17～图22可看出，水深对平台的6个自由度运动的影响都比较大。由于环境载荷沿船长方向，所以纵荡运动最激烈。运动幅度随着水深的减小而增大，水深越浅纵荡越大且不太稳定。横荡运动随着水深的减小而减小，艏摇运动随着水深的减小而减小。垂荡、横摇和纵摇运动比较稳定。

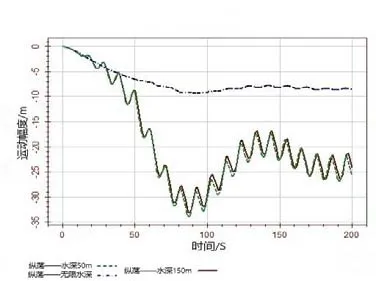
图17 不同水深情况下纵荡运动时历曲线

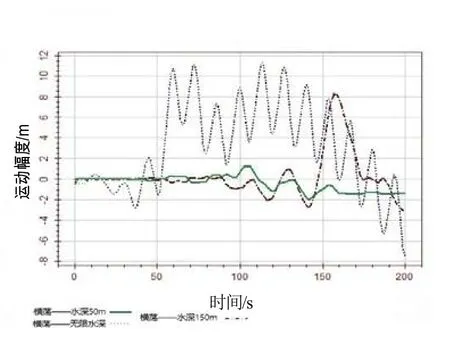
图18 不同水深情况下横荡运动时历曲线

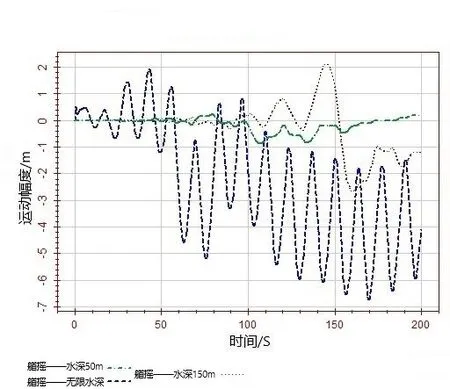
图19 不同水深情况下艏摇运动时历曲线

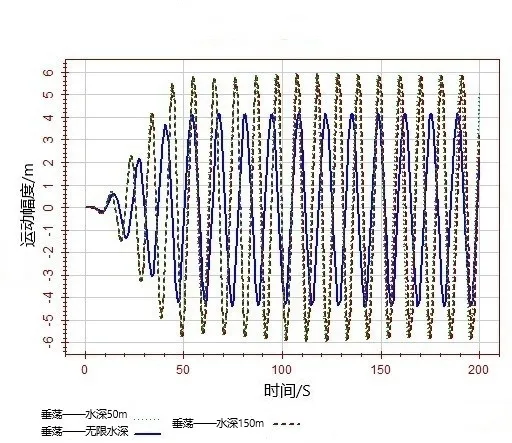
图20 不同水深情况下垂荡运动时历曲线

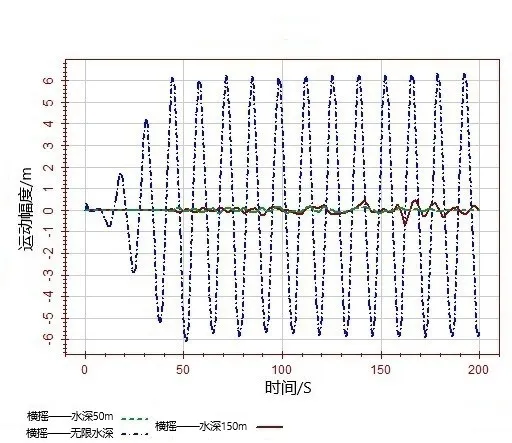
图21 不同水深情况下横摇运动时历曲线

图22 不同水深情况下纵摇运动时历曲线

6 结论

本文对比分析了桩腿不同下放高度对平台运动响应的影响，对运动响应进行了短期预报，根据预报极值预估桩腿发生触底时桩腿下放高度。研究表明浪向角及波浪周期对平台运动影响较大，平台的运动响应存在随着桩腿下放而变小的规律，但总体响应幅值变化不大，根据桩腿触底分析提出适合平台就位的环境条件。通过与DNV规范值对比，平台的波浪诱导载荷预报极值在规范规定范围内。