水下监测设备翼型导流罩三维流固耦合研究

代绍岭，管 官

（1. 黄海造船有限公司，山东威海 264309；2. 大连理工大学 船舶工程学院，辽宁大连 116024）

0 引言

随着海洋开发事业的不断发展进步，解决水下目标的信息特征, 以实现对水下目标的探测、定位和识别越来越受到人们的重视。而使用水下监测设备进行信息采集时，在水流影响下常常存在设备失稳及振动等问题，不利于信息的准确收集。

为维持水下监测设备稳定，学者们从很多方面进行了研究，如潜标系统、浮标系统及导流罩等。其中导流罩方案方便监测设备与其他器件的整合封装，故本文重点研究此方案。

如何评判导流罩的稳定效果也一直是研究重点，主要分为理论推导、模型仿真及试验测试几个方法。由于设计过程中构件复杂性及试验条件的限制，本文针对模型仿真法进行研究。由于流固耦合计算所需计算资源庞大，而较计算复杂模型的流固耦合响应就更难完成，故目前学者们往往选择二维流固耦合计算来分析导流罩稳定作用，这种分析方法简便但对运动分析不够准确。故本文针对所设计的翼型导流罩进行三维流固耦合计算，并对所得振动响应进行分析，证明了导流罩对水下监测设备的稳定作用。

1 流固耦合

针对水下监测设备稳定性问题，本文重点分析海流影响。流固耦合研究的是流体和固体之间的相互影响和相互作用，是多场耦合问题在科学和工程中的应用之一。

1.1 湍流模型

常见的湍流模型有 k-ε模型、k-ω 模型、Spalart-Allmaras模型和雷诺应力模型等，本文选取的是k-ε模型，它将理论及经验公式结合，利用实验总结出道经验公式解决粘性底层内的流动问题，是兼具内存占用小和高精度的常用湍流模型。

1.2 耦合交界面

流固耦合也遵循最基本的守恒原则，流固耦合交界面上应遵守应力守恒、位移守恒、热流量守恒以及温度守恒，如式（1）所示。

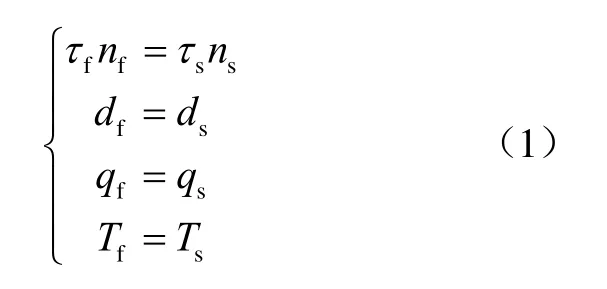
式中：τ为应力；d为位移；q为热流量；T为温度；下标f和s分别表示流体和固体。

1.3 流固耦合分类

流固耦合的大致分类情况见图 1，本文所研究的水下监测设备及导流罩流固耦合，须同时考虑固体对流体以及流体对固体的的相互影响，故选择双向流固耦合。

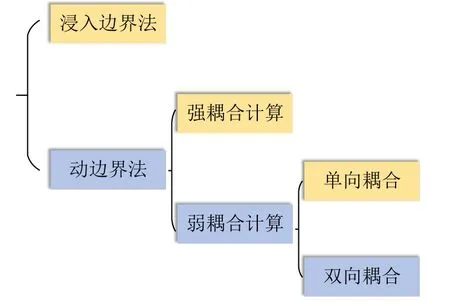
图1 流固耦合分类

2 仿真计算

为分析导流罩对水下监测设备的稳定作用，分别对水下监测设备及加装导流罩的监测设备进行流固耦合分析，通过对比二者的位移响应来进行分析判断。

ANSYS Workbench可建立分析流程并在流程中激活相关的应用程序，工作界面友好，操作人性化。故选用ANSYS Workbench进行双向流固耦合，以得出涡激振动位移响应。

2.1 双向流固耦合平台搭建

选用Ansys进行固体动力学分析，Fluent进行流体计算。在 Analysis Systems栏和 Component Systems栏中分别调出流体模块（Fluid Flow）、结构模块（Transient Structural）以及系统耦合器（System Coupling），并连接形成双向流固耦合分析系统（见图 2）。

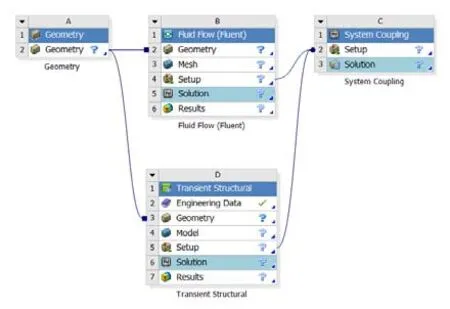
图2 双向流固耦合分析

2.2 模型建立

为对比带导流罩监测设备对振动的抑制作用，本文选用某一水下监测设备安装导流罩前后2个模型进行流固耦合计算。此监测设备为一250 mm长变截面柱体，被尼龙绳牵拉置于流体中，流固耦合几何模型见图3。流域尺寸为0.5 m×0.5 m×0.3 m。应用Transient Structural和Fluid Flow中的modal模块分别对水听器和流域划分网格，得到有限元模型见图4。

图3 水下监测设备流固耦合几何模型（未安装导流罩）

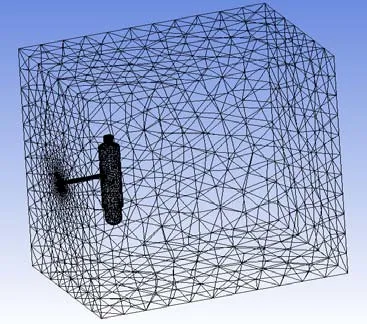
图4 水下监测设备流固耦合有限元模型（未安装导流罩）

导流罩为930 mm长的翼型截面柱体，同样被尼龙绳牵拉置于流体中。为更好地捕捉流体运动轨迹，设置流域尺寸宽20 d，长40 d，与入口距离10 d（

d

为翼型截面弦长），最终得出流域尺寸为14 m×28 m×5 m。安装导流罩监测设备的几何模型见图5，对其划分网格，得到有限元模型见图6。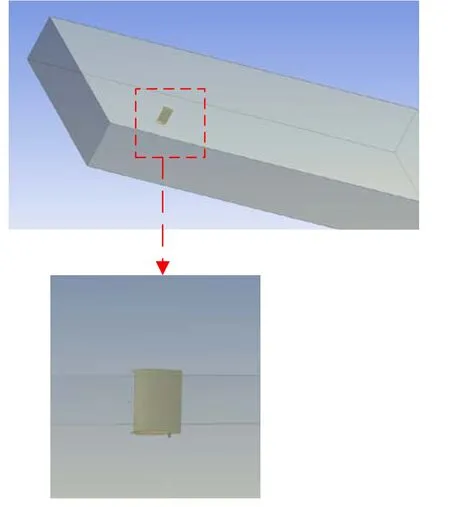

图5 水下监测设备流固耦合几何模型（安装导流罩）

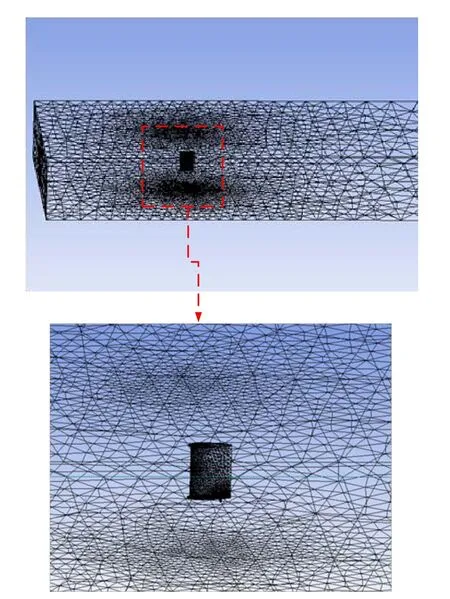
图6 水下监测设备流固耦合有限元模型（安装导流罩）

2.3 参数设置

流固耦合分析中，重点在于流体分析的参数设置。在流体分析中涉及到的重要参数设置包括湍流模型选择、边界条件设置以及动网格设置。

1）湍流模型：Fluent提供了多种湍流模型，本文选择标准

k-ε

模型。标准

k-ε

模型系数由经验公式给出，计算比较稳定。

2）边界条件：位于计算流域的左端面处的速度入口设置端面上为均匀来流，速度为1.5 m/s；位于计算流域右端面处出口边界设置为outflow；其余流体边界设置为wall。

3）动网格：动网格技术用于模拟仿真计算区域随时间的变化。本文应用弹簧光顺法（Spring-Based Smoothing）进行分析，它能够根据边界节点上已知的位移，平滑地调整流域内节点的位置。通过基于弹性变形的网格光滑更新体网格，而不改变网格之间的连通性。

2.4 流固耦合响应结果分析

经过对水下监测设备及带导流罩监测设备的流固耦合分析，得到了监测设备下端点的振动响应。

未安装导流罩的水下监测设备振动响应的稳定部分结果见图7，从图7可看出其位移相对杂乱且频率高，红线为其拟合的正弦函数曲线，函数为

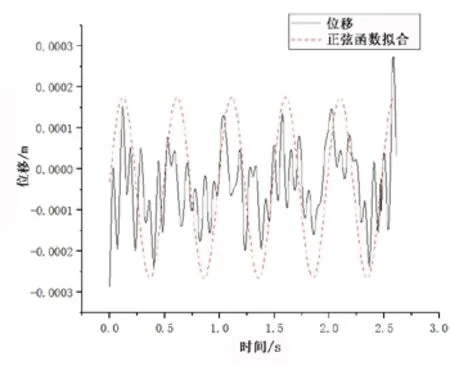
图7 水下监测设备振动响应位移结果（未安装导流罩）

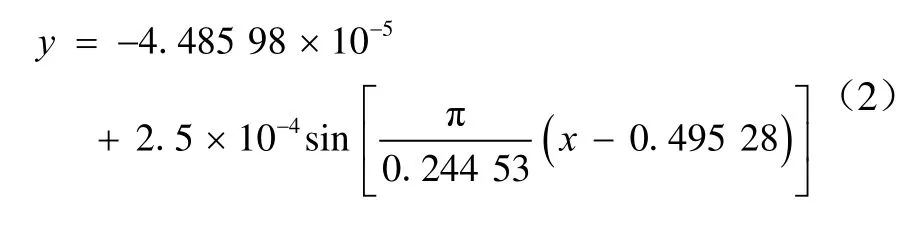
未安装导流罩的水下监测设备振动的振幅为2.5×10m，周期为0.489 s。

安装有导流罩的监测设备振动位移响应相对稳定部分结果见图 8，位移有下降趋势，结果的正弦函数拟合曲线为图8中红线，函数为

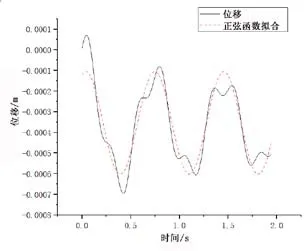
图8 水下监测设备振动响应位移结果（安装导流罩）

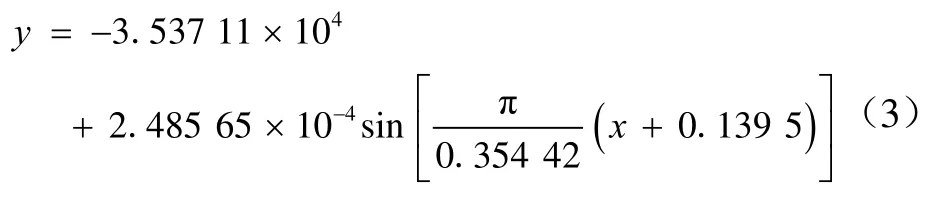
安装有导流罩的水下监测设备振动的振幅为2.485 65×10m，周期为0.708 s。

对比可知，安装导流罩后水下检测设备振动平稳，周期明显增大，也就是频率有效减小，这代表其位移响应相对稳定。此外，振幅也略微减小。

3 结论

在海洋环境中，水下监测设备往往无法保持稳定正常工作，故为其加装翼型导流罩。本文对水下监测设备及带导流罩监测设备分别进行了三维流固耦合计算，得到振动位移响应。经分析证明了无论从振幅还是频率方面，安装导流罩均有降低作用，可增强监测设备在水中的稳定性。