改进的L-矩阵线性系统的预条件迭代法
程 军,李正彪,朱 彪
(曲靖师范学院 a.学前与初等教育学院,b.数学与统计学院,中国 曲靖 655011)
求解线性方程组
Ax=b,
(1)
其中A∈Rn×n是非奇矩阵,且b∈Rn×1,x∈Rn×1。若A=M-N,且M是非奇异矩阵。式(1)的基本迭代解法可以表示为
Mxk+1=Nxk+b,k=0,1,…。
当aii≠0,i=1,2,…,n时,假设
A=I-L-U,
(2)
其中I是单位矩阵,U是严格上三角矩阵,L是严格下三角矩阵,通过对矩阵A进行如上形式的分裂[1],可得相应的SOR迭代法:
x(i+1)=(I-ωL)-1[(1-ω)I+ωU]x(i)+(I-ωL)-1ωb,i=1,2,…。
其迭代矩阵为
Lω=(I-ωL)-1[(1-ω)I+ωU],
(3)
其中参数ω(ω≠0)称为松弛因子。显然,当ω=1时,SOR迭代法就转化为Gauss-Seidel迭代法。当迭代矩阵谱半径小于1时,其迭代法是收敛的,且谱半径越小,其收敛速度越快。为了加快其迭代法的收敛速度,通常用预条件迭代法来求解方程组(1),即
PAx=Pb,
其中P为预条件子,且P为非奇异矩阵。类似地,如果假设
PA=D*-L*-U*,
就可以得到相应的预条件SOR迭代法,其迭代矩阵为
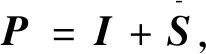
拟消去A的次对角线上的元素,进而提高了其相应的迭代法的收敛速度,其中A为L-矩阵且需满足条件0 为方便起见,首先给出相关字义和引理。设C=(cij)∈Rn×n是n阶实矩阵,diag(C)是对角矩阵,并且其对角矩阵的对角元素为cii,设A=(aij)和B=(bij)是n阶实矩阵。如果aij≥bij(i,j=1,2,…,n),记A≥B。如果A≥0(aij≥0)(i,j=1,2,…,n)称矩阵A是非负矩阵,如果A≥B,则A-B≥0。ρ(·)表示矩阵的谱半径。 定义1 矩阵A是一个L-矩阵,如果aii≥0i=1,2,…,n,并且aij≤0,对所有的i,j=1,2,…,n且i≠j。 引理1[9]若A≥0是不可约的n×n矩阵,则 (1)A有一个正的实特征值等于它的谱半径; (2)ρ(A)对应的特征向量x>0; (3)ρ(A)是A的单特征值。 引理2[10]若A是非负矩阵,则 (1)如果αx≤Ax对某一个非负向量x且x=0成立,那么α≤ρ(A); (2)如果Ax≤βx对某一个正向量x成立,那么ρ(A)≤β,进一步,如果A是不可约并且若有0≠αx≤Ax≤βx,αx≠Ax和Ax≠βx对某一非负向量x成立,那么α<ρ(A)<β且x是一正向量。 引理3[9]设A=M1-N1=M2-N2为A的两个正则分裂且A-1≥0。如果N2≥N1≥0,那么 0≤ρ(M1-N1)≤ρ(M2-N2)<1。 进一步,如果A-1>0且N2≥N1≥0,那么除等号外 0<ρ(M1-1-N1)<ρ(M2-1N2)<1。 阵且存在一个非零集合α⊂N={1,2,…,n-1}使得 考虑预条件线性方程组 (4) 对式(4)运用SOR迭代法,得到其相应的迭代矩阵为 (5) 为了得到证明一下主要结果,需要用到以下引理: 证:由于矩阵A是L-矩阵,可知L≥0,而且矩阵L是一个严格下三角矩阵。则(I-ωL)-1=I+ωL+ω2L2+…+ωn-1Ln-1≥0由式(3),可得 Lω=(I-ωL)-1[(1-ω)I+ωU]=[I+ωL+ω2L2+…+ωn-1Ln-1][(1-ω)I+ωU]= (1-ω)I+ωU+ω(1-ω)L+ω2LU+(ω2L2+…+ωn-1Ln-1)[(1-ω)I+ωU]= (1-ω)I+ωU+ω(1-ω)L+T, 其中 T=ω2LU+(ω2L2+…+ωn-1Ln-1)[(1-ω)I+ωU]≥0, 即得Lω是非负的,又由文献[6]中的引理1,可知Lω是不可约的。由式(5)得 其中 定理1 设式(3)和(5)分别由SOR迭代法作用于式(1)和(4)得到的迭代矩阵。0<ω<1,如果A是一个L-矩阵且存在一个非零集合α⊆N={1,2,…,n-1}使得 则 Lωx=λx, 其中λ=ρ(Lω),即得: [(1-ω)I+ωU]x=λ(I-ωL)x。 对于x>0,则 设 其中μi=-(ω-1)ai,i+1ai+1,ixi-ai,i+1xi+1≥0,i=1,2,…,n-1。 注:显然,如果α=N,预条件因子即转化为[11]中的预条件因子。 易知,当ω=1时,SOR迭代法就转化为Gauss-Seidel迭代法。进而,可得到如下推论: 那么 证:设 其中 注2通过上面的讨论,易知,ω=1是SOR迭代法的最优数值。即,在满足0<ω≤1条件下,Gauss-Seidel迭代法的收敛速度比SOR迭代法的收敛速度快。 这里给出相应的数值算例,来说明前面迭代法的结果。 例:设式(1)的系数矩阵A为 类似地,PG-S表示用本文中提出的预条件Gauss-Seidel迭代法,PEG-S表示用预条件Gauss-Seidel迭代法。表1和表2给出了当取不同参数ω和n的值时,迭代矩阵谱半径的大小、迭代次数、CPU时间和误差。表中的数值是通过Matlab 7.0计算获得。 表1 定理1的数值实验Tab. 1 Numerical experiment of theorem 1 表2 推论1的数值实验Tab. 2 Numerical experiment of inference 1 通过表1和表2中的数值实验表明,在满足定理1以及推论1条件的情况下,其结论同样是成立的。且我们提出的预条件子比很多文献中提出的预条件子较优。同时,该数值算例的结果也说明了在满足0<ω≤1下,预条件Gauss-Seidel迭代法的收敛速度比预条件SOR迭代法的收敛速度快一些。1 预备知识
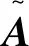
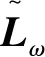
2 预条件SOR迭代法
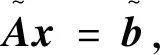
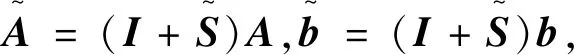
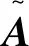
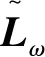
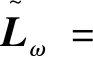
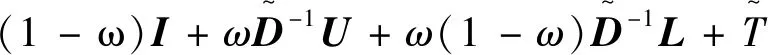
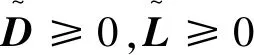
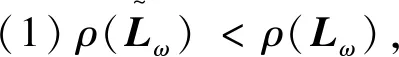
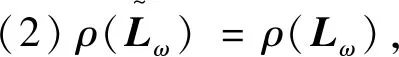
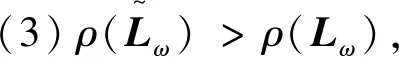
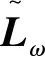
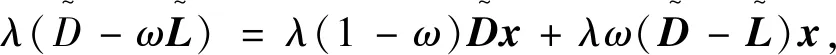
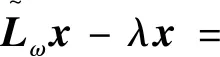
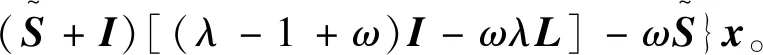
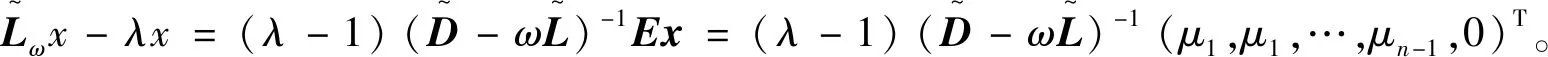
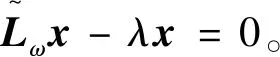
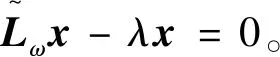
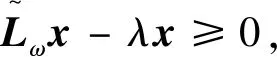
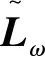
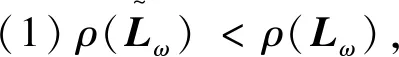
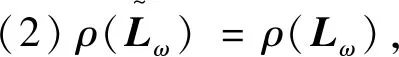
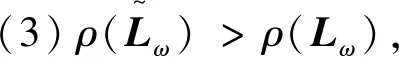
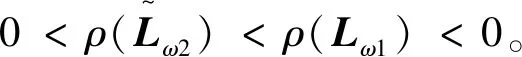
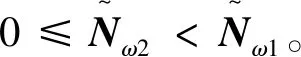
3 数值算例
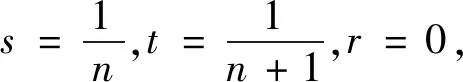


4 结论

