多漏斗放矿过程中散体介质力链演化特征量化研究

陈庆发，刘恩江，秦世康

(广西大学资源环境与材料学院，广西南宁，530004)

对于由矿石颗粒组成的散体介质体系，目前的研究大多从宏观尺度描述其流动规律，但未从细观尺度对散体内部复杂的力学特性进行探讨[1−3]。而散体介质具有独特的多尺度结构，即单个颗粒(微观尺度)、接触力沿接触路径传递所形成的力链(细观尺度)以及散体介质整体(宏观尺度)[4−5]。随着对散体介质研究的深入，多尺度研究法受到了人们的广泛关注。在孙其诚等[6]提出的“颗粒−力链−散体介质”多尺度结构研究框架中，力链是连接单个颗粒与散体介质整体的桥梁，力链网络的复杂响应决定了散体介质体系的宏观行为。因此，开展放矿过程中散体介质体系内部力链演化特征研究具有重要意义。

近年来，学者们针对力链受力特性及其演化特征开展了大量研究。在散粒体宏观形变方面，安令石[7]基于有限差分−离散元耦合原理，建立冻土路基耦合计算模型，分析了路基土颗粒间力链演化规律及平均配位数的变化规律，从细观角度揭示了路基的变形机理；罗滔等[8]以尖角堆石颗粒材料为研究对象，借助于力链网络形态演化规律，分析了试样先缩减后剪胀的宏观特性。在散体介质力学行为方面，TORDESILLAS 等[9]从力链演化和运动学的角度研究了应变局部化过程中非共轴性的微观力学起源，探讨了单剪试验和双轴试验中试样宏观力学特性的关系；胡超[10]通过堆石体双轴压缩多尺度数值试验，在细观层面研究了堆石颗粒体系的力学特性；ESTEP等[11−12]采用光弹性技术和数字图像处理方法分别研究了密集颗粒流中颗粒的位移与运动方向、力链的动态力学行为对颗粒流系统基底的影响，并对力链中的损伤点进行了预测。

上述研究表明，散体介质宏观行为与力链存在密不可分的关系。因此，本文构建多漏斗放矿数值试验模型，并对多漏斗放矿过程中散体介质体系内部力链数量、长度、强度、方向等演化特征进行量化研究，以期揭示散体介质体系细观层面的力学特性，加强对放矿过程中矿石流动规律的认知。

1 数值试验模型的构建

1.1 数值试验模型尺寸参数的选择

考虑模型的可实现性及试验的便利性，结合文献[13]中关于试验模型相似常数的取值，确定物理试验模型与实际矿块原型的相似比为1∶25[13−14]。

物理试验模型与矿块结构原型参数取值对比如表1所示。

表1 物理试验模型与矿块结构原型参数取值对比Table 1 Comparison of parameter values between physical test model and ore block structure prototype

本文数值试验模型与文献[14]中物理试验模型参数保持一致。

1.2 矿石散体参数的测定

有关矿石颗粒密度、块度、内摩擦角和黏聚力等物理力学参数的测定详见文献[14]，下面对部分参数的测定过程进行介绍。

1.2.1 自然安息角的测定

自然安息角φz是指自然湿度条件下，散体介质在某一特定条件下堆积，其自然静止坡面与水平面之间的夹角。安息角可用无底圆筒法进行测量，计算公式为

式中：φz为自然安息角；hzd为椎体高度；dzd为椎体底面直径。

散体介质安息角测定实验结果如表2所示。

表2 安息角测定实验结果Table 2 Experimental results of repose angle measurement

由表2 可知，多次测定后，安息角均值为35.79°。因此，数值试验模型中的矿石散体的自然安息角设定为35.79°。

1.2.2 矿石块度的测定

松散矿石的块度U是指松散矿石中不同尺寸矿石质量分数，其计算公式为

式中：mj为某一粒级石样的质量；mz为石样总质量。

试验中，矿石块度的测定采用筛分法。首先，将石块按粒径划分为不同等级，并选取4个相对应尺寸的筛格，孔径分别为2，4，7 和12 mm；然后，随机选取石样，用四分法对石样进行缩分，将缩分后的石样用选取的筛格进行筛分，筛分时必须按规定的给料制度给料并保证一定的震荡时间，确保筛分结果具有可比性；最后，在筛分完成后，称取筛出的某一级块度范围内的石子质量，计算出某一块度石子的质量分数。

矿石块度测定实验结果如表3所示。

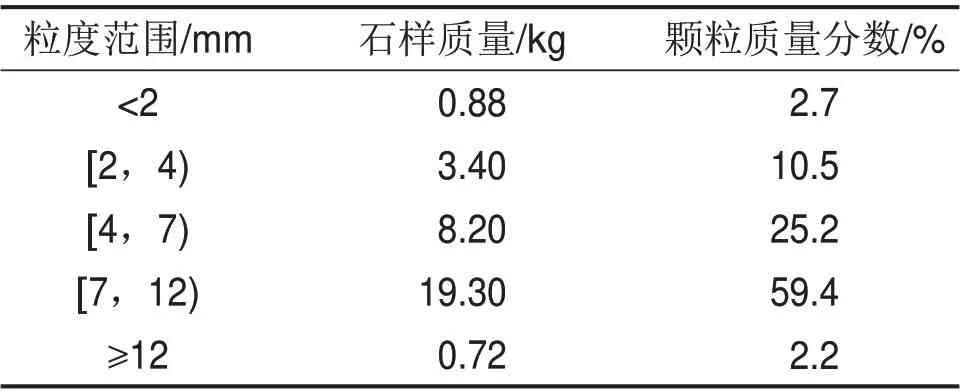
表3 矿石块度测定实验结果Table 3 Experimental data of ore block size determination

1.3 接触模型及其细观参数的选择

以矿石散体物理力学参数测定结果为基础，选择合理接触模型并设定其细观参数。

矿石颗粒是由大量形态不同的块体组成，若采用随机分布的方法生成矿石颗粒，则在后续分析过程中会频繁出现漏斗堵塞的情况，影响最终的统计结果。WENSRICH 等[15]建议通过调整抗转动摩擦因数来反映颗粒形态对散体介质体系流动的影响。在PFC 软件所提供的接触模型中，抗滚动线性接触模型增加了抗滚动系数，会降低颗粒的转动能力，颗粒间接触与非均匀块体间的接触相似[16]。因此，本文选取抗滚动线性接触模型模拟矿石颗粒之间的接触，以抵消矿石颗粒形态对矿岩散体流动的影响，并根据表3中的矿石块度测定结果，选取颗粒质量分数最大的粒度范围作为参考，将数值试验模型中矿石颗粒半径设置为8 mm。

抗滚动线性接触模型细观参数主要包括颗粒的有效模量、法向刚度比和切向刚度比、摩擦因数、抗转动系数。其中，有效模量与岩石颗粒的弹性模量有关，法向刚度比和切向刚度比与岩石的泊松比有关，这2个参数可通过相关的力学试验获得，其余参数则可通过颗粒的自然安息角进行标定[17]。本文在安息角测定结果的基础上，通过矿石颗粒堆积数值试验，并结合数值试验模型的实际情况，设定模型中的摩擦因数及抗转动系数。

1.4 模型的构建

多漏斗放矿数值试验模型的构建过程如下。

1)墙体生成。利用“wall creat”命令构建1个长为168 cm，宽为128 cm，放矿口间距为24 cm的多漏斗放矿数值试验模型。整个模型的边壁由23面墙组成，其中，底部由7 个尺寸相同(从左到右依次编号为1～7 号)的放矿口组成，放矿口侧壁与水平面呈45°夹角，所有放矿口共计21面墙；剩余2面墙代表数值试验模型的边壁。

2)初始颗粒的生成。通过“ball generate”命令在墙体模型y轴正方向0.08～128.00 cm 范围内生成若干矿石颗粒，这些颗粒的重力加速度g=9.81 m/s2，其细观力学参数如表4 所示。为使散体介质体系内的颗粒尽快充填密实，初始颗粒的接触模型设置为线性接触模型，颗粒之间的摩擦因数取0.3；同时，为方便观察放矿过程中矿石颗粒的流动现象，待模型平衡后，以10 cm为间隔将矿石颗粒标记为不同的颜色。

表4 墙体及初始矿石颗粒力学参数Table 4 Mechanical parameters of wall and initial ore particles

3)真实颗粒的生成。模型平衡后，将颗粒接触模型由线性接触模型变为抗滚动线性接触模型，此时散体介质体系内颗粒的细观力学计算参数如表5 所示。打开放矿口后，矿石颗粒从放矿口放出，矿石流动随即开始。放矿过程中，每计算若干时步，关闭放矿口，待模型在自重作用下解算平衡后，再次打开放矿口，进入下一循环计算过程，直至放矿结束。

表5 真实颗粒的力学参数Table 5 Mechanical parameters of real particles

构建的放矿数值试验模型如图1所示。

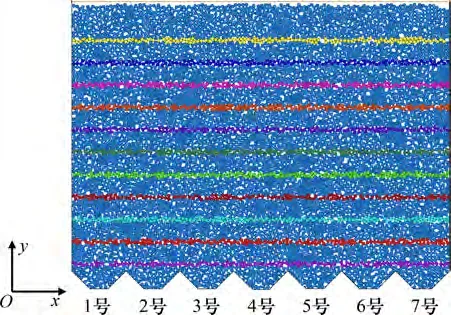
图1 放矿数值试验模型Fig.1 Numerical model of ore drawing

2 力链的识别

力链的形成需满足3 个条件[18−20]：1)颗粒串内相互接触颗粒之间的接触为强接触；2)必须由3个及3个以上相互接触的颗粒组成颗粒串；3)颗粒串内相邻接触之间的夹角应小于某个角度α。

根据以上3 个成链条件，设置力链识别判据如下。

2.1 强接触判据

强接触为接触力大于或等于平均接触力的接触，散体介质体系内平均接触力-F为

式中：N为接触总数，Fi为接触编号为i的接触力。

因此，强接触判据为：Fˉ≤Fi。

2.2 力链长度判据

颗粒串必须由3个及3个以上相互接触颗粒所组成，即该颗粒串中接触的个数必须大于或等于2，故力链的长度L表达式为

式中：n为1条力链上所含接触的个数。

因此，力链长度判据为：L≥3。

2.3 接触夹角判据

在离散元模型中，接触为2个颗粒中心点之间的连线，假如颗粒I，Ⅱ和Ⅲ之间存在2个接触，颗粒I和Ⅱ之间的接触为AB，其法向量为(xAB，yAB)，颗粒Ⅱ和Ⅲ之间的接触为BC，其法向量为(xBC，yBC)，那么接触AB与接触BC之间的夹角θ为

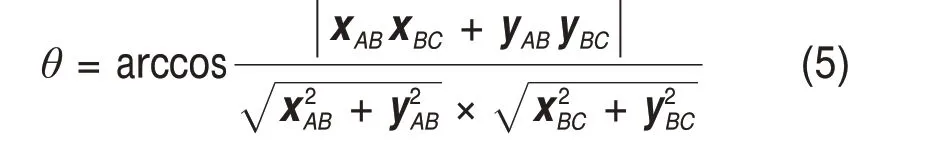
颗粒成链的角度阈值α为

式中：-Z为模型内颗粒的平均配位数。

因此，颗粒成链的接触夹角判据为：α≥θ。

根据力链识别判据，编写力链识别程序，实现力链的自动检索及识别。力链自动检索及识别的具体流程如下：首先，利用PFC2D导出不同放矿节点条件下散体介质体系内部颗粒位置、半径及接触位置、接触力等信息；然后，为实现条件1)中所提要求，筛选出体系中的强接触；最后，依据条件2)与条件3)，利用Matlab 软件编制力链识别程序，实现对力链的检索及识别。

3 力链演化特征

3.1 力链数量及长度变化

基于放矿数值试验模型，利用PFC2D输出的不同放矿节点条件下散体介质体系内部接触力信息，对所有接触力中的强接触进行筛选，并在筛选出的强接触基础上，利用力链识别程序实现对力链接触的筛选。不同放矿节点条件下散体介质体系内部力链数量统计结果如图2所示。

图2 多漏斗放矿过程中散体介质体系内部力链数量变化规律Fig.2 Variation law of internal force chain of bulk medium system during multi-funnel drawing

由图2可知，多漏斗放矿过程中，体系内部力链数量由第1次放矿结束时的503条逐渐减少至放矿结束时的69条，总体上呈指数形式减少。同时，根据力链形成所需具备的3个条件可知，即便是强接触，也并不能全部参与力链的组成。

多漏斗放矿过程中强接触与力链接触占比如图3 所示。由图3 可以看出，多漏斗放矿过程中，大部分接触为弱接触，强接触占比较小，保持在37%左右，变化幅度不超过3%；而力链接触占比仅14%左右，变化幅度也不超过3%。

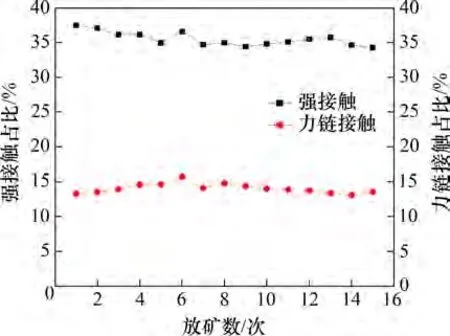
图3 多漏斗放矿过程中强接触与力链接触占比Fig.3 Proportions of strong contact and force chain contact during multi-funnel drawing

综合图2 和图3 可知，在多漏斗放矿过程中，随着矿石颗粒的持续放出，体系内部矿石颗粒逐渐减少，接触总数也在不断减少，但体系内部力链不断发生断裂重组，并在断裂重组过程中达到新的平衡，且由于强接触占比与力链接触占比均保持相对稳定，使得力链数量随放矿次数呈指数形式减少。

基于对力链数量及强接触、力链接触占比的研究，将不同放矿节点条件下体系内部力链数进行归一化处理，进一步对不同放矿节点条件下体系内部力链长度的分布概率进行统计，结果如图4所示。

图4 多漏斗放矿过程中力链长度概率分布Fig.4 Probability distribution of force chain length in multi-funnel drawing process

通过图4可知，不同放矿节点条件下，力链长度的分布概率表现出相似的变化规律，即力链长度越长，其形成的概率越小，两者呈指数关系递减(需要注意的是，存在力链长度大于15 的情况，但在力链长度统计过程中，长度大于15 的力链数量极少，不会对其变化规律产生影响)。对多漏斗放矿过程中散体介质体系内部力链长度概率分布进行拟合：

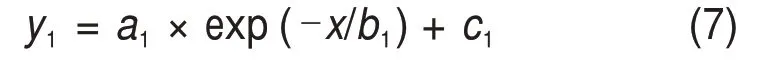
式中：a1=15.71，b1=0.93，c1=0.04。拟合相关系数R2=0.998，说明拟合效果好。

利用式(7)对不同放矿节点条件下力链长度概率分布进行拟合时，拟合相关系数均达到0.99 以上，说明拟合效果好。对比发现，本文得到的不同放矿节点条件下力链长度概率分布规律与文献[21−22]中所得规律一致。

根据图4中力链长度概率分布的规律，将长度等于3的力链视为短力链，长度为4～6的力链视为中等长度力链，长度大于6的力链视为长力链，统计不同放矿节点条件下3种力链的概率分布，如图5所示。

图5 多漏斗放矿过程中3种类型力链概率分布Fig.5 Probability distribution of three types of force chains during multi-funnel drawing

由图5 可知：在多漏斗放矿过程中，3 种力链的整体分布规律是一致的，即不同放矿节点下，短力链出现概率最大，中等长度力链出现概率次之，长力链出现概率最小。但3种力链的分布也有一定的差别：对于短力链和中等长度力链而言，在不同放矿节点中总是呈现出相反的变化规律即短力链出现概率增加时，中等长度力链出现概率就会减小，且短力链与中等长度力链出现概率波动幅度较大；而对于长力链，从放矿开始直至第12 次放矿过程结束，其分布概率保持相对稳定，但从第13 次放矿开始至整个放矿过程结束，其分布概率逐渐减小为0。

在放矿前中期，散体介质体系内部力链发生断裂重组，导致体系内部一方面不断形成长力链，另一方面，长力链断裂、弯曲形成中等长度力链及短力链；随着放矿的进行，体系内部不断重复发生力链断裂重组，使得3种力链的分布情况保持基本不变；至放矿后期，受体系内矿石颗粒数量的影响，形成长力链的概率变小，但长力链仍断裂、弯曲形成中等长度力链及短力链，使得力链分布呈现出以短力链和中等长度力链为主，长力链逐渐减少的现象。

3.2 力链强度演变过程

力链强度为某条力链中所有法向接触力的均值，其表达式为

式中：f为力链强度。

在多漏斗放矿过程中，不同放矿节点条件下力链强度演变规律如图6所示。

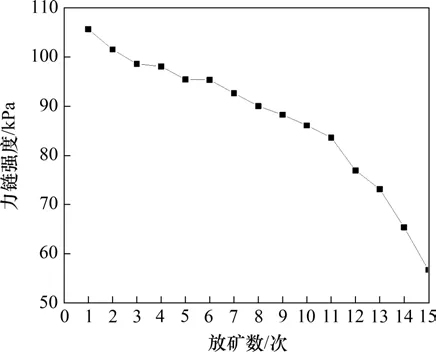
图6 多漏斗放矿过程力链强度演化规律Fig.6 Strength evolution law of force chain during multifunnel drawing

从图6可知，在多漏斗放矿过程中，随着矿石颗粒放出，力链强度呈指数形式减小，这是因为：在放矿初期，受到矿石颗粒自身重力影响，颗粒之间接触紧密，因此力链强度较大，而随着矿石颗粒放出，矿房内的颗粒逐渐减少，颗粒之间接触的紧密程度有所下降，颗粒与颗粒之间的接触力逐渐变小，力链强度也逐渐减小。

根据不同放矿节点条件下散体介质体系内部力链强度的变化规律，对体系内部力链强度的概率分布进行统计，结果如图7 所示。由图7 可知，在多漏斗放矿过程中，不同放矿节点条件下力链强度的分布概率均先呈指数形式上升，再呈指数形式下降，并在0.65处出现峰值；同时，不同放矿节点条件下力链强度概率分布规律相似，这表明在由矿石颗粒组成的散体介质体系内部，力链网络大部分是由弱力链组成，强力链只占力链网络的小部分，强力链和弱力链相互交织构成一个完整力链网络，共同维持着整个散体介质体系的稳定。

图7 不同放矿节点条件下力链强度概率分布Fig.7 Probability distribution of force chain strength under different ore drawing node conditions

对不同放矿节点条件下散体介质体系内部的力链强度分布概率进行拟合：

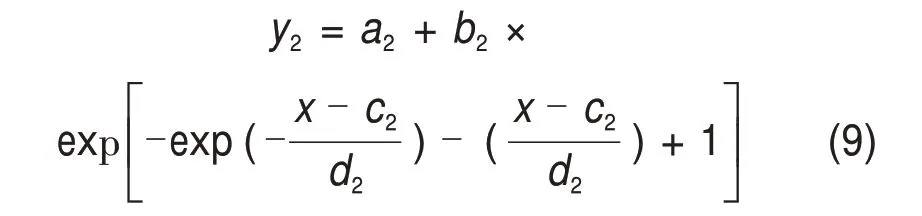
式中：a2=0.019，b2=0.616，c2=0.756，d2=0.253。

利用式(9)对力链强度分布进行拟合后发现，拟合相关系数达到0.99以上，拟合程度较好。

3.3 力链方向分布变化

为了解放矿过程中散体介质体系内部力链方向分布的变化规律，将360°等分为36 个区间，并对每个区间内力链数量及强度进行统计，求出每个区间内力链的平均强度，由此可得不同放矿节点条件下力链方向分布，如图8 所示(图中仅选择具有代表性的力链方向)。

图8 多漏斗放矿过程中力链方向演化规律Fig.8 Evolution law of force chain direction during multifunnel drawing

为定量描述散体介质体系内部力链方向的变化规律，结合ROTHENBURG等[23]的研究成果，对散体介质体系内部力链强度与方向的统计结果进行拟合：

式中：fn(θ)为力链强度的分布函数；f0为力链平均强度；βn为傅里叶级数，表示力链方向分布的各向异性程度；θn为力链的主方向角；ω为频率。

通过对力链方向进行拟合发现，式(10)能较好地反映对应放矿节点力链方向的波峰，总体拟合效果较好。不同放矿节点条件下参数拟合结果如表6所示。

综合图8及表6可知，在第12次放矿前，矿房内矿岩颗粒呈整体下移的状态，体系自重是力链方向角的主要影响因素。因此，力链主要沿铅垂方向分布，故散体介质体系内部力链分布主方向角θn始终保持在90°左右，力链方向分布形态呈花生状；对于各向异性程度表征参数βn而言，由于除铅垂方向外，其余各方向的力链逐渐减少，导致第12 次放矿结束前各向异性程度表征参数βn逐渐增大。而自第13次放矿开始，体系内部颗粒减少，放矿口侧壁逐渐成为影响力链方向分布的主要因素，使得与水平方向呈45°的力链逐渐增多，体系内部力链分布主方向角θn由84.40°变化为30.16°，力链方向分布形态呈花瓣状；由于与水平方向呈±45°的力链逐渐增多，使得各向异性程度表征参数βn逐渐减小。

表6 不同放矿节点条件下参数拟合结果Table 6 Fitting results of parameters under different drawing nodes

对于体系内部力链平均长度f0而言，因为其经过归一化处理，所以一直保持不变。

4 结论

1)在多漏斗放矿过程中，力链数量总体上呈指数形式减少，但不同放矿节点条件下力链的组成情况相同，即短力链占比最大，中等长度力链占比次之，长力链占比最小；不同放矿节点条件下力链长度的概率分布也呈指数形式减少。

2) 在放矿过程中，力链强度波动范围较大，总体上随放矿次数增加而呈指数形式减少；不同放矿节点条件下力链强度的概率分布规律也具有一致性，即力链强度的分布概率均先呈指数形式上升，后呈指数形式下降，并在0.65-F处达到峰值。

3)在放矿前中期，散体介质体系内部力链分布主方向角θn始终保持在90°左右，各向异性程度表征参数βn逐渐增大；在放矿后期，与水平方向呈45°的力链逐渐增多，体系内部力链分布主方向角θn由84.40°变化为30.16°，各向异性程度表征参数βn逐渐减小。