应力三轴度对聚乙烯材料损伤及断裂的影响

韩丽美，张毅,2，叶贵根，薛世峰，贾朋

(1. 中国石油大学(华东)储运与建筑工程学院，山东青岛，266580；2. 阿尔伯塔大学机械工程系，加拿大埃德蒙顿，T5J4P6)

聚乙烯(polyethylene，PE)是一种高分子聚合物材料，具有耐磨、耐腐蚀、耐冲击和耐化学性等优点，广泛应用于燃气管、水管等管道制造业中。在燃气管制造业中，PE 管道已经成为主要的管道类型，特别是在中低压燃气管网中，PE 管道是新铺设管道和旧管道修复及更新的主要甚至是唯一的选择[1]。在PE 管道生产、运输、安装及使用过程中，会不可避免地出现微裂纹、微孔隙等损伤，损伤导致的PE 管道失效甚至爆炸事故在世界各地都有发生，因此，研究PE 材料损伤与破坏机理具有重大意义。

对于半结晶聚合物，损伤和断裂通常基于层间微孔洞导致断裂的假设进行建模[2−3]。CDM模型是一种唯象型模型，从宏观现象出发模拟宏观力学行为，其基本假设是将损伤视为嵌入不可逆过程热力学中的内部变量，使得含损伤变量的本构关系能真实描述受损材料的宏观力学行为。JEAN[4]将损伤变量引入材料应力−应变本构方程，建立了CDM模型的框架，并提出用弹性模量的衰减计算材料的损伤程度；BONORA 等[5−6]提出了材料的损伤演化方程，并采用实验和有限元分析相结合的方法研究了低合金钢在三轴应力状态下的韧性损伤行为；CELENTANO等[7]也采用实验和有限元分析相结合的方法研究了钢在塑性大变形下的损伤演化；ZHANG 等[8]对高密度聚乙烯(HDPE)材料的损伤演化进行了表征，研究了应变率对损伤演化的影响；ZHANG 等[9]研究了加载历史对PE材料损伤演化的影响，发现PE 材料损伤演化与加载速度和加载方式无关；黄学伟等[10]结合实验与有限元分析，确定了Q690D 钢材的连续损伤模型参数，并应用此模型分析了圆棒试样和带初始间隙试样在不同加载制度下的断裂破坏；ZHANG 等[11]引入了基于应力的损伤变量来表征PE 材料的延性损伤，并通过实验与数值模拟相结合的方法发现基于应力的损伤变量与基于能量等效方法的损伤变量具有良好的一致性；王铎等[12]将拉伸实验与ABAQUS 数值模拟相结合，推演出延性金属的弹塑性损伤模型，得出损伤变量；李非凡等[13]介绍了预测金属延性断裂行为的非耦合唯象型延性断裂准则，并进一步总结了唯象型延性断裂准则在镁合金断裂预测中的应用现状。上述研究大多针对金属材料损伤断裂机理，而对PE 材料这方面的研究很少。

材料的损伤断裂机理不仅与材料本身性质有关，而且与材料的应力状态有关。当应力状态不同时，材料内产生的塑性变形与应力集中程度不同，材料的损伤及断裂机理也将发生变化，为了简明反映材料受力时不同的应力状态情况，引入应力状态参数的概念。研究中常见应力三轴度、应力状态软性系数和罗德参数3 种应力状态参数。相较于应力状态软化系数和罗德参数，应力三轴度(即平均正应力与等效应力之比)能更合理地体现应力状态对塑性变形与断裂破坏的影响[14]。

BRIDGMAN[15]研究了应力三轴度对金属材料延性的影响，建立了带有缺口的圆柱试样应力三轴度的计算公式。直接从BRIDGMAN解析式得到是初始应力三轴度，而应力三轴度随着变形过程而不断变化，为此，BØRVIK 等[16−18]修正了应力三轴度的计算公式。近年来，人们针对应力三轴度对聚合物材料的影响进行了研究。CASTAGNET等[19]发现当三轴度越高时，径向应变的变化越小。BOISOT 等[20]用扫描电子显微镜(SEM)观察聚酰胺11 断流实验中微切口表面，并结合数值模拟，发现应力三轴度随径向应变增大而减小，在应力软化阶段体积变化可以降低应力三轴度比。OGNEDAL等[21]对含预加工缺口和不含预加工缺口的矿物填充聚氯乙烯(PVC)和HDPE 进行拉伸实验和数值模拟，证明了唯象型本构模型可以在高应力三轴度条件下得到应用。PVC 材料是静水压力的敏感材料，塑性膨胀随静水应力变化而变化，HDPE是非静水压力敏感材料，但当应力三轴度较高时体积变化明显。HAN 等[22]通过实验测试与数值模拟相结合的方法研究了应力三轴度对PE 材料损伤的影响，发现损伤随应力三轴度增加而增大。SAWADA[23]采用指数函数法和有限元法研究了聚四氟乙烯断裂前应力三轴度与等效塑性应变之间的关系。

相较于金属材料，应力三轴度对PE 的损伤断裂机理尚不成熟。因此，本文采用实验与数值模拟相结合的方法，建立不同应力状态条件下PE 材料的损伤本构模型，分别得出有损伤与无损伤的真实应力−应变曲线，分析临界损伤参数和临界断裂应变随应力三轴度的变化，研究不同应力状态对PE材料损伤及断裂的影响。

1 拉伸实验

实验的所有试样均由HDPE材料加工而成。圆棒形缺口试样可以有效模拟三轴应力状态，使单轴拉伸后的试样的缺口处产生复杂应力状态[24]，因此，本文采用缺口半径分别为20.0，5.0，2.0和0.5 mm的圆棒试样进行实验。所有试样均以1 mm/min 的恒定速度在实验机上进行单轴拉伸实验，直至断裂。试样均为轴对称结构，缺口处的最小截面的直径均为6 mm。图1所示为试样模型图。

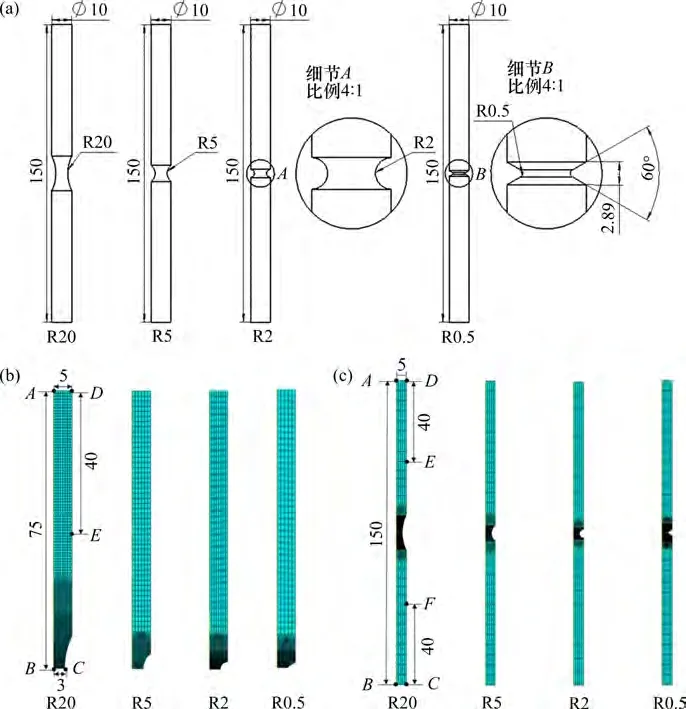
图1 试样模型图Fig.1 Specimens models

2 数值模拟

2.1 有限元模型

利用ABAQUS/CAE(2016)建立缺口试样的二维轴对称有限元模型，确定试样在变形过程中的真实应力−应变曲线和变形后的应力三轴度、损伤参数及临界断裂应变。

1)不考虑损伤的有限元模型。由于试样具有几何对称性，所以采用图1(b)所示的1/4 二维轴对称模型。边界条件与实验条件一致，具体如下：AB边限制x方向移动，BC边限制y方向移动，在DE边设置位移载荷，模拟采用的位移载荷与实验的位移载荷相同。采用CAX8R 轴对称8 节点单元对整个模型网格进行有规则地划分。

2)包含损伤的有限元模型。为了在ABAQUS中直观看到模型的断裂现象，在考虑损伤时采用图1(c)中的1/2 二维轴对称模型。边界条件设置与不考虑损伤的有限元模型相同。

2.2 损伤本构模型

PE的本构模型和损伤模型是研究PE材料的力学性能的有效工具，近年来有很多学者进行了相关研究，寻找一个与PE材料对应的精确本构模型。KWON 等[25]提出一种简单的修正因子来确定有限元模型输入所需要的等效Mises应力，再现实验所得的变形行为，且需要的迭代步骤也大幅减少。武艳霞等[24,26−28]采用KWON修正后的模型研究了PE材料，证明了KWON 修正后本构模型的适用性。本文也使用KWON提出的本构模型进行研究。

本构模型包括线弹性阶段、非线性弹性阶段、颈缩阶段和应变硬化阶段4 个部分。NEALE 等[29]采用胡克定律描述线弹性阶段的变形，KWON等[25]采用修正后OGDEN 公式[30]描述非线性弹性阶段的变形，HUTCHINSON等[31]将G'SELL等[32]提出的经验公式进行了修正，并描述了颈缩和应变硬化阶段的变形。

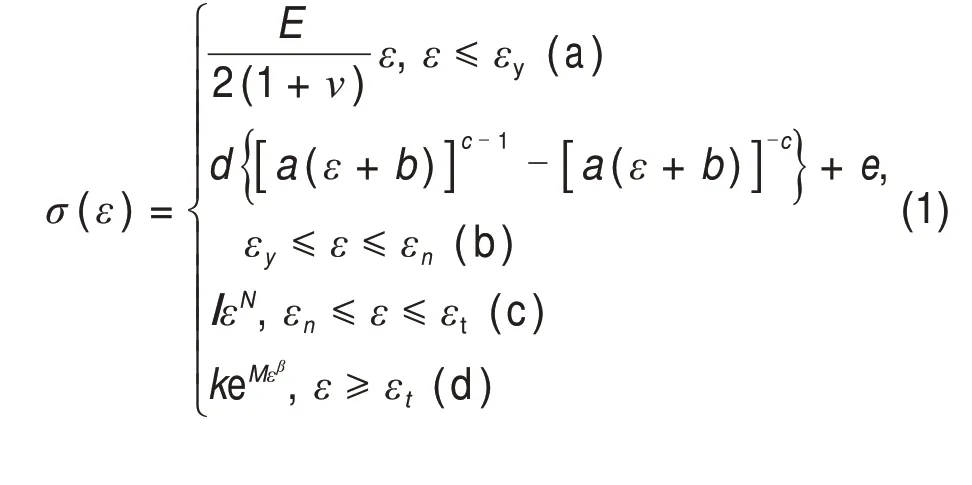
式中：σ为等效应力，MPa；ε为等效应变；εy为线弹性到非线弹性的临界应变点；εn为颈缩起始应点；εn为硬化起始应变点。其他参数如a，b，c，d，e，l，k，N，M，β，A，n和m均是用户自定义参数，修改这些参数与应变区间，直到可以通过有限元模拟重现实验所得的工程应力−位移曲线为止。

将由本构模型得出的应力−应变曲线输入有限元模型中，计算后得出工程应力−位移曲线，当由有限元模拟获得的工程应力−位移曲线与实验吻合时，即得出准确的有限元模型。

3 实验与数值模拟结果

3.1 拉伸实验结果

图2所示为实验得出的工程应力−位移曲线，4种缺口试样均拉伸至断裂。由图2可见：随缺口半径减小，屈服应力逐渐增加，断裂位移显著减小。因此，PE 材料有明显的缺口效应，随缺口半径减小，PE材料由塑性转为脆性。

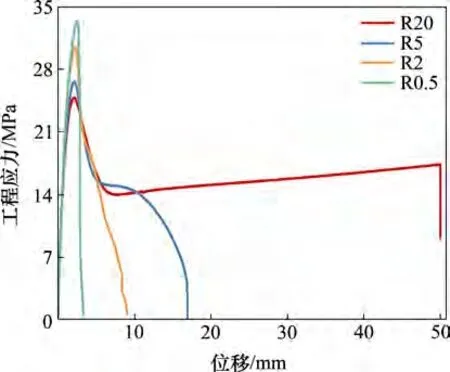
图2 缺口半径为0.5，2.0，5.0和20.0 mm PE试样的工程应力−位移曲线Fig.2 Engineering stress-displacement curves from PE specimens with notch radii of 0.5,2.0,5.0 and 20.0 mm

3.2 数值模拟结果

3.2.1 不考虑损伤的数值模拟结果

图3所示为实验与有限元分析得出的工程应力−位移曲线对比图。从图3可见：在不考虑损伤时，有限元模拟可以重现断裂前的实验结果，但不能模拟断裂部分的应力−应变曲线。式(1)中具体的参数与应变区间分别在表1与表2中列出。由实验与有限元结合的方法得出的试样变形过程中的真实应力−应变曲线如图4 所示。由图4 可见：在真实应变小于0.3 时，缺口半径越大，真实应力越大；在应变大于0.3时，随缺口半径减小，真实应力增加越快；断裂时，真实应力随缺口半径增大而增大。

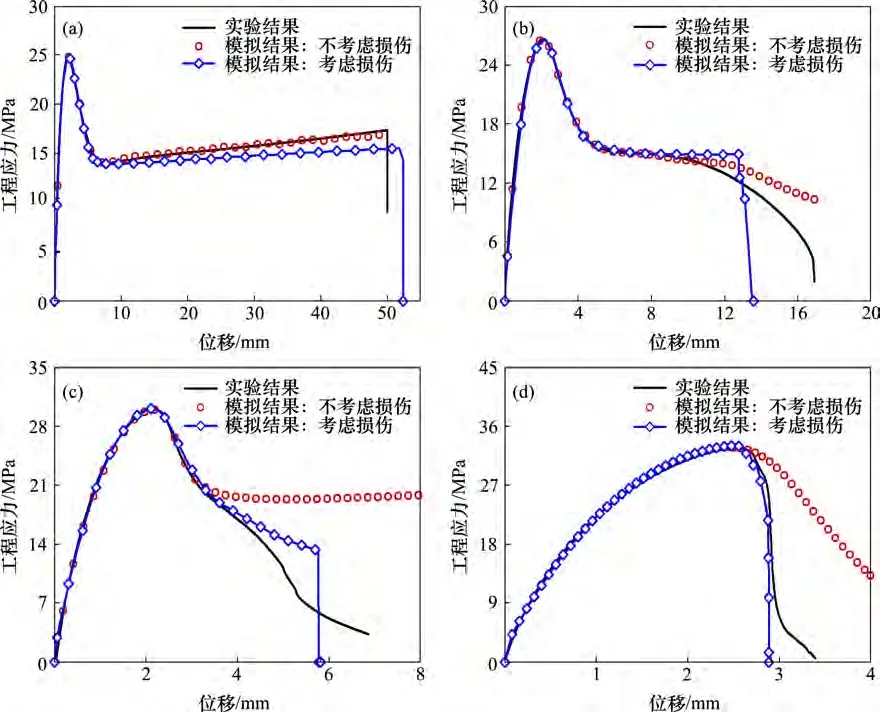
图3 不同缺口半径试样实验结果与有限元模拟结果的对比Fig.3 Comparison between experimental testing results and FE simulation results from specimens with different notch radius

表1 有限元模拟确定的公式(1)中参数值Table 1 Values for parameters in Eq.(1)determined from FE simulation

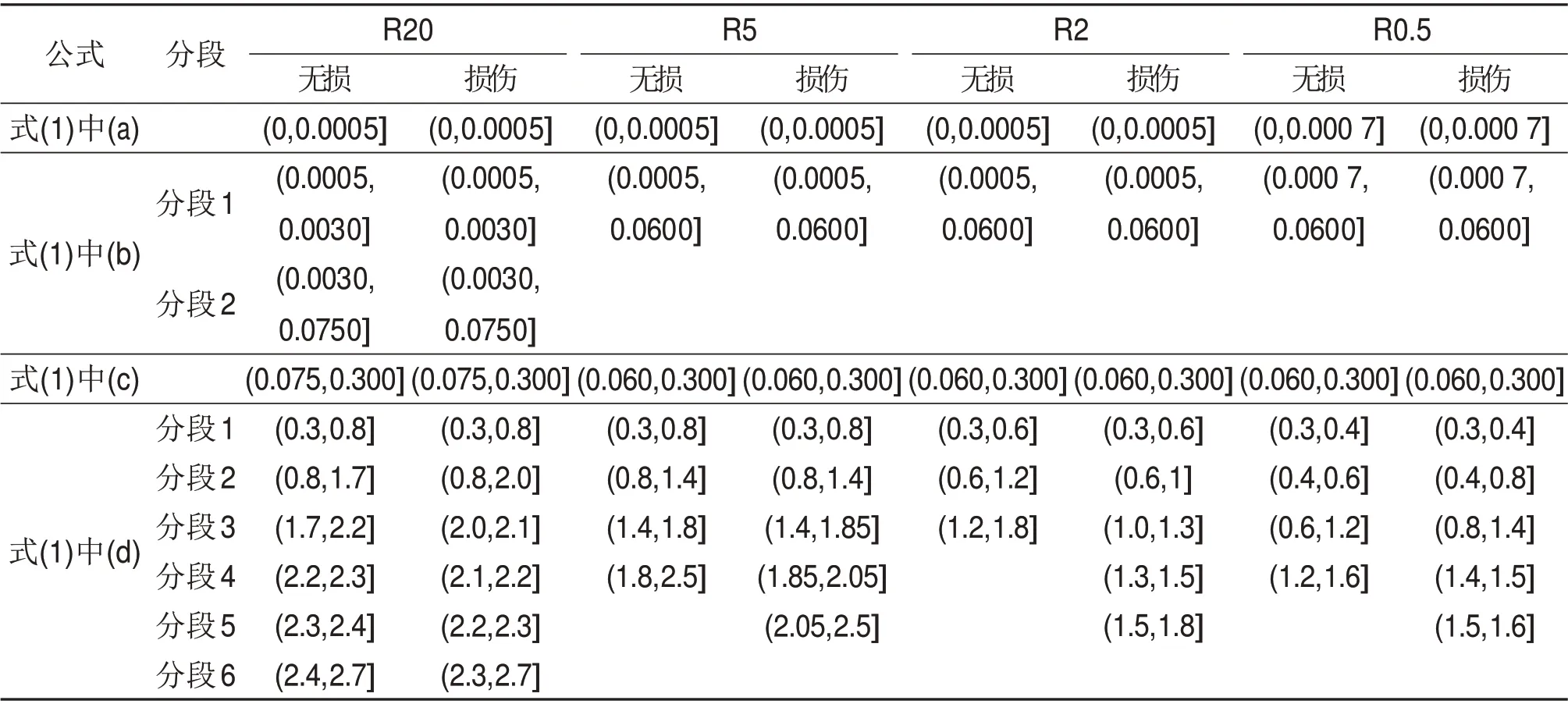
表2 有限元模拟确定的公式(1)中应变范围Table 2 Strain ranges in Eq.(1)determined from FE simulation

3.2.2 包含损伤的数值模拟结果

由图3可见：在模拟中引入损伤模型后，有限元模拟可以重现试样变形断裂全过程，并得出图4中的无损伤真实应力−应变曲线，表明本文得出的损伤模型可以准确模拟PE材料的损伤断裂。

PAWLAK等[33−34]发现HDPE材料在屈服点附近开始出现空洞，因此，认为PE 材料在屈服点时开始损伤。本文采用CDM模型，模拟中采用的指数型损伤演化如图5所示，具体参数见表3。

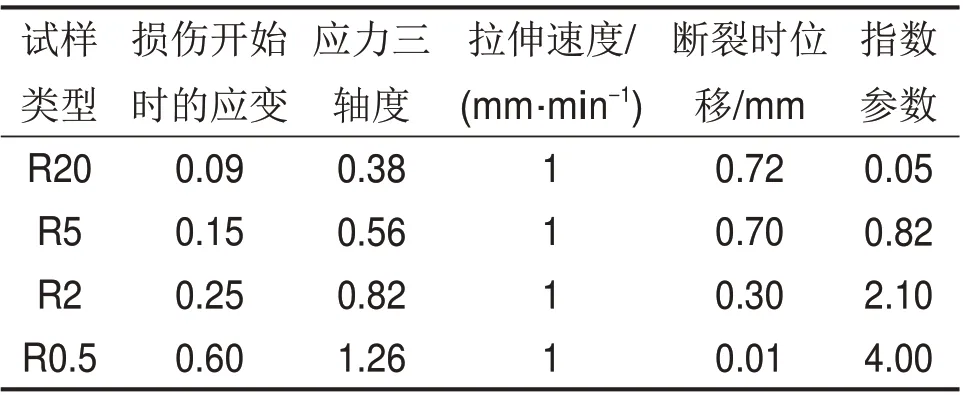
表3 有限元模拟中使用损伤参数Table 3 Damage parameter in FE simulation

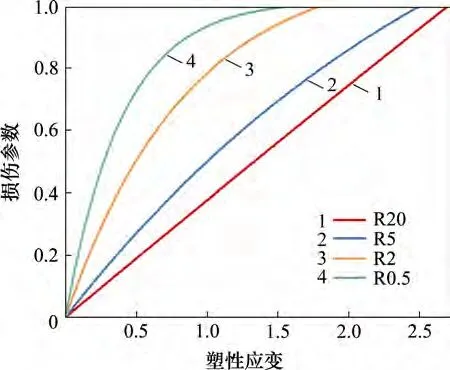
图5 有限元模拟中采用的损伤演化Fig.5 Damage evolution used in FE simulation

由图4 可以看出损伤出现前的真实应力−应变曲线没有变化，在损伤出现后，真实应力较无损伤真实应力明显增加，且有损伤与无损伤真实应力之间的差值随缺口半径减小而增大。

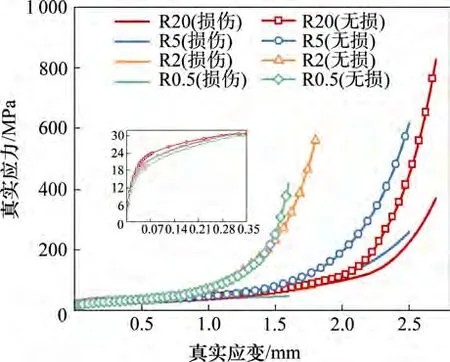
图4 有损伤与无损伤的真实应力−应变曲线Fig.4 True stress-strain curves from damaged FE and undamaged FE

4 讨论

4.1 不同阶段应力/应变的分布规律

记录最小横截面上应力应变分布的取点位置如图6 所示，据此研究PE 试样拉伸到点1(屈服前)、点2(屈服点)、点3(应变软化)和点4(应变硬化)横截面上径向/轴向应力、应变分布规律。径向应力在最小截面上沿径向方向的变化如图7 所示。从图7 可见，4 个点的径向应力都随缺口半径减小而增大，且径向应力随离中心点距离增大而减小。轴向应力的变化趋势与径向应力有所不同，从点1到点4，轴向应力随缺口半径减小而减小，如图8所示。

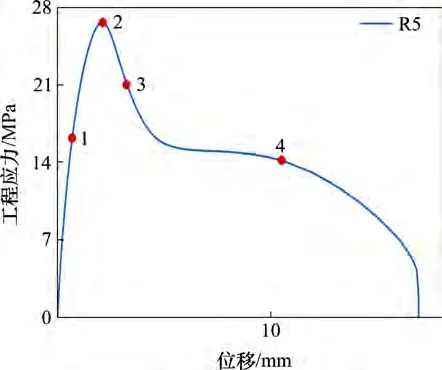
图6 记录最小横截面上应力应变分布的取点位置Fig.6 Schematic description of the positions at which the stress and strain distribution within the minimum cross section is recorded

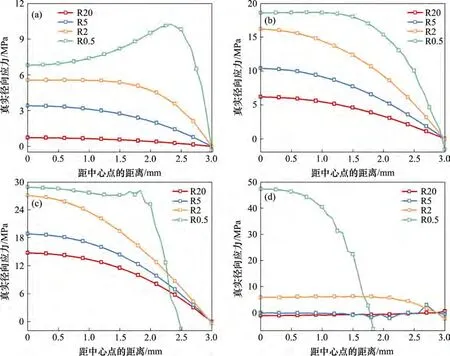
图7 径向应力在PE试样最小横截面上沿径向方向的变化Fig.7 Variation of radial stress along radial direction at minimum cross section of PE specimen

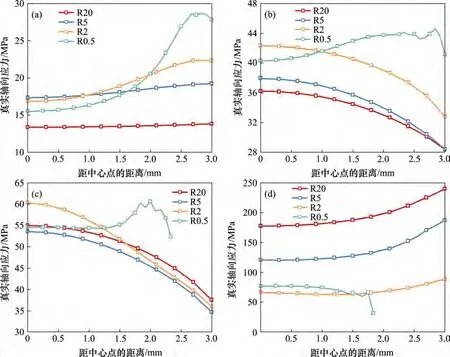
图8 轴向应力在PE试样最小横截面上沿径向方向的变化Fig.8 Variation of axial stress along radial direction at minimum cross section of PE specimen

图9所示为径向应变在最小截面上沿径向方向的变化。从图9可见：点1、点2和点3的变化趋势相同；在横截面的中心位置，径向应变变化平缓且随缺口半径增大而增大；在距中心点2 mm位置处径向应变开始有较大变化，最终在横截面的边界部位变为径向应变随缺口半径增大而减小，点4的径向应变始终随缺口半径增大而增大。图10 所示为轴向应变在PE 试样最小横截面上沿径向方向的变化，由图10 可见轴向应变变化与径向应变变化趋势基本相同，径向应变与轴向应变从1 点到4点持续增加。需要注意的是，图7～10 中R0.5 试样在点3 和点4 距中心点的距离小于3 mm 的原因是此时R0.5试样已经开始断裂。

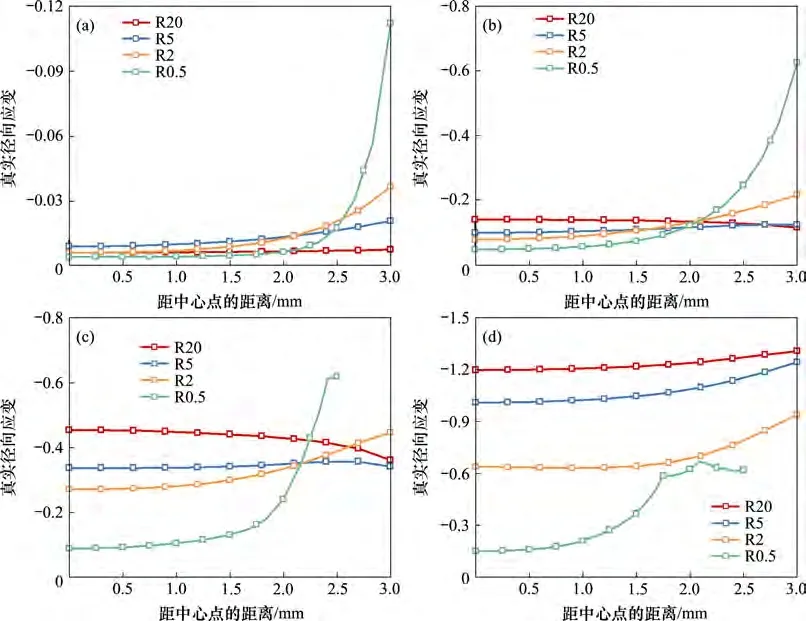
图9 径向应变在PE试样最小横截面上沿径向方向的变化Fig.9 Variation of radial strain along radial direction at minimum cross section of PE specimen

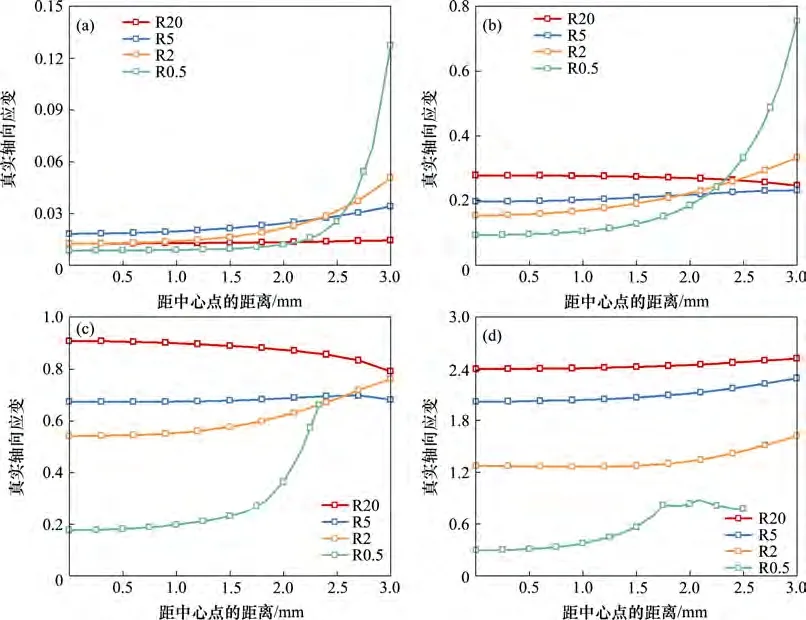
图10 轴向应变在PE试样最小横截面上沿径向方向的变化Fig.10 Variation of axial strain along radial direction at minimum cross section of PE specimen

4.2 应力三轴度

应力三轴度定义为平均应力与等效应力的比[15]，计算公式为

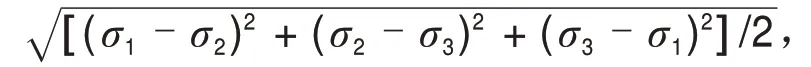
4.2.1 应力三轴度随位置的变化

基于数值模拟得出损伤本构模型，利用有限元得到4种缺口试样单轴拉伸情况下试样最小横截面上应力三轴度。X为取样点到中心点的距离，将有限元分析得出的数据代入式(2)，得到如图11 所示的4种不同缺口半径的试样应力三轴度随变化曲线。图11 中的应力三轴度均为变形最初阶段的应力三轴度。

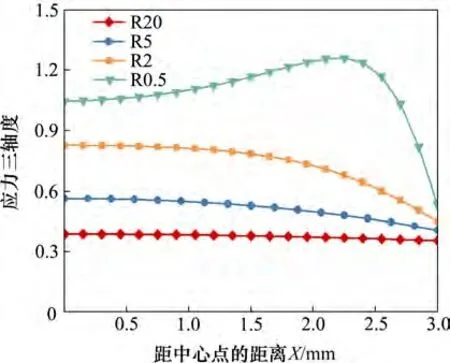
图11 4种试样应力三轴度随X的变化曲线Fig.11 Variation of stress triaxiality with X for four specimens

从图11 可见：R20，R5 和R2 这3 种试样在最小截面中心部位(即X=0处)应力三轴度最大，然后随X增大，应力三轴度减小；但R0.5 试样的应力三轴度在截面中心点到边界的变化趋势为先增大后减小，在X=2.25 mm 处应力三轴度最大。因为应力三轴度在最小截面上的分布不均匀，且最小截面中心处的应力三轴度最大，所以，多数研究者都选用最小截面中心点的应力三轴度。但是，这种选择对缺口半径小的试样并不适合，因为对于缺口半径小的试样，其应力三轴度最大的位置并不在中心点处，而在最小截面中心与边界之间的某个位置。LAIARINANDRASANA 等[35,21]认为当试样的最小直径明显大于缺口半径R时，从试样截面中心到边界的应力三轴度不再单调减小。

由图11 还可以看出：随缺口半径减小，应力三轴度明显增加；且缺口半径越大，应力三轴度随位置变化的曲线越趋于平滑。本文取每种试样最小截面上的最大应力三轴度作为修正后的应力三轴度。R20，R5，R2 和R0.5 试样的应力三轴度分别取0.386 8，0.563 8，0.934 6和1.218 2。

4.2.2 应力三轴度对损伤的影响

损伤变量D被定义为有损伤真实应力与无损伤真实应力的比，即

式中：σd为有损伤真实应力；σn为无损伤真实应力。

本文将每种试样断裂时真实应力比作为该试样临界损伤参数，并应用到有限元模拟中。将图4中真实应力代入式(3)，计算得出不同缺口半径PE材料的损伤演化规律，如图12 所示。由图12 可见：缺口半径越小，PE 材料的损伤发展越快。图13 所示为临界损伤参数和临界断裂应变随应力三轴度的变化。由图13 可见：随应力三轴度增加，临界损伤参数也随之增加。因此，损伤随应力三轴度增加而增大。

图12 不同缺口试样的损伤演化过程Fig.12 Damage evolution of different notched specimens

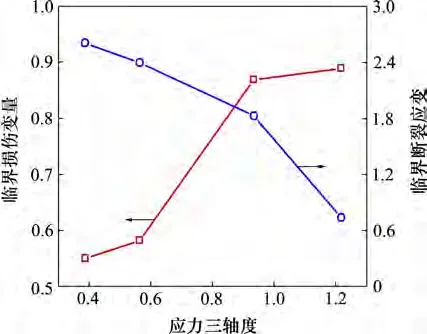
图13 临界损伤参数和临界断裂应变随应力三轴度的变化Fig.13 Variation of critical damage parameter and critical fracture strain with stress triaxiality

4.2.3 应力三轴度对断裂的影响

图14所示为R2试样的等效应变图。由图14(a)可见：最小截面上边界处等效塑性应变最大，离中心轴越近等效塑性应变越小，与应力三轴度在最小截面上的变化规律相反。由图14(b)可见：试样在最小截面的边界处开始断裂，即在等效塑性应变最大处开始断裂。其他3种缺口试样等效塑性应变在最小截面上的变化规律与断裂起始位置都与R2 试样的相同，这与BØRVIK 等[36]的研究结果一致。

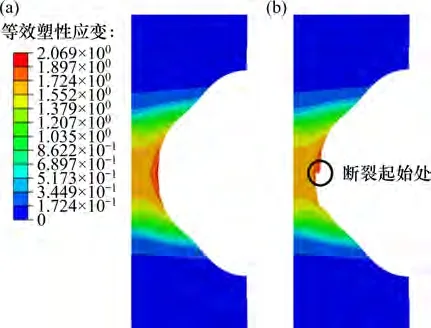
图14 R2试样的等效应变图Fig.14 The equivalent strain diagram of R2 specimen

PE 材料拉伸变形很大，拉断后的试样直径不便于直接测量，因此，利用有限元损伤模型获得各试样断裂起始时的等效塑性应变作为临界断裂应变。应力三轴度与临界断裂应变的关系如图13所示，可以看出临界断裂应变随应力三轴度增大而减小。

5 结论

1)随缺口半径减小，屈服应力逐渐增加，断裂位移显著减小。PE 材料有明显缺口效应，随缺口半径减小，PE材料由塑性转为脆性。

2)有损伤和无损伤的真实应力都在应变小于0.3时随着应力三轴度减小而增大，在应变大于0.3时，有损伤和无损伤的真实应力随着应力三轴度增大而增大。在应变相同时，无损伤与有损伤真实应力之间的增幅随缺口半径减小而增大。

3)应力三轴度在试样最小横截面上分布不均匀，随着应力三轴度增大，应力三轴度最大位置由中心点向外移动到离中心点2/3半径的位置；应力三轴度随着缺口半径减小而增大。

4)损伤演化和临界损伤参数随应力三轴度增加而增大，PE 材料的损伤随应力三轴度增加而增大。

5) 临界断裂应变随应力三轴度增加而减小，三轴度越高的PE试样越容易达到断裂临界点。