基于可靠性的天然气管道设计和评价技术

张振永*，白芳

（中国石油天然气管道工程有限公司）

0 引言

根据中国中长期油气管网规划，截至2025年，中国油气长输管道总里程将达到24×104km，其中天然气管道里程数将达到 16.3×104km，因此未来一段时期内仍将有大量天然气管道项目持续开工建设。为提升输送效率，建设大口径、高压力管道是一种发展趋势。提升管道输送效率的途径主要包括：①提高钢级至X90、X100；②提高输气管道设计系数；③使用1 422 mm大口径输送管道。为科学量化输气管道新材料、新工艺带来的管道安全可靠性问题，同时采取最优方案提升和保障管道的安全可靠性，在以往国内外研究基础上，中国管道企业从2012年开始，系统开展了天然气管道可靠性方面的相关研究。

国外从20世纪90年代即开展了大量的基于可靠性管道设计和方法评价研究，取得的成果相继纳入一些标准中。如：2006年，ISO（国际标准化组织）在其发布的标准ISO 16708-2006Petroleum and Natural Gas Industries—Pipeline Transportation Systems — Reliability-based Limit State Methods（《石油和天然气工业—管道传输系统—基于可靠性的极限状态法》）中正式阐述了油气管道可靠性设计方法；2007年，加拿大标准协会发布CSA Z662-2007Oil and Gas Pipeline System（《油气管道系统》），在该标准的附录O中表述了基于可靠性的陆上非含硫天然气输送管道设计与评估方法。此外，挪威船级社DNV-OS-F101-2013Submarine Pipeline Systems（《海底管线系统》）也加入了管道可靠性设计内容。CSA Z662-2007Oil and Gas Pipeline System中给出了天然气管道基于可靠性设计和评价的一些基本流程、管道极限状态和状态方程，以及管道在材料、腐蚀和第三方挖掘方面的不确定性参数，同时也明确了天然气管道的目标可靠度，但该成果是基于北美天然气管道的建设和运行维护水平研究建立的，中国和北美的地形地貌和人口密度差异较大，管道材料、施工和运行维护水平也存在诸多不同，如，中国新建的X80高钢级管道较多，在整个管道系统中占比较大，北美高钢级管道占比较少，CSA Z662-2007Oil and Gas Pipeline System中管道爆裂和破裂极限状态方程多基于X70及以下低钢级开发，这些极限状态方程不便直接应用于中国高钢级管道［1-4］。

结合国外已有研究成果和标准，在分析国内外差异的基础上，中国科技人员重点开展了：①管道目标可靠度确定方法研究；②材料性能、管道荷载、运行参数等不确定性研究；③不同失效模式下的管道极限状态方程建立；④管道可靠度计算模型及方法研究。通过5年的研究，建立了适合中国国情的天然气管道的目标可靠度；构建或修订了包含适用于X80等高钢级管道在内的天然气管道极限状态方程；通过大数据统计分析，建立了管材性能、腐蚀、第三方挖掘和环焊缝性能等不确定参数库；通过对不同极限状态方程的算法研究，优化了蒙特卡洛仿真模拟计算方法，开发了配套计算软件；基于上述成果，首次建立了中国天然气管道的可靠性设计和评价标准，为该方法的推广和应用奠定了基础。

中俄东线天然气管道工程为中国首条1 422 mm大口径管道，采用X80钢级，设计压力12 MPa。中国缺少建设和运行维护经验，管道的安全可靠性是政府主管部门和企业共同高度关注的问题。为验证GB 50251—2015《输气管道工程设计规范》中所定设计系数的适用性，采用建立的天然气管道可靠性设计和评价方法，科学论证了按现行设计系数选取壁厚的1 422 mm管道可靠度能够满足要求，为工程建设解决了一个重大问题。

1 天然气管道可靠性设计和评价方法

1.1 工作流程

基于可靠性的设计和评价方法的实质是对影响管道安全状态的不确定因素进行定量分析，利用分析结果计算管道可靠性水平，并寻求达到同样安全可靠度水平下的多种解决方案中的最佳经济性方案，以实现工程的安全性和经济性目标。天然气管道基于可靠性的设计和评价方法工作流程见图1［5］。

1.2 关键技术问题

基于可靠性的设计方法理论较成熟，但是此方法属于一种新的设计方法。该方法的核心是天然气管道目标可靠度、极限状态方程、不确定性参数库、概率计算模型和算法。根据中国与北美国家在天然气管道方面的建设和运行环境差异对比，为把此方法应用于中国的陆上天然气管道设计和评价，需要解决的关键技术包括：

（1）管道目标可靠度确定方法，即如何确定国内天然气管道的目标可靠度。借鉴国外的研究思路，利用基于风险的理念，在推演计算目前天然气管道风险的基础上，综合国内石油石化行业的风险水平，并参考国外天然气管道风险水平，最终确定中国天然气管道的风险水平。在确定可接受风险水平的基础上，利用风险与后果之比可得到最大允许失效概率，见下式：

式中：RT——天然气管道目标可靠度；Pmax——允许最大失效概率；rmax——天然气管道可接受风险；C——天然气管道的失效后果。

（2）国内管道材料性能、现场施工和运行参数库。可靠性计算是一种定量计算方法，在相关极限状态可靠性计算中，需要管材、腐蚀、第三方机械挖掘施工和环焊缝等大量数据，尤其是这些不确定参数的分布类型和特征参数。目前国内尚未有可利用的参数数据，需要针对国内的材料制造、管道施工和运行维护参数进行统计分析。

（3）不同失效模式下的管道极限状态方程。国外已建的极限状态方程大多基于X65及以下钢级，对于 X70、X80等高钢级适用性未知；同时已有的极限状态方程不全，未涵盖地面位移条件下的极限状态方程。国内需在国外已有成果的基础上，通过理论推导、有限元模拟并辅以必要实物验证等方法，分析现有极限状态方程的适用性，并对相关极限状态方程进行制修订。

（4）管道可靠度计算模型和方法构建。对于极限状态方程的计算，可以通过多种方法完成，其中包括一阶和二阶可靠性方法及各种模拟方法，如蒙特卡洛方法、重要性抽样方法和拉丁超立方抽样方法。管道可靠性计算涉及多个极限状态方程，且每个方程涉及众多参数，计算繁琐、耗时较长，需要研究制定优化的计算流程和算法，并开发专用的计算软件工具。

2 关键技术成果

2.1 天然气管道目标可靠度

2.1.1 天然气管道风险确定

调研收集了中国国内 3.7×104km已建天然气管道基础数据，根据压力、管径、钢材等级、各地区等级管段长度确定了148种场景（国内天然气管道典型压力、典型钢级和典型管径的组合）。每种场景，都根据实际场景的腐蚀和设备撞击情况，修正了失效计算模型。在失效后果计算过程中，选取约2×104km不同地区等级管段，统计了各地区等级的平均人口密度［6］。

基于中国国内在役管道148种场景，计算天然气管道社会风险，并与中国石油石化行业的整体风险水平，以及国外研究和标准做比对，进而确定中国天然气管道的整体社会风险水平为 2.0×10-5人/（a·km），如表1所示。

表1 不同数据来源管道社会风险水平值

参照国外CSA Z662-2007Oil and Gas Pipeline System，ISO 16708-2006Petroleum and Natural Gas Industries—Pipeline Transportation Systems—Reliability-based Limit State Methods标准，并结合国家安全生产管理相关要求，中国天然气管道个体风险可接受标准确定为：

一级地区10-4/a，二级地区10-5/a、三四级地区10-6/a。

2.1.2 极端极限状态（ULS）目标可靠度

极端极限状态是导致出现泄漏并产生重大安全危险的极限状态。为了确定该极限状态下管道的目标可靠度，图2所示为结合了基于固定期望社会风险、基于规避社会风险和基于个体风险的可靠性目标。

根据图2，推荐的最终目标可靠性RT可以利用下列公式计算：

式中：ρ——人口密度，人/hm2；P——设计压力，MPa；D——管外径，mm。

2.1.3 泄漏极限状态（LLS）目标可靠度

泄漏极限状态为导致出现泄漏，但不会产生重大安全危害的极限状态。参考ASME B31.8-2010Gas Transmission and Distribution Piping Systems（《气体输送和分配管道系统》）中给出的小泄漏率1.5×10-3次/（a·km），以及国内外的统计历史数据，确定泄漏极限状态最大容许失效概率为 1×10-3次/（a·km）。

2.1.4 服役极限状态（SLS）目标可靠度

服役极限状态定义为不满足设计或服务要求，但不会导致出现泄漏的极限状态，包括屈服、椭圆化、凹痕和过度塑性变形。参考标准ISO 16708-2006Petroleum and Natural Gas Industries—Pipeline Transportation Systems—Reliability-based Limit State Methods对于不同安全等级的规定，确定服役极限状态最大容许失效概率为 1×10-1次/（a·km）。

2.2 管道极限状态方程

2.2.1 总体情况

针对不同极限状态相关参数的特点，分析其承受的主要荷载和提供抗力情况，建立极限状态函数表达式。根据建立的表达式，对管道的抗力模型进行筛选，找出适合的已有模型进行对比分析。对比分析中要综合考虑模型表达形式、所需参数、模型精度以及方便工程应用等因素，确定一种最为合适的模型，并基于采用的模型通过模型校订，取得模型偏差系数，最后构建极限状态方程［7］。

针对中国天然气管道实际工况，经相关研究分析，直接采纳、修订和新建了不同失效模式下的管道极限状态方程共计21种，如表2所示。

表2 极限状态方程修订或新建情况

2.2.2 高钢级管道腐蚀引起的非透壁缺陷爆裂极限状态方程修订（例）

为说明极限状态的修订方法，以高钢级管道腐蚀引起的非透壁缺陷爆裂极限状态方程为例进行分析。国内外学者认为，对于X70钢，现有模型已经过试验验证；而对于X80及以上高钢级，现有模型是否合适还有待于进一步验证。研究中收集了 50组X80、X100高钢级腐蚀试验数据，利用收集的50组数据对ASME B31G MO（B31G准则修正版模型）、PCORRC（管道腐蚀准则，国外工业界开发的一种腐蚀评价模型）、LPC（一种腐蚀评价模型，由ASME B31G模型改进而来）、CFER（加拿大C-FER公司开发的管道腐蚀评价模型）等4种模型进行了对比，具体结果见表3。通过对 4种模型进行比较，认为LPC模型相对准确，对X80及以上钢级推荐采用LPC模型。

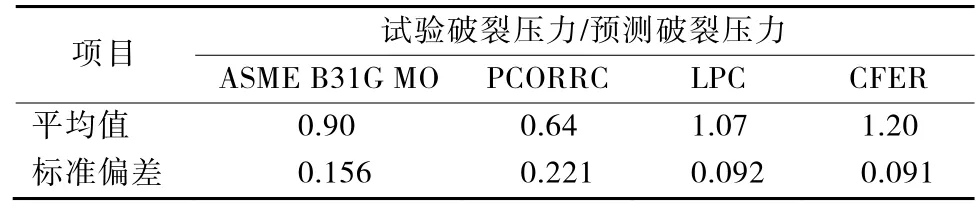
表3 X80及以上钢级4个模型的偏差情况

确定采用 LPC基本模型的基础上，利用 50组数据进行处理分析，得到X80及以上钢级的非透壁缺陷爆裂极限状态方程为：

式中：Pb——腐蚀管道的预测失效压力，MPa；σu——管道抗拉强度，MPa；t——管壁厚度，mm；D0——管道平均直径，mm；d——平均腐蚀深度，mm；L——最大缺陷长度，mm；B1、B2——模型修正系数，其中B1为 1.036；B2均值为-0.001 69，标准偏差为0.001 63（正态分布）；Q——长度校正系数；P0——无缺陷管道的破裂压力，MPa；Pr——试验破裂压力，MPa；g——极限状态方程表达符号，g≥0表示安全，g＜0表示失效。

2.3 不确定性参数库构建

2.3.1 总体情况

目标可靠度的参数不确定性来源于参数的随机变化性、参数测量的不确定性及参数模型的不确定性。

对于管道的荷载参数，首先通过对国内外资料和文献的收集得到了管道主要部位的压力数值；其次对管道安全运行产生最大威胁的第三方活动进行统计分析，得出第三方开挖施工中使用的挖掘机设备占统计事故的70%。因此以挖掘机为重点，通过调研挖掘机设备参数，对挖掘机操作重量、铲斗挖掘力数据进行回归分析，建立了适用于中国的挖掘机作用力计算模型。

对于钢管机械特性参数，在研究过程中，对不同钢级钢管的机械性能指标进行了大量统计分析。使用SPSS（统计产品与服务解决方案，是IBM公司推出的一系列用于统计学分析运算、数据挖掘、预测分析和决策支持任务的软件产品）和 Matlab（矩阵实验室，是美国MathWorks公司出品的商业数学软件）对统计数据样本量、最大值、最小值、平均值、标准差、离散系数和分布类型等进行分析确定。同时，为了计算管道在地面位移情况下的管道拉伸断裂和压缩屈曲失效概率，还对管道不同焊接方式环焊缝的力学性能参数进行统计。

除上述外，还对钢管的几何参数和缺陷特征（包括管体不完整度、制管焊缝缺陷、环焊缝缺陷、管体凹坑-划痕、管道外部腐蚀等）进行统计分析，分别得出适用于中国的数据类型和分布特征。

2.3.2 深度方向腐蚀速率（例）

不同钢级在不同环境下的腐蚀速率是可靠性计算所需的一个重要参数。为获得腐蚀速率等不确定性参数，基于国内外文献资料、标准、国家材料环境腐蚀站数据资料，以及收集的国内6 000 km已有管道的内检测数据和室内开展的对 X80、X90钢管加速腐蚀试验等，综合确定了外部腐蚀参数及分布类型，如外腐蚀缺陷深度方向腐蚀速率，具体见表4所示。

表4 外腐蚀缺陷深度方向腐蚀速率

2.4 目标可靠度计算方法［8-10］

管道可靠度的计算在不同情况下需要考虑的极限状态不同，每个方程涉及众多参数，其中大部分参数又是服从一定概率分布的随机变量。通过对FOSM（一次二阶矩法）、SORM（二次二阶矩法）以及蒙特卡洛、重要性抽样和拉丁超立方抽样等方法的研究，最终选取模特卡洛模拟作为基本计算方法。

为提升算法效率和精度，构建了优化的失效概率算法流程，并在计算中对抽样数据拟合和计算结果处理做了大量优化，开发了PRADA（管道可靠性设计和评价）计算软件。管道失效概率计算流程如图3所示。

3 基于可靠性设计和评价方法在中俄东线天然气管道的应用

为论证中俄东线天然气管道工程1 422 mm管道的安全可靠性，利用可靠性设计和评价方法对 3种壁厚的管道极端极限状态进行失效概率分析。

3.1 管道失效概率计算

管道运行过程中，根据其运行环境，需要考虑多种极限状态。根据国内外的管道失效因素统计分析，管道的失效原因依次为外部干扰、腐蚀、材料制造与施工缺陷、带压开孔、地面移动以及其他未知原因，其中，外力破坏和腐蚀是造成管道失效的主要原因，占整个失效事故的60%～76%。为简化计算，结合中俄天然气管道实际情况，在可靠性计算中考虑的主要极端极限状态包括内压作用下管道腐蚀造成的大孔泄漏、管道破裂以及第三方机械挖掘造成的大孔泄漏和管道破裂。在计算上述失效概率后再乘 1.5倍的系数，为管道的总失效概率，具体计算公式如下：

式中：PULS——总极端极限状态失效概率，次/（a·km）；——腐蚀造成的管道破裂失效概率，次/（a·km）；——第三方机械挖掘造成的管道破裂失效概率，次/（a·km）；——腐蚀造成的大孔泄漏失效概率，次/（a·km）；——第三方机械挖掘造成大孔泄漏失效概率，次/（a·km）［11-14］。

3.2 数据来源及计算结果

可靠性评价所需的数据主要从管道公司内部和外部（如行业管理数据）获取，包括基础数据和参数变量数据。基础数据有管道设计参数、环境数据等；参数变量数据有钢管性能数据、施工数据、运行维护数据等。对于收集到的钢管管道的内外腐蚀和运行压力等参数，进行参数的不确定性分析和概率建模，形成各种参数的分布类型和特征值。本次可靠性评价，1 422 mm钢管的性能参数全部来源于实际生产统计数据。

对于腐蚀、第三方挖掘破坏失效概率，模拟抽样次数为1×108次，计算时间周期为30 a。通过对失效概率的计算（如表5所示）可以看出，3种壁厚的管道总体失效概率均小于最大允许失效概率，说明依据现行设计系数计算得到的管道目标可靠度满足 1 422 mm中俄东线天然气管道工程目标可靠度的要求。

表5 中俄东线天然气管道工程（1 422 mm）失效概率计算结果

4 结束语

为保障管道的安全可靠性，国内通过对可靠性设计和评价方法的系统研究，形成了较为完整的技术成果，弥补了现有设计和评价方法的不足，可根据管道的实际失效形式进行设计和评价，避免采用不合理或过于保守的设计，使设计更加科学合理。

该技术成果为中国首条1 422 mm天然气管道的设计系数适用性论证提供了科学支撑，进一步说明该方法可用于指导高钢级、大口径和高压力的管道设计方案的制定和优化，在保障管道安全运行的前提下，可以带来明显的经济效益和社会效益。