掺氢天然气输送管道阀室泄漏扩散规律研究

贾文龙*，温川贤，杨明，黄军，吴瑕，李长俊

（1.西南石油大学石油与天然气工程学院；2.国家管网集团西部管道有限责任公司；3.汉正检测技术有限公司）

0 引言

氢能是一种清洁的二次能源载体，能方便地转换成电和热，转化效率较高且燃烧能实现碳的零排放［1］。在“碳中和、碳达峰”背景下，实现氢的高效的输送和利用是能源发展的战略需求［2］。将氢气掺入天然气管道进行输送，在节省巨额管道建设费用的同时，可实现氢气大规模、长距离输送［3］，是目前国内外氢气输送研究的热点。荷兰、英国、意大利等国家已经开展了氢气体积浓度 10%～20%的天然气掺氢输送工业化试验［3-4］。

通常，长输管道沿线隔一定距离及在特殊地段设有阀室［5］，主要用于长输管道的维修、检修及事故工况下截断管道，减少天然气放空时间和放空量。但阀室本身也面临地基下沉、焊缝破损、静密封处密封不严等风险［6］，可能会造成阀室内部的气体泄漏。由于氢气密度、最小点火能远低于甲烷，爆炸浓度极限范围远大于甲烷，在泄漏后更加容易扩散［7］，并可能在气体与管壁的摩擦等因素作用下点燃爆炸，严重威胁管道的安全运行。

有效的检测气体的泄漏是防止气体燃爆事故发生、减轻事故后果的关键。目前，主要采用在阀室内布置可燃气体检测器的方式监测气体泄漏，但其布置方式主要是根据天然气的泄漏扩散特征确定的［8］，并未考虑到氢气、天然气的密度等物性参数差异带来的扩散特征变化，现有可燃气体检测器的布置方式能否适用于掺氢天然气尚无指导性建议。在缺乏实验数据的条件下，基于数值模拟方法，探究掺氢天然气的泄漏扩散特征，进而评价可燃气体检测器布置方式的适应性，对于保证管道的安全运行具有重要意义。

1 模型建立

1.1 控制方程

阀室内天然气的泄漏扩散属于高压射流条件下的湍流流动过程，目前普遍采用的数值模拟方法有直接数值模拟、大涡模拟和雷诺平均法［9］等，其中雷诺平均法由于计算量小且具有一定精度，在工程上得到广泛应用。雷诺平均法的基本时均控制方程如下所示：

标准 k-ε模型作为雷诺平均法布斯涅斯克（Boussinnesq）模型中双方程模型的一种，是最简单且完整的湍流模型［10］。使用标准 k-ε模型求解掺氢天然气泄漏扩散问题时，除需满足连续性方程、动量方程、能量方程、k方程、ε方程和黏性系数方程等六大控制方程之外，还应满足组分输运模型。即对于掺氢天然气这类多组分气体，在泄漏扩散过程中的气体浓度分布需满足以下组分守恒关系：

式中：Yi——可压缩湍流中组分i的脉动扩张项；Ji——组分i的扩散通量；Ri——第i种物质的化学净源项；Si——离散相和用户定义源项的产生率；Xi——组分i的摩尔分数，%；Dij——二元扩散系数，表示i组分在j组分中的扩散速率，m2/s。

扩散通量Ji表示单位时间内气体垂直通过某个面的流量，可基于气体扩散系数与Fick扩散定量计算得到，其取值对于掺氢天然气泄漏扩散行为的计算具有重要影响。

1.2 多组分非理想气体扩散系数

采用PR状态方程对Fuller二元扩散系数以及热力学因子计算方法进行校正，可克服传统方法将天然气假设为单一组分气体、难以描述氢气与天然气由密度等物性参数不同而带来扩散系数差异的不足［11-12］。本文将掺氢天然气简化为氢气、甲烷两组分混合物，基于校正的 Fuller模型计算了二元物系非理想状态扩散系数，并以此为基础计算掺氢天然气泄漏扩散通量。

1.2.1 二元物系非理想状态扩散系数

Fuller模型是一种精度较高的二元气体扩散系数经验公式。考虑掺氢天然气的非理想性，引入了压缩因子Z对其进行校正，如下所示：

1.2.2 多组分理想气体扩散系数

在多组分物系传质过程中，由于组分间存在交互作用，某一组分的传质通量除了与其自身质量浓度梯度有关，还与其他组分的质量浓度梯度有关。对于n组分体系，其扩散通量表示为：

式中：Ji——组分i的摩尔扩散通量，kmol/（m2·s）；——组分i与组分k之间二元物系传质过程Fick扩散系数；c——扩散物质的质量浓度，kg/m3；∇xk——质量浓度梯度；“-”表示扩散方向为质量浓度梯度反方向。

Fick扩散系数可用矩阵形式进行如下表示：

式中：Dij、Din和Dik——组分之间的二元扩散系数，由式（4）计算得到，其中下标i、j、n、k代表不同组分，m2/s。ijδ——Kronrcker函数，当i=j时，ijδ=1；当i≠j时，ijδ=0。Iniφ——组分i的逸度系数。

1.2.3 掺氢天然气扩散系数

假设掺氢天然气中仅含甲烷和氢气，且空气为单一组分气体，则掺氢天然气的泄漏扩散过程构成CH4/H2/Air三组分物系扩散过程，基于上述方法得到的Fick扩散系数矩阵如表1所示（其中空气为参考组分）［13］，并将该Fick扩散系数矩阵作为模拟各组分间的扩散特性的基础参数。

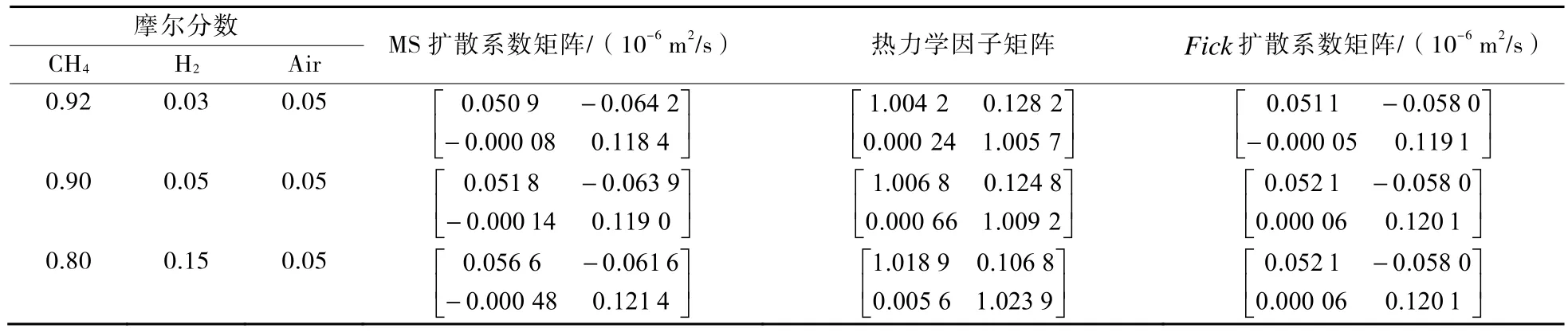
表1 5 MPa、温度293.15 K下不同含氢量掺氢天然气Fick扩散矩阵

2 数值模拟

2.1 几何模型

以西气东输一线某典型阀室为对象，研究掺氢天然气泄漏扩散规律。阀室的物理模型如图1所示，阀室主体房屋为15 m×11 m的矩形，房屋四周墙壁高3.5 m，中心屋顶高4.1 m。房屋墙上每隔1 m设置一个矩形的通风口和通风窗，通风口高0.17 m、长0.8 m，底部距离地面0.15 m；通风窗高0.2 m、长0.8 m，底部距离地面2.6 m。房屋外有2.5 m高的围墙，距离房屋墙壁水平距离4.5 m或5 m。为模拟自然风，以阀室为中心，建立一个长32 m、宽29 m、高15 m的长方体作为模型边界。阀室内管道旁通支管外径为273 mm，在阀室中的横跨距离约为4 m，建立的泄漏口位于支管中部，如图 2所示。采用Fluent软件开展数值模拟，当计算网格数增加至94×104以上时，计算结果无明显变化，为此确定计算总网格数为949 932个。

2.2 边界条件

主要边界条件设置如下：

入口边界：在模型四周任取一面设为速度入口，自然风垂直于阀室围墙均匀吹向阀室。

出口边界：模型四周，除自然风入口外，另外三面及模型顶面设为压力出口。

壁面边界：壁面上施加无滑移边界条件。

泄漏源：根据天然气管网掺氢输送情况，设定管道运行压力为5 MPa，泄漏口径分别为100 m、50 mm和20 mm，氢气体积浓度为0、3%、5%和15%［3］。

求解算法：采用压力和速度耦合求解的PISO算法，扩散系数按照表1取值。

模拟时间：考虑气体泄漏后，可燃气体检测器检测到气体泄漏的时间，模拟时长取60 s。

3 泄漏扩散特征

3.1 泄漏扩散规律

阀室内安装的可燃气体检测器检测到甲烷浓度达到爆炸下限浓度的40%（40% LEL）时即触发报警。对于甲烷，触发报警的浓度为2%；若安装氢气检测器，触发报警的氢气浓度为1.6%。本文主要分析报警浓度以上的甲烷和氢气泄漏及浓度分布规律。

首先，以泄漏口竖直向上、风速5 m/s、氢气体积浓度为15%、泄漏口径为50 mm的泄漏工况为例，分析泄漏发生1 s、10 s和30 s时甲烷和氢气的浓度扩散趋势，可检测气体体积浓度等值线如图3所示。

由图3可知，掺氢天然气泄漏后，由于其密度小于空气且具有一定的初始动能，首先会朝泄漏口所正对阀室边界进行扩散，随后再沿着墙壁向四周扩散，直至充满整个阀室。但由于在混合气体中氢气体积浓度远低于甲烷，且氢气在空气中扩散速度更快，导致同一时刻在报警浓度以上的甲烷的覆盖范围要远大于氢气的。从相同时刻甲烷和氢气扩散情况的对比可以发现，对于阀室内任意位置，甲烷均能在氢气之前达到可检测浓度。

在泄漏发生后，可燃气体检测器与泄漏点之间的相对距离、与阀室房顶的间距是影响可燃气体检测器能否快速准确地检测到甲烷和氢气泄漏的主要因素。为此，选择泄漏发生60 s后，甲烷和氢气在阀室顶部的平均聚集厚度、阀室壁面上的最低可检测高度作为评价指标，定量分析甲烷和氢气的泄漏扩散特征。这两个指标的取值方法如图 4和图5所示。

在氢气体积浓度分别为0、3%、5%、10%和15%，风速为3 m/s、5 m/s、8 m/s和12 m/s，泄漏口径为20 mm、50 mm和100 mm条件下，甲烷、氢气在阀室顶部的聚集厚度、在墙壁上的最低可检测高度模拟结果如图6、图7和图8所示。其中，阀室顶部聚集厚度4.1 m代表气体充满整个阀室；最低可检测高度0 m代表阀室内至少有一面墙被气体聚集占满，3.5 m代表阀室内所有墙壁上均无气体聚集。

3.1.1 风速的影响

由图6、图7和图8可知，当泄漏口径为20 mm时，风速对甲烷在阀室顶部的聚集厚度有明显影响。具体表现为各种氢气体积浓度下，12 m/s风速下的甲烷聚集厚度为3 m/s风速下的40%～45%。当泄漏口径大于50 mm时，风速对甲烷在阀室顶部聚集厚度及墙壁最低可检测高度影响甚微。相比于地面天然气管道的泄漏扩散［14］，自然风对阀室内掺氢天然气的影响更小，其主要原因是自然风受阀室周围2.5 m高围墙的阻挡改变了流向，难以直接吹进阀室稀释泄漏的掺氢天然气，导致泄漏气体主要依靠浓度差及阀室内外压力差进行对外扩散。

3.1.2 氢气体积浓度的影响

随着氢气体积浓度的增大，甲烷在混合气体中的浓度减小，甲烷在阀室顶部的聚集厚度稍有减少。相比于氢气体积浓度为0的情况，氢气体积浓度为15%、各风速条件下的甲烷在阀室顶部的聚集厚度仅减小不到0.05 m。随着氢气体积浓度的增大，氢气在阀室顶部的聚集厚度逐渐增大，但只有在泄漏口径不小于50 mm、氢气体积浓度不小于5%的泄漏工况下，才会在阀室顶部出现大于可检测浓度范围的氢气聚集；氢气在阀室墙壁上的最低可检测高度会减小，即氢气的聚集位置距离地面越来越近。

3.1.3 泄漏口径的影响

当泄漏口径为20 mm时，各工况下甲烷在阀室顶部的聚集厚度不超过0.4 m。当泄漏口径为50 mm时，各工况下甲烷均能占满整个阀室，但氢气仅在阀室顶部的聚集厚度不超过0.3 m，在阀室墙壁上无明显聚集。当泄漏口径为100 mm时，各工况下甲烷均能占满整个阀室，氢气在阀室顶部的聚集厚度为0～2.6 m。出现差异的主要原因是在风速和压力相同的条件下，泄漏口径对泄漏体积流量影响较大。

3.1.4 泄漏方向的影响

在实际输气管道运行过程中发生泄漏时，泄漏口的朝向可能发生在各个方向上，气体泄漏聚集规律也会不同。为此，模拟了泄漏口方向为水平（向左、向右）及向下、泄漏口径20 mm、50 mm、100 mm，氢气体积浓度15%、风速8 m/s条件下甲烷、氢气在阀室顶部和墙壁的聚集情况，结果如表2和表3所示，其中泄漏口朝左时甲烷的浓度分布如图9所示。结果表明：当泄漏口向左或者向右时，泄漏气体首先向阀室墙壁扩散，随后天然气沿墙壁底部向上扩散，部分天然气通过通风口流出阀室，形成墙角底部气体聚集多、顶部气体聚集少的情况；当泄漏口朝下时，氢气在阀室顶部无聚集，且氢气在墙壁上的聚集量小于泄漏口朝上的工况。

表2 不同泄漏方向下的甲烷聚集情况

表3 不同泄漏方向下的氢气聚集情况

3.2 结果验证及讨论

在泄漏口朝上的情况下，氢气体积浓度每增加1%，甲烷在阀室顶部的聚集厚度减小约0.02 m，氢气在阀室顶部的聚集厚度增大约0.01～0.1 m。泄漏口朝水平方向和向下时，相比于向上泄漏，甲烷和氢气在阀室顶部的聚集量将减少。无论哪种泄漏工况下，在阀室内的任意一点，可燃气体检测器均可在氢气达到泄漏检测浓度前检测到甲烷泄漏并报警。

欧洲的 NaturalHy天然气管网掺氢输送示范项目［15］、Lowesmith 等［16］在英格兰北部 Advantica 试验场开展的典型房屋中泄漏口径5 mm和10 mm下的掺氢天然气泄漏扩散实验表明：氢气在室内的聚集体积随着氢气含量的上升而增加，但氢气体积浓度小于 30%时气体聚集体积近乎不变；氢气体积浓度小于50%时聚集体积增加不明显，上述趋势与本文模拟结果是一致的。但国内外在掺氢天然气室内泄漏扩散实验研究方面刚刚起步，在具备条件的情况下，可系统地开展相关实验并验证模拟结果的准确性。

4 可燃气体检测器安装建议

目前我国在工程中主要根据气体相对密度结合标准规范决定室内可燃气体检测器的布置方式。对于天然气及掺氢天然气这些密度小于空气的气体，常用标准规范及其建议安装位置见表4［12］。

表4 标准规范中推荐的可燃气体检测器安装位置

数值模拟结果表明：氢气浓度小于15%的掺氢天然气发生泄漏后，在阀室内的任意一点，可燃气体检测器均可在氢气达到泄漏检测浓度前检测到甲烷泄漏并报警。据此，对阀室内可燃气体检测器提出建议如下：

在进行氢气浓度小于15%的天然气掺氢输送时，阀室内现有的可燃气体检测器可保持现状。若要更加有效的检测横向或向下方向的泄漏，可考虑在四周墙壁处增设甲烷检测器，增设位置视具体情况而定。

在进行掺氢浓度15%及以下掺氢输送时可不单独设置氢气检测器。若要单独检测氢气，氢气检测器安装位置建议为贴近房顶0.1～0.2 m处的四周墙壁上，氢气体积浓度大于15%时需另行评估。

5 结论

基于压缩因子修正的多组分非理想气体扩散系数模型，建立了西气东输一线管道某阀室泄漏扩散三维模型，分析了掺氢天然气泄漏扩散瞬态过程，以及风速、氢气体积浓度、泄漏口径、泄漏口朝向对泄漏扩散的影响。

泄漏口朝上时，在泄漏60 s后，氢气体积浓度每增加1%，甲烷在阀室顶部的聚集厚度减小约0.02 m，氢气的聚集厚度增大约0.01～0.1 m。泄漏口水平方向和向下时，甲烷和氢气在阀室顶部的聚集量相比于向上泄漏时较少。当氢气浓度小于15%时，阀室内可燃气体检测器可在氢气达到泄漏检测浓度前检测到甲烷泄漏并报警。

在进行氢气浓度小于15%的天然气掺氢输送时，阀室内现有的甲烷可燃气体检测器可保持现状。若必须进行氢气检测，可燃气体检测器安装位置建议为贴近房顶0.1～0.2 m处的四周墙壁上。

在具备条件的情况下，可以进一步开展掺氢天然气室内泄漏扩散实验，验证模拟结果的准确性，并为进一步完善掺氢天然气输送场站泄漏应急处理预案提供支撑。