一种改进格林元方法及在渗流问题中的应用

方思冬， 程林松， 饶 翔， 吴永辉

(1.中国石化石油勘探开发研究院，北京 100083; 2.中国石油大学(北京)，石油工程学院，北京 102249)

1 引 言

渗流问题在实际工程中有着广泛的应用，如地下水、热工、化工和石油等领域，由于求解区域和边界条件的复杂性，很难得到有效的解析解，因此，数值方法是求解渗流问题的有效方法之一[1-3]。

常见的数值方法主要有有限元、有限差分、有限体积和边界元法等[4,5]。与有限元、有限差分和有限体积等数值方法相比，边界元类方法具有半解析、降低一阶维数和处理无限域问题的优势[6,7]，在一些工程和科学问题中，如石油的渗流方程、水渗流方程和热传导方程等应用广泛。

基于边界积分方程，Taigbenu等[8-11]提出了原始的格林元方法，该方法结合了边界元方法和有限元方法的思想。与边界元方法类似的是，格林元方法也是基于边界积分方程推导的；不同的是，格林元方法结合了有限元方法的思想将计算区域划分成了网格，并在每一个网格中应用边界积分方程进行离散。在该方法中，计算区域划分为多边形网格，并选用多边形的顶点作为压力值求解的节点，同时采用离散后压力表达式的微分来估计每个节点处的外法线流量，这样的处理方式使得整个数值方法仅显式考虑了节点处的压力值，导致整体精度下降，即只有一阶精度。Archer[12，13]通过使用更大范围的插值基函数来提高对流量项估计的精度，但仅能在矩形网格的情况下实施该方法，并且该方法在区域边界存在源汇项时会计算困难。文献[14-18]提出了基于流量向量的格林元方法，并成功在矩形网格和三角形网格的情况下使用，该方法显式考虑了节点的压力值和外法向流量值，将格林元方法提高到了二阶精度。然而，按照该方法的计算原理，压力和外法向流量在相邻的网格上不连续，不符合实际的物理过程，因此可能一定程度上降低了计算结果的精度。Lorinczi等[19]提出了一种显式考虑节点压力和外法线流量的格林元方法用以数值求解科学工程中的二阶非线性偏微分方程，但是该方法为解决方程组封闭性而提出的公式缺乏严格的证明，计算精度不能保证。随后，Lorinczi等[20]仍采用原始格林元方法中利用离散后压力表达式的微分来近似外法线流量的做法，但使用二次多项式函数作为压力值的插值基函数，使得微分后的外法线流量项是空间坐标的一次多项式函数，从而一定程度提高了计算精度，但仍只是显式考虑了节点的压力值。

为了进一步提高格林元方法的精度并使计算原理更符合实际的物理过程，本文借鉴了混合有限元方法中压力和流量(通量)的求解方法，提出了格林元方法流量和压力处理的新方法，并命名为混合边界元方法，该方法在不增加额外未知数的情况下提高了计算精度。

2 材料和方法

2.1 原始格林元方法

Taigbenu[8]针对式(1)的二阶偏微分方程的数值求解问题，提出了原始的格林元方法，该方法基于边界积分方程，并结合了有限元网格划分的特点，其基本推导过程为

·(Kh)=c(∂h/∂t)+f

(1)

基于拉普拉斯方程的基本解，方程(1)可以写为

(2)

式中Ψ=lnK,ν=1/K,σ=cv,基于格林定理和对应方程在无限大空间中的基本解(2G=δ(r-ri))，方程(2)对应的边界积分方程为

(3)

式中q=-Kh·n为通量，下标i表征源点或者配点，λ表征节点的角度值。方程(3)可以转化为边界元方程，而区域积分可以通过高斯积分或者DRM方法转换到边界积分上求解。引入插值函数可以将离散方程应用到每个子区域里，表示为Λe,方程表示为

Ri jhj+Li j(q/K)j-Ui m jΨmhj+

Wi m j[σm(dhj/dt)+υmfj]=0

(4)

式中

Wi m j=∬ΛeG(r,ri)ΩmΩjdA

方程(4)简化形式为

(5)

式中Ei j=Ri j-Ui m jΨm,Bi j=Li j(1/K)j

Ci j=Wi m jσm,Fi=Wi m jυm

关于时间的偏导数可以写成有限差分的形式为

dh/dt=(h(2)-h(1))/Δt

(6)

方程的显隐式程度可以由关于时间的权重因子θ来控制，将θ代入方程(5)，并联立方程(6)，得到方程关于压力和流量的表达式为

(7)

式中上标1表示已知时刻，上标2表示下一时刻。

主变量h的处理方法与有限元相似,如图1所示，为网格的节点，而流量的处理存在多种方法，最简单的是采用节点之间的压力插值求解，但该方法对方程(7)流量的精度由二阶降到一阶。

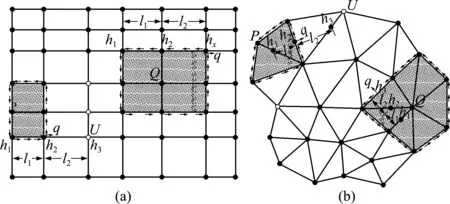
图1 格林元网格

2.2 混合边界元方法的建立

格林元类方法关于流量的处理主要有两大类，第一类采用网格节点值局部插值得到每个节点的压力梯度，然后求解出流量，但该方法精度低；第二类为将流量显式求解，但该方法增加了计算量，对于大网格数计算效率低。

本文基于格林元边界积分法，借鉴了混合有限元压力和流量(通量)的求解方法，提出了格林元流量和压力处理的新方法，该方法在不增加额外未知数的情况下提高了计算精度。

对于局部网格e，基于方程(5)，求解流量q对应系数矩阵B的逆矩阵，将方程等号左边写成流量，右边写成流量关于网格边界积分和压力的函数。

(8)

代入时间权重因子，方程变换为

(9)

为了简洁，方程写为

(i=1,2,…,n;j=1,2,…,n)(10)

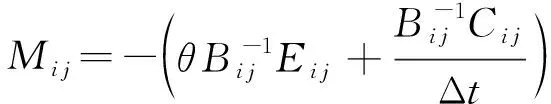
方程类似于混合有限元流动方程关于速度的插值积分形式，其中流量采用常单元体表征,如 图2 中 edge -base element，即每个边界处流量均匀分布，而压力也采用常单元,如图2中 edge -base element。压力未知数与流量未知数相同，矩阵耦合后为方阵。

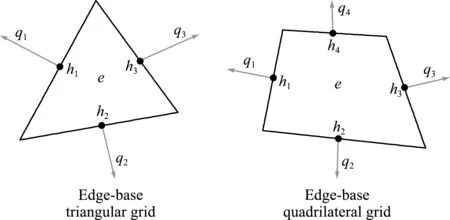
图2 混合边界元局部网格未知数

以两个单元(图3)为例，说明全局矩阵如何由局部矩阵构成。对于单元e1方程组为

(11)

对于单元e2方程组为

(12)

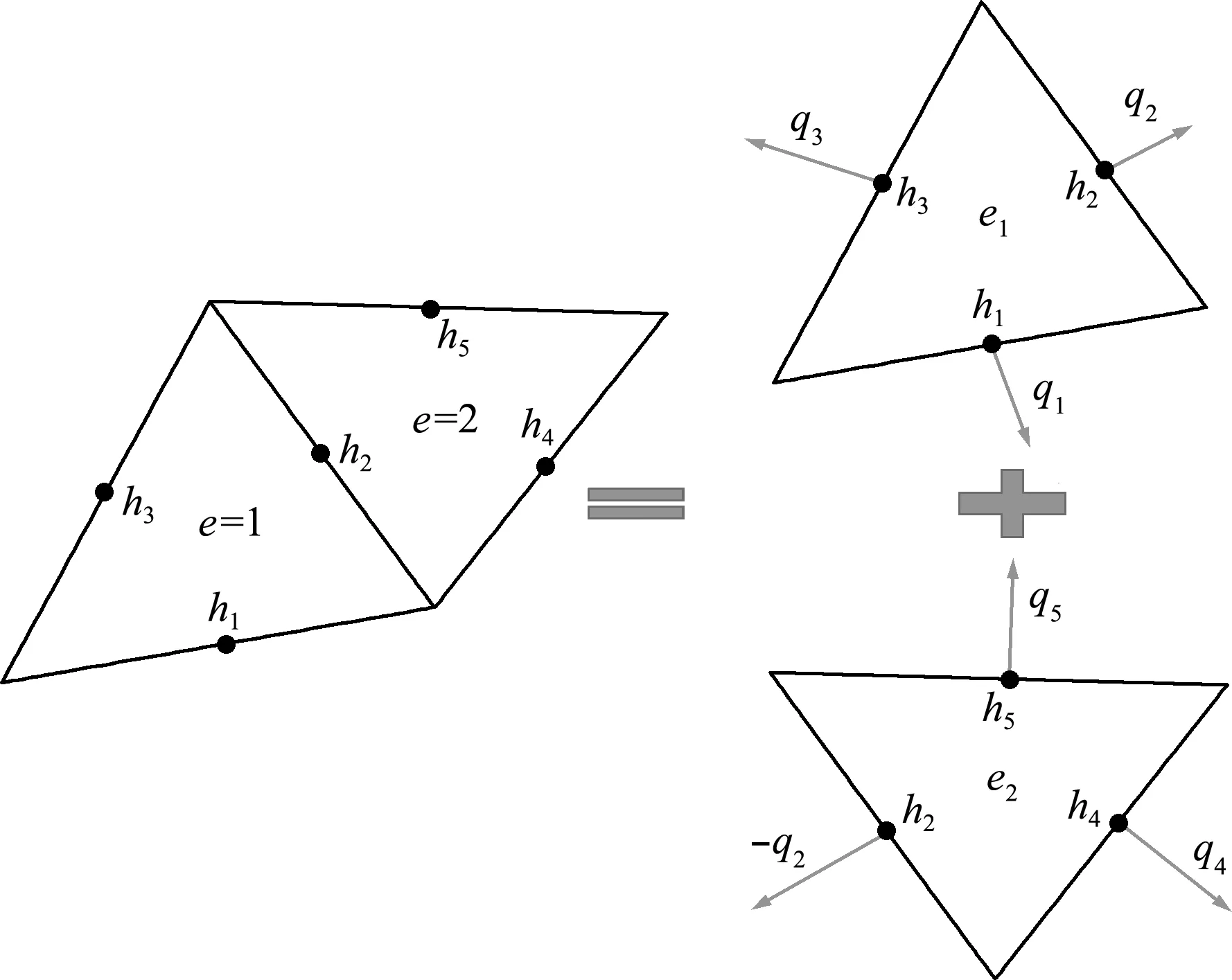
图3 相邻网格关系

合并方程组(11,12)，并假设网格外边界流量为0(封闭边界)，可得全局方程组为

(13)

方程(4)中单元边界积分项Ri j和Li j包含格林函数的积分和格林函数导数的积分，边的参数关系如图4所示，其中沿着图4粗线方向的坐标为

(14，15)

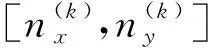
(16)

图4 三角形边参数

格林函数积分和格林函数导数积分表达式为

(17)

(18)

式中A(k )=[l(k )]2

方程(17,18)的解析表达式分别为

(19)

(20)

方程(4)关于单元面积分项Ui m j和Wi m j的计算，需要利用单元节点对单元体内部的插值。本文采用边节点为主变量，单元体采用非协调线性单元，即在每条边中点主变量连续，而在三角形网格顶点处不同网格值不同，如图5所示；而与非协调元对应的是协调线性单元，该类方法是有限元中最常见的插值方法，格林元方法同样运用该类型单元，即顶点处为主变量，如图6所示，单元体内部的值由以三角形顶点值线性插值得到。

三角形线性单元的插值函数为

Ni(x,y)=ai+bix+ciy(i=1,2,3)

(21)

图5 三角形协调线性单元

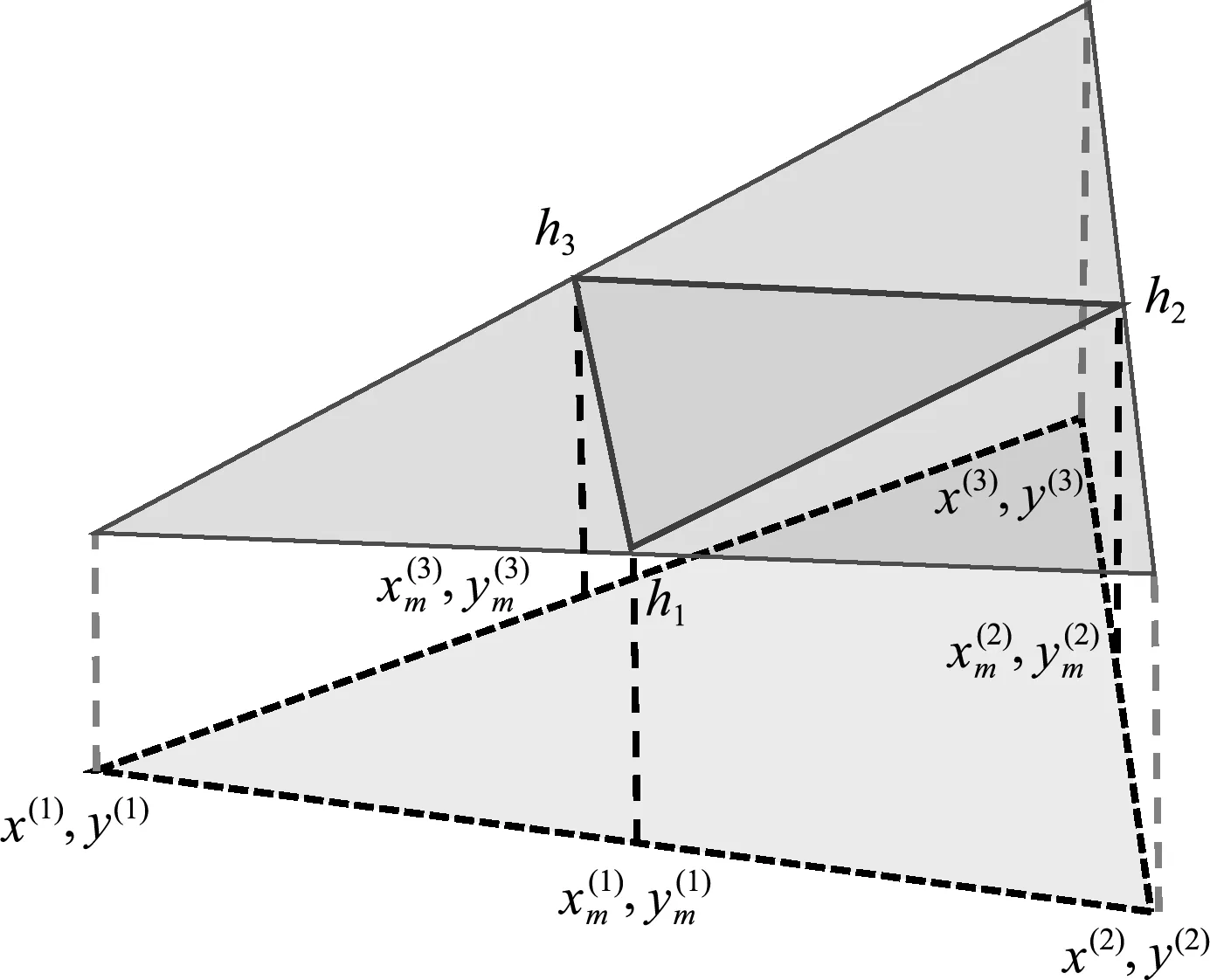
图6 三角形非协调线性单元

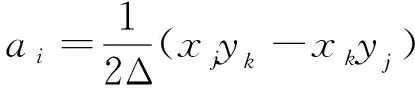
在计算时，当i=1，则j=2，k=3；当i=2，则j=3，k=1；当i=3，则j=1，k=2；其中，Δ为单元体面积，

(22)

3 数值计算实例

本节建立五个实例，分析计算结果以及其变化特征等，并对比混合边界元法与格林元类方法的精度，文献[11]对比了相同计算节点数格林元类方法和有限元方法的计算误差，证明两类方法整体误差相当。

一滴水可以折射出太阳的光辉，一个企业的发展历程也可以映证一个国家经济变革的风貌。西北石油局进疆40年风雷激荡的雄浑篇章，也是40年改革开放取得辉煌成就的一个缩影和历史见证。西北油田正是乘着改革开放的春风，以非凡胆识与创新精神，取得一个个重大突破。沙参二井的重大发现，犹如“沙漠春雷”拉开了塔里木油气勘探开发大会战的序幕；沙48井的高产油气流，拉开了10亿吨储量级缝洞型油藏开发的序幕，并使塔河油田快速跻身国内陆上十大油田之列。如今，西北油田已发生脱胎换骨的变化，一跃成为在低油价时率先盈利，在高油价时创效最多的标杆企业 ，以强劲的发展势头，划出一条激情上扬曲线。

(1) 拉普拉斯方程求解。拉普拉斯方程又称调和方程或位势方程，求解拉普拉斯方程是电磁学、天文学和流体力学等领域经常遇到的一类重要的数学问题，因为这种方程以势函数的形式描写了电场、引力场和流场等物理对象(一般统称为保守场或有势场)的性质。在石油渗流方面，拉普拉斯描述均质地层稳定渗流。

问题描述。区域范围是0.5×0.5，左边界和上边界均满足第一类边界条件，内部区域没有源汇项，方程可以写为

2h=0

(23)

边界条件为

h(0,y)=0， (∂h/∂x)(0.5,y)=0

(∂h/∂y)(x,0)=0,h(x,0.5)=sin(πx)

(24)

以上方程的精确解析解为

h=cosh(πy)sin(πx)/[cosh(π/2)]

(25)

基于混合边界元方法，计算了四套网格的值(2×2，4×4，8×8和16×16)，其中网格大小分别为0.25，0.125，0.0625和0.03125，并与格林元、流量格林元和修正格林元方法的计算结果对比，平均误差表达式为

(26)

式中上标e和上标n代表精确解和数值解，N是节点个数，如图7所示，数值解精度随着网格数目增加而增加，混合边界元法在四种大小的网格下误差都是最小，但与修正格林元方法差距不大。利用混合边界元方法计算了外边界的流量值并与精确解对比(8×8网格数)，如图8所示，混合边界元数值解与精确解完全重合。

模拟了相同几何区域不同网格形态对计算结果的影响，网格类型为矩形网格、任意四边形网格和三角形网格，如图9所示。模拟结果发现，当网格数相近时(网格大小相近)，模拟精度几乎相同，计算结果不会因为网格形式不同而发生较大变化。

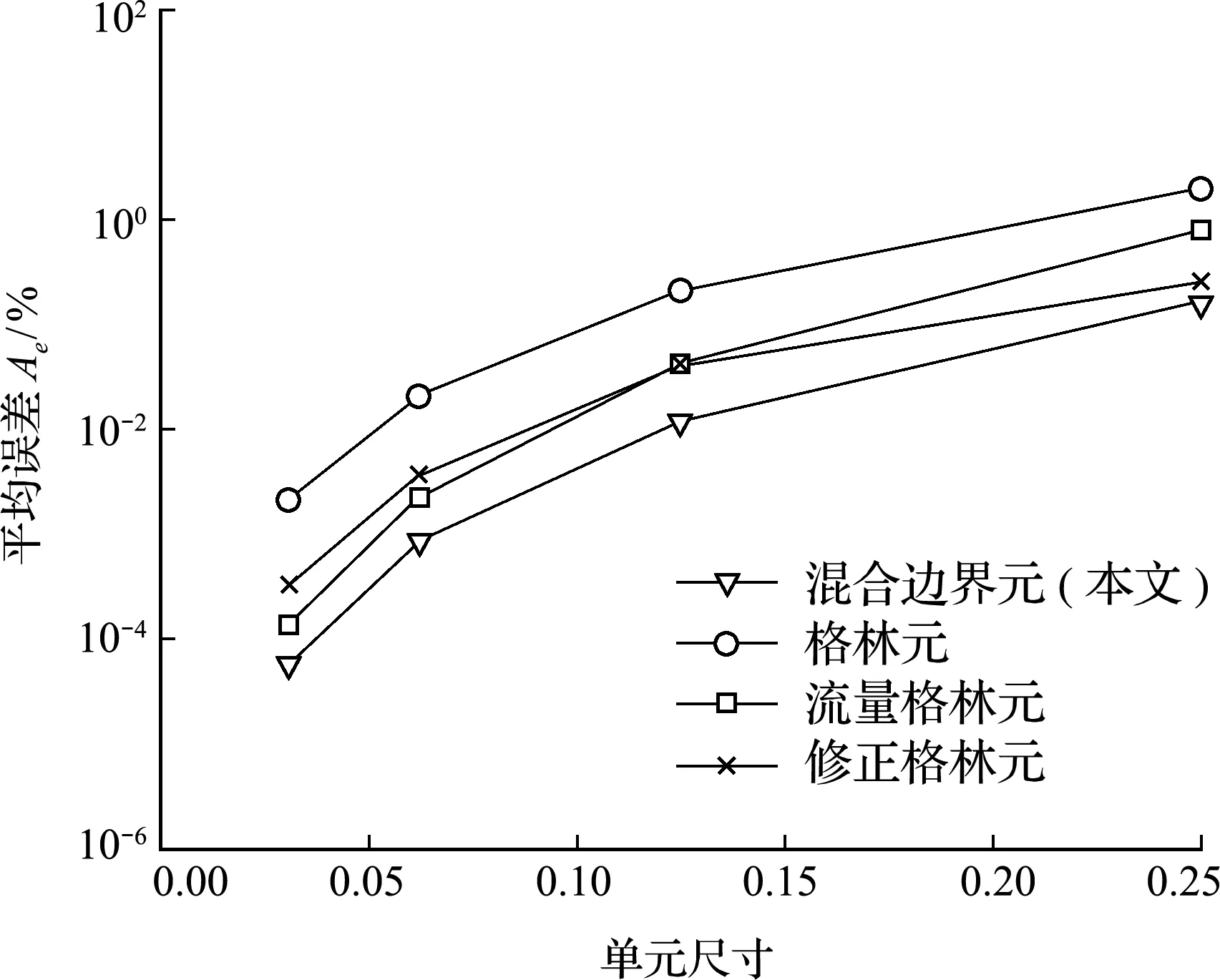
图7 四种数值方法误差对比(实例1)

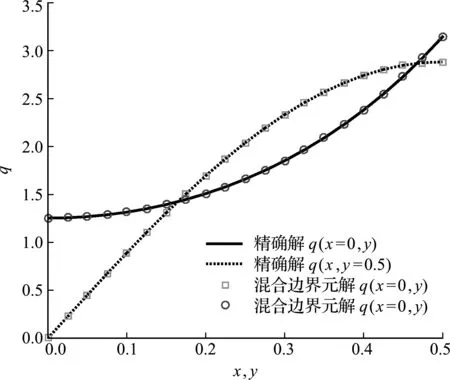
图8 外边界流量(实例1)

图9 三种网格对比

图10 三种网格形态区域内相应的的3D场图(实例1)

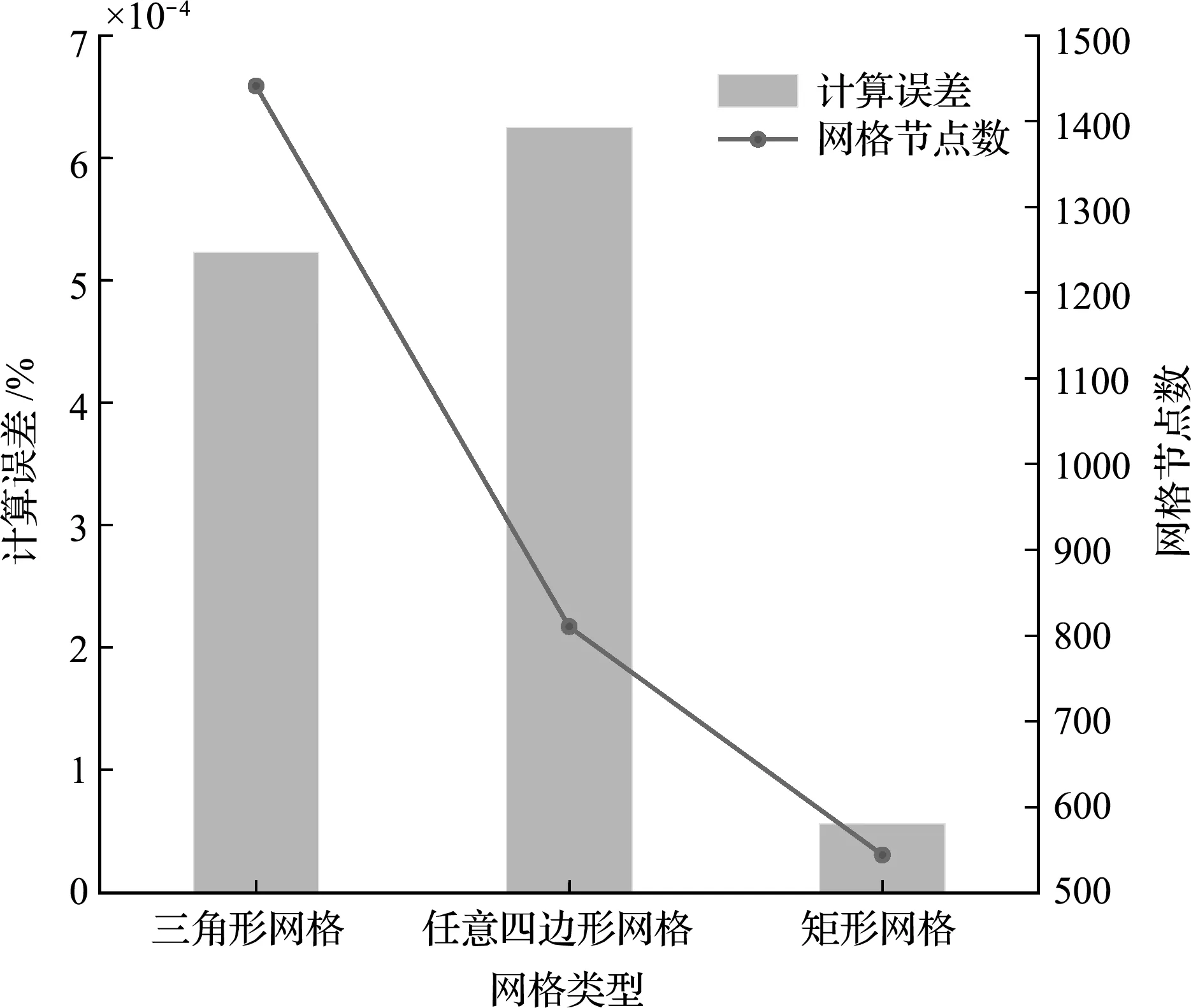
图11 三种网格形态相应的计算误差(实例1)

(2) 非均质区域稳态流。区域范围是1×1，区域范围里的流动是稳定渗流，材料参数为非均质，渗透率满足分布K=1+x3，左右边界条件满足第一类边界条件，上下边界满足封闭边界条件，内部区域没有源汇项，其稳定渗流方程可以写为

·(Kh)=0

(27)

其中边界条件为

h(0,y)=0，h(1,y)=1

(28)

计算了五套网格，其网格数目为(3×1，4×1，5×1，8×1，10×1)，不同数值方法误差对比如 图12 所示，混合边界元方法误差比以往的方法小一个数量级，故混合边界元更能准确模拟非均质流动问题。结果分布如图13所示。

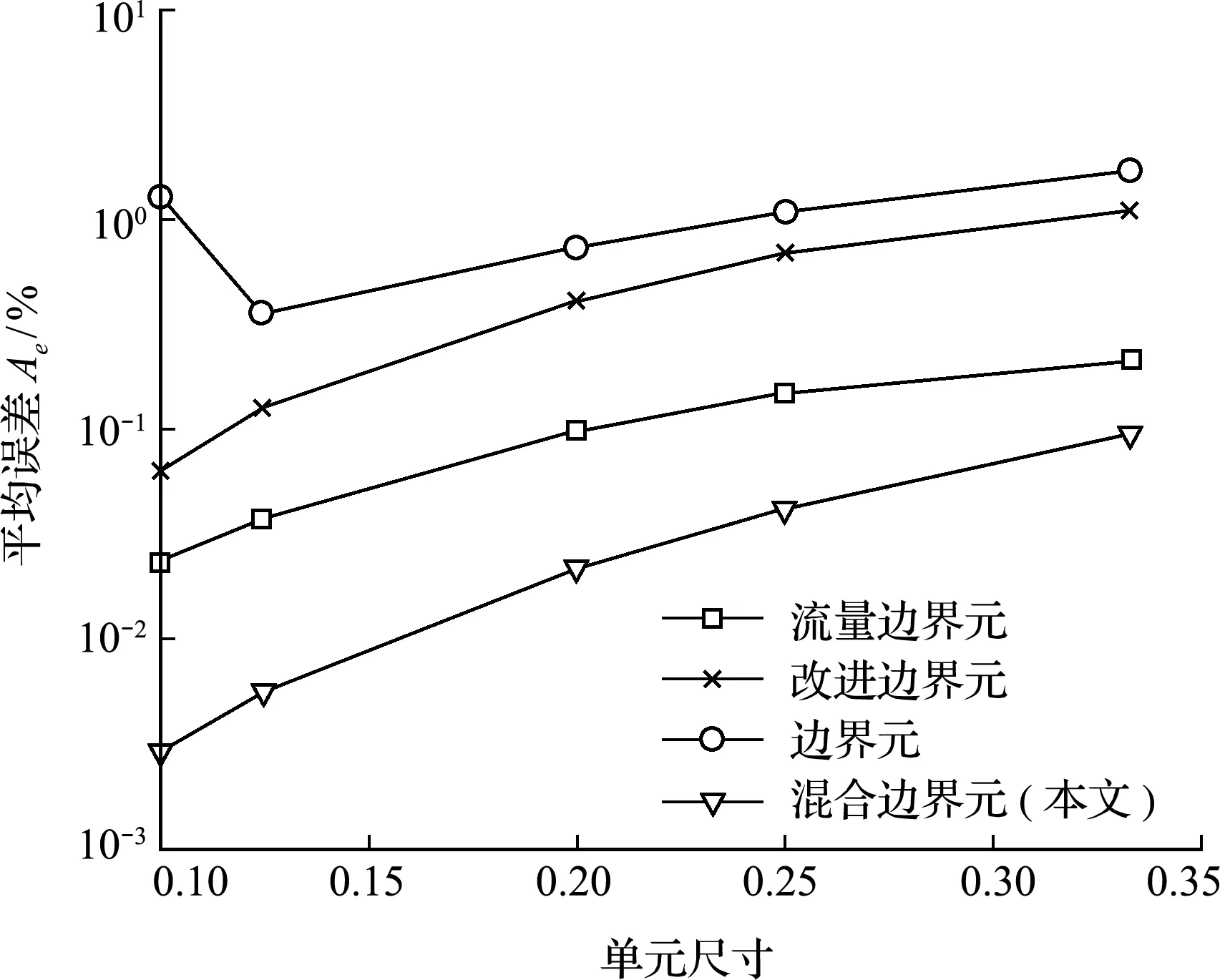
图12 四种数值方法误差对比(实例2)

(3) 非均质介质非稳态热传导问题。该问题的偏微分方程以及边界条件为

·(Kh)=c(∂h/∂t)

(29)

图13 结果3D场图(实例2)

边界条件和初始条件为

h(x=0)=1，h(x=1)=20，h(x,t=0)=1

(30～32)

材料介质的参数分别给出两套值，分别为

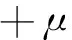
基于以上方程，建立了1×1正方形区域，对于第一套参数例子模拟，采用两套网格，10×1的粗网格，网格大小为0.1×1；20×1的细网格，网格大小为0.05×1。第二套参数采用20×1的细网格，网格大小为0.05×1。方程采用全隐式求解(θ=1)。时间步长为0.02，对比不同数值方法，第一套参数粗网格误差如图14所示，细网格误差如图15所示。第二套参数细网格误差如图16所示。可以看出，混合边界元方法在粗网格和细网格都具有稳定并且最小的误差值。利用混合边界元方法建立并对比了不同点温度随时间变化的曲线，如图17所示。

图14 四种数值方法误差对比(K =exp(3 x )，10个网格)(实例3)

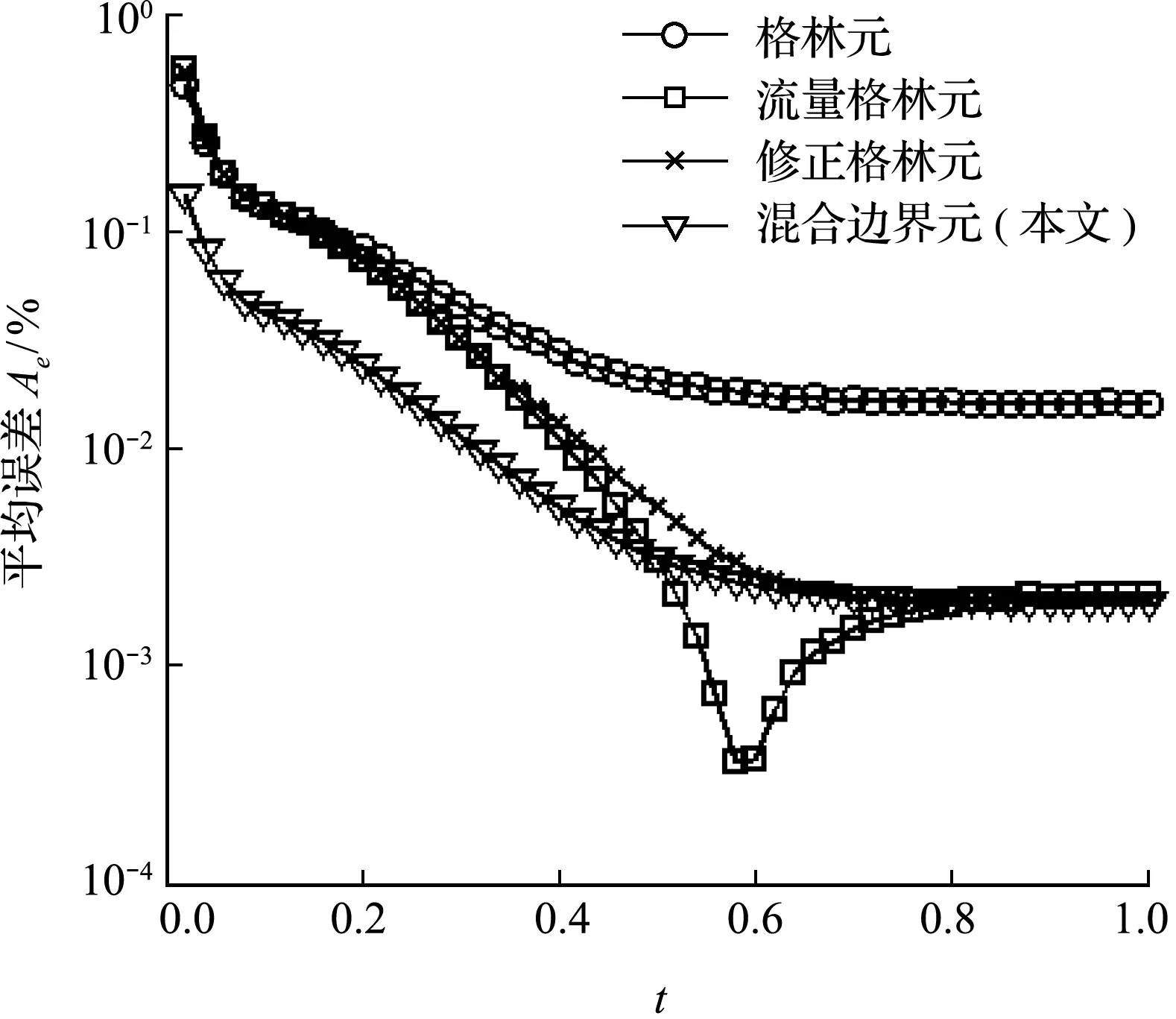
图15 四种数值方法误差对比(K =exp(3 x )，20个网格)(实例3)

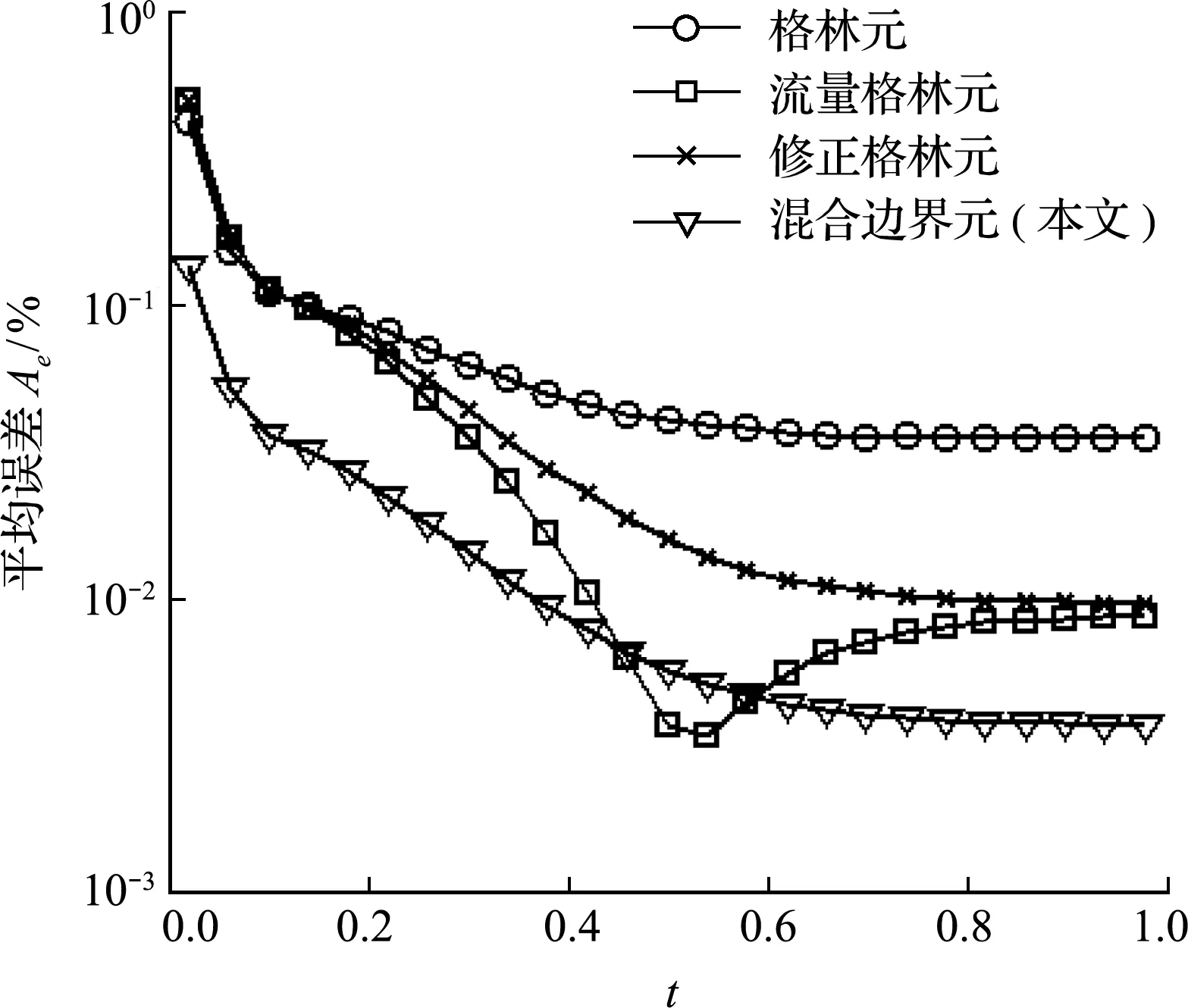
图16 四种数值方法误差对比(K=(1+3 x)2，20个网格)(实例3)

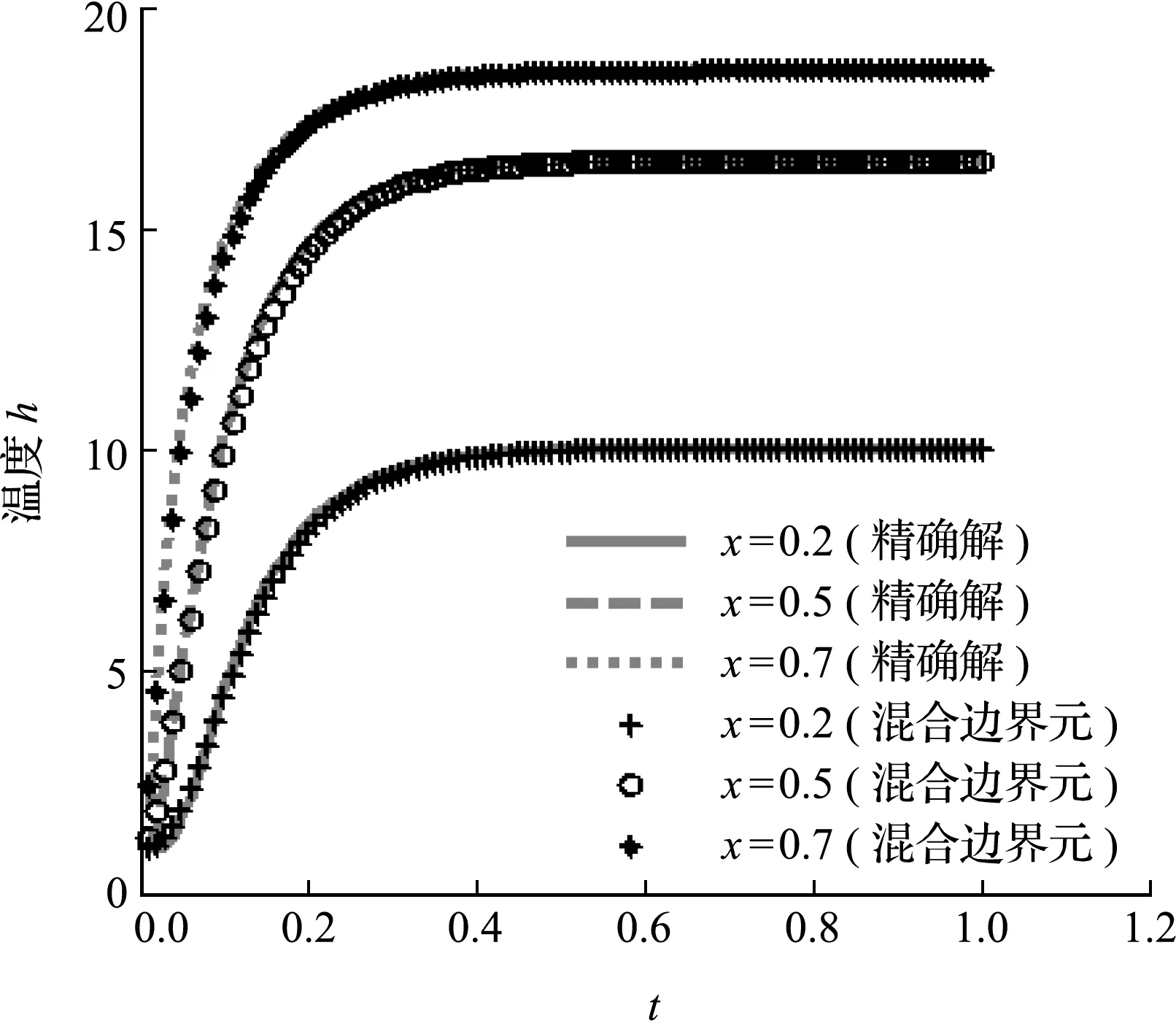
图17 温度剖面(K =(1+3 x )2)(实例3)

K=(1+3x)220 grids

(4) 非线性非稳态问题。该问题由方程(33)表征，但没有f项，K值大小由主变量h决定。问题主要描述自由水体在X方向的瞬态流动，左端水头随着时间变化，右端封闭，其偏微分方程和边界条件可以写为

边界条件为

(34)

初始条件为

h(x,t=0)=x(x-x/6)

(35)

基于以上方程，建立了1×3正方形区域，划分12个网格，网格大小为0.25×1，当时间小于等于1时，时间步长为0.05，当时间大于1时，时间步长为 0.25，时间权重因子θ=0.67，不同时间水头剖面如图18所示，混合边界元计算的剖面与解析解完全重合，平均误差随时间变化如图19所示。可以看出，对于非线性问题，混合边界元精度比以往方法高一个数量级。因此，混合边界元法很适合求解非线性问题。

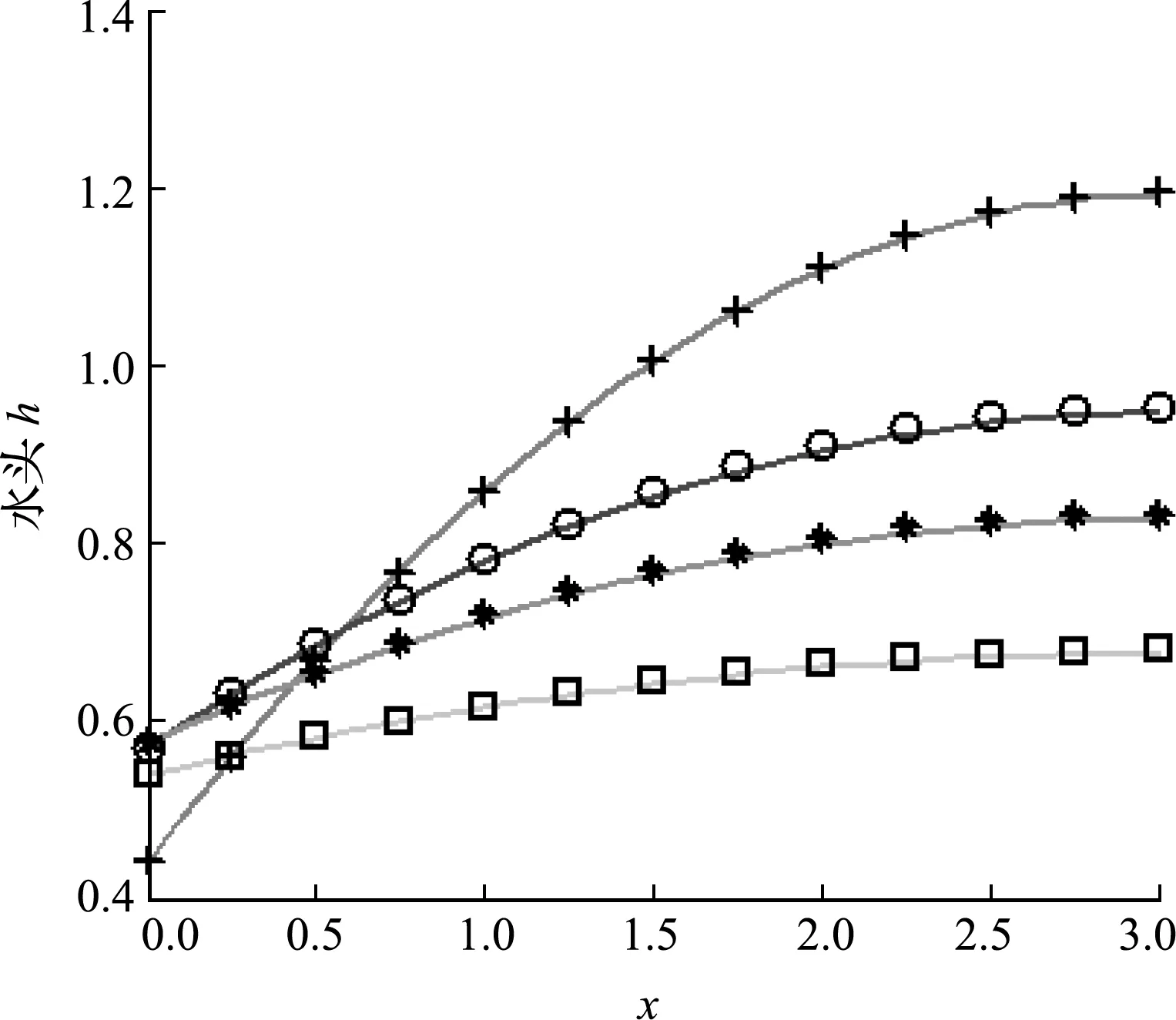
图18 不同时间水头剖面

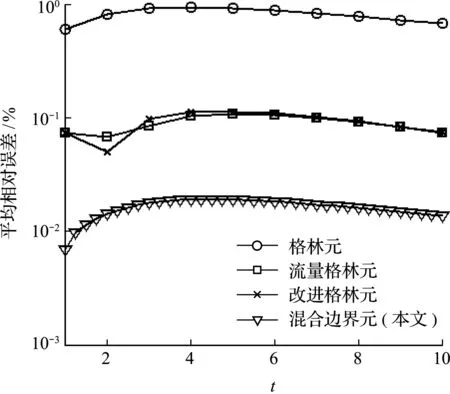
图19 四种数值方法误差对比(实例4)

(5) 圆形油藏生产模拟。本算例建立300 m圆形油藏，中心有一口直井，定产量生产，具体区域及网格剖分如图20所示，利用混合边界元方法计算无因次井底压力及压力导数曲线，如图21所示。可以看出，利用混合边界元方法计算得到井底压力及压力导数曲线与解析解之间误差很小，因此混合边界元方法适用于油藏数值模拟，具有较广阔的应用前景。

图20 圆形油藏网格剖分情况

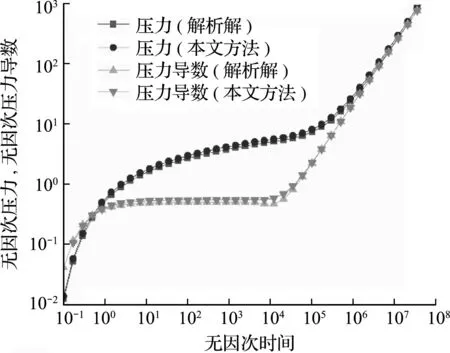
图21 计算结果对比

4 结 论

本文借鉴了混合有限元压力和流量(通量)的处理方法，并利用两相邻网格公共边的外法向流量代数和为0的特点，使得求得的数值解相较于以往的格林元类方法在计算区域上精度更高，具有广泛的应用前景。

模拟了不同网格形态对计算结果的影响，网格类型为矩形网格、任意四边形网格和三角形网格，模拟结果发现，当网格数相近时(网格大小相近)，模拟精度几乎相同，计算结果不会因为网格形式不同而发生较大变化。

通过实例计算发现，对于非线性问题，混合边界元精度比以往方法高一个数量级。因此，混合边界元法很适合求解非线性问题。

利用混合边界元方法计算得到井底压力及压力导数曲线与解析解之间误差很小，因此混合边界元方法可用于油藏数值模拟。