阶梯圆柱形耦合声场的特征正交-里兹法建模及声学特性分析

钟 锐， 谢 非， 秦 斌， 王青山*

(1.中南大学 高性能复杂制造国家重点实验室，长沙 410083；2.中南大学 交通运输工程学院，长沙 410083)

1 引 言

阶梯圆柱形耦合封闭声场是一种外径参数沿长度方向呈现阶梯变化的声场。作为典型的室内声学建筑，这类声场广泛存在于船舶舱室、海洋平台、运输管道和回转类建筑等工程领域，有关其内部噪声控制的研究始终是室内声学领域关注的热点和难点，而进行室内噪声控制研究有赖于精准有效的声场建模和声学特性分析。因此，对阶梯圆柱形耦合声场进行理论建模及声学特性研究具有重要的科学意义和实用价值。

目前，对等径圆柱形封闭声场已有丰富的研究成果[1-4]，有助于了解和认识阶梯柱形耦合声场的声学特性，但由于该类声场几何形状的不规则性以及声学边界的复杂性，一般认为无法获得精确的解析解[5,6]。Williams[1]通过改进格林函数描述声压函数进而求解了圆柱形声场的声学问题，这一研究仅考虑了诺伊曼边界和狄利克边界。Chen等[2]结合边界元法(BEM)和Helmholtz外部积分公式法分析了圆形和矩形声场的声学特性，但研究仅局限于等径柱形声场。Xiao等[3]提出三维改进傅里叶级数方法建立了不同阻抗边界下单一环形段声场的声学模型，考察了角度、半径比、阻抗大小及阻抗壁面数目对声场声学特性的影响，对回转类柱形耦合声场的研究具有一定的借鉴意义。Zhang等[4]从能量的角度提出了任意阻抗壁面条件下包含锥形、柱形和球形在内的回转类封闭声场的统一求解方法，丰富了现有的回转类声场计算体系，但并未涉及几何形状更为复杂的柱形耦合声场的研究。Choi等[7]基于波动方程提出一种解析法，获得了环形声场的自然频率和固有模态，探讨了声学特性与声场介质局部偏差的关系。Shao等[8]提出了一种基于格林函数原理的简化声学模型，对有限长柱形管的声场模态特性进行了分析，有效提高了柱形管声场模态的计算效率。基于近场全息原理，王健等[9]构建了两端封闭的有限长圆柱壳体内部声场，但该方法仅适用于低频率段声学问题求解。熊路[10]根据真空中、内部充液和浸没在流场中几种情况下的椭圆柱壳和单层偏心圆柱薄壳的特性，分别采用双Fourier级数展开法、传递矩阵法和Helmholtz方程对其振声特性进行了系统研究。除上述提及的数值方法外，研究人员也提出了有限元法[11-13]和边界元法[14]等数值手段用于封闭声场的声学特性研究。事实上，利用数值方法如有限元法可以对阶梯柱形耦合声场进行分析，但随着计算波数和频率的增加，数值方法往往需要占用大量计算资源，且对具有耗散壁面的声学问题，数值方法缺乏灵活性和普适性。另外，分析已有的文献可以发现，对几何形状沿长度方向呈现阶梯变化的柱形耦合声场的研究尚不多见，且由于声学设计指标的高要求，对于具有一定能量耗散作用的声学阻抗壁面研究有迫切需求。因此，开展阻抗壁面下阶梯圆柱形耦合声场的建模及声学特性研究具有重要的意义。

近来，Qin等[15]利用特征正交-里兹法研究了具有任意边界条件的圆柱薄壳结构的自由振动特性。本文在此基础上，将特征正交-里兹法扩展到柱形耦合声场，建立包含任意阶梯分段和阻抗壁面在内的声场模型，通过数值对比分析验证本建模方法的可靠性，进而研究声场几何参数、阻抗边界以及声源幅值对于其声学特性的影响。

2 阶梯柱形耦合声场建模

2.1 柱形耦合声场物理模型

图1给出了沿长度方向阶梯变化的柱形耦合声场几何参数和坐标系统。坐标原点O在耦合声场的最底面，沿长度方向柱形耦合声场根据外径大小分割为N段柱形声场，Ri表示第i段声场外径，Li表示第i段声场在长度方向上的分段长度，耦合声场总长定义为L，所有分段的内径统一设为R0。图中为耦合声场的横截面示意图，该截面绕中心轴旋转θ=2π，即可获得周向封闭的柱形耦合声场。另外，对于声学稳态特性，通过在声场内部设置点声源Q的方式来开展相应的声场内部声压响应研究。

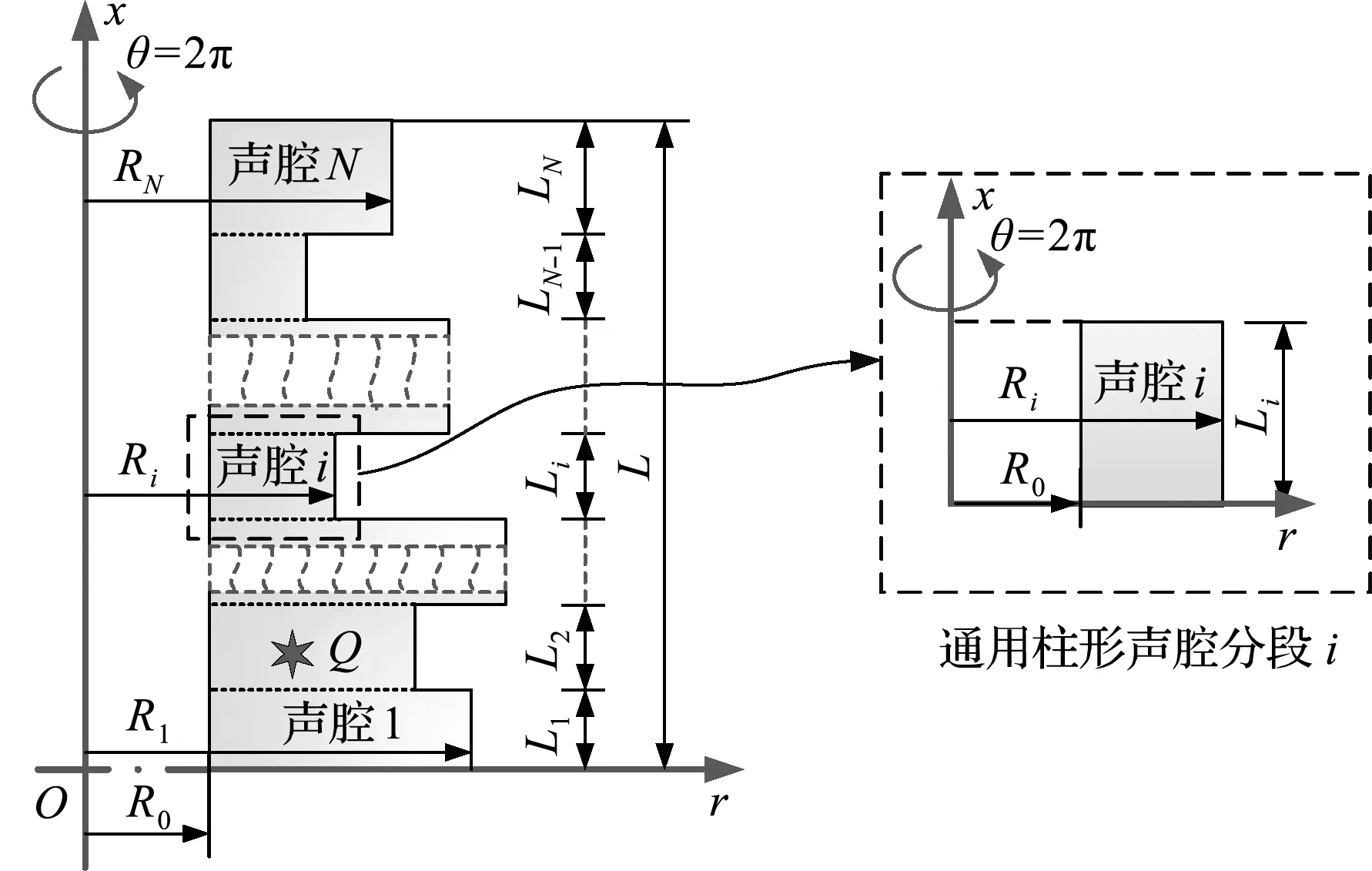
图1 柱形耦合声场的几何参数和坐标系统

2.2 基于特征正交-里兹法的声压容许函数

圆柱形耦合声场沿长度方向x和以外径Ri为依据进行阶梯分段变化，从本质上讲，每段声场均为等径的柱形封闭声场，因而具有通用性。本文建模思路分为两部分，首先构建单段声场的声学求解模型；在此基础上，借鉴有限元或者区域能量分解的思想，建立柱形耦合声场分段与分段之间的声学协调方程，并将各声场分段在整体系统声学变量下进行组装，进而获得任意阻抗壁面条件下任意阶梯分段的圆柱形耦合声场声学特性求解方程。由于分段i具有通用性，因而声学建模主要基于通用柱形分段声场i进行。就耦合声场而言，其内部声场变量在空间中具有对称性，可将其沿周向坐标方向采用傅里叶级数进行展开，同时根据Zhang等[4]提出的三维声压函数构造形式，给出基于特征正交多项式的单段柱形声场i的声压容许函数表达式

P(x,r,θ)Aiei ω t

(1)

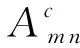
(m≥1)(2a)

(q≥1)(2b)

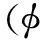
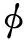
(4)

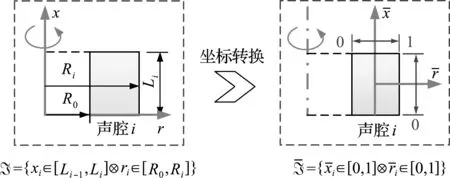
图2 求解区域转换

2.3 柱形耦合声场能量方程

基于声学原理建立阻抗声学壁面条件下的柱形耦合声场分析模型的能量方程，阶梯分段的柱形耦合声场拉格朗日能量方程可表示为

(5)

对于第i段柱形声场，其动能和势能表达式分别为

(6)

(7)

式中ρ为腔内声学介质密度，c为声波在声学介质中的传播速度，ω为耦合声场的圆频率，pi为腔内的声压梯度函数。柱形封闭声场包含内径柱面(r=R0)、外径柱面(r=Ri)、下表面(x=0)和上表面(x=Li)在内的四个阻抗壁面，其壁面耗散能表示为

(8)

对于研究封闭声场的内声场特性而言，其侧重点一般是通过场内放置一个单极子点声源来对声场内部的声场特性进行激振，进而开展不同声学阻抗壁面条件下的声场特性研究。而单极子点声源一般是由脉动压力球构成，其入射压力可表示为

(9)

式中点声源幅值(kg/s2)和声源的辐射距离分别采用符号A和r表示；声波波数k与波速c以及圆频率ω之间存在等式关系，即k=ω/c。根据以上描述，单极子点声源的声源强度Qpoint(m3/s)可以表示为

Qpoint=4πA/(jρck)

(10)

由此，点声源Qpoint所做的功WS可表示为

δδ=δ(x-x0)δ(r-r0)δ(θ-θ0)

(11)

式中δ为三维狄拉克函数，Q是点声源的体积速度幅值，(x0,r0,θ0)为点声源在声场内的加载位置坐标。

本文建立的分析模型适用于阶梯柱形耦合声场系统，此时需要考虑分段与分段之间的声学协调条件。由于耦合声场系统是沿长度方向x进行阶梯变化，因此分段与分段之间的耦合界面是在第i段柱形声场单元的上表面x=Li和第i+1段柱形声场单元下表面x=0之间。在此耦合界面上，第i段和第i+1段声场的声压大小和粒子速度保持一致，具体可表示为

(12)

{Pi +1(0,r,θ)Ai +1Pi,i +1}rdrdθ

(13)

图3 耦合界面积分区域

2.4 柱形耦合声场求解

将能量表达式(6～8,11,13)代入阻抗壁面下柱形耦合声场总的拉格朗日能量方程的表达式(5)，并结合瑞利-里兹能量法，对系统的拉格朗日能量方程LC求极值，可得

∂LC/∂A=0

(A=[A1…Ai…AN])(14)

将式(13)以矩阵形式给出得

(K+C-ωZ-ω2M)A=Q

(15)

式中K和M分别为耦合声场的整体刚度矩阵和质量矩阵，Z为因引入阻抗壁面而产生的耗散矩阵，C为柱形耦合声场的耦合矩阵，Q为外部单极子点声源的力矢量。

对于方程(15)，通过令等式右边为零，同时设Y=ωA，可以将方程(15)转换为求解待求圆频率的特征方程问题[16-18]，即

(R-ωS)H=0

(16)

(17)

通过求解线性方程组(16)，即可获得柱形耦合声场的声学固有频率和声压函数展开表达式的未知展开系数。将获得的未知展开系数代入方程(1)，即可获得柱形耦合声场的声压分布云图。

3 柱形耦合声场声学特性分析

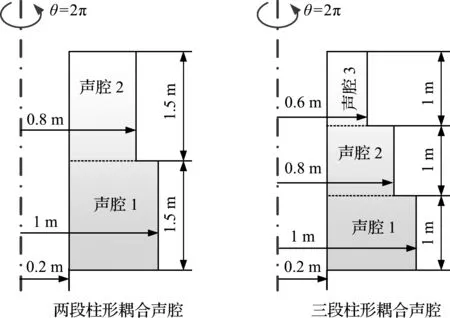
图4 两种典型柱形耦合声场算例

3.1 收敛性和数值验证

本文建立的分析模型计算精度及效率取决于声压函数的截断数Mc和Qc，表1和表2分别给出了两段柱形耦合声场和三段柱形耦合声场的前20阶固有频率收敛性结果，截断数Mc和Qc保持在 4～20之间同步变化。由表1和表2可知，当截断Mc和Qc都等于12时，本文方法的计算结果已完全收敛；对于两段和三段耦合声场而言，Mc×Qc=12×12的计算结果与截断值Mc×Qc=20×20的计算结果之间的绝对误差不超过0.05%。因此，在接下来的数值计算中，声压容许函数的截断值统一选取为Mc×Qc=12×12。

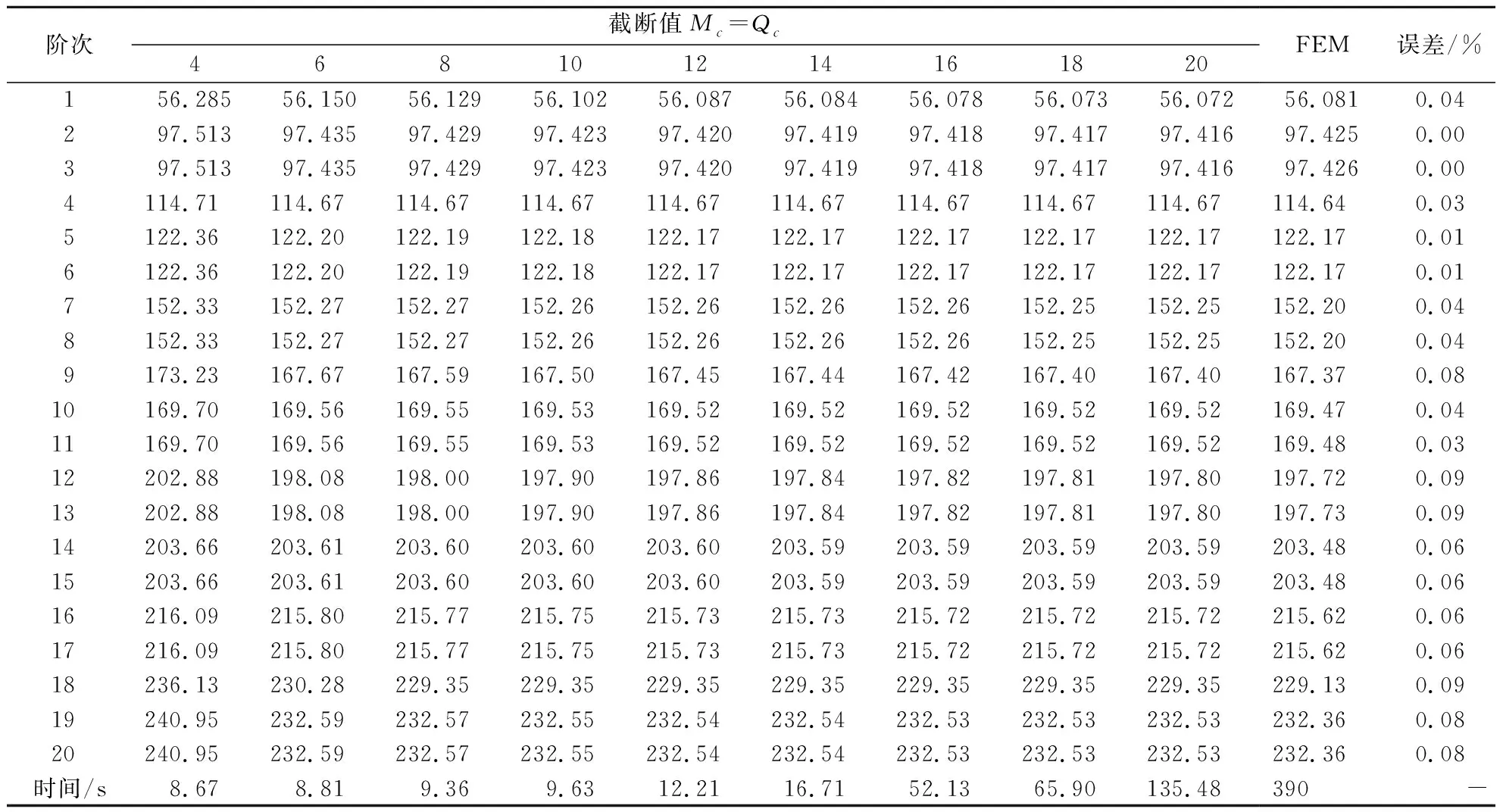
表1 两段柱形耦合声场前20阶固有频率(Hz)的收敛性与正确性分析Tab.1 Convergence and accuracy of the first twenty frequencies (Hz) for two section cylindrical coupled sound field

本文给出本方法的计算正确性分析，由于关于此类问题的文献结果缺失，因此采用基于有限元法获得的结果作为参照来验证所建立分析模型的正确性。有限元分析模型的单元类型为标准的六面体声学单元，单元尺寸全局设置为0.03 m。相关的有限元结果已在表1和表2给出，由表1和表2可知，基于本方法的预测结果和有限元数值结果之间的最大绝对误差不超过0.09%。表中也给出了不同截断值下本方法的计算时间与有限元法的对比，可以看出，尽管随着截断值的增加，本方法的计算时间也随之增加，但本方法在Mc×Qc=12时已完全收敛，满足计算精度要求，此时本方法的计算耗时远小于有限元法计算耗时，表明在保证计算准确性的前提下，本方法可以有效提高耦合声场的计算效率。此外由式(15)可知，除了能获得固有频率信息，还能获得声场的声压分布云图，而声压分布云图有助于理解声场的内部声场特性。图5和图6分别呈现了通过本方法所获得的两段和三段柱形耦合声场的前8阶声压云图，同时也给出了与之对应的基于有限元法的声压云图。可以看出，本方法不仅能够预测精确的固有频率信息，同时能够获得对应的声压分布云图。

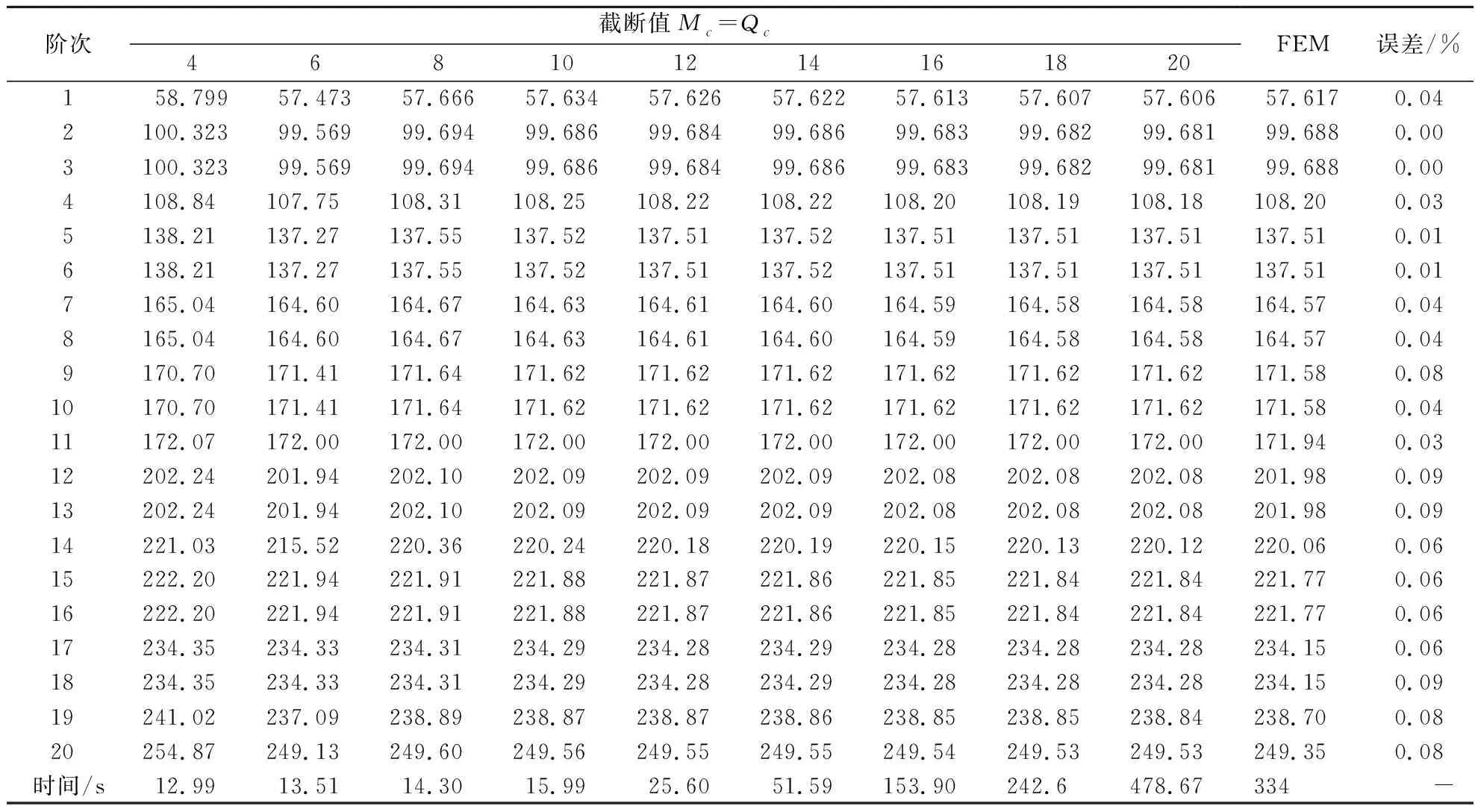
表2 三段柱形耦合声场前20阶固有频率(Hz)的收敛性与正确性分析Tab.2 Convergence and accuracy of the first twenty frequencies (Hz) for three section cylindrical coupled sound field

图5 两段柱形耦合声场声压分布云图

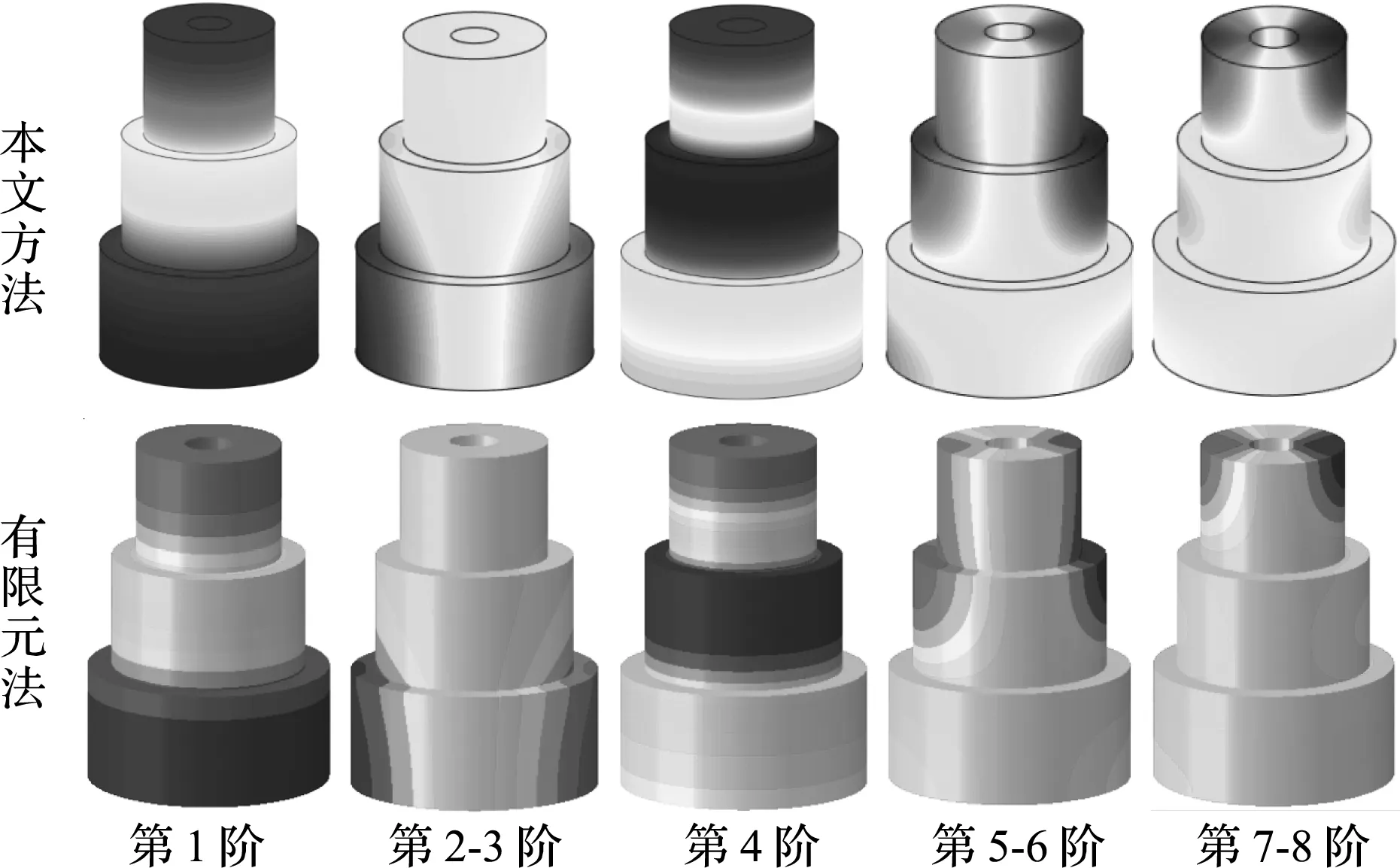
图6 三段柱形耦合声场声压分布云图

图7和图8分别给出了通过本方法和有限元法得到的两段耦合声场和三段耦合声场的声学稳态响应对比曲线。在两段耦合声场算例中，声压观测点1、点2和点3的坐标分布定义为(r1,θ1,x1)=(0.2,0,1)，(r2,θ2,x2)=(0.4,180°,1)，(r3,θ3,x3)=(0.3,0,2)，声源激励点位置为(r0,θ0,x0)=(0.3,0,1)。在三段耦合声场算例中，声压观测点1、点2和点3的坐标分布定义为(r1,θ1,x1)=(0.55,0,0.5)，(r2,θ2,x2)=(0.3,0,1.5)和(r3,θ3,x3)=(0.35,0,2.5)，声源激励点位置为(r0,θ0,x0)=(0.4,0,0.5)。声源幅值Q=1 kg/s2。可以看出，由本文方法及有限元法预测的稳态响应曲线具有良好的一致性。综合以上对比研究，证明本文提出的建模方法适用于具有任意阶梯分段的柱形耦合声场声学问题的求解。

3.2 声学特性分析

本节详细讨论关键参数对于声场声学特性的影响。表3给出了两段柱形耦合声场在不同外径参数R2下的固有频率结果，可以看出，其变化规律整体上是随着外径参数R2增大，声场固有频率普遍增大，但少数模态阶次(n=1)呈现先减小后增大的趋势，这表明耦合声场外径参数对固有频率的影响与模态阶次存在较大的关联性。图9给出了声场深度参数对于声场在n=1和n=6下的前4阶固有频率变化规律。耦合声场几何参数除了整体深度变化，其余参数和图4保持一致。必须说明的是，图9的横坐标为声场整体深度L，纵坐标为频率差Δf(Δf=f(x)-f(2))。可以看出，声场的腔深L对声场特性有着重要影响，随着腔深L的增加，固有频率参数逐渐减小，而且不同模态阶次的变化趋势也存在一定差异，这表明腔深对声场的影响也与模态阶次相关联。

图7 两段柱形耦合声场在单位点声源激励下的声压响应

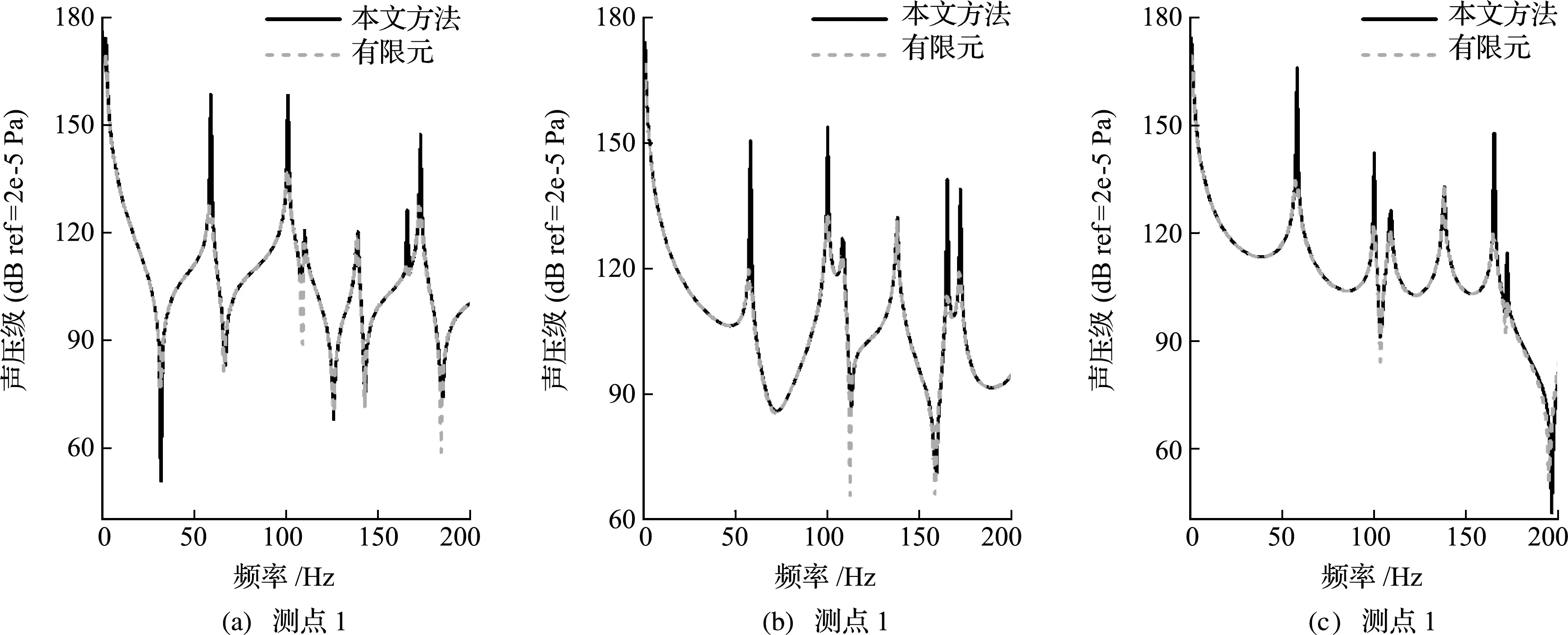
图8 三段柱形耦合声场在单位点声源激励下的声压响应

通过图9和表3的分析可知，声场的几何参数对于声场固有模态特性具有至关重要的作用，而且这种影响从本质上是对声场刚度矩阵和质量矩阵的影响。

由本文模型建立可知，声源激励的幅值和声场的阻抗壁面对于声学稳态响应比较敏感，因此开展上述参数的声学稳态特性研究。图10给出了不同阻抗壁面条件下，柱形耦合声场在单位点声源激励下的声压响应，本文阻抗壁面的位置设置于柱形耦合声场的上下底面，即x=0和x=L的环形面。声源激励位置和声压观测点位置和图7及图8保持一致，三种阻抗壁面的阻抗值分布定义为Z1=ρc0(20-j)，Z2=ρc0(50-j)和Z3=ρc0(100-j)。同时，完全刚性壁面条件下的计算响应曲线也在图中给出。通过对比可知，由于阻抗壁面的存在，声学稳态响应的共振峰值能受到有效抑制。可以看出，随着阻抗值的降低，阻抗壁面吸收耗散能的能力变强，使得声场内部的声学响应共振峰值的抑制效果越显著。但需注意，阻抗壁面的引入对其声场共振频率的影响甚微。

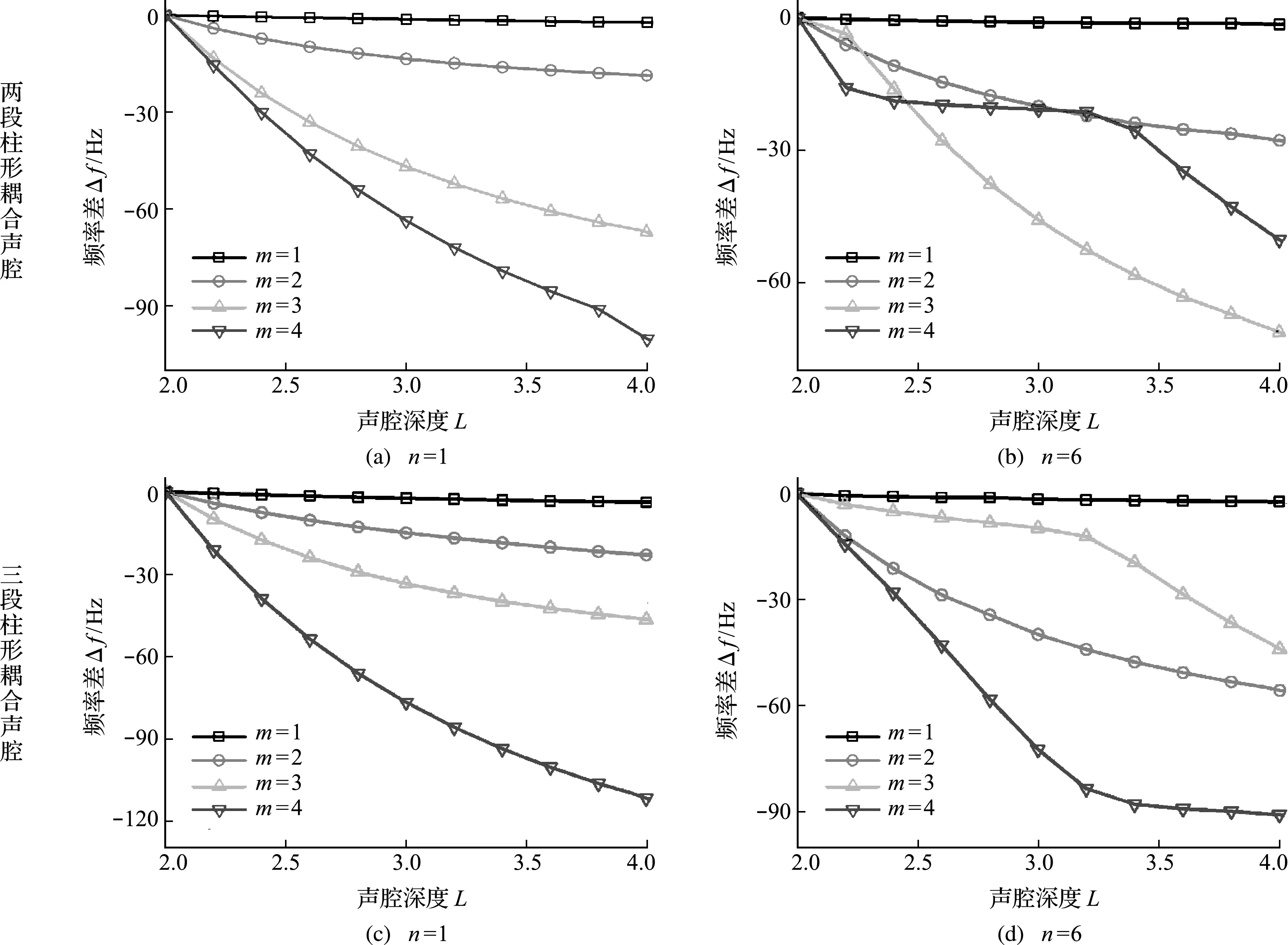
图9 在不同深度下柱形声场的频率变化曲线

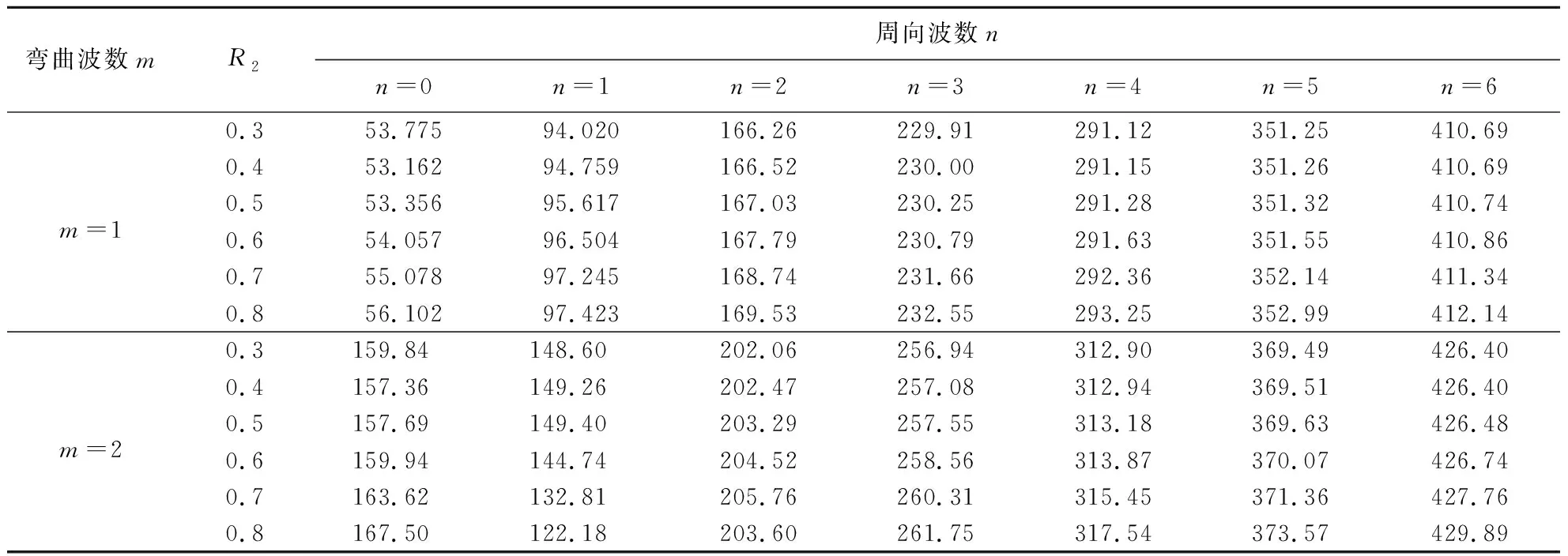
表3 两段柱形耦合声场在不同外径参数R2下固有频率(Hz)计算结果Tab.3 Natural frequencies of the two section cylindrical coupled cavity with various outside diameter parameter R2

不同外界激励幅值下柱形耦合声场声压特性曲线如图11所示。其中，声源激励位置和声压观测点位置与图7和图8保持一致，所有壁面均设定为刚性，算例采用三种声源幅值，即A=1 kg/s2，2 kg/s2和3 kg/s2。通过图11的响应曲线能够看出，声源幅值A的变化会导致声压响应曲线的幅值在纵向发生偏移，而且当激励幅值增大时，声压响应幅值也会增大。产生这种线性变化的主要原因是随着声源激励自身强度的增加，声场内部的声学响应特性也会增强，但是由于声场自身的声学模态特性不变，因此最终仅影响其自身声压级的大小。另外，从以上声场特性的研究可以发现对于声场特性的研究，本建模方法仅修改相关参数即可实现，无需重新推导编程，因而具备较强的灵活性。

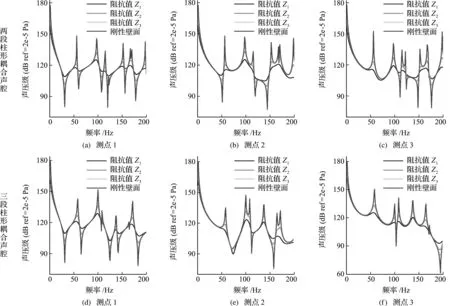
图10 不同阻抗边界条件下柱形声场在单位点声源激励下的声压响应

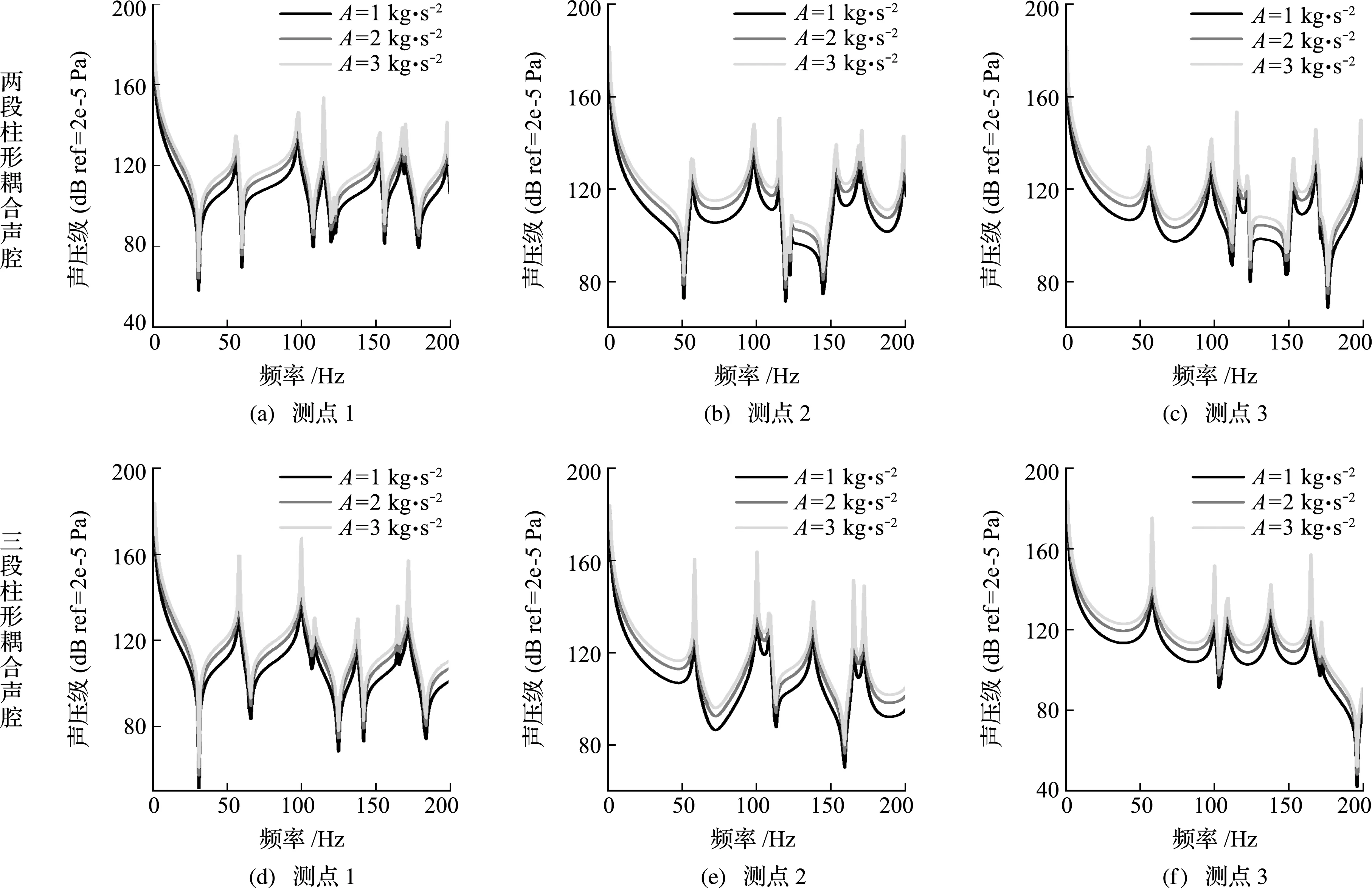
图11 不同幅值下柱形声场在点声源激励下的声压响应

4 结 论

本文提出基于特征正交-里兹能量原理的阶梯圆柱形耦合声场建模方法，该方法采用二维特征正交多项式和傅里叶级正余弦级数构建耦合声场子分段声压函数，从能量角度建立了邻近声场间耦合能量方程，进而结合里兹法对圆柱形耦合声场声学问题进行求解。对不同分段的柱形耦合声场声学特性研究结果表明，在保证计算准确性的前提下，本文建模方法改善了传统有限元法计算效率不高的问题，并且对于声场特性规律的研究仅修改相关参数即可实现，因而具备较强的灵活性；另外，对声场进行参数化研究发现，随着声场外径R2增加，声场固有频率普遍增大，并且这种现象与模态阶次相关联，而腔深L的影响呈现相反的变化规律；降低阻抗壁面和声源幅值的大小可抑制声场的声学响应幅值。