Q420十字组合截面角钢轴压稳定性能试验研究

吴 刚，李布辉，余 亮，宁帅朋，张 庆

(中国能源建设集团江苏省电力设计院有限公司，江苏 南京 211102)

0 引言

随着大容量、高电压和多回路的输电线路工程日益增加，铁塔所承受的挂点荷载和塔身风荷载成倍增加，Q420高强钢材得到了广泛应用[1]。Q420十字截面组合角钢被应用于超高压、特高压输电线路工程中。在传统的设计程序(如TTT和MYL等)中，格构式铁塔属于理想的空间桁架结构体系，铁塔杆件两端铰接且轴心受力，拉杆规格通过净截面受力计算求得，压杆规格通过净截面受力和整体稳定受力求得[2-3]。特高压输电铁塔真型试验结果表明，试验结果与设计结果相差较大，腿部主材在达到计算最大承载力之前发生提前破坏，组合角钢主要沿虚轴发生屈曲失稳，而不是最小轴[4-5]。

TEMPLE M等[6]开展组合角钢的试验，研究填板形式和布置对构件承载能力的影响。ZHUGE Yan等[7]开展三种填板形式十字组合角钢的试验研究，结果表明十字填板组合角钢的承载能力大于其他填板构件UNGKURAPINAN N等[8]开展了36个节点的承载力试验，研究螺栓滑移对构件承载力和变形性能的影响。FONG M等[9]和AHMED K等[10]研究了螺栓滑移对铁塔承载力性能的影响，结果表明螺栓滑移增大了铁塔位移，螺栓滑移产生的偏心效应降低了构件的承载力。然而，关于组合角钢不同分肢之间受力方面的研究较少，现行设计规范的计算方法也不够准确。杆塔设计人员对结构的实际安全余度没有把握，往往通过加大杆件规格来增大其安全余度。本文开展了12个组合角钢试件的轴压试验研究，并建立了角钢的简化计算模型，最后提出了组合角钢修正长细比计算方法。

1 试验研究

为了充分了解Q420十字组合角钢的轴压稳定承载力性能及不同角钢分肢的受力情况，开展组合角钢试件的轴压试验研究。

1.1 试件设计

根据实际工程中角钢规格的使用频率和试验条件的限制，选取试验角钢规格分别为2L125×8、2L140× 12和2L160×10，分肢角钢之间的间隙为14 mm，每种试件的长细比为30、40、50和60，角钢材质为Q420B。试件共分为12组，每组3个，如表1所示。

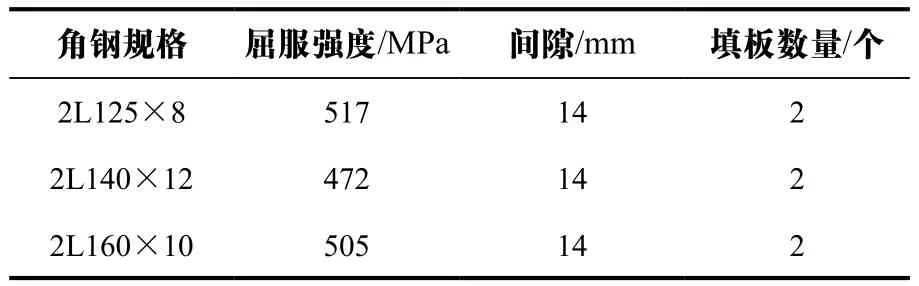
表1 组合角钢试件概况

填板形式为焊接十字填板，板厚为14 mm。对于规格为L125×8和L140×12的角钢，每个剪切面的螺栓为3M20；对于规格为L160×10的角钢，每个剪切面的螺栓为4M20，采用8.8级高强螺栓，如图1所示。试验开始之前，开展角钢板材的材性拉伸试验，Q420板材没有明显的屈服台阶，取残余应力为0.2%对应的应力作为屈服强度，得到8 mm、10 mm和12 mm厚钢板的屈服强度分别为517 MPa、505 MPa和472 MPa。

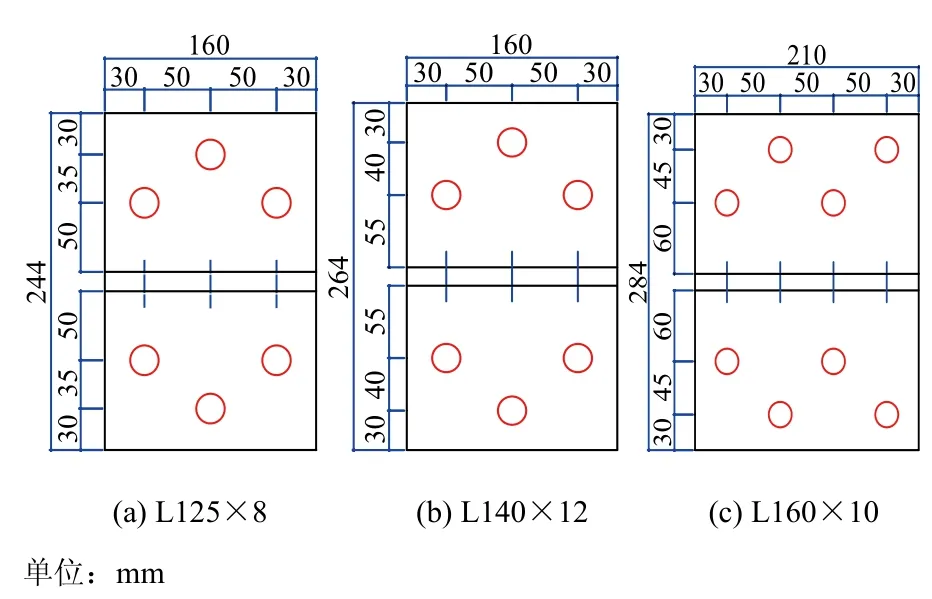
图1 填板螺栓布置

1.2 试验加载

试验加载方案如图2所示。试验采用卧位加载的方式进行，试验段两侧分别连有公共段和加载段，不同段之间通过包角钢和节点板相连。加载段两侧分别布置球铰，球铰直径为450 mm，高度为120 mm。公共段的角钢为L160×14，且长细比与试验段角钢一致；加载段角钢为L160×14，长度为500 mm，加载段两端焊有40 mm厚钢板，钢板宽度为500 mm。

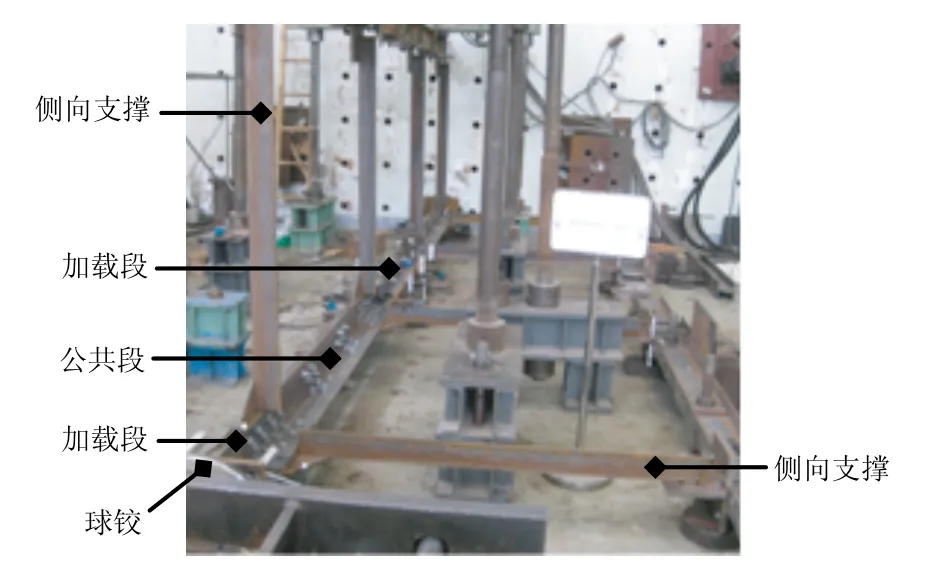
图2 试验加载方案

在试验段—公共段接头处，公共段—加载段接头处沿2个垂直方向分别布置侧向支撑模拟塔腿主材的实际受力；支撑角钢规格为L75×6，按不小于试验段角钢内力的2.5%设计。侧向支撑一端与节点板连接，另一端与固定H型钢的翼缘相连，连接螺栓采用2M20，H型钢通过锚栓与地面连接。采用液压千斤顶施加轴向压力，千斤顶最大可加荷载3 000 kN。

采用分级加载的方法逐步施加轴向压力，每级持荷1～2 min。试验开始之前，采用几何对中方法确保试件轴心受力，并在试件各典型部位布置位移测点和应变测点，如图3所示。试验段中间截面布置12个应变测点，每肢角钢6个；角钢每边3个，分别为肢背、肢中和肢尖；在两侧L/4截面和3L/4截面处分别布置4个应变测点，位于角钢的肢尖。应变片的平面尺寸为10.0 mm×4.0 mm，最大测得应变为2%～3%。同时，为了测量试件的轴向压缩量，在加载端板的4个角点分别布置量程为±100 mm的位移计。在每级荷载持荷过程中，采用静态应变测试仪保存应变和变形读数。

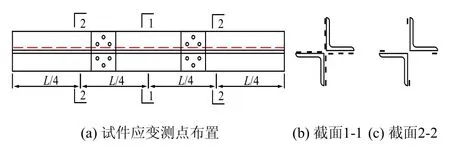
图3 试验角钢应变测点布置

1.3 试验结果

试验得到组合角钢试件的破坏模式和稳定承载力如下所示，根据中间截面测点的应变数据可计算得到分肢角钢之间的受力差异。

1.3.1 破坏模式

刚开始加载时，试件处于弹性阶段，并没有明显的变形，应变和位移基本呈线性发展；随着轴压力的增加，应变发展开始出现分叉；当达到极限承载力时，应变迅速下降，且轴向变形发展迅速，构件出现明显的整体弯曲变形和局部屈曲变形。

组合角钢试件的破坏模式如图4和图5所示，组合角钢试件呈现整体弯曲破坏和局部屈曲破坏的混合破坏模式。总体而言，当长细比λ为30和40时，试件发生明显的局部屈曲变形，并发生微小的整体弯曲变形；当长细比λ为50和60时，试件发生明显的整体弯曲变形和局部屈曲变形。由试件破坏模式可知试件主要绕虚轴(w-w轴)发生弯曲变形，与真型塔试验现象吻合较好。产生这种现象的原因可能是，填板连接螺栓为粗制螺栓，螺孔与螺杆之间存在间隙，加载过程中试件失稳产生的剪力主要由虚轴方向的螺栓承担，随着荷载增加，螺栓发生相对滑移，使得试件沿虚轴的变形增加，导致试件沿虚轴发生弯曲变形。

图4 试件整体弯曲变形

图5 试件局部弯曲变形

局部屈曲变形主要发生在十字填板附近的主材上，因为填板部位的主材具有较大的连接刚度，不能与其他部位主材发生协调变形，因此，在填板附近主材存在较大的局部应力集中，最终导致屈曲变形。试验结束后，观察发现十字填板和连接螺栓均没有明显的变形。

1.3.2 稳定承载力

以λ=40的组合角钢2L125×8作为分析对象，2L125×8的中间截面应变发展情况如图6所示。在加载过程中，试验段中间截面分肢角钢肢尖的应变发展差异较大；肢背应变发展趋势基本一致，但是其中一肢的应变发展速度明显快于另一肢。分析认为加载过程中螺栓滑移在分肢角钢间产生次弯矩，该弯矩导致分肢角钢受力不均匀。对于十字组合截面，各角钢的肢背紧靠着截面中心点，次弯矩在该点产生的截面应力基本可以忽略，所以该点处的应力反映了分肢角钢的实际受力情况，可以通过式(1)和式(2)求得。

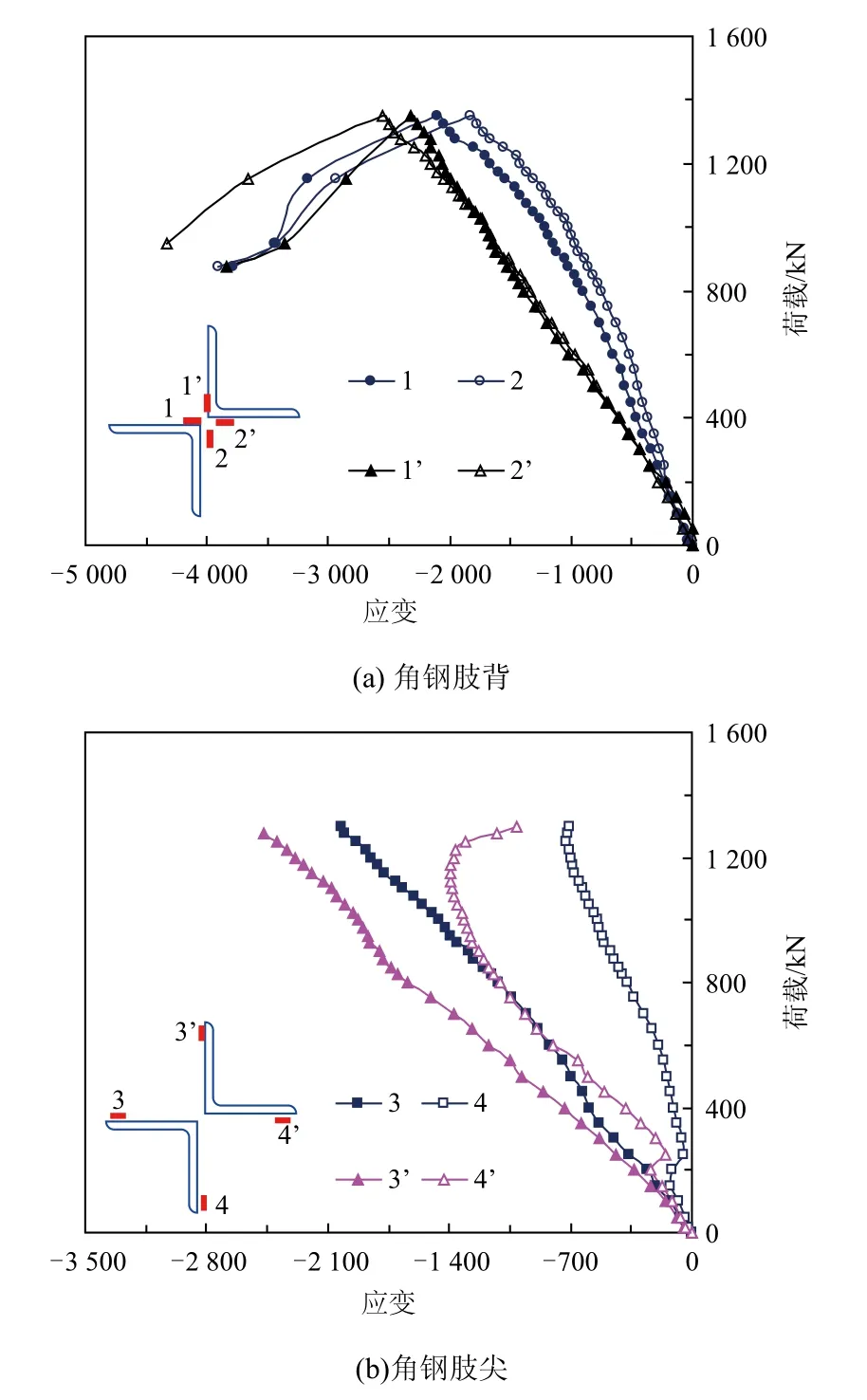
图6 中间截面应变发展过程

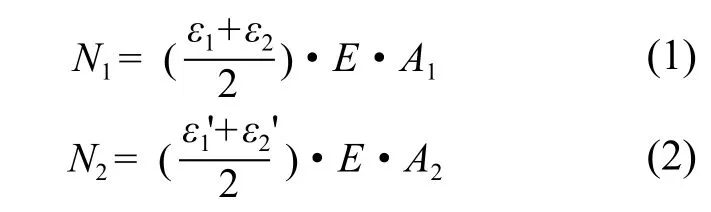
式中：N1、N2分别为分肢角钢的计算荷载；A1、A2为分肢角钢的截面面积；ε1、ε2为单肢角钢应变；ε1'、ε2'为另一肢角钢应变；E为钢材弹性模量。

表2列出了根据实测应变计算得到的截面轴力，可以发现：分肢受力比值N1/N2的范围为1.04～1.31，平均值为1.157，与真型试验塔主材测试结果吻合。因此，组合角钢构件设计过程中应重视分肢角钢受力不均匀的问题。

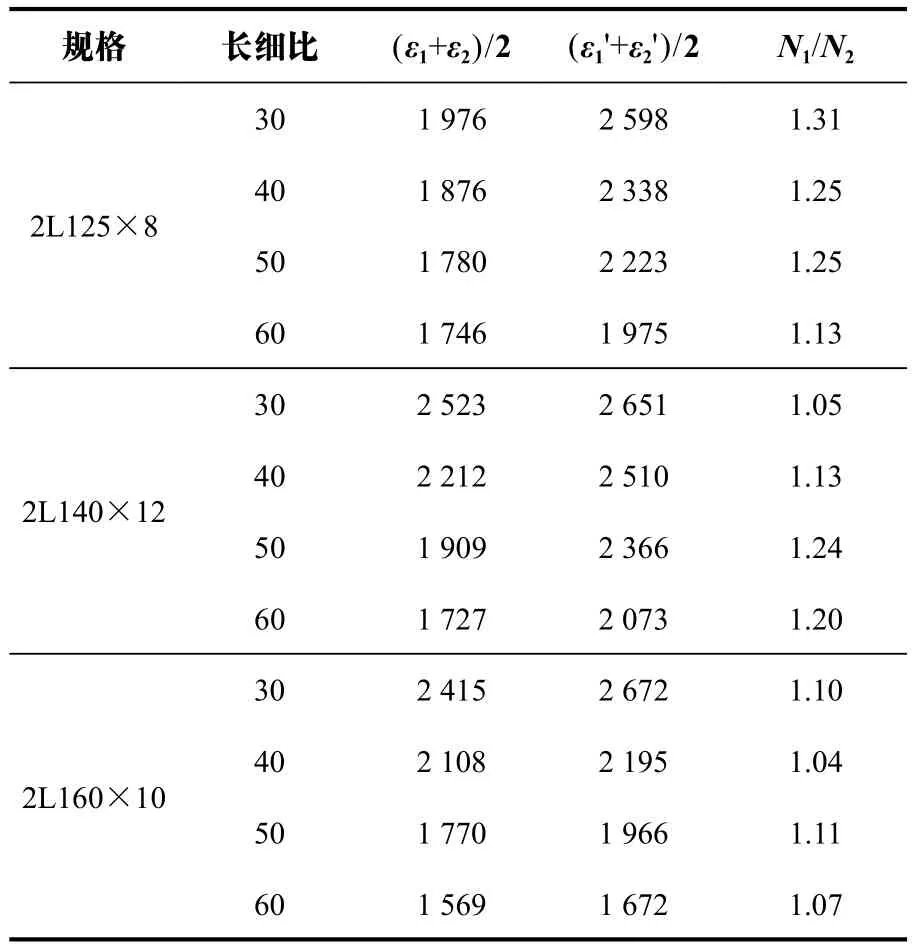
表2 分肢角钢内力

2 有限元数值模拟

采用有限元分析程序建立组合角钢的简化计算模型，并将模拟结果与试验结果进行对比。考虑到角钢的平面尺寸与厚度相差较大，同时为了节省计算时间，降低建模难度，采用Shell181单元代替实体单元模拟角钢和填板。钢材采用双线性弹塑性模型模拟，材料强度参考材性试验结果，两侧端板采用Solid45单元模拟。

在简化计算模型中，将填板与角钢对应节点的三向平动自由度(ux，uy，uz)进行耦合模仿螺栓连接。首先，开展试件的模态分析，根据试件破坏现象，施加L/1000的绕虚轴方向的初始弯曲变形作为试件的初始缺陷。施加轴向压力并开展计算分析。模拟得到试件的破坏模式与试验现象相似，组合角钢沿虚轴发生整体弯曲且局部屈曲变形明显，角钢应力分布如图7所示。组合角钢试验承载力PExp与模拟承载力PFEA的比值平均值为1.06。有限元分析结果与试验结果吻合较好，该简化模型可用于分析十字组合截面角钢的轴压稳定性能。

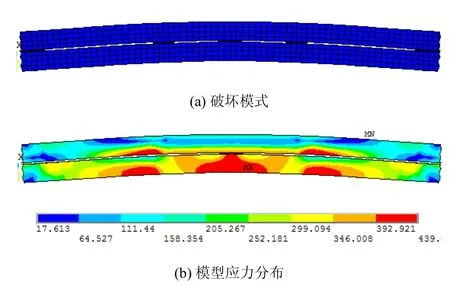
图7 组合角钢有限元分析

3 试件受力分析

根据试验结果和模拟分析结果开展组合角钢试件受力的理论分析，对比不同变形模式下的屈曲临界应力，并提出十字合角钢构件修正长细比计算方法。

3.1 局部屈曲变形

基于小变形屈曲理论单向均匀压缩薄板的平衡微分方程如式(3)所示。角钢可视为一边简支三边自由的平板，屈曲系数k为0.425。如式(5)，角钢局部屈曲应力决定于其宽厚比b/t。国家标准GB 50017—2017《钢结构设计标准》[11]规定，局部屈曲失稳不能先于整体稳定失稳，并给出了角钢的宽厚比限值。其中，u为钢材泊松比，取0.3。

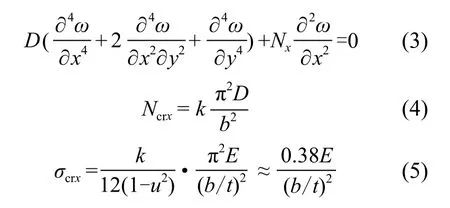
式中：D为柱面刚度；Ncrx为局部屈曲临界压力；σcrx为局部屈曲临界应力；b为角钢肢宽；t为角钢肢厚。

3.2 截面扭转变形

在轴向压力作用下，十字组合角钢通常会发生沿截面纵轴的扭转屈曲变形。基于临界状态下，两端简支构件发生微小扭转变形的平衡微分方程见式(6)：

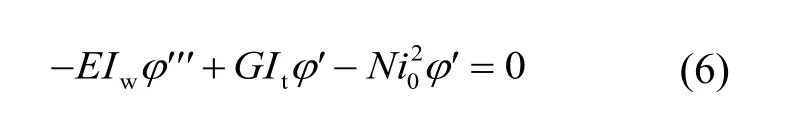
对于角钢，截面翘曲系数Iw、截面面积A、扭转惯性矩It、极回转半径i0和剪切模量G分别表达如下：

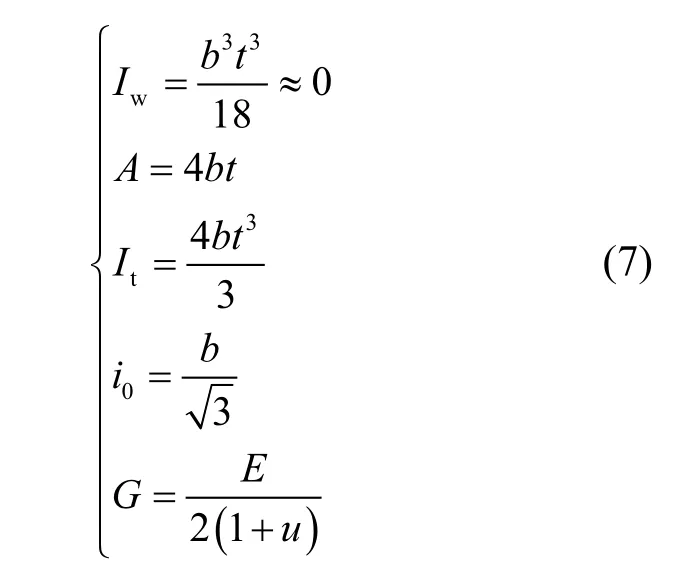
试件换算扭转长细比λZ可以表达为：

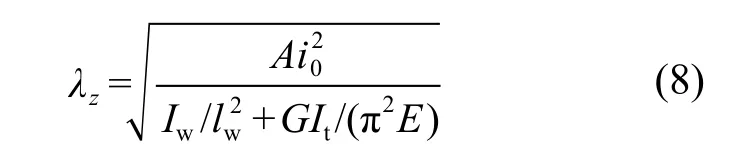
式中：lw为构件长度。

将以上变量代入式(7)，可以得到换算扭转长细比λZ为：

式(9)表明，角钢等效扭转长细比只与其宽厚比b/t有关，与构件的长度没有关系。角钢临界扭转应力用式(10)和(11)表达：

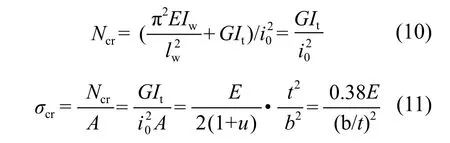
式中：Ncr为构件扭转屈曲临界压力；σcr为构件扭转屈曲临界应力。

对比式(5)和式(11)可以发现，对于十字组合截面角钢，局部屈曲临界应力和扭转屈曲临界应力是相等的。因此，在设计过程中，如果考虑了局部屈曲效应，可以不必考虑扭转屈曲效应的影响。电力行业标准DL/T 5154—2012《架空输电线路杆塔结构设计技术规定》[12]明确给出了角钢压杆稳定折减系数mN的计算方法。

3.3 修正长细比

根据试验结果和模拟分析结果发现：十字组合角钢的破坏模式为绕虚轴的整体弯曲并伴有明显的局部屈曲，且分肢角钢受力不对称，试验结果与计算假定条件相矛盾。关于组合角钢压杆稳定计算，电力规范中给出了详细的计算方法，如式(12)所示。本文在式(12)的基础上，参考GB 50017—2017采用修正长细比λe计算组合角钢的稳定承载力。

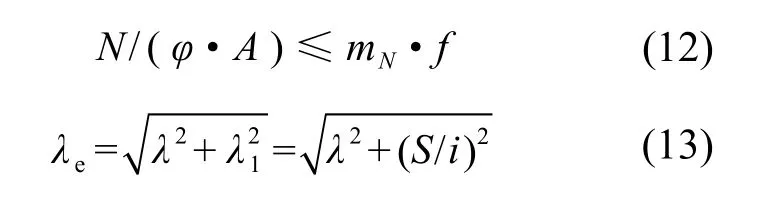
式中：λe为构件修正长细比；λ为构件修正长细比；S为填板间距；φ为构件压杆稳定系数；f为钢材强度设计值。

表3列出了采用修正长细比的计算承载力PMO与试验承载力PExp的对比情况，以及模拟承载力PFEA和规范计算值PDL。由表3可知：PExp/PDL的平均值为0.93，说明按DL/T 5154—2012的计算结果偏小；PExp/PMO的平均值为1.03，说明根据修正长细比计算得到的试件稳定承载力与试验结果吻合较好，建议在实际工程中推广使用。

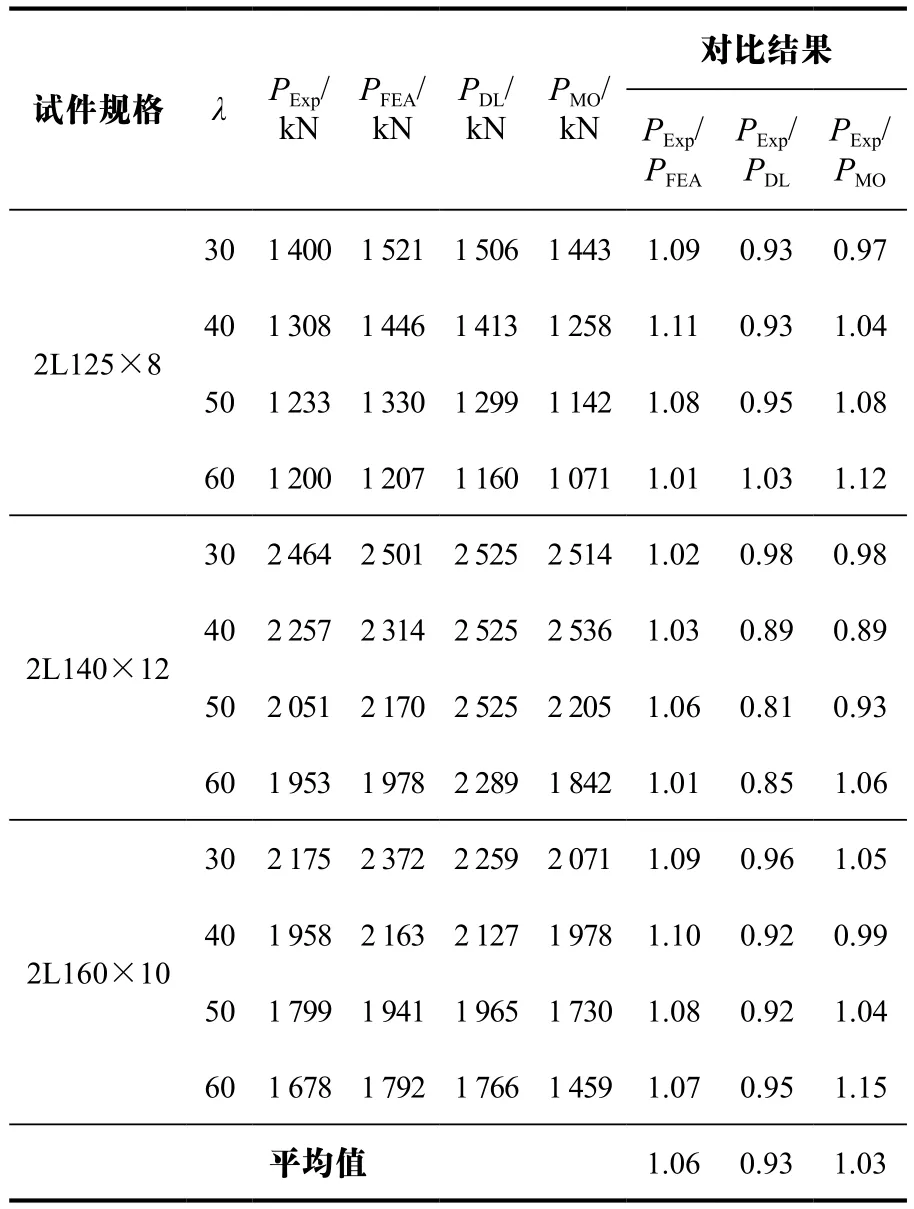
表3 试验承载力和设计承载力对比情况

4 结语

本文开展了十字组合截面角钢试件压杆稳定性试验研究，数值模拟和理论分析，主要结论如下：

1)组合角钢试件呈现整体弯曲破坏和局部屈曲破坏的混合破坏模式。当长细比为30和40时，试件发生明显的局部屈曲变形，并发生微小的整体弯曲变形；当长细比为50和60时，试件发生明显的整体弯曲变形和局部屈曲变形，且主要沿虚轴(w-w轴)弯曲变形；

2)试验表明，分肢角钢内力分布不均匀，且分肢受力比值N1/N2的范围为1.04～1.31，平均值为1.157，设计过程中应重视分肢角钢受力不均匀的问题；

3)对于十字组合截面角钢，局部屈曲临界应力和扭转屈曲临界应力是相等的。因此，在设计过程中，如果考虑了局部屈曲效应，可以不必考虑扭转效应的影响；

4)采用修正长细比计算组合角钢轴压稳定承载力，根据修正长细比计算得到的试件稳定承载力与试验结果吻合较好，建议在实际工程中推广使用。