基于组合模型的浙江省GDP预测研究

张秀华, 马佳杰, 徐 雷, 张国栋, 田 旭

(1.浙江沪杭甬高速公路股份有限公司， 杭州 310020； 2.浙江数智交院科技股份有限公司， 杭州 310030)

高速公路的建设与区域的经济发展水平密切相关，区域经济的良好发展推动高速路网的有序扩张，高速路网的平稳运行反哺区域的社会和谐与经济繁荣。国内生产总值(gross domestic product，GDP)可以反映一个国家或者一个地区的经济发展水平和人民的生活状况，也可以衡量和评价国家和地区未来的发展趋势。实际上，地区的GDP发展状况也常常成为高速公路路线走向设计的重要参考依据。因此，对于GDP预测研究显得尤为重要，它不仅可以评估某个区域未来总体的经济水平变化情况，而且可以提供某个区域高速路网规划的数据支撑。

浙江省既是21世纪海上丝绸之路圈定的五省之一，又是长江经济带三极之一长江三角洲城市群的重要组成部分，也是环杭州湾发达城市集中区域。落实“一带一路”、长江经济带发展和大湾区建设，必然会对区域内外交通运输系统的时效性、便捷性和安全性提出更新、更高的要求。因此，及时准确地掌握浙江省GDP发展趋势，对于推进现代交通“五大建设”、打造“畅通浙江”和完善区域高速公路网具有十分重要的意义。

历史的GDP数据是一组带有时间标签的数值，数值的大小随着时间而变化。对于时间序列的研究是GDP预测过程中必不可少的一部分。如果将GDP数据作为时间序列进行建模，需要考虑其自身包含的线性关系和非线性关系。首先，本文分别构建ARIMA模型和BP神经网络模型对浙江省GDP进行预测，并得到模型评价结果；其次，在ARIMA模型基础上，挖掘出残差序列的非线性关系，并设置合适的BP神经网络结构；最后，优化ARIMA和BP神经网络组合模型，并比较3种模型的预测结果。

1 研究现状综述

时间序列经过变换后，能够以3项相加的形式进行表示。时间序列分析的目的就是从一个时间序列提取并分解出趋势项、周期项和随机误差项[1]。经典回归通常不足以解释时间序列的所有特性。因此，Peter Whittle在1951年提出了自回归(autoregressive，AR)和自回归移动平均(autoregressive moving average，ARMA)[2]。1970年，Box和Jenkins首次提出了差分自回归移动平均(autoregressive integrated moving average，ARIMA)，标志着时间序列分析进入了新的应用阶段[3]。该模型基于历史数据的相关性分析，得出当前期与滞后期之间的相关系数，并利用最小二乘法建立时间序列中当前项和滞后项之间的线性关系。ARIMA模型以优越的短期预测效率在不同学科领域得到广泛应用，特别是在经济和金融领域的研究。王鄂等通过构建ARIMA(1，1，2)最优模型对湖南省GDP进行预测研究，发现湖南省将在2020年达成全面建成小康社会的目标，并且人均GDP将超过一万美元[4]。郑梦琪等基于浙江省1978—2018年的全省GDP数据，结合一阶差分、AIC和BIC原则，建立ARIMA(5，1，5)模型，并预测浙江省未来3年的GDP数据，为区域发展战略规划提供依据[5]。基于安徽省历年的GDP数据，游文倩等分别建立ARIMA(0，1，1)模型、Holt-Winters模型和组合预测模型(ARIMA-holt-winters，无季节性模型)，结果发现组合预测模型能够更加准确地得到短期预测结果[6]。

传统的时间序列预测模型是通过分析某一学科领域的机理，将各类影响因素与目标结果之间建立数学关系，从而实现时间序列的预测。除此以外，基于机器学习技术的时间序列预测模型是对大量时间序列数据进行反复学习和优化，从而获得数据预测能力[7]。人工神经网络(artificial neural network，ANN)是机器学习领域热门的研究理论，通过构建多样的网络结构处理复杂的关联关系。BP(back propagation)神经网络是人工神经网络的一个分支，是由Rumelhart和McClelland在1986年提出的一种误差反向传播学习机制，经过不断改进和完善，目前已经广泛应用，如函数逼近、模式识别、造价预测等[8]。刘莉等利用BP神经网络对宿迁市降水量数据的剩余平稳序列成分进行模拟，并构建时间序列预测模型，结果表明基于BP神经网络的时间序列预测模型具有较高的精度和稳定性，预测结果优于传统的时间序列加法模型[9]。孟毅选取ARIMA时间序列、BP神经网络和BP-ARIMA组合模型3种方法对中国的月度CPI数据进行建模和预测，结果表明BP-ARIMA组合模型预测效果最优[10]。张建辉将趋势模型的残差时序数据作为BP神经网络的输入数据，训练能够捕捉时序细微震荡特征的残差神经网络，结合时序趋势模型和残差神经网络，实现更为精准的时间序列预测[11]。

2 研究方法

2.1 ARIMA(p，d，q)模型

博克斯-詹金斯(Box-Jenkins)提出的时间序列分析方法主要是用来解决数据中潜在的随机性、平稳性和季节性问题。该方法基本的表现形式包括自回归模型(AR)、移动平均模型(MA)、自回归移动平均模型(ARMA)、整合移动平均自回归模型(ARIMA)。AR、MA和ARMA主要是针对平稳序列数据，然而本文研究GDP数据属于非平稳时间序列，其方差、均值将随时间的变化而变化。由于非平稳序列的不确定性较高，难以借助已知信息完成预测，因此考虑使用ARIMA模型先对非平稳序列进行差分处理，将其转化为平稳序列之后，再进行分析和预测。假设时间序列{Xt,t∈T}为非平稳序列，{∇dXt}表示经过d阶差分运算后的平稳序列，那么ARIMA(p，d，q)模型的表达式为

(1)

式中：B为延迟算子，BkXt=Xt-k；Φ(B)为自回归系数多项式，Φ(B)=1+φ1B+φ2B2+…+φpBp；Θ(B)为移动平均多项式，Θ(B)=1+θ1B+θ2B2+…+θqBq；εt为零均值的白噪声序列。

ARIMA模型中参数p、d、q分别代表滞后期阶数、差分阶数和滞后随机波动项的阶数。当d=0时，ARIMA(p，d，q)模型就是ARMA(p，q)模型；当d=q=0时，ARIMA(p，d，q)模型就是AR模型；当d=p=0时，ARIMA模型就是MA模型；当d=q=p=0时，ARIMA(0，0，0)就是白噪声序列函数。ARIMA(p，d，q)模型中自回归阶数p和移动平均阶数q是通过自相关系数(ACF)和偏自相关系数(PACF)进行确定。

ACF的公式为

ρt,s=Corr(Xt,Xs),t、s=0,±1,±2,…

(2)

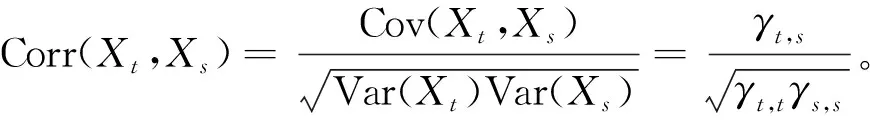
PACF的公式为

φk=ρXt,Xt-k|Xt-1,…,Xt-k+1=

(3)

偏自相关系数只计算当前期与k阶滞后期的相关性：φk接近于±1时，表示相关性增强；φk接近于0时，表示相关性减弱；φk=0时，表示当前期与k阶滞后期不相关。

2.2 BP神经网络模型

BP神经网络的基本思想是通过训练误差反向传播进行参数修正，以梯度下降的方法寻找网络结构的输出值与实际值之间的最小均方误差[12]。Hecht-Nielsen的研究表明BP神经网络可以逼近任何一个非线性函数[13]。良好的拟合效果和简单的操作过程使BP神经网络得到不断推广和应用。

BP神经网络主要由输入层、隐藏层和输出层3部分组成，其中输入层和输出层均为单层结构，而隐藏层可为多层结构。BP神经网络的训练过程主要分为两个部分：①信息前向传播，是指信息从输入层传入，经过隐藏层神经元的非线性映射，传入输出层输出结果；②误差向后传播，是指通过比较输出值与实际值的误差，若超出预先设置的误差阈值，则误差信息逐步向后传回，同时调整每一个隐藏层的权重，直到误差在控制范围之内。

在解决预测问题时，BP神经网络主要有两种应用方式，一种是基于多因素的预测，另一种是基于时间序列的预测。本文重点研究BP神经网络在时间序列方面预测应用。例如：存在时间序列Xt,Xt+1,Xt+2,…,Xt+m，若要预测该序列之后t+m+k(k>0)时刻的值Xt+m+k，那么可以将Xt,Xt+1,Xt+2,…,Xt+m整体作为输入变量，构建Xt+m+k与过去m个值的函数关系。

BP神经网络的建模过程如下：

1)数据归一化。BP神经网络模型对数据的量纲较为敏感，通常将原始数据进行归一化处理，使数据大小落在[0，1]范围内，归一化公式为

(4)

(5)

2)网络结构的确定。包括神经网络层数的确定，输入层、隐藏层和输出层节点数的确定，以及激活函数的选择。

3)初始化各连接的权重和阈值。

4)输入归一化后的数据，经由神经网络结构正向传播。

5)观察模型误差是否在预设的范围内。若是，则建模过程结束；若否，则进行反向传播，重新计算各连接的权重和阈值，并返回上一步，直到模型的最小均方误差小于设置的误差要求。

6)利用训练后的模型进行时间序列的预测。

2.3 组合模型

组合模型的预测精度往往优于单一模型。考虑到浙江省GDP的增长趋势受到不同因素的影响，是非平稳序列。序列中既存在线性特征，也存在非线性特征。因此，本文将ARIMA模型和BP神经网络模型进行组合，构建预测模型，以期提升预测效果。组合模型的建立过程如下：

1)ARIMA模型预测浙江省GDP的线性部分。ARIMA模型的实质是建立当前期数据和滞后期数据之间的线性回归，因此将ARIMA模型的预测结果作为组合模型的线性部分。此外，ARIMA模型预测结果中的残差，即白噪声，在序列的线性部分之外，不再适用于线性预测模式，需要通过非线性的预测方法提取潜在的价值信息。

2)BP神经网络模型预测浙江省GDP的非线性部分。先对ARIMA模型预测所得的残差序列进行矩阵变换和归一化处理，再通过训练的BP神经网络模型得到浙江省GDP时间序列非线性部分的预测值，最后将ARIMA模型的线性拟合值和BP神经网络模型的残差预测值相加，即为组合模型的预测结果。

3 案例分析

选取浙江省1978—2019年的全省GDP数据作为研究对象。将数据划分为训练集和测试集两部分，1978—2016年的39个GDP数据作为模型的训练集，2017—2019年的3个GDP数据作为模型的测试集。1978—2019年浙江省GDP数据见表1。

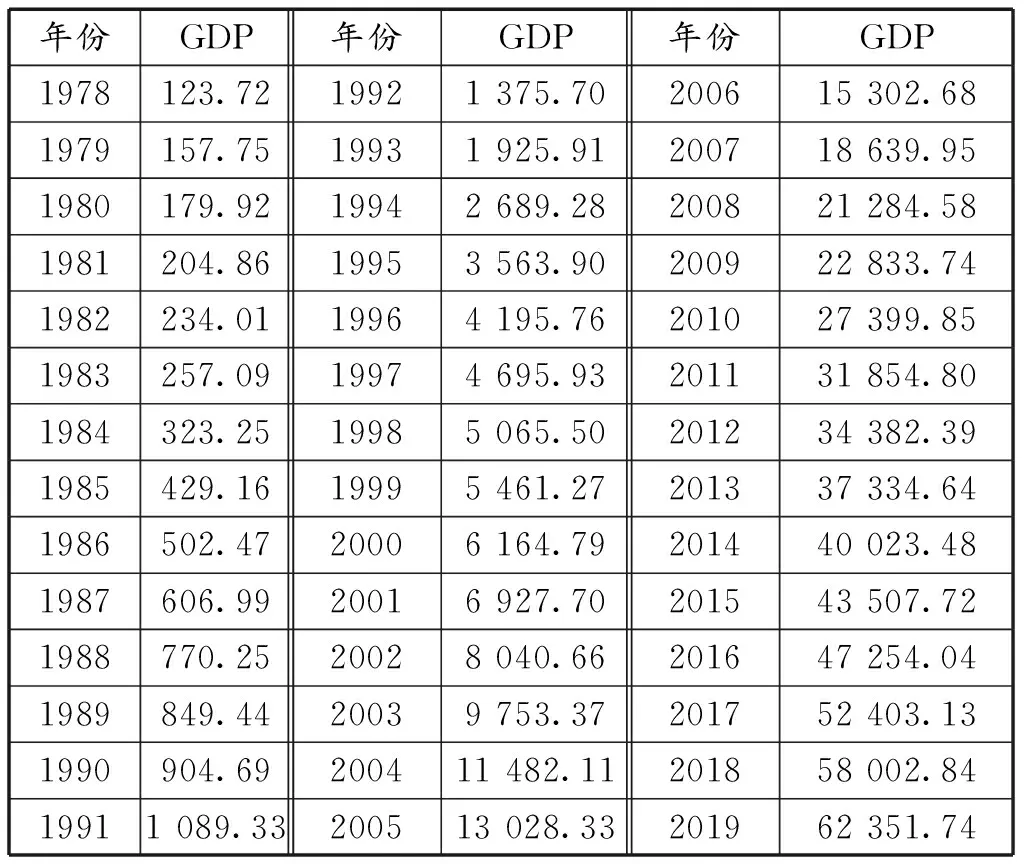
表1 1978—2019年浙江省GDP数据

3.1 ARIMA预测结果

观察1978—2019年浙江省的GDP时间序列(图1)，发现GDP数值随着时间的变化呈现上升的趋势，因此是一个非平稳序列，需要进行差分处理将其转化为平稳序列。

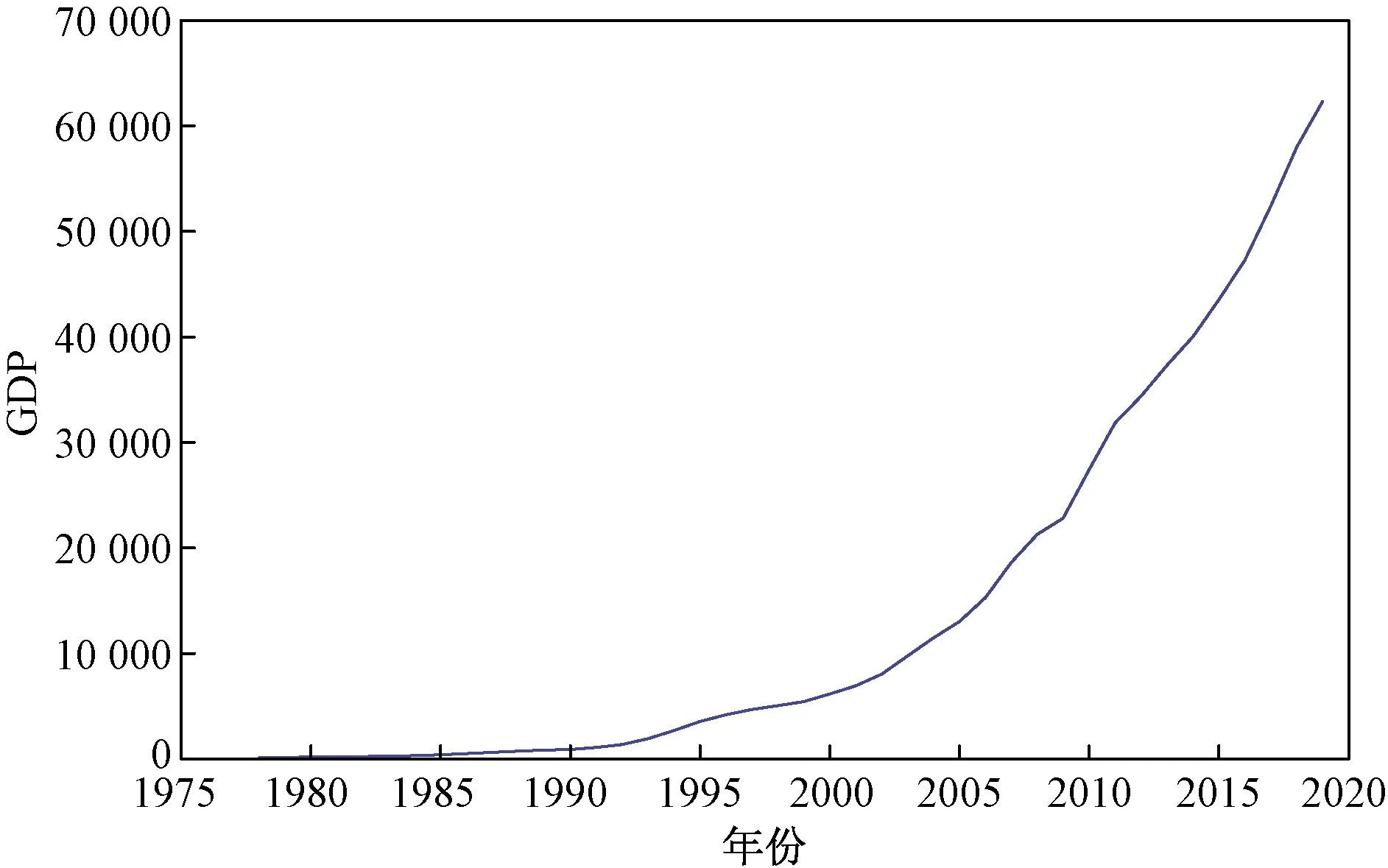
图1 1978—2019年浙江省的GDP时间序列

为了消除浙江省GDP时间序列中的递增趋势，对其进行一阶差分运算和二阶差分运算，具体结果如图2所示。可以发现，一阶差分处理后的GDP时间序列仍然存在单调上升的趋势，是非平稳序列；二阶差分处理后，时序折线围绕0值上下波动，符合平稳序列的特征。

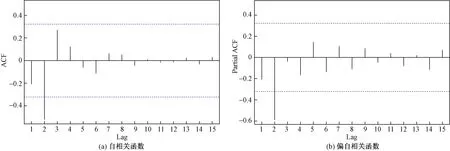
图4 二阶差分GDP时间序列的自相关函数和偏自相关函数

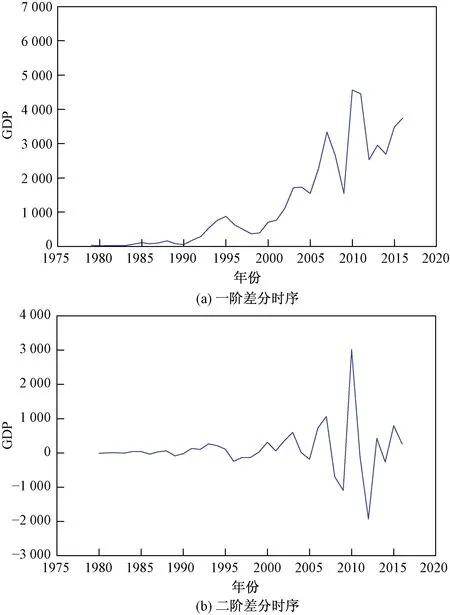
图2 差分处理后的浙江省GDP时间序列

进一步利用R语言tseries包中的adf.test函数对二阶差分运算后的GDP时间序列作ADF检验(augmented dickey-fuller test)，检验结果如图3所示。结果显示ADF检验的p值小于0.01，即拒绝序列存在单位ADF根的原假设，说明二阶差分的浙江省GDP时间序列是静止的，已经成为平稳序列。

图3 ADF检验结果

通过观察自相关函数ACF和偏自相关函数PACF(图4)，确定ARIMA模型中的p和q两个参数，即滞后波动项的阶数和滞后项的阶数。二阶差分GDP时间序列在2阶延迟位置的自相关性最大(2阶截尾)，偏自相关性同样在延迟阶数为2时达到最大(2阶截尾)，这表明可以构建ARIMA(2，2，2)模型。但是，仅仅通过图像确定的p值和q值可能有失偏颇，因此本文考虑以ACF图和PACF图为参考，利用赤池信息量准则(akaike information criterion，AIC)检验多对不同的模型参数，从而选取使得模型结果最优的阶数。

从二阶差分GDP时间序列的ACF图和PACF图中选取若干可能的参数对，拟合模型并计算AIC值，具体结果见表2。AIC的值越小，模型的拟合效果越好。结果表明，AIC值最小的是ARIMA(2，2，0)，因此本文确定其为拟合浙江省GDP时间序列的最优模型。

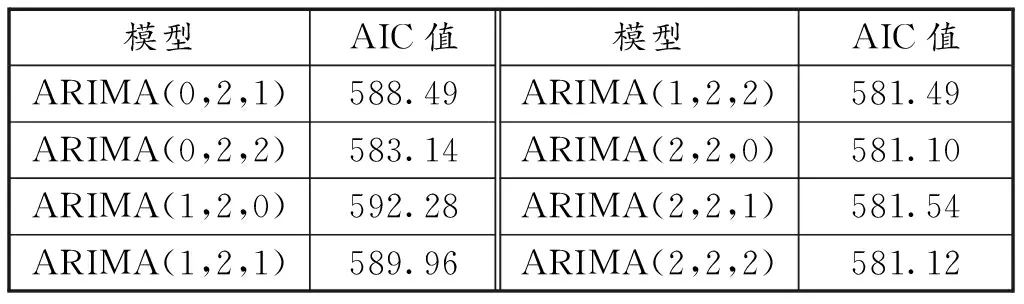
表2 不同ARIMA模型所对应的AIC值

通过观察模型残差序列的ACF图(图5)，发现自相关系数全部落于置信区间内，说明残差序列中不存在自相关性。此外，利用R语言中Box.test函数对残差序列进行Ljung-Box检验，如图6所示；结果显示P值为0.529，远远大于0.05，即接受序列平稳的原假设，证明模型的残差序列为白噪声序列。

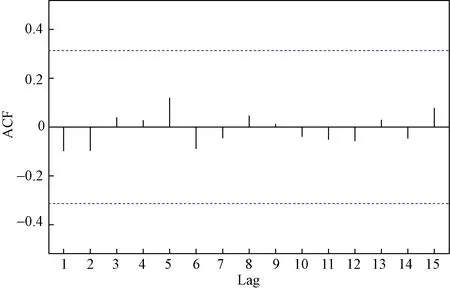
图5 残差序列ACF图

图6 Ljung-Box检验结果

运用训练数据所确定的ARIMA(2，2，0)模型，预测2017—2019年3年的浙江省GDP，预测结果如图7所示。

图7 ARIMA(2，2，0)模型预测结果

基于绝对误差和相对误差比较浙江省GDP的预测值和真实值，以评估模型的预测效果。绝对误差等于真实值减去预测值，相对误差等于绝对误差的绝对值除以真实值。模型预测结果见表3。

一般而言，相对误差在10%以内时，可以认为模型预测是有效的[14]。由表3可知，模型预测结果的平均相对误差为6.30%。因此，根据时间序列预测方法所构建的ARIMA(2，2，0)模型，可以有效地预测浙江省GDP。

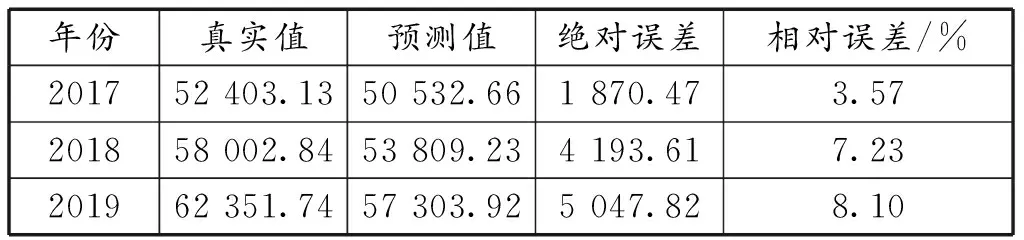
表3 ARIMA模型预测结果分析

3.2 BP神经网络预测结果

1)确定模型的网络层数。BP神经网络的层数过多，会导致训练过程复杂，出现数据过拟合的情况；网络层数过少，则无法充分挖掘数据价值，导致模型预测能力不足。以往研究表明，三层BP神经网络结构能够准确拟合任何非线性的连续函数[15]。因此，本文采用包含1个隐藏层的三层BP神经网络模型进行浙江省GDP预测。

2)确定输入层的神经元节点数。利用BP神经网络预测浙江省GDP时间序列，需要将时序值通过移动窗口的方式建立一个输入矩阵。输入节点数过多，会减小模型运行速度；输入节点数太少，会降低模型预测精度。因此，本文依次选取GDP时序的5个数据作为输入向量，之后的1个数据作为输出向量，建立前5个数据和之后1个数据的映射关系。39个浙江省GDP时序值可以产生34个输入样本，见表4。表4中的前34行数据为训练集输入样本，第35行数据为测试集输入样本。根据BP神经网络对于输入数据的要求，需要将原始数据集进行归一化处理。

通过Kolmogorov定理可以得到最佳的隐藏层神经元节点数目，然后在理论的最佳节点数目附近选取若干值进行程序试验，最终确定使得模型误差最小的隐藏层神经元节点数。Kolmogorov定理的公式为

n2=2n1+1

(6)

式中：n1为输入层神经元；n2为隐藏层神经元。

3)选取合适的激活函数。根据以往的经验和研究，本文选取具有良好的非线性映射能力的tan-sigmoid函数作为激活函数，同时选取线性函数purelin作为输出层的函数。

通过数据预处理和确定的网络结构，借助R语言中的AMORE包构建BP神经网络模型，并且实现浙江省GDP时间序列的预测。将表4中第35行数据作为测试样本输入训练后的模型，计算得到第一个预测值；测试样本向后滑动，依次计算得到剩余两个预测值，见表5。

为了得到最终的GDP预测值，需要将模型输出的直接结果进行逆归一化处理。通过计算绝对误差和相对误差，分析模型的预测效果，见表6。

表4 BP神经网络训练集样本

表5 BP神经网络测试样本

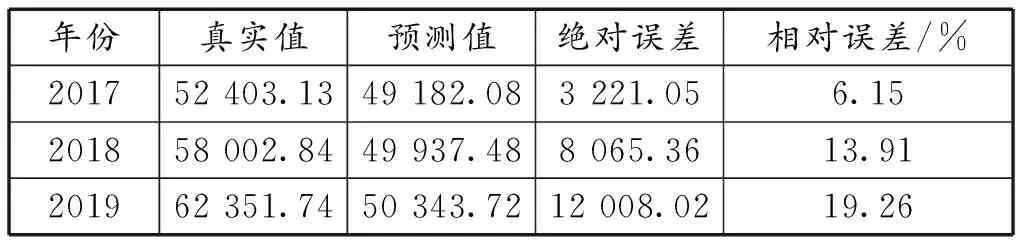
表6 BP神经网络预测结果分析

基于BP神经网络模型预测浙江省2017—2019年的GDP数值。模型预测结果的平均相对误差为13.10%，说明模型的有效性不充分。此外，模型的相对误差随着预测年份的增大而增大，说明模型的预测效果不稳定。由此可见，单一的BP神经网络模型预测效果不够理想。

3.3 组合模型预测结果

选择ARIMA(2，2，0)模型拟合浙江省GDP时间序列，并得到模型的39个残差值，见表7。

神经网络结构确定为3层，经过比较和验证，输入层设置3个神经元，输出层设置1个神经元，所以39个残差值滑动生成36个训练数据，其中第37行数据作为测试样本。经过归一化处理后的残差序列可以作为BP神经网络模型输入矩阵，见表8。

由Kolmogorov定理可知，模型隐藏层最佳的神经元节点个数为7。隐藏层选择tan-sigmoid函数，输出层选择purelin函数。借助R语言中的AMORE包构建BP神经网络模型，设置网络结构参数，并将36个残差训练数据导入模型。利用训练完的模型拟合测试样本的Y值，然后依次滑动拟合得到其他两个残差序列的预测值。最后，将预测的3个残差值进行逆归一化处理，并与ARIMA模型拟合的GDP预测值相加，得到组合模型的预测结果，见表9。

表7 ARIMA(2，2，0)模型预测残差序列

表8 残差序列样本集

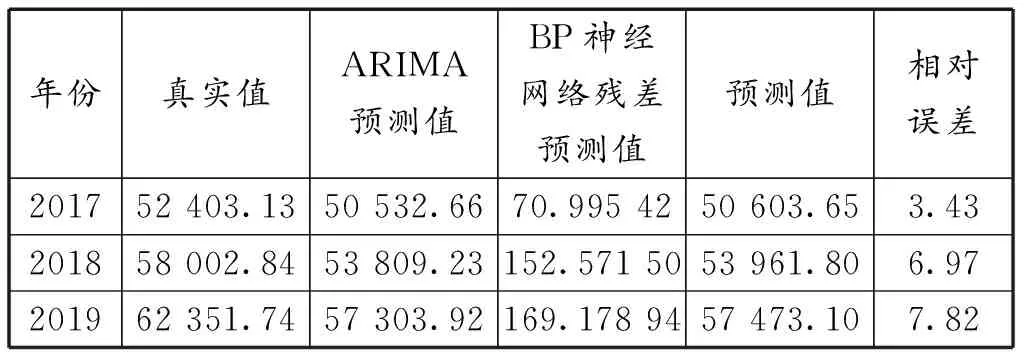
表9 组合模型预测结果分析

基于组合模型预测浙江省2017—2019年的GDP值，模型结果的平均相对误差是6.08%，优于ARIMA(2，2，0)模型和单一的BP神经网络模型。因此，通过将ARIMA模型和BP神经网络进行组合，可以得到更为准确的GDP预测结果。

4 结语

区域经济的发展和高速公路的建设紧密联系。经济发展态势好、增速快，有利于推进高速公路的建设，促进产业结构的转型升级；高速路网密度高、布局优，有利于带动区域经济的发展，加强生产生活的稳定有序。GDP是衡量区域经济发展水平的一个基本指标。及时准确地了解GDP的变化趋势，可以更加科学合理地规划高速路网。

基于浙江省1978—2019年的GDP数据，分别构建3个预测模型，分析GDP的未来走势。①ARIMA模型：先将非平稳的时间序列进行差分处理转为平稳时序，再通过ACF图、PACF图以及AIC值确定模型参数，最后建立ARIMA(2，2，0)模型进行预测分析。②BP神经网络模型：先将GDP时序值以移动窗口的方式生成训练集和测试集，再确定BP神经网络结构、激活函数和各层的神经元节点数，最后用训练数据建立预测模型，并用测试数据评估模型预测效果。③组合模型：先利用ARIMA(2，2，0)模型得到GDP时间序列的预测值，再利用BP神经网络模型得到GDP时序的残差预测值，最后将两个预测值相加得到组合模型的预测结果。通过计算3个模型的相对误差并进行比较，发现组合模型的预测准确度最高。