声谱图生成方法及实现

中国电子科技集团公司第三十六研究所 周欣 李洋锐 马国峰

通信接收机的语音信号解调结果为时域数据,反映了语音的时域特性,而要对语音信号进行深度处理需获取语音频域特征信息。声谱图体现了语音信号的频域特征,本文研究了语音声谱图生成的相关技术,首先介绍了语音WAVE文件格式,以及通过短时傅里叶变换从时域数据获取频域数据的原理,最后依据时间、频率、幅度信息实现了声谱图生成。

0 引言

语音是由大部分稳定以及部分动态变化的状态构成的连续音频流。声谱图是依赖于傅里叶变换的显示图形,实际上是一种动态的频谱图,能够直观的显示出语音中包含的各种频率信号随时间的能量强弱变化情况。声谱图纵轴为频率,横轴为时间,任意一个给定频率成分在给定时刻的能量强弱用点的颜色来表示。语音特征向量可以从声谱图中提取出来[1]。语音音素的属性可以从声谱图里观察出来,通过观察声谱图共振峰和它们的转变可以更好地识别声音,隐马尔科夫模型就是对声谱图进行建模以达到好的识别性能。声谱图可以直观地评估TTS(Text to Speech)系统的好坏,直接对比合成的语音和自然的语音声谱图的匹配度。由此,将语音时域数据转化为声谱图是非常重要的一步。

1 WAVE文件格式

WAVE文件格式是符合RIFF(Resource Interchange File Format,资源交互式文件格式)规范的一种数据编码。对于音频流的编码,WAVE没有严格的规则,几乎任何支持ACM(Audio Codec Manager,音频编解码器管理器)规范的编码都可以用来对音频数据流进行编码。最基本的WAVE文件格式是PCM(Pulse Code Modulation,脉冲编码调制)格式。PCM是没有经过任何压缩的声音采样数据格式,声卡能够直接播放。而其他采用压缩编码的声音数据,需要把压缩的数据按照编解码格式解码成PCM格式,再送到声卡才能正常播放。WAVE文件包括RIFF文件头(File Header)和一系列数据块(Data Chunk),而其中最主要的“WAVE”数据块由“fmt”子数据块和“data”子数据块组成。“fmt”数据块用于详细说明数据格式,“data”数据块包含实际的采样数据。数据块是WAVE文件最基本的组成单元,数据块中包含的字段有“类型块标识”(该字段为可选字段)“标识符”“数据大小”和“数据”。其中“类型块标识”只在部分数据块中用到,如“WAVE”数据块就使用了“类型块标识”,当使用了“类型块标识”时,该数据块就没有“标志符”“数据大小”及“数据”字段项。“类型块标识”表示下面嵌套有别的数据块,只作为文件读取解析时的一个标志,通常先找到这个类型块标识,再以它为起点读取后面嵌套的其他数据块。WAVE文件的具体格式如表1所示:

表1 WAVE文件的具体格式Tab.1 The specific format of the WAVE file

描述PCM数据的基本单元是“Sample”(采样),一个Sample代表采样一次得到的数据。如果用44kHz采样,将在一秒中得到44000个Sample。每个Sample可以用8位、16位表示,位数越高,音频质量越好。如果是单声道文件,采样数据按时间顺序存储,它的基本组织单位是一个字节(8位)或字。如果是双声道的文件,采样数据按时间先后顺序交叉存入,左右声道数据交叉存储在一起,先存储第一个Sample的左声道数据,然后存储第一个Sample的右声道数据。

2 短时傅里叶变换

傅里叶变换是一种分析信号的方法,它可分析信号的成分,也可用这些成分合成信号,在信号分析中,主要用于平稳信号的处理[2]。欧拉公式可以将任意函数转化为一系列正(余)弦函数之和,任意函数在这里指我们的时域信号,而正(余)弦函数包含信号的频率和对应振幅信息。傅里叶变换可以将0～t时间信号(时域、水平轴时间、垂直轴大小)分解到不同的频率分量(频域、水平轴频率、垂直轴大小),通过傅里叶变换可以获取一段信号总体上包含哪些频率的成分,但是对各成分出现的时刻无法得知[3]。因此对于非平稳信号,傅里叶变换就显示出了它的局限性,而我们日常生活中的绝大多数音频都是非平稳信号的。解决这个问题的方法是使用短时傅里叶变换来处理语音信号。短时傅里叶变换的思想是将全部时域过程分解为很多等长的小进程,每一个小过程近似平稳,然后对每一个小过程举行傅里叶变换。短时傅立叶变换采用滑动窗口机制,设定窗口大小和步长,让窗口在时域信号上滑动,分别计算每个窗口的傅立叶变换。把函数和窗口函数相乘,然后通过滑动窗口函数做傅里叶变换,得到一系列的傅里叶变换结果,形成不同时间窗口对应的频域信号,然后将结果进行排列,通过时间叠加累积得到一个随时间变化的二维时频信号声谱数据矩阵[4]。

3 声谱图生成

生成声谱图时,语音被分成许多帧,每一帧对应一个代表频率和能量之间的关系的频谱。在实际应用中,有三种频谱,即线性振幅谱、对数振幅谱和自功率谱,本文采用对数振幅谱。对数振幅谱中需对振幅做对数运算,其纵坐标的单位是分贝。对数振幅谱中振幅较低的成份相对高振幅成份得以拉高,从而可以观察到掩盖在低幅噪声中的周期信号。从音频文件生成声谱图的过程描述如下:

(1)读取音频文件,处理得到一个保存音频数据的数组、采样频率和时长等信息;

(2)确定所需要用到的窗函数、窗长度、重叠长度、傅立叶点数等相关参数,在傅里叶变换计算过程中需加窗进行平滑处理,以减弱非同步采样造成的栅栏效应和频谱泄漏[5],常用的窗函数有矩形窗、汉宁窗、平顶窗、指数窗等,本文使用的是汉宁窗;

(3)将输入数据做短时傅里叶变换处理,得到其中一帧语音的频谱图(频率-幅度),对连续多帧语音进行相同处理,得到含时间、频率序列的二维数组数据;

(4)根据处理后的时频矩阵绘制声谱图,以帧号(时间)为x轴,频率为y轴,以颜色表示幅度。通过增加时间这个维度,就可以显示一段语音而不是一帧语音的频谱。声谱图生成的流程图如图1所示。

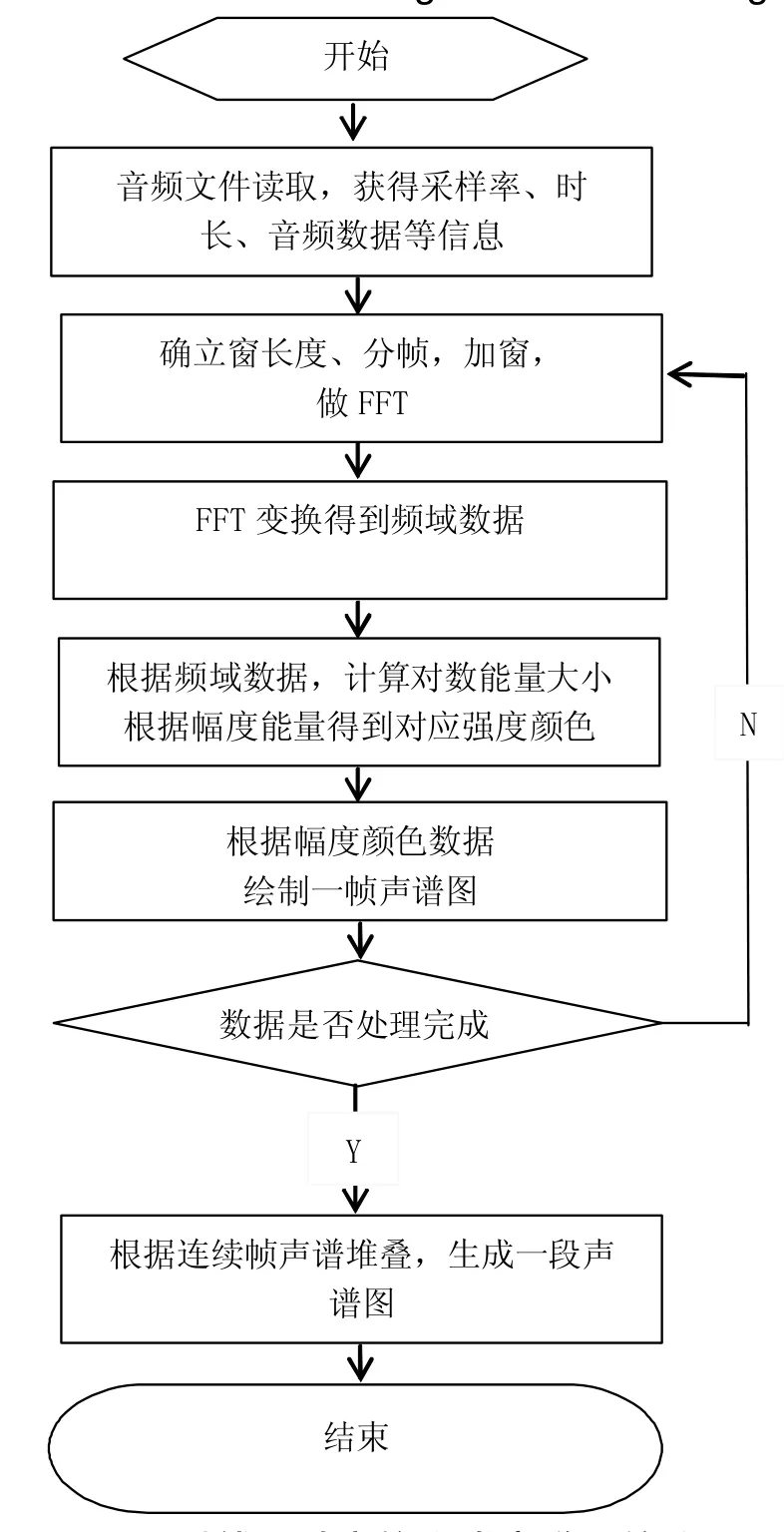
图1 短时傅里叶变换生成声谱图的流程图Fig.1 The flow chart of short-time Fourier transform to generate a spectrogram

声谱图生成结果示意如图2所示。

图2 声谱图生成结果示意图Fig.2 Schematic diagram of the result of spectrogram generation

4 结语

本文介绍了如何通过语音信号解调结果数据生成声谱图的方法,通过分析WAVE格式,解析WAVE文件,采用短时傅里叶变换实现时域数据到频域数据的生成,然后根据时间-频率-幅度信息得到了语音信号的语谱,为后续语音信号深度处理如降噪增强、端点检测、语音识别等提供基础支撑。

引用

[1] 孔旭,关佶红.以声谱图相似度为度量的波形音乐检索[J].计算机工程与应用,2009,45(13):136-141.

[2] 孙端.短时傅里叶变换在工业测量中的应用[J].机电信息,2020(26):14-15.

[3] 张子涛.基于小波和PNCC特征参数的语音识别技术研究[D].重庆:重庆大学,2018.

[4] 胡航.现代语音信号处理[M].北京:电子工业出版社,2014.

[5] 刘会衡,王正强,宋立新.数字信号处理课程中利用DFT分析模拟信号频谱的几个问题[J].计算机时代,2020(06):13-16.