主蒸汽管道在瞬态流作用下的结构动力分析

刘 浪

(1.核电安全监控技术与装备国家重点实验室，广东深圳 518172;2.深圳中广核工程设计有限公司，广东深圳 518172)

0 引言

根据ANS 58.2—1988Designbasisforprotectionoflightwaternuclaearpowerplantsagainsttheeffectsofpostulatedpiperupture规定，核电厂压水堆的管道应考虑假想管道破裂。管道破裂会产生动态效应，主要包括甩击、喷射、瞬态流等(见图1)。每个假想破裂应分别作为单个假想始发事件来考虑，如果要求论证核电厂安全停堆，则需要针对管道系统的未破裂部分或相连管道系统进行上述动态效应的载荷分析，评定管道系统的完整性，并采取相应的防护措施[1-2]，以保证在核电厂管道系统发生假想破裂后，它们仍能执行核安全功能。

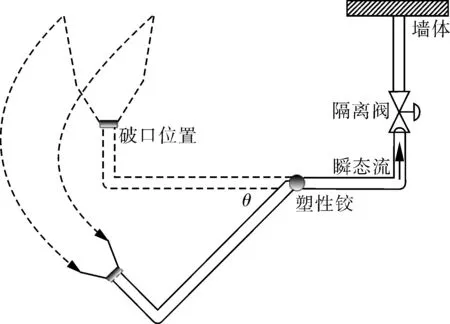
图1 管道破裂动态效应示意

管道破裂后，在其余未破的管道内部产生瞬态流[3]，流体介质从破口泄放，管道内部流体突然降压，在断裂管道上产生压力波载荷；该载荷对管道系统而言是一个巨大的瞬时冲击，它不同于管道系统力学分析中考虑的另一个动载荷——地震，瞬态流的持续时间短(通常是毫秒级)、峰值大[4]，对管道、阀门、支架、埋板等产生很大影响，决定了管道系统的结构设计。在实际工程中，针对瞬态流这种特殊载荷，需要在通常管道有限元简化模型基础上，对各种简化方法进行深入的敏感分析研究，确保建立正确的管道有限元力学模型，得到准确的动力响应结果。

建立管道有限元力学模型时，考虑到安全性和可行性两个因素，通常会进行很多简化处理[5]，比如支架刚度和阀杆刚度通常按无限大考虑，即软件取默认的刚度极大值，而不是用支架和阀杆实际刚度，这样做极大地降低了模型建立难度，经过验证这种简化方法对管道在自重、内压、地震等载荷下的影响不大，可以接受；然而上述简化方法对瞬态流冲击载荷是否仍然适用是本文的研究目的。本文针对核电厂主蒸汽管道的约束刚度和阀杆刚度进行分析，研究这两个参量对管道系统在瞬态流作用下动力响应的影响，并建立适用于瞬态流的管道有限元力学简化模型。

1 计算模型

本文以图2所示的管道结构为研究对象,图中1号位置是C形封头；管道系统中的一个固定点，8号位置是贯穿件；管道系统中的另一个固定点，6号位置是导向支架(简称GL支架)，对管道起到径向平动约束作用；7号位置是管道在线设备(阀门)。从1号～6号位置，管道外径850 mm，壁厚40 mm；从6号～8号位置，管道外径880 mm，壁厚55 mm；管材密度8.203×10-9t/mm3，管道介质密度0.042×10-9t/mm3；阀门偏心在管道轴线正上方1 224 mm，重量9 t；管材弹性模量为185 000 MPa。

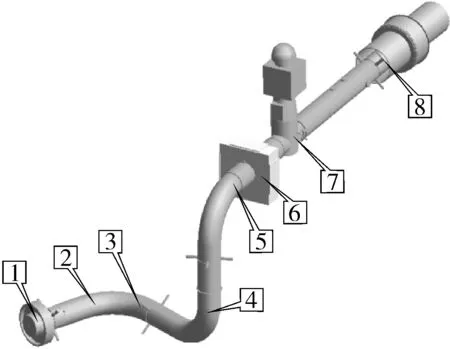
图2 管道结构示意

本文用ANSYS程序[6]建立管道有限元计算模型，如图3所示。直管采用Pipe 16单元，弯管采用Pipe 18单元，GL支架采用Combin 14单元，阀门偏心采用Mass 21单元[7]。图2中的1号位置和8号位置6个自由度全约束，6号位置约束水平和竖向平动，2,3,4,5号位置是瞬态流载荷加载点。

图3 管道有限元模型

2 管道瞬态流计算

管道破裂后，在其余未破的管道内部产生瞬态流载荷，作用于管道弯头处，本文采用RELAP程序计算瞬态水力参数，该程序以两相非均匀、非平衡模型为基础，应用汽相、液相完全独立的6个质量、动量、能量守恒方程求解系统各处的热工水力参数的变化。假定1号位置C形封头的下游(管内介质从8号位置流向1号位置)出现破裂，利用下式即可由瞬态水力参数计算得到各弯头位置的瞬态流载荷(见图4)：

(1)

图4 2号～5号位置瞬态流载荷

式中，Fi为管道受到来自内部容纳流体水力载荷，管壁对流体作用力的反作用力，N；ρ为流体密度，t/mm3；v为流速，mm/s；Pi为排放出口的流体静压，MPa；Pa为环境压力，通常为标准大气压，MPa；Si为管道截面积，mm2。

3 管道动力分析对比

本节对比计算管道系统在瞬态流载荷作用下，GL支架刚度和阀杆刚度分别按无限刚度(简化模型)和真实刚度(详细模型)考虑时，管道动力响应结果的差异。

3.1 GL支架刚度

GL支架(见图5)是管道的一处约束点，约束管道水平和竖直两个径向平动，通常情况下，在管道的有限元计算简化模型中，约束刚度按无限刚度考虑，即软件取默认的刚度极大值。本文计算了支架的真实刚度，分析该参量对管道系统在瞬态流作用下动力响应的影响。GL支架在两个约束方向结构基本一致，经计算，平动刚度为19.6×106N/mm。

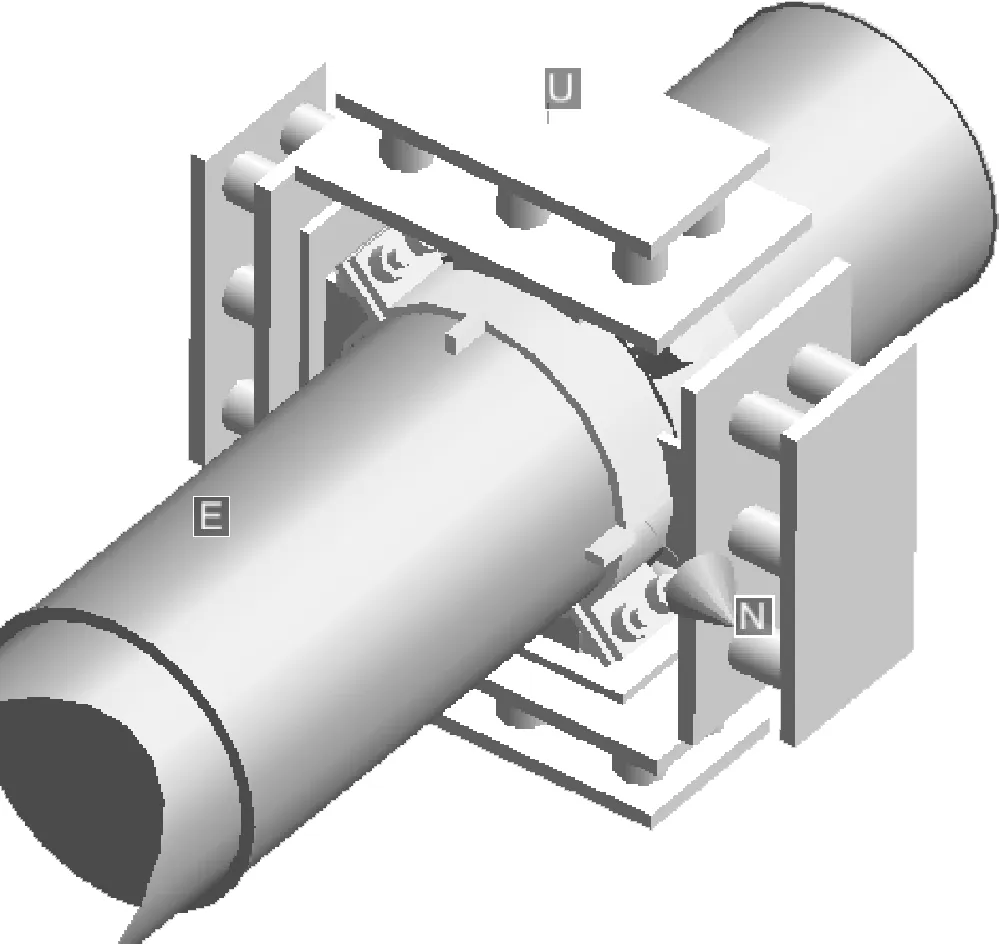
图5 GL支架结构示意

3.2 阀杆刚度

阀门是管道系统中的在线设备，管道力学分析时需要加以考虑。通常情况下，认为阀体和阀杆比管道刚度大，在管道的有限元计算简化模型中阀体和阀杆设置为刚性单元，即软件取默认的刚度极大值。

实际阀门结构以电动阀(见图6)为例，由三部分组成：阀本体、轭架和电动头，其中阀本体和电动头的刚度足够大，可以依然设置为刚性单元(见图7)；轭架相对阀本体和电动头刚度较小，可以设置为弹性梁单元(见图8)，因为弹性梁截面扭转模量较抗弯模量大很多，所以可以只考虑截面抗弯模量。本文提供一种计算阀门轭架弹性梁单元截面抗弯模量的简化方法[8]，实现在瞬态流作用下更加精准地考虑阀门整体刚度对管道系统动力响应的影响。

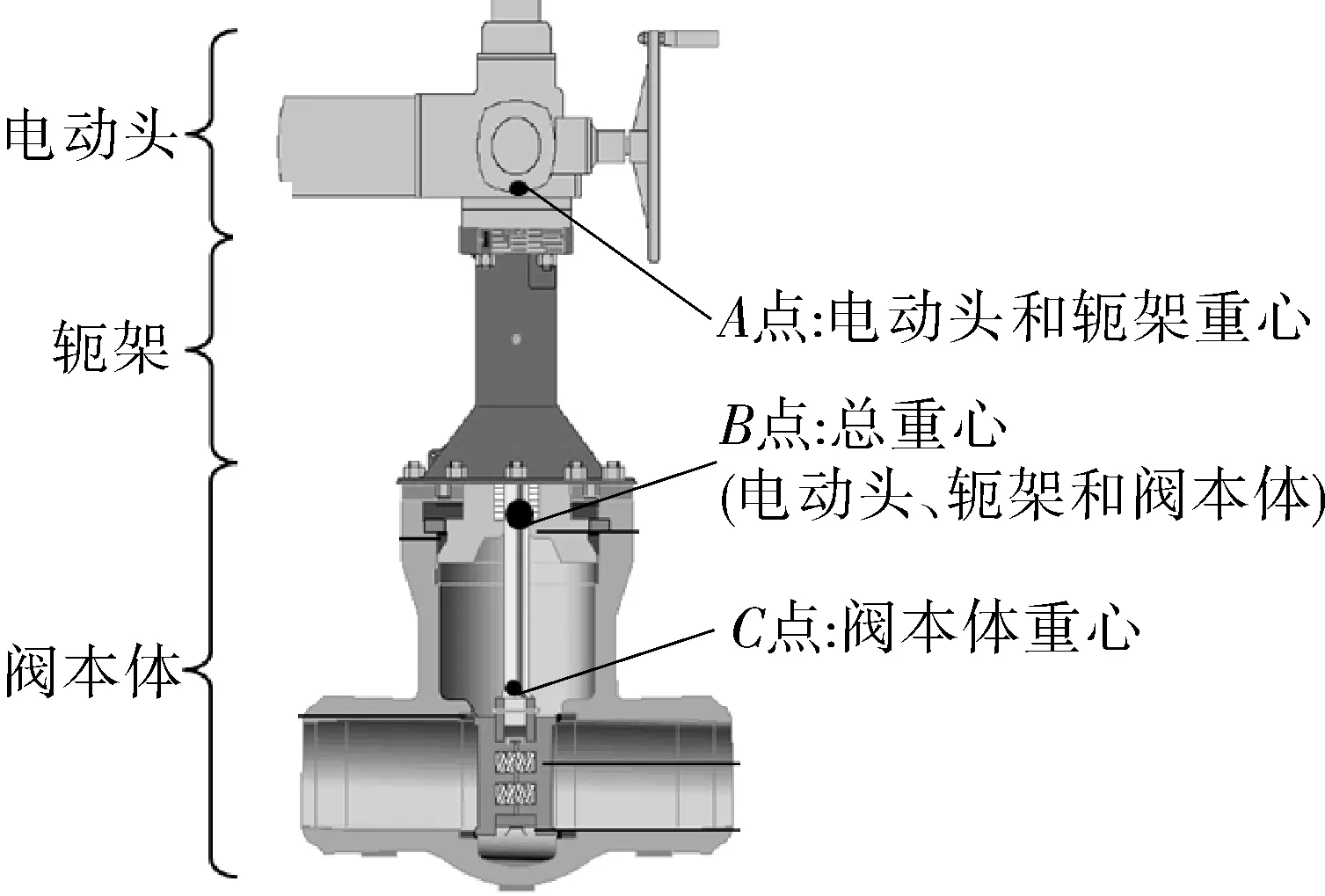
图6 电动阀结构示意

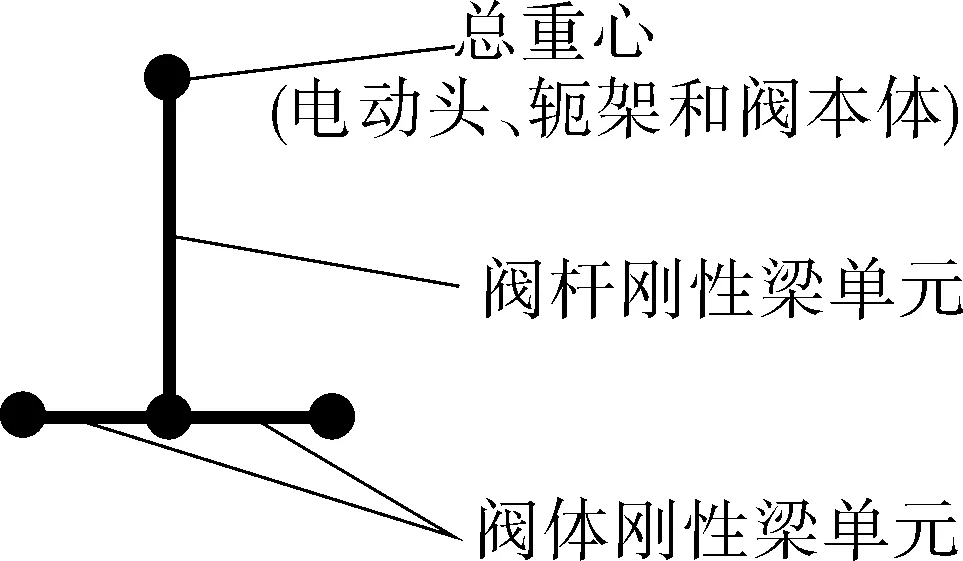
图7 用于简化计算的有限元模型

图8 用于详细计算的有限元模型

首先将法兰E点到电动头和轭架重心A点简化为单自由度变截面悬臂梁，设悬臂梁顶端即电动头和轭架重心A点质量为m；法兰D点到电动头和轭架重心A点长度为a，截面抗弯模量为Ia；法兰E点到法兰D点长度为b，截面抗弯模量为Ib；阀门一阶频率为f。通过以下两个步骤计算截面抗弯模量Ib。

(1)求悬臂梁最大挠度。

①a段。

弯矩方程：

M(x)=-Fx(0≤x≤a)

(2)

挠曲线近似微分方程[9]:

EIaδ″a=-M(x)=Fx(0≤x≤a)

(3)

积分：

(4)

②b段。

弯矩方程：

M(x)=-Fx(a≤x≤b)

(5)

挠曲线近似微分方程：

EIbδ″b=-M(x)=Fx(a≤x≤b)

(6)

积分：

(7)

③由θ(x=a+b)=0，δ(x=a+b)=0和θb(x=b)=θa(x=b)，可以求得系数C1,C2,D1,D2，从而求得单自由度变截面悬臂梁顶点处最大挠度：

(8)

(2)求悬臂梁轭架段截面抗弯模量Ib。

①利用式(8)求柔度系数λ。

(9)

②单自由度自由振动方程[10]。

(10)

式中，f为频率；m为质量。

③求Ib。

将式(9)代入式(10)得：

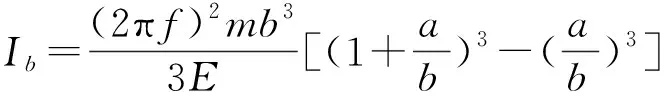
(11)

综上所述，管道力学分析考虑阀杆实际刚度时，公式(11)可以用于计算阀杆轭架部分对应的有限元弹性梁单元的截面抗弯模量。本文利用式(11)计算出管道上阀门轭架部分对应的有限元弹性梁单元的截面抗弯模量为1.06×1012mm4。

3.3 计算结果对比

将管道GL支架刚度和阀杆刚度分别按无限刚度(简化模型)和真实刚度(详细模型)条件下动力响应结果进行对比，包括对比约束点反力、管道典型位置应力和阀门加速度。

(1)GL支架处水平向反力。

由图9可以看出，两种模型计算得到的GL支架处水平向反力相差不大。

图9 两种模型GL支架处水平向反力对比

(2)4号位置管道应力。

由图10可以看出，两种模型计算得到的4号位置管道应力相差不大。对其他位置的管道应力也进行了对比，结果类似。

图10 两种模型4号位置管道应力对比

(3)阀门加速度

由图11可以看出，两种模型计算得到的阀门加速度相差不大。

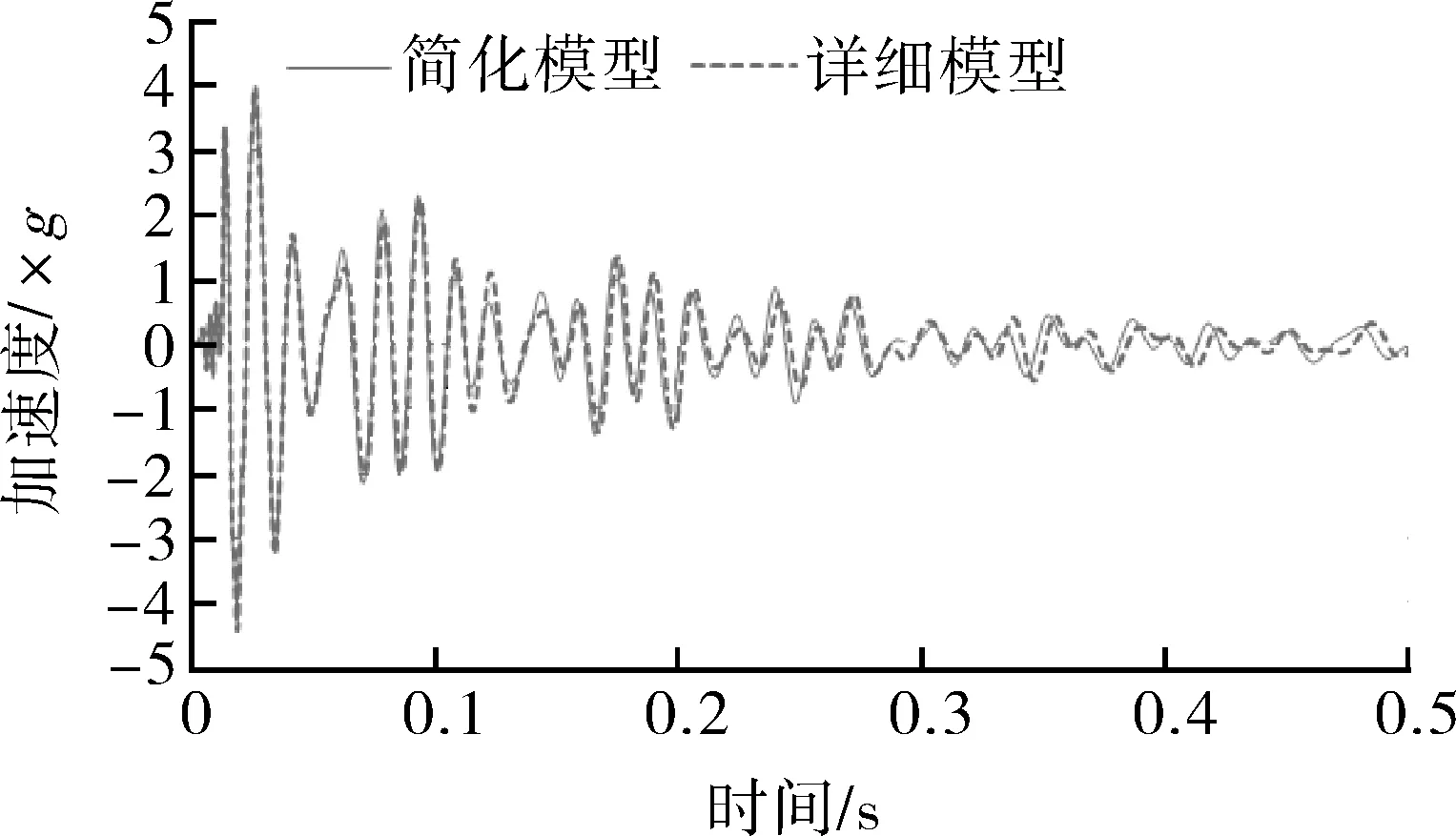
图11 两种模型阀门水平加速度对比

4 管道动力分析敏感性研究

本节分析管道动力响应结果对GL支架刚度的敏感性，即GL支架取不同刚度值，对比分析管道系统在瞬态流载荷作用下动力响应结果。核电厂管道系统力学分析时，支架约束的最小刚度取值通常为相连管道刚度的10倍，该参量往往成为支架设计选型的决定性因素，通过本节敏感性分析，寻找降低支架最小刚度的可能性，从而在保证核电厂安全性的前提下，减小高能管道支架钢结构和埋板的尺寸，提升安装的便捷性和建造的经济性。

GL支架的刚度为19.6×106N/mm，首先取GL支架真实刚度1/10并设定为K；然后在管道计算模型中分别将GL支架的刚度设置为K的1倍、2倍、3倍，依次递增到10倍，即达到GL支架的真实刚度(GL支架刚度变化过程中,支架对管道的约束能力增强)；最后对比计算结果，包括阀门水平向加速度、GL支架反力和管道4号位置应力值。

对比计算结果(见图12)可以看出，随着GL支架刚度变大：(1)GL支架反力变大，但是GL支架刚度在5倍K值以后反力变化不大；(2)管道4号位置应力变小，但是GL支架刚度在5倍K值以后应力变化也不大；(3)阀门水平向加速度几乎没有变化。

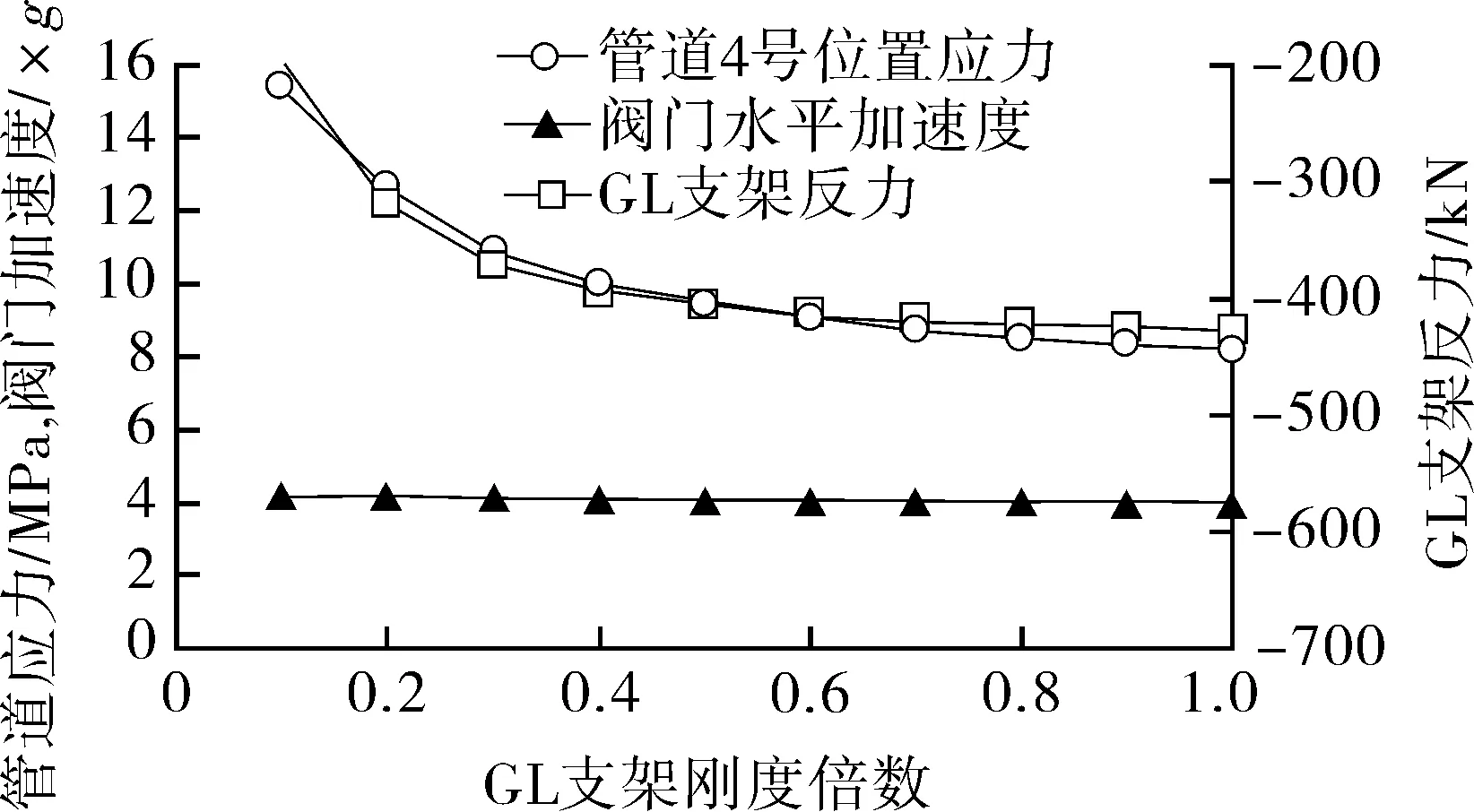
图12 管道计算结果随GL支架刚度增大的变化趋势

5 结论

(1)管道GL支架刚度和阀杆刚度分别按无限刚度和真实刚度计算，管道系统模态分析结果、约束点的反力、管道应力水平、阀门加速度差别不大；通常工程做法是，在力学分析中将支架刚度和阀杆刚度按无限刚度考虑，但考虑到阀门结构的多样性，建议按本文第3.2节给出的阀杆有限元力学模型简化方法建立阀杆模型，在不影响安全性和工作效率的情况下，使计算结果更加精确。

(2)核电厂管道系统力学分析时，GL支架的最小刚度取值通常为相连管道刚度的10倍。经过敏感性分析可以发现，可以进一步减小支架最小刚度，从而减小支架的钢结构和埋板尺寸，对安装和造价都起到很大改进作用；但不能仅依据某一个载荷，来进行支架刚度的折减，需要对全部载荷进行分析后，才能给出支架刚度折减的具体数值。