基于多尺度建模方法的蠕变-疲劳寿命预测

李凯尚，王润梓，张显程，涂善东

(华东理工大学 机械与动力工程学院,上海 200237)

0 引言

在循环热载荷作用下，飞机起降会导致疲劳损伤，同时在巡航过程中也会产生蠕变损伤[1-2]。此外，考虑到通风和机械连接，涡轮盘中将不可避免地引入几何不连续性，最终在应力集中区域发生过早的蠕变-疲劳失效[3-4]。因此，对几何不连续结构进行可靠的蠕变-疲劳寿命评定是保证其安全服役的前提。

与标准光滑试样相比，几何不连续结构的循环变形和损伤演化需要借助有限元仿真方法进行描述[5]。在宏观尺度框架下，连续损伤力学被广泛应用于评估单因素驱动的蠕变/疲劳损伤和复杂的蠕变-疲劳交互损伤。虽然宏观的本构模型符合损伤评估和寿命设计要求，但是无法合理描述微观组织损伤演化和解释裂纹萌生机制，因此，晶体塑性有限元被提出和广泛的使用。其中，MANONUKUL等[6]提出了疲劳指示因子，并使用这个因子预测疲劳裂纹萌生寿命；在此基础上，LI等[7]提出了蠕变-疲劳指示因子的概念，并成功预测了蠕变-疲劳裂纹萌生寿命。

考虑到计算成本，传统晶体塑性有限元无法描述整个部件的应力-应变状态。因此，研究人员结合宏微观尺度的有限元模型,提出了多尺度建模方法[8]。本文借助该方法,实现含孔结构的蠕变-疲劳寿命预测，并对某型航空涡轮盘进行拓展应用。

1 数值模拟过程

1.1 数值模拟概述

基于多尺度建模方法的非连续结构蠕变-疲劳寿命评估的总体流程如图1所示。

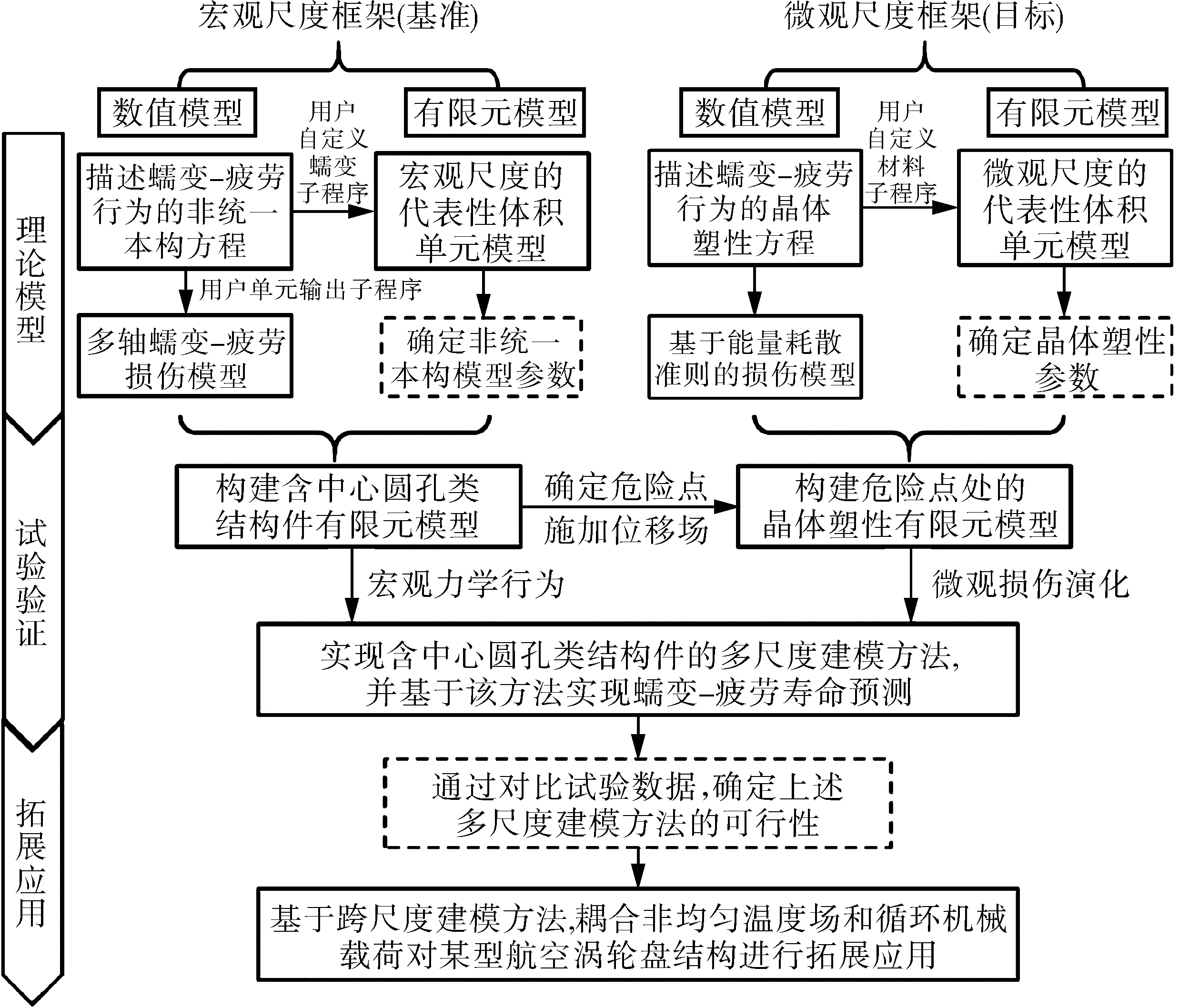
图1 多尺度建模方法的流程

首先，根据标准蠕变-疲劳试验数据确定本构模型参数，并构建相应的损伤模型。其次，将非统一本构方程和蠕变-疲劳寿命模型应用于含孔类结构的有限元模型中，通过数值模拟确定该类结构的最危险点，利用ABAQUS软件的子模型技术构建危险点处的晶体塑性有限元模型，并将宏观尺度下获得的位移场施加到晶体塑性有限元模型中作为边界条件，通过这种建模方法可以获得非连续结构的微观损伤演化规律以及实现寿命预测。最后，通过试验和模拟结果的对比,确定这种多尺度建模方法的可行性，并将该方法应用到某型航空涡轮盘的寿命评估。

1.2 粘塑性理论

在宏观尺度框架下，使用非统一本构方程描述材料的蠕变-疲劳行为，表达式如下[9]：

(1)

其中：

(2)

(3)

(4)

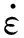
屈服公式可以表示为：

(5)

式中,σ*为偏应力张量;χ*为偏背应力张量;R为各向同性变形阻力。

背应力可以表示为：

(6)

式中,上标l(l=1,2,3)为总的背应力张量被分成3个部分;ζ(l),r(l)为材料参数。

各向同性变形阻力可以表示为：

(7)

式中,Rsat为各向同性变形阻力的饱和值;b为趋于该饱和值的速度。

采用临界平面法的疲劳损伤参量描述多轴应力状态下的疲劳损伤，表达式如下[10]：

(8)

式中,τmax为某一循环的最大剪应力;τ′f为某一循环的剪切疲劳强度;Δγ/2为剪切应变幅;σn,max为某一循环的最大正应力;σ′f为疲劳强度常数;Δεn/2为正应变幅;G为剪切模量;b0,c0为关于疲劳强度和延性的指数；γ′f为剪切延性强度。

在蠕变损伤方程中,通过引入弹性跟随因子Z和多轴延性因子(MDF)描述多轴应力状态对蠕变-疲劳寿命的影响[3]，每周次的蠕变损伤表达式如下：

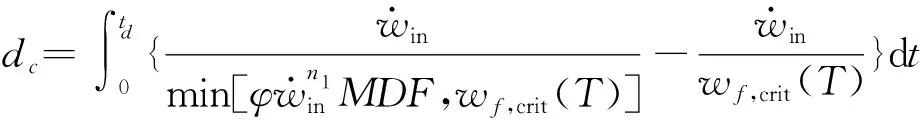
(9)

其中：

(10)

(11)

(12)

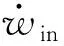
1.3 晶体塑性理论

(13)

式中,N为滑移系个数;mα，nα为α滑移系的滑移方向和滑移面法向。

晶体塑性滑移率的流动准则与分解剪应力τα、背应力Bα和滑移阻力Sα有关，表示如下：

×sgn(τα-Bα)

(14)

分解剪应力τα的表达式为：

τα=FeTFeT*:(sα⊗mα)

(15)

式中，T*为第二Piola-Kirchoff应力。

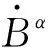
(16)

式中，hB为材料相关的硬化参数；rD为动态恢复参数；rS为静态恢复参数。

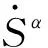
(17)

式中,hαβ为α和β滑移系的交叉硬化矩阵;S0,Ssat为初始和饱和滑移阻力;Sβ为β滑移系的滑移阻力。

为了描述材料在蠕变-疲劳载荷下的损伤演化规律，本文利用累积能量耗散W作为裂纹萌生的判据准则，其表达式为：

(18)

累积能量耗散的临界值Wcrit等于试验的裂纹萌生周次与模型预测的单周累积能量耗散的乘积，即：

Wcrit=NiWcyc

(19)

对于蠕变-疲劳加载工况，累积能量耗散可以看成由两部分组成，一部分是由循环加载引起的能量耗散;另一部分是在保载过程中产生的能量耗散,基于线性损伤叠加准则可以获取蠕变-疲劳裂纹萌生寿命[12]。其中，每周次的疲劳损伤可以表示为：

(20)

(21)

式中,Wf,crit为由循环加载产生的累积能量耗散临界值;Wc,crit为由保载产生的累积能量耗散临界值。

2 有限元模型

2.1 试件有限元模型

通常情况下，借助代表性体积单元和试验数据拟合的方法获取所需的模型参数。图2(a)示出宏微观尺度的代表性体积单元,以及代表性体积单元的边界条件，其中微观尺度的代表性体积单元根据VT算法构建，一共包含300个晶粒。

图2 不同尺度下的有限元模型

2.2 类结构件有限元模型

图2(b)示出了含孔类结构件的多尺度建模方法。首先，构建宏观尺度的含孔类结构有限元模型，并借助非统一本构方程实现蠕变-疲劳数值模拟；其次，提取危险位置处的位移场，作为晶体塑性有限元子模型的边界条件；最后，通过对子模型的有限元模拟便可以实现对孔根部(最危险点)的蠕变-疲劳行为分析。

在宏观尺度框架下，将含孔类结构简化为二维对称问题，采用CPE4单元，中心圆孔根部的网格尺寸较密，远离孔根部的网格尺寸较粗。模型左边采用对称边界条件，底边施加y方向的固定约束，上面施加y方向的位移载荷。在微观尺度框架下，采用VT算法构建晶体塑性有限元子模型，单元类型为CPE4单元，子模型的大小应包含孔根部裂纹萌生区，将含孔类结构有限元模型输出的位移场作为子模型的边界条件，实现微观尺度的有限元模拟。

2.3 结构件有限元模型

采用多尺度建模方法对某型航空涡轮盘结构进行拓展应用，多尺度建模方法参考第2.2节。考虑到涡轮盘的对称性以及计算成本，采用三维实体旋转模型的二维横截面进行有限元模拟，如图2(c)所示。对该结构件二维有限元模型施加轴对称边界条件，以Y轴为旋转轴设置涡轮盘的离心力，网格类型为CAX8R单元。同样，利用VT算法在危险位置建立晶体塑性有限元子模型，单元类型为CPE4单元，子模型的边界条件为整体结构件有限元模型输出的位移场。此外，在涡轮盘运行过程中，由温度梯度产生的热应力是无法忽略的，因此，本文通过温度场模拟涡轮盘运行过程中的温度变化。

3 本构及损伤模型参数

根据《中国航空材料手册》，可以获得材料在不同温度下的杨氏模量E、热膨胀系数αT、热传导率λ，如表1,2所示。其余温度参数由ABAQUS自动线性插值获得。

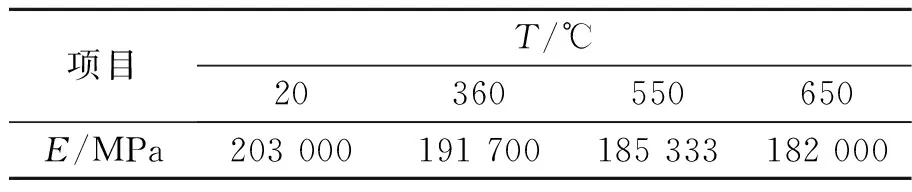
表1 不同温度下的杨氏模量

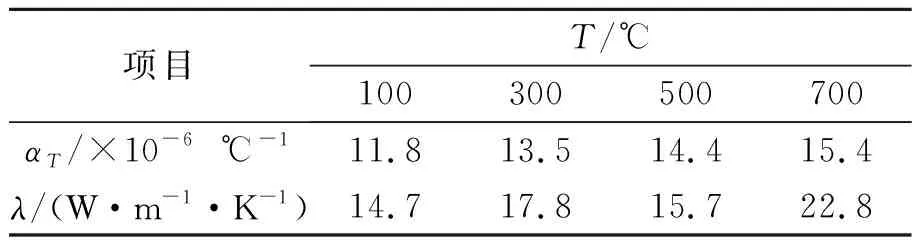
表2 不同温度下的热膨胀系数和热传导率

在宏观尺度框架下，需要分别确定非统一本构模型和损伤模型参数，参数标定过程件参考文献[13]，本文不再陈述。表3，4分别列出不同温度下的蠕变和疲劳本构参数。在微观尺度框架下，通过“试错法”标定不同温度下的晶体塑性模型参数，具体标定过程见参考文献[7]。

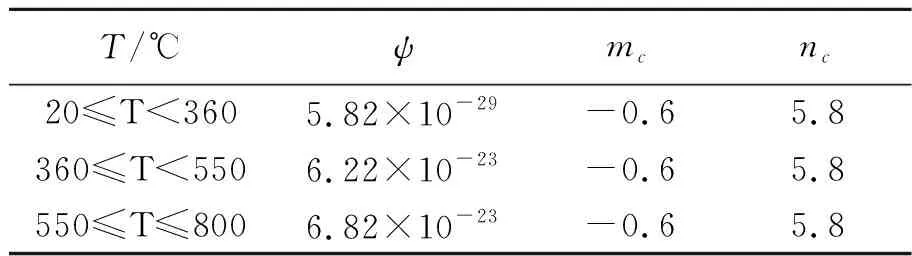
表3 不同温度下的蠕变本构参数

表4 不同温度下的疲劳本构参数

为了验证模型参数的有效性，图3示出基于非统一本构方程和基于晶体塑性的模拟结果，与650 ℃下的试验曲线对比发现，模拟结果和试验数据相吻合，说明本文给出的模型参数可以用于多尺度有限元模拟中。

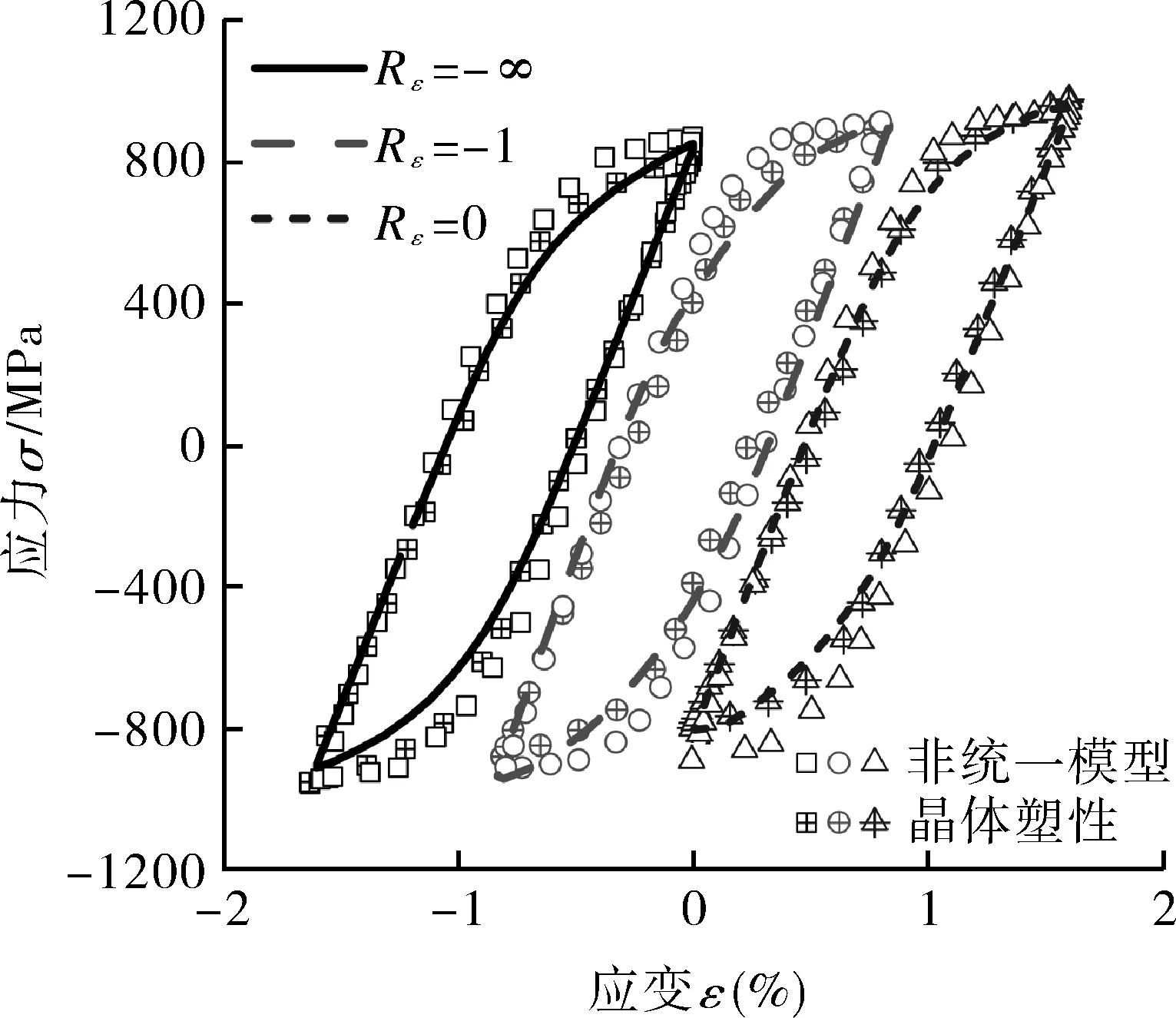
(a)疲劳迟滞回线的对比

4 结果分析与讨论

4.1 含孔类结构件

4.1.1 累积塑性应变分布

图4(a)为基于非统一本构方程模拟获得的塑性应变云图。由于几何不连续效应，最大塑性应变出现在孔的根部，且塑性应变沿着孔径往内部呈梯度减弱。不同于宏观尺度的模拟结果，图4(b)示出了基于晶体塑性获得的塑性应变云图，可以看出，在低变形量下最大塑性应变出现在孔的根部，随着变形量的增加，最大塑性应变从孔的根部往内部转移且呈现非均匀分布，这种现象可能是由于应力集中效应和晶粒取向差的相互作用导致的。

(a)宏观尺度下的塑性应变演化

4.1.2 累积塑性应变分布

图5(a)示出宏观尺度下的蠕变和疲劳损伤随着循环周次的演化规律，可以看出，蠕变损伤和疲劳损伤均随着循环周次的增加而线性增加，此外，累积蠕变损伤随着保载时间的增加而增加，但是疲劳损伤表现出保载时间无关性。图5(b)示出微观尺度下的累积能量耗散随着循环周次的演化规律。与宏观尺度下的累积损伤演化规律相似，累积能量耗散同样随着循环周次呈线性增加，但是考虑晶体塑性的复杂性以及有限元计算的费时性，基于晶体塑性的有限元仿真只能描述较少周次的损伤演化规律。

(a)宏观尺度下的蠕变和疲劳损伤演化

4.1.3 蠕变-疲劳寿命预测

针对含孔试样进行蠕变疲劳试验，总应变幅为0.3%和0.4%，保载时间为0～1 800 s，应变比0.1。图6示出基于多尺度建模方法的蠕变-疲劳寿命预测结果，绝大多数含孔试样的寿命数据点在2.0倍的误差带范围，展现了较高的寿命预测精度，同时验证了本文提出的多尺度建模方法的可行性。因此，本文将基于这种建模方法，同时耦合非均匀温度场和循环机械载荷对某型航空涡轮盘结构进行拓展应用。

图6 基于多尺度建模方法的蠕变-疲劳裂纹

4.2 某型航空涡轮盘结构

4.2.1 载荷谱和温度场

图7 稳态周次的转速-时间载荷谱和温度场-时间载荷谱

航空涡轮盘在实际工作过程中，承受由涡轮盘本身高速旋转产生的离心力、由不均匀温度场产生的温度应力、涡轮盘本身的重力以及运行过程中产生的振动载荷等[1]。由于涡轮盘的自重和振动载荷的影响远小于高速旋转的离心力，因此本文仅考虑由离心力产生的循环机械载荷对蠕变和疲劳损伤结果的影响，稳态周次下的转速-时间载荷谱如图7所示。

此外，航空涡轮盘在运行过程中经历非均匀温度场的影响，本文将稳态周次的温度场归一化处理，如图7所示。假设在起飞和降落的时间点处涡轮盘处于20 ℃的室温环境，而在巡航过程中涡轮盘承受的温度最高，将温度场进行归一化处理，其温度分布如图8所示。

图8 巡航过程中的温度场分布

4.2.2 损伤演化规律

图9(a)示出航空涡轮盘经历稳态周次以后的蠕变损伤分布情况，可以看出，最大蠕变损伤位置出现在几何不连续处，其数值为3.47×10-3。图9(b)示出了航空涡轮盘经历稳态周次以后的疲劳损伤分布情况，最大疲劳损伤位置仍然出现在轮缘几何不连续处的表面，其数值为2.34×10-4。稳态周次下最大的总损伤数值大约为3.64×10-3，如图9(c)所示。在此工况下，表现出以蠕变损伤为主导的失效模式。以最大损伤值作为每周次蠕变-疲劳损伤的典型数值，可以获得某型涡轮盘在此工况下的裂纹萌生寿命，为274周。图9(d)示出最大总损伤位置处的晶体塑性有限元模拟结果，可以看出，最大累积能量耗散出现在轮缘几何不连续处的次表面，这与晶粒取向和应力集中的竞争关系相关。由于本节只对多尺度建模方法的扩展应用进行研究，晶粒取向和应力集中之间的协同与竞争关系将在未来的工作中进行深入的探究。

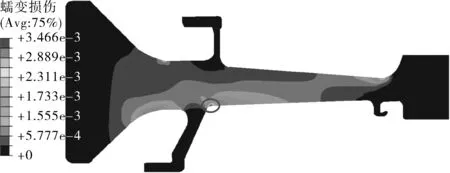
(a)稳态周次的蠕变损伤

5 结论

(1)从宏观有限元模型中提取的局部位移场作为晶体塑性有限元模型的边界条件，从而实现多尺度有限元模拟以及蠕变-疲劳裂纹萌生寿命预测。

(2)宏观尺度框架下的有限元模拟结果作为多尺度有限元分析的前提和基准。一方面，宏观有限元模型可以获得整体结构的损伤分布，为多尺度建模提供了裂纹萌生的位置；另一方面，通过对照宏观尺度的模拟结果来论证多尺度建模方法的合理性。

(3)通过含孔类结构的蠕变-疲劳试验结果，验证了多尺度建模方法的可行性，预测的蠕变-疲劳寿命与试验数据相吻合，该多尺度建模方法被成功地应用到某型航空涡轮盘的损伤评估。