车载LNG气瓶液体晃动数值分析方法对比

许海洋，杨宁祥，梁 琳，刘 蕊，范海贵，刘培启

(1.大连理工大学 化工学院，辽宁大连 116024；2.广东省特种设备检测研究院 珠海检测院，广东珠海 519002；3.中国特种设备检测研究院，北京 100029)

0 引言

车载LNG气瓶是液化天然气汽车储存燃料的关键设备，其安全性能对汽车的安全行驶至关重要[1-2]。车辆在行驶时的加减速和转弯操作都会引起气瓶内LNG液体的晃动，从而对气瓶产生冲击载荷，这种晃动在气瓶非满载的情况下更加明显。如果气瓶设计不合理，过大的冲击载荷可能会超过气瓶材料的许用强度极限，引起气瓶开裂造成泄漏甚至火灾等危险事故，因此对气瓶进行准确的应力强度分析非常重要。

工程应用时，对于气瓶受到惯性载荷引起液体晃动的问题，一般将其简化为静力学问题来计算[3-5]。刘德玉[6]将刹车时气瓶内介质的冲击作用等效为内胆内壁面上均布的压力，压力载荷作用面为液体在内胆冲击方向上的投影；周天送等[7-8]采用虚拟质量法，把液体晃动载荷定义为均布质量耦合在与介质接触的内胆壁面上，认为内胆所受的LNG冲击载荷近似和LNG的惯性力相等。这两种简化方法认为满载时气瓶液体晃动较小，且轴向防波板、真空腔和防过充的存在进一步增加了液体晃动阻尼，因此可以忽略液体晃动引起的应力，然而实际车载LNG气瓶在不同工况下的受力情况如何，尚缺少相关计算验证[9]。

另一种计算气瓶应力强度的方法是流固耦合分析，许多学者都对流固耦合方法进行过研究，并通过试验验证了其可行性。EDWARDS[10]改进了原有的壳理论，提取液体表面压强施加在流固交界面上进行流固耦合分析，得到了在地震时储液容器受力情况，计算出在地震载荷下储液罐的应力和位移响应，提出了在校核强度时必须考虑液体冲击作用。李海鸣等[11]以铁路客车水箱为对象，用VOF多相流模型计算水箱内流体流动情况，根据单向流固耦合，得到了水箱和防波板受到的最大应力，从而确定了箱体结构的薄弱位置。龙飞等[12]分别对液体小幅晃动和大幅晃动对水箱的瞬态动力响应进行了计算，结果表明，小幅晃动时，水箱即使共振也不会强度失效，而大幅晃动时铝合金所制造的水箱会强度失效。洪洋等[13]针对板翅式换热器的开裂现象，结合FLUENT与ABAQUS分析软件对冷却器进行了流固耦合分析并根据分析结果进行结构优化，将模拟得到的结构疲劳断裂和通过电镜扫描观察的断口形貌对比，对流固耦合计算结果进行了可靠的验证。NICOLICI等[14]结合有限元应力分析和流体力学分析进行耦合计算，预测了含液容器晃动波幅值、对流模态频率、壁面压力以及晃动对锚固点力的影响，并将流固耦合模型的结果与设计规范中简化力学模型的结果进行了比较，发现耦合现象影响了壁面弹性对冲击压力的放大作用，通过流固耦合计算可以准确地将各个时刻的液体晃动压力加载到气瓶上，但是该方法计算量较大，耗费时间较长，不如等效静力法使用方便。

本文以某型号1 000 L车载LNG气瓶为研究对象，分别用流固耦合法和等效静力法对气瓶不同工况下受力进行分析，提出晃动影响系数的概念，根据不同工况下的流固耦合计算结果对等效静力法进行修正，并给出晃动影响系数的上限值，为车载LNG气瓶的工程设计提供参考。

1 计算方法

1.1 等效静力法

为了简化计算过程，工程上常用等效静力法来计算充液容器的结构强度。其基本原理是假设结构各区域振动形态相同，将最大运动加速度引起的惯性载荷看作静力施加在整体结构上，再通过静力分析方法计算结构的位移和受力情况。该方法认为液体波动很小，将复杂流固耦合问题简化为固体静力学问题，极大地减少了计算量[15]。具体计算时只需改变与内部流体接触的固体壁面壁单元的密度即可，因此又被称为虚拟质量法，等效密度的计算公式[16]为：

(1)

式中，mliquid为与充装液体质量，kg；mwall为液体边界固壁的质量，kg；ρwall为液体边界壁面的密度，kg/m3。

1.2 单向流固耦合

根据文献[11,17]，气瓶等储液容器在车载工况下受到液体冲击时不会产生大变形,固体变形对流体域影响很小,因此本文采用单向流固耦合的方法，主要研究流体晃动引起结构上的应力。

在气瓶晃动过程中，气瓶内存在两相流体，即液态的LNG和其饱和蒸汽，汽车变工况时介质在内胆里晃动，具有很强的随机性。目前有限体积法(VOF法)[18-21]是实时追踪自由液面位置的最好方法，所以本文采用VOF多相流模型模拟液体晃动行为。

为了验证在流体计算过程中使用的VOF计算方法的准确性，对张恩慧[22]做的油箱内燃油晃动试验进行了数值计算，其和气瓶的液体晃动问题区别仅在于容器形状和流体物性，试验中油箱初速度为0，1 s内保持0.1g加速度在导轨内滑行，试验和模拟结果如图1所示。

图1 试验曲线和模拟值曲线

模拟得到的压力变化曲线和试验得到的曲线趋势基本一致，在同样的时刻，前壁面和后壁面分别达到极值，极值误差如表1所示，可以看出最大误差不超过5%，所以本文采用的VOF方法是准确的，后续计算中，只需将流体压力导入气瓶内胆壁面来计算结构应力。

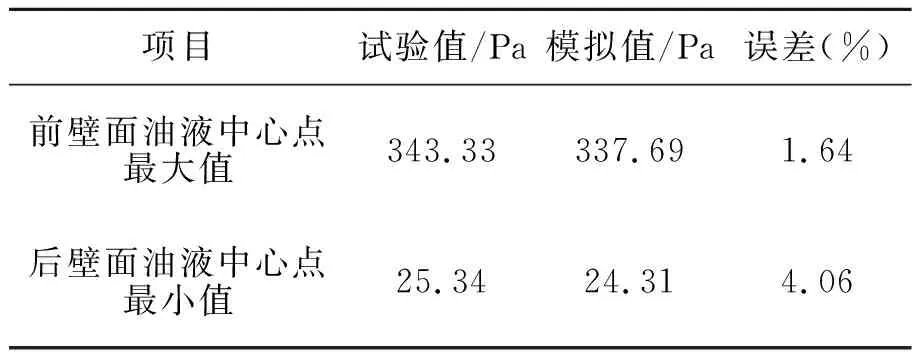
表1 试验和模拟极值对比

2 建立气瓶模型及准确性验证

2.1 建立气瓶模型及设置边界

所选气瓶公称容积1 000 L，忽略了液位计、管路系统、保温层等众多对结构强度影响小的组件，从最危险情况考虑，本文假设该气瓶没有设置防波板。经过以上简化可建立气瓶的固体模型，气瓶整体结构如图2(显示1/2模型)所示。

图2 气瓶整体结构

气瓶内胆和外壳均采用06Cr19Ni10奥氏体不锈钢，其密度为7 930 kg /m3，屈服强度205 MPa，抗拉强度520 MPa，弹性模量209 GPa，泊松比0.278[23]。整体以Solid 186单元划分网格，气瓶有限元模型如图3所示。

图3 气瓶有限元模型

在固体模型上施加的边界条件如下。

(1)设计压力：内胆施加1.37 MPa压力，内胆与外壳之间施加-0.1 MPa压力。

(2)惯性力：汽车行驶时，由于加速度改变会导致瓶体受到不同方向的惯性载荷，GB/T 34510—2017《汽车用液化天然气气瓶》规定的大容积气瓶振动试验振动加速度幅值为5g，为考虑最危险情况，也对固体模型施加不同方向5g的加速度。

(3)液体晃动载荷：对于流固耦合法，采用Fluent软件计算不同时刻的流体壁面压力，再将压力映射到内胆内壁上计算气瓶结构应力；对于等效静力法，通过增加单元材料密度，等效流体的冲击力。

(4)约束：气瓶固定架由支座和绑带组成，用来防止瓶体因汽车振动而松动或脱落，可近似认为其约束了整个约束环面的平动和旋转，因此在建模过程中没有对固定用的绑带和支架建模，而是将其约束作用转化为对于绑带接触的外壳表面节点的全约束，约束环面位置见图2。

2.2 气瓶模型准确性验证

为了验证所建立气瓶固体域模型是否准确，本节对其加载第2.1节边界条件中的设计压力和约束，计算得到其应力分布如图4所示。

图4 气瓶应力强度分布

沿图4上路径A-A提取内胆内壁的应力曲线如图5所示，从封头到内胆筒体段的应力变化符合压力容器椭圆封头和圆柱筒体应力分布规律[24]，内胆筒体段应力恒定，环向和轴向应力分别为150.21 MPa和73.72 MPa。

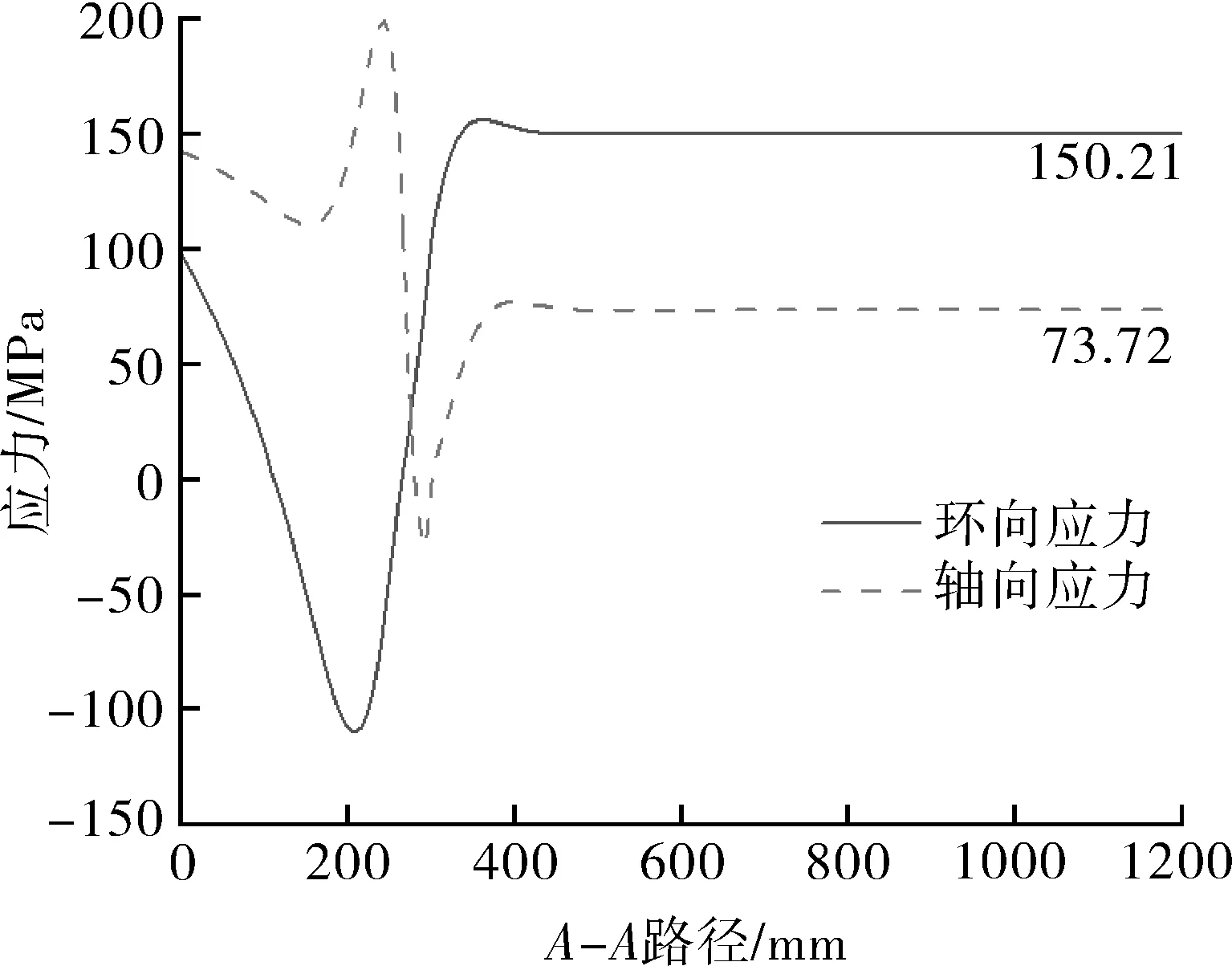
图5 沿路径得到的内胆内壁应力曲线

根据薄壁容器无矩理论[24]可得环向和轴向应力的理论解分别为：

(2)

(3)

式中，P为设计压力，MPa；R为内胆内径，mm；δ为内胆筒体壁厚，mm。

模拟值与理论值相差1%以内，可以认为模型准确。

3 流固耦合计算结果

3.1 流体域计算设置

用流固耦合法计算气瓶应力强度，首先要提取出不同时刻流体对固体的压力，流体域主要包括气液两相：气相为液化天然气的饱和蒸汽(密度为21.8 kg/m3，动力黏度为4.98×10-2cP)，液相为液化天然气(密度为345.6 kg/m3，动力黏度为6.69×10-3cP)，流体域网格如图6所示。

图6 流体域网格

在FLUENT软件中选择VOF瞬态模型和真实k-ε模型，用压力求解器求解，时间步长为0.001 s，选择PISO算法加快计算速度。

3.2 液体晃动过程

以70%充装率为例，流体域初始静止，在0 s时突然受到5g轴向负向加速度，加速时间共1 s。其0～1 s内介质晃动情况如图7所示，可以看出，液体先是冲击前封头，受到前封头阻挡后液体翻腾，一部分液体涌向后封头，最后在0.8 s时液体晃动趋于稳定。

图7 液体晃动过程

液体晃动过程中，气瓶内胆表面静压分布如图8所示，随着时间增加，压强值呈现先增加、再减小、然后趋于稳定的趋势，在t=0.116 s时，压强值达到最大36 200 Pa，约为初始状态下最大压强的16倍。

图8 流体压力变化

3.3 气瓶结构强度计算

将流体静压作为介质冲击载荷传递到气瓶内胆的流固耦合面上，再加上第2.1节中所述的设计压力、惯性力和约束，计算可得气瓶各时刻应力强度云图如图9,10所示，图9示出外壳筒体部分应力均很小，应力较大区域主要集中在内胆以及内胆与外壳连接处附近(见图10)，因此后续只显示气瓶内侧应力强度云图。如图10所示，气瓶在t=0.116 s时应力强度达到最大，最大应力点为外壳前封头开孔连接处，之后应力逐渐减小，最大应力转移到内胆前封头和小筒体连接处，如图11所示。

图9 t=0.116 s时气瓶外侧应力强度云图

图10 t=0.116 s时气瓶内侧应力强度云图

图11 t=1 s时应力强度云图

提取不同时刻外壳前封头开孔连接处以及内胆前封头和小筒体连接处应力强度，拟合得到应力曲线如图12所示，其中0 s时刻气瓶仅受到设计压力、惯性力以及液体静止时的静压，0 s之后液体晃动引起气瓶应力变化。可以看出，以上两点的应力强度均呈现先增大至峰值、再减小至相对稳定的趋势，气瓶危险区域的应力强度均在0.116 s达到最大，然后在0.5 s左右趋于相对稳定，应力波动较小。

图12 危险位置应力强度变化曲线

4 等效静力法计算结果及其修正

等效静力法计算时，只需通过将等效密度施加在和液体接触的固体壁面上即可，根据虚拟质量法的计算公式，70%充装率气瓶的固壁等效密度为17 206 kg/m3。施加第2节所述的边界条件后，得到气瓶的应力计算结果如图13所示。

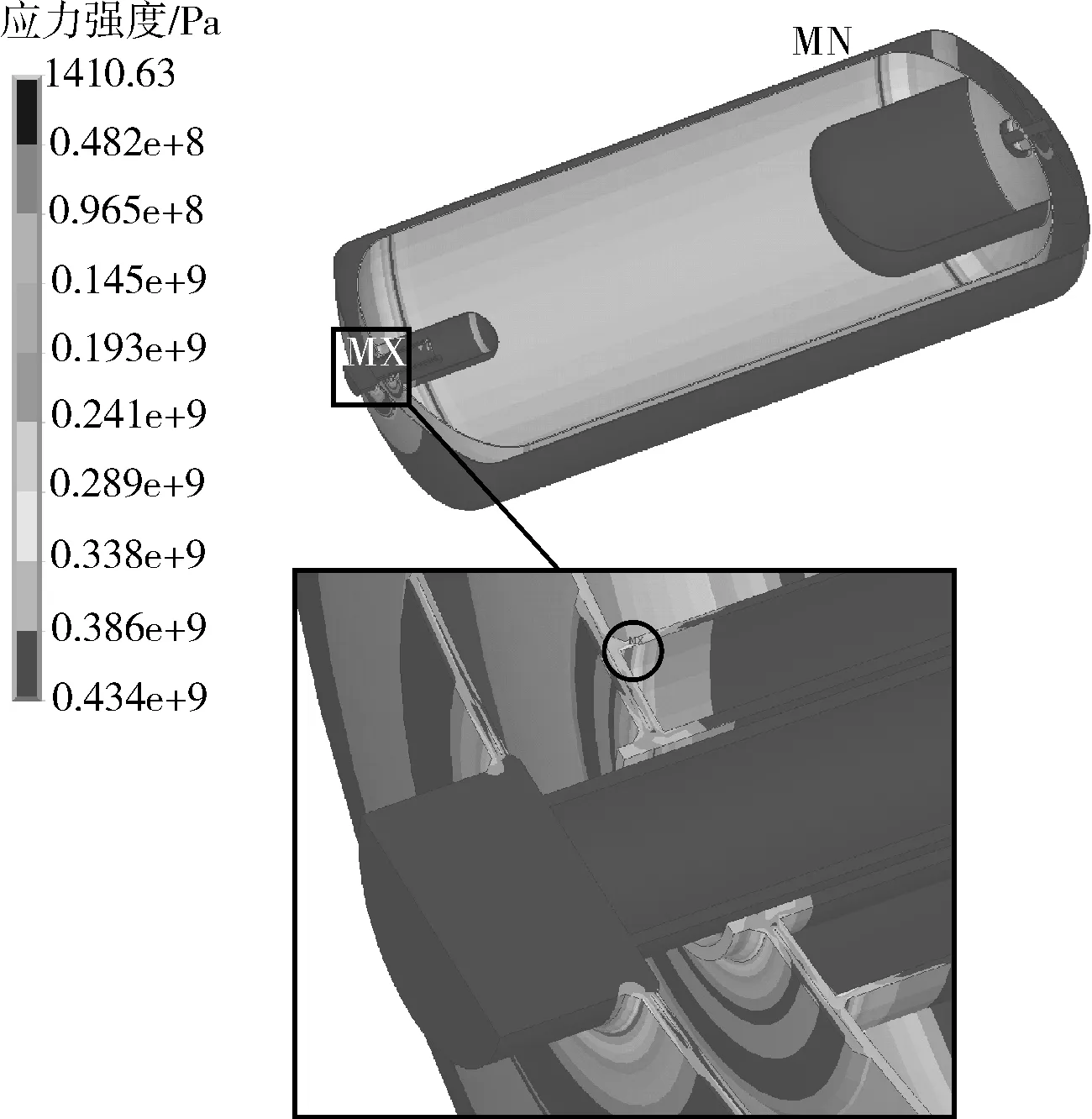
图13 等效静力法修正前得到的应力强度云图

由图13可以看出，等效静力法计算结果和流固耦合计算得到的晃动相对稳定时的应力云图(见图11)几乎相同，而与图10晃动最剧烈时(t=0.116 s)则相差较大，因此需要对等效静力法进行修正，修正后的等效密度计算公式如下：

(4)

式中，α为晃动影响系数，该系数与防波板配置、充装率、惯性加速度大小、方向及加载速度有关,其下限值为1，即忽略液体晃动影响，在惯性加速度很小且防波板合理配置时可以实现，上限值将在下一节给出。

对受到5g轴向负向加速度、70%充装的计算工况，晃动影响系数为1.23，修正后通过等效静力法得到静力强度云图如图14所示，应力分布和图10基本一致。修正前后危险点应力如表2所示，可以看出，修正后误差在2%以内。

图14 等效静力法修正后得到的应力强度云图

表2 等效静力法修正前后危险点应力比较

5 不同工况下晃动影响系数上限值

想要准确得到所有情况下晃动影响系数值较困难，但是可以取最危险工况来计算晃动影响系数的上限值，本文取瞬间加载的最大惯性加速度5g，不设置防波板，对不同方向充装率和惯性加速度气瓶的晃动影响系数进行计算，得到了车载LNG气瓶晃动影响系数的上限值。

考虑到充装率对液体的晃动影响很大，分别对受到轴向负向加速度以及充装率为25%,50%,70%,90%(满载)时的液体晃动进行了计算，在不同充装率下，用流固耦合计算得到的外壳前封头开孔连接处应力强度曲线如图15所示。可以看出，随着充装率增加，液体晃动引起的气瓶最大应力增加，最大应力可达到静止状态的2倍左右；随着充装率增加，气瓶应力增加的幅度减小，应力强度很快便达到相对稳定，说明液体晃动冲击作用在逐渐减弱。

图15 不同充装率时，参考点应力强度的变化曲线

在行驶时，由于加减速、急转弯和路面颠簸等工况，车载LNG气瓶会受到轴向负向、轴向正向、水平径向和竖直径向这几个方向的惯性加速度作用，针对所有工况，根据流固耦合计算结果修正等效静力法，得到不同充装率的晃动影响系数上限值如图16所示。

图16 不同惯性加速度方向、充装率时的晃动影响系数上限值

由图16可看出，轴向正向加速度作用下，晃动影响系数最大，竖直径向加速度下，晃动影响系数最小，随着充装率的增加，晃动影响系数逐渐减小；考虑到满载时气瓶应力最大，此充装率下晃动影响系数最大值为1.3，是由轴向正向加速度作用引起的，因此实际工程应用时，可取晃动影响系数为1.3来校核不同工况下的气瓶强度。

6 结论

本文运用等效静力法和流固耦合法分别对车载LNG气瓶进行应力强度计算，在此基础上提出了晃动影响系数的概念，从而对等效静力法进行了修正，主要结论如下。

(1)当气瓶受到液体晃动冲击载荷时，最大应力强度呈现先增大、后减小的趋势，最后趋于稳定值，最大应力可达静止状态的2倍左右。

(2)获得了不同方向惯性加速度作用下气瓶的液体晃动影响系数上限值，随着充装率增加，液体晃动冲击作用减弱，各方向的晃动影响系数均逐渐减小。

(3)满载时气瓶应力最大，实际工程应用时可取晃动影响系数为1.3来校核不同工况下的气瓶强度。