面内和面外约束相关的反应堆压力容器结构钢断裂性能及预测

刘 争，王 昕，陈 旭,3

(1.天津大学 化工学院，天津 300350；2.天津市化工安全与装备技术重点实验室，天津 300354；3.天津大学 浙江研究院，浙江宁波 315200)

0 引言

反应堆压力容器(RPV)是核反应堆冷却剂压力边界屏障中的一个重要且不可更换设备，主要是装载反应堆堆芯、高温高压和密封的冷却剂，要求在各种常规工况和极端工况下均能保证结构的完整性。然而，RPV长期在高温、高压和高中子辐照环境下运行，RPV结构钢不可避免地劣化，抗断裂性能降低；另一方面，在RPV制造和使用过程中，缺陷不可避免地存在或萌生。因此，如何准确预测含裂纹反应堆压力容器在各种工况下的断裂行为，对RPV的安全服役具有重要的意义[1]。

目前，核电站广泛采用的仍然是基于常规断裂力学的结构完整性评定方法，认为一个断裂参数，如应力强度因子K或J积分可以唯一地表征裂纹尖端的应力应变场，从而断裂韧性测试标准ASTM E1820-20b建议采用高约束断裂试样，如单边缺口弯曲(SENB)试样和紧凑拉伸型(CT)试样。实践证明，采用单参数法得到的结果过于保守，造成大量的结构钢浪费。基于此，在过去二十年中，断裂力学领域寻求发展约束相关的断裂力学，发展了一系列双参数法，如J-T11方法、J-QSSY(QHRR)方法和J-A(A2)方法等，其中T11，QSSY，QHRR，A，A2为约束参数。然而，上述发展的双参数法，在一定程度上可以量化和描述面内约束效应的影响，但依然无法解决试样厚度、面外载荷和二维裂纹所导致的三维约束效应。

最近，LIU等[2-6]采用低约束断裂试样(夹持式SENT试样)，研究了面内和面外约束对API X80油气管线钢和16MND5结构钢断裂性能的影响；同时，提出了新的面外约束参数(T33-vT11)，分别使用名义应力归一化的T11和T33-vT11，定义为F11和V33，量化面内和面外约束效应，发展了J-F11-V33方法，该方法已被试验结果证实是有效的。然而，T11和T33-vT11的理论基础均是线弹性断裂力学，且T11只适用于小尺度屈服或一定屈服状态下，不适合在大尺度屈服或全塑性下使用。因此，验证V33的合理性及在大尺度屈服下的适用性，并且与大尺度屈服下适用的面内约束参数相结合，发展新的三维面内和面外约束相关的断裂力学方法就极为重要。

综上所述，在本研究中先介绍基于16MND5结构钢展开的断裂试验，随后采用三维弹塑性数值分析，求解不同几何尺寸下的A和V33，验证V33的适用性；最后，发展适用于大尺度屈服的三维面内和面外约束相关的断裂力学方法，建立16MND5钢面内和面外约束统一的断裂性能函数，从而实现对其他断裂试样或裂纹结构进行预测。

1 夹持式SENT断裂试验

1.1 试验材料及试样设计

试验材料为16MND5低合金钢，其化学成分列于表1中，其弹性模量E=215.4 GPa，泊松比v=0.3，屈服应力σYS=411.5 MPa，抗拉强度σUTS=575.4 MPa，应变硬化指数n=9.21。

表1 16MND5钢化学成分

根据文献[7]的推荐，试样为夹持式SENT试样(见图1)，其中试样宽度W=15 mm，夹持端尺寸为 4W，夹距H分别设计为8W和10W，裂纹深度与试样宽度的比a/W和试样厚度与试样宽度的比B/W见表 2，其中编号A～F为H/W=10.0，编号G，H,K为H/W=8.0。同时，为了得到较为平齐的裂纹前沿，所有的试样均开侧槽，侧槽深度为0.1B，角度60°，切口的根部半径为 0.5 mm。

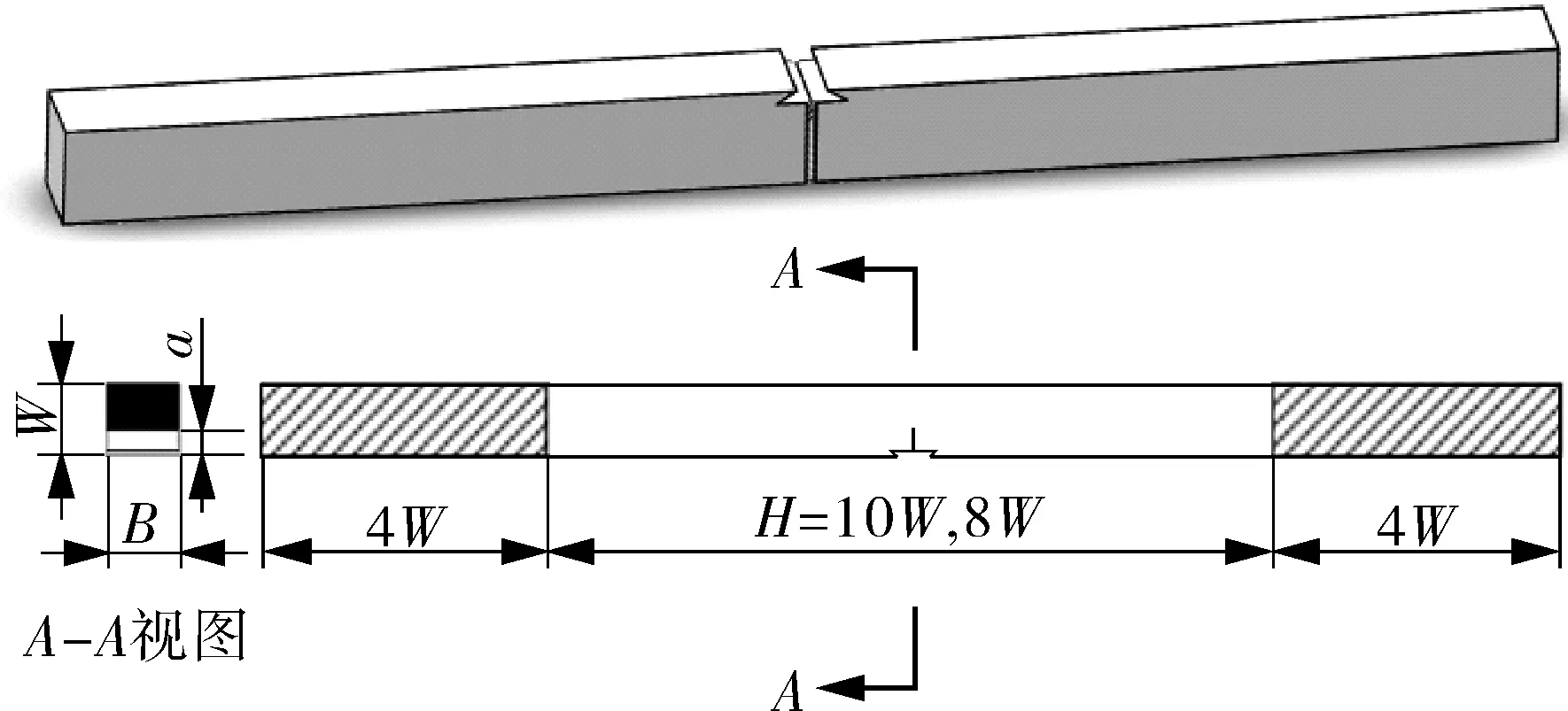
图1 夹持式SENT试样结构示意

表2 夹持式SENT试样几何尺寸

1.2 试验过程及试验结果

试验在MTS E64试验机上进行，裂纹张开位移采用COD引伸计测量。试验过程采用卸载柔度法，加载为应变控制，卸载是载荷控制，其中加载速率为 0.01 mm/s，卸载速率为0.1 kN/s。有明显的裂纹扩展，或载荷到达峰值载荷后，下降不超过峰值载荷的20%停止试验。随后，对数据进行处理，计算实时裂纹长度及对应的J积分，采用幂律函数对其进行拟合：

J=CJ1ΔaCJ2

(1)

式中，CJ1,CJ2为J-R曲线拟合参数。

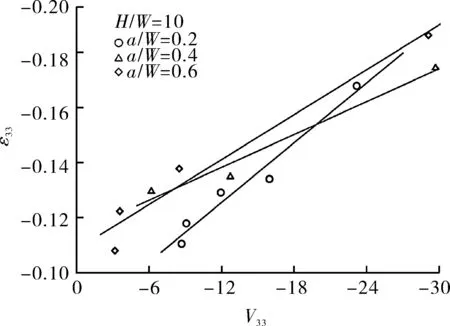
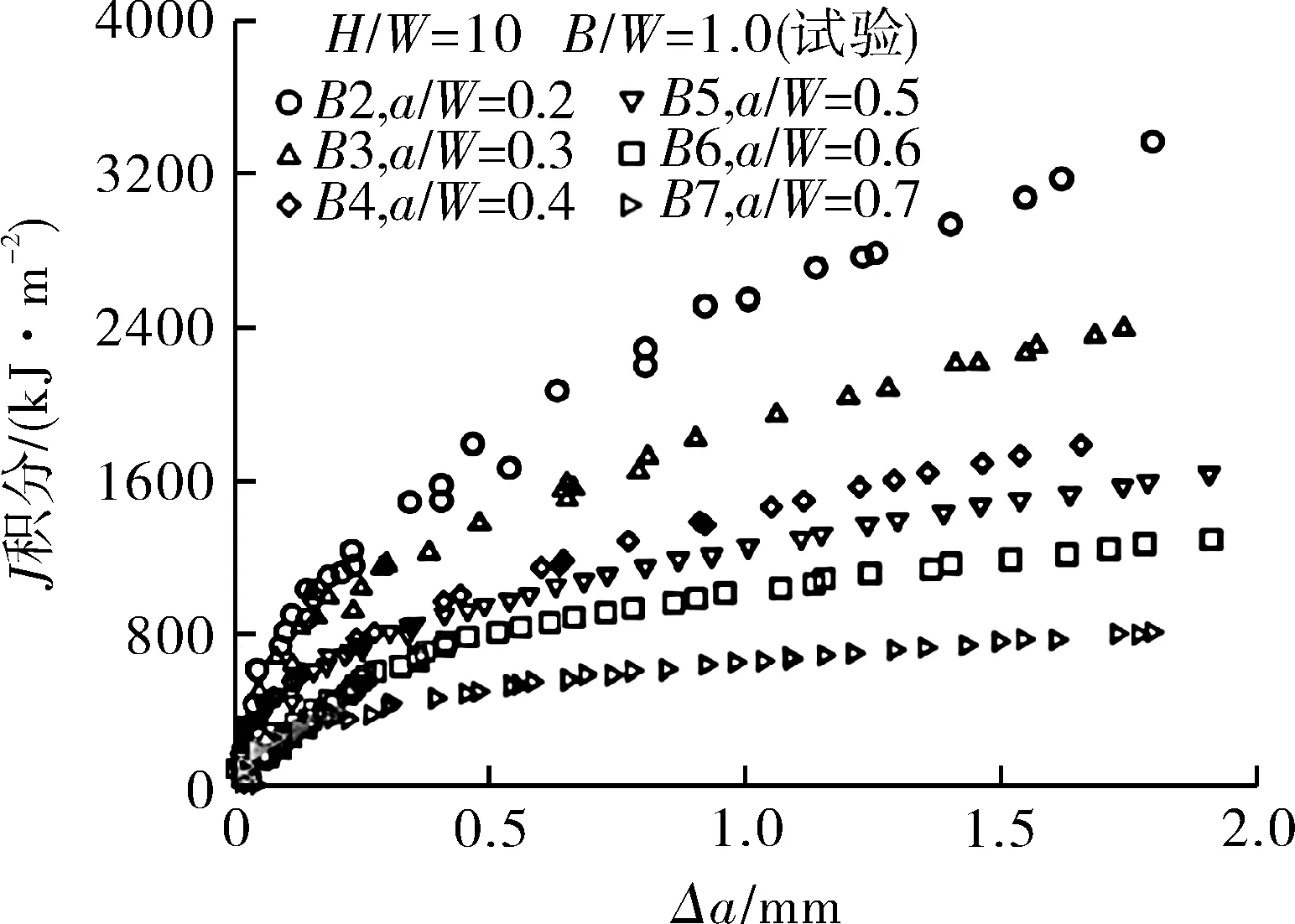
阻力曲线结果如图2所示。可以看出J-R曲线显著依赖于试样的几何尺寸，整体规律是随着裂纹深度和试样厚度的增大而递减。另外，Δa=0.2 mm处的平均厚度应变ε33结果列于图3中。可以看出，随着试样厚度的增大，平均厚度应变单调递增，表明逐渐接近平面应变状态，其结果可以较好地量化试样厚度的影响。

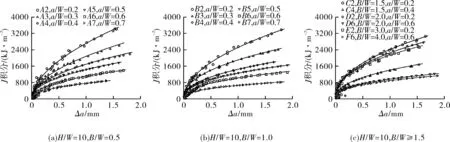
图2 试验测试得到的不同几何尺寸下的J-R曲线

2 三维弹塑性数值分析

2.1 有限元模型及约束参数求解

材料模型和试验材料一致，针对三维夹持式SENT试样，其几何尺寸与试验一致，对所有的有限元模型采用ABAQUS四分之一建模，网格单元为C3D20R。为了得到较为精确的模拟结果，采用聚焦环式网格，最小网格尺寸为1 μm。另外，考虑到裂纹尖端附近较大的弹塑性非线性变形，设置一个半径为0.001 mm的1/4圆形缺口，其网格示意如图4所示。设置对称边界条件，夹持的区域和一个参考点完全耦合约束，限制参考点在除了加载方向上的全部自由度，一个集中力P施加在参考点上。

图4 夹持式SENT试样有限元网格划分

考虑到由断裂试验确定的极限载荷为1.3Py，因此，对于每个试样，施加的集中力P最大值为1.5Py，其中Py为：

Py=BNbσY

(2)

式中，BN为净厚度尺寸,mm;b为韧带长度,mm,b=W-a;σY为流动应力,MPa,σY=(σYS+σUTS)/2。

对一个含Ⅰ型裂纹的二维弹塑性体在平面应变状态下，根据NIKISHKOV等[8]的研究，裂纹尖端附近的应力可以用三项渐进式表示为：

(3)

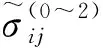
A0=(αε0In)s

(4)

式中，In为无量纲积分常数，是硬化指数n的函数。

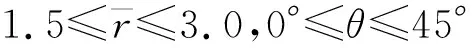
另一方面，针对面外约束参数，由于T33=Eε33+vT11，从而，新提出的面外约束参数在数值上等于Eε33，使用名义应力进行载荷无关性归一化，表示为：

(5)

式中,σn为名义应力，σn=P/[(BNB)0.5W]。

最后，考虑到弹塑性下，面内和面外约束参数依赖于施加的载荷大小。因此，本研究选择启裂断裂韧性J0.2处的A和V33作为面内和面外约束参数。

2.2 数值分析结果

面内约束参数A的结果见图5。

图5 面内约束参数A的变化曲线

从图5可以看出，A均为正值，对于H/W=10的试样，任意一个试样厚度下，随着裂纹深度的增大，A单调减小；当H/W=8时，发现A并不随裂纹深度的变化而单调变化，这一现象是由于夹持

式SENT试样，其裂纹尖端的应力场由H/W，B/W和a/W耦合决定，且A的变化与试验结果较为一致，从而可以较好地量化面内约束效应。

对于面外约束参数，首先建立其与平均厚度应变的关系(见图6(a))。可以看出，对于任意给定的裂纹长度，V33均与ε33,avg有较好的线性关系，ε33随着V33的减小而减小，且a/W越小，斜率越大，表明裂纹深度会影响面外约束效应。V33在弹塑性下的适应性通过试验结果得以验证。

另外，不同几何尺寸下的V33如图6(b)所示。随着试样厚度的增大，V33单调递增，当B/W≥2.0时，变化不大，表明接近平面应变状态。另外，针对不同a/W和H/W的影响，V33也表现出一定的单调性。综上，V33作为面外约束参数，适用于大尺度屈服条件。

(a)随平均厚度应变的变化

3 三维面内和面外约束相关的断裂力学方法

3.1 面内和面外约束相关的断裂力学方法的建立

针对A和V33相关的J-R曲线，其形式为：

J(Δa,A,V33)=CJ1(A,V33)(Δa)CJ2(A,V33)

(6)

假设已知两个裂纹扩展长度Δa1和Δa2，其对应的J积分为：

J(Δa1,A,V33)=CJ1(A,V33)(Δa1)CJ2(A,V33)

(7)

J(Δa2,A,V33)=CJ1(A,V33)(Δa2)CJ2(A,V33)

(8)

则：

(9)

(10)

因此，如果已知阻力曲线上任意2个点(Δa1，JΔa1),(Δa2，JΔa2)，就可以得到整条阻力曲线，为了保证结果的相对准确性，推荐的2个裂纹扩展长度的范围为0.2～1.0 mm。

3.2 面内和面外约束相关的16MND5钢断裂性能函数

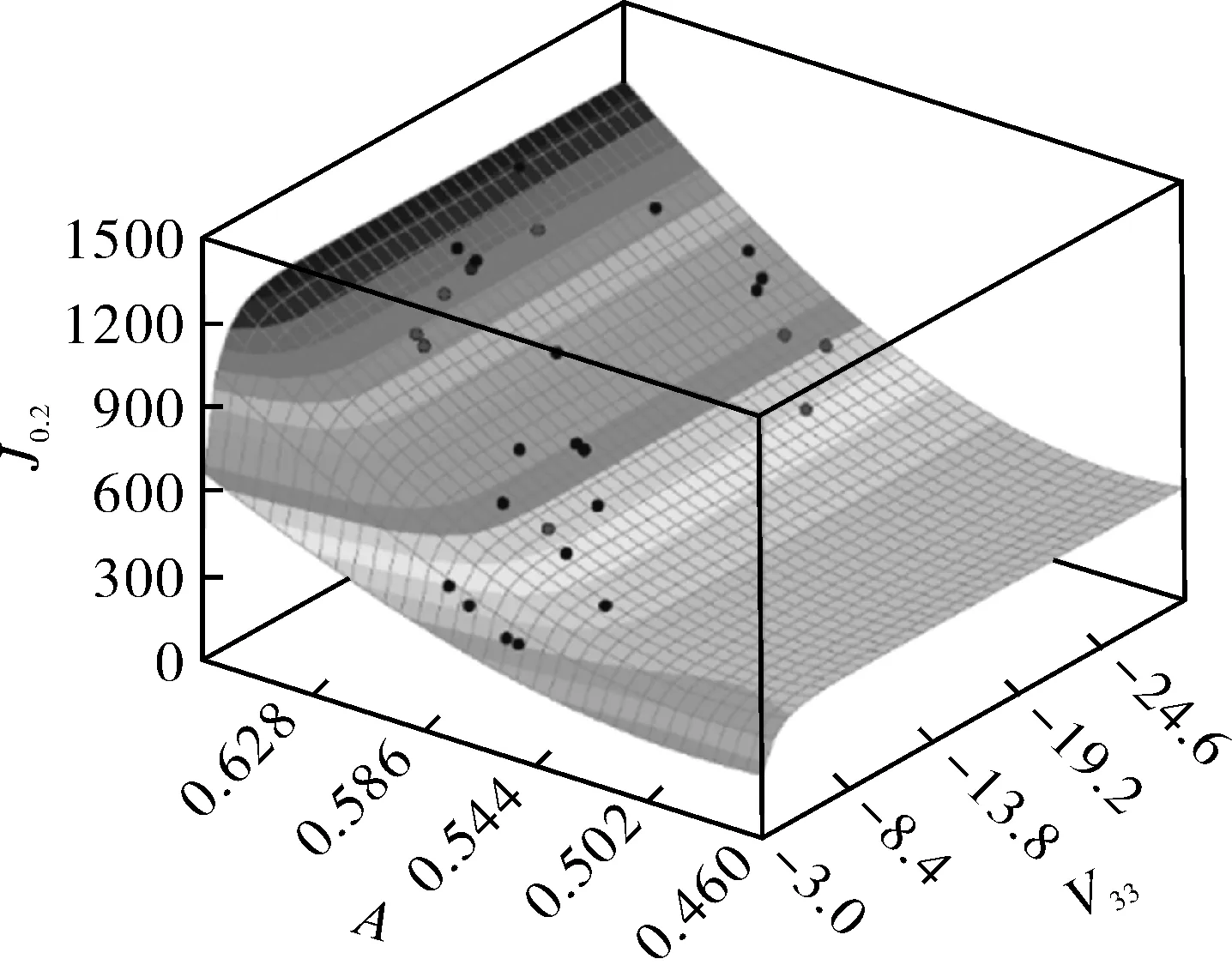
首先，基于J-A-V33方法，针对16MND5钢面内和面外约束相关的J-R曲线，本文选择裂纹扩展长度为0.2 mm和0.4 mm，其对应的J积分为J0.2和J0.4，随后，J0.2和J0.4关于A和V33的失效曲面如图7所示，并用如下公式进行拟合：

JΔa=(a+bA+cA2+dA3+eA4+fA5)

(11)

(a)J0.2

式中，a～j为拟合参数。

从图7可以看出，J0.2和J0.4高度依赖于A和V33，并且随着A和V33的降低而单调增大；同时，可以看出J积分主要是由面内约束水平决定，J积分在一定范围内，对面外约束水平不敏感，表现出相对较小的变化。

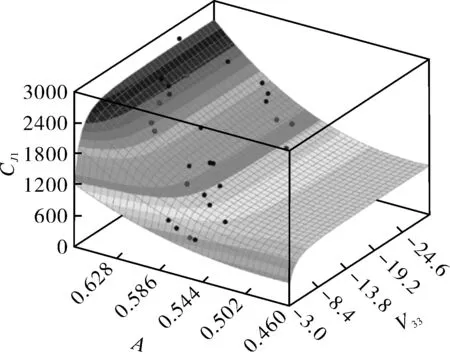
随后，将(0.2，J0.2)和(0.4，J0.4)代入式(9)(10)，CJ1(A,V33)和CJ2(A,V33)即可以得到，表示为：

CJ=(a+bA+cA2+dA3+eA4+fA5)

(12)

求解的CJ1(A,V33)和CJ2(A,V33)见图8。

(a)CJ1

一旦已知RPV结构钢的CJ1(A,V33)和CJ2(A,V33)，将式(12)代入式(6)就可以得到面内和面外约束相关的J-R曲线。为了验证当前提出的面内和面外约束相关的J-R曲线，将通过式(6)预测的J-R曲线与试验测试得到的J-R曲线进行对比(见图9)。从图9可以看出，当前J-A-V33方法可以很好地重现不同面内和面外约束下的J-R曲线结果。

(a)H/W=10,B/W=1.0试样的试验结果

4 阻力曲线预测

销轴式SENT试样也是BS 8571—2018标准推荐的低约束试样。首先，基于柔度法，开展基于销轴式SENT试样的断裂试验，随后使用当前发展的面内和面外约束相关的断裂性能函数预测的阻力曲线，并与试验结果进行对比。

关于销轴式SENT试验，所用试验材料仍然为16MND5钢。根据BS 8571—2018标准的推荐，其中试样宽度W=15 mm，B/W=1.0，a/W=0.2,0.3,0.4,0.5。同时，为了实现较为平齐的裂纹前沿，所有的试验均设计侧槽，侧槽尺寸与夹持式SENT试样一致。试验基于柔度法，具体试验过程与夹持式SENT试样一致。J积分的计算公式列于参考文献[9]。

另外，对于销轴式SENT试样，其中间平面的面内和面外约束参数A和V33由数值分析计算。将相关的A和V33代入式(6)，就可以得到本三维面内和面外约束相关的断裂力学方法所预测的J-R曲线，如图10所示。

(a)试验结果

从图(10)中可以看出，预测和试验测得的J-R曲线随着裂纹深度的增大而单调递减，浅裂纹试样(a/W=0.2)有着最低的约束状态，因此有最高的阻力曲线。同时，两种方法得到的阻力曲线，不仅趋势一致，具体数值也非常相近。以上结果再一次证明当前发展的面内和面外约束相关的断裂力学方法的准确性。

5 结论

基于对夹持式SENT试样的三维弹塑性数值分析，与16MND5钢断裂试验相结合，验证了所提出的面外约束参数V33在大尺度屈服下的适用性；同时，将V33与面内约束参数A相结合，发展了三维面内和面外约束相关的断裂力学方法(J-A-V33方法)；最后，建立了16MND5钢面内和面外约束相关的断裂性能函数，并成功预测销轴式SENT试样在不同裂纹深度下的J-R曲线。这一研究对含缺陷RPV结构的安全评定具有重要的意义。