考虑挡风板的车辆侧风效应研究

刘宏伟

(乌兰察布市公路管理局，乌兰察布 012000)

0 概述

车辆在行驶过程中的气流场特性十分复杂，包括湍流边界层、气流在车辆表面上分离和再附；在车辆的后部剪切层演变和转捩、分离涡等特征的流动现象。此外，当雷诺数(Reynolds number)较大时，车辆周围的流场呈现复杂的湍流状态，使得气流变化十分复杂[1]。这些特征流动对车辆空气动力学特性具有巨大影响，特别对安全行车具有决定性作用。

行驶车辆周围三维特征流场的研究已成交通安全领域的重要课题。特别是在横风环境中，车辆空气动力学特性取决于来流风向变化；同时，在风向变化条件下准确获取车辆气动力分布和变化以及车辆周围的特征风速场等。然而，与飞行器、潜水艇等交通设备相比，地面行驶车辆周围特征流场主要为顿体流动效应，包括分离、再附、转捩等现象，使得车辆气动特性愈发复杂。

高速公路上通常采用挡风板(windbreak fence，见图1)降低行驶车辆的横风效应。对挡风板、诸如植被屏障、多孔栅栏进行风致效应研究多用风洞试验和数值仿真的方法，为了降低仿真分析的计算消耗，通常将挡风板作为多孔介质处理[2-6]。达西定律(Darcy’s Law)是最早建立的用于描述穿过多孔介质的流动压降数学模型，该模型认为流经多孔介质的流体平均流体速度与压力梯度成正比，与流体动力粘度成反比[7]。然而，达西定律仅适用于粘性主导流动流问题，面向该缺陷，forchheimer[8]在达西模型基础上增加了惯性损失项。Joseph等[9]在forchheimer模型基础上又考虑惯性阻力影响，用以解决多孔介质导致的动量损失。

图1 公路挡风板示意图

本文采用ANSYS-FLUENT仿真平台结合darcy-forchheimer模型，给出车辆在不同路况条件下的几何模型、计算域、网格构造、边界条件等详细数据；基于该数值模型获取不同路况和挡风板下车辆气动力特性，为车辆在横风环境下安全行驶提供数值依据，为相应挡风板设计提供参考[10-12]。

1 数值方法

1.1 湍流模拟方法

ANSYS-FLUENT采用有限体积法求解平稳Navier-Stokes方程，采用剪应力输运SST模型求解湍流模型。由于湍流脉动的多尺度性质，高雷诺数湍流包含很宽的尺度范围，实现这种湍流的直接数值模拟需要巨量的网格数，也就是需要天文数字的计算机内存，于是一种湍流数值模拟方法被提出来，即大涡模拟方法。该方法通过过滤湍流运动，将湍流分解为可解尺度湍流(包含大尺度脉动)和不可解尺度湍流运动(包含小尺度脉动)，可解尺度湍流运动用数值计算方法直接求解。小尺度湍流脉动的质量、动量和能量输运对大尺度脉动的作用采用建立亚格子模型的方法，从而使可解尺度运动方程封闭。由于运动边界对小尺度脉动的影响较小，亚格子模型可能对广泛的复杂的湍流运动有较好的适用性。

通过在涡粘表达式中引入阻尼项，或在湍流模型中加入附加项(低雷诺数模型)，可在一定程度上改善涡粘模型的性能。但是这类方法会使湍流模型更依赖于初始条件和离散格式的选取，易造成非物理的流动现象，会降低计算稳定性。基于上述原因，研究人员提出k-ω模型以及剪应力输运(Shear Stress Transport，SST)k-ω模型来克服上述问题。

k-ω模型在保持湍动能的输运方程不变的前提下，以比耗散率ω(specific dissipation rate)的控制方程替代单位质量耗散率ε的控制方程，则稳态的k-ω控制方程为：

(1)

式中：σk,σω分别为控制方程的湍动能扩散系数和耗散率扩散系数，σk=1.0,σω=1.2；Gk为湍动能生成项；ρ为气流密度；k为湍动能；uj为风速分量；β*为常量，β*=0.09；xj为方向坐标；μ为气体粘性；μt为湍流粘度；α为描述低雷诺数特性的阻尼函数，在高雷诺数区，α=1，在低雷诺数区，其表达式为：

(2)

式中：Ret为雷诺数，Ret=ρk/μω；α∞，α0，Rω均为常数，α∞=0.52，α0=1/9，Rω=2.95；α*为湍流粘性阻尼函数，其表达式为：

(3)

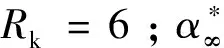
结合α*得到k-ω模型的湍流粘性μt表达式为：

(4)

k-ω模型对流动分离的计算效果优于k-ω系列模型，特别对于近壁流动的处理，模型本身可以考虑低雷诺数效应而无需采用壁面函数模型，从而保证模型的健壮性及稳定性。

对于边界层流动问题，标准k-ω对粘性子层和负压梯度的计算稳定性和准确性比较理想。但是，对于强负压梯度以及分离等流动现象的计算效果较差。为此，Menter等提出剪应力输运(Shear Stress Transport，SST)k-ω模型。所谓剪应力输运是指假定边界层内的湍流剪应力τ与湍动能k之间满足线性关系，即τ=a1ρk，a1为常数，再将其引入到涡粘假定中，得到SSTk-ω模型。其表达式为：

(5)

湍流粘度μt为：

(6)

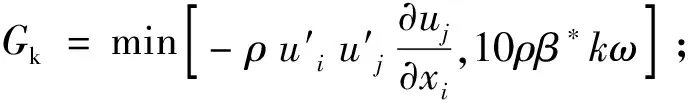
(7)

式中：

均为系数。

SST模型结合了k-ω模型和k-ω模型的优点，克服了标准k-ω模型的缺陷，使得该模型更适用于工程结构绕流研究。

1.2 边界条件

来流条件根据大气边界层气流分布特点，采用指数率剖面作为平均风来流u表达式：

(8)

式中：yref为参考高度；uref为该高度处的风速值；y为距地面高度；αr为地表粗糙类别参数；Yb,YG分别为不同粗糙类别对应的粗糙高度。

地表粗糙类别分为4类，地表粗糙类别参数αr如表1所示。

不同地面地表粗糙类别参数 表1

采用湍流强度I和湍流特征尺度L，T来表征大气边界层的湍流流动特性。基于RANS理论，可以将湍流特征量(k，ε及ω等)表示为湍流强度的函数，即可得到AIJ湍流来流条件。

(9)

大气湍流运动主要是由于地面粗糙元以及建构筑物的阻碍效应产生的。因此，湍流强度Iyr可以由下式确定：

(10)

结合指数律入口和规范对边界层湍流强度的定义，即可得到湍流来流条件表达式。基于k-ε系列模型，湍动能k可以表示为平均风来流u和湍流强度Iyr表达式的函数，即：

(11)

由湍流长度尺度Lyr和湍动能k可以得到耗散率ε的表达式：

(12)

式中Cμ为常数，Cμ=0.43。

综合上述表达式，可以得到SSTk-ω湍流模型的来流表达式为：

(13)

出口边界条件为采用压力出口边界，在流动分布的详细信息未知，但边界的压力值已知的情况下，使用恒压边界条件，在本文中取参考压力为一个大气压，假定垂直于出口方向的速度分量是零梯度的；流体域顶部和两侧为自由滑移的壁面条件；车体表面和地面为无滑移的壁面条件。

2 几何模型与数值模型

计算模型依据实际工程路面、车辆、挡风墙情况建立几何模型(图2，3)，并使用混合网格方案对整个流体区域进行划分。本文在计算过程中建立了全尺度模型(图4)，计算域尺寸为L(x)×L(y)×L(z)=110m×160m×60m，L(x)，L(y)，L(z)分别为车辆模型沿x，y，z方向的计算长度。图5为计算域网格细部网格。

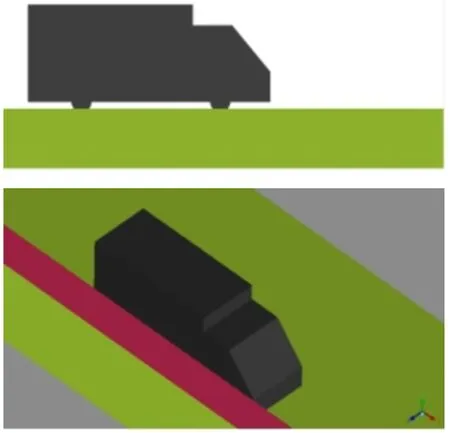
图2 车辆、道路与挡风墙模型

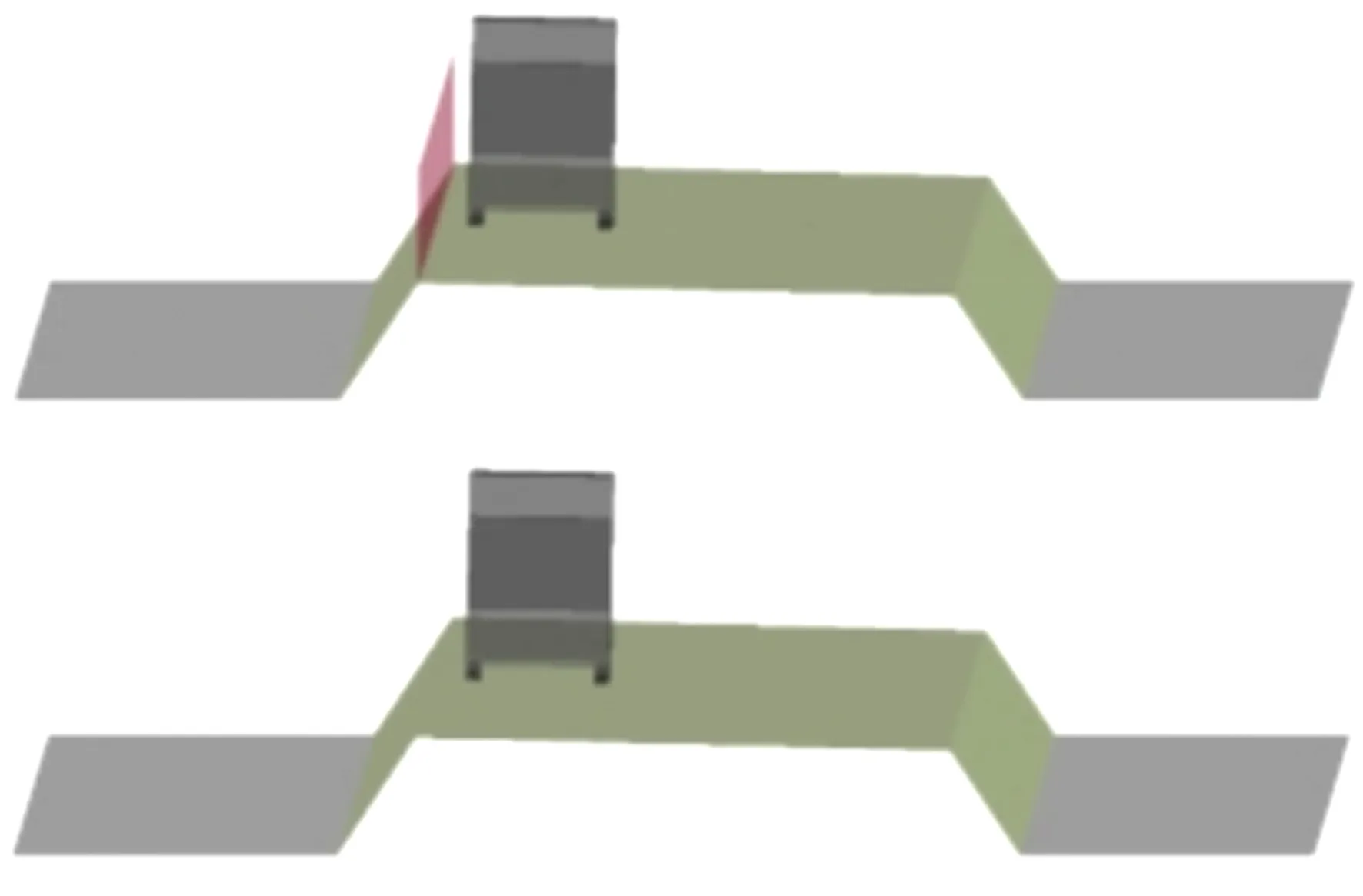
图3 车辆、路堤、道路与挡风墙模型

图4 计算模型具体布置

图5 车体细部网格

在生成网格过程中，由于该模型的形体比较高大，计算域比较广，使得网格划分变得十分困难。为此，在数值模拟中对车体以及周围流场采用非结构化网格，并且采用了渐变比为1.05以实现网格由疏到密的过渡，以保证计算不溢出，从而得到了质量较好的流体网格；对绕流外部的流场采用结构化六面体网格，在保证计算精度的前提下降低了计算量(图4，5)。为了保证计算精度，计算中将车体附近可能发生强烈流动变化的区域进行网格加密；为满足网格独立性要求，选取网格数量为1 780万混合网格方案。

3 仿真结果分析

为了分析横风作用下车辆在道路上行驶时的侧滑问题，由风产生的横向风力和升力的计算具有重要意义。考虑挡风墙的挡风效应，将有无挡风墙的车辆气动力分布进行对比。基于前述网格策略，在来流0°风向角下，分析车辆的气动升力和气动侧向力的特性。

3.1 无路堤条件下，无、有挡风板时车辆气动侧向力与升力

基于前述无路堤模型与网格策略，以车顶高度处风速为6.45m/s为参考风速，无、有挡风板时车身气动侧向力系数分别为0.855，0.483。图6为无路堤条件下，无挡风板和有挡风板时车辆气动侧向力云图。由图6可知，相比于无挡风板的工况，挡风板显著降低了车身上的侧向风力，确保车辆的在侧风条件下不出现滑移事故。

图6 无路堤条件下，无、有挡风板时车辆气动力分布

同样工况下，无、有挡风板时车顶上气动升力系数分别为-0.475，-0.860。相比于无挡风板的工况，尽管挡风板显著降低了车身上的侧向风力，但是由于顿体绕流的原因，气流绕过车身在车顶位置增大了升力数值，此时需根据轮上气动升力和车身气动升力综合考虑车辆的在侧风条件下的翻转事故的可能性。

3.2 有路堤条件下，无、有挡风板时车辆气动侧向力与升力

基于前述有路堤模型与网格策略，同样以6.45m/s为参考风速，无、有挡风板时车身气动侧向力系数分别为1.831，0.846。图7为有路堤条件下，无、有挡风板时车辆气动力分布。由图7可知，相比于无挡风板的工况，挡风板显著降低了53.8%车身上的侧向风力，然而与不考虑路堤工况相比，此时车身侧向力显著增大，主要是由于地面边界层风速沿高度变化增加了风速幅值，因此车身上侧向力幅值增大。尽管如此，考虑挡风板条件仍可以显著降低车身侧向力，确保车辆的在侧风条件下不出现滑移事故的可能性。

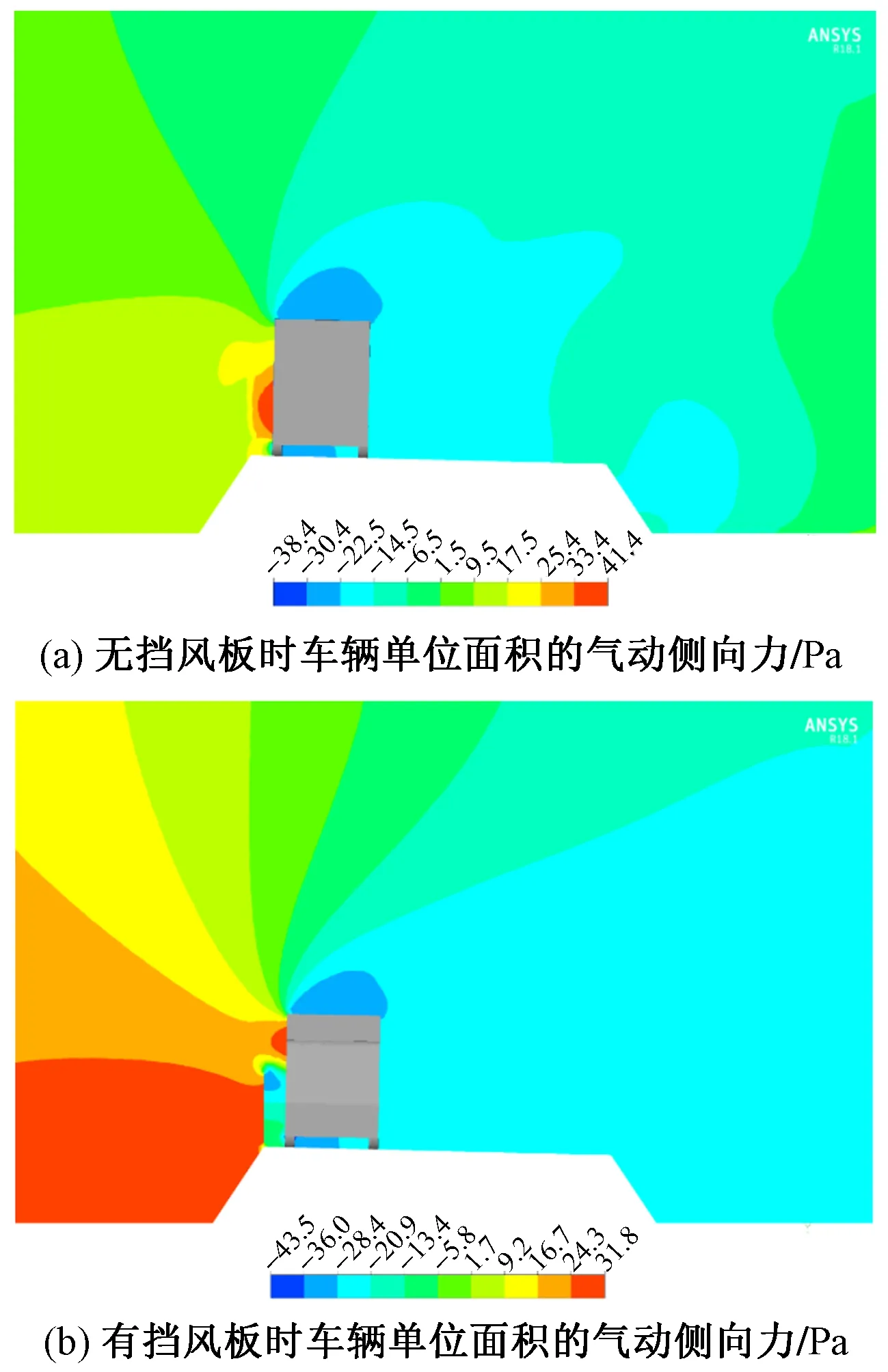
图7 有路堤条件下，无、有挡风板时车辆气动力分布

同样工况下，无、有挡风板时车顶上气动升力系数分别为-1.085，-1.267。由图7可知，相比于无挡风板的工况，尽管挡风板显著降低了车身上的侧向风力，但是由于车顶上方流速提高，整体涡尺度变大，因此车顶部升力系数提高16.7%，此时需根据轮上气动升力和车身气动升力综合考虑车辆的在侧风条件下的翻转事故的可能性。

3.3 有路堤条件下，挡风板分别为25%，50%透风率时车辆气动侧向力与升力

基于前述有路堤模型与网格策略，将全封闭挡风板改为25%和50%透风率的工况进行分析，挡风板采用Darcy-Forchheimer多孔模型进行仿真。同样以6.45m/s为参考风速，挡风板透风率分别为25%，50%时车身气动侧向力系数分别为1.423，1.439。图8为有路堤条件下，车辆附近气动力分布。由图8可知，考虑开洞的挡风板车身上的侧向风力接近；与有路堤无挡风板工况相比，挡风板透风率分别为25%，50%时车身侧向力分别降低22.3%，21.4%，可见，考虑挡风板作用仍可以显著降低车身侧向力，确保车辆的在侧风条件下不出现滑移事故。

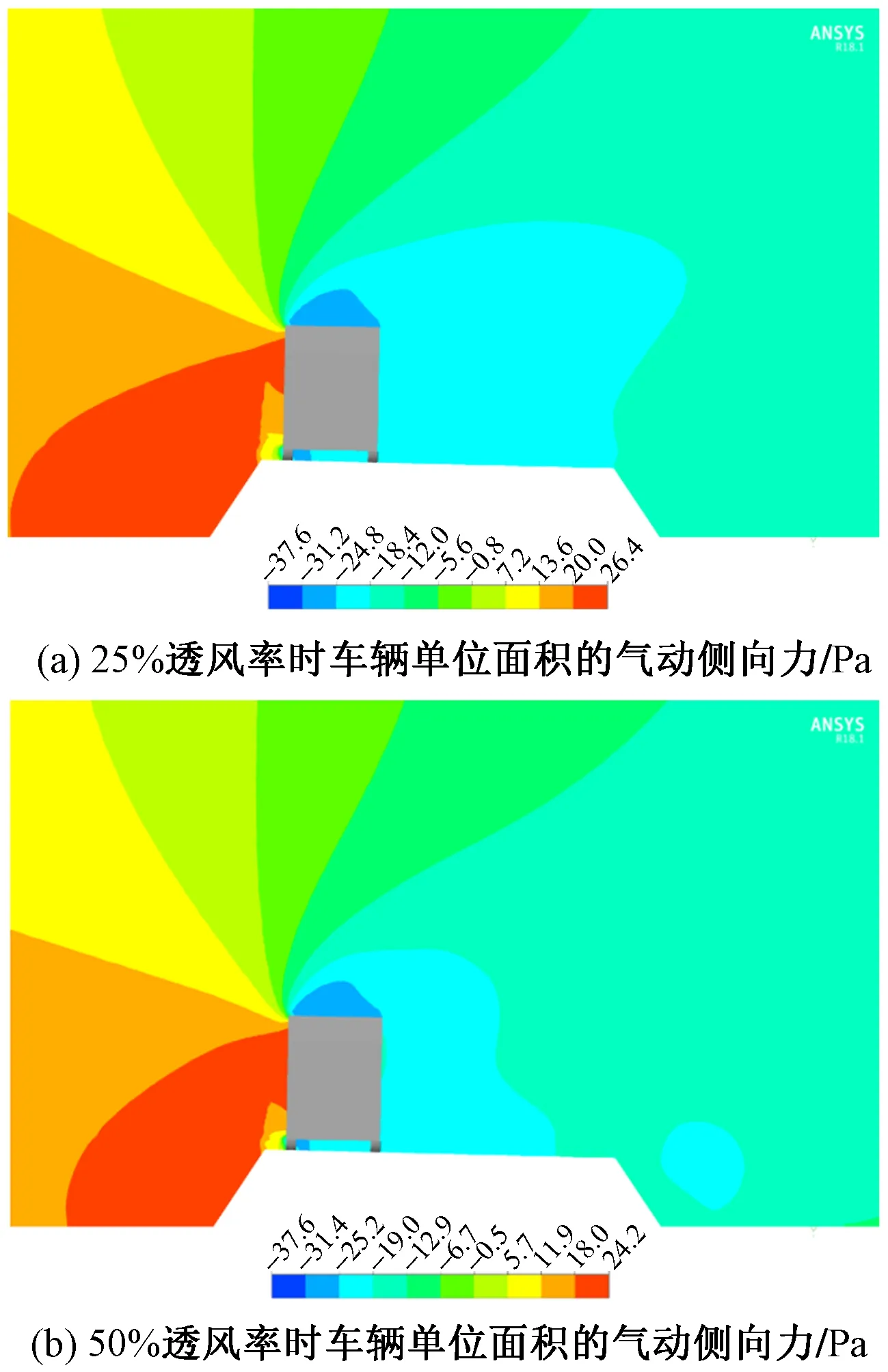
图8 有路堤条件下，挡风板透风率分别为25%，50%时车辆气动力分布

同样工况下，挡风板透风率分别为25%，50%时车顶上气动升力系数分别为-1.040，-1.055。由图8可知，相比于无挡风板的工况，开洞挡风板工况下车顶升力与无挡风板工况接近，透风率分别为25%，50%时比全挡板工况升力系数分别降低了17.9%，16.7%，可见，开洞挡风板在有效提高抵抗侧向风荷载作用的前提下，比全挡风板的气动升力更小，更能确保车辆的在侧风条件下避免翻转事故。

4 结语

研究发现，开孔挡风板的压降与粘性阻力呈二次方关系，与惯性阻力呈线性变化关系。采用开孔挡风板适用于公路行车的侧风安全性研究，特别当采用数值计算方法时，带有开孔的挡风板能够正确地捕捉流场与压力场的平均特性。需要注意的是，风场的脉动特性仍需高阶湍流模型进行模拟，特别对于来流具有强阵风特性时，还需考虑特征来流的能量分布与尺度特征；此外，对更大范围的挡风板孔隙率，特别是还需考虑植被、地势和地貌等因素的影响时，尽管多孔模型适用于此类问题的研究，但是仍需大量的风洞试验或数值计算确定孔隙率与对应粘性阻力和惯性阻力的关系。