基于dSPACE的工业机器人运动控制系统仿真分析及实验

路博凡, 韩家哺, 张艳伟

(上海工程技术大学 机械与汽车工程学院，上海 201620)

0 引 言

近些年来，越来越多的汽车工厂在一定精度工业生产[1]中开始用串联机器人打磨轮毂来代替人工打磨，做法有着低成本高效率等优点，所以对于串联机械臂控制的研发也是一种大趋势。之前在国内对串联机械臂以传统方法控制较多，是以求出六自由度的机器人的正解[2]、IPC+PMAC的控制方法在RTLinux上开发工业机器人的控制系统[3]。求解的逆利用仿生机器人[4],机器人进行运动学标定[5]、或是进行焊接路径的视觉识别与轨迹规划[6]用运行程序、停止程序运行以及反馈界面从而实现了实验平台的搭建[7]。但这种控制方法设计周期长成本高，现在使用Lapusan与Simulink的便利实现了，机器人的仿真模型和末端轨迹反映实验并借助 dSPACE 搭建了机器人的控制系统[8]。因为MATLAB/Simulink是同一家公司生产的所以可以在操作使用上无缝连接，通过 Simulink 建模仿真的方法模拟控制器，可以在现实开发中节约成本以及减少因为硬件配套而要重新开发驱动的时间从而缩短了串联机器人控制系统研发周期[9-10]。

在正常快速搭建控制模型的基础上对电机参数及机械臂的Simscape物理模型进行改进，从而得到更好的控制效果。

1 ER20-1700机器人的运动建模

ER20-1700机器人是国内市场上主流机械臂的一种，主要用于切割、打磨、上下料等场合，具有6个自由度，并且末端位置和姿态存在解耦关系。ER20-1700实物模型如图1所示。

图1 ER20-1700机器人结构

2 机器人运动学正逆解

2.1 确定机器人改进D-H参数

用改进D-H方法进行运动学建模，坐标系的X轴方向和连杆两端连接关节的公垂线共线，坐标系的Z轴方向和连杆所连接的左端关节的轴线共线，根据右手定则，来确定Y轴方向，然后连杆、连杆左端关节以及坐标系都是同一个编号i-1。ai-1为两个关节轴线之间的公垂线长度即连杆长度。di,θi描述了关节自身的运动状态，其中di被称为关节偏距，θi被称为关节转角。

图2为机器人的运动模型图，图中{O-XYZ}是机器人的基座标系，{ot-xtytzt}是机器人末端坐标，L0,L1,L2,L3,L4,Hb是对应机器人的连杆之间的距离，分别是50、270、70、299、78.5和321.5 mm,机器人的DH参数见表1。

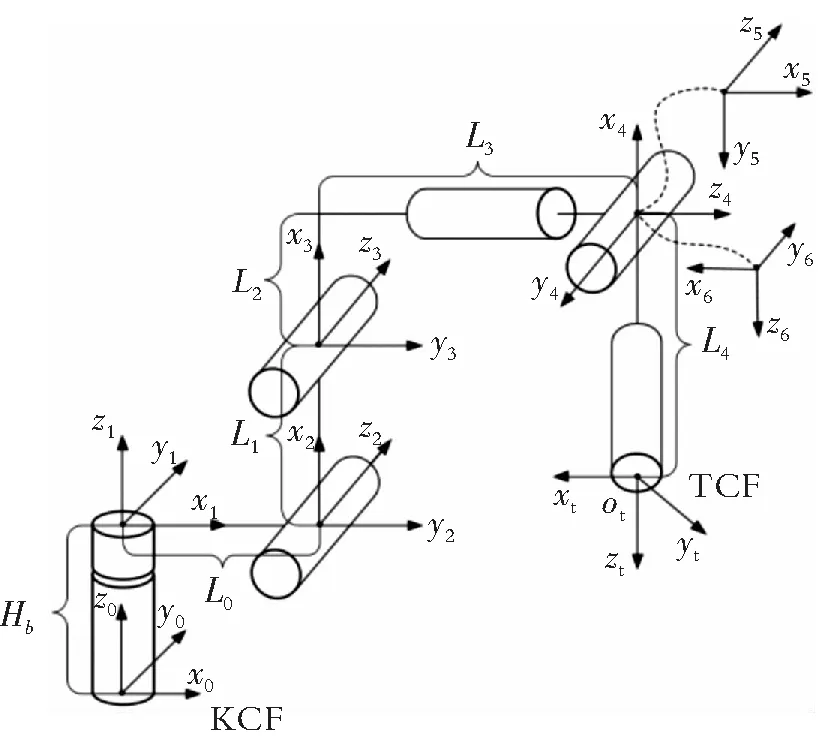
图2 机器人运动模型图

表1 机器人DH参数表

2.2 机器人运动学逆解

根据末端坐标系和基座标系之间的关系矩阵：

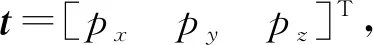
采用代数法来分析机器人的逆运动学。根据前面建立的机器人的MDH坐标图，可知机器人的4、5、6轴交于机器人末端的一个点，所以这3轴的变化不会影响该点的位置变化，因此可以先求解前3轴，再求解后3轴，求解步骤如下：

(1) 对θ1求解。

其中矩阵各元素的具体表达式为

这里ci,si，表示cos(ti)和sin(ti)的缩略形式，等式右边中第2行第4列元素为零，联立m24=pyc1-pxs1-L4ayc1+L4axs1可以解出θ1：

(2) 对θ3求解。

1T2-10T1-1T6Te-1=

在等式右边的结果中，选取和θ2相关的部分，分别是第1行第4个结果和第2行第4个结果：

c2m34+(m14-L0)s2=L1+L2c3-L3s3(m14-L0)c2-

s2m34=L3c3+L2s3

对上式进行平方相加整理可得：

A1c3+B1s3=C1

其中：

A1=37 800B1=-161 460

C1=2 500-100m14+m142+m342-167 201

β1=arctan(A1/B1)

θ3=±arcsin(C1/2.6*1010)-β1

(3) 求解θ2。

将求得的θ3结果代入下式

c2m34+(m14-L0)s2=L1+L2c3-L3s3

可以求得θ2其中：

(4) 求解θ4，θ5，θ6。

取MDH中变换矩阵的旋转部分R1～R6，这样可以构建等式：

R3-1R2-1R1-1R=R4R5R6

分别取等式两边矩阵中第3列，第1行和第3行的元素相除，可得：

当c5=0的时候，机器人第4轴和第6轴重合，机器人失去一个自由度，关节进入奇异位置，这是在规划机器人关节空间运动时需要避免的情况。

当cos(θ4)≠0的时候，可以利用R3-1R2-1R1-1R=R4R5R6等式中第3列第2行除以第3列第1行，解得θ5：

θ5=arctan(c4(axc23c1+ayc23s1-azs23)/

axs23c1+ays23s1+azc23)

当cos(θ4)=0的时候，可以利用R3-1R2-1R1-1R=R4R5R6中第3列第2行除以第3列第3行，解得θ5：

当c5=0时，可以充分利用R3-1R2-1R1-1R=R4R5R6中第二行第二列除以第二行第一列，解得θ6：

3 ER20-1700机器人控制系统设计

3.1 基于SimMechanic工具箱的机器人建模

首先将打开已经完成的三维建模装配体，注意关节之间的约束关系并在导入Matlab之前要尽量简化模型，使之保证导入的完整性和正确性。

(1) 在工具栏内点击Simscape Multibody Link内的Export来生成MATLAB可以读取的step和xml格式文件。

(2) 导出xml格式文件之后，在MATLAB命令窗口中输入指令:smimport；来生成Simscape物理模型。

(3) 将Torque设置为Automatically Computed，Motion设置为Provide By Input，将传感器的信号勾选作为输出。对于六自由机械臂而言，需要控制的是6个旋转坐标系，为了实现控制，对其内部属性进行修改。

关节1配置完后如图3所示。

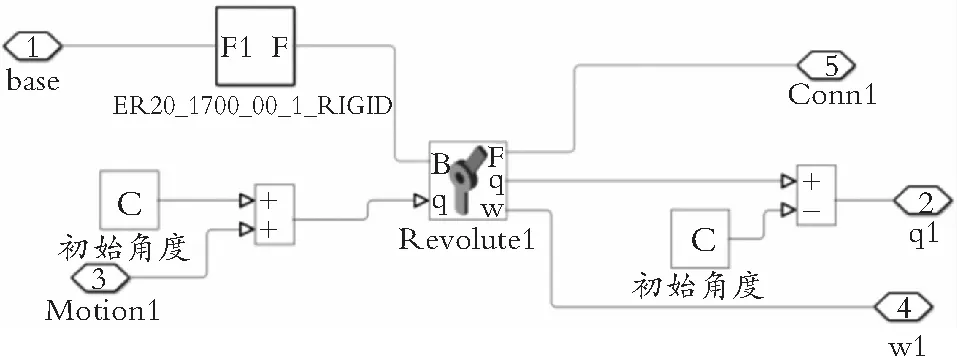
图3 关节1模型图

(4) 将每个Rotation配置成这样之后，就可以将外部的角度信号输入给机械臂Simscape模型中的每个关节,输出信号选择为角度值。配置完毕之后选中所有单击右键Creat Subsystem from Select将整个Simscape封装。改进后的机械臂Simscape物理模型如图4所示。

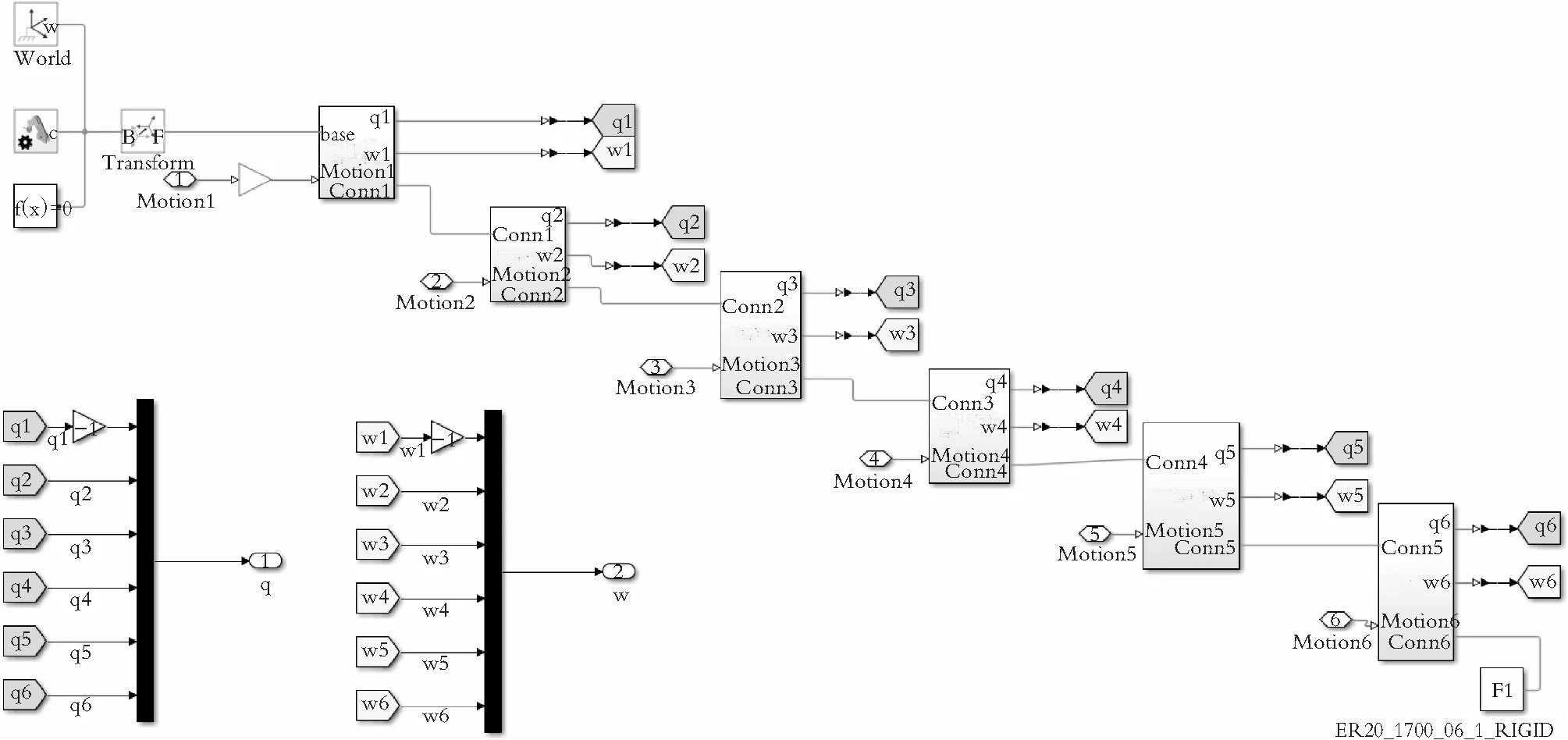
图4 改进后的机械臂Simscape物理模型

3.2 搭建电机驱动Simscape物理模型

因为在Simulink中步进电机模型输出的是位置信号并且不需要编码器来检测所以可以很好地满足角度输出的要求，并且给到的PWM信号通过步进电机模可以输出扭矩R。因此需要搭建步进电机模型。

(1) 在MATLAB命令窗口输入elec_motor_stepper指令直接创建步进电机模型。将默认输入给电机的阶跃信号改为Input1，再除上步距角1.8°得到步进电机的步数，再给到电机的控制器，将步数转化为对应的PWM信号。

(2) 为了让电机信号能够输出给各个关节，并且适应不同初始角度状态的Simscape，需要在电机的输出a后接PS-Simulink元件将电机的物理角度信号转换成Simulink的模拟值，修改后的电机模型如图5所示。

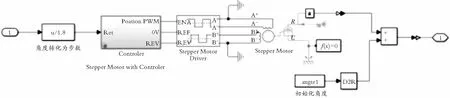
图5 改进后步进电机模型图

3.3 机械臂Simscape正逆解仿真

将上面两个模块进行封装整理后，并加入之前做好的机械臂的正解逆解算法。经整理后最终的仿真模型如图6所示。

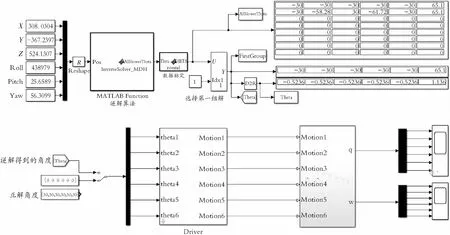
图6 机械臂仿真模型图

在模型下，在下方输入角度可以得到通过正解算法得到机器人末端的位置。在上方输入末端位置坐标可以使仿真模型中的机械臂转动相应角度。为验证其仿真的准确性，把之前的正逆解算法通过编程写入MATLAB的机器人工具箱中，出仿真结果。先验证正解的准确性同时输入各关节角度(-30,-60,100,-30,60,-30)与之前的仿真结果对比完全一致，如图7所示。

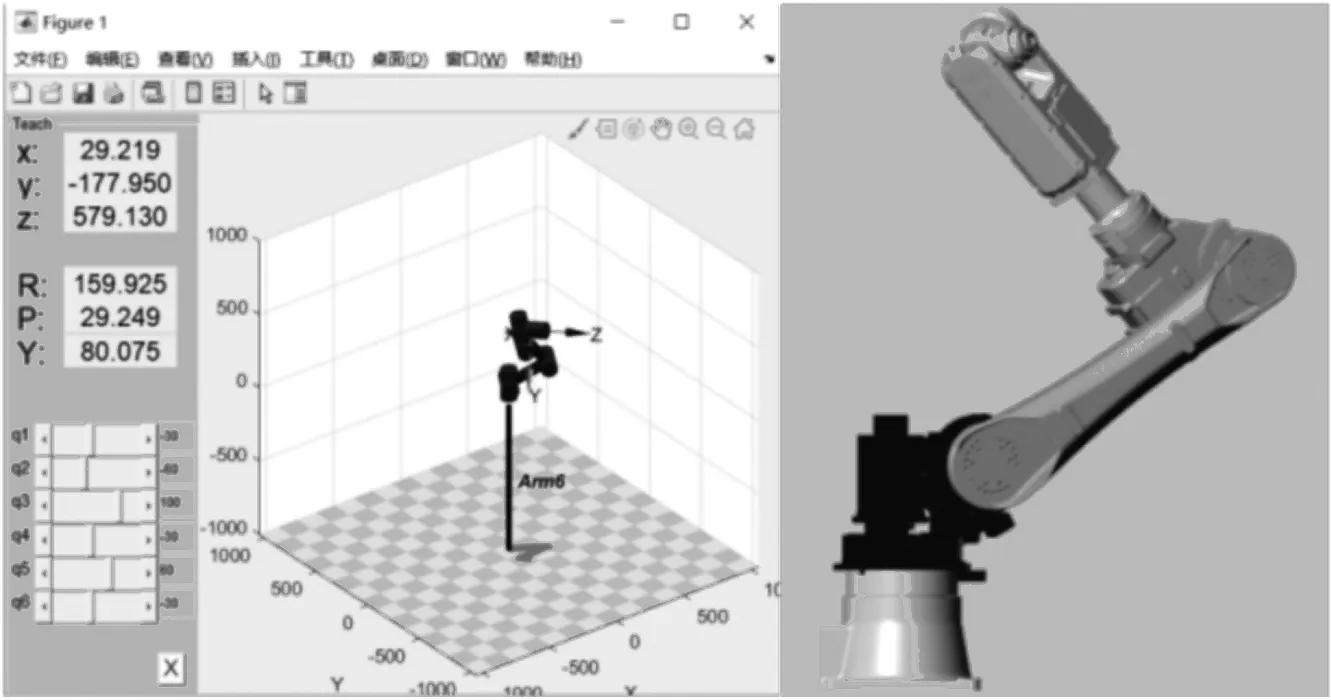
图7 仿真结果比对图

然后，再开始验证逆解准确性在仿真模型上端输入末端位置(x=29.219,y=-177.95,z=578.13,R=159.925,P=29.249,Y=80.075)然后可以通过模型中scope模块观察到各个关节旋转的角度，如图8所示。

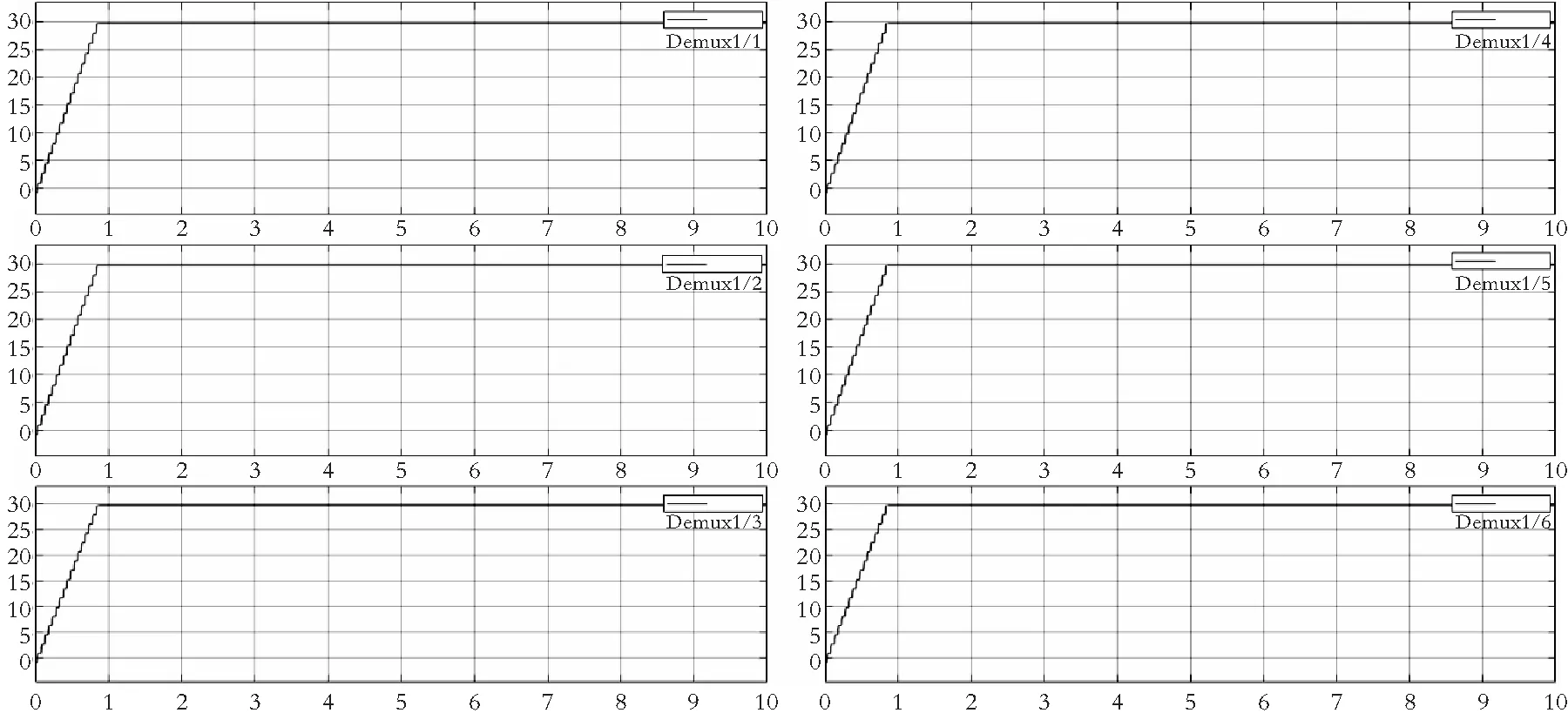
图8 各关节旋转角度仿真结果图

比对图7可得仿真模型在输入末端指令后的 2 s 内达到指定姿态。由图10可知关节1在1 s内达到-30度位置，关节2在2 s内达到-60度位置，关节3在2 s内达到100度位置，关节4在1 s内达到-30度位置，关节5在1 s内达到60度位置，关节6在1 s内达到-30度位置，于逆解运算结果保持一致。由此可得逆解算法正确。

3.4 机械臂的轨迹规划

在轨迹规划中，首先在MATLAB中运用编程建立机器人模型。定义轨迹规划中的初始关节角度(First_Theta)和终止关节角度(Final_Theta)并定义其步数为777。随后使用jtraj函数带入初始角度、终止角度和步数后，可以得到关于位置、速度和加速度的一个6*777的矩阵，随后把得到的数据用编程制成图像。可得机械臂运动时各关节的位置曲线、速度曲线和加速度曲线如图9所示。

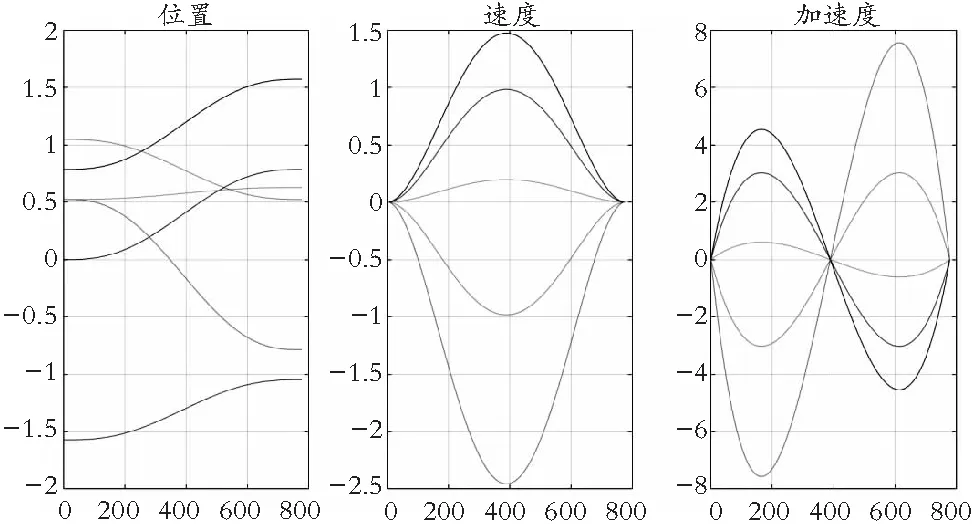
图9 各关节的位置曲线、速度曲线和加速度曲线图

然后通过之前计算的正运动学公式输入初始关节角度和终止关节角度可以得到起始和终止的位姿矩阵。接下来就利用ctraj在笛卡尔空间规划轨迹，在ctraj函数中输入步数起始和终止的位姿矩阵，就可以得到表示2点之间运动信息的齐次旋转矩阵，是一个6*777的矩阵，使用transl函数在齐次旋转矩阵中提取移动变量，相当于笛卡尔坐标系的点的位置。最后用编程的手段画出A1到A2直线和B2圆的轨迹,如图10所示。

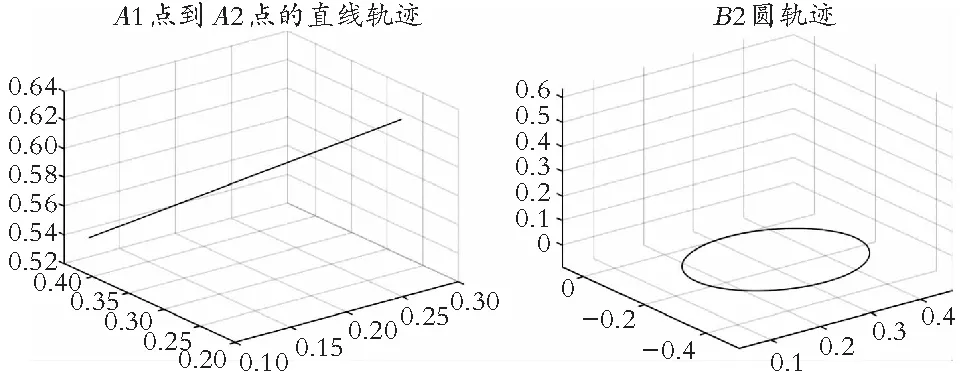
图10 A1到A2直线和B2圆轨迹图

4 实验平台的搭建与结果

4.1 实验设备介绍

实验平台由dSPACEDS1007组件系统，包含12个DA接口、12个编码器接口、2路RS422接口和24个IO接口;一台电机伺服驱动器、一块转接板、一台ER20-1700机械臂、紧急制动装置、一台pc控制台以及力矩传感器组成如图11所示。

图11 串联机器人实验平台图

4.2 实验过程与结果

由于Dspace和Simulink是由同一家公司生产的，所以可以直接把仿真环境下系统转化为程序导入其中。当在Simulink软件中编译好程序后，需要在Control Desk软件中进行调试和变量的读取。打开Control Desk软件后，先加载Simulink软件编译的sdf文件，然后可以看见一个调试界面，通过配置完以后的实验界面先控制机械臂以0.05 m/s的速度走完0.05 m长的直线再控制机械臂以0.025 m/s的速度走完半径为0.025 m的圆为观测其数值显示变量的历史变化轨迹，让灵活的触发式测量和多个控件同步比较。

如图12所示，给出了机械臂跟踪直线和圆时机械臂的关节误差。通过Dspace把实验数据导入MATLAB中制作成实验对比图。其中虚线是系统规划在x、y坐标系下走的路径，实线是机械臂在x、y坐标系下的实际移动距离。最大跟踪误差小于 3 mm。故证明了系统及方法的有效性。

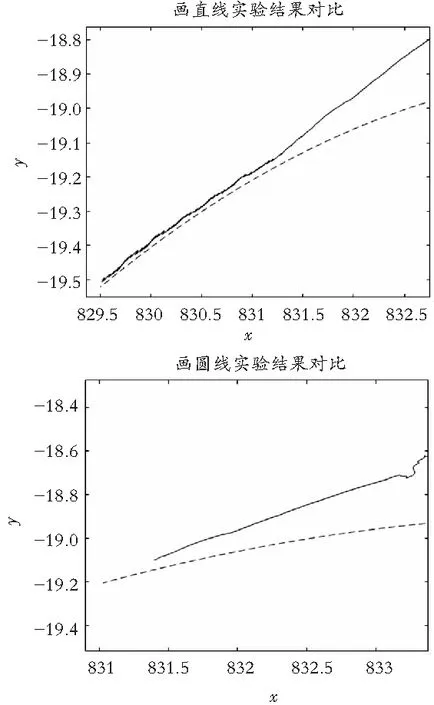
图12 走直线与圆实验结果对比图

5 结 论

从零搭建ER20-1700机器人的控制系统,先在 MATLAB/SIMULINK 中搭建仿真模型并进行仿真实验。 仿真结果表明,逆解算法搭建成功。再在进行实际实验，通过dSPACES进行走直线和画圆实验。实验结果表明最大跟踪误差小于3 mm，控制方法可行。