考虑边缘磁通的内磁式音圈电机磁路计算模型

何竞雄，杨 镜，赵全斌，李 雨，郑文鹏

(中国电子科技集团公司第二十一研究所，上海 200233)

0 引 言

音圈电机是一种特殊结构的直驱电机，它可以将直流电信号直接转化为动子的位移，不需要中间的机械传动结构[1]。得名“音圈”是因为这种电机的工作原理与扬声器类似，为洛伦兹力原理[2]。相较于传统的旋转电机传动系统，音圈电机省去了电机与负载间的转换机构，没有累积误差。它具有体积小、结构简单、动态响应速度快等优势[3-4]，在磁悬浮系统[5]、精密相机调焦[6]、微细电火花加工[7]等特殊应用场合具有广阔的应用前景。

从运动方式上分类，音圈电机可以分为旋转型和直线型。旋转型音圈电机因其较小的转矩波动和较高的控制精度常用于替代有限转角电机[8]。而对于精密定位、主动减震等应用场合常用的是直线型音圈电机，根据其磁路形式的不同，又可将直线型音圈电机分为内磁式和外磁式。相较于外磁式音圈电机，内磁式音圈电机磁路短，能够充分利用永磁体的磁力线[9]；并且，内磁式音圈电机采用圆柱形轴向充磁磁钢，相比于外磁式电机采用环形充磁磁钢，可以大幅降低电机的结构复杂度和加工周期。

针对音圈电机的磁场计算和综合设计，文献[10]和文献[11]通过有限元法对两种圆柱形音圈电机的结构进行了设计和优化。但是有限元方法需要占用大量的计算机资源，计算耗时长，不利于在电机初始设计阶段确定电机的主要尺寸。文献[12]基于高斯积分方法计算了一种圆柱形磁钢音圈电机的推力，相比于有限元法，该方法可以减少一定的计算时间。但是高斯积分方法作为一种数值计算方法，依然需要专业数学软件对高阶积分进行迭代运算。为了达到理想的精度，该方法的计算时间依然较长。

在计算机技术发展前，磁路计算是计算电机电磁性能的唯一选择。即使是在计算机软硬件性能非常强大的今天，磁路计算因有助于加深对电机物理现象的理解和快速的运算速度，依然吸引着国内外学者的注意力。文献[8]和文献[13]通过等效磁路法对一种旋转式音圈电机电磁性能进行了解析计算，由于在计算推力的过程中将气隙磁场等效成了均匀磁场，解析计算结果与有限元仿真结果有较大的偏差。

造成磁路计算方法不精确的主要原因是线圈所处的磁场计算不准确。如图1所示，线圈运动范围内的磁场分布并不均匀，除了气隙磁通外，位于定子外侧的边缘磁通对电机的推力有较为明显的影响。如果忽略边缘磁通，将线圈的磁场等效为匀强磁场，仅采用F=NBLI计算电机推力，则推力计算值与实际值的误差不可避免。

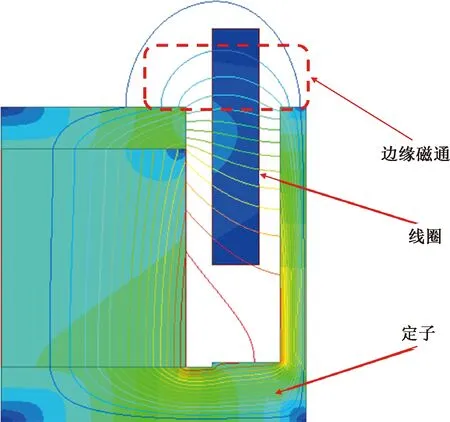
图1 边缘磁通示意图

因此，本文提出了一种改进的磁路计算方法，该方法考虑了边缘磁通对磁密和推力的影响。在研究了音圈电机的磁路特点后，作了必要的简化和等效。分别计算各支路的磁阻值，推导出了电机推力的解析表达式。由于采用磁路方法计算，有效缩短了电机的计算时间，降低了分析难度。本文以一台内磁式音圈电机为例，通过磁路计算结果与仿真结果和实测结果的比较，证明了上述方法的准确性。

1 内磁式音圈电机的结构与磁路模型

1.1 电机结构

本文研究的内磁式音圈电机结构如图2所示。电机由线圈组件、静铁心Ⅰ、磁钢和静铁心Ⅱ组成。线圈组件包含线圈和线圈骨架，组成了电机的动子，静铁心Ⅰ、磁钢和静铁心Ⅱ组成了电机的定子。线圈骨架为非导磁的铝合金材料制作，静铁心Ⅰ和静铁心Ⅱ采用高饱和磁密的1J22铁钴钒合金，磁钢为轴向充磁。线圈通电后因为洛伦兹力的作用电机将在轴向产生推力。

图2 内磁式音圈电机结构

根据内磁式音圈电机的三维结构，本文对该电机进行了参数化建模，如图3所示。对应电机的主要参数如表1所示。

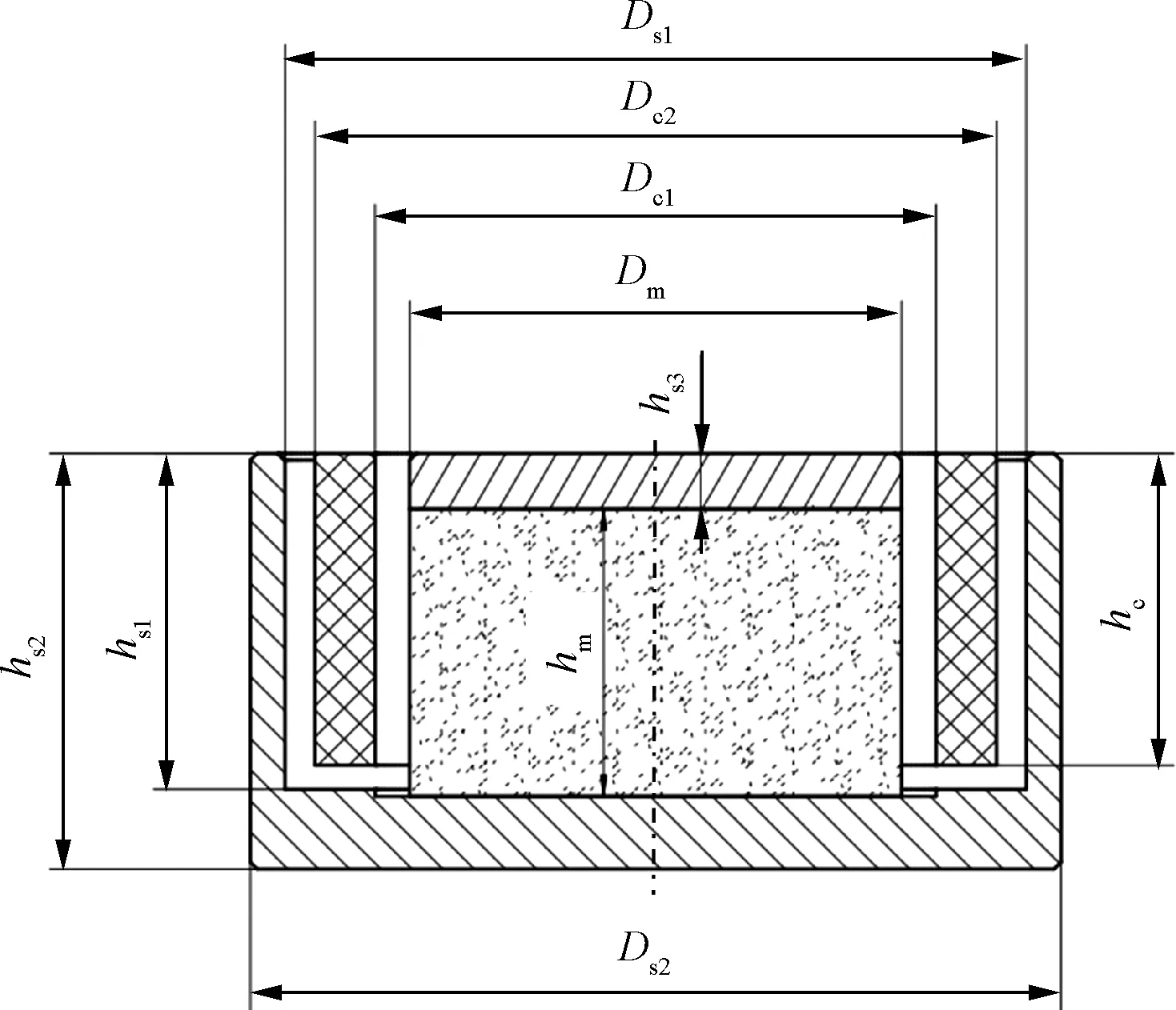
图3 电机的参数化模型

表1 电机主要参数

1.2 电机磁路模型

本文研究的电机在圆周方向上具有高度的对称性，在构建磁路模型时可以对电机结构进行简化。根据二维模型的磁场分布规律，考虑边缘磁阻后可以得到空载情况下电机的等效磁路图，如图4所示。

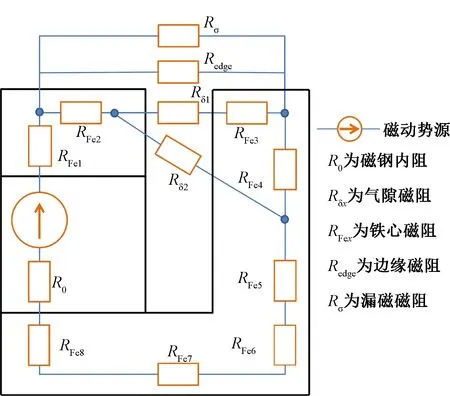
图4 电机的二维等效磁路图

磁路和电路具有相似性，因此可以根据磁路的基尔霍夫定律推导出各个支路磁通的表达式。1J22铁钴钒合金材料的磁导率远大于磁钢和空气的磁导率，在计算磁路时可以忽略所有的铁心磁阻。另外，气隙磁阻可以等效为一个整体。即图4中的RFex均为零，Rδ1和Rδ2等效为Rδ，磁路得以简化。在磁路计算前，需要分析电机的工作状态：

1)电机的磁轭部分采用高饱和磁密的1J22材料，该材料的饱和磁通密度可以达到2.2 T以上。电机在电磁设计时留有充分裕量，故不考虑饱和对磁路的影响，将磁路近似为线性。

2)由于电机额定工作点的电流很小，仅有0.6 A，加上该结构的气隙较大，故不考虑电枢反应对磁路的影响。

2 磁路分析

2.1 磁阻单元的等效

在进行磁阻模型计算时，通常会将磁阻单元划分等效为三种基本形状，分别为矩形、梯形和扇环形，如图5所示。多数磁导单元都可以方便地通过基本磁导公式直接计算。例如，磁钢内阻R0可以参考图5(a)的矩形单元，将矩形的底面转换为圆形底面即可。而气隙磁阻Rδ则可以直接等效为图5(b)的梯形径向磁路磁阻单元。

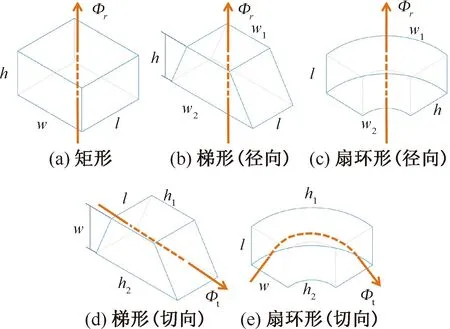
图5 常用的基本磁阻单元

矩形单元的磁阻RR可以通过式(1)计算：

(1)

式中：μ表示磁阻单元的绝对磁导率。

梯形单元和扇环形单元的径向磁路磁阻Rr和切向磁路磁阻Rt的计算公式分别如下[14]：

(2)

本文的研究重点是边缘磁通对内磁式音圈电机推力的影响，因此在磁路计算时需要特别注意边缘磁阻的等效计算方法。定子外侧的磁场分布十分复杂，虽然静铁心Ⅰ的直径远大于静铁心Ⅱ的外壁厚度，但实际上从静铁心Ⅰ出发能够经铁心外侧进入到静铁心Ⅱ并与线圈交链的磁通是有限的。为了简化计算，可以将与线圈交链的部分磁通等效为图5(e)的扇环形切向磁路，而不与线圈交链的部分以漏磁计算。边缘磁通的等效过程如图6所示。

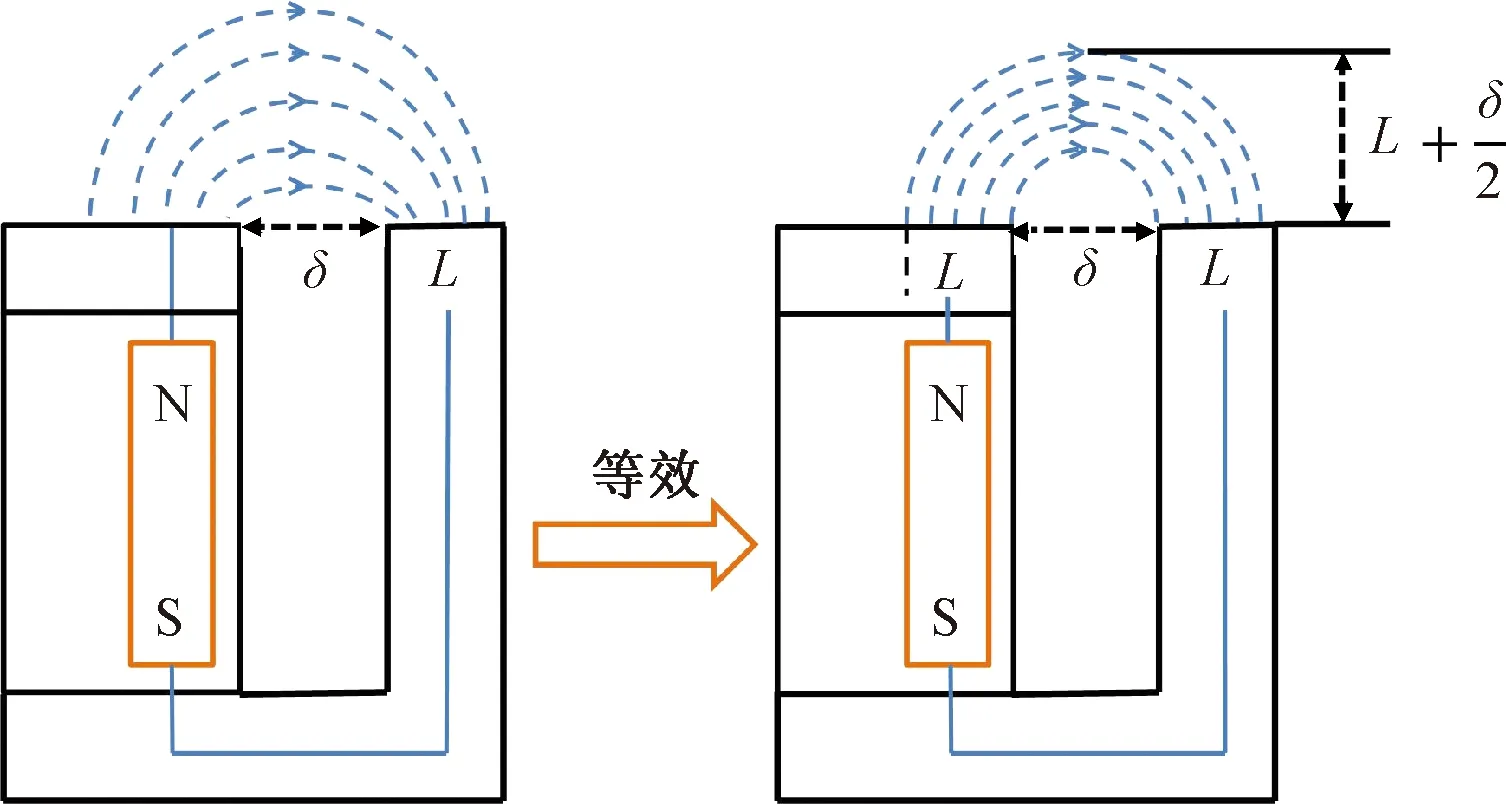
图6 边缘磁通的等效

图6中，δ和L表示电机的气隙长度和静铁心Ⅱ外壁厚度，分别可以由式(3)和式(4)计算：

(3)

(4)

2.2 电机磁路计算

2.2.1 磁阻计算

根据图3的参数化模型，用式(1)和式(2)计算磁路中的各个磁阻单元的阻值。根据磁钢的充磁方向可知，磁钢的充磁面积Sm：

(5)

根据式(1)的通用磁阻表达式，可以计算出磁钢内阻R0：

(6)

由图6的简化模型可知，边缘磁阻Redge的横截面为扇环形，磁通方向为切向。而对于磁阻的有效长度，则需要利用近似方法。参考文献[14]提出的扇环形单元切向磁通计算方法，结合式(2)计算得到边缘磁阻Redge如下：

(7)

气隙部分的磁阻Rδ则可以等效为梯形磁阻单元，磁路方向为径向。梯形单元的上下表面可以分别用电机静铁心Ⅰ的外侧面S1和静铁心Ⅱ的内侧面S2表示，S1和S2的计算式如式(8)，利用式(2)计算气隙磁阻Rδ可由式(9)表示：

(8)

(9)

计算漏磁磁阻Rσ时，因为定子外的一部分磁通以边缘磁通计算，漏磁系数不应选得过高。本磁路中取漏磁系数σ=1.1，则有：

(10)

2.2.2 磁通密度计算

电机的等效磁路模型中磁动势仅由永磁体产生，故磁路中的磁动势Fm可以由式(11)表示。进而可以求出电机等效磁路模型中的总磁通Φ：

Fm=HcBhm

(11)

(12)

由式(11)和式(12)可以进一步求出气隙磁通Φδ和边缘磁通Φedge，分别如下：

(13)

(14)

在计算线圈运动位置处的磁通密度前，需要将各处磁通的截面积进行一定的近似等效[15]。计算线圈边的平均有效长度Lc可以近似：

(15)

则气隙磁密Bδ和边缘磁密Bedge分别如下：

(16)

2.2.3 推力计算

设电机动子的轴向位移为x，定义初始状态线圈的上沿与静铁心Ⅰ的上表面平齐，即图3的状态，在该状态下x=0。由于边缘磁通的影响，电机线圈所处的磁场并不均匀。根据电机动子的运动方式，线圈的轴向中点从初始位置运动至静铁心Ⅰ附近时，随着穿过线圈的磁通增加，电机的推力不断增加。当电机的位移超过这个值时，由于线圈的有效匝数减少，电机的推力会逐渐减小。因此，可以推导出本文研究的内磁式音圈电机静态推力与轴向位移x的函数关系如下：

(17)

式中：KI为修正系数，本文取KI=0.75。

将式(17)的分段函数表示为统一的推力表达式，可得：

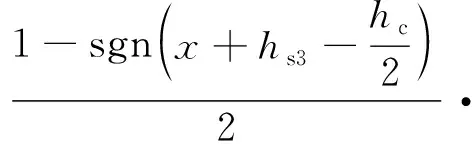
(18)

3 仿真和实验验证

3.1 仿真验证

本文在ANSYS EM 18.0软件中搭建了表1的内磁式音圈电机的二维有限元仿真模型。由于电机的尺寸较小，不宜采用自适应网格剖分。为了使仿真达到足够的计算精度，铁心和磁钢的最大单元边长取0.5 mm，线圈和气隙的最大单元边长取0.3 mm。二维有限元仿真模型和磁场仿真结果如图7所示。

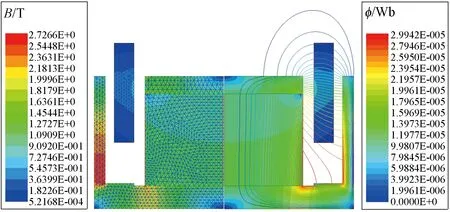
图7 二维有限元仿真模型

为了验证改进磁路模型对电机推力计算的准确性，分别给定子绕组通入0.4 A、0.5 A、0.6 A、0.7 A的直流激励。在不同的动子位移下，分别将本文的改进磁路计算模型、传统磁路计算模型和有限元仿真得到的推力曲线进行对比，对比结果如图8所示。

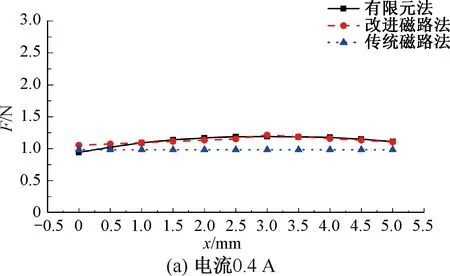
图8 推力的对比验证

由图8可知，传统的磁路计算模型仅考虑了气隙磁通，电机推力随动子位移的变化近似为一条直线。传统模型在动子初始状态下吻合度较好，但是随着动子位移的增加，计算误差会逐渐增大，不能反映出电机实际推力的变化趋势。而本文的改进磁路模型由于考虑了边缘磁通，相较于传统的磁路计算模型可以较准确地反映出内磁式音圈电机随着动子位移的增加，推力先增大后减小的电磁特性，在电机动子的有效位移范围内有较高的吻合度。

传统磁路法的计算结果与有限元仿真结果的平均误差达到了12.8%，而改进磁路法的平均误差仅有2.8%。结果证明本文的改进磁路法相比于传统磁路法在计算精度上有较大的提升。

3.2 实验验证

音圈电机的推力测量实验平台如图9所示，样机通过工装与弹簧拉压试验机相连。固定完毕后用直流电源给电机的绕组通入给定电流，电流值为0.6 A。通过调整测试仪的高度即可调整电机动子的位移。电机推力可由测试仪上的传感器示数读出。

图12 推力测量实验平台

为了消除电机加工误差的影响，本文加工制造了5台样机。样机的结构尺寸相同，采用相同的方法测试了5台电机在不同动子位移下的推力，并与有限元法和改进磁路法的结果进行比较。实验结果如表2所示。

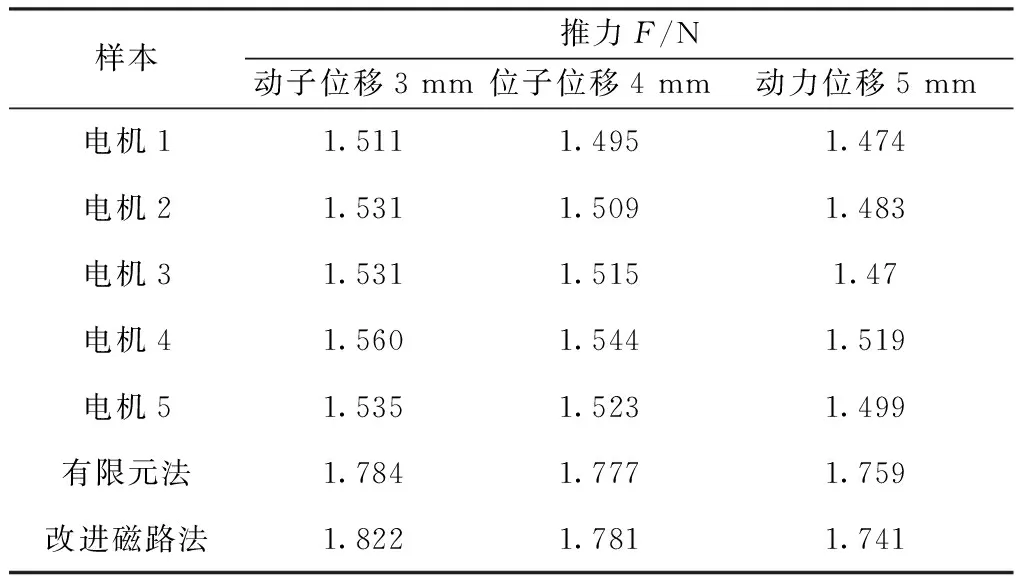
表2 不同动力位移时的推力实验结果

3.3 误差分析

由表2的实验结果可知，5台样机推力的一致性较好。推力和动子位移的变化趋势与有限元法和改进磁路法相同，但是推力值有一定的误差。经过分析，造成推力误差的原因主要有：

1) 电机磁钢的充磁并不完全，磁钢实际的剩磁与矫顽力和计算时使用的参数有一定的误差。

2)实验测量平台是通过测量电机动子对测试仪上的应力得到电机的推力值。由于推力值较小，测量结果与实际值存在一定的误差。

3)电机本体的尺寸较小，在安装时的机械公差会造成定子和动子的偏心，即动子线圈和磁钢中心有微小的偏差。该偏差也会造成电机的推力与仿真结果和计算结果有误差。

4 结 语

本文针对内磁式音圈电机推力的快速建模计算问题，综合考虑了该类型电机轴向充磁以及气隙磁场分布不均匀的特点，重点研究了边缘磁通对电机推力的影响，并对一种内磁式音圈电机的推力特性进行了分析，得出以下结论：

1)通过对内磁式音圈电机结构特点和电磁特性的分析，提出了一种磁路模型的等效建立方法，该方法考虑了边缘磁通，实现了不同动子位移和电枢电流下电机推力的快速计算。相比于传统的磁路计算模型，改进后的磁路模型保证了较高的计算精度。

2)与二维有限元模型相比，磁路模型建模阶段的时间较长，但是在计算阶段能够节省大量时间。

3)小型音圈电机的推力值普遍较小，实验平台的误差会被放大。采用弹簧拉压试验机测试微型电机的推力时，精度较低。更高精度的电机推力测试方法需要进一步研究。

4)电机定子和动子的偏心问题同样会造成一定的实验误差，特别是在小尺寸音圈电机上这种误差会被放大。如何在解析模型中考虑偏心的影响有待深入研究。