二阶常系数非齐次线性微分方程特解

鲁 琦

(蚌埠学院 数理学院,安徽 蚌埠 233030)

0 引言及预备知识

通常会用y″+py′+qy=0的通解与py′+qy=f(x)的特解合并表示y″+py′+qy=f(x)的通解,即全体解.特解往往随着f(x)形式的复杂而变得难以求出.

在文献[1]中,作者基于待定系数法,给出f(x)为2种特殊形式的方程的特解求法.按文献[1]中对形如f(x)=eλxPm(x)方程的分析,其中Pm(x)是m次多项式,可假设特解是y*=R(x)eλx, 则由文献[1]可知,形如方程y″+py′+qy=eλxPm(x)的特解归结为研究2个多项式的相等,即

R″(x)+(2λ+p)R′(x)+

(λ2+pλ+q)R(x)=Pm(x).

(1)

再依据λ和特征方程的关系,即是不是特征方程的根、或者是单根、复根等情形,推出相应的特解形式.文献[2]对f(x)的几种类型,介绍了升降法、公式法和拼凑法解法.文献[3]基于多项式之间相等的定义,对f(x)=aeλx,f(x)=(ax+b)eλx等形式的方程给出了比教材更加简洁的方法. 文献[4-7]的结果丰富了二阶线性微分方程的相关研究成果.

本文将y″+py′+qy=eλxPm(x)作为主要研究对象,分析文献[1]中对形如f(x)=eλxPm(x)的方程特解所作假设的合理性,并证明了按文献[1]中假设,最终求出的特解有且只有一个.

1 引例

下面将通过微分方程y″-5y′+6y=xe2x来讨论其特解形式.

假设特解形式为y*=R(x)e2x,由于y*=R(x)e2x满足y″-5y′+6y=xe2x,将其代入方程,注意到λ=2是特征方程r2-5r+6=0的根(且为单根),结合式(1),整理可得R″(x)-R′(x)=x,所以R′(x)是一次多项式,从而R(x)是二次多项式.

按文献[1]中所作分析及假设,可令特解为y*=R(x)e2x=xR1(x)e2x,此时

R(x)=xR1(x).

(2)

故对上例,可令R(x)=xR1(x)=x(b0x+b1),其中R1(x)=b0x+b1按文献[1]中例2,即可求出特解.

然而,R(x)作为二次多项式,一般包含常数项.假设R(x)=ax2+bx+c,利用代数基本定理可得R(x)有2个复根,分别记为x1和x2,故可得

R(x)=a(x-x1)(x-x2)=

(x-x1)a(x-x2)=(x-x1)R1(x)，

(3)

其中:R1(x)=a(x-x2).

对比式(2)和(3),不难发现,式(2)需求出2个未知量,式(3)则需求出3个.

另一方面,对于本例,考虑到R′(x)是一次多项式,可设R′(x)=ax+b,则R″(x)=a,得-ax+(a-b)=x,解得a=b=-1,故可得R′(x)=-x-1.利用微积分相关知识,求得R(x)为

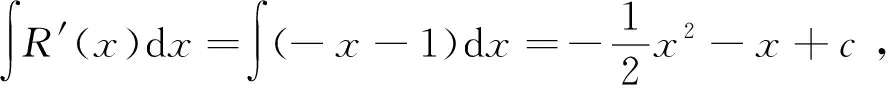
(4)

R(x)=xR1(x).

从上述例子的分析可以看出,一般特解的选取不唯一,而按文献[1]的方法,所得特解却只有一个.文献[1]中从R(x)=xR1(x)的假设出发,求出的R(x)无常数项,求得对应的特解也满足原方程,且相当于在式(4)中c=0时的情形.对于文献[1]中不出现常数项的假设方法,是不是广泛适用,下文将对其进行证明.

2 y″+py′+qy=eλxPm(x)特解

仅讨论λ是特征方程单根的情形,复根的情形可作类似分析.当λ是特征方程的单根时,R′(x)是m次多项式,此时R(x)是m+1次多项式.一般考虑到R(x)比R′(x)次数多1,需令R(x)=(ax+b)Rm(x),而文献[1]中为减少未知量的个数,令R(x)=xRm(x),相比令R(x)=(ax+b)Rm(x),减少了未知量个数,计算相对简便.从前例的分析也可看出文献[1]的假设具有可行性.下面对所作假设R(x)=xRm(x)的合理性进行证明.

设Pm(x)=a0xm+a1xm-1+…+am,若满足λ2+pλ+q=0.现令R(x)=xRm(x),可以得出

y*=eλxR(x)=eλxxRm(x)=eλxx(b0xm+

b1xm-1+…+bm)=eλx(b0xm+1+b1xm+…+bmx),

其中Rm(x)=b0xm+b1xm-1+…+bm.

(y*)′=eλx{λ(b0xm+1+b1xm+…+bmx)+[(m+1)b0xm+mb1xm-1+…+bm]}

(y*)″=eλx{λ2(b0xm+1+b1xm+…+bmx)+

2λ[(m+1)b0xm+mb1xm-1+…+bm]+

通常情况下深基坑支护工程的施工环节较多，其中包括：地质土方挖掘-边坡稳定调整-混凝土放点成孔-灌浆注浆-混凝土养护技术等等。想要确保各类型施工技术能够有良好应用环境条件，就需要勘查人员在实践中做好地质探测工作，为下一步计划提供基础数据支持，我国幅员辽阔，所以各地区地质条件有明显区别，因此在勘查工作进行时一定要结合当地实际情况，确认建筑分布，以免造成不必要的永久性影响。

[(m+1)mb0xm-1+m(m-1)b1xm-2+…+2bm-1]}.

将上述(y*)″,(y*)′,y*及eλxPm(x)代入方程y″+py′+qy=eλxPm(x),得

λ2b0xm+1+λ2b1xm+λ2b2xm-1+λ2b3xm-2+…+λ2bm-1x2+λ2bmx+2λ(m+1)b0xm+2λmb1xm-1+2λ(m-1)b2xm-2+…+ 2λ3bm-2x2+2λ2bm-1x+2λbm+ (m+1)mb0xm-1+m(m-1)b1xm-2+…+4·3bm-3x2+ 3·2bm-2x+2bm-1+λpb0xm+1+λpb1xm+λpb2xm-1+λpb3xm-2+…+λpbm-1x2+λpbmx+p(m+1)b0xm+pmb1xm-1+p(m-1)b2xm-2+…+p·3bm-2x2+p·2bm-1x+pbm+qb0xm+1+qb1xm+qb2xm-1+qb3xm-2+…+qbm-1x2+qbmx=a0xm+a1xm-1+a2xm-2+…+am-2x2+am-1x+am.

利用多项式相等的定义,可得如下等式,即

(λ2+λp+q)b0=0,

(2λ+p)(m+1)b0+(λ2+λp+q)b1=a0,

(m+1)mb0+(2λ+p)mb1+(λ2+λp+

q)b2=a1m(m-1)b1+(2λ+p)(m-1)b2+

…

4·3bm-3+(2λ+p)·3bm-2+(λ2+λp+q)bm-1=am-23·2bm-2+(2λ+p)·2bm-1+(λ2+λp+q)bm=am-12bm-1+(2λ+p)·bm=am.

(5)

注意到λ2+pλ+q=0,上面的第一个等式对b0为任意数显然成立.把第二个等式至最后一个等式联立成一个m+1元线性方程组,若可解出b0,b1,…,bm,就可以定出特解y*.从而说明从最初的假设R(x)=xRm(x)出发,是可以解出满足方程的相应结果,因此有其合理性.下面证明上述m+1元线性方程组有解,且解是唯一的.

将式(5)中除第一个方程外的其他方程合并写成矩阵形式(注意此时λ2+pλ+q=0),可得,

因为A为下三角矩阵,所以|A|=(2λ+p)m+1.(m+1)!.再由λ是特征方程的单根可得2λ+p≠0,故|A|≠0,即A可逆.进而可得b=A-1a.因此,由逆矩阵的唯一性可知上述方法得到的b是唯一的,即b0,b1,…,bm是唯一的,故相应的特解有且只有一个.