基于极限平衡理论的滑坡稳定性分析

郑志威，张莉丽，代一鸣，王仁龙，张耀文

（1.防灾科技学院，河北三河 065201；2.北京市地质矿产勘查开发总公司四川分公司，四川成都 610051；3.河北省地震动力学重点实验室，河北三河 065201）

0 引言

我国幅员辽阔，地貌、地质构造多样，自然以及人为因素都会造成地质灾害频发［1］，尤其是雨水充沛的南部地区尤为严重。因此滑坡的稳定性问题一直是工程上的热点问题之一［2］。1916年K.E.Pettersson最先提出计算滑坡稳定性的基本思想——条分法［3］，胡尔顿在其基础上提出了瑞典圆弧法［4］。1927年，Fellenius将摩擦力和黏聚力作为主要的影响因素分析边坡稳定性，探索出了滑动过程变化的规律［5］。Janbu改进了瑞典圆弧法，提出了适用于任意形状滑坡稳定性计算方法——普通条分法，也称为Janbu法［6］。A.W.Bishop［7］在Janbu法的基础上进行进一步的研究和完善，提出了土坡稳定安全系数的概念，这便是 Bishop 法。 二十世纪六七十年代，Morgenstern-Prce 法［8］、Spencer 法［9］、Sarma法［10］及Baker-Garber临界滑面法［11］等极限平衡法相继被提出来，极限平衡理论已经逐步发展成为了一套成熟的边坡稳定性分析理论。目前，常用的滑坡稳定性的分析方法是极限平衡法和有限单元法［12］，尤其基于极限平衡法的传递系数法在我国的工程界被广泛的应用。苏爱军［13］对滑坡稳定性的传递系数计算法进行了改进，何木［14］基于方向角的修正改进了传递系数法等。近几十年来各位专家学者们对滑坡的研究更加深入，已经能将实际情况与理论有机结合起来［15］，并取得了丰硕的成果［16-20］。

本文以眉山渡槽村螃蟹堰滑坡为例，在研究滑坡工程地质条件的基础上，对该滑坡的变形特征及成因展开分析研究，并进行天然、暴雨、地震等工况下的计算及稳定性分析，为今后类似边坡工程的滑坡治理提供参考。

1 研究区概况

眉山渡槽村螃蟹堰滑坡位于四川省眉山市仁寿县黑龙滩镇渡槽村，地理坐标为（104°04′01.24″E，30°08′39.40″N），距离仁寿县城区约35km。滑坡前缘有国道老G213线横跨。研究区属侵蚀构造低山区，微地貌属斜坡地形，坡向约255°，坡面形态为陡折线型，总体地形坡度约20°～25°。滑坡位于斜坡中上部，平均地形坡度约25°～30°，斜坡中下部老G213公路横贯，路堑开挖和前人采石活动呈陡坡，临空条件发育，为滑坡的发育提供了地形地貌基础条件，滑坡全貌如图1所示。

图1 螃蟹堰滑坡全貌图Fig.1 Overall view of Crab W eir landslide

研究区上覆第四系全新统残坡积、第四系全新统滑坡堆积以及侏罗系上统蓬莱镇组地层。残坡积岩性为夹少量碎石黏土，含大量植物根系，紫红色、塑性、松散、碎石含量在5%～10%，粒径为2～10cm，厚度为0.3～0.8m，棱角状，无分选性。滑坡堆积上覆黏土夹少量碎石，厚约0.3～0.5m，下伏碎裂黏土岩，成块状散体结构。蓬莱镇组地层以内陆浅水湖相沉积为主，兼有滨湖相和河流相沉积。岩性主要为紫红色黏土岩夹透镜状泥质粉砂岩。区内主要有基岩风化带裂隙水和上层滞水两种地下水类型，未见泉点出露。地下水径流排泄方式较简单，就地补给，顺坡径流交替强烈，直接下渗补给。

2 滑坡特征

滑坡位于斜坡中上部，平面形态呈舌形，坡向约255°，滑坡边界特征明显，前缘位于老G213线靠山侧，后缘位于斜坡中上部，左侧以冲沟和剪切裂缝为界，右侧以冲沟和剪切裂缝为界。滑体上覆松散堆积层，主要为黏土夹少量碎石，下伏侏罗系上统蓬莱镇组黏土岩，风化呈碎屑状，碎裂呈块状结构。滑坡相对高差约75m，滑动前地形剖面呈直线，滑动变形后地形剖面总体呈凸形，地形坡度20°～25°。滑坡顺坡长约190m，平均宽约100m，面积约1.9×104m2，滑体厚度8～12m，平均厚度约10m，总体积19×104m3，属中型岩质滑坡。螃蟹堰滑坡地质剖面图如图2所示。

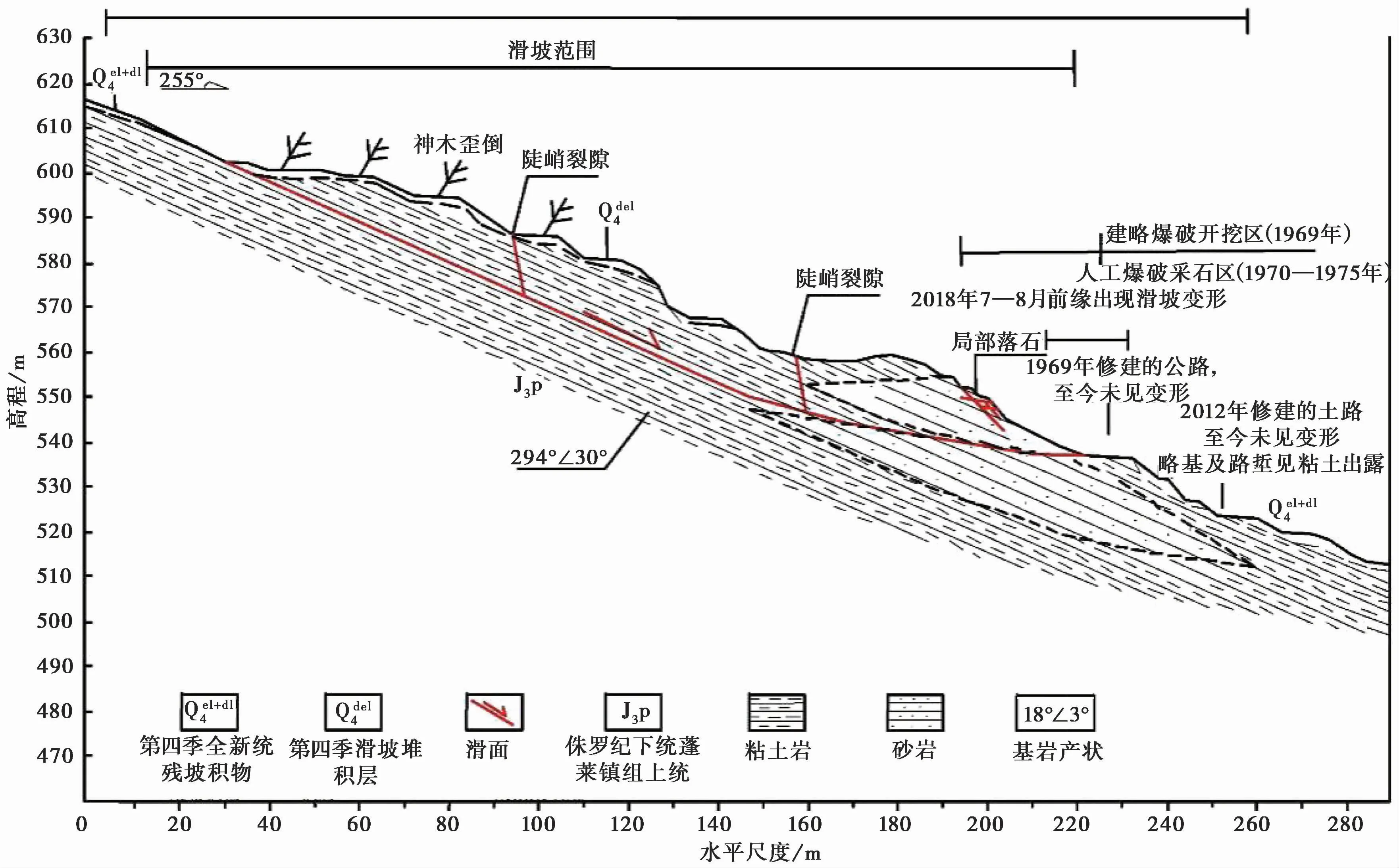
图2 螃蟹堰滑坡地质剖面图Fig.2 Geological p rofile of C rab W eir landslide

根据野外工程地质勘察测绘发现，滑坡的基岩发育2组共轭节理裂隙：节理裂隙1产状为343°∠75°，间距3m，宽约2cm，泥质充填；节理裂隙2的产状为282°∠73°，间距2m，宽约2cm，泥质充填。通过分析可知，影响滑坡稳定性的结构面主要是节理裂隙1和节理裂隙2。滑坡和结构面及其组合线的产状见表1。

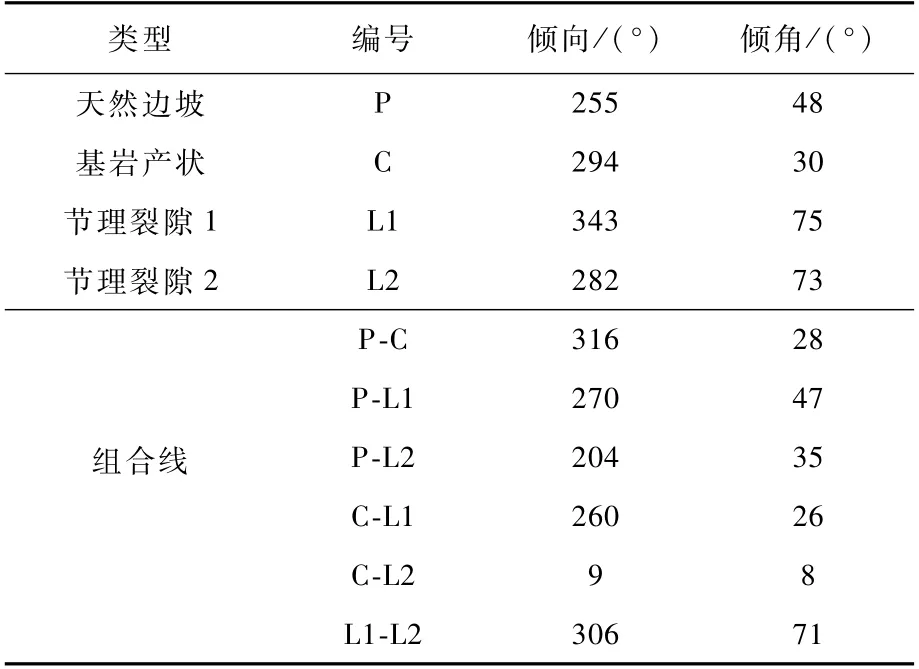
表1 滑坡和结构面及其组合线产状Tab.1 O ccurrences of the landslide，the structu ral p lane and their com bination line

应用赤平投影法，由表1中的综合产状作上半球极射赤平投影图，如图3所示。节理裂隙1属于外倾，倾角大于坡角，走向与坡向相交约30°，节理裂隙1与层面组合交线位于坡面附近，交线倾向与坡向的关系属外倾，交线倾角小于坡角，组合交线位于层面倾向线外侧，层面是控滑面，滑坡沿层面方向滑动，节理裂隙1起侧向切割的作用。节理裂隙2属外倾，倾角大于坡角，走向与坡向近于垂直，滑体拉张裂缝为该结构面张开引起的变形，节理裂隙2与层面组合交线远离坡面附近，交线倾向与坡向的关系属外倾，交线倾角远小于坡角。节理裂隙1与节理裂隙2组合交线倾向于外倾，交线倾角大于坡角。因此，层面属于外倾，倾角小于坡角，对滑坡稳定性影响大。由此可知，滑坡体受两组结构面切割，沿层面单方向滑动。

图3 滑坡主滑方向与节理裂隙组合关系Fig.3 The relationship of the com bination between the m ain sliding d irection of landslide and the joint fissure

3 滑坡稳定性分析

3.1 稳定性计算

滑坡稳定性计算采用以极限平衡理论为依据的折线形滑面条分法和传递系数法来计算。传递系数法的计算模型如图4所示。

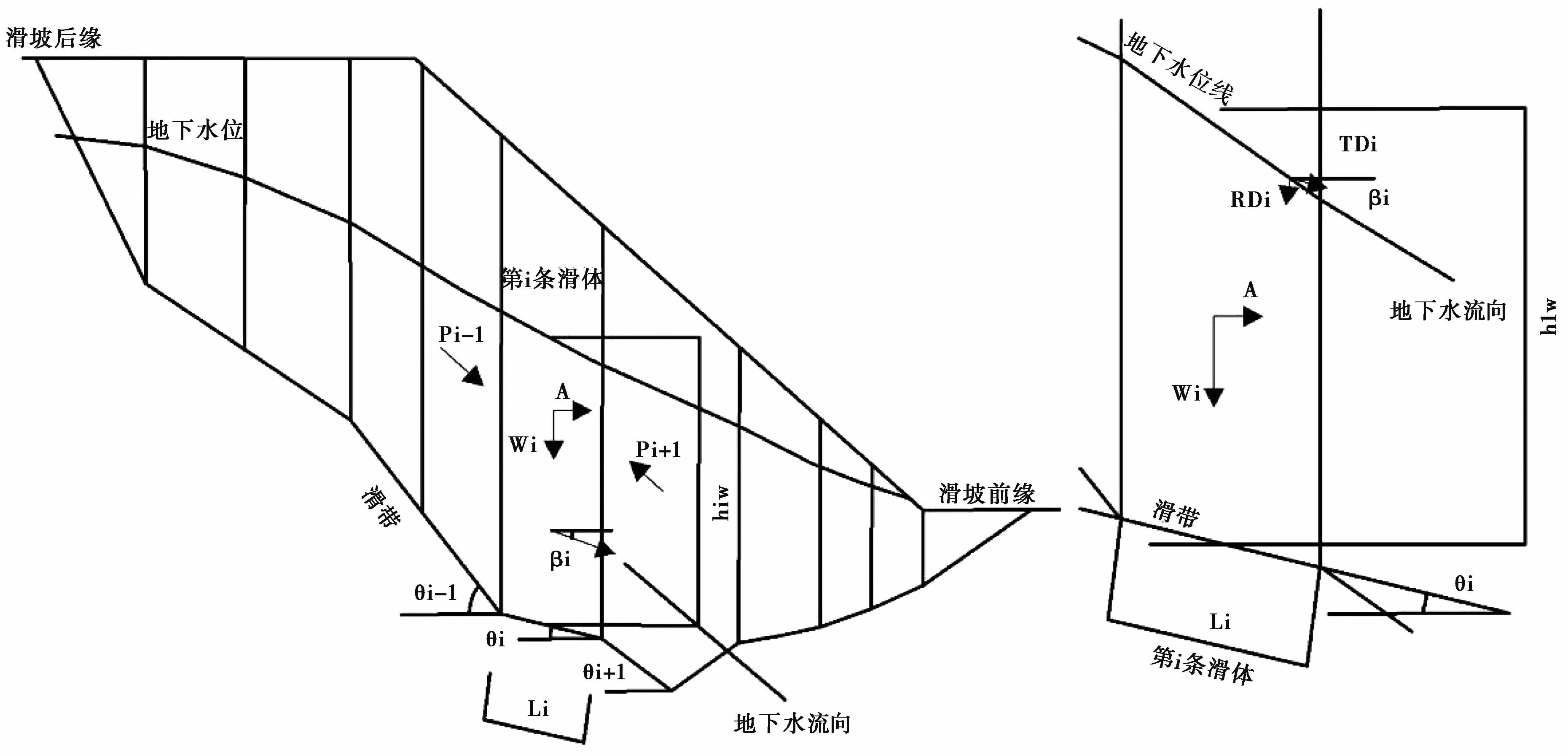
图4 传递系数法（折线型滑面）计算模型Fig.4 Calcu lation m odel of the transfer coefficientm ethod（sliding surface of landside being a broken line）

稳定性系数计算公式可表示为：

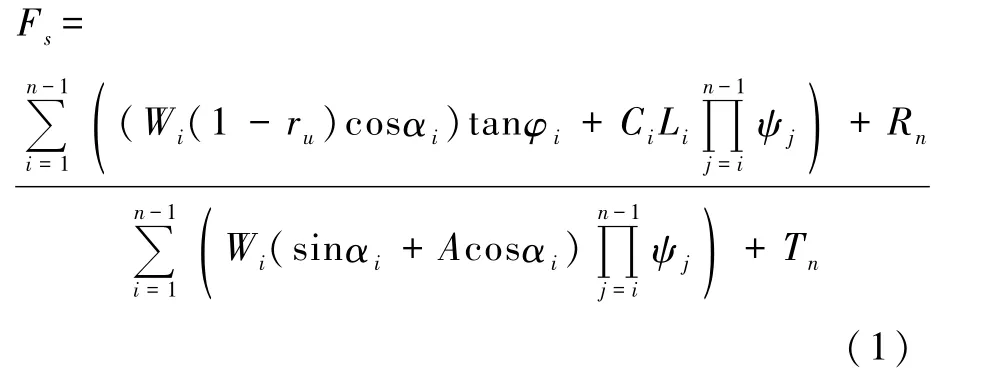
其中，

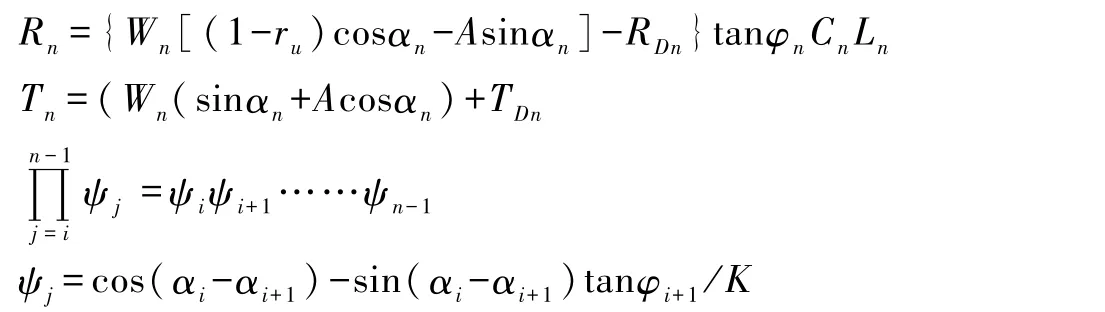
式中，Fs为稳定系数；Wi为第i条块的重量（kN／m）；ru为孔隙压力比；αi为第i条块滑带倾角（°）；φi为第i条块内摩擦角（°）；Ci为第i条块内聚力（kPa）；Li为第i条块滑带长度（m）；ψj为第i块段的剩余下滑力传递至第i+1块段时的传递系数（j＝i）；A为地震加速度（重力加速度g）；βi为第i条块地下水流方向（°）。

剩余下滑推力计算公式可表示为：

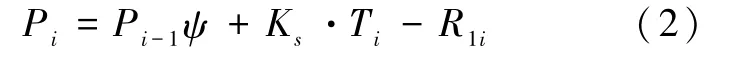
式中，传递系数ψ＝cos（ai-1-ai）-sin（ai-1-ai）·tanφi；下滑力Ti＝Wisinαi+A cosαi；抗滑力Ri＝（Wi（cosαi-A sinαi）+CiLi；Pi为第i条块推力（kN／m）；Pi-1为第 i条块的剩余下滑力（kN／m）；Wi为第i条块的重量（kN）；Ci、φj为第i块的内聚力（kPa）及内摩擦角（°）；Li为第i条块长度（m）；αi为第i块的滑带倾角（°）；A为地震加速度（重力加速度g）；Ks为设计安全系数。

根据滑坡的地质环境背景及形成机制，分析计算中主要考虑暴雨、地震等因素，滑坡稳定性计算分析选取3种工况类型：工况Ⅰ自重、工况Ⅱ自重+暴雨、工况Ⅲ自重+地震。根据《滑坡防治工程设计与施工技术规范》［21］，滑坡防治工程等级为Ⅲ级，故工况Ⅱ设计降雨强度为重现期为20年一遇暴雨。工况Ⅲ条件下的地震动峰值加速度取0.05 g，地震烈度值为Ⅵ度。3种工况条件下的安全系数分别为1.10、1.05、1.05。滑坡剖面分区图如图5所示，稳定性系数计算结果见表2。

表2 滑坡不同工况下稳定性系数Tab.2 Stability coefficien ts of the landslide under different work ing conditions

由表2可知，同一工况下，不同剖面的稳定性相同。不同工况条件下：自重以及自重+地震两种工况下，滑坡基本稳定；自重+暴雨的工况下，滑坡欠稳定。

3.2 稳定系数影响敏感性分析

影响滑坡稳定性的主要因素包括滑带土抗剪强度参数（C、φ值）、滑体饱水情况及滑体容重的变化等，而C、φ值的取值中影响因素较复杂。

本次研究主要以C、φ值为主要对象，分析2-2′剖面在暴雨工况下对滑坡稳定性的影响。选取暴雨工况C＝11.2kPa、φ＝13.2°，C值每增加1kPa和φ值每增加1°的情况下，分别计算相应的稳定系数。暴雨工况下滑带土抗剪强度和内摩擦角对滑坡稳定系数影响敏感性分析见表3。

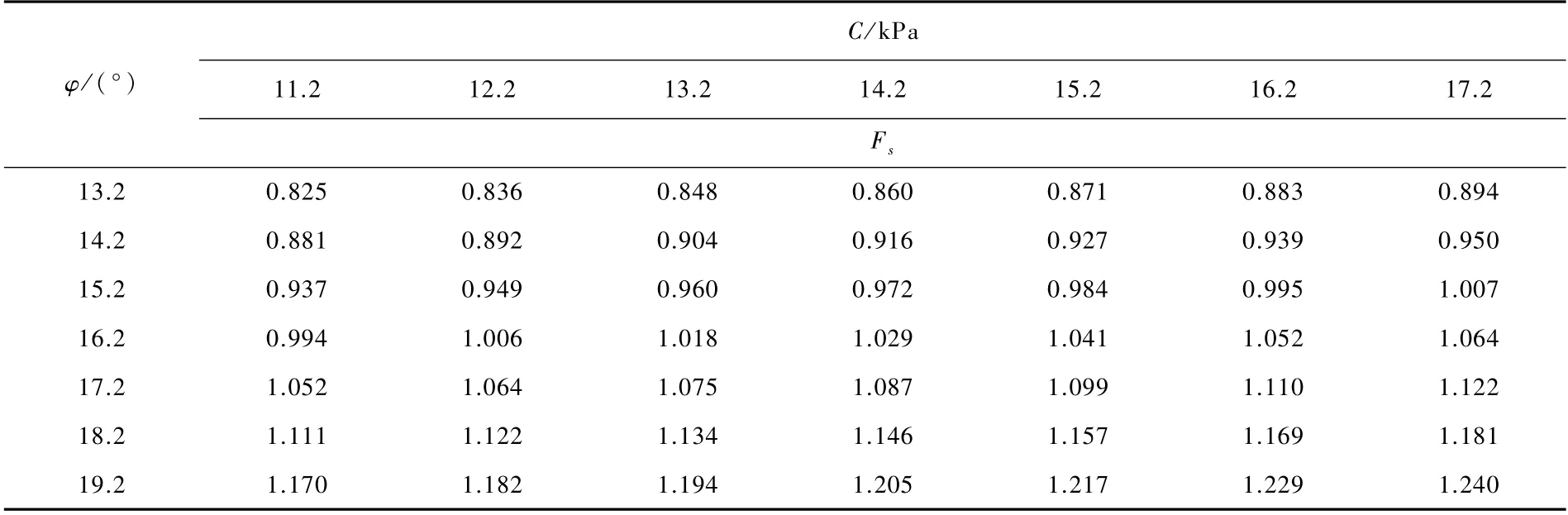
表3 暴雨工况下滑带土抗剪强度参数大小对滑坡稳定系数影响敏感性分析Tab.3 Sensitivity of the influence of shear strength param eters of the soils in the sliding zone on stability coefficients of the landslide under the rainstorm condition

由表3可绘制稳定性系数Fs与任意C值和φ值的关系曲线，以C＝13.2kPa、φ＝15.2°为例，见图6。暴雨工况下滑带土抗剪强度敏感性分析图，见图7。

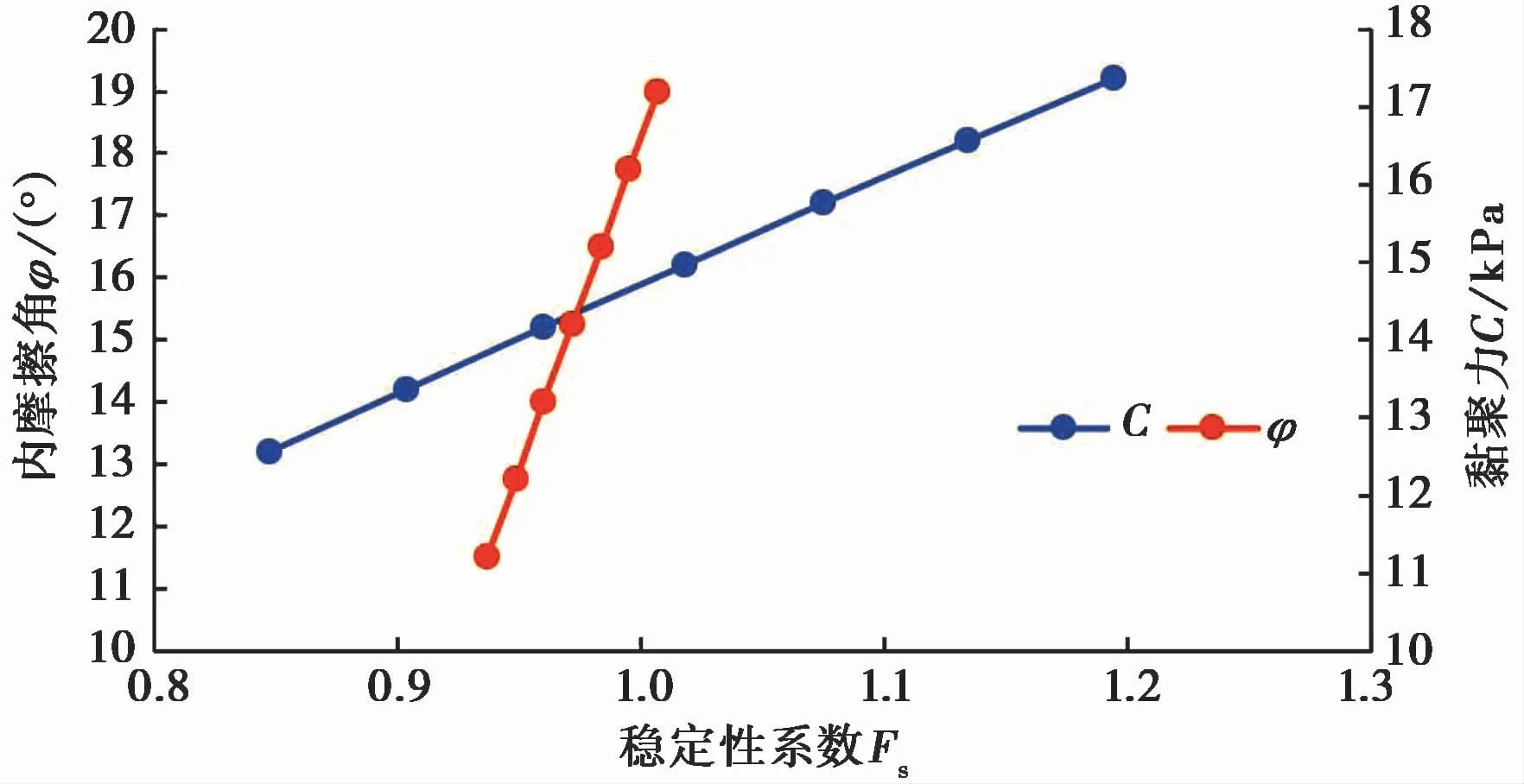
图6 滑坡稳定性系数Fs与黏聚力C和内摩擦角φ关系Fig.6 The relationship betw een the stability coefficien t Fs w ith the sliding cohesion C and the in ternal friction angleφof the landslide

图7 暴雨工况下滑带土抗剪强度敏感性分析Fig.7 Sensitivity analysis of shear strength of the soils in the sliding zone soil shear under the rainstorm condition

由图6和图7分析可知，滑坡稳定性系数与黏聚力和内摩擦角值存在明显线性关系。随着C值的增加滑坡稳定性系数缓慢增加，而随着φ值的增加滑坡稳定性系数显著增加。暴雨工况下φ值斜率远大于C值斜率，φ变化对滑坡稳定性起决定性作用，为影响滑坡稳定性最主要的敏感因素。目前滑坡整体处于基本稳定状态，在暴雨、地震等不利条件下，整体处于欠稳定状态。计算结果与野外地质勘察基本一致。

4 结论与建议

本文基于极限平衡理论对滑坡进行了稳定性分析，得到如下结论：

（1）滑坡边界特征明显，平面形态呈舌形，坡向约255°，属中型岩质滑坡。

（2）滑坡在正常工况下能保持整体稳定状态，滑坡的三个剖面在暴雨工况下稳定性系数偏低，分别为1.029、1.029、1.036，处于欠稳定状态，其他情况下都处于稳定状态。

（3）暴雨工况下φ变化对滑坡稳定性起决定性作用，为影响滑坡稳定性最主要的敏感因素。

（4）雨季出现变形的危险性较大，因此，应急治理工程完成前，应继续加强地质灾害的监测预警工作，防止地质灾害带来的损失。