碰撞阻尼器中颤振发生的恢复系数区间研究

杜妍辰，张洪源，林俊文

(上海理工大学 医疗器械与食品学院，上海 200093)

碰撞阻尼属于振动的被动控制技术，它利用振动过程中自由质量与主系统的碰撞来控制主系统的响应。目前，碰撞阻尼的研究成果通常采用每周期两次对称碰撞作为碰撞阻尼器的典型的运动模式[1-2]。通过数值模拟发现：碰撞阻尼在减振效果较好情况下，其运动轨迹中存在颤振和黏滞的现象，即颤振和黏滞有可能是碰撞阻尼器取得良好减振效果的新的有效途径[3]。所谓颤振，是指自由质量在短时间内与主系统之间发生很多次甚至无穷次碰撞的情况。关于颤振方面的研究,Budd等[4]对一类单自由度冲击振荡器在周期激励下的颤振和黏滞运动进行系统的研究，推导出了该系统周期颤振行为的存在以及周期的颤振行为与混沌运动的关系。Toulemonde等[5]在对谐和激励的碰撞振子的动力学行为进行研究时，发现了黏滞运动，并对单自由度和多自由度中的周期黏滞运动进行了研究。Wagg等[6-9]研究了谐和激励的二自由度碰撞振动系统中存在的周期运动、混沌颤振运动和黏滞运动，在颤振和黏滞运动的研究中发现了滑动分岔和“隆起”现象，并以双侧约束的碰撞系统为例讨论了黏滞现象出现的条件。Demeio等[10]研究了倒立摆碰撞中颤振持续时间的近似计算方法，研究表明，颤振持续时间主要与振幅有关，与激振频率和阻尼比关系不大。Alzate等[11]利用试验和数值的方法，对一类基于齿轮传动系统的碰撞模型引发的颤振行为进行了研究。Nordmark等[12]通过引入局部非连续映射的算法，对碰撞系统中颤振行为的稳定性及分岔进行了研究。Quintana等[13]对工业和学术研究中关于颤振的研究进展与方法分类进行了总结。Hös等[14]研究了减压阀碰撞模型，讨论了该模型存在的分岔、颤振行为及由分岔到颤振的路径。杨智春等[15]采用等效线化法和数值仿真法对利用碰撞阻尼器抑制机翼颤振问题进行了研究，提出了“模态转移抑颤”的概念。Yin等[16]研究了一根悬臂梁与一根钢棒碰撞的问题，发现了颤振和黏滞现象。Luo等[17]对带有刚性约束的两自由度碰撞振动系统进行了研究，低频时发现了颤振和黏滞现象的存在。冯进铃等[18]以典型的Duffing单边碰撞系统为例，通过引入彗尾映射的概念和有效的数值方法，研究了系统中的完全颤振和不完全颤振现象，同时分析了系统的颤振分岔。李飞等[19]对一类多约束碰撞振动系统的黏滞运动进行了分析。张惠等[20]对一类两自由度含间隙和预紧弹簧的碰撞振动系统动力学模型建立了Poincaré映射，推导出了映射的Jacobian矩阵。苏芳等[21]推导了一类两自由度单边刚性约束碰撞系统周期运动的解析解和Poincaré映射，并分析了系统周期运动的稳定性及系统在适当参数下发生分岔现象与混沌演化。王小斌等[22]引入一种不连续拉回映射的方法对一类双自由度碰撞振动系统的完全颤振进行了研究，得到了其碰撞运动的颤振完成点及其颤振时间。朱喜锋等[23-24]利用数值仿真法对两自由度弹性碰撞系统的颤振运动及转迁规律进行了研究。

目前国内外对振动冲击系统的动力学研究大多是基于固定约束的多自由度系统，未见对无固定约束的非线性系统颤振和以恢复系数控制的变化规律的研究。由于碰撞阻尼器中的约束是一个自由质量，需要采用无固定约束的模型，因此本文关于碰撞阻尼器中的颤振研究与现有的研究有较大的不同。本文建立了非固定约束碰撞振动系统的动力学模型，以恢复系数为主要控制参数分析了系统周期运动及其分岔区域，揭示了系统的颤振运动特性。得到了在不同质量比和频率比条件下，碰撞阻尼器发生颤振现象的恢复系数区间。

1 系统力学模型和运动微分方程

图1为一个碰撞阻尼器的力学模型。图1中对部件相同的力学性能进行合并，并以力学符合给予表示，其中：M1为腔体和外部支撑的质量；M2为自由质量，K为系统刚度；C为系统阻尼；F为系统的激励力；X为M1的位移；Y为M2的位移。M2是位于M1其中的，当F作用于M1时，M1与M2会发生相对碰撞，碰撞表示以它们之间的位移差确定。K与C作用于M1，对M1的运动施加控制力。能量交换在CKM1M2之间相互出现，塑性变形的能量消耗发生与M1与M2之间，C消耗了部分能量。

图1 两自由度动约束碰撞振动系统

为方便计算，采用以下几个基本假设：

(1)自由质量(冲击器)只沿腔体进行水平运动，摩擦因数f=0；

(2)M1与地面摩擦因数f=0;

(3)自由质量此时视为质点；

(4)碰撞过程由恢复系数r决定，且碰撞为瞬时的。

在不发生碰撞情况时，振子M1的运动微分方程为

(1)

对方程进行无量纲化处理为

(2)

小球在未发生碰撞时视为匀速直线运动

y(t)=y0+v0t

(3)

式中：y(t)为小球的位移；y0，v0分别为小球的初始位移和初始速度(或碰撞后小球速度)。

(4)

当|y-x|=δ/2时，振子与小球发生碰撞，且碰撞被理想化为一个不连续的过程，根据动量守恒定律及碰撞恢复系数r的定义，可得

(5)

(6)

由式(5)和式(6)可求得碰撞后速度的解析表达式

(7)

(8)

在振子与小球组成的碰撞阻尼模型中，由于两次碰撞间振子的运动方程式(2)为一个非齐次的二阶常系数线性微分方程，因此，方程式(2)的解应该由相应齐次方程的通解和非齐次方程的特解两部分组成，即

x(t)=x1(t)+x2(t)

(9)

式中，x1(t)为系统有阻尼的自由振动，在小阻尼情况下

x1(t)=e-ξωnt(c1cosωdt+c2sinωdt)

(10)

式中：ωn=K/M1；ωd为振子有阻尼振动的固有频率；c1，c2由振子的初始位移和初始速度决定；x1(t)为衰减振动，称为瞬态振动或瞬态响应。

式(11)中x2(t)为系统有阻尼的受迫振动，设为

x2(t)=Bsin(ωt-θ)

(11)

式中：B为响应振幅；θ为相位差。将式(11)代入式(2)中解方程得到

(12)

(13)

式中：ω为激励力的频率；λ=ω/ωn为频率比；σ为阻尼比。式(2)所表示的总运动形式是间歇运动，而式(9)说明运动由两部分组成，这两部分都是间歇运动，其中：x1(t)为自由振动；x2(t)为强迫振动，即带有激励的振动，它的角频率即是激励力的角频率，当激励频率与系统固有频率接近的时候，就是进入了共振点附近的区域，此时会发生共振现象，振幅显著增大。而自由振动相对强迫振动在一个较长的时间轴上，不断衰弱，强迫振动因为能量的输入持续保持或增大振幅，故在这里，对自由振动的部分可忽略不计，即x1(t)在一定程度上不作考虑。

在碰撞发生前，振子与冲击小球的运动状况即方程所示，但碰撞发生，则运动情况就会改变，因此定义碰撞前后时间即可，例如t0=t+。对于所建模型的位移和速度的初始条件定义，及碰后时刻的状态，都由恢复系数r确定。碰撞的持续时间很难量化，但对于颤振的研究，作为颤振持续时间来说，这个过程必须量化。所以在方程的解式(10)中设其经过了很小的一段时间Δt，经过这段时间后，碰撞再次发生，这个方法解决了碰撞间隔问题，其中，每次的碰撞都符合式(7)和式(8)的恢复系数速度变化条件，通过这些办法，我们就可以求出位移与速度的变化，继而得到碰撞的变化情况，以此来求解系统的碰撞规律。

2 系统的分岔运动分析

碰撞振动系统往往是一个多参数系统，当某个参数或几个参数变化至某个临界值时，周期解的个数及稳定性将发生变化，产生所谓的分岔现象，这种现象只能通过计算机数值计算观察。通过无数次的分岔，系统可能进入混沌状态。恢复系数作为在碰撞过程中的控制参数，在计算过程中简化了许多问题，将碰撞过程由恢复系数决定，速度与能量的变化会产生一个跳跃，则会对分岔与颤振产生极大的影响。

设置参数，μm=0.050，μm=0.001,ω=1,δ=0.005,r∈(0,1)，通过对r进行连续变化，研究恢复系数分岔的规律。

图2与图3是不同质量比的全局分岔图。由图2和图3可以发现，在r=0.5之后系统普遍发生了大面积分岔，分岔面积不断扩大。

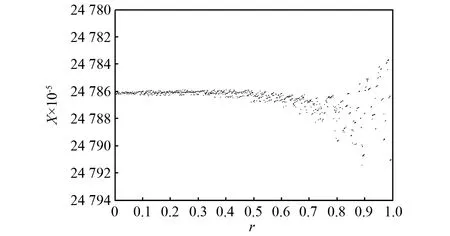
图2 当μm=0.050时r的分岔图

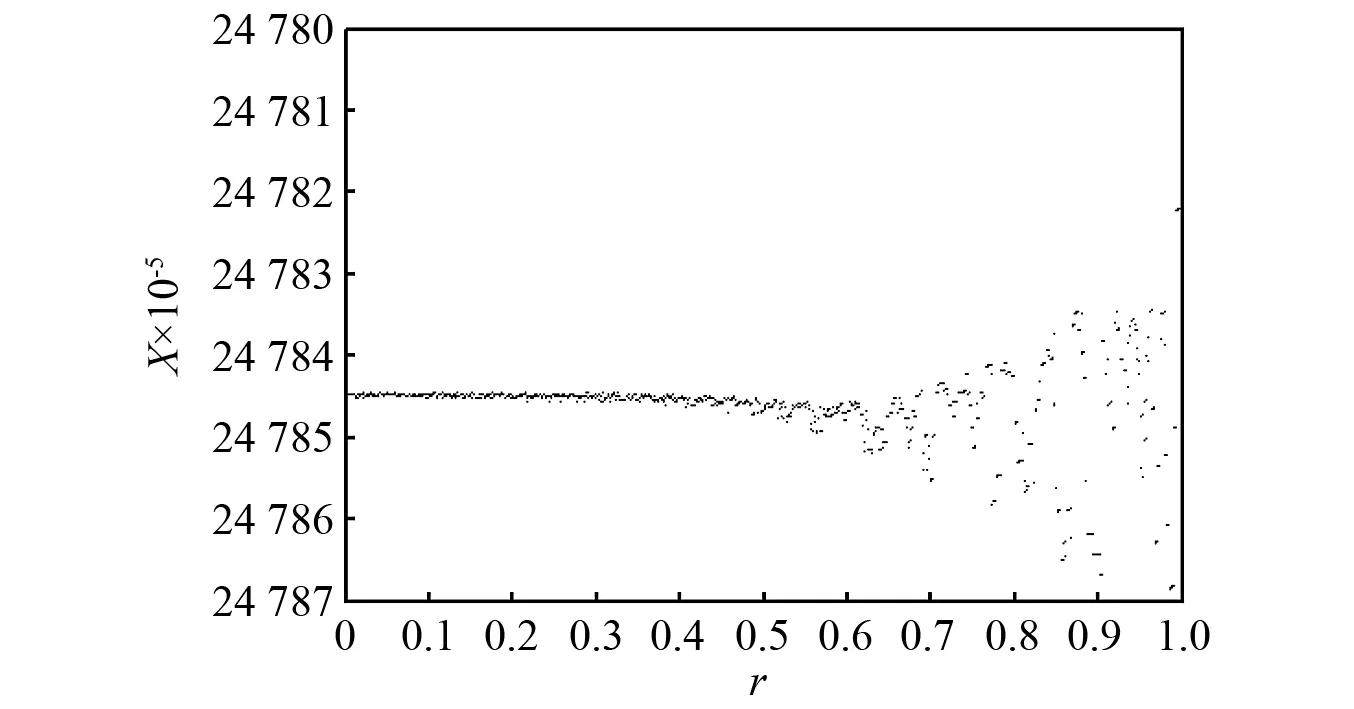
图3 当μm=0.001时r的分岔图

为了更清晰地观察分岔发生的情况，在图4和图5中绘制了相平面图与Poincare映射图，选取分岔前后的各一个点，r=0.2与r=0.8的两面，分别可以看出在r=0.5前后系统的分岔明显有较大差异，在r=0.2时系统处于周期或拟周期运动，在r=0.5之后则会进入混沌运动。颤振现象多发于分岔较为集中的区域，下面将在分岔区间进行颤振行为的研究。

图4 r为分岔参数时的分岔规律(μm=0.050)

图5 r为分岔参数时的分岔规律(μm=0.001)

3 系统的颤振运动分析

第2章已经对双边动态约束系统的分岔现象进行了深入地分析，本章将研究恢复系数对颤振的影响。颤振现象是非光滑动力系统学的一个分支，也是非光滑系统的一个常见现象。在碰撞振动系统中发生颤振，冲击器必须保持一系列的低速碰撞运动，如果这一系列的碰撞运动的速度最后趋近于零，与约束保持相对静止，则就从颤振进入黏滞。当系统相对碰撞超过5次(包含5次)，即判定为颤振发生。颤振后有黏滞现象的出现为完全颤振，反之为不完全颤振。设置参数，μm=0.250，μm=0.100，μm=0.050，μm=0.001,δ=0.005,r∈(0,1)，在ω=1，3，4条件下通过对r进行连续变化，绘制振动系统不同恢复系数的时域图。

图6～图8为质量比为0.250时不同恢复系数下的时域波形图。

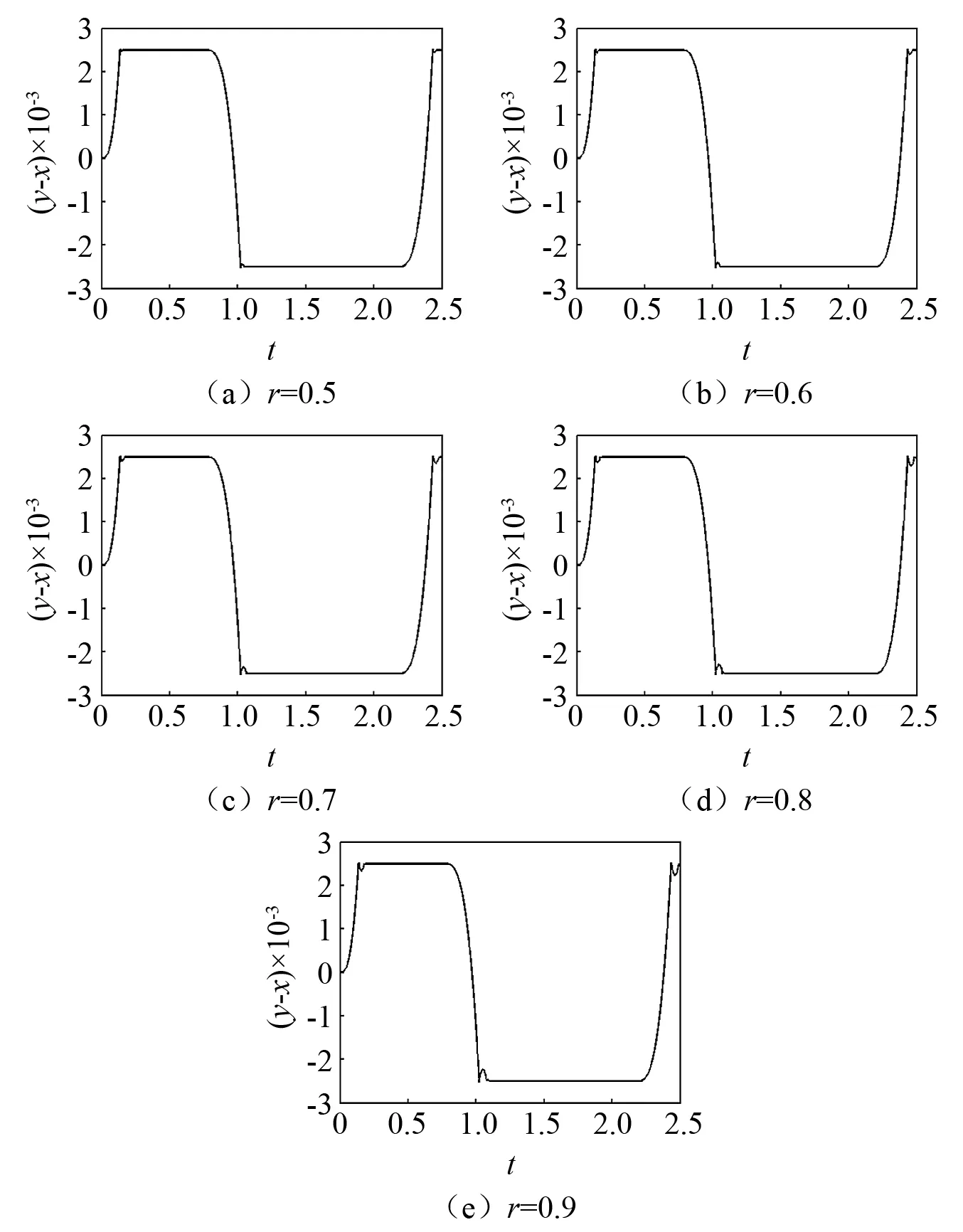
图6 不同恢复系数下的时域波形图(μm=0.250，ω=1)

图7 不同恢复系数下的时域波形图(μm=0.250，ω=3)

图8 不同恢复系数下的时域波形图(μm=0.250，ω=4)

图6为ω=1条件下不同恢复系数下的时域波形图。由图可以看出，图6(a)～图6(e)都以单周期1～2次的碰撞为主，故未发生颤振。碰撞结束后，系统处于长期黏滞状态，之后进入下一周期运动。随着恢复系数增大，初次碰撞相对位移有增大趋势。

图7为ω=3条件下不同恢复系数下的时域波形图。由图7(a)～图7(e)发现，恢复系数增大使初始碰撞位移增大且连续碰撞次数增多。图7(c)中，在t=1.75处，发生了单周期内5次的连续碰撞，此时判定发生颤振，并且在颤振发生后有短暂的黏滞发生，为完全颤振。图7(d)中，在t=0.25，t=1.25，t=2.25处均发生了5次以上的连续碰撞且伴随黏滞，为完全颤振。图17(e)中，在t=0.25处发了颤振现象并伴随黏滞，为完全颤振。故颤振的恢复系数区间为r∈(0.7,0.9)，完全颤振的恢复系数区间为r∈(0.7,0.9)。

通过函数调用，将上市公司全称与境外投资企业名称进行精确匹配；处理上市公司名称，删除 “集团”、“股份”、“控股”、“有限”、“公司”等字样，再一次进行模糊匹配；进一步利用关联交易文件确定上市公司与对外直接投资企业间是否存在关联关系。本文认为其母子公司或同一集团控股子公司间接参与对外直接投资活动，符合本文研究上市公司对外直接投资活动对整个企业集团绩效影响的初衷。

图8为ω=4条件下不同恢复系数下的时域波形图。由图8(a)～图8(e)发现，恢复系数增大使初始碰撞位移增大且连续碰撞次数增多。图8(a)～图8(c)以单周期2次碰撞为主。图8(d)～图8(e)以单周期3次碰撞为主。故此条件下的恢复系数区间均未发生颤振现象。

图9～图11为质量比为0.1时不同恢复系数下的时域波形图。

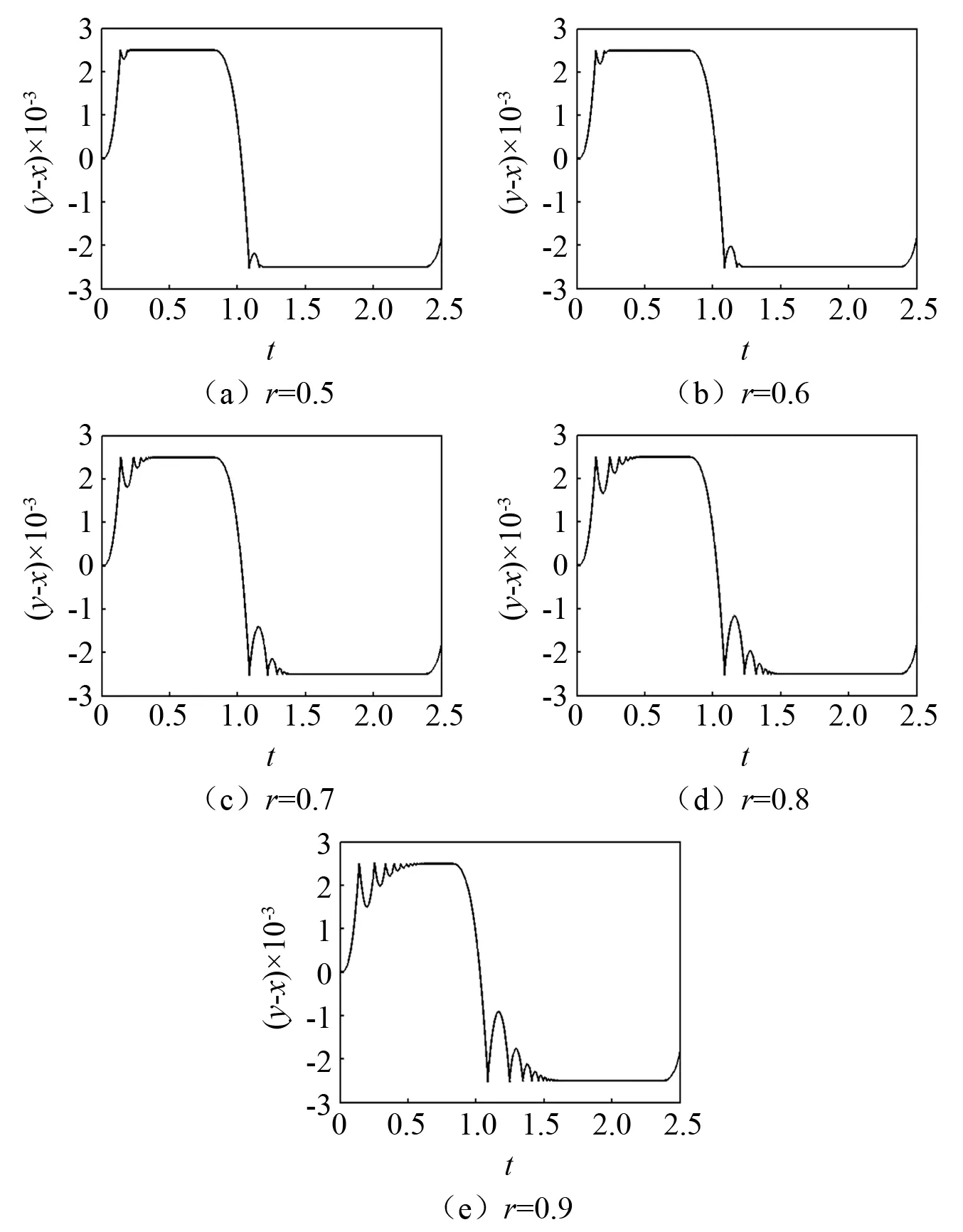
图9 不同恢复系数下的时域波形图(μm=0.100，ω=1)

图10 不同恢复系数下的时域波形图(μm=0.100，ω=3)

图11 不同恢复系数下的时域波形图(μm=0.100，ω=4)

图9为ω=1条件下不同恢复系数下的时域波形图。图9(a)和图9(b)中，碰撞次数不断增多，初始碰撞位移不断增大，单周期碰撞次数为1～4次，均未发生颤振。图9(c)中，在t=0.2，t=1.2处发生5次以上的碰撞并伴随黏滞，为完全颤振。图9(d)中，在t=0.3，t=1.3处发生5次以上的碰撞并伴随黏滞，为完全颤振。图9(e)中，在t=0.3，t=1.3处发生5次以上的碰撞并伴随黏滞，为完全颤振。故颤振的恢复系数区间为r∈(0.7,0.9)，完全颤振的恢复系数区间为r∈(0.7,0.9)。

图10为ω=3条件下不同恢复系数下的时域波形图。图10(a)～图10(e)中，碰撞次数不断增多，初始碰撞位移不断增大。图10(a)～图10(c)中，以单周期1～4次的碰撞为主，未发生颤振。图10(d)在t=0.3，t=0.6，t=1.1，t=1.3，t=2.1，t=2.3处发生了5次以上的碰撞并伴随黏滞，为完全颤振。图10(e)中，在t=0.5，t=0.8，t=1.1，t=1.4，t=1.7，t=2.1，t=2.4处发生了5次以上的碰撞未伴随黏滞，在碰撞后直接进入下一个周期，为不完全颤振。故颤振的恢复系数区间为r∈(0.8,0.9)，完全颤振的恢复系数区间为r=0.8附近。

图11为ω=4条件下不同恢复系数下的时域波形图。图11(a)～图11(e)中，碰撞次数最多为单周期3次，初始碰撞位移随恢复系数增大而增大。故在此条件下未发生颤振。

图12～图14为质量比为0.05时不同恢复系数下的时域波形图。

图12 不同恢复系数下的时域波形图(μm=0.050，ω=1)

图13 不同恢复系数下的时域波形图(μm=0.050，ω=3)

图14 不同恢复系数下的时域波形图(μm=0.050，ω=4)

图12为ω=1条件下不同恢复系数下的时域波形图。图12(a)中，在t=0.2，t=1.2处发生5次以上的碰撞并伴随黏滞，为完全颤振。图12(c)中，在t=0.3，t=1.3处发生5次以上的碰撞并伴随黏滞，为完全颤振。图22(d)中，在t=0.5，t=1.5处发生5次以上的碰撞并伴随黏滞，为完全颤振。图22(e)中，在t=1.0，t=3.0处发生5次以上的碰撞并伴随黏滞，为完全颤振。故颤振的恢复系数区间为r∈(0.6,0.9)，完全颤振的恢复系数区间为r∈(0.6,0.9)。

图13为ω=3条件下不同恢复系数下的时域波形图。图13(a)中，以单周期1～4次的碰撞为主，未发生颤振。图13(b)中，在t=0.2，t=0.5，t=1.2，t=1.7，t=2.2处发生了5次以上的碰撞并伴随黏滞，为完全颤振。图13(c)中，在t=0.2，t=0.5，t=1.2，t=1.7，t=2.2处发生了5次以上的碰撞并伴随黏滞，为完全颤振。图13(d)在t=0.6，t=1.2，t=1.6，t=2.2处发生了5次以上的碰撞并伴随黏滞，为完全颤振。图13(e)中，在t=0.5，t=1.1，t=1.6，t=2.2处发生了5次以上的碰撞未伴随黏滞，在碰撞后直接进入下一个周期，为不完全颤振。故颤振的恢复系数区间为r∈(0.6,0.9)，完全颤振的恢复系数区间为r∈(0.6,0.8)。

图14为ω=4条件下不同恢复系数下的时域波形图。图14(a)中，碰撞次数最多为单周期3次，初始碰撞位移随恢复系数增大而增大。图14(b)中，在t=0.2，t=0.5，t=0.8，t=1.3，t=1.7，t=2.2处发生了5次以上的碰撞并伴随黏滞，为完全颤振。图14(c)中，在t=0.5，t=0.8，t=1.3，t=1.7，t=2.2处发生了5次以上的碰撞并伴随黏滞，为完全颤振。图14(d)中，在t=0.5，t=1.0，t=1.3，t=1.7，t=2.2处发生了5次以上的碰撞但未伴随黏滞，为不完全颤振。图14(e)中，只在t=0.5，t=1.3处发生了5次碰撞，则未发生颤振。故颤振的恢复系数区间为r∈(0.6,0.9)，完全颤振的恢复系数区间为r∈(0.6,0.7)。

图15～图17为质量比为0.001时不同恢复系数下的时域波形图。

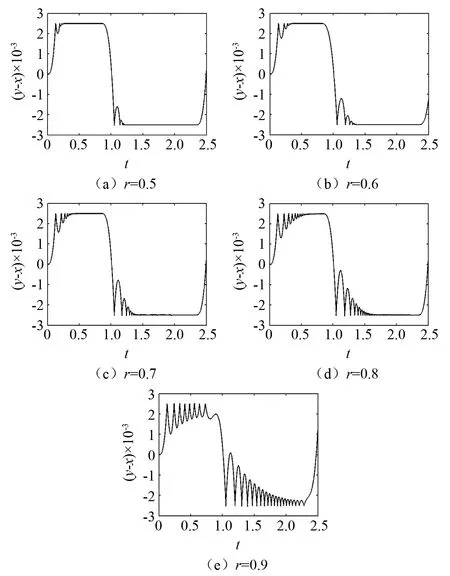
图15 不同恢复系数下的时域波形图(μm=0.001，ω=1)

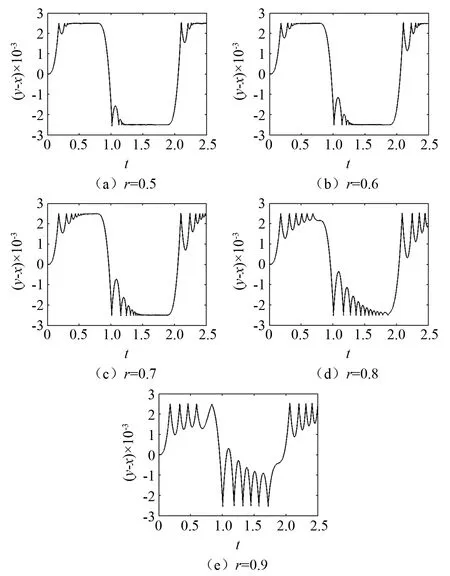
图16 不同恢复系数下的时域波形图(μm=0.001，ω=3)

图17 不同恢复系数下的时域波形图(μm=0.001，ω=4)

图15为ω=1条件下不同恢复系数下的时域波形图。图15(a)图中，在t=1.2处发生了5次碰撞并伴随黏滞，为完全颤振。图15(b)中，在t=0.3，t=1.3处发生5次以上的碰撞并伴随黏滞，为完全颤振。图15(c)中，在t=0.5，t=1.5处发生5次以上的碰撞并伴随黏滞，为完全颤振。图15(d)中，在t=1.5处发生5次以上的碰撞并伴随黏滞，为完全颤振。图15(e)中，在t=1.5处发生5次以上的碰撞未伴随黏滞，为不完全颤振。故颤振的恢复系数区间为r∈(0.5,0.9)，完全颤振的恢复系数区间为r∈(0.5,0.8)。

图16为ω=3条件下不同恢复系数下的时域波形图。图16(a)～图16(e)中，碰撞次数不断增多，初始碰撞位移不断增大。图16(a)中，在t=0.2，t=0.5，t=1.2，t=1.7，t=2.2处发生了5次以上的碰撞并伴随黏滞，为完全颤振。图16(b)中，在t=0.5，t=1.2，t=1.7，t=2.2处发生了5次以上的碰撞并伴随黏滞，为完全颤振。图16(c)在t=0.5，t=1.2，t=1.6，t=2.2处发生了5次以上的碰撞未伴随黏滞，为不完全颤振。图16(d)中，发生5次碰撞并未伴随黏滞，为不完全颤振。图16(e)中，发生5次碰撞并未伴随黏滞，为不完全颤振。故颤振的恢复系数区间为r∈(0.5,0.9)，完全颤振的恢复系数区间为r∈(0.5,0.6)。

图17为ω=4条件下不同恢复系数下的时域波形图。图17(a)中，在t=0.2，t=0.5，t=0.8，t=1.3，t=1.7，t=2.2处发生了5次以上的碰撞并伴随黏滞，为完全颤振。图17(b)中，在t=0.5，t=1.2，t=1.7，t=2.2处发生了5次以上的碰撞未伴随黏滞，为不完全颤振。图17(c)在t=0.5，t=0.8，t=1.2，t=1.6，t=2.2处发生了5次以上的碰撞未伴随黏滞，为不完全颤振。图17(d)中，在t=0.8处发生了5次碰撞未伴随黏滞，为不完全颤振。图17(e)中，未发生5次以上的碰撞，无颤振。故颤振的恢复系数区间为r∈(0.5,0.8)，完全颤振的恢复系数区间为r=0.5附近。

根据上述分析所得到的发生颤振的恢复系数区间，列于表1。通过表1可以看出在不同质量比和频率比条件下，发生颤振的恢复系数在0.5～0.9，所以大恢复系数容易发生颤振现象，由于大部分碰撞材料的恢复系数位于0.5～0.9，所以碰撞阻尼器中颤振是经常发生的现象。而且小质量比容易发生颤振。

表1 颤振现象恢复系数区间表

4 结 论

本文通过建立非固定约束碰撞振动系统的力学模型，通过连续改变恢复系数的参数值得到了全局分岔图，并以此得出在各个恢复系数下的相位图、Poincare映射图、时域图，得到了在不同质量比和频率比条件下，碰撞阻尼器发生颤振现象的恢复系数区间。结论如下：

(1)根据恢复系数分岔图可以看出，恢复系数大于0.5时系统发生了明显的分岔现象，且分岔面积不断扩大。

(2)通过分析不同恢复系数下的系统位移时域图，表明发生颤振的恢复系数在0.5～0.9，且随着质量比减小，颤振发生的恢复系数区间扩大；随着频率比增大，颤振发生的恢复系数区间缩小。

(3)碰撞阻尼器中采用大恢复系数材料在小质量比条件下容易发生颤振。