多空沟对弹性波的散射及隔振性能分析：SH波入射

周凤玺，梁玉旺，刘 佳

(1.兰州理工大学 土木工程学院，兰州 730050；2.兰州理工大学 西部土木工程防灾减灾教育部工程研究中心，兰州 730050)

近年来，随着城镇化建设的快速发展，由交通运输，工程施工等人工振动引起的环境污染问题得到了广泛的关注，地基振动及其控制已经成为岩土工程领域亟待解决的课题之一。空沟作为常见的波障之一，由于施工简单，造价低廉而广泛应用于隔振工程。国内外学者对空沟的隔振效果也进行了大量的试验研究和理论分析。在试验方面：早在1962年，Barkan[1]就通过试验分析了空沟和板桩墙的隔振性能。Woods[2]对空沟的近场隔振和远场隔振方面进行了一系列的现场原位测试研究，并通过振幅衰减比来评价屏障的隔振效果。Ahmad等[3-4]通过现场试验对屏障尺寸，屏障位置进行了设计研究，并通过隔振效果提出了一些设计原则。Haupt[5]通过室内试验研究了混凝土填充沟对激励荷载的隔振效果，之后，Erkan[6]、Murillo等[7]、Ulgen等[8]也研究了空沟和填充沟对激振荷载的隔振效果，并对激振荷载的频率、土层参数、尺寸等参数进行了分析。徐平等[9]通过落锤式弯沉仪(falling weight deflectometer，FWD)试验分析了空沟深度、宽度及空沟-荷载间距对交通冲击荷载的隔离效果。在数值模拟方面：Saikia等[10]利用有限元程序PLAXIS对简谐波载荷作用下的空沟隔振问题进行了数值分析。Shrivastava等[11]考虑不同几何参数下，通过三维有限元模型研究了空沟与填充沟屏障对Rayleigh波的隔离效果。基于边界元法，Emad等[12]分析了任意形状二维浅沟的隔振效果，发现只有在中频范围内，浅沟可以减少25%的地基扰动，且空沟形状对隔振效果的影响较小。之后，Beskos等[13-15]采用此方法研究了空沟隔振性能。巴振宁等[16-17]采用2.5维间接边界元方法(indirect boundary element method，IBEM)研究了空沟对层状饱和地基中列车移动荷载的隔振性能。Andersen等[18]和Adam等[19]则借助边界元-有限元耦合法分析了列车荷载作用下空沟尺寸和位置对隔振效果的影响。结合薄层法和边界元法，李伟等[20-21]分析了二维和三维黏弹性层状地基中空沟的隔振效果，结果表明地基分层参数对空沟隔振效果影响显著。在解析分析方面：Cao等[22]采用半解析方法研究了移动荷载作用下饱和土地基中单空沟的隔振效果。徐平等[23-24]将复变函数方法应用于空沟隔振理论，建立了单空沟对弹性波隔离效果的理论解答。

目前，对空沟的隔振效果的研究成果主要集中在单空沟在不同载荷以及不同地层等条件下。而工程实践中由于空沟深度受土体稳定性所限，单空沟很难达到理想的隔振效果，尤其是在低频激励情形下。设置多排空沟是一种有效的隔振措施，可以对振动波的传播路径进行多次阻断来达到理想的隔振效果。Younesian等[25]通过数值分析研究了单相场地中多沟屏障对列车荷载引起地面振动的屏蔽效果，而且研究发现对于相同的隔振效果，多沟屏障所需沟深远小于单沟。Hwang 等[26]通过试验研究了三个浅沟屏障对冲击荷载的隔振效果，但是由于沟深较小，并没有获得明显的隔振效果。

基于弹性波散射的基本理论，在复数域上进行波函数展开，由空沟四周自由应力的边界条件，借助保角映射方法和多极坐标变换技术建立了方程组，通过对方程组的求解得到了多空沟对弹性SH波散射的解析解答，最后对多空的隔振效果进行了分析。

1 多空沟对SH波散射问题解析解答

图1 多空沟布置及坐标设置

1.1 波场分析

设SH波的入射频率为ω，在全局坐标系(x,y)下，入射SH波的位移势函数可以表达为

Wi=W0exp[iks(xcosα+ysinα)]

(1)

式中：上标i为入射；W0为入射SH波的幅值;α为入射SH波与水平方向(x轴)的夹角;ks=ω/cs为SH波的波数;cs为SH波的波速。

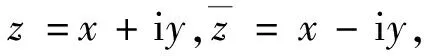
(2)

(3)

(4)

(5)

通过叠加，观测点A处总的散射SH波位移场可以表达为

(6)

1.2 待定复系数的求解

由复变函数理论，通过保角映射函数zj=ωj(ζ)可将z平面上任一第j个空沟边界对应映射为ζ平面上第j个单位圆，保角映射后的坐标系统如图2所示，相应的保角映射公式[28]为

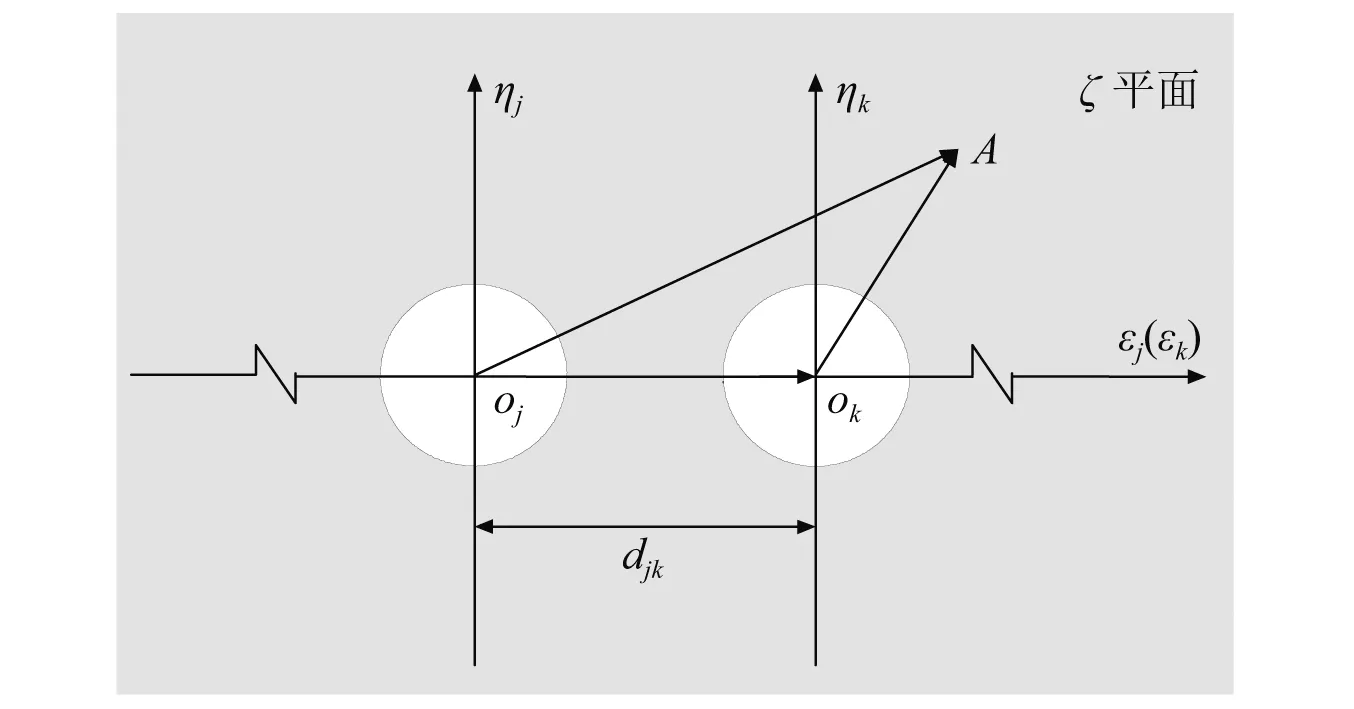
图2 保角映射后的坐标系统

(7)

c1=cos(2kπ)

(8a)

(8b)

(8c)

(8d)

式中：k取决于空沟的长宽比b/a的系数，其值可采用试算法计算；系数c1～c5仅与k有关；R为与空沟尺寸相关的实数，由于式(9a)和式(9b)计算结果相等，因此R值可由下式中的任何一式进行计算

(9a)

(9b)

(10)

(11)

式中,μ为土体的剪切模量，引入保角映射之后，式(10)和式(11)可进一步表达为

(12)

(13)

空沟边界上满足应力自由边界条件

(14)

(15)

将式(3)和式(6)代入式(12)中，由式(14)可得

(16)

其中,

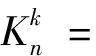
(17a)

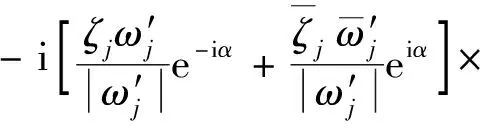
(17b)

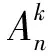
(18)

其中,

(19a)

(19b)

2 隔振效果分析

2.1 解的正确性验证

对多空沟的隔振效果分析时，限于篇幅，本文仅对双沟的隔振效果进行了算例分析。并引入振幅比|W/W0|(设置屏障后土体内某点由入射波和散射波产生总的位移与未设置屏障时由入射波单独产生的位移之间的比值)来评价双空沟对SH波的隔振效果，位移比值小于1时说明有隔振效果，且比值越小说明隔振效果越好。

为了验证本文解答收敛性，取级数项n=5, 剪切波速为cs=100 m/s，SH波入射频率为75 Hz，空沟间距d12/a=20，宽度a=0.4,长度b=3 m，由图3给出了双空沟周边应力分布图，从图中可以看出，空沟1(j=1)和空沟2(j=2)周边应力最大值在τθjz=2.5×10-9以内，满足计算精度要求。

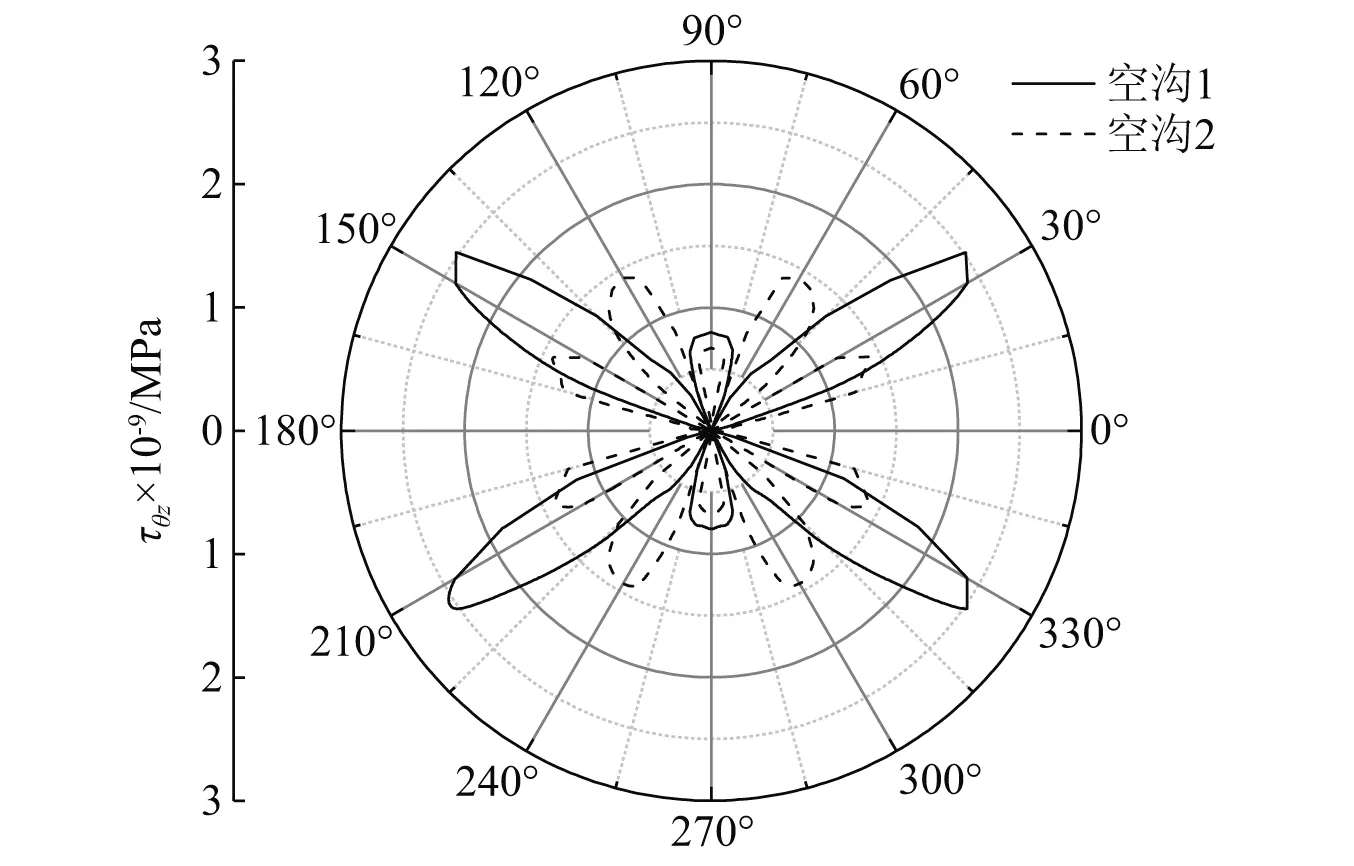
图3 双空沟周边应力分布图

为了进一步验证本文解答及计算程序的正确性，首先，取N=1时将本文公式退化为单空沟公式，与徐平等研究中的公式一致，说明了本文公式推导的正确性；然后，选取土体的剪切波速为cs=100 m/s，固有圆频率为75 Hz，空沟的宽度取a=0.4 m，长度b=4.0 m，图4给出了本文计算结果与徐平等的研究结果。从图4中可以看出，两者位移比值非常吻合，说明了计算过程的正确性。

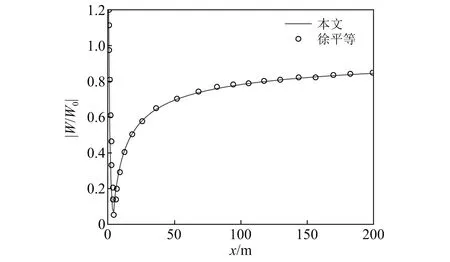
图4 振幅比|W/W0|对比曲线

2.2 隔振效果分析

为了分析空沟间距d12对隔振效果的影响，取SH波入射频率为75 Hz，空沟宽度a=0.4 m长度b=3 m，图5给出了不同空沟间距下地基表面振幅比|W/W0|等值线图，从图5中可以看出，随着空沟间距d12/a和空沟长度的增大，相同|W/W0|等值线所占屏蔽区域面积明显增大，并且最佳屏蔽区域靠近空沟。

图5 不同空沟间距下振幅比|W/W0|等值线

为了进一步分析空沟间距d12的影响，图6给出了在y/a=8时空沟后地基表面振幅比随x/a变化曲线，并且与单空沟隔振效果做了对比。从图6中可以明显的看出，空沟间距越大隔振效果越好，且双空沟的隔振效果明显优于单空沟的隔振效果。

图6 不同空沟间距在y/a=8处振幅比|W/W0|随x/a的变化曲线

为了分析空沟长度b对隔振效果的影响，取空沟间距d12/a=20，宽度a=0.4时，图7给出了不同空沟长度取值时对应的振幅比|W/W0|等值线图，从图7中可以看出，随着空沟长度的增大，相同|W/W0|等值线所占区域的面积增大更为显著。以空沟后侧为研究区域，空沟长度分别为3 m,4 m和5 m时对SH波隔离效果大于40%的屏蔽区域面积占比分别为5%,39%和46%。

图7 不同空沟长度下振幅比|W/W0|等值线

同样地，为了进一步分析空沟长度b的影响，图8给出了在y/a=8时空沟后地基表面振幅比随x/a变化曲线。从图中可以明显的看出，空沟长度的越大振幅比越小，说明隔振效果越好。

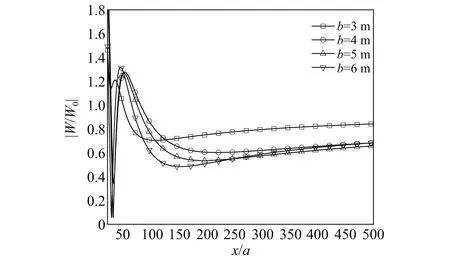
图8 不同空沟长度在y/a=8处振幅比|W/W0|随x/a的变化曲线

为了分析入射波频率(无量纲频率η=ωa/(πcs))对隔振效果的影响，取空沟长度b=4 m，宽度a=0.4 m，空沟间距d12/a=20，图9给出了不同入射波频率的SH波入射下，y/a=0处地基表面振幅比值|W/W0|随x/a的变化曲线。

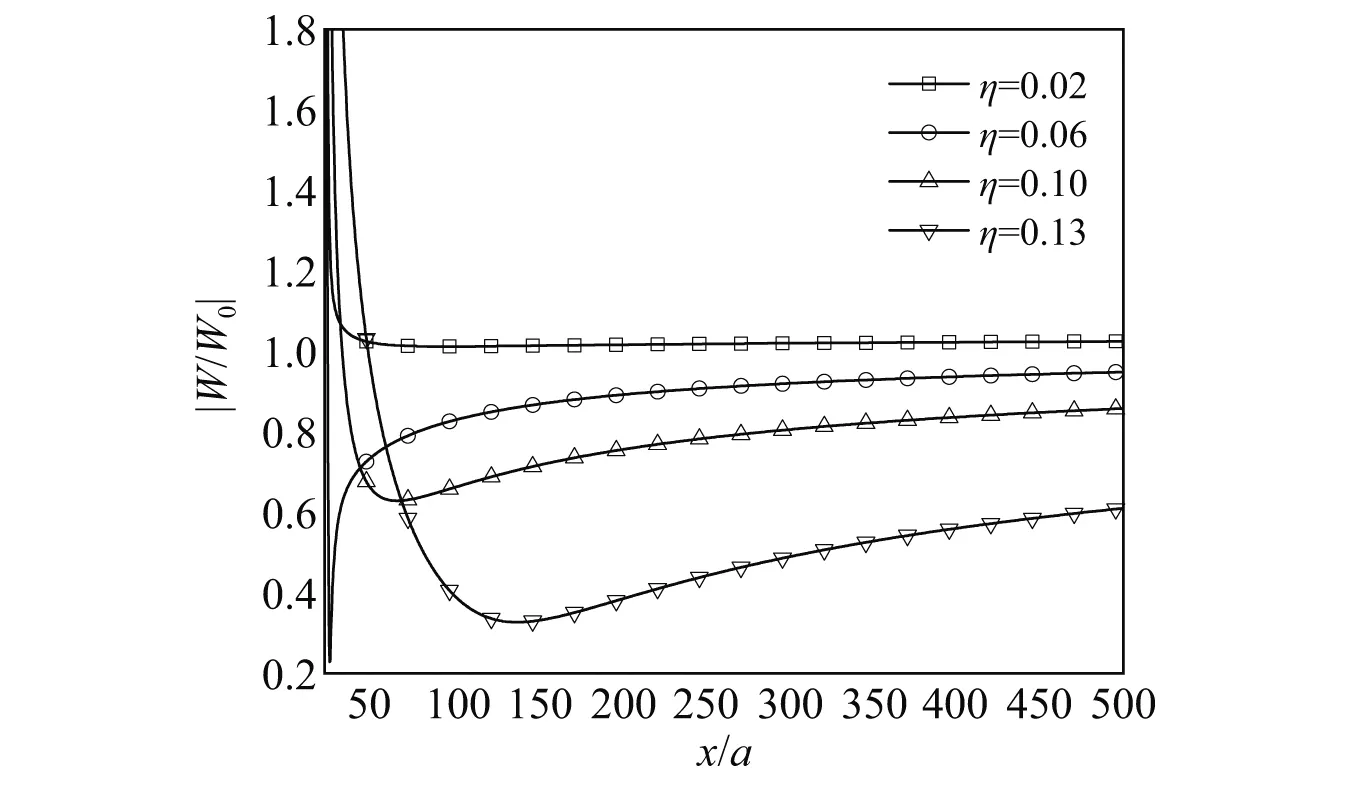
图9 不同入射波频率在y/a=8处振幅比|W/W0|随x/a的变化曲线

3 结 论

基于弹性波散射的基本理论，在复数域上进行波函数展开得到多空沟对平面SH波散射的解析解答。通过公式退化和数值计算与已有单沟的结果进行对比，验证了本文公式和计算方法的正确性。通过对双排空沟的隔振效果进行分析，得到了以下主要结论：

(1)双空沟的隔振效果明显优于单空沟的隔振效果，并且最佳屏蔽区域靠近空沟。

(2)随着空沟长度和空沟间距的增加，屏蔽区域面积明显增大，并且空沟长度对隔振效果的影响更为显著。

(3)随着入射波频率的增大，隔振效果越好。